On the Complementarity of Sparse L0 and CEL0 Regularized Loss Landscapes for DOA Estimation
Abstract
:1. Introduction
2. Sparse DOA Estimation Problem
2.1. On-Grid Array Signal Modeling
2.2. Vectorized Covariance Matrix Model
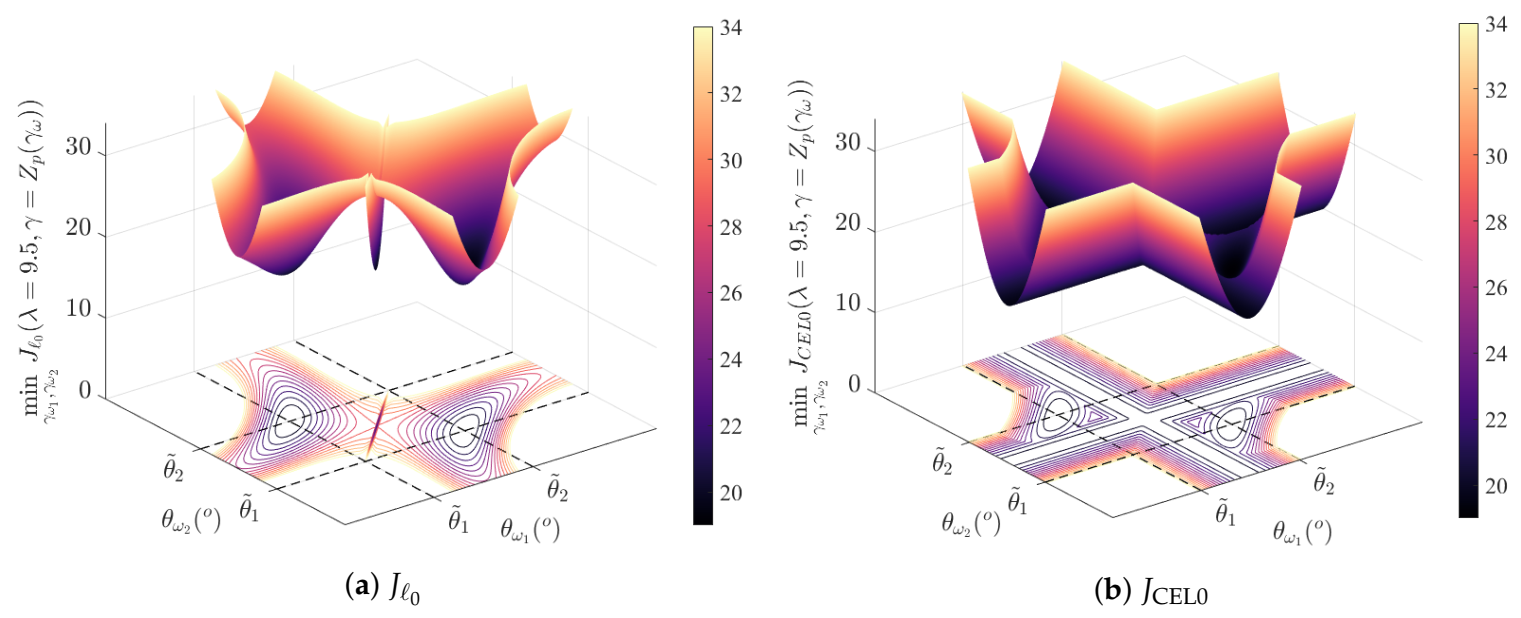
3. Description and Numerical Investigations of the Minimizers of and
3.1. Simulation Setup
3.2. Minimizers of
3.3. Minimizers of
4. Alternating between Loss Surfaces
| Algorithm 1. Optimization Scheme ALICE-L0 (Alternated Landscapes Iterations for Complementary Enhancement for ) |
| Input: dictionary , observation , , L Lipschitz-constant of , , , stopping criteria |
| Initialization:, , |
| • |
| while and do |
| • |
| • Compute weighting vector by: , |
| • , , |
| while and do (weighted FISTA iterations) |
| • , |
| • |
| • |
| • |
| end while |
| • |
| while and do (IHT iterations) |
| • , |
| • |
| end while |
| • , |
| end while |
| return |
5. Statistical Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Trees, H.L. Optimum Array Processing; Part IV of Detection, Estimation, and Modulation Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Avitabile, G.; Florio, A.; Coviello, G. Angle of Arrival Estimation Through a Full-Hardware Approach for Adaptive Beamforming. IEEE Trans. Circuits Syst. II: Express Briefs 2020, 67, 3033–3037. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, Maximum Likelihood, and Cramer-Rao Bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Wang, W.; Wu, R. High Resolution Direction of Arrival (DOA) Estimation Based on Improved Orthogonal Matching Pursuit (OMP) Algorithm by Iterative Local Searching. Sensors 2013, 13, 11167–11183. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhou, W.; Juwono, F.H. Joint Smoothed l0-Norm DOA Estimation Algorithm for Multiple Measurement Vectors in MIMO Radar. Sensors 2017, 17, 1068. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Z.; Li, J.; Stoica, P.; Xie, L. Chapter 11 - Sparse methods for direction-of-arrival estimation. In Academic Press Library in Signal Processing; Chellappa, R., Theodoridis, S., Eds.; Academic Press: Cambridge, MA, USA, 2018; Volume 7, pp. 509–581. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Zhu, W.; Yan, J. A high-resolution DOA estimation method with a family of nonconvex penalties. IEEE Trans. Veh. Technol. 2018, 67, 4925–4938. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wu, X.; Li, C.; Zhu, W.P. An ℓp-Norm Based Method for Off-Grid DOA Estimation. Circuits Syst. Signal Process. 2019, 38, 904–917. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, J.; Du, R.; Lv, G. Sparse Method for Direction of Arrival Estimation Using Denoised Fourth-Order Cumulants Vector. Sensors 2018, 18, 1815. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soubies, E.; Chinatto, A.; Larzabal, P.; Romano, J.M.T.; Blanc-Féraud, L. Direction-of-Arrival Estimation Through Exact Continuous ℓ2,0-Norm Relaxation. IEEE Signal Process. Lett. 2021, 28, 16–20. [Google Scholar] [CrossRef]
- Nikolova, M. Relationship between the optimal solutions of least squares regularized with L0-norm and constrained by k-sparsity. Appl. Comput. Harmon. Anal. 2016, 41, 237–265. [Google Scholar] [CrossRef] [Green Version]
- Delmer, A.; Ferréol, A.; Larzabal, P. L0-Sparse DOA Estimation of Close Sources with Modeling Errors. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2020. [Google Scholar]
- Delmer, A.; Ferréol, A.; Larzabal, P. On Regularization Parameter for L0-Sparse Covariance Fitting Based DOA Estimation. In Proceedings of the ICASSP 2020, IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 4–8 May 2020. [Google Scholar]
- Marmin, A.; Castella, M.; Pesquet, J.C. How to Globally Solve Non-convex Optimization Problems Involving an Approximate L0 Penalization. In Proceedings of the ICASSP 2019, IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019; pp. 5601–5605. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J. The Restricted Isometry Property and Its Implications for Compressed Sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Selesnick, I. Sparse Regularization via Convex Analysis. IEEE Trans. Signal Process. 2017, 65, 4481–4494. [Google Scholar] [CrossRef]
- Wen, F.; Chu, L.; Liu, P.; Qiu, R.C. A Survey on Nonconvex Regularization-Based Sparse and Low-Rank Recovery in Signal Processing, Statistics, and Machine Learning. IEEE Access. 2018, 6. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [Green Version]
- Soubies, E.; Blanc-Féraud, L.; Aubert, G. A Continuous Exact L0 penalty (CEL0) for least squares regularized problem. SIAM J. Imaging Sci. 2015, 8, 1102492. [Google Scholar] [CrossRef]
- Nikolova, M. Description of the minimizers of least squares regularized with ℓ0-norm. Uniqueness of the global minimizer. SIAM J. Imaging Sci. 2013, 6, 904–937. [Google Scholar] [CrossRef]
- Soubies, E.; Blanc-Féraud, L.; Aubert, G. New Insights on the Optimality Conditions of the l2-l0 Minimization Problem. J. Math. Imaging Vis. 2020, 62, 808–824. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delmer, A.; Ferréol, A.; Larzabal, P. On the Complementarity of Sparse L0 and CEL0 Regularized Loss Landscapes for DOA Estimation. Sensors 2021, 21, 6081. https://doi.org/10.3390/s21186081
Delmer A, Ferréol A, Larzabal P. On the Complementarity of Sparse L0 and CEL0 Regularized Loss Landscapes for DOA Estimation. Sensors. 2021; 21(18):6081. https://doi.org/10.3390/s21186081
Chicago/Turabian StyleDelmer, Alice, Anne Ferréol, and Pascal Larzabal. 2021. "On the Complementarity of Sparse L0 and CEL0 Regularized Loss Landscapes for DOA Estimation" Sensors 21, no. 18: 6081. https://doi.org/10.3390/s21186081
APA StyleDelmer, A., Ferréol, A., & Larzabal, P. (2021). On the Complementarity of Sparse L0 and CEL0 Regularized Loss Landscapes for DOA Estimation. Sensors, 21(18), 6081. https://doi.org/10.3390/s21186081





