Area-Efficient Post-Processing Circuits for Physically Unclonable Function with 2-Mpixel CMOS Image Sensor
Abstract
:1. Introduction
2. Overview of CIS PUF
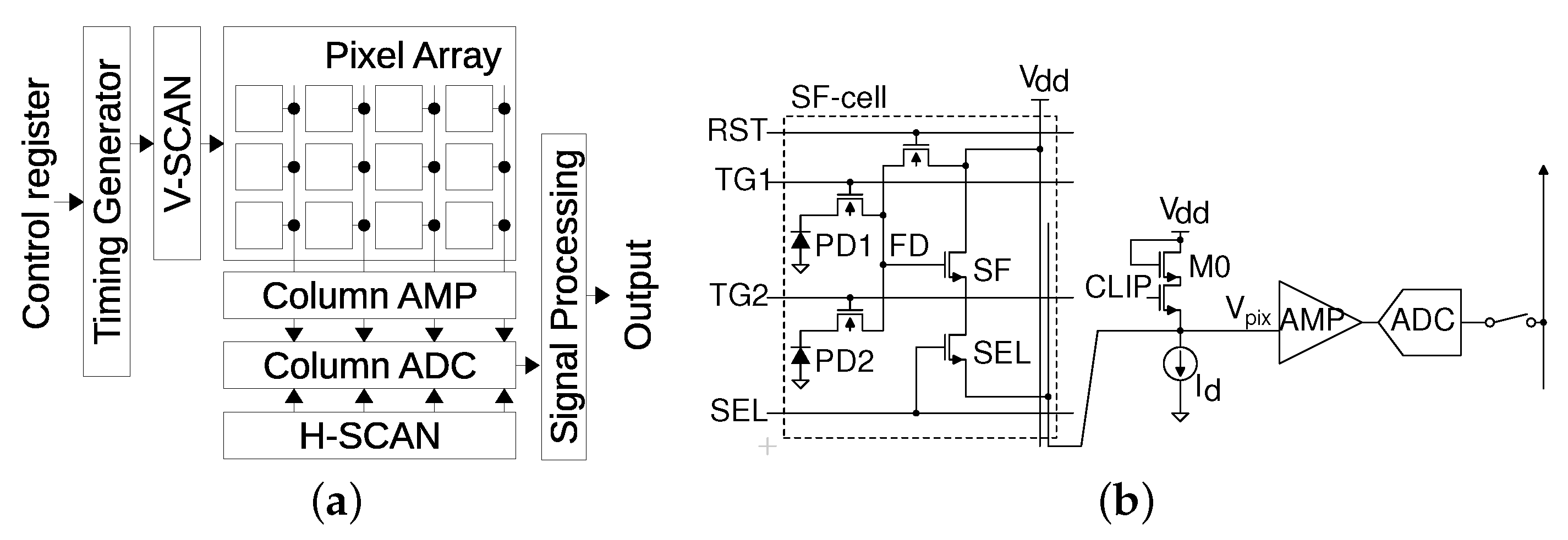
2.1. Circuits and Operations
2.2. Signal Processing to Generate PUF Response
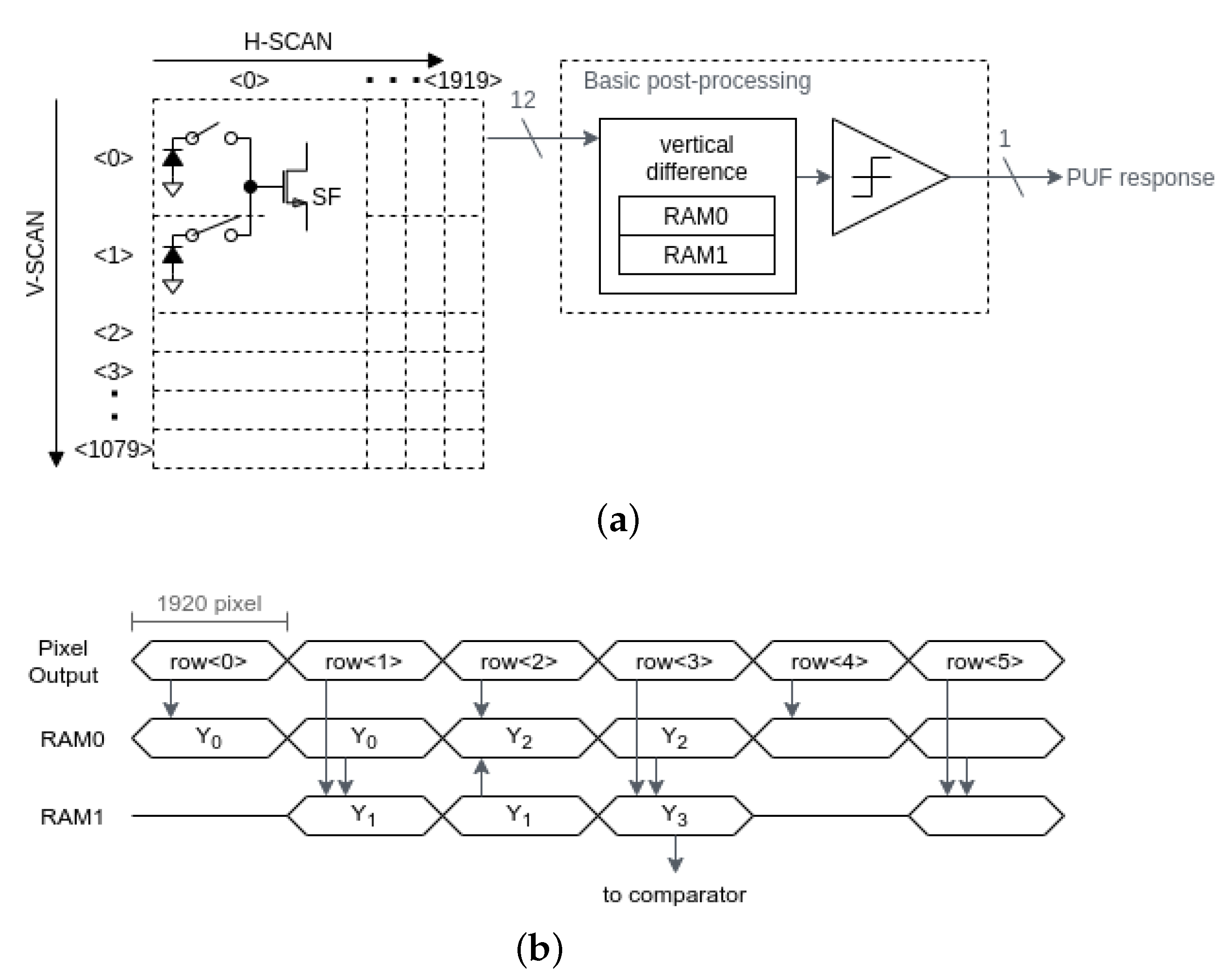
2.2.1. Basic Signal Processing
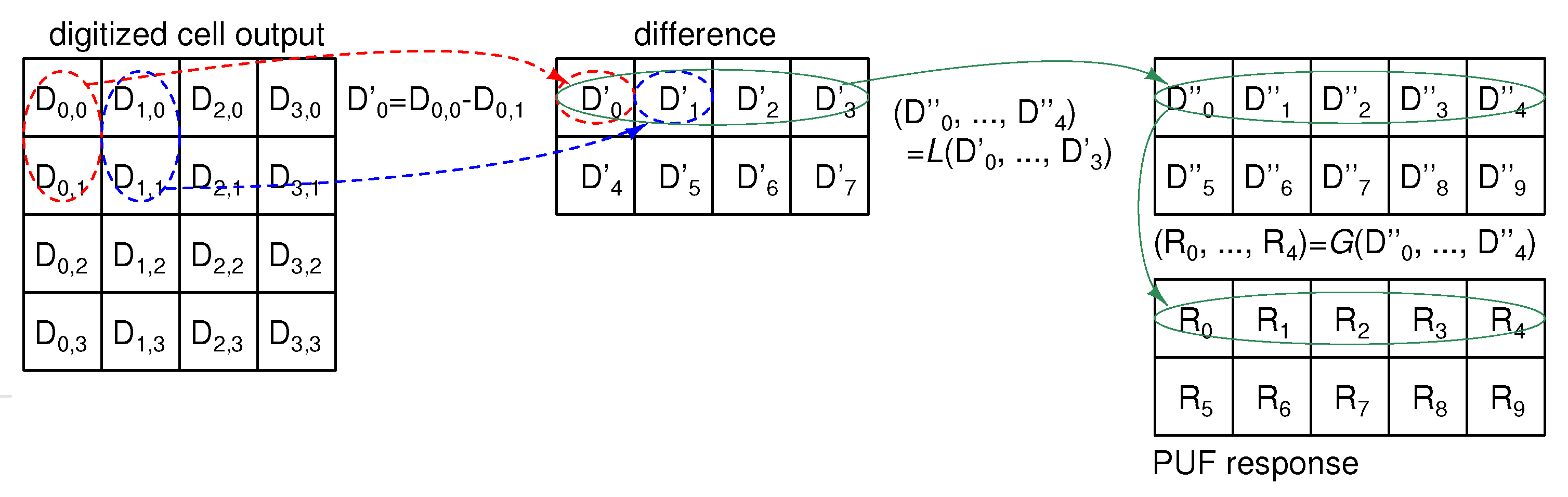
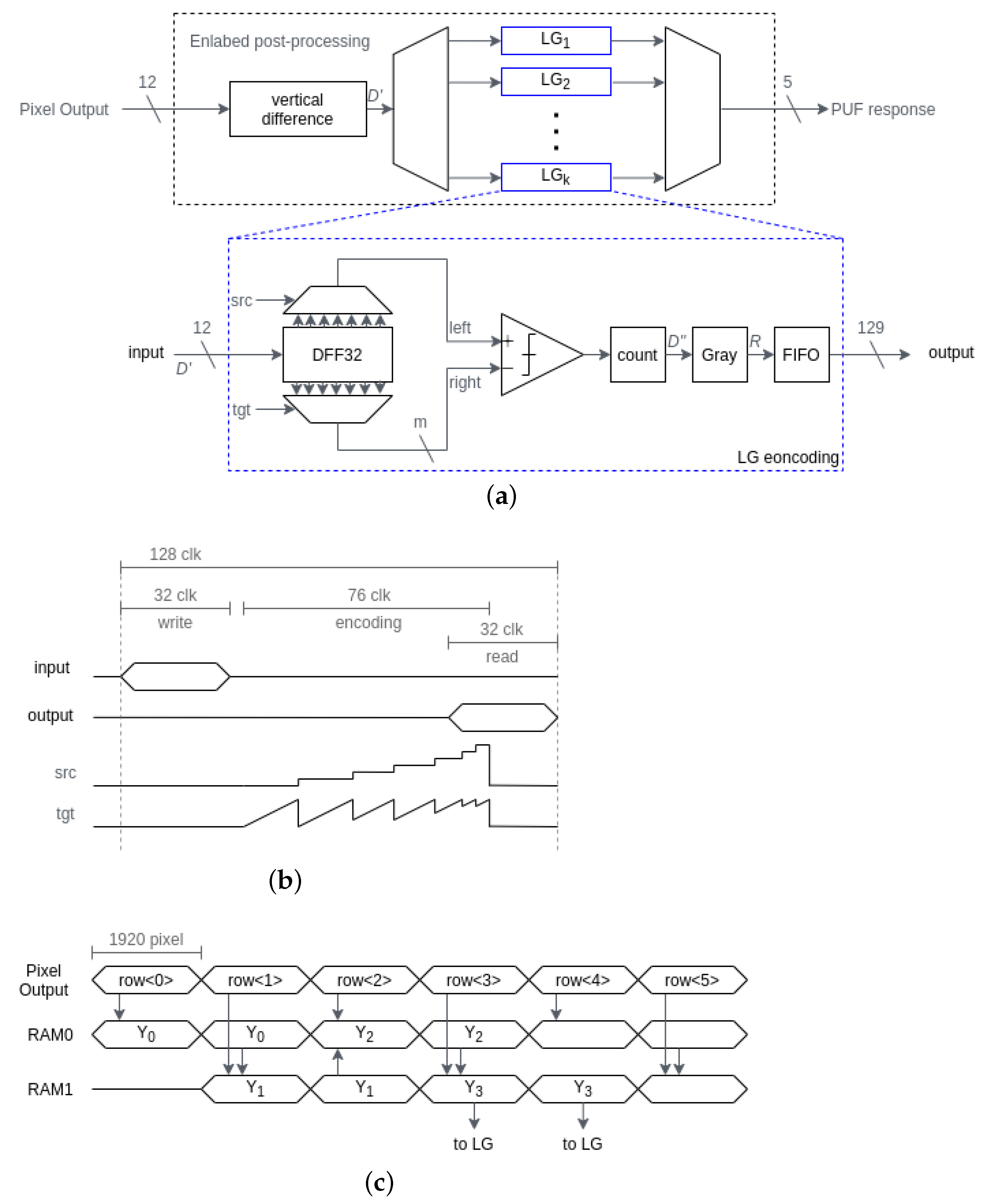
2.2.2. L.G. Signal Processing
2.3. Operation Confirmation of Device Authentication
3. Evaluation of PUF Properties
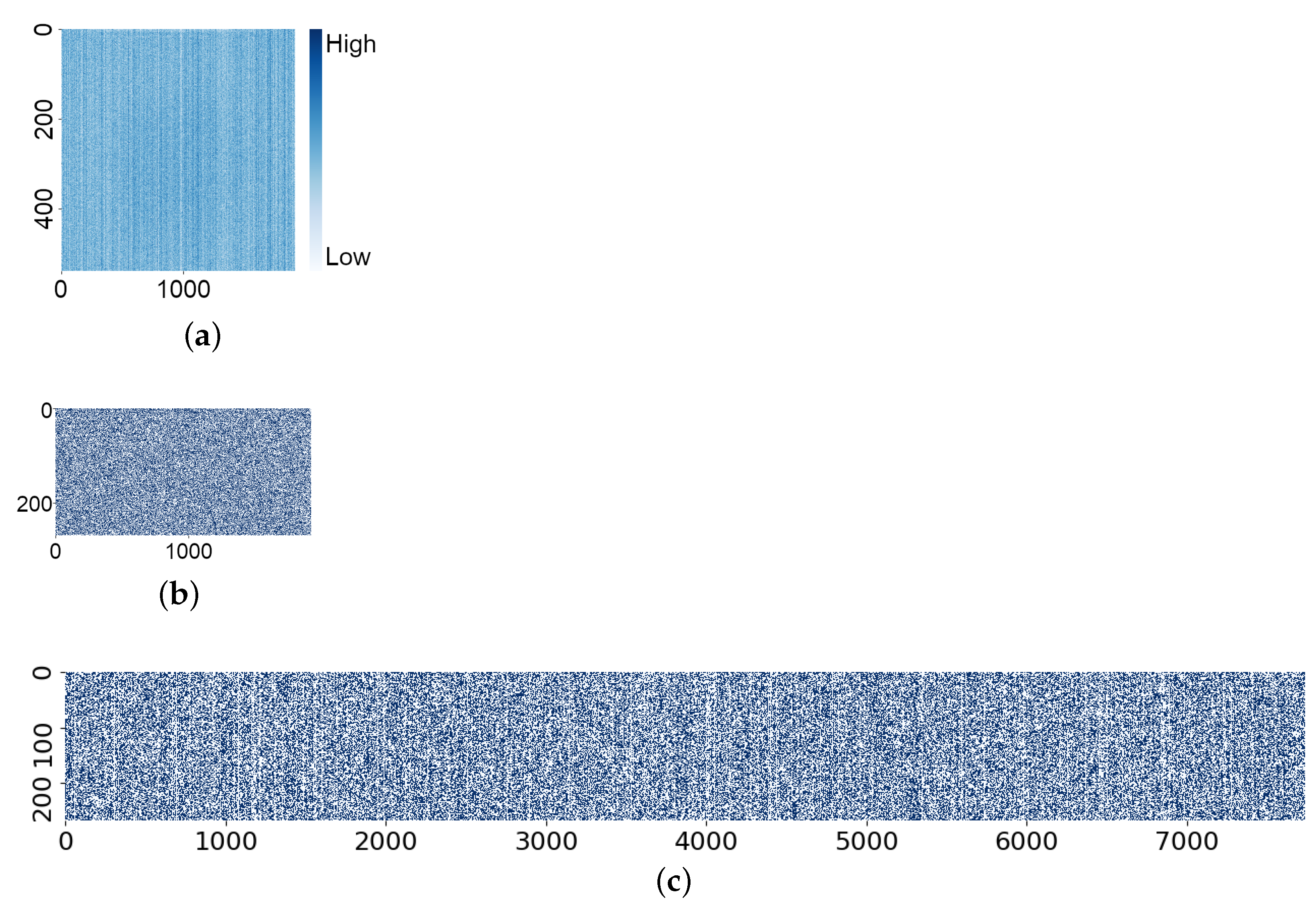
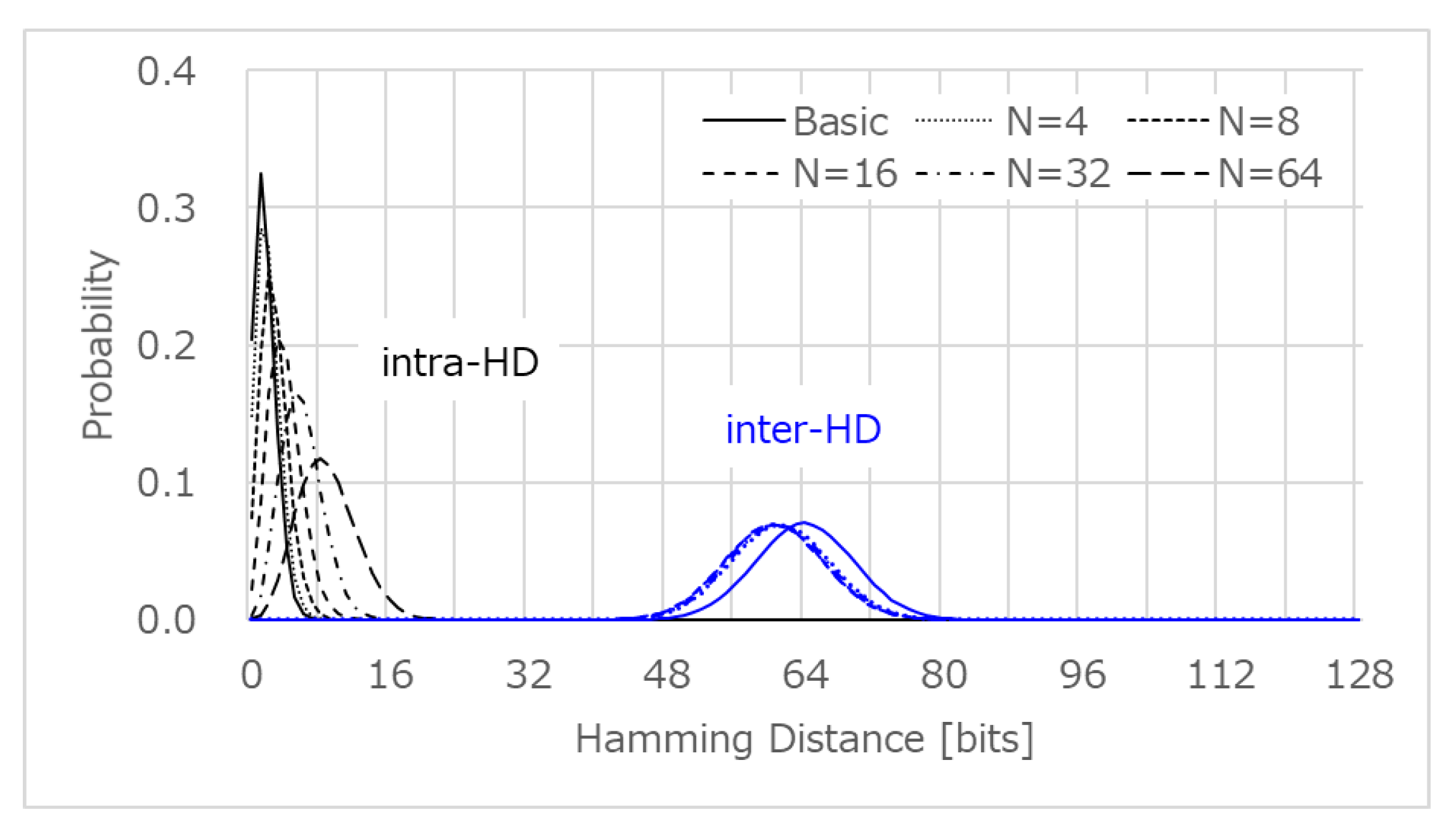
3.1. Reliability and Uniqueness
3.2. Device Authentication Error Rate
4. Post-Processing Circuit Design
4.1. Basic Post-Processing Circuit
4.2. L.G. Post-Processing Circuit
4.3. Circuit Area and PUF Response Length
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- The Route to a Trillion Devices: The Outlook for IoT Investment to 2035. Available online: https://community.arm.com/cfs-file/__key/telligent-evolution-components-attachments/01-1996-00-00-00-01-30-09/Arm-_2D00_-The-route-to-a-trillion-devices-_2D00_-June-2017.pdf (accessed on 30 January 2021).
- Hassija, V.; Chamola, V.; Saxena, V.; Jain, D.; Goyal, P.; Sikdar, B. A Survey on IoT Security: Application Areas, Security Threats, and Solution Architectures. IEEE Access 2019, 7, 82721–82743. [Google Scholar] [CrossRef]
- Halak, B.; Zwolinski, M.; Mispan, M.S. Overview of PUF-based hardware security solutions for the internet of things. In Proceedings of the 2016 IEEE 59th International Midwest Symposium on Circuits and Systems (MWSCAS), Abu Dhabi, United Arab Emirates, 16–19 October 2016; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Pappu, R.; Recht, B.; Taylor, J.; Gershenfeld, N. Physical One-Way Functions. Science 2002, 297, 2026–2030. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Seok, M. A 3.07 μm2/bitcell physically unclonable function with 3.5% and 1% bit-instability across 0 to 80 °C and 0.6 to 1.2V in a 65nm CMOS. In Proceedings of the 2015 Symposium on VLSI Circuits (VLSI Circuits), Kyoto, Japan, 17–19 June 2015; pp. C250–C251. [Google Scholar] [CrossRef]
- Yoshimoto, Y.; Katoh, Y.; Ogasahara, S.; Wei, Z.; Kouno, K. A ReRAM-based physically unclonable function with bit error rate < 0.5% after 10 years at 125 °C for 40nm embedded application. In Proceedings of the 2016 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 14–16 June 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Willers, O.; Huth, C.; Guajardo, J.; Seidel, H. MEMS Gyroscopes as Physical Unclonable Functions. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS), Vienna, Austria, 24–28 October 2016. [Google Scholar]
- Chen, J.; Tanamoto, T.; Noguchi, H.; Mitani, Y. Further investigations on traps stabilities in random telegraph signal noise and the application to a novel concept physical unclonable function (PUF) with robust reliabilities. In Proceedings of the 2015 Symposium on VLSI Technology (VLSI Technology), Kyoto, Japan, 16–18 June 2015; pp. T40–T41. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, L.; Zalivaka, S.S.; Chang, C.H.; Chen, S. CMOS Image Sensor Based Physical Unclonable Function for Coherent Sensor-Level Authentication. IEEE Trans. Circuits Syst. I 2015, 62, 2629–2640. [Google Scholar] [CrossRef]
- Hiller, M.; Önalan, A.G. Hiding Secrecy Leakage in Leaky Helper Data. In Cryptographic Hardware and Embedded Systems—CHES 2017; Fischer, W., Homma, N., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 601–619. [Google Scholar]
- Liu, K.; Min, Y.; Yang, X.; Sun, H.; Shinohara, H. A 373-F2 0.21%-Native-BER EE SRAM Physically Unclonable Function With 2-D Power-Gated Bit Cells and VSS Bias-Based Dark-Bit Detection. IEEE J. Solid Circuits 2020, 55, 1719–1732. [Google Scholar] [CrossRef]
- Liu, K.; Chen, X.; Pu, H.; Shinohara, H. A 0.5-V Hybrid SRAM Physically Unclonable Function Using Hot Carrier Injection Burn-In for Stability Reinforcement. IEEE J. Solid Circuits 2021, 56, 2193–2204. [Google Scholar] [CrossRef]
- Okura, S.; Nakura, Y.; Shirahata, M.; Shiozaki, M.; Kubota, T.; Ishikawa, K.; Takayanagi, I.; Fujino, T. A Proposal of PUF Utilizing Pixel Variations in the CMOS Image Sensor. 2017. pp. 66–69. Available online: http://www.imagesensors.org/Past%20Workshops/2017%20Workshop/2017%20Papers/P01.pdf (accessed on 8 September 2021).
- Information Security, Cybersecurity and Privacy Protection—Physically Unclonable Functions—Part 1: Security Requirements Standard; International Organization for Standardization: Geneva, Switzerland, 2020.
- Rührmair, U.; Sölter, J.; Sehnke, F.; Xu, X.; Mahmoud, A.; Stoyanova, V.; Dror, G.; Schmidhuber, J.; Burleson, W.; Devadas, S. PUF Modeling Attacks on Simulated and Silicon Data. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1876–1891. [Google Scholar] [CrossRef] [Green Version]
- Yamada, H.; Okura, S.; Shirahata, M.; Fujino, T. Modeling attacks against device authentication using CMOS image sensor PUF. IEICE Electron. Express 2021, 18, 20210058. [Google Scholar] [CrossRef]
- Maes, R.; Van Herrewege, A.; Verbauwhede, I. PUFKY: A Fully Functional PUF-Based Cryptographic Key Generator. In Cryptographic Hardware and Embedded Systems—CHES 2012; Prouff, E., Schaumont, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 302–319. [Google Scholar]
- Shiozaki, M.; Hori, Y.; Fujino, T. Entropy Estimation of Physically Unclonable Functions with Offset Error. Cryptology ePrint Archive, Report 2020/1284. 2020. Available online: https://eprint.iacr.org/2020/1284 (accessed on 8 September 2021).
- Lehmer, D.H. Teaching combinatorial tricks to a computer. In Proceedings of Symposia in Applied Mathematics; American Mathematical Society: Providence, RI, USA, 1960; Volume 10, pp. 179–193. [Google Scholar]
- Wild, A.; Becker, G.T.; Güneysu, T. A fair and comprehensive large-scale analysis of oscillation-based PUFs for FPGAs. In Proceedings of the 2017 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Hori, Y.; Yoshida, T.; Katashita, T.; Satoh, A. Quantitative and Statistical Performance Evaluation of Arbiter Physical Unclonable Functions on FPGAs. In Proceedings of the 2010 International Conference on Reconfigurable Computing and FPGAs, Cancun, Mexico, 13–15 December 2010; pp. 298–303. [Google Scholar] [CrossRef]
- Maes, R. Physically Unclonable Functions; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Onodera, H.; Hirata, A.; Kitamura, T.; Kobayashi, K.; Tamaru, K. P2Lib: Process Portable Library and Its Generation System. Trans. Inf. Process. Soc. Jpn. 1999, 40, 1660–1669. [Google Scholar]





| PUF | CIS | CIS (L.G.) | SRAM | Latch | DFF | RO | RO (L.G.) |
|---|---|---|---|---|---|---|---|
| Area Overhead [Gate] | #PUF Response [Bit] | Efficiency [Gate/Bit] | |
|---|---|---|---|
| Basic | 26 k | 518 k | 0.050 |
| L.G. | 44 k | 1902 k | 0.023 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okura, S.; Aoki, M.; Oyama, T.; Shirahata, M.; Fujino, T.; Ishikawa, K.; Takayanagi, I. Area-Efficient Post-Processing Circuits for Physically Unclonable Function with 2-Mpixel CMOS Image Sensor. Sensors 2021, 21, 6079. https://doi.org/10.3390/s21186079
Okura S, Aoki M, Oyama T, Shirahata M, Fujino T, Ishikawa K, Takayanagi I. Area-Efficient Post-Processing Circuits for Physically Unclonable Function with 2-Mpixel CMOS Image Sensor. Sensors. 2021; 21(18):6079. https://doi.org/10.3390/s21186079
Chicago/Turabian StyleOkura, Shunsuke, Masanori Aoki, Tatsuya Oyama, Masayoshi Shirahata, Takeshi Fujino, Kenichiro Ishikawa, and Isao Takayanagi. 2021. "Area-Efficient Post-Processing Circuits for Physically Unclonable Function with 2-Mpixel CMOS Image Sensor" Sensors 21, no. 18: 6079. https://doi.org/10.3390/s21186079
APA StyleOkura, S., Aoki, M., Oyama, T., Shirahata, M., Fujino, T., Ishikawa, K., & Takayanagi, I. (2021). Area-Efficient Post-Processing Circuits for Physically Unclonable Function with 2-Mpixel CMOS Image Sensor. Sensors, 21(18), 6079. https://doi.org/10.3390/s21186079






