4.1. Representation of Particles and Scheduling Scheme
In the study of GA-MOCA and ACO-CMS, solutions for this problem are usually based on a string-based notation. For example, GA-MOCA defined a string-based notation to represent the number of containers for each microservice, as well as the allocation of these containers to the physical machines, as shown in
Figure 4.
After investigating this method, we found that it has several problems: First, according to the characteristics of the ACO-CMS algorithm, when it tries to find a suitable schedule scheme, it has to traverse each container, microservice, and physical node separately, which results in significant search times. If there are x containers, y microservices, and z physical nodes, and the ACO-CMS algorithm has a population of m particles and n iterations, the time complexity of the ACO-CMS algorithm is .
Second, in the GA-MOCA algorithm, when the crossover and mutation operations occur, unreasonable solutions are always generated (i.e., growth mutation, swap mutation, and shrink mutation). Growth mutation adds a physical node to a microservice randomly, for example, if , then perhaps after mutation. Swap mutation exchanges the allocation of microservices, for example, if and , then and after mutation. Shrink mutation reduces the physical node that the microservice has been allocated, for example, if , then perhaps after mutation. Therefore, if only has two container instances when the operations occur, may not fill the quantity limit or exceed the resources that the physical nodes can provide. This can generate an invalid schedule scheme. This is the case for all of the other operations, as well.
Third, when there are large amounts of containers and microservices, the representation method uses significant amounts of memory to record the allocation order of containers when the algorithm is running, and the allocation order of containers has no direct impact on the optimization of the scheduling plan; however, this is suitable for the operation of their algorithm, specifically.
Considering the above problems, we define a new scheduling scheme expression, based on the number of containers. Each scheduling scheme is represented by a two-dimensional array, each row representing a microservice
, and each column represents a physical node
. The element
represents the number of containers of microservice
allocated to physical node
. Consider the simple application we mentioned above (shown in
Figure 2) as an example; one of its schedule schemes (or particles) is shown in
Figure 5.
Figure 5 shows the original state of the particle, which is randomly initialized by the MOPPSO-CMS algorithm. As microservice1 has two container instances, the total number of rows in
is two. The allocations
and
are randomly initialized, where one of the
containers is assigned to
and the other is assigned to
. Compared to the previous representation method, this method has several advantages:
First, the new representation method and the characteristics of MOPPSO-CMS algorithm have reduced time complexity. When the MOPPSO-CMS algorithm begins, it first initializes the particles (shown in
Figure 5), then finds the suitable schedule scheme by changing the number of containers in the physical node, instead of traversing each container and physical node. Thus, if there are
x containers,
y microservices, and
z physical nodes, and the MOPPSO-CMS algorithm has a population of
m particles and
n iterations, the time complexity of the MOPPSO-CMS algorithm is
.
Second, the transfer and copy operations, which are discussed later, can avoid generating an invalid schedule scheme while looking for a suitable schedule scheme, as they do not change the total number of containers.
Third, the memory resource of the new representation method only depends on the number of microservices and the physical nodes. The amount of containers will not significantly affect the new representation method.
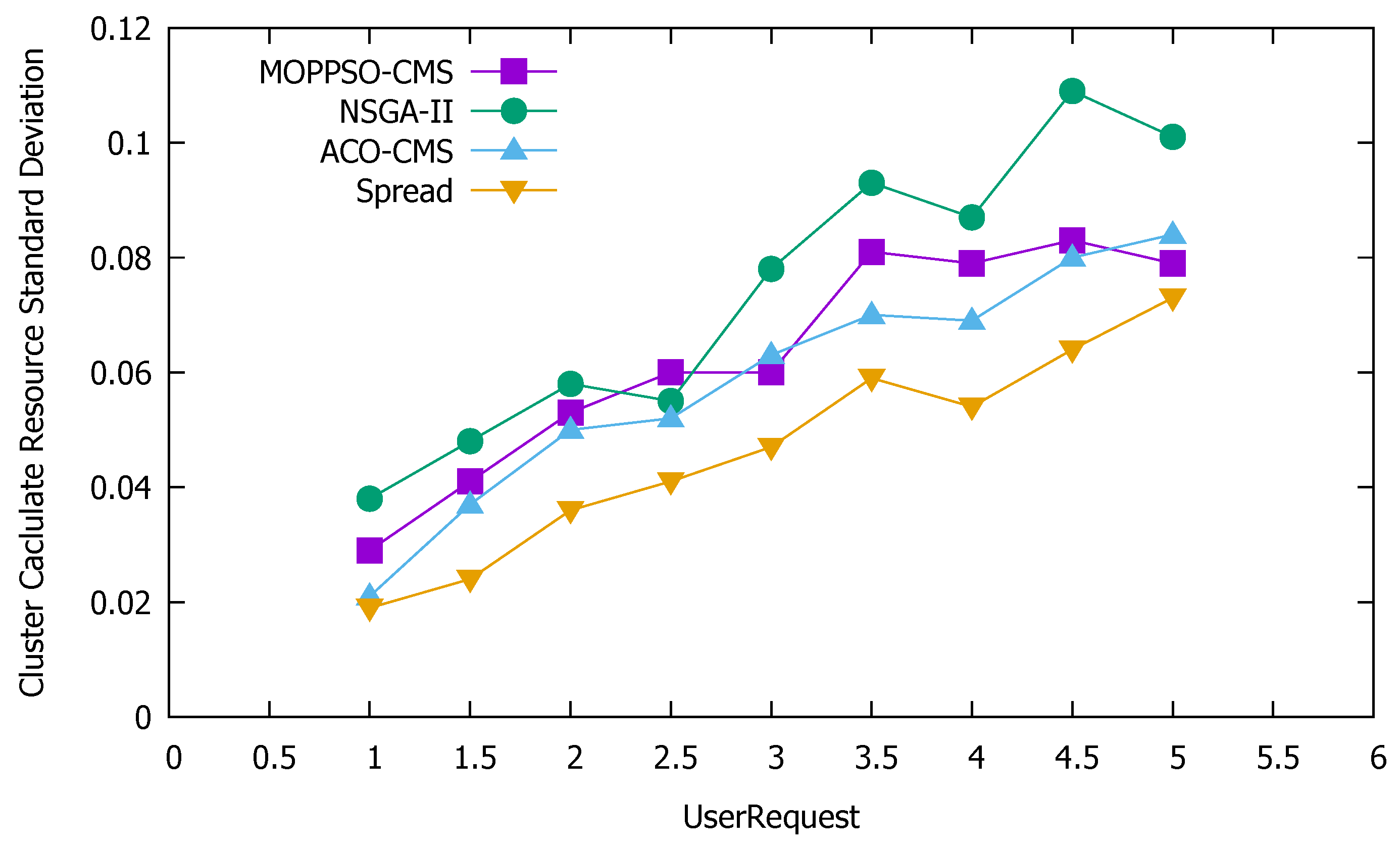
In conclusion, the new representation method combines the advantages and overcomes the shortcomings of both ACO-CMS and GA-MOCA. ACO-CMS will not generate an invalid schedule scheme, as it picks the containers in order to find suitable physical nodes; however, this may result in increased time complexity. The GA-MOCA may have less time complexity, but can generate many invalid schedule schemes. The new representation will reduce the time complexity and avoid generating invalid schedule schemes at the same time, thus combining the advantages of both methods.
4.2. Transfer and Copy Operations
The original update method of the PSO [
18] is shown in Equations (
1) and (
2). Obviously, the original update method of the particle swarm does not apply to the algorithm in this paper. To solve this problem, we improve the update method based on the original. The first is the transfer operation. In order to ensure the optimization ability of the particle itself, each particle is transferred according to a probability; namely, the inertia factor
. The transfer operation of particles is illustrated in
Figure 6.
In the figure, there is a 0.5 probability for the transfer operation to occur in each position of the particle. If the transfer occurs, the microservice would randomly transfer its containers to other physical nodes. For example, if a transfer occurs at , the containers in the physical node are randomly transferred to . Similarly, if a transfer occurs at , the containers in the physical node are randomly transferred to and . The number of the transfer containers are random, for example, for , it could transfer one or two to . If the number of containers in the position is 0, no transfer occurs.
Further, in order to increase the global optimization ability and optimization efficiency, the copy operation is integrated into the process of particle swarm optimization. Each row in the particle will copy the individual extremum
and the global extremum
according to a specified probability (i.e., the learning factors
and
), taking the particle itself and the individual extremum
as an example. The copy operation of the particle is illustrated in
Figure 7.
In the figure, the left side is the particle, and the right side is the individual extremum of the particle. According to the learning factor, the probability of a copy operation occurring is 0.5. The copy operation occurs at , and the particle copies the elements of the same row in , covering their own elements to achieve the purpose of learning from the individual extremum.
4.3. Parallel Particle Swarm Optimization Algorithm
The traditional PSO algorithm only uses one swarm when running; in contrast, the parallel particle swarm optimization algorithm in this paper uses multiple swarms operating at the same time. First, the MOPPSO-CMS algorithm is used to initialize the particles, as shown in
Figure 5. Then, the algorithm calculates
and
, according to the fitness function. The fitnesses of the particles are defined as an array
; the quality of the particles is assessed by means of an objective function of optimization problems [
34]; and each element of the array is calculated using Equations (
9), (
19) and (
24), respectively. These three equations represent the fitness function used in our method. The smaller the fitness, the better the particle.
In the MOPPSO-CMS algorithm, each swarm has their own , , and Pareto-optimal front. Within the swarm, after initializing, the particle is updated through the transfer and copy operations mentioned above. First, according to , it executes the transfer operation; the containers allocated are transferred to other physical nodes. Second, the particle copies the rows from , according to , to execute the copy operation. Third, the particle copies the rows from , according to , to execute the copy operation.
When the particle is initialized or changed, its fitness is calculated. According to Pareto optimality theory, if the new fitness (which, in our approach, is named ) Pareto-dominates , then is replaced by , and the schedule scheme of is also replaced by the schedule scheme of . Otherwise, we keep and the associated schedule scheme. Then, the or Pareto-optimal front is updated to the same operation.
When the iteration is finished, the fitness of each particle is compared to that of the others. One with fitness that is Pareto-dominated by another particle will be dropped. The rest is the , and forms the Pareto-optimal front. It is difficult to find the best solution in a multi-objective optimization problem. Therefore, the is not unique in this algorithm. According to the Pareto optimality theory mentioned above, each Pareto-optimal solution is a , and the set of (or Pareto-optimal solutions) is a Pareto-optimal front.
Each iteration generates a new set of , with the in the new set denoted by . The are compared with in the Pareto-optimal front. All that are Pareto-dominated by the are dropped, and the are added to the Pareto-optimal front. If any is Pareto-dominated by any one of the , then it is dropped. If does not Pareto-dominate any , and all do not Pareto-dominate , then is added to the Pareto-optimal front.
When the Pareto-optimal front of the swarm is updated, inter-process communication is carried out. The swarm uploads the
that was added most recently to the Pareto-optimal front and the shared memory. The other swarm downloads the
from the shared memory, all the local
Pareto-dominated by the
are dropped, and the
are added to the Pareto-optimal front. The
are uploaded to the shared memory again, for the rest of the swarm to download. If the
is Pareto-dominated by any one of the local
, then the
is dropped. If
does not Pareto-dominate any
, and all
do not Pareto-dominate
, then the
is added to Pareto-optimal front, and the
is uploaded again. The operation of inter-process communication is shown in
Figure 8.
The particle or schedule scheme is output, which has the minimum value of a sum of fitness in the Pareto-optimal front. The algorithm pseudo-code is shown in Algorithm 2.
| Algorithm 2: Parallel particle swarm optimization algorithm |
![Sensors 21 06212 i002]() |