Clutter Suppression Method for Off-Grid Effects Mitigation in Airborne Passive Radars with Contaminated Reference Signals
Abstract
:1. Introduction
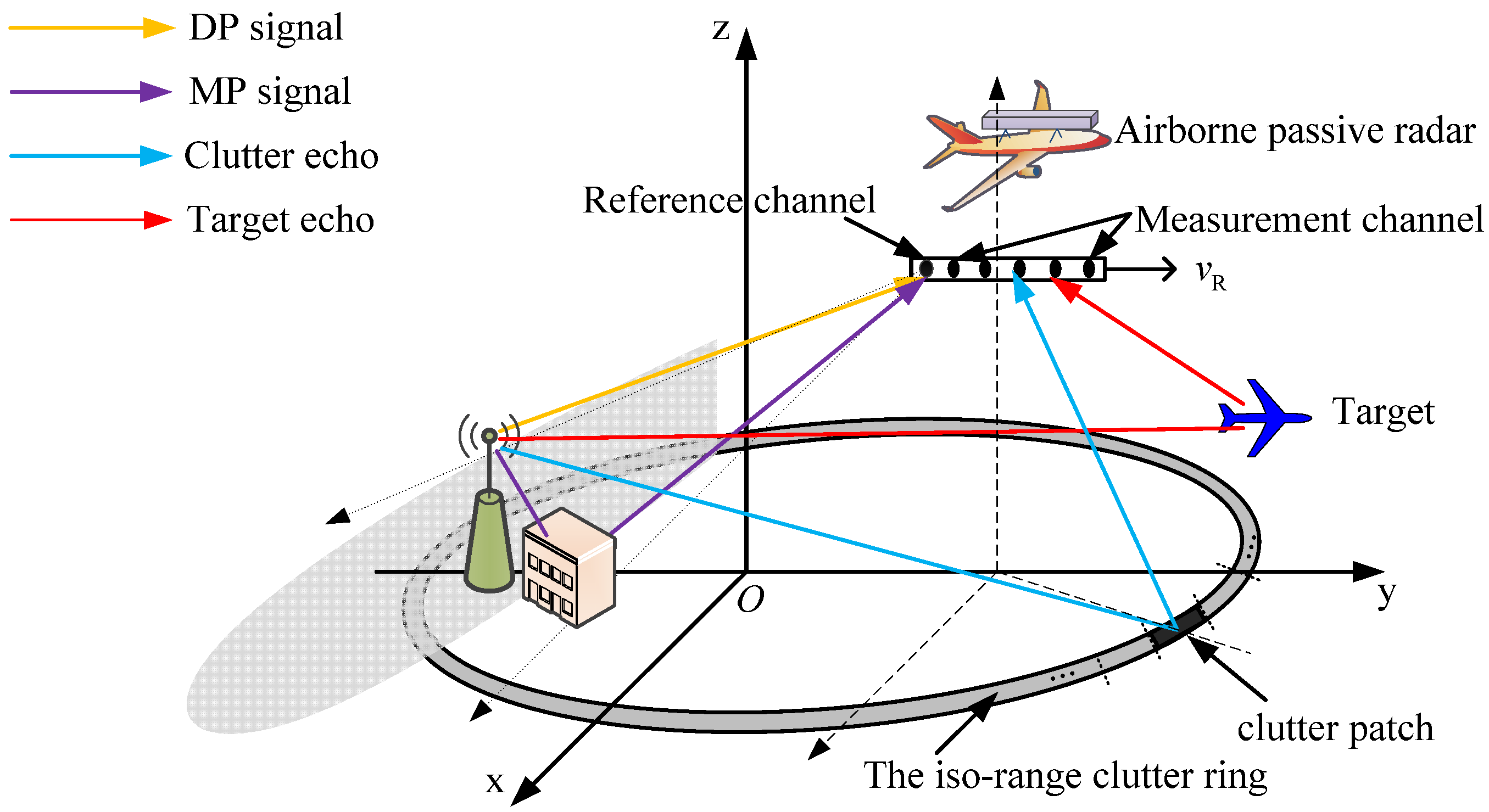
2. Signal Model
3. The Proposed CM for MP Clutter Suppression and Off-Grid Effects Mitigation
3.1. Review of the Exiting CMs
3.2. The Proposed CM for Clutter Suppression and Off-Grid Effects Mitigation
| Algorithm 1: The proposed CM for off-grid effects mitigation |
 |
3.3. Analyses of Computational Complexity
4. Simulations and Performance Analyses
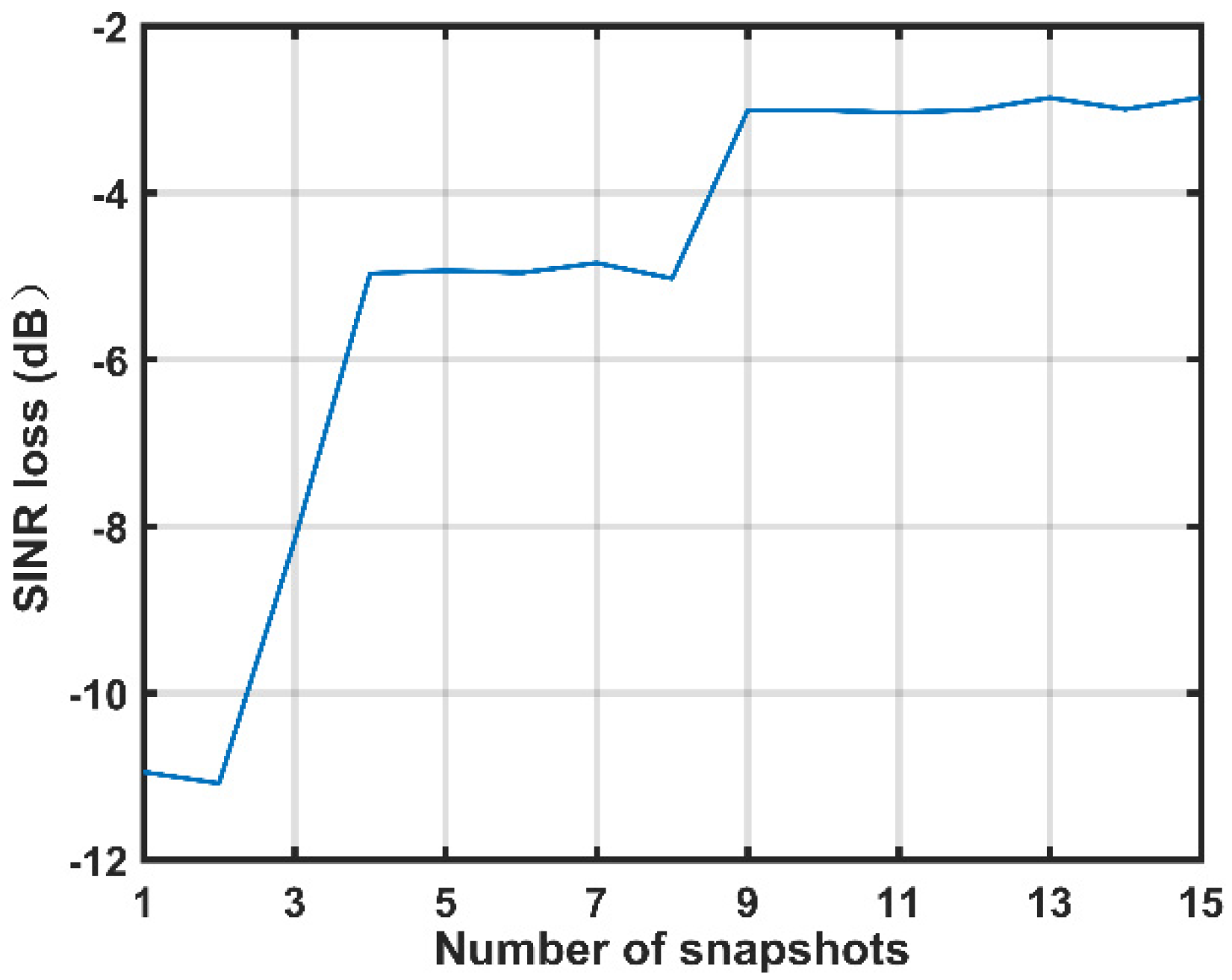
4.1. Setting of the Number of Snapshots in Range Dictionary
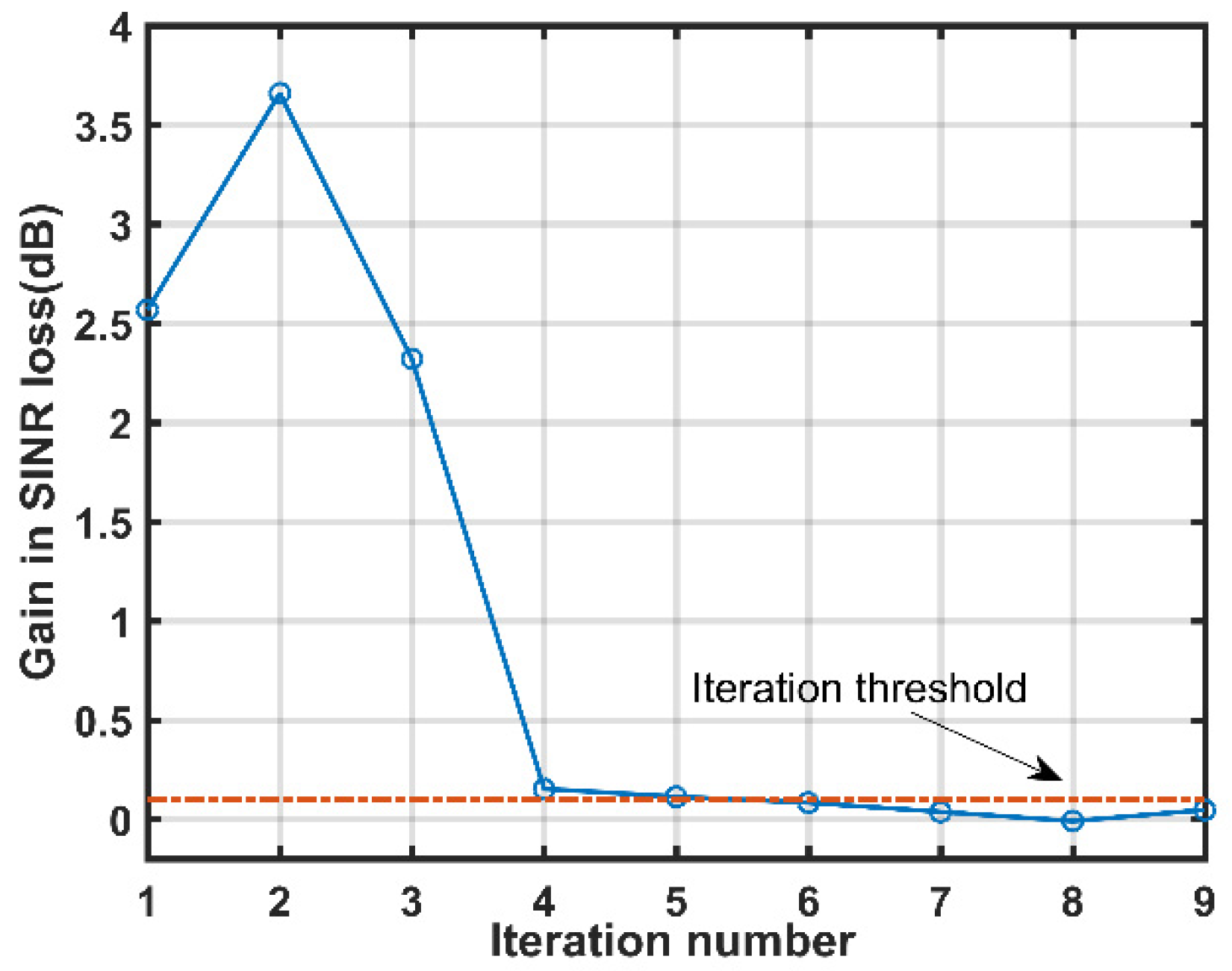
4.2. Setting of the Iteration Threshold
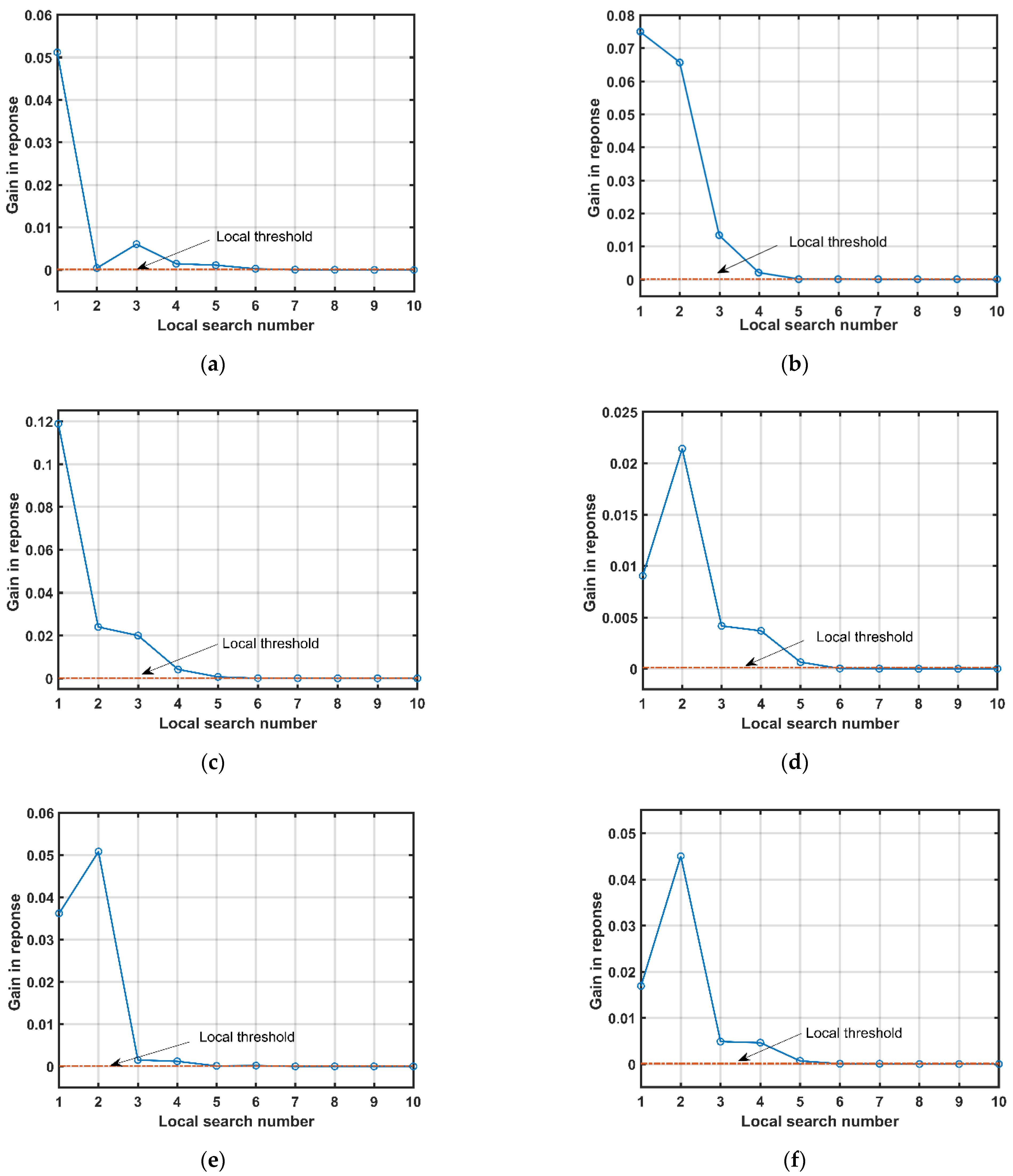
4.3. Setting of the Local Threshold
4.4. Distribution of Selected Atoms in the Range-Doppler Plane
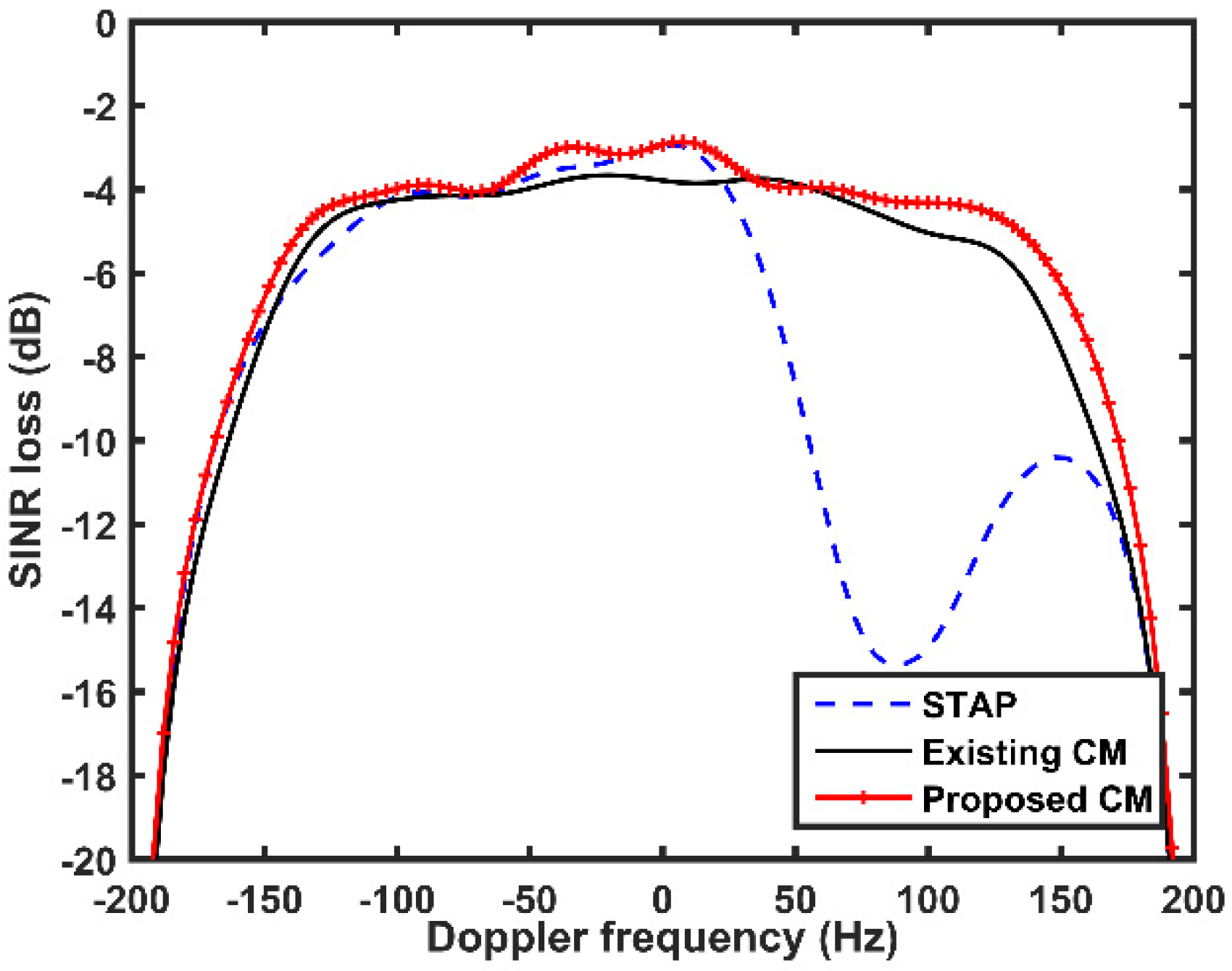
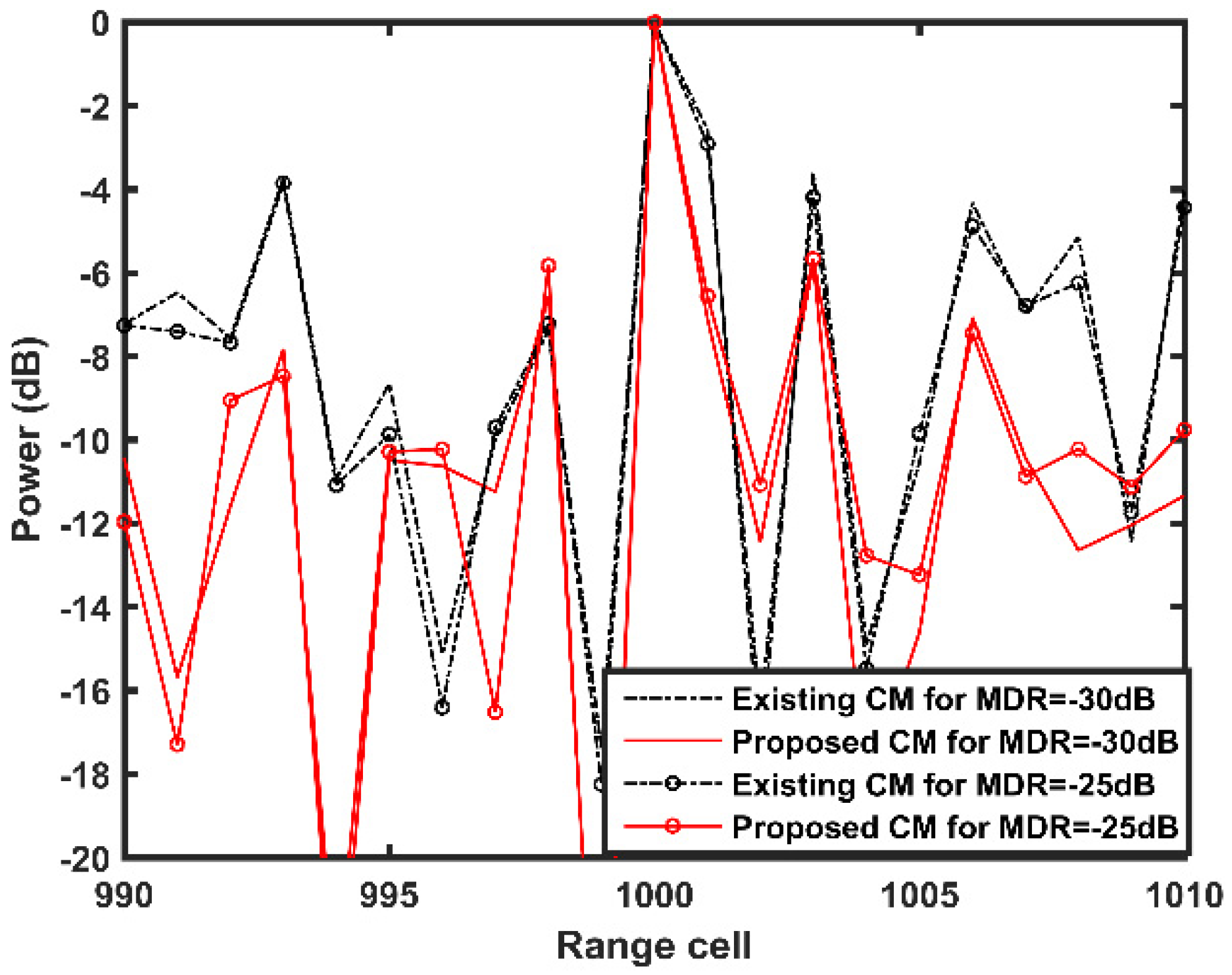
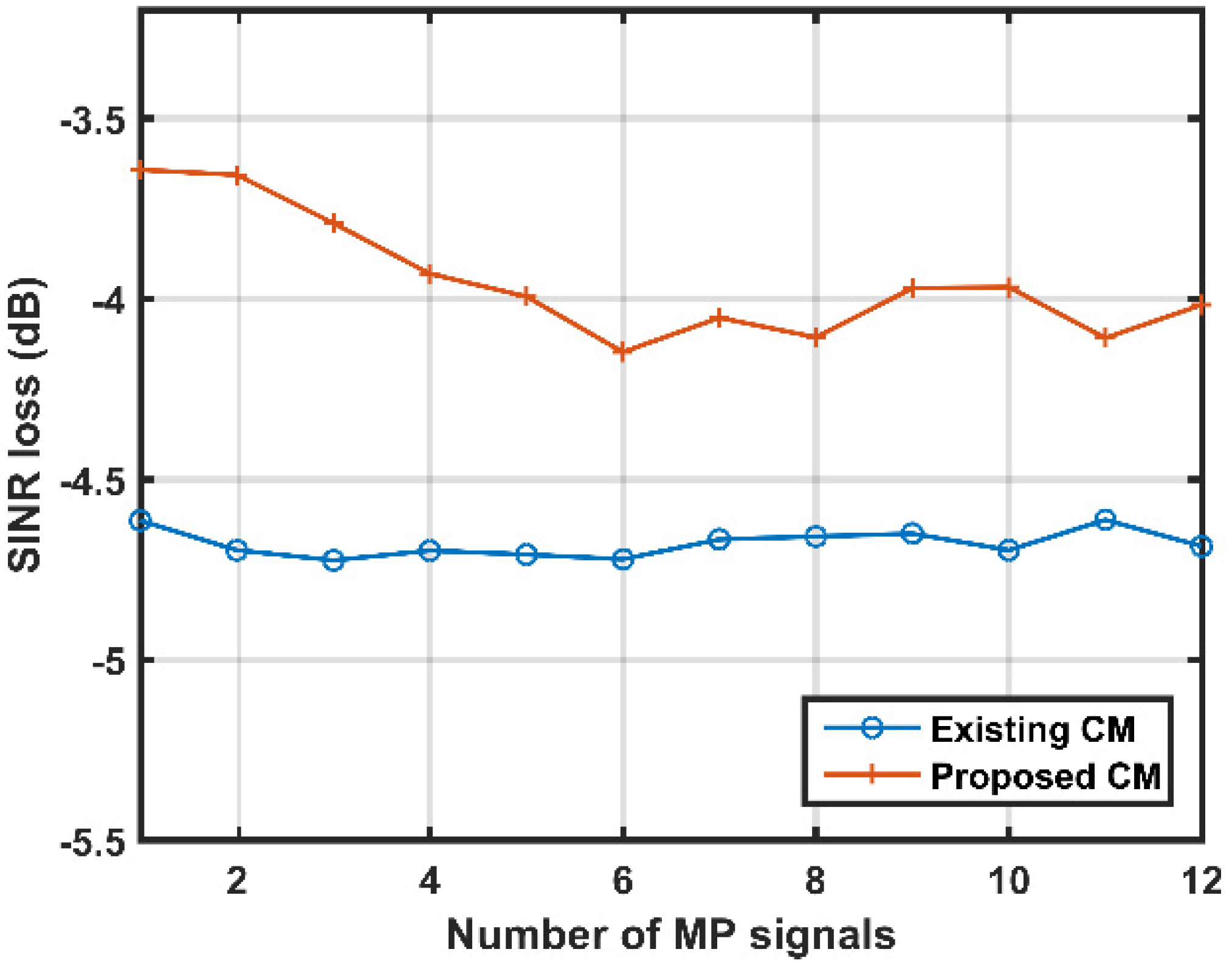
4.5. Comparison with the Existing CM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, W.; Zhang, C.; Zhao, Z.; Liu, F.; Chen, T. Low-complexity channelizer based on FRM for passive radar multi-channel wideband receiver. Circuits Syst. Signal Process. 2020, 39, 420–438. [Google Scholar] [CrossRef]
- Shan, T.; Liu, S.; Zhang, Y.D.; Amin, M.G.; Tao, R.; Feng, Y. Efficient architecture and hardware implementation of coherent integration processor for digital video broadcast-based passive bistatic radar. IET Radar Sonar Navig. 2016, 10, 97–106. [Google Scholar] [CrossRef]
- Dawidowicz, B.; Kulpa, K.S.; Malanowski, M.; Misiurewicz, J.; Samczynski, P.; Smolarczyk, M. DPCA Detection of Moving Targets in Airborne Passive Radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1347–1357. [Google Scholar] [CrossRef]
- Tan, D.K.P.; Lesturgie, M.; Sun, H.; Lu, Y. Space–time interference analysis and suppression for airborne passive radar using transmissions of opportunity. IET Radar Sonar Navig. 2014, 8, 142–152. [Google Scholar] [CrossRef]
- Wojaczek, P.; Colone, F.; Cristallini, D.; Lombardo, P. Reciprocal-Filter-Based STAP for Passive Radar on Moving Platforms. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 967–988. [Google Scholar] [CrossRef]
- Brown, J.; Woodbridge, K.; Griffiths, H.; Stove, A.; Watts, S. Passive bistatic radar experiments from an airborne platform. IEEE Aerosp. Electron. Syst. Mag. 2012, 27, 50–55. [Google Scholar] [CrossRef]
- Ward, J. Space-Time Adaptive Processing for Airborne Radar. In Proceedings of the IEE Colloquium on Space-Time Adaptive Processing, London, UK, 6 April 1998. [Google Scholar]
- Klemm, R. Principles of Space-Time Adaptive Processing, 3rd ed.; Institute of Electical Engineering: London, UK, 2006. [Google Scholar]
- Zhou, Y.; Wang, L.; Chen, X.; Wen, C.; Jiang, B.; Fang, D. An improving EFA for clutter suppression by using the persymmetric covariance matrix estimation. Circuits Syst. Signal Process. 2018, 37, 4136–4149. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, L.; Li, Y.; Wen, C.; Jiang, B. A fast iterative three-dimensional joint domain localized method in airborne MIMO radar. Circuits Syst. Signal Process. 2019, 38, 3370–3383. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Huang, J.; de Lamare, R.C. Robust two-stage reduced-dimension sparsity-aware STAP for airborne radar with coprime arrays. IEEE Trans. Signal Process. 2020, 68, 81–96. [Google Scholar] [CrossRef]
- Chen, S.; Kong, L.; Yang, J. Adaptive clutter nulling Approach for heterogeneous environments. Circuits Syst. Signal Process. 2015, 34, 987–1000. [Google Scholar] [CrossRef]
- Yang, X.; Sun, Y.; Zeng, T.; Long, T.; Sarkar, T.K. Fast STAP method based on PAST with sparse constraint for airborne phased array radar. IEEE Trans. Signal Process. 2016, 64, 4550–4561. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Pallotta, L.; Farina, A. Median matrices and their application to radar training data selection. IET Radar Sonar Navig. 2014, 8, 265–274. [Google Scholar] [CrossRef]
- Han, S.; Fan, C.; Huang, X. A novel STAP based on spectrum-aided reduced-dimension clutter sparse recovery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 213–217. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Wang, H.; Fa, R. Knowledge-aided STAP with sparse-recovery by exploiting spatio-temporal sparsity. IET Signal Process. 2016, 10, 150–161. [Google Scholar] [CrossRef]
- Sun, G.; He, Z.; Tong, J.; Zhang, X. Knowledge-aided covariance matrix estimation via Kronecker product expansions for airborne STAP. IEEE Geosci. Remote Sens. Lett. 2018, 15, 527–531. [Google Scholar] [CrossRef]
- Tan, X.; Roberts, W.; Li, J.; Stoica, P. Sparse learning via iterative minimization with application to MIMO radar imaging. IEEE Trans. Signal Process. 2011, 59, 1088–1100. [Google Scholar] [CrossRef]
- Aubry, A.; Carotenuto, V.; De Maio, A.; Govoni, M.A. Multi-snapshot spectrum sensing for cognitive radar via block-sparsity exploitation. IEEE Trans. Signal Process. 2019, 67, 1396–1406. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Duan, K.; Xie, W. Subspace-augmented clutter suppression technique for STAP radar. Geosci. Remote Sens. Lett. 2016, 13, 462–466. [Google Scholar] [CrossRef]
- Yang, Z.; de Lamare, R.C.; Liu, W. Sparsity-based STAP using alternating direction method with gain/phase errors. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2756–2768. [Google Scholar]
- Yang, Z.; Qin, Y.; de Lamare, R.C.; Wang, H.; Li, X. Sparsity-Based direct data domain space-time adaptive processing with intrinsic clutter motion. Circuits Syst. Signal Process. 2017, 36, 219–246. [Google Scholar] [CrossRef]
- Guo, S.; Wang, J.; Ma, H.; Wang, J. Modified blind equalization algorithm based on cyclostationarity for contaminated referent signal in airborne PBR. Sensors 2020, 20, 788. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, Y.; Wang, J.; Luo, Z.; Guo, S. Cascaded suppression method for airborne passive radar with contaminated reference signal. IEEE Access 2019, 7, 50317–50329. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, S.; Zhu, Q.; Zhang, L.; Li, W. Clutter suppression methods based on reduced-dimension transformation for airborne passive radar with impure reference signals. J. Appl. Remote Sens. 2021, 15, 016514. [Google Scholar] [CrossRef]
- He, P.; He, S.; Yang, Z.; Huang, P. An off-grid STAP algorithm based on local mesh splitting with bistatic radar system. IEEE Signal Process. Lett. 2020, 27, 1355–1359. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; He, X.; Guo, Y. Low-complexity off-grid algorithm based on local search clutter subspace estimation. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1862–1866. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, W.; Yan, J. Direction of arrival estimation for off-grid signals based on sparse Bayesian learning. IEEE Sensors J. 2016, 16, 2004–2016. [Google Scholar] [CrossRef]
- Dai, J.; Bao, X.; Xu, W.; Chang, C. Root sparse Bayesian learning for off-grid DOA estimation. IEEE Signal Process. Lett. 2017, 24, 11–15. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse inference. IEEE Trans. Signal Process. 2013, 61, 38–43. [Google Scholar] [CrossRef] [Green Version]
- Duan, K.; Liu, W.; Duan, G.; Wang, Y. Off-grid effects mitigation exploiting knowledge of the clutter ridge for sparse recovery STAP. IET Radar Sonar Navig. 2018, 12, 557–564. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, J.; Liang, S. Efficient joint probabilistic data association filter based on Kullback–Leibler divergence for multi-target tracking. IET Radar Sonar Navig. 2017, 11, 1540–1548. [Google Scholar] [CrossRef]
- Gao, Z.; Tao, H. Robust STAP algorithm based on knowledge-aided SR for airborne radar. IET Radar Sonar Navig. 2017, 11, 321–329. [Google Scholar]
- Kulpa, K.S.; Czekala, Z. Masking effect and its removal in PCL radar. IEE Proc. -Radar Sonar Navig. 2005, 152, 174–178. [Google Scholar] [CrossRef]
- Ciuonzo, D.; De Maio, A.; Orlando, D. On the statistical invariance for adaptive radar detection in partially homogeneous disturbance plus structured interference. IEEE Trans. Signal Process. 2016, 65, 1222–1234. [Google Scholar] [CrossRef]
- Addabbo, P.; Besson, O.; Orlando, D.; Ricci, G. Adaptive detection of coherent radar targets in the presence of noise jamming. IEEE Trans. Signal Process. 2019, 67, 6498–6510. [Google Scholar] [CrossRef] [Green Version]
- Rabideau, D.J. Clutter and jammer multipath cancellation in airborne adaptive radar. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 565–583. [Google Scholar] [CrossRef]
- De Maio, A.; De Nicola, S.; Huang, Y.; Zhang, S.; Farina, A. Adaptive detection and estimation in the presence of useful signal and interference mismatches. IEEE Trans. Signal Process. 2008, 57, 436–450. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Number of elements | 10 |
| Number of equivalent pulses in a CIT | 10 |
| Main beam look direction | Side-looking |
| Equivalent PRF | 400 Hz |
| Channel spacing | |
| Platform velocity | 100 m/s |
| Target range cell index | 1000 |
| Target Doppler frequency | −100 Hz |
| True and Ghost MP Clutter | Ture 1 | Ture 2 | True 3 | Ghost 1 | Ghost 2 | Ghost 3 |
|---|---|---|---|---|---|---|
| Time bin | 3 | 4 | 9 | 6 | 7 | 8 |
| Normalized Doppler frequency | −0.25 | −0.18 | −0.33 | 0.5 | −0.43 | −0.36 |
| MDR Value (dB) | −15 | −20 | −25 | −30 | −35 | −40 |
|---|---|---|---|---|---|---|
| Existing CM (dB) | −4.961 | −4.721 | −4.725 | −4.624 | −4.542 | −4.519 |
| Proposed CM (dB) | −3.946 | −4.077 | −3.801 | −3.925 | −3.981 | −3.930 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Li, W.; Zhang, S.; Wang, F.; Xiao, W.; Cui, Z. Clutter Suppression Method for Off-Grid Effects Mitigation in Airborne Passive Radars with Contaminated Reference Signals. Sensors 2021, 21, 6339. https://doi.org/10.3390/s21196339
Deng Y, Li W, Zhang S, Wang F, Xiao W, Cui Z. Clutter Suppression Method for Off-Grid Effects Mitigation in Airborne Passive Radars with Contaminated Reference Signals. Sensors. 2021; 21(19):6339. https://doi.org/10.3390/s21196339
Chicago/Turabian StyleDeng, Yaqi, Wenguo Li, Saiwen Zhang, Fulong Wang, Weichu Xiao, and Zhi Cui. 2021. "Clutter Suppression Method for Off-Grid Effects Mitigation in Airborne Passive Radars with Contaminated Reference Signals" Sensors 21, no. 19: 6339. https://doi.org/10.3390/s21196339
APA StyleDeng, Y., Li, W., Zhang, S., Wang, F., Xiao, W., & Cui, Z. (2021). Clutter Suppression Method for Off-Grid Effects Mitigation in Airborne Passive Radars with Contaminated Reference Signals. Sensors, 21(19), 6339. https://doi.org/10.3390/s21196339





