Wildfire Risk Assessment of Transmission-Line Corridors Based on Naïve Bayes Network and Remote Sensing Data
Abstract
:1. Introduction
2. Study Area and Data Collection
2.1. Study Area
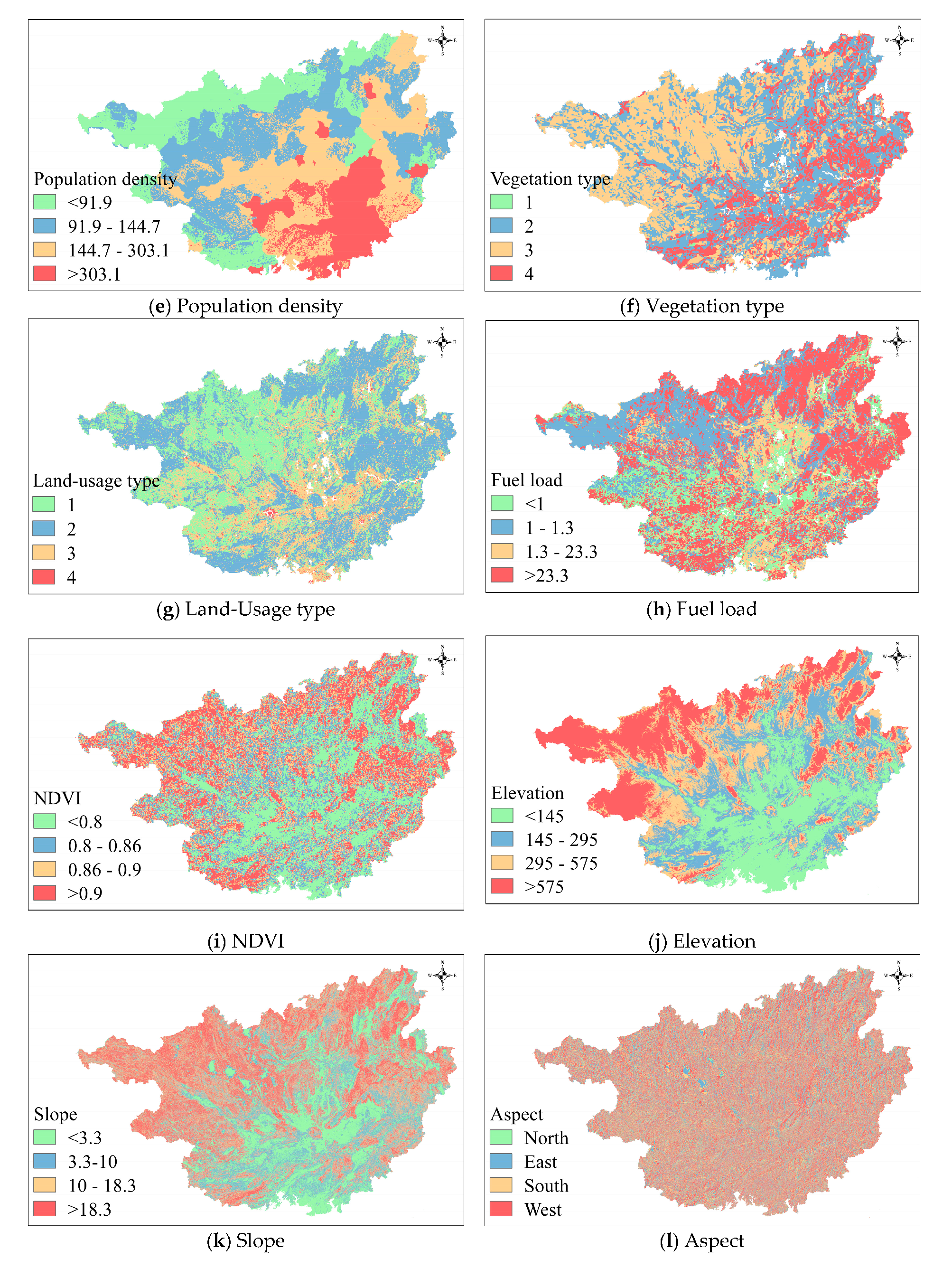
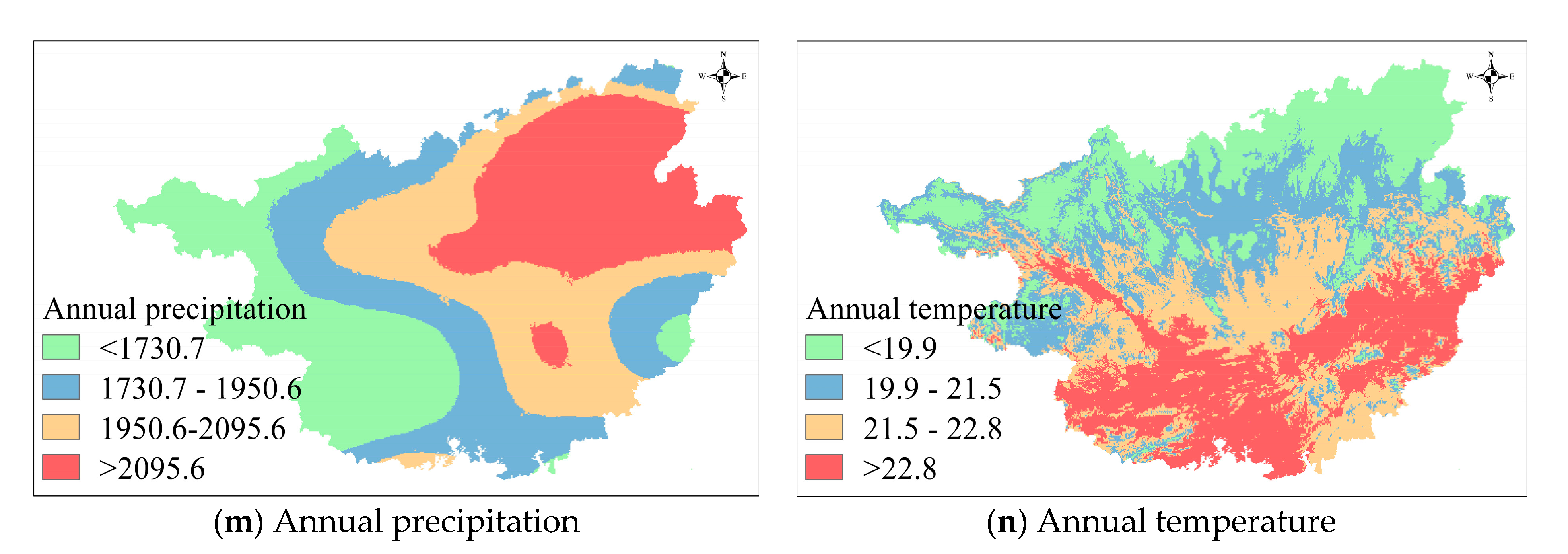
2.2. Wildfire-Related Factors
2.2.1. Anthropogenic Factors
2.2.2. Physiographic Factors
2.2.3. Meteorologic Factors
2.3. Sample Preparation and Pre-Processing
2.4. Spatial Distribution of Factors
3. Importance of Wildfire-Related Factors
- (1)
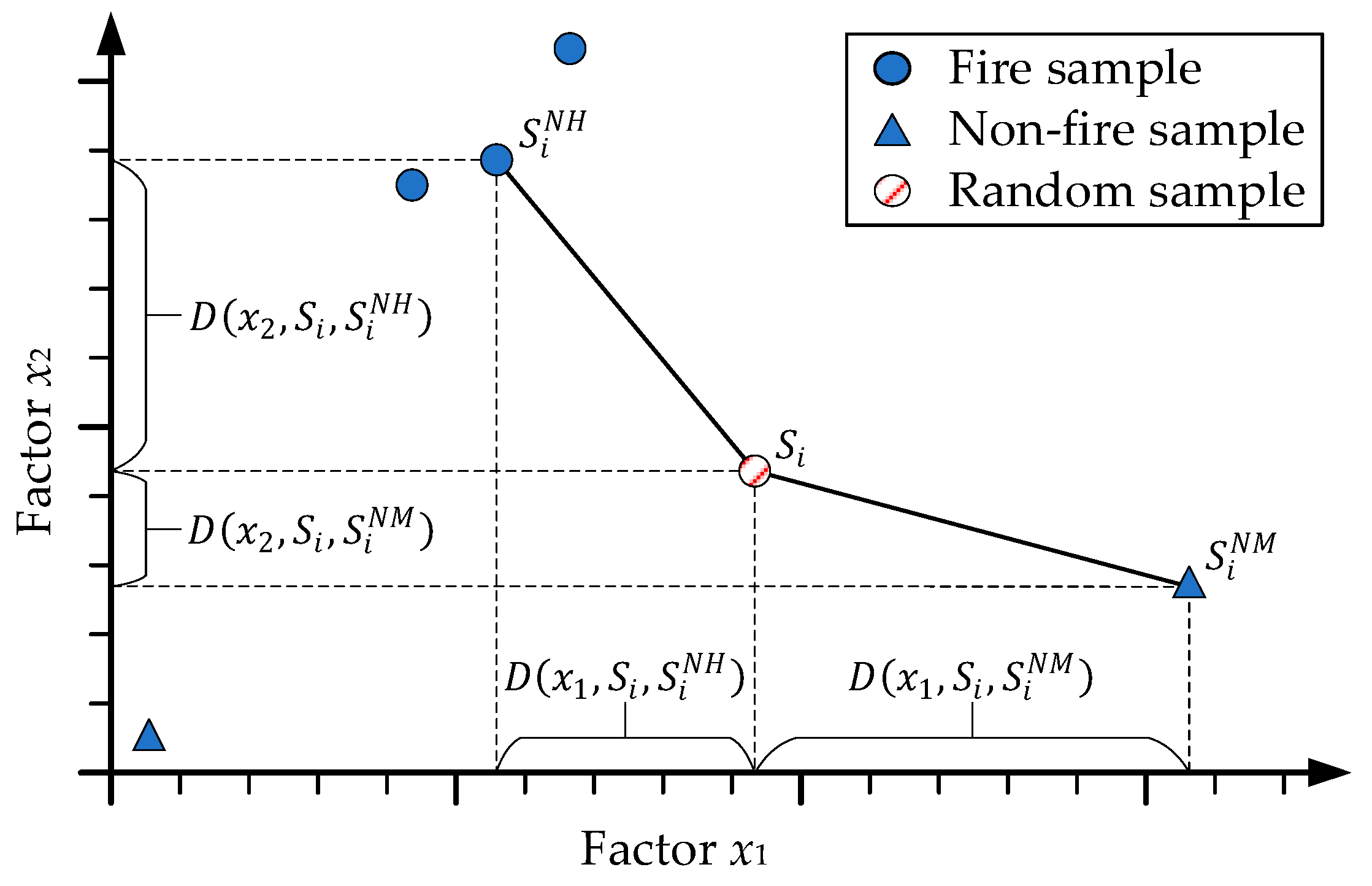
- Take a sample randomly from the dataset .
- (2)
- Go through the dataset and find the closest same-class sample and different-class sample of the .
- (3)
- Calculate the distance between the closest samples about a certain factor . If the factor is a discrete variable,else,In this study, the most of factors are continuous variables, except the Vegetation Type and Land-Usage Type.
- (4)
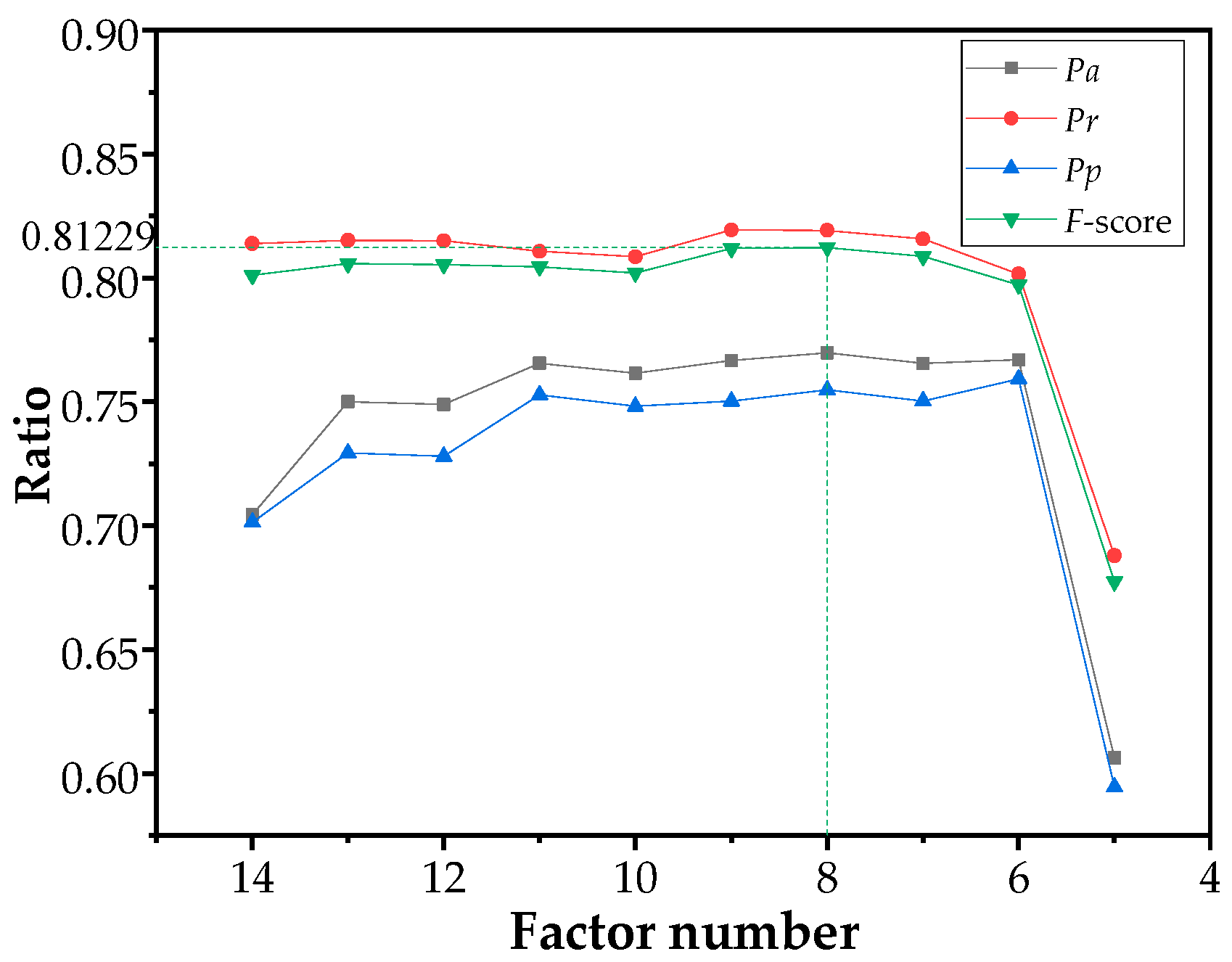
- Update the weight of factor after multiple samplingwhere and are the initial and updated weight, respectively. is the number of random sampling. The calculated weights of the 14 wildfire-related factors are listed in Table 4.
4. Naïve Bayes Network-Based Wildfire Risk Assessment
4.1. Bayes Theorem and Independence Assumption
4.2. Model Construction
- (1)
- Sample preparation from the grids. The fire samples are the grids where fire-spots have been monitored by satellites in the years from 2015 to 2019. A total of 20,348 fires were recorded. In addition, a same number of non-fire samples were extracted randomly excluding buffer zones of 3 km around the fire samples. Then the samples were graded according to the discretization standards in Table 3. The training subset was randomly chosen from 70% of the samples, the remaining samples were used as the testing subset to evaluate the model’s performance. In addition, the spatial distribution of samples in the testing subset are shown in Figure 3.
- (2)
- By using the training subset, the probabilities of factors are obtained under fire and non-fire condition based on the maximum likelihood estimation.where is the ith wildfire-related factor fall in jth level; and is the number of . represented the discretization level of factors. and are the probabilities of for the girds with non-fires and fires, separately.
- (3)
- The conditional probability and of samples in the testing subset were calculated based on the Bayes’ theorem. In addition, the final wildfire occurrence probability P(Y) was obtained after normalization.
- (4)
- To test and optimize model’s performance, the value of 0.5 was selected as the threshold to divide the samples into two classes: “Prone to fire” and “Prone to non-fire”. The least important factors were then eliminated in turn to study the influence of factors composition on the model’s performance.
4.3. Model Assessment
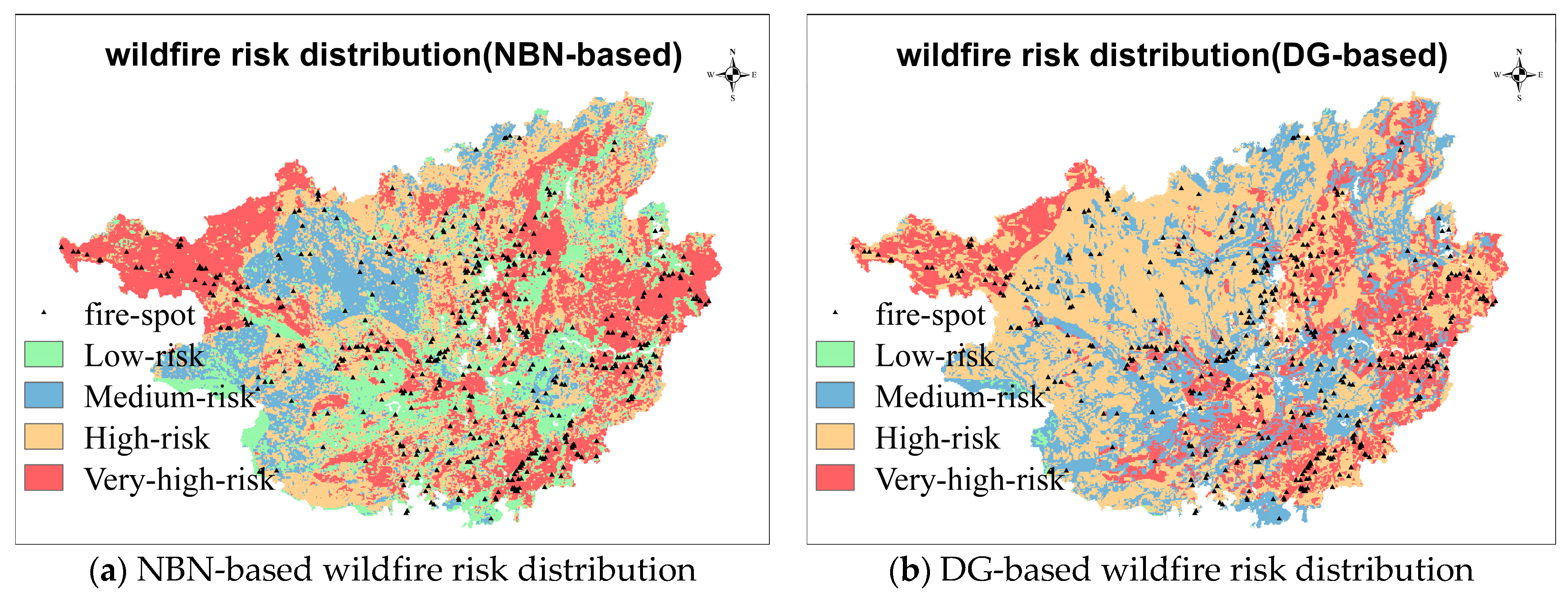
5. Visualization of Wildfire Risk and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, S.; Yao, C.; Wang, S.; Han, W. A Model Design for Risk Assessment of Line Tripping Caused by Wildfires. Sensors 2018, 18, 1941. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Chen, R.; Shi, J.; Wan, J.; Yi, H.; Zhong, J.J.I.G. Determination of the power transmission line ageing failure probability due to the impact of forest fire. IET Gener. Transm. Distrib. 2018, 12, 3812–3819. [Google Scholar] [CrossRef]
- Wu, T.; Ruan, J.; Zhang, Y.; Chen, C.; Pu, Z.H.; Wang, G.L. Study on the statistic characteristics and identification of AC transmission line trips induced by forest fires. Power Syst. Prot. Control 2012, 40, 138–143. [Google Scholar]
- Li, P.; Huang, D.; Pu, Z.; Ruan, J. Study on DC Voltage Breakdown Characteristics of Gap under Fire Conditions. In Proceedings of the Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Shenzhen, China, 20–23 October 2013; pp. 338–341. [Google Scholar]
- Fonseca, J.; Tan, A.; Silva, R.; Monassi, V.; Assuncao, L.; Junqueira, W.; Melo, M. Effects of agricultural fires on the performance of overhead transmission lines. IEEE Trans. Power Deliv. 1990, 5, 687–694. [Google Scholar] [CrossRef]
- Chou, Y.H.; Minnich, R.A.; Salazar, L.; Power, J.; Dezzani, R.J. Spatial autocorrelation of wildfire distribution in the Idyllwild quadrangle, San Jacinto Mountain, California. Remote Sens. 1990, 56, 1507–1513. [Google Scholar]
- Sakellariou, S.; Cabral, P.; Caetano, M.; Pla, F.; Painho, M.; Christopoulou, O.; Sfougaris, A.; Dalezios, N.; Vasilakos, C. Remotely Sensed Data Fusion for Spatiotemporal Geostatistical Analysis of Forest Fire Hazard. Sensors 2020, 20, 5014. [Google Scholar] [CrossRef] [PubMed]
- El-Zohri, E.H.; Abdel-Salam, M.; Shafey, H.M.; Ahmed, A. Mathematical modeling of flashover mechanism due to deposition of fire-produced soot particles on suspension insulators of a HVTL. Electr. Power Syst. Res. 2013, 95, 232–246. [Google Scholar] [CrossRef]
- You, F.; Zhang, Y.; Chen, H.X.; Zhang, L.H.; Zhu, J.P.; Zhou, J.J. Preliminary studies on flashovers of high-voltage transmission lines induced by wildfires by field survey and experimental tests. Procedia Eng. 2013, 52, 557–565. [Google Scholar] [CrossRef] [Green Version]
- Giglio, L.; Descloitres, J.; Justice, C.O.; Kaufman, Y. An enhanced contextual fire detection algorithm for MODIS. Remote Sens. Environ. 2003, 87, 273–282. [Google Scholar] [CrossRef]
- Giglio, L.; Csiszar, I.; Restás, Á.; Morisette, J.T.; Schroeder, W.; Morton, D.; Justice, C.O. Active fire detection and characterization with the advanced spaceborne thermal emission and reflection radiometer (ASTER). Remote Sens. Environ. 2008, 112, 3055–3063. [Google Scholar] [CrossRef]
- Chiang, S.H.; Ulloa, N.I. Mapping and Tracking Forest Burnt Areas in the Indio Maiz Biological Reserve Using Sentinel-3 SLSTR and VIIRS-DNB Imagery. Sensors 2019, 19, 5423. [Google Scholar] [CrossRef] [Green Version]
- Barmpoutis, P.; Papaioannou, P.; Dimitropoulos, K.; Grammalidis, N. A Review on Early Forest Fire Detection Systems Using Optical Remote Sensing. Sensors 2020, 20, 6442. [Google Scholar] [CrossRef]
- Choobineh, M.; Ansari, B.; Mohagheghi, S. Vulnerability assessment of the power grid against progressing wildfires. Fire Saf. J. 2015, 73, 20–28. [Google Scholar] [CrossRef]
- Sánchez, Y.; Martínez-Graña, A.; Santos Francés, F.; Mateos Picado, M. Mapping Wildfire Ignition Probability Using Sentinel 2 and LiDAR (Jerte Valley, Cáceres, Spain). Sensors 2018, 18, 826. [Google Scholar] [CrossRef] [Green Version]
- Sadasivuni, R.; Cooke, W.; Bhushan, S. Wildfire risk prediction in southeastern Mississippi using population interaction. Ecol. Model. 2013, 251, 297–306. [Google Scholar] [CrossRef]
- Lu, J.; Liu, Y.; Xu, X.; Yang, L.; Zhang, G.; He, L. Prediction and early warning technology of wildfire nearby overhead transmission lines. High Volt. Eng. 2017, 43, 314–320. [Google Scholar]
- Dian, S.; Cheng, P.; Ye, Q.; Wu, J.; Luo, R.; Wang, C.; Hui, D.; Zhou, N.; Zou, D.; Gong, X. Integrating wildfires propagation prediction into early warning of electrical transmission line outages. IEEE Access 2019, 7, 27586–27603. [Google Scholar] [CrossRef]
- Deeming, J.E. National Fire-Danger Rating System; Rocky Mountain Forest and Range Experiment Station, Forest Service: Fort Collins, CO, USA, 1972; Volume 84. [Google Scholar]
- Wang, X.; Wotton, B.M.; Cantin, A.S.; Parisien, M.A.; Anderson, K.; Moore, B.; Flannigan, M.D. cffdrs: An R package for the Canadian forest fire danger rating system. Ecol. Process. 2017, 6, 5. [Google Scholar] [CrossRef]
- State Grid Corporation of China. Drawing Guidelines for Region Distribution Map of Wildfires Near Overhead Transmission Lines. 2016. Available online: http://www.doc88.com/p-3837473228466.html (accessed on 21 October 2017).
- Costafreda-Aumedes, S.; Comas, C.; Vega-Garcia, C. Human-caused fire occurrence modelling in perspective: A review. Int. J. Wildland Fire 2018, 26, 983–998. [Google Scholar] [CrossRef]
- Rodrigues, M.; Jiménez, A.; de la Riva, J. Analysis of recent spatial–temporal evolution of human driving factors of wildfires in Spain. Nat. Hazards 2016, 84, 2049–2070. [Google Scholar] [CrossRef] [Green Version]
- Albuquerque, M.T.D.; Gerassis, S.; Sierra, C.; Taboada, J.; Martín, J.; Antunes, I.M.H.R.; Gallego, J.R. Developing a new Bayesian Risk Index for risk evaluation of soil contamination. Sci. Total Environ. 2017, 603, 167–177. [Google Scholar] [CrossRef] [PubMed]
- Depicker, A.; De Baets, B.; Baetens, J. Wildfire ignition probability in Belgium. Nat. Hazards Earth Syst. Sci. 2020, 20, 363–376. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Zhou, T.; Wu, C.; Li, B.; Tan, Y.; Zhu, Y. Fault statistics and analysis of 220 kV and above power transmission line in province-level power grid. High Volt. Eng. 2016, 42, 200–207. [Google Scholar]
- Dlamini, W.M. A Bayesian belief network analysis of factors influencing wildfire occurrence in Swaziland. Environ. Model. Softw. 2010, 25, 199–208. [Google Scholar] [CrossRef]
- Archibald, S.; Roy, D.P.; van Wilgen, B.W.; Scholes, R.J. What limits fire? An examination of drivers of burnt area in Southern Africa. Glob. Chang. Biol. 2009, 15, 613–630. [Google Scholar] [CrossRef] [Green Version]
- O’Donnell, A.J.; Boer, M.M.; McCaw, W.L.; Grierson, P.F. Vegetation and landscape connectivity control wildfire intervals in unmanaged semi-arid shrublands and woodlands in Australia. J. Biogeogr. 2011, 38, 112–124. [Google Scholar] [CrossRef]
- Saglam, B.; Bilgili, E.; Dincdurmaz, B.; Kadiogulari, A.I.; Kücük, Ö. Spatio-Temporal Analysis of Forest Fire Risk and Danger Using LANDSAT Imagery. Sensors 2008, 8, 3970–3987. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Liu, Y.; Wu, C.; Zhang, H.; Zhou, T. Study on satellite monitoring and alarm calculation algorithm of wild fire near transmission lines. Proc. Csee 2015, 35, 5511–5519. [Google Scholar]
- Parisien, M.A.; Moritz, M.A. Environmental controls on the distribution of wildfire at multiple spatial scales. Ecol. Monogr. 2009, 79, 127–154. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. The Feature Selection Problem: Traditional Methods and a New Algorithm. In Proceedings of the Tenth National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; pp. 129–134. [Google Scholar]
- Liu, R.; Chen, Y.; Wu, J.; Gao, L.; Barrett, D.; Xu, T.; Li, L.; Huang, C.; Yu, J. Assessing spatial likelihood of flooding hazard using naïve Bayes and GIS: A case study in Bowen Basin, Australia. Stoch. Environ. Res. Risk Assess. 2016, 30, 1575–1590. [Google Scholar] [CrossRef]



| Level | Description |
|---|---|
| 1 | Desert, Swamp, Cultivated plants |
| 2 | Meadow, Grassland, Alpine vegetation |
| 3 | Broad-leaved forest, Shrub |
| 4 | Coniferous forest, theropencedrymion |
| Level | Description |
|---|---|
| 1 | Paddy field, Dry land, Water area, Unused land, Urban-rural fringe, Industrial and mining land, Residential land |
| 2 | Meadow, Grassland, Alpine vegetation |
| 3 | Broad-leaved forest, Shrub |
| 4 | Coniferous forest, Theropencedrymion |
| Factors | Discrete Intervals |
|---|---|
| GDP (10,000 yuan/km2) | (0, 194), (194, 400), (400, 638), (638, ∞) |
| Fuel load(t/km2) | (0, 1), (1, 1.3), (13, 23.3), (23.3, ∞) |
| NDVI | (0, 0.8), (0.8, 0.86), (0.86, 0.90), (0.90, 1] |
| Population density (people/km2) | (0, 91.9), (91.9, 144.7), (144.7, 303.1), (303.1, ∞) |
| Elevation (m) | (0, 145), (145, 295), (295, 575), (575, ∞) |
| Fire-spot density (unit/(100 km2·year)) | (0, 1), (1, 2.4), (2.4, 4.5), (4.5, ∞) |
| Annual precipitation (mm) | (0, 173.1), (173.1, 195.1), (195.1, 209.6), (209.6, ∞) |
| Annual temperature (°C) | (0, 19.9), (19.9, 21.5), (21.5, 22.8), (22.8, ∞) |
| Slope (°) | (0, 3.3), (3.3, 10), (10, 18.3), (18.3, 90] |
| Aspect (°) | North (0°, 45°) ∪ (315°, 360°), East (4 5°, 135°), South (135°, 225°), West (225°, 315°) |
| DS (m) | (0, 356.5), (356.5, 635.7), (635.7, 1041.8), (1041.8, ∞) |
| DR (m) | (0, 832.6), (832.6, 2043.7), (2043.7, 3860.3), (3860.3, ∞) |
| Wildfire-Related Factor | Weight |
|---|---|
| DS | 0.1265 |
| Vegetation Type | 0.1227 |
| DR | 0.1182 |
| Annual precipitation | 0.1043 |
| Fire-spot density | 0.0997 |
| Land-Usage Type | 0.0922 |
| Elevation | 0.0873 |
| NDVI | 0.0789 |
| Aspect | 0.0554 |
| Fuel load | 0.0376 |
| Population density | 0.0297 |
| Annual temperature | 0.0245 |
| Slope | 0.0134 |
| GDP | 0.0096 |
| Samples in Testing Subset | Predicted Results | ||
|---|---|---|---|
| Prone to Fire | Prone to Non-fire | ||
| Actual events | Fire | ||
| Non-fire | |||
| Predicted Results | ||||
|---|---|---|---|---|
| Prone to Fire | Prone to Non-fire | Total | ||
| Actual events | Fire | 4839 | 1161 | 6000 |
| Non-fire | 1641 | 4359 | 6000 | |
| Total | 6480 | 5520 | — | |
| 76.65% | ||||
| 80.65% | ||||
| 74.68% | ||||
| -score | 81.23% | |||
| NBN-Based Map | DG-Based Map | |||
|---|---|---|---|---|
| Fire Proportion | Area Proportion | Fire Proportion | Area Proportion | |
| Low-risk | 8.92% | 19.94% | 0.00% | 0.28% |
| Medium-risk | 9.30% | 16.93% | 22.20% | 26.40% |
| High-risk | 36.43% | 31.46% | 45.35% | 50.32% |
| Very-high-risk | 45.35% | 31.67% | 32.45% | 23.00% |
| R-score | 6.15 | 6.62 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Zhou, Y.; Zhou, E.; Xiang, Z.; Zhou, W.; Lu, J. Wildfire Risk Assessment of Transmission-Line Corridors Based on Naïve Bayes Network and Remote Sensing Data. Sensors 2021, 21, 634. https://doi.org/10.3390/s21020634
Chen W, Zhou Y, Zhou E, Xiang Z, Zhou W, Lu J. Wildfire Risk Assessment of Transmission-Line Corridors Based on Naïve Bayes Network and Remote Sensing Data. Sensors. 2021; 21(2):634. https://doi.org/10.3390/s21020634
Chicago/Turabian StyleChen, Weijie, You Zhou, Enze Zhou, Zhun Xiang, Wentao Zhou, and Junhan Lu. 2021. "Wildfire Risk Assessment of Transmission-Line Corridors Based on Naïve Bayes Network and Remote Sensing Data" Sensors 21, no. 2: 634. https://doi.org/10.3390/s21020634
APA StyleChen, W., Zhou, Y., Zhou, E., Xiang, Z., Zhou, W., & Lu, J. (2021). Wildfire Risk Assessment of Transmission-Line Corridors Based on Naïve Bayes Network and Remote Sensing Data. Sensors, 21(2), 634. https://doi.org/10.3390/s21020634




