Experimentally Verified Analytical Models of Piezoelectric Cantilevers in Different Design Configurations
Abstract
:1. Introduction
2. Model of Piezoelectric Vibration Energy Harvester
2.1. Bimorph Cantilever Beam with Piezoelectric Layers in Series
2.1.1. Effect of Chosen Mode Shape Function on Model Output
2.1.2. Single DOF Model of Bimorph Configuration
2.2. Modification of Single DOF Model for Unimorph Configuration
3. Verification of Analytical Model Based on Experimental Results
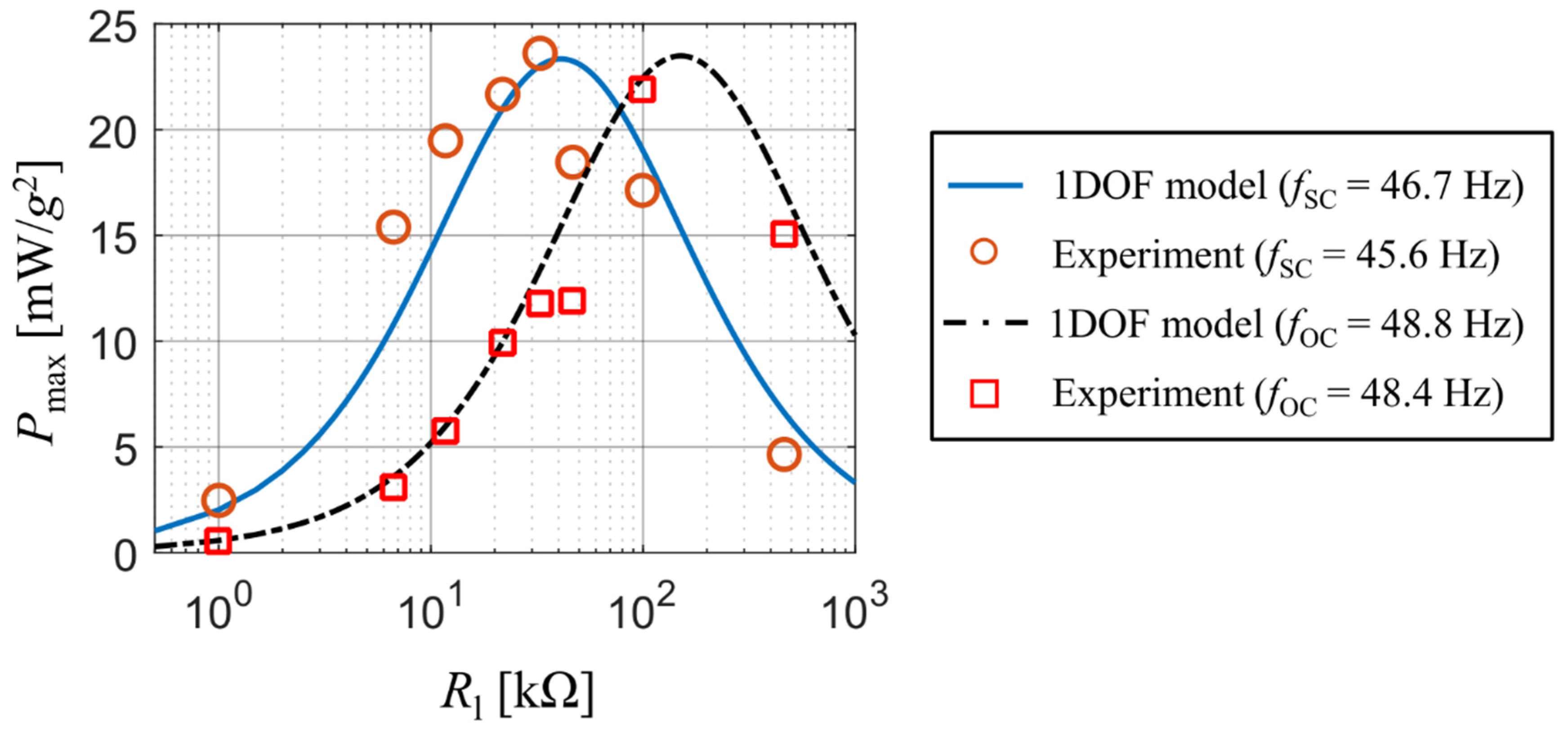
3.1. PZT-5A Bimorph with a Full Electrode Length and a Linear Response
3.2. PZNN-PLZT Bimorph with Partial Electrode Length and Weak Non-Linear Response
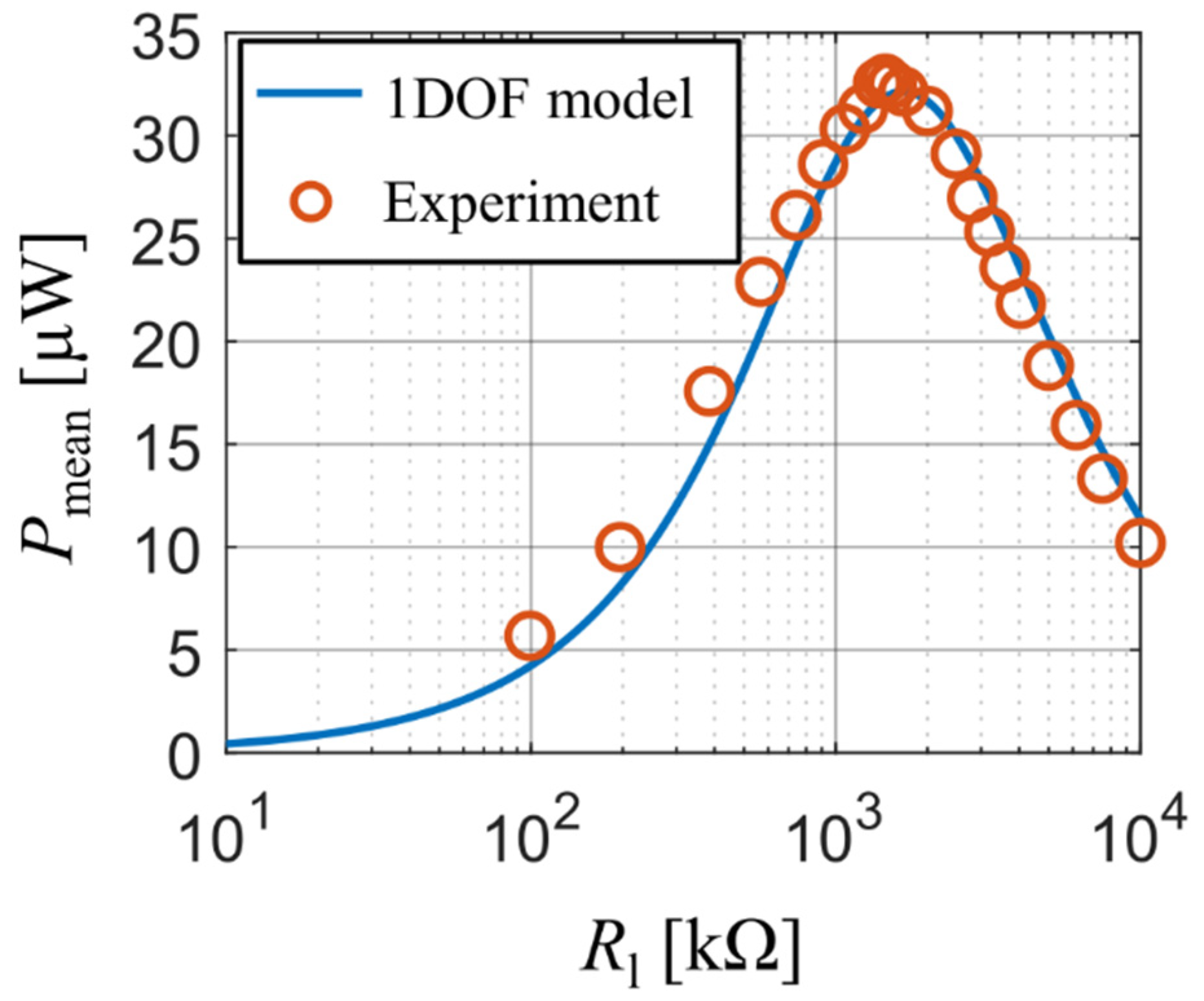
3.3. PVDF Unimorph with a Partial Electrode Length and a Linear Response
3.4. Single DOF Model Parameters of Considered Harvesters
4. Comparison of Piezoelectric Materials for Kinetic Energy Harvesting Purposes
4.1. Harmonic Vibrations Case
4.2. Random Vibrations Case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.; Rao, G.K.; Holmes, A.S.; Green, T. Energy Harvesting From Human and Machine Motion for Wireless Electronic Devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef] [Green Version]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1142. [Google Scholar] [CrossRef] [Green Version]
- Hadas, Z.; Smilek, J.; Rubes, O. Analyses of electromagnetic and piezoelectric systems for efficient vibration energy harvesting. In Smart Sensors, Actuators, and MEMS VIII; Fonseca, L., Prunnila, M., Peiner, E., Eds.; SPIE MICROTECHNOLOGIES: Barcelona, Spain, 2017. [Google Scholar]
- Gljušćić, P.; Zelenika, S.; Blažević, D.; Kamenar, E. Kinetic energy harvesting for wearable medical sensors. Sensors 2019, 19, 4922. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Tofel, P.; Hadas, Z.; Smilek, J.; Lošák, P.; Skarvada, P.; Macku, R. Investigation of a cantilever structured piezoelectric energy harvester used for wearable devices with random vibration input. Mech. Syst. Signal Process. 2018, 106, 303–318. [Google Scholar] [CrossRef] [Green Version]
- Paulo, J.; Gaspar, P.D. Review and future trend of energy harvesting methods for portable medical devices. In WCE 2010—World Congress on Engineering 2010; Ao, S.I., Gelman, L., Hukins, D., Eds.; IAENG Society of Electrical Engineering: London, UK, 2010. [Google Scholar]
- Zelenika, S.; Hadas, Z.; Bader, S.; Becker, T.; Gljušćić, P.; Hlinka, J.; Janak, L.; Kamenar, E.; Ksica, F.; Kyratsi, T.; et al. Energy Harvesting Technologies for Structural Health Monitoring of Airplane Components—A Review. Sensors 2020, 20, 6685. [Google Scholar] [CrossRef] [PubMed]
- Duarte, F.; Ferreira, A. Energy harvesting on railway tracks: State-of-the-art. Proc. Inst. Civ. Eng. Transp. 2017, 170, 123–130. [Google Scholar] [CrossRef]
- Cahill, P.; Hanley, C.; Jaksic, V.; Mathewson, A.; Pakrashi, V. Energy harvesting for monitoring bridges over their operational life. In Proceedings of the 8th European Workshop on Structural Health Monitoring, EWSHM 2016, Bilbao, Spain, 5–8 July 2016; Volume 4, pp. 1–11. [Google Scholar]
- Bowen, C.R.; Kim, H.A.; Weaver, P.M.; Dunn, S. Piezoelectric and ferroelectric materials and structures for energy harvesting applications. Energy Environ. Sci. 2014, 7, 25–44. [Google Scholar] [CrossRef] [Green Version]
- Panda, P.K.; Sahoo, B. PZT to lead free piezo ceramics: A review. Ferroelectrics 2015, 474, 128–143. [Google Scholar] [CrossRef]
- Bai, Y.; Tofel, P.; Palosaari, J.; Jantunen, H.; Juuti, J. A Game Changer: A Multifunctional Perovskite Exhibiting Giant Ferroelectricity and Narrow Bandgap with Potential Application in a Truly Monolithic Multienergy Harvester or Sensor. Adv. Mater. 2017, 29, 1700767. [Google Scholar] [CrossRef] [PubMed]
- Tofel, P.; Machu, Z.; Chlup, Z.; Hadraba, H.; Drdlik, D.; Sevecek, O.; Majer, Z.; Holcman, V.; Hadas, Z. Novel layered architecture based on Al2O3/ZrO2/BaTiO3 for SMART piezoceramic electromechanical converters. Eur. Phys. J. Spec. Top. 2019, 228, 1575–1588. [Google Scholar] [CrossRef]
- Pozzi, M.; Canziani, A.; Durazo-Cardenas, I.; Zhu, M. Experimental characterisation of macro fibre composites and monolithic piezoelectric transducers for strain energy harvesting. In Smart Structures (NDE); Kundu, T., Ed.; SPIE: Bellingham, DC, USA, 2012. [Google Scholar]
- Sappati, K.K.; Bhadra, S. Piezoelectric polymer and paper substrates: A review. Sensors 2018, 18, 3605. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, J.; Zhao, G.; Li, B.; Wang, J. Design optimization of PVDF-based piezoelectric energy harvesters. Heliyon 2017, 3, e00377. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Dugundji, J.; Wardle, B.L. Efficiency of piezoelectric mechanical vibration energy harvesting. Smart Mater. Struct. 2015, 24, 055006. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Issues in mathematical modeling of piezoelectric energy harvesters. Smart Mater. Struct. Smart Mater. Struct 2008, 17, 065016. [Google Scholar] [CrossRef] [Green Version]
- Liao, Y.; Liang, J. Maximum power, optimal load, and impedance analysis of piezoelectric vibration energy harvesters. Smart Mater. Struct. 2018, 27, 075053. [Google Scholar] [CrossRef]
- Li, X.; Upadrashta, D.; Yu, K.; Yang, Y. Sandwich piezoelectric energy harvester: Analytical modeling and experimental validation. Energy Convers. Manag. 2018, 176, 69–85. [Google Scholar] [CrossRef]
- Mendonca, L.S.; Martins, L.T.; Radecker, M.; Bisogno, F.; Killat, D. Normalized Modeling of Piezoelectric Energy Harvester Based on Equivalence Transformation and Unit-Less Parameters. J. Microelectromech. Syst. 2019, 28, 666–677. [Google Scholar] [CrossRef]
- Machů, Z.; Ševeček, O.; Hadas, Z.; Kotoul, M. Modeling of electromechanical response and fracture resistance of multilayer piezoelectric energy harvester with residual stresses. J. Intell. Mater. Syst. Struct. 2020, 31, 2261–2287. [Google Scholar] [CrossRef]
- Meitzler, A. 176-1987 IEEE Standard on Piezoelectricity; IEEE: New York, NY, USA, 1988. [Google Scholar]
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics Extended, 9th ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Flores-Domínguez, M. Modeling of the Bending Stiffness of a Bimaterial Beam by the Approximation of One-Dimensional of Laminated Theory. J. Eng. Res. Appl. 2014, 4, 492–497. [Google Scholar]
- Zhao, J.; You, Z. Models for 31-Mode PVDF Energy Harvester for Wearable Applications. Sci. World J. 2014, 2014, 893496. [Google Scholar] [CrossRef] [PubMed]
- Hadas, Z.; Rubes, O.; Tofel, P.; Machu, Z.; Riha, D.; Sevecek, O.; Kastyl, J.; Sobola, D.; Castkova, K. Piezoelectric PVDF Elements and Systems for Mechanical Engineering Applications. In Proceedings of the 2020 19th International Conference on Mechatronics—Mechatronika (ME), Prague, Czech Republic, 2–4 December 2020. [Google Scholar]
- Rubes, O.; Machu, Z.; Sevecek, O.; Hadas, Z. Crack Protective Layered Architecture of Lead-Free Piezoelectric Energy Harvester in Bistable Configuration. Sensors 2020, 20, 5808. [Google Scholar] [CrossRef]
- Rubes, O.; Hadas, Z. Design and Simulation of Bistable Piezoceramic Cantilever for Energy Harvesting from Slow Swinging Movement. In Proceedings of the 2018 IEEE 18th International Conference on Power Electronics and Motion Control, PEMC 2018, Budapest, Hungary, 26–30 August 2018. [Google Scholar]
- Rubes, O.; Brablc, M.; Hadas, Z. Nonlinear vibration energy harvester: Design and oscillating stability analyses. Mech. Syst. Signal Process. 2019, 125, 170–184. [Google Scholar] [CrossRef]
- Fitzgerald, P.C.; Malekjafarian, A.; Bhowmik, B.; Prendergast, L.J.; Cahill, P.; Kim, C.-W.; Hazra, B.; Pakrashi, V.; Obrien, E.J. Scour Damage Detection and Structural Health Monitoring of a Laboratory-Scaled Bridge Using a Vibration Energy Harvesting Device. Sensors 2019, 19, 2572. [Google Scholar] [CrossRef] [Green Version]
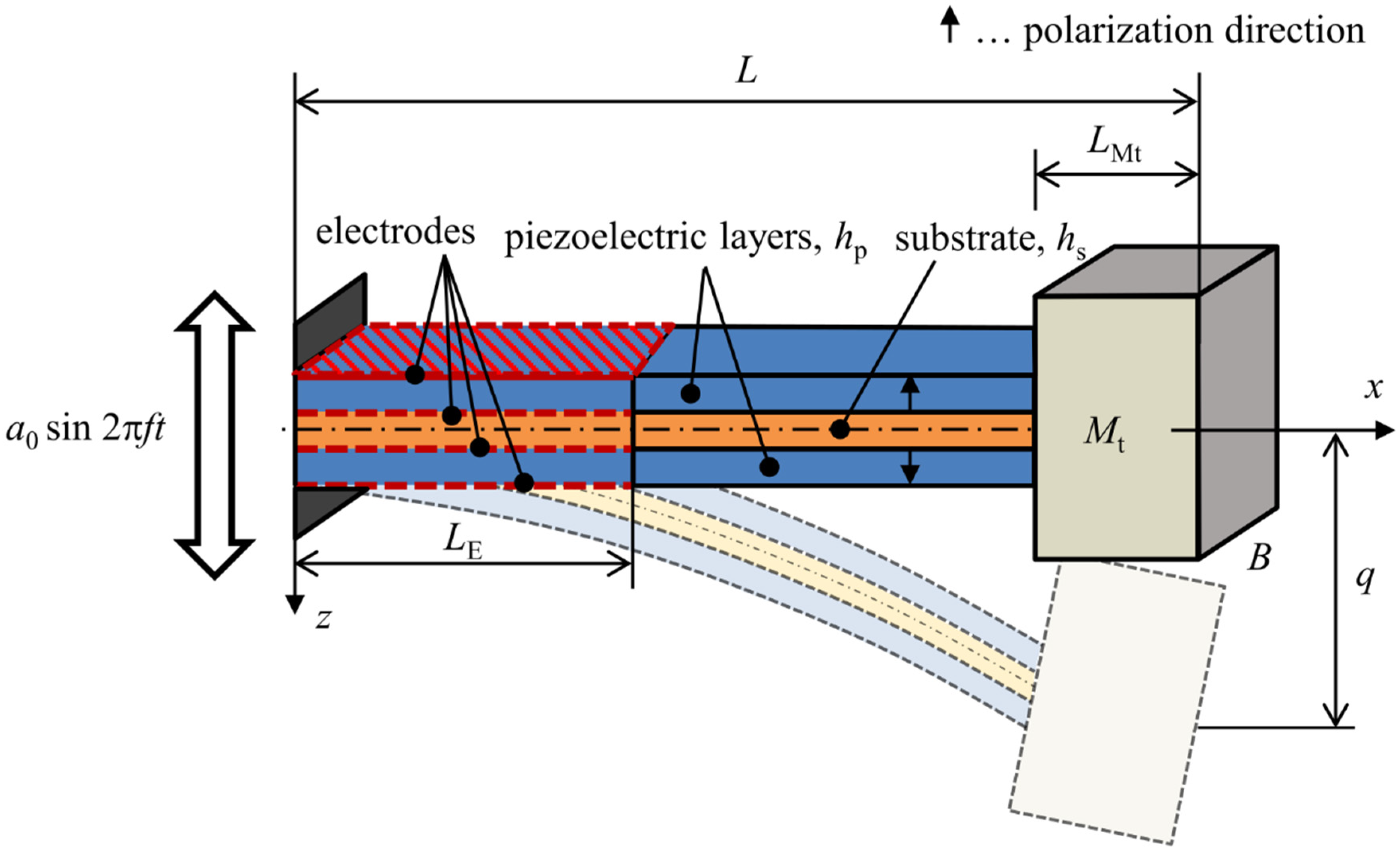








| Harvester Type (Configuration) | L [mm] | B [mm] | |||||
|---|---|---|---|---|---|---|---|
| PZT-5A (bimorph) | 50.8 | 50.8 | – | 31.8 | 0.14 | 0.26 | 12 |
| PZZN-PLZT (bimorph) | 40 | 25 | 15 | 10 | 0.1 | 0.2 | 10 |
| PVDF (unimorph) | 71.9 | 49.2 | 4 | 10 | 0.3 | 0.13 | 2.6 |
| Harvester Type (Configuration) | Material | Ρ [kg/m3] | Y [GPa] | ||
|---|---|---|---|---|---|
| PZT-5A (bimorph) | PZT-5A | 7800 | 66 | –190 × 10–12 | 1500 |
| Brass shim | 9000 | 105 | – | – | |
| PZZN-PLZT (bimorph) | PZNN-PLZT | 7800 | 62.5 | –195 × 10–12 | 1850 |
| Steel shim | 7850 | 210 | – | – | |
| PVDF (unimorph) | PVDF | 1760 | 2 | –19 × 10–12 | 12 |
| Steel shim | 7850 | 210 | – | – |
| Harvester Type | Meff [g] | Beff [Ns/m] | Keff [N/m] | Feff [N/g] | θeff [N/V] | Ceq [F] |
|---|---|---|---|---|---|---|
| PZT-5A | 14.1 | 2.24 × 10–1 | 1218.10 | 1.51 × 10–1 | 2.20 × 10–3 | 4.12 × 10–8 |
| PZZN-PLZT | 6.10 | 5.13 × 10–2 | 164.56 | 7.90 × 10–2 | 6.03 × 10–5 | 3.65 × 10–9 |
| PVDF | 2.90 | 4.40 × 10–3 | 40.38 | 3.27 × 10–2 | 1.21 × 10–6 | 3.08 × 10–10 |
| Harvester Type (Configuration) | L [mm] | [mm] | [mm] | B [mm] | [mm] | [mm] | [g] |
| PZT-5A (bimorph) | 68.8 | 40 | 5 | 10 | 0.15 | 0.26 | 3.67 |
| PZZN-PLZT (bimorph) | 54.3 | 40 | 5 | 10 | 0.15 | 0.26 | 3.99 |
| PVDF (unimorph) | 71.9 | 40 | 5 | 40 | 0.3 | 0.13 | 2.60 |
| Harvester Type (Configuration) | [g] | [Ns/m] | [N/m] | [Hz] | [N/1g] | [N/V] | [F] |
| PZT-5A (bimorph) | 4.21 | 4.45 × 10–2 | 161.25 | 31.13 | 5.02 × 10–2 | 5.14 × 10–4 | 1.02 × 10–8 |
| PZZN-PLZT (bimorph) | 4.21 | 4.20 × 10–2 | 161.05 | 31.13 | 4.75 × 10–2 | 6.36 × 10–5 | 4.50 × 10–9 |
| PVDF (unimorph) | 4.21 | 1.07 × 10–2 | 161.25 | 31.13 | 5.40 × 10–2 | 5.54 × 10–6 | 1.30 × 10–9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machu, Z.; Rubes, O.; Sevecek, O.; Hadas, Z. Experimentally Verified Analytical Models of Piezoelectric Cantilevers in Different Design Configurations. Sensors 2021, 21, 6759. https://doi.org/10.3390/s21206759
Machu Z, Rubes O, Sevecek O, Hadas Z. Experimentally Verified Analytical Models of Piezoelectric Cantilevers in Different Design Configurations. Sensors. 2021; 21(20):6759. https://doi.org/10.3390/s21206759
Chicago/Turabian StyleMachu, Zdenek, Ondrej Rubes, Oldrich Sevecek, and Zdenek Hadas. 2021. "Experimentally Verified Analytical Models of Piezoelectric Cantilevers in Different Design Configurations" Sensors 21, no. 20: 6759. https://doi.org/10.3390/s21206759
APA StyleMachu, Z., Rubes, O., Sevecek, O., & Hadas, Z. (2021). Experimentally Verified Analytical Models of Piezoelectric Cantilevers in Different Design Configurations. Sensors, 21(20), 6759. https://doi.org/10.3390/s21206759








