Conical Statistical Optimal Near-Field Acoustic Holography with Combined Regularization
Abstract
:1. Introduction
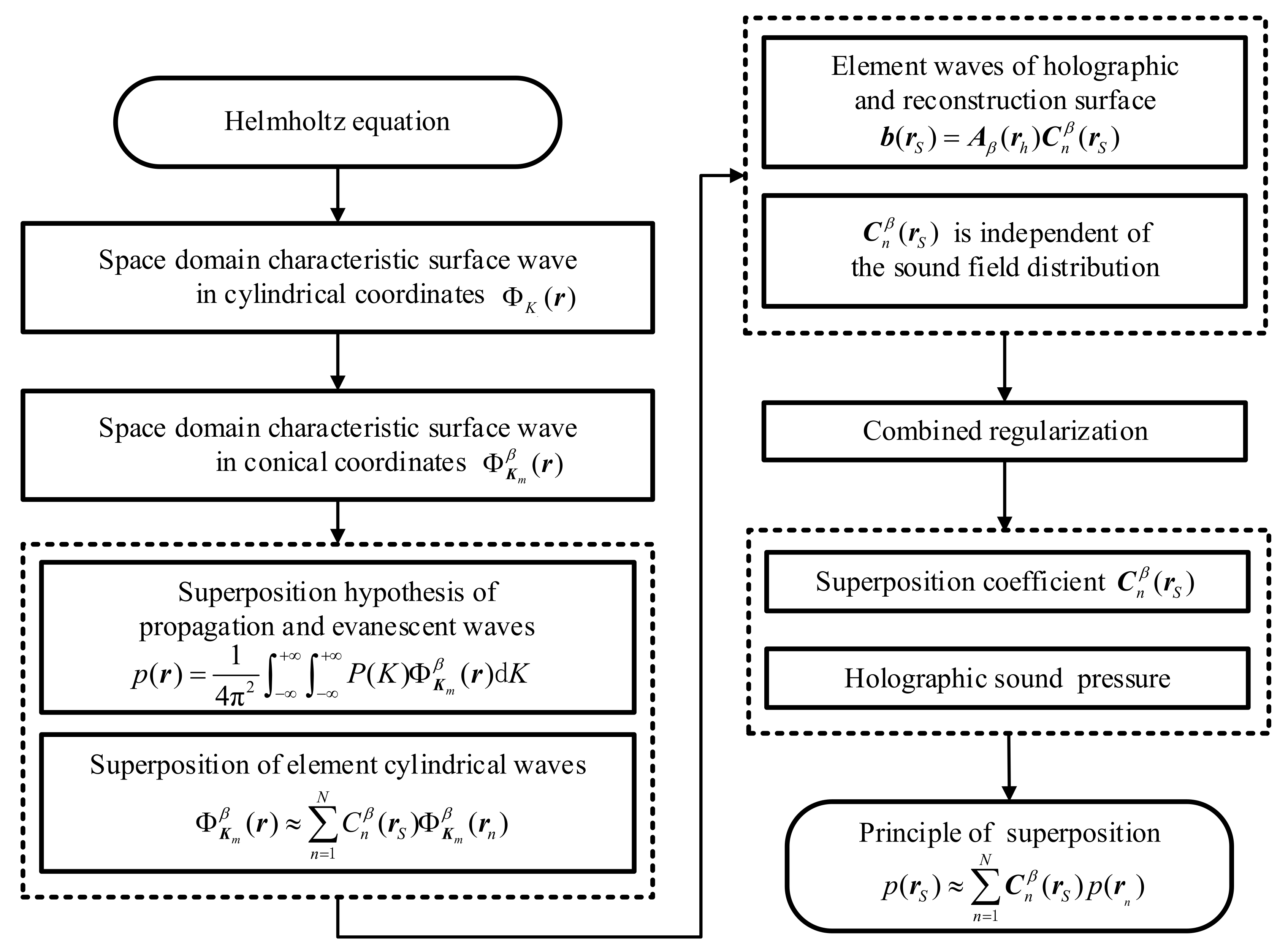
2. Theories of Conical SONAH
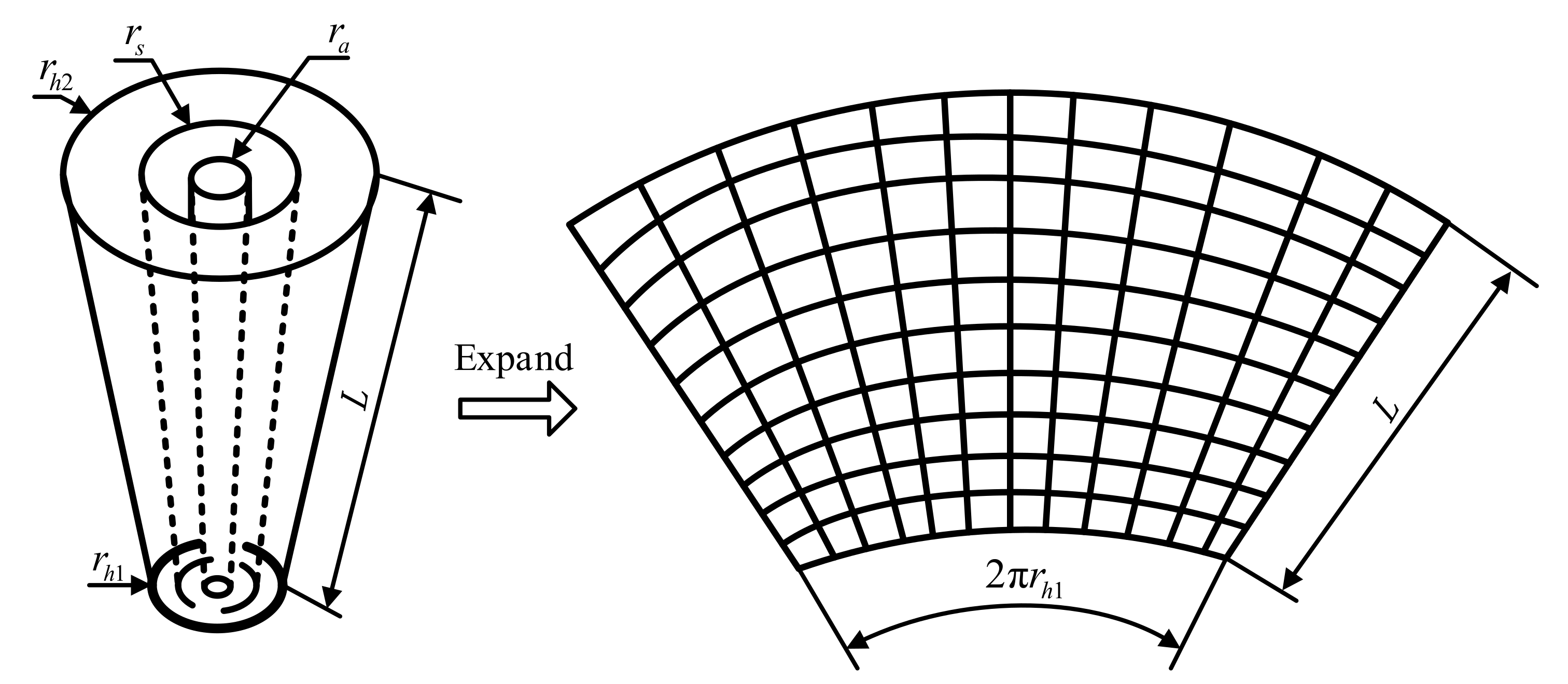
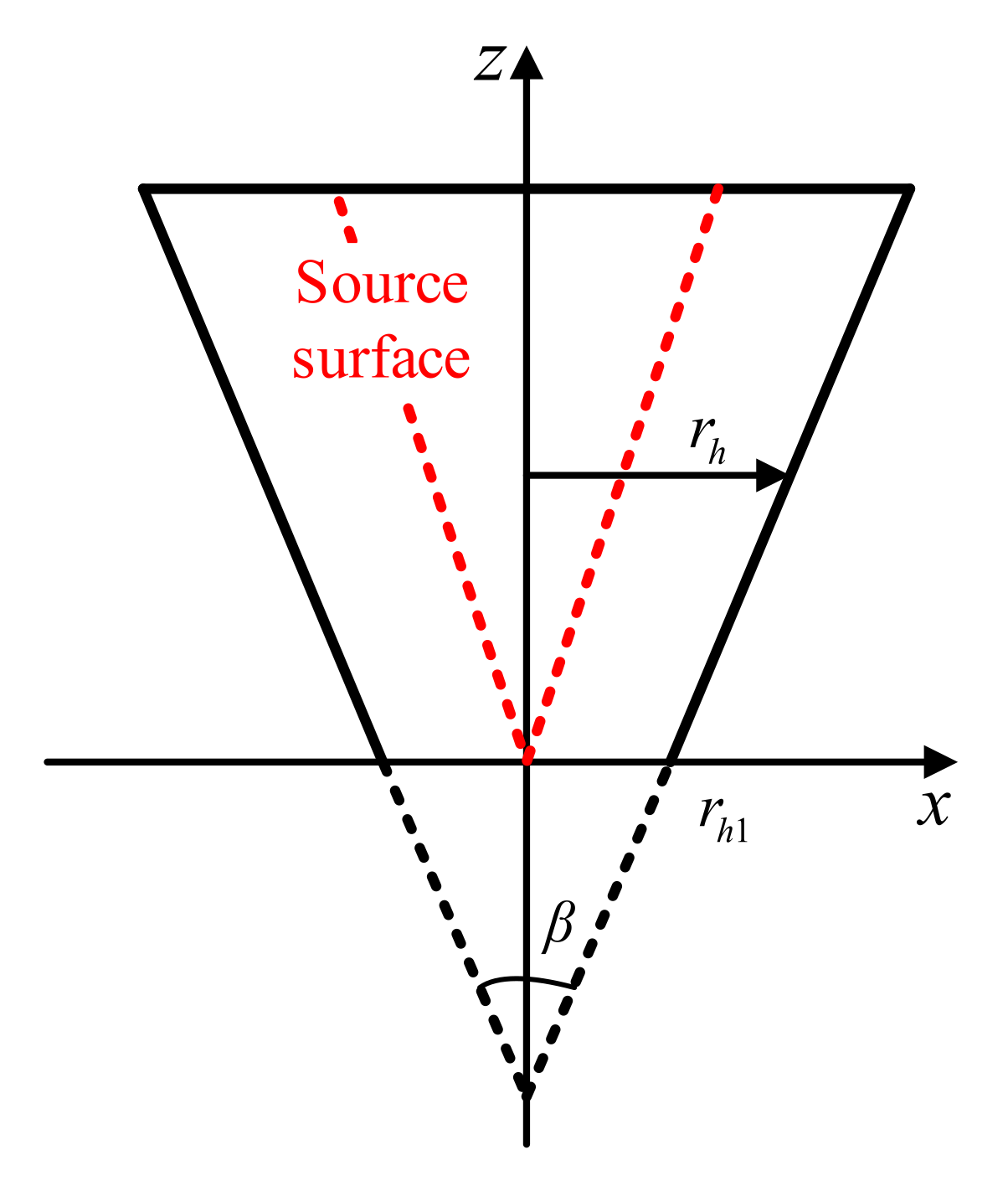
2.1. Implementation Process of Conical SONAH
2.2. Theories of the Combined Regularization Method
2.2.1. Truncated Singular Value Decomposition (TSVD)
2.2.2. Tikhonov Regularization
2.2.3. Combined Regularization Method
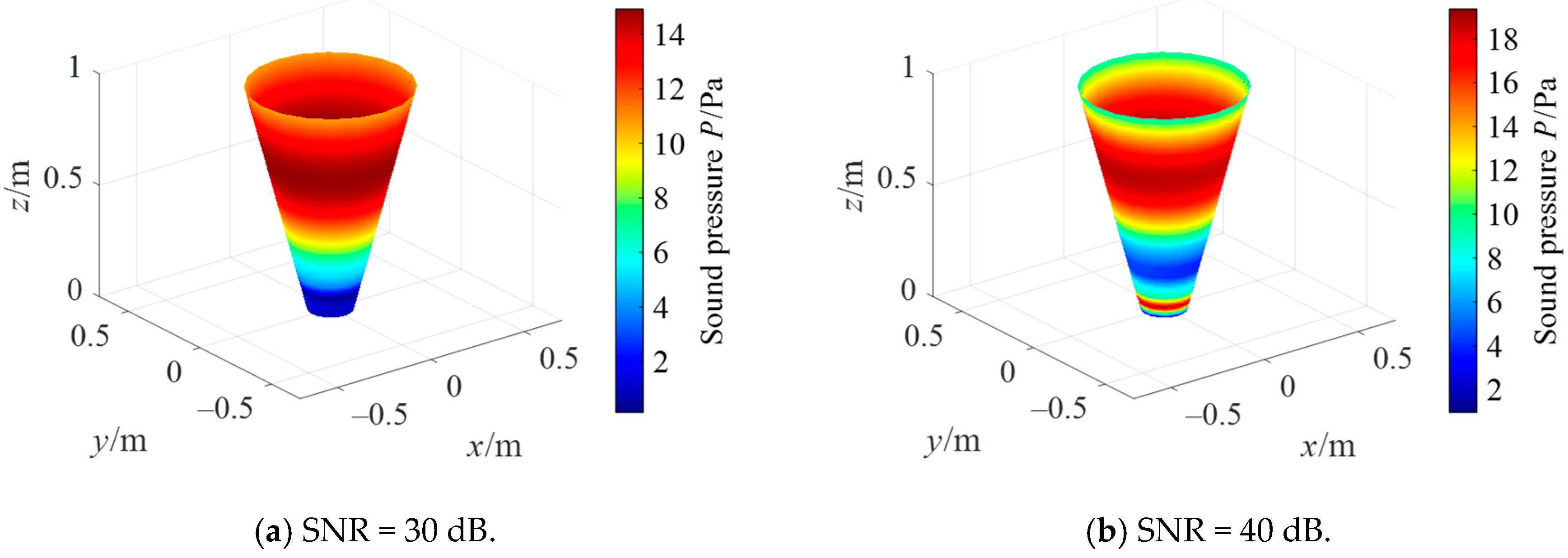
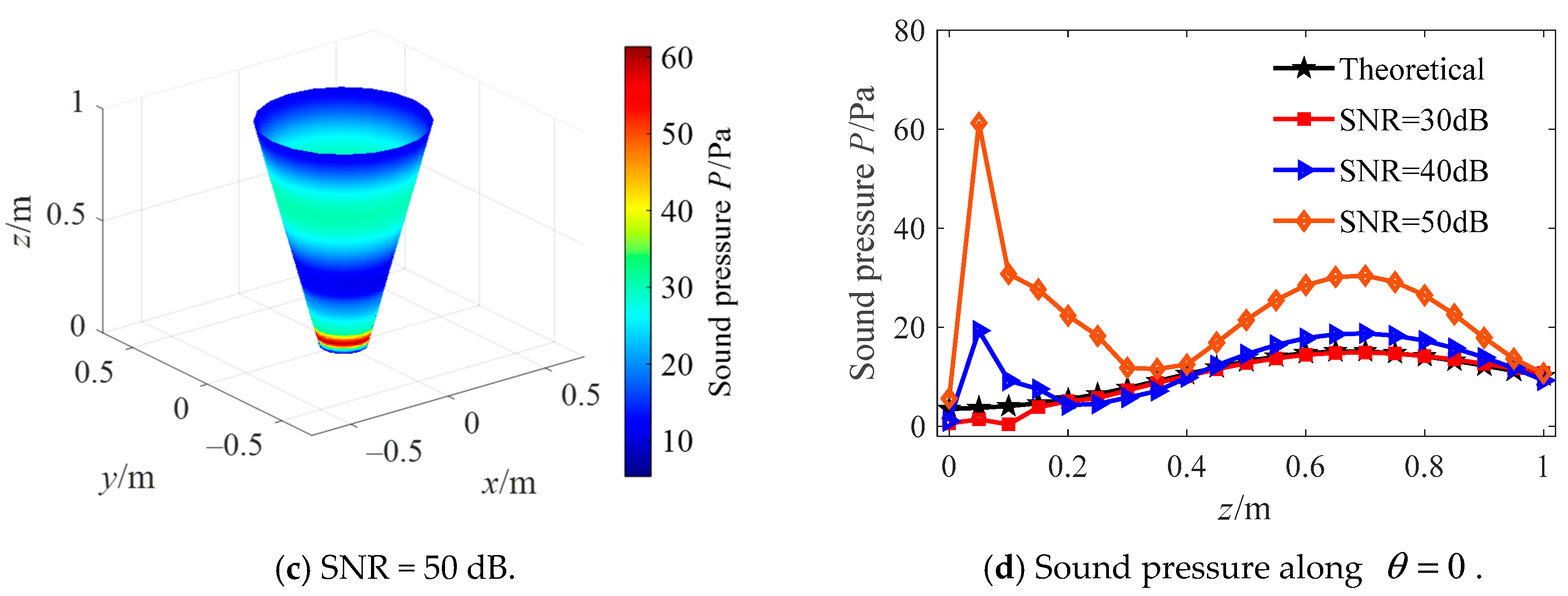
3. Numerical Case Studies
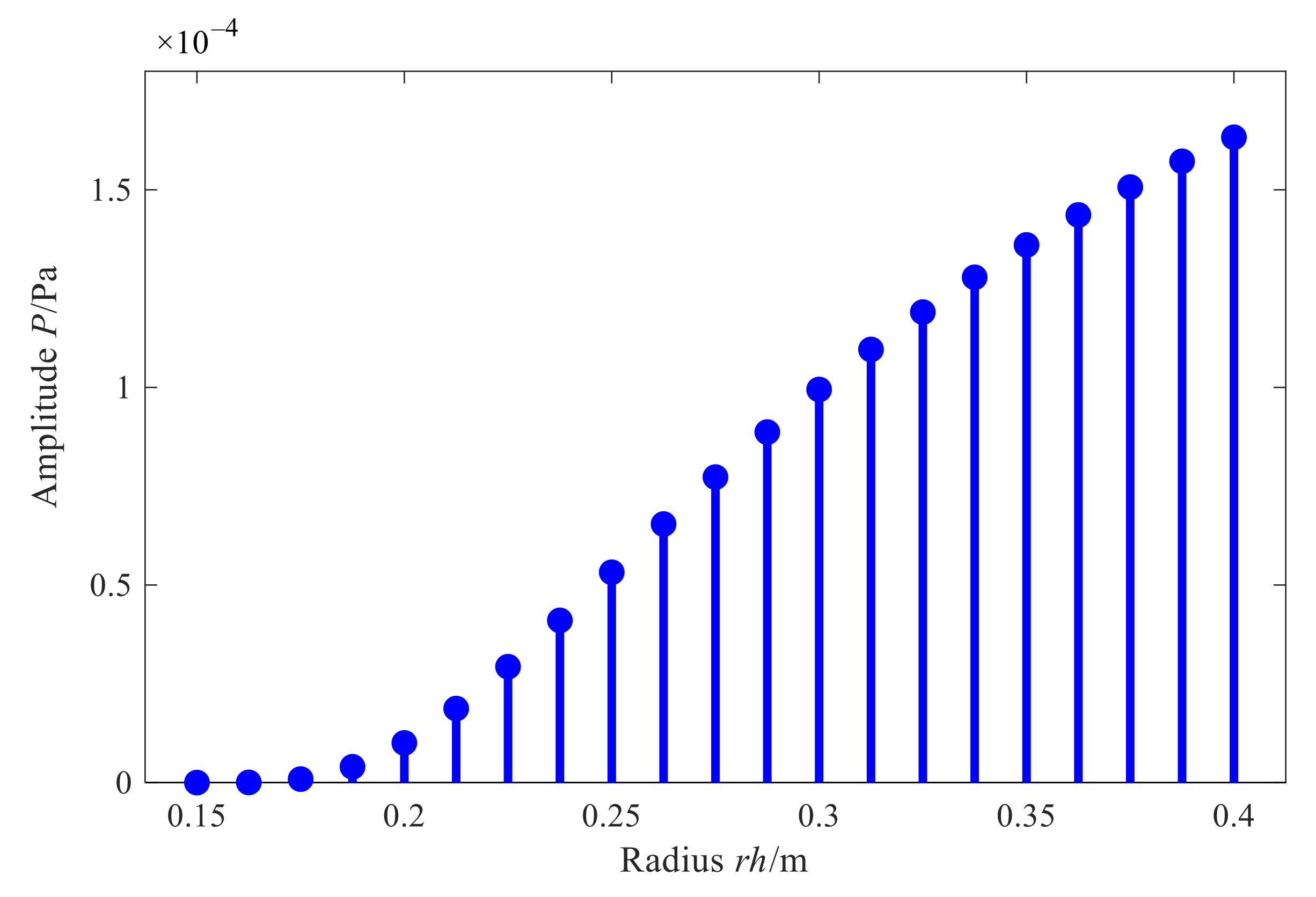
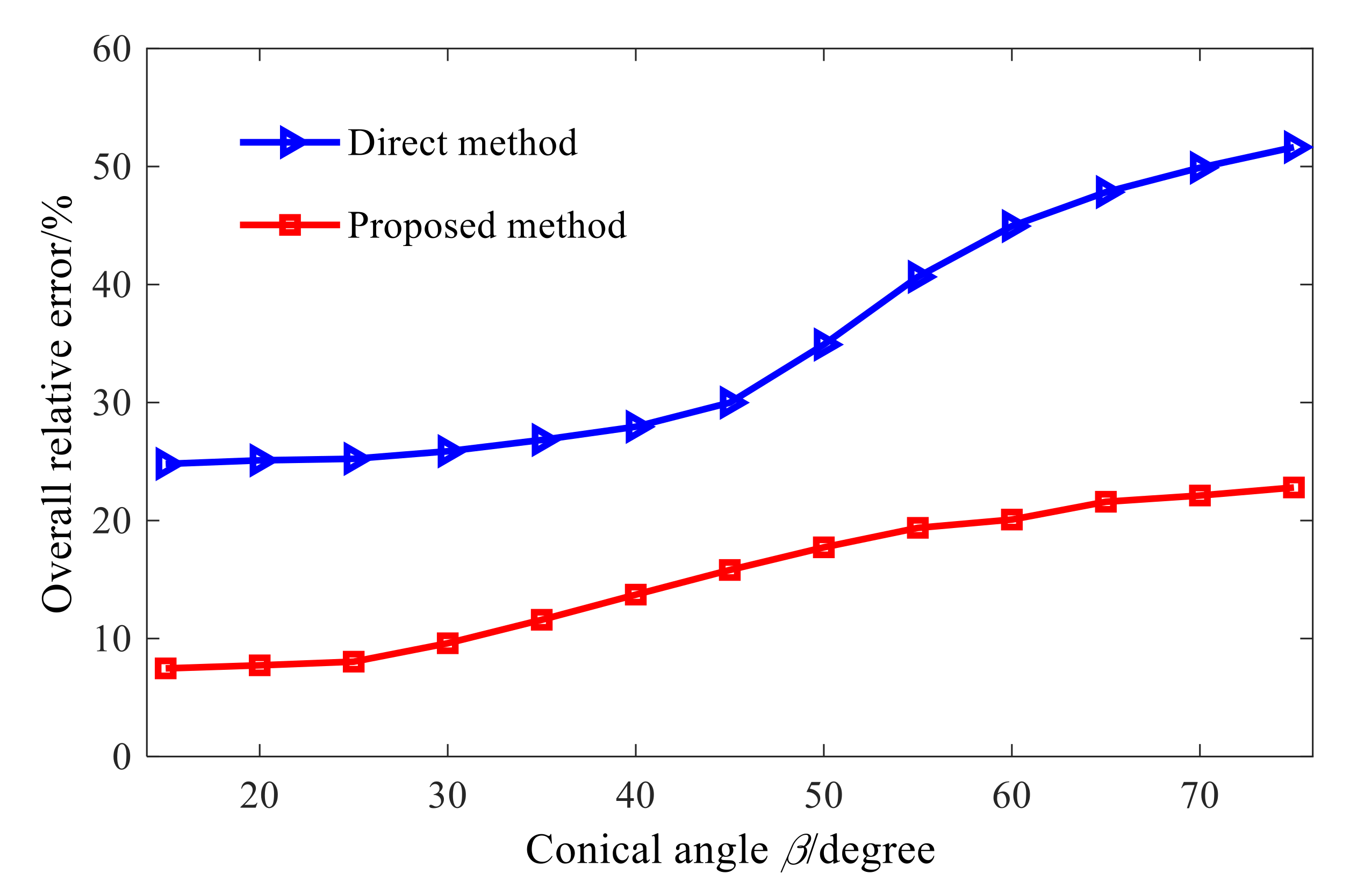
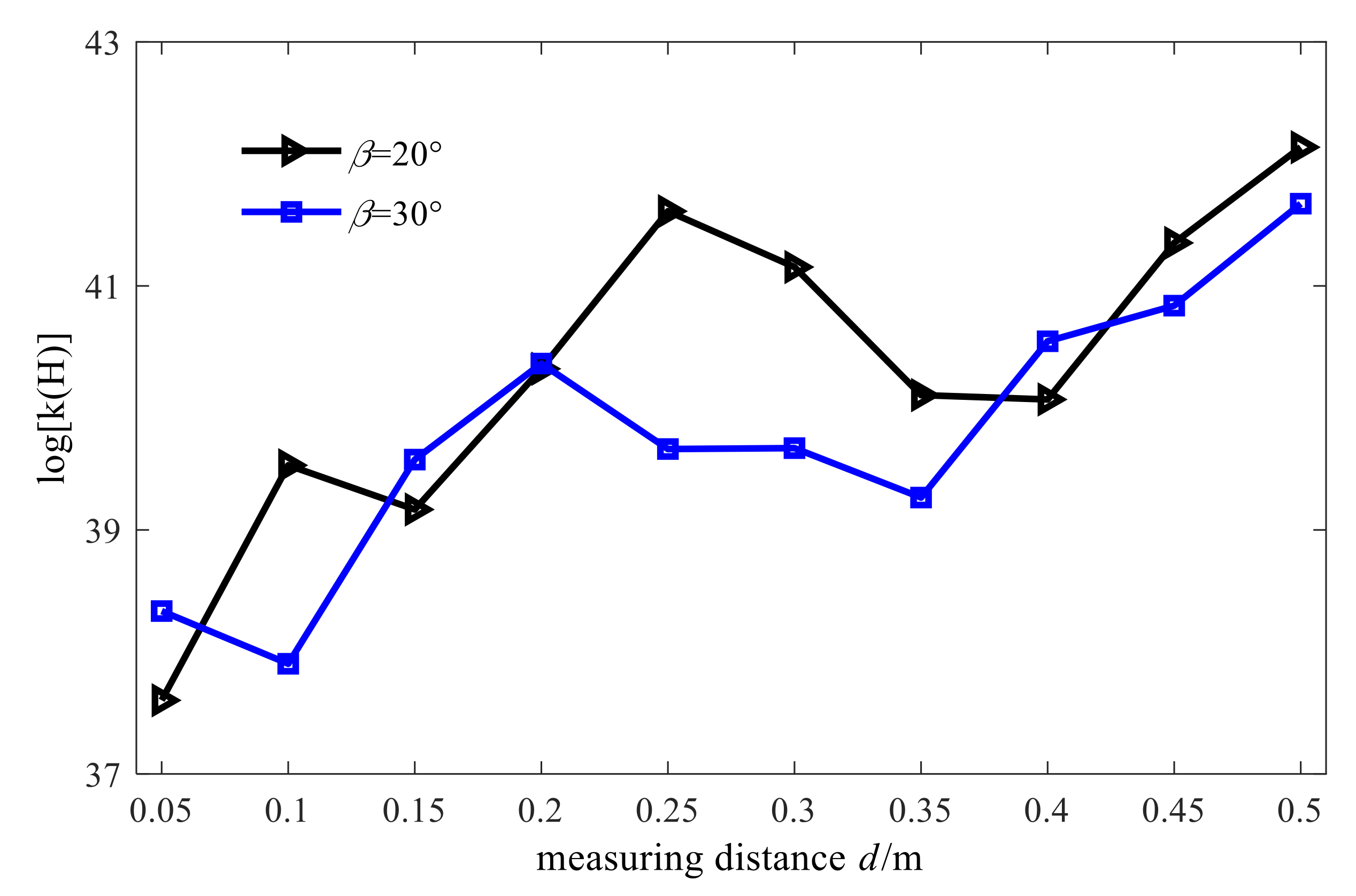
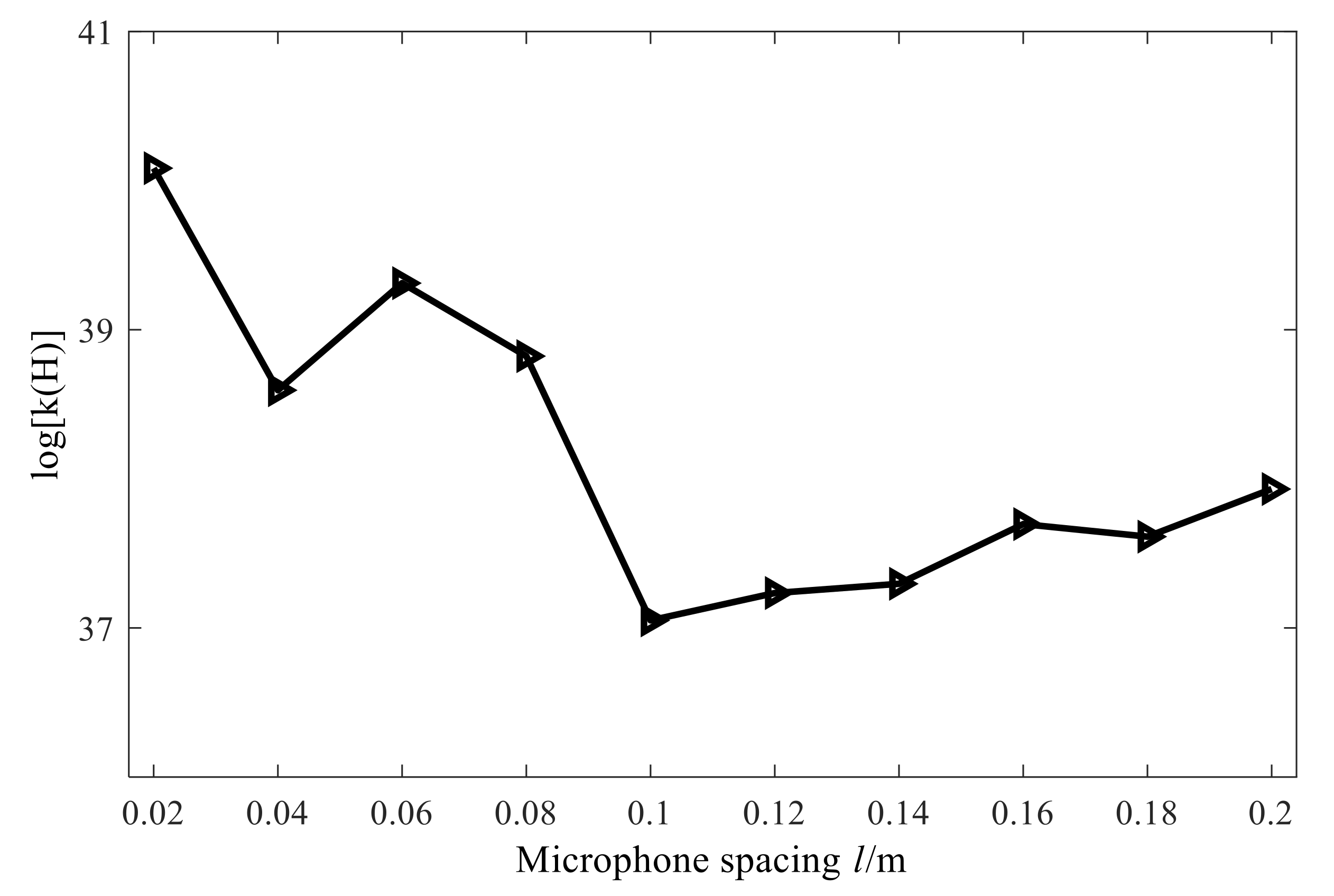
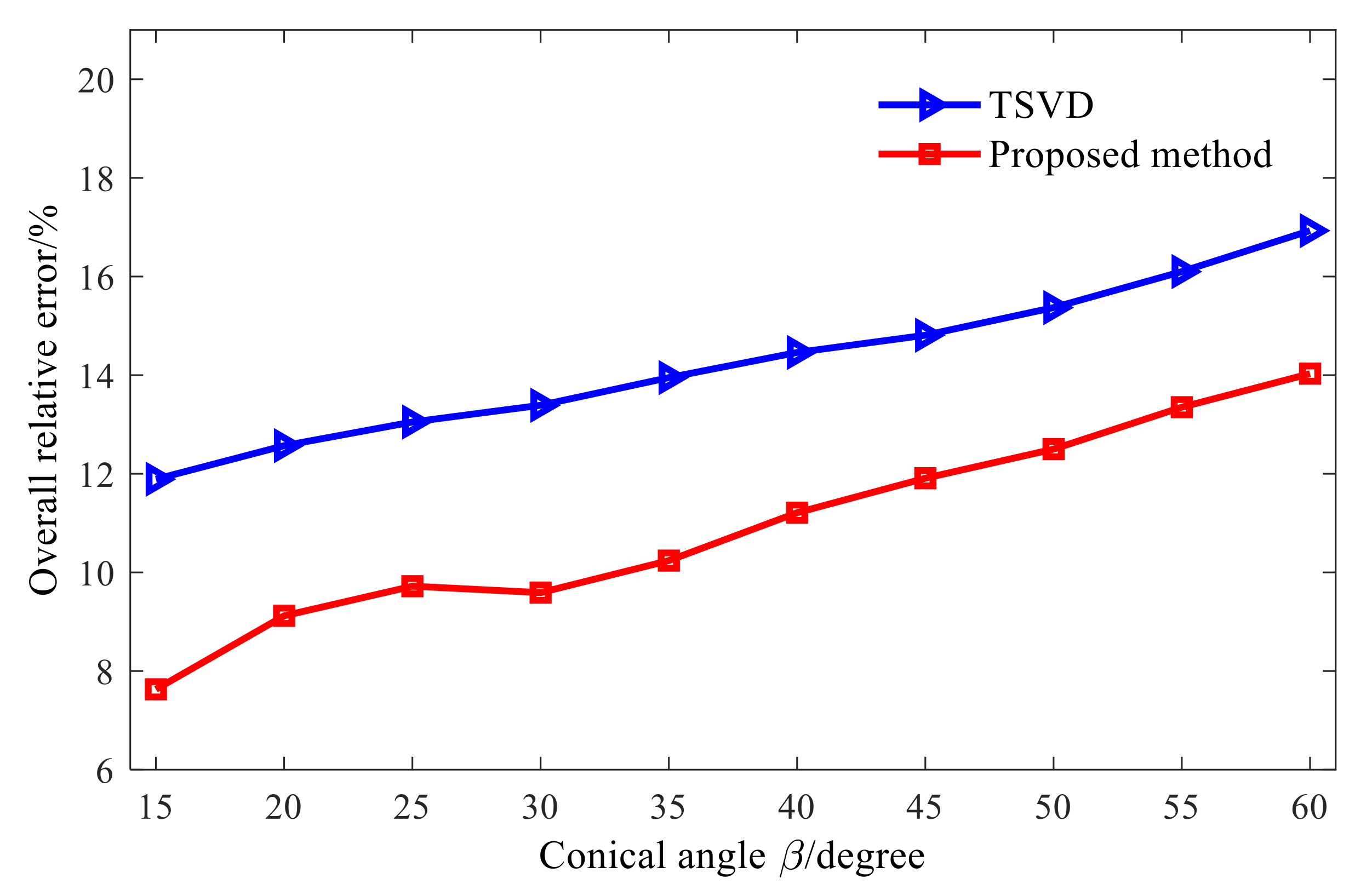
3.1. Quantitative Study on the Influence of Cone Angle
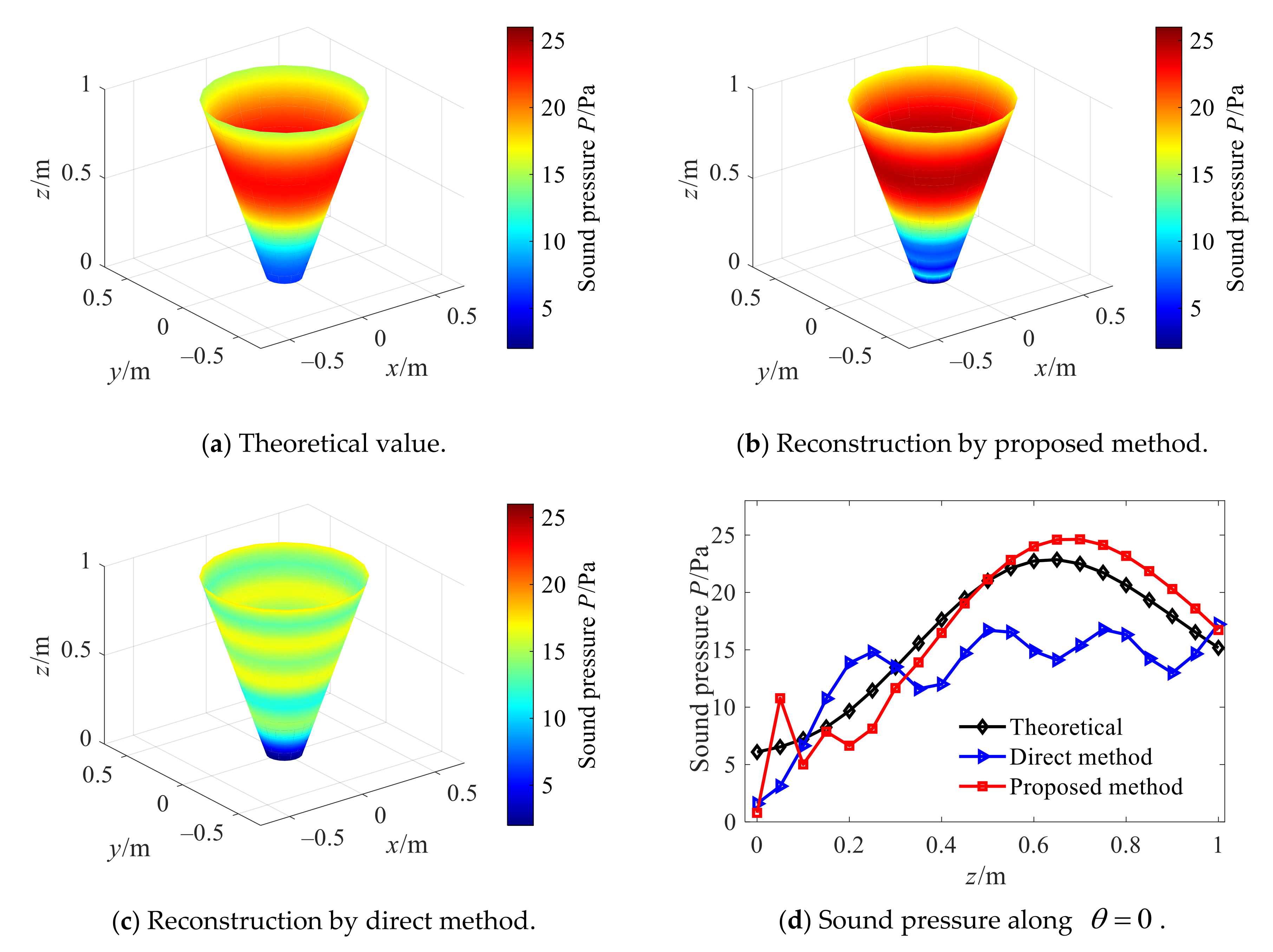
3.2. Comparative Study of Conical and Cylindrical SONAH
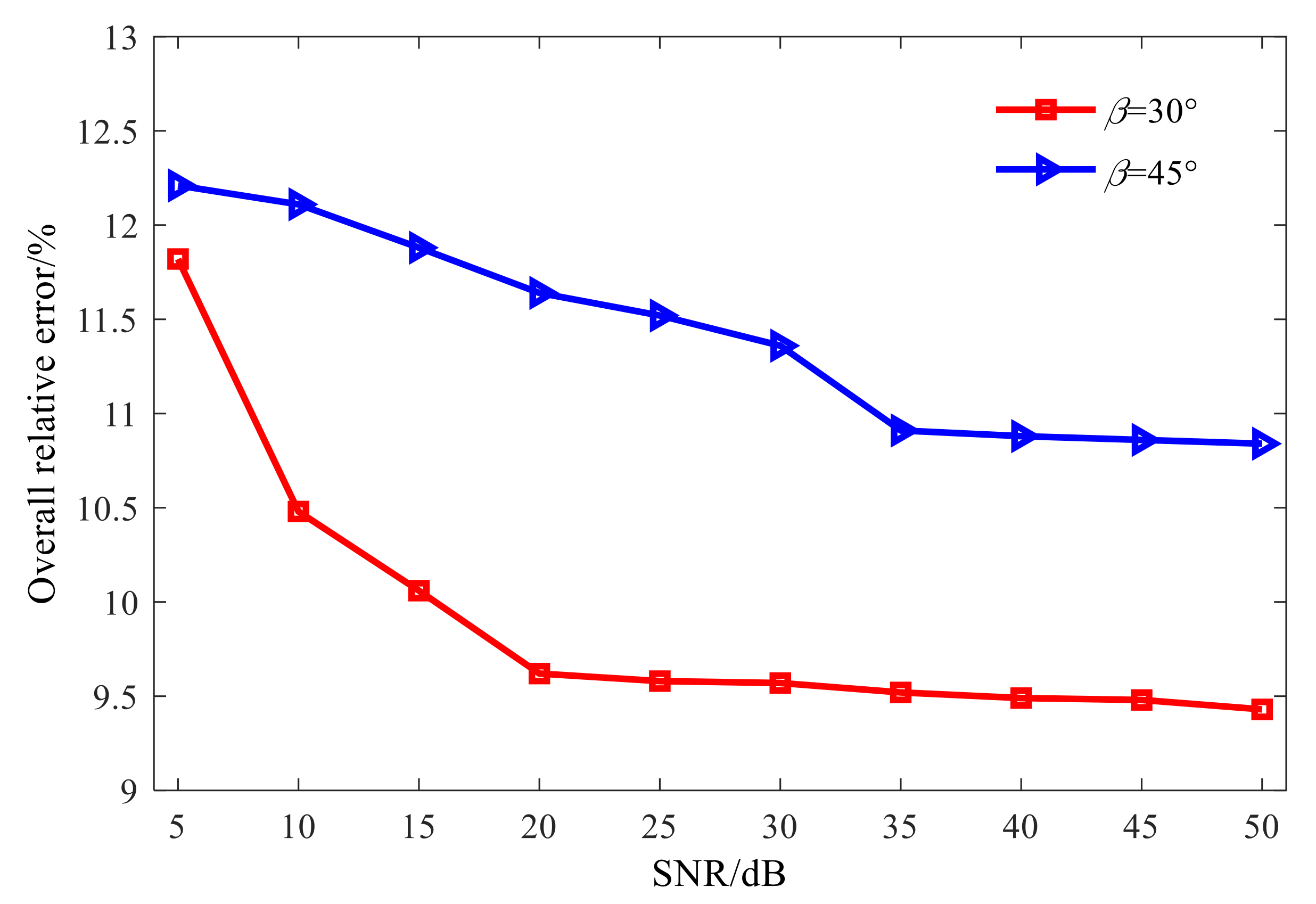
3.3. Quantitative Study of Combined Regularization Method
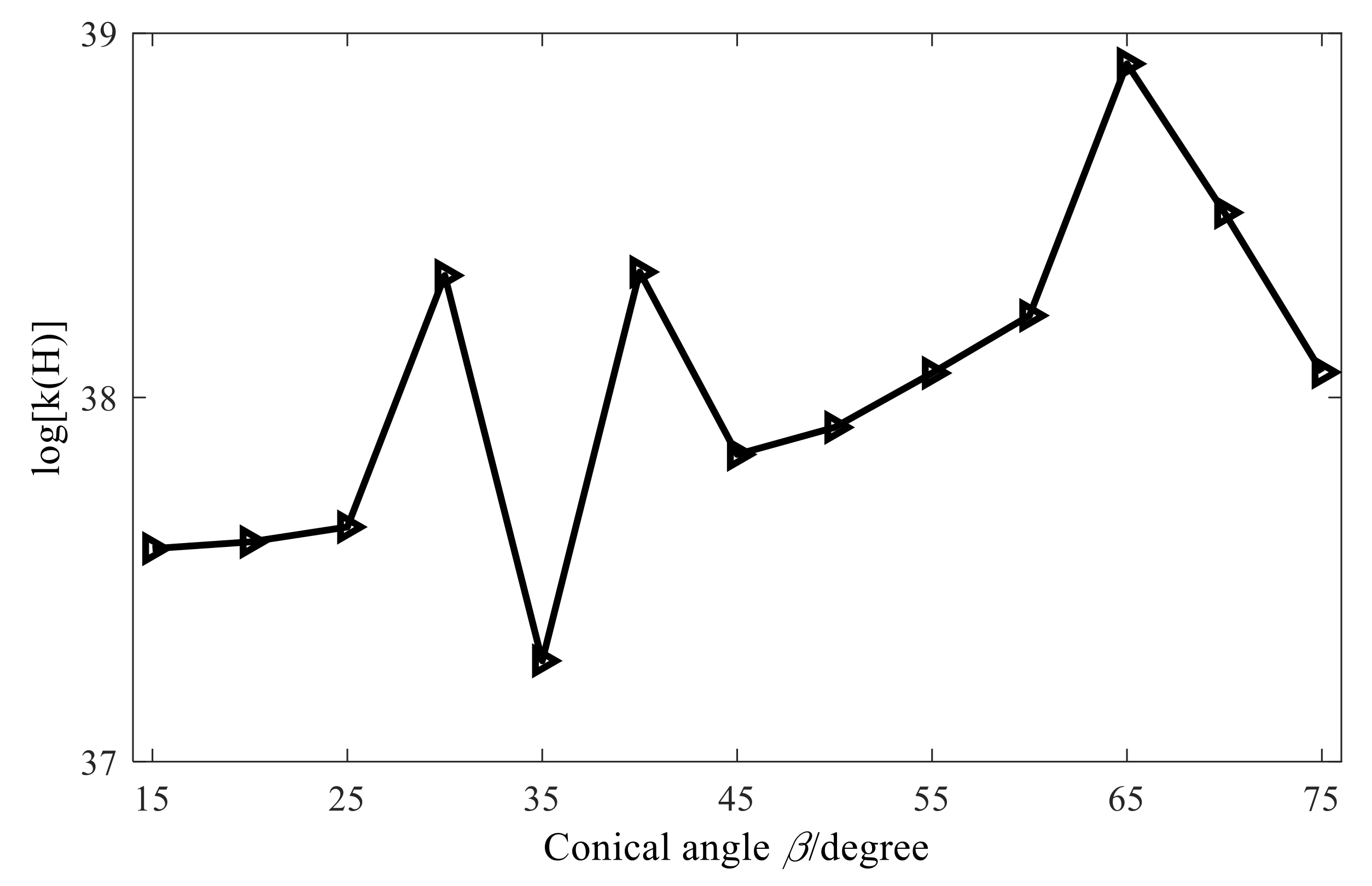
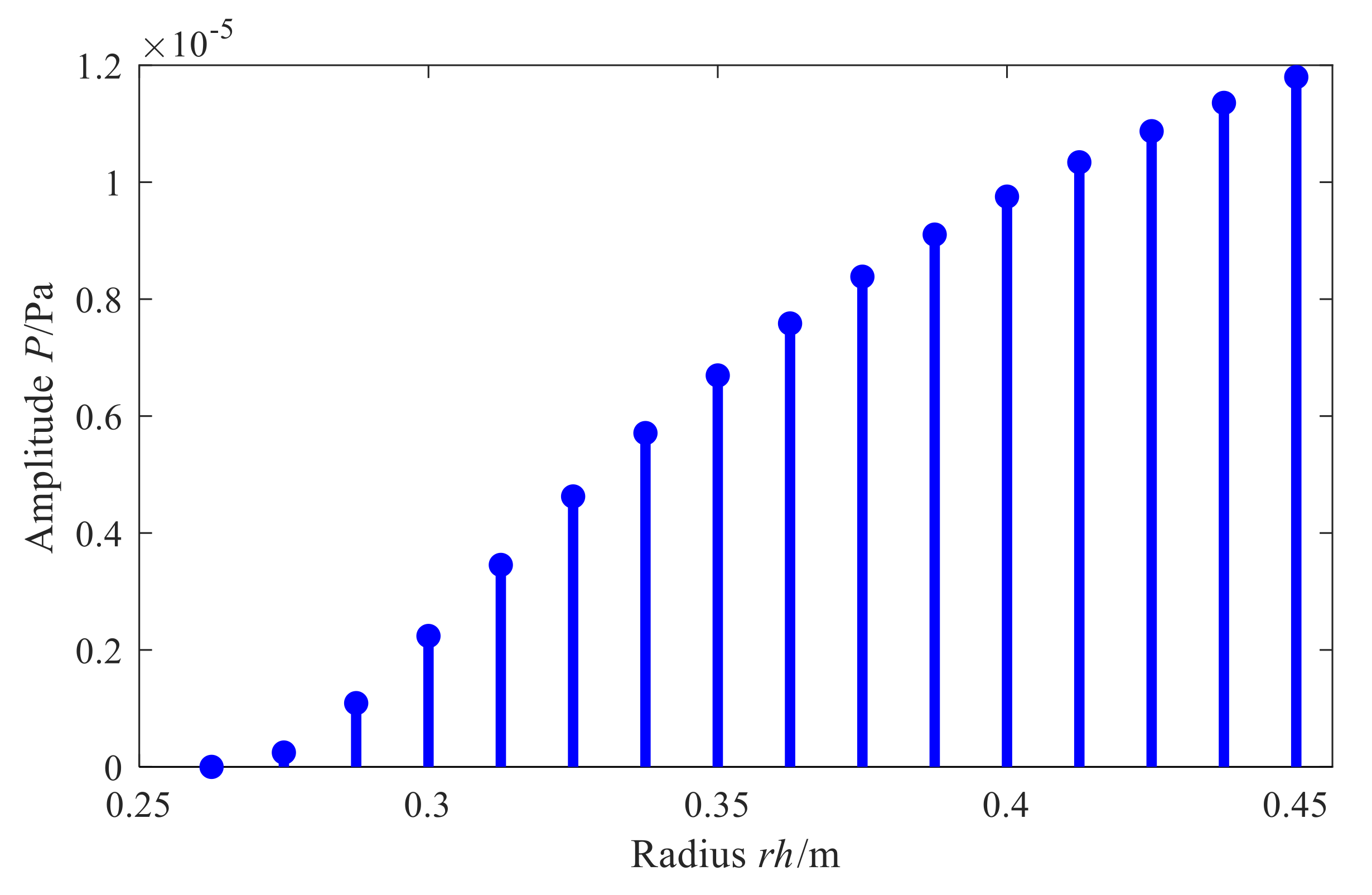
3.3.1. Ill-Condition Analysis of Acoustic Transfer Matrix
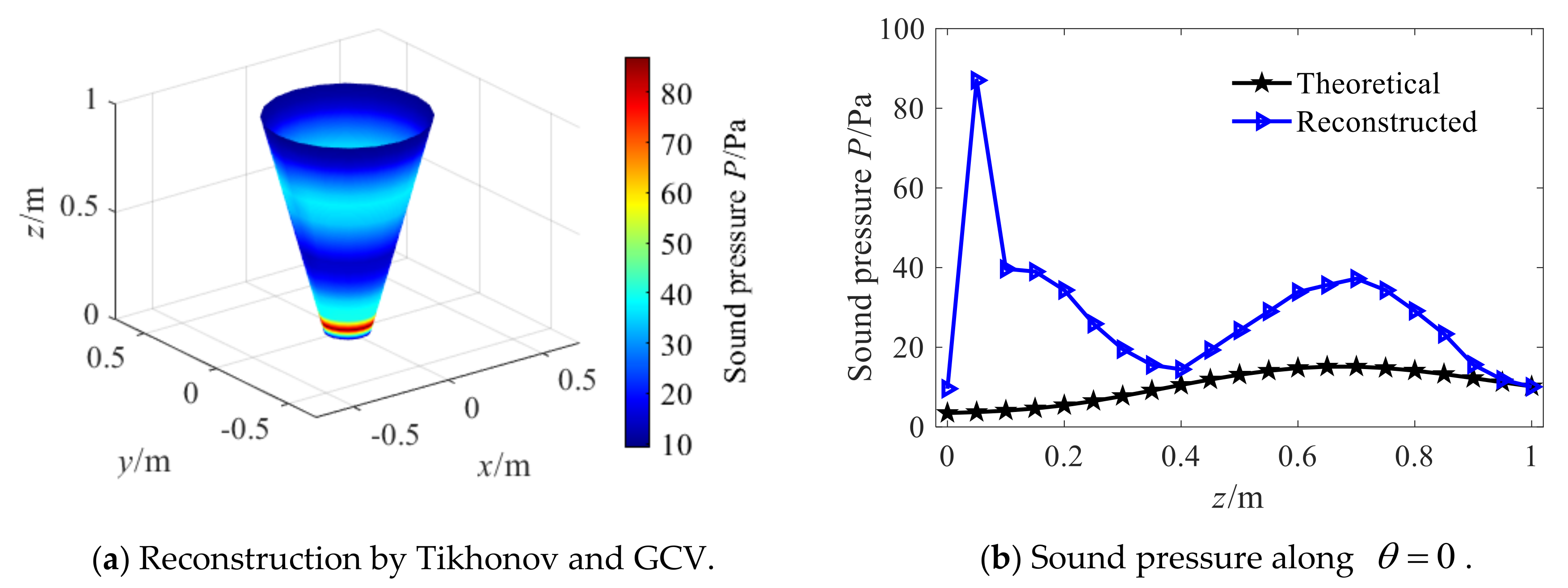
3.3.2. Comparative Studyof Different Regularization Methods
4. Experimental Case Studies
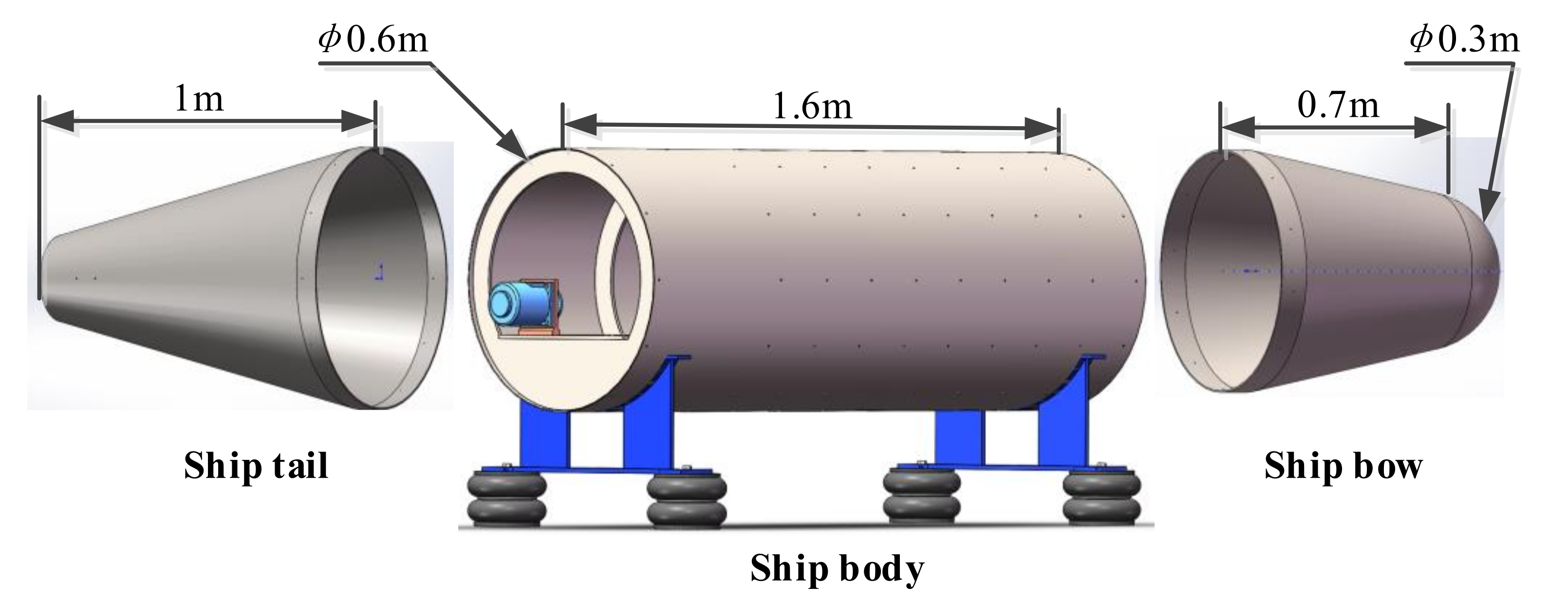
4.1. Introduction of Experimental System
4.2. Test Implementation
4.2.1. Sensor Arrangement and Signal Acquisition
4.2.2. Test Implementation Steps
- (1)
- As shown in Figure 23, connect the experimental equipment, set relevant parameters, pre-sample and roughly analyze the measurement data, and ensure that all equipment and channel signals are good.
- (2)
- Start the large motor alone and slowly adjust the motor speed to 1800 r/min. At this time, the vibration generated by the motor is transmitted to the cylindrical shell through the motor support, and then to the cone through the connection between the cone and the cylindrical shell, causing the vibration of the conical shell and thus radiating sound field into space.
- (3)
- The microphone bracket is rotated from one side of the shell to the other side at a circumferential interval of 22.5° to collect data of each circumferential angle position. Since the experimental conditions are limited, the radiative sound pressure of the upper part of the conical shell is measured.
- (4)
- The measurement distance is adjusted to the position 0.01 m away from the shell surface, and the above steps are repeated to obtain the radiation sound pressure data of the conical shell surface under the same condition.
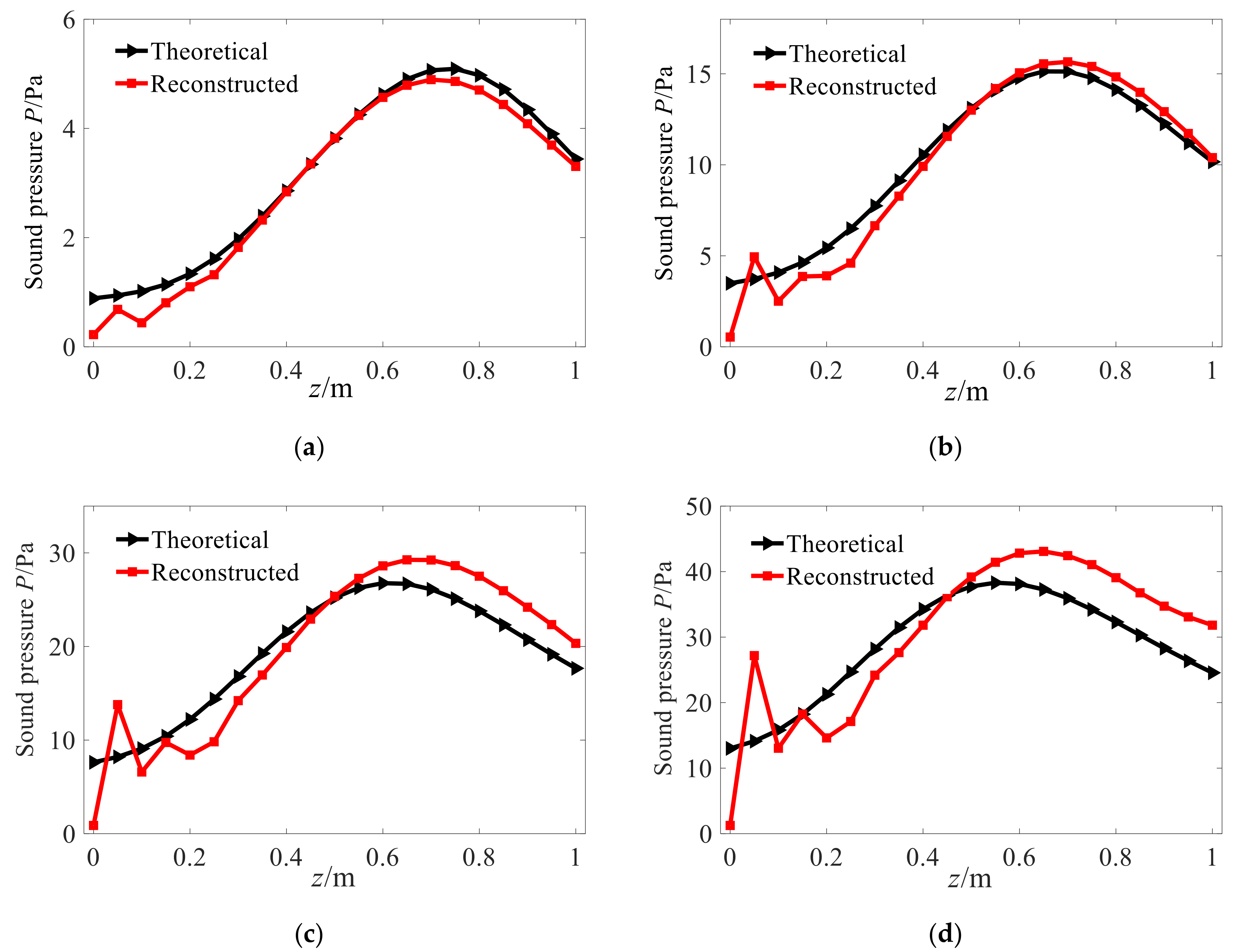
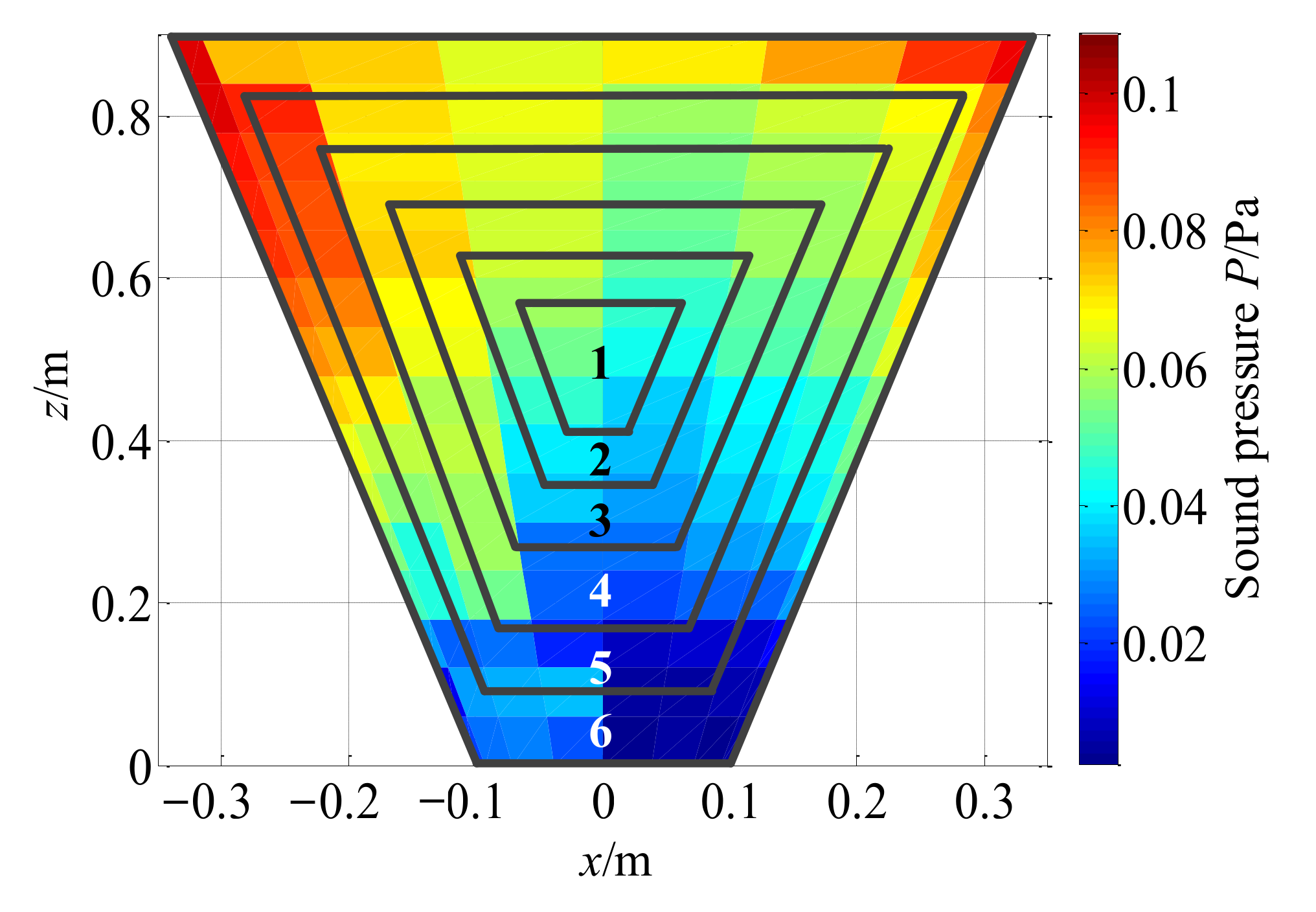
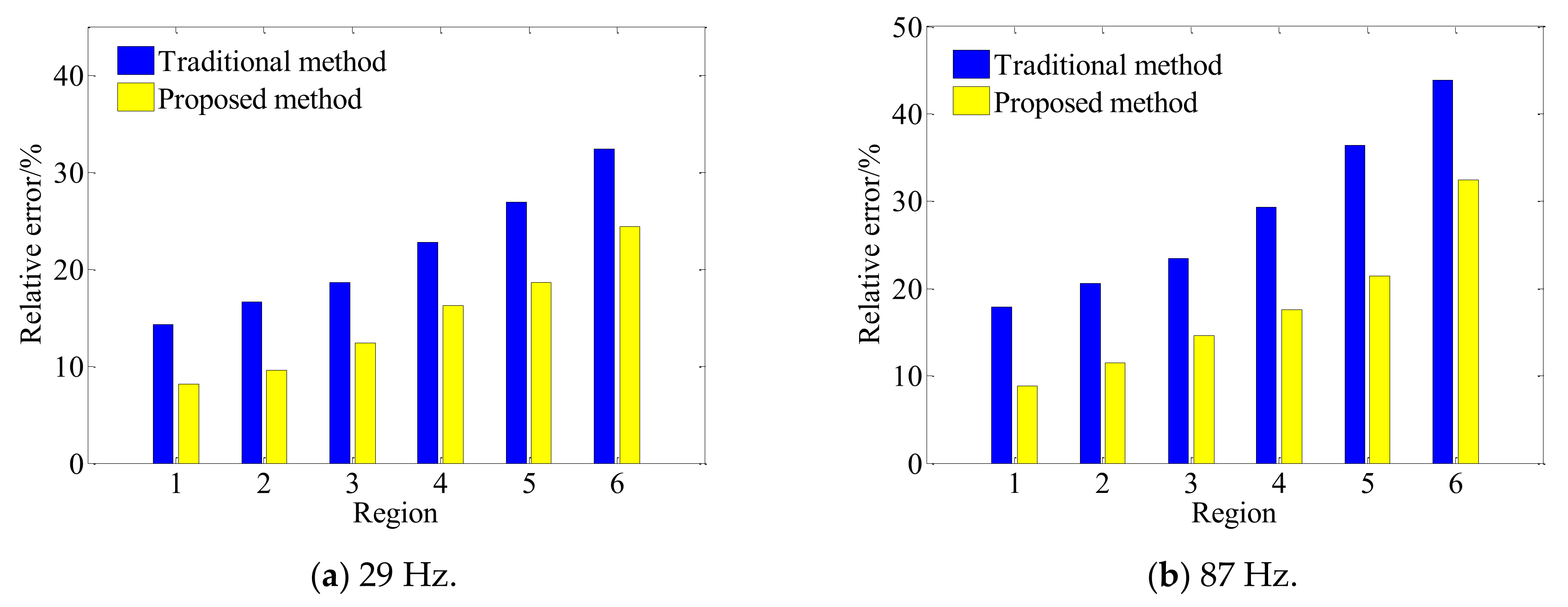
4.3. Analysis of Test Data
5. Conclusions
- (1)
- In the theoretical framework, based on the cylindrical SONAH, the elementary cylindrical wave is transformed into the characteristic elementary wave suitable for the radiated sound field of the conical surface through the cylinder-cone orthogonal coordinate transformation method, and the matrix of characteristic elementary wave in the conical spatial domain is formed. Then, the sound pressure is expressed as the superposition of this characteristic elementary wave. Next, by incorporating the advantages of TSVD and Tikhonov, a combined regularization method is proposed to obtain a stable and meaningful solution to the inverse problem so that the superposition coefficient is solved according to the principle of superposition of wave field. Lastly, the reconstructed conical pressure is expressed as a linear superposition of the holographic conical pressure.
- (2)
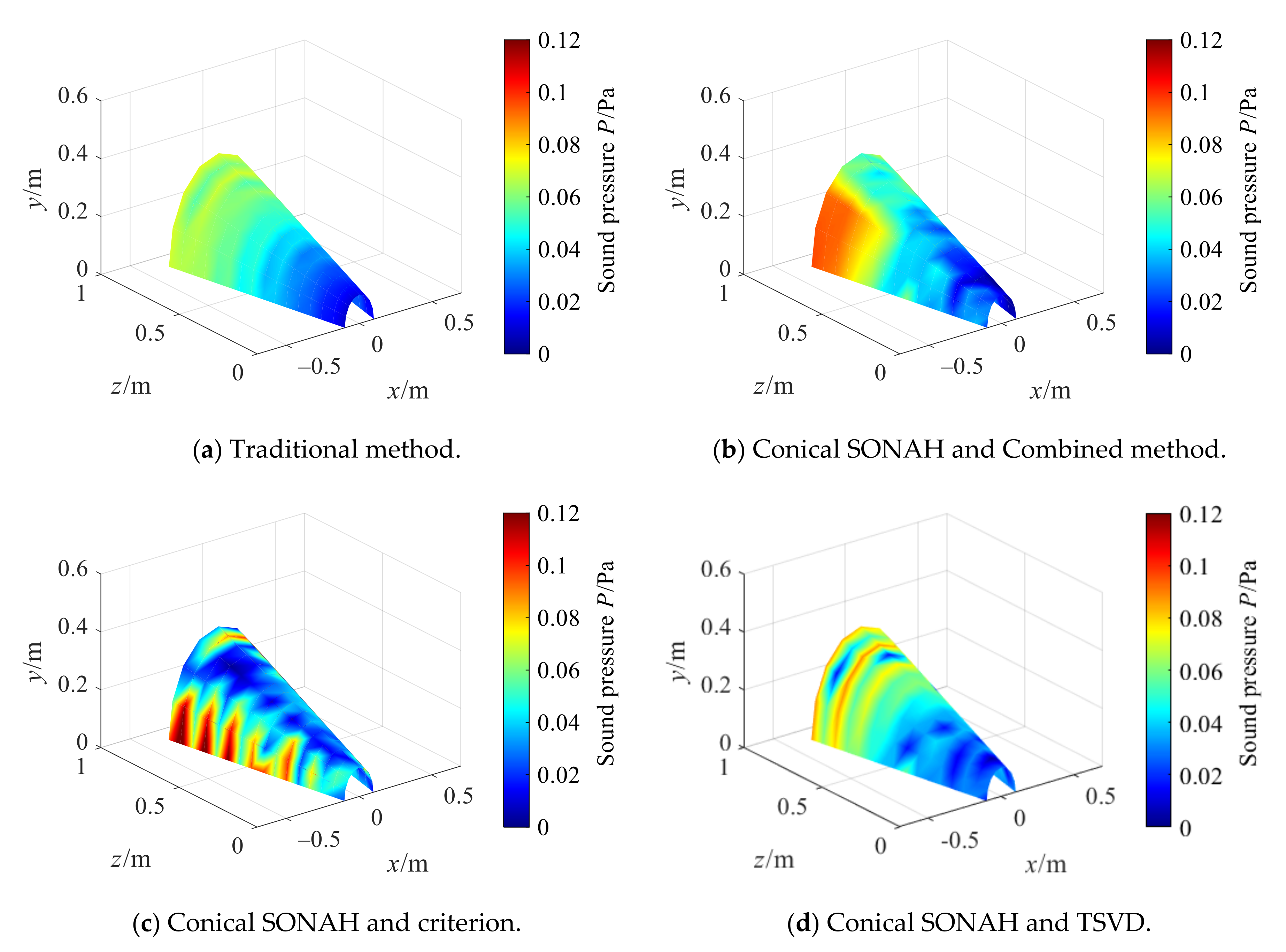
- Simulation investigations demonstrated that the proposed conical SONAH can reconstruct the sound field of conical sound source efficiently. When the cone angle increases gradually, the reconstruction error of the sound field will increase accordingly at different frequencies. As compared to cylindrical SONAH, the proposed conical SONAH has better reconstruction accuracy under different cone angles, and the relative reconstruction error can be reduced by about 15%. As compared to the standalone Tikhonov regularization combined with GCV and TSVD method, the reconstruction error of the proposed combined method is reduced by 90% and about 5%. Therefore, the proposed combined regularization method is more accurate and stable.
- (3)
- The effectiveness of the modified method was validated through a set of experiments, and the results verified the better reconstruction performance of the modified method in comparison to the direct reconstruction method of cylindrical SONAH. It is difficult to achieve the effective reconstruction of the sound field with a single regularization method, while the proposed combination regularization method based on TSVD and Tikhonov can effectively solve the acoustic inverse problem to obtain high reconstruction accuracy. The relative error of the largest value is 11.14%, while that of the traditional method is 34.70%. Furthermore, the overall relative errors of different regions of the reconstruction surface are reduced by 10–15% with different frequencies. Therefore, the proposed method can effectively reconstruct the sound field radiated by the conical source. This study can provide a reference for the engineering application of conical SONAH and can benefit vibration and noise monitoring, reduction, and control for mechanical systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Williams, E.G.; Maynard, J.D.; Skudrzyk, E. Sound source reconstructions using a microphone array. J. Acoust. Soc. Am. 1980, 68, 340–344. [Google Scholar] [CrossRef]
- Leete, K.M.; Wall, A.T.; Gee, K.L.; Neilsen, T.B.; Downing, J.M.; James, M.M. Numerical validation of using multisource statistically-optimized near-field acoustical holography in the vicinity of a high-performance military aircraft. Proc. Meet. Acoust. 2017, 31, 040007. [Google Scholar] [CrossRef] [Green Version]
- Wall, A.T.; Gee, K.L.; Neilsen, T.B.; McKinley, R.L.; James, M.M. Military jet noise source imaging using multisource statistically optimized near-field acoustical holography. J. Acoust. Soc. Am. 2016, 139, 1938–1950. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.R.; Xing, Y.S.; Chen, H.Y. Experiment verification of underwater noise localization based on cylindrical near-field acoustic holography. Noise Vib. Control 2018, 38, 1006–1355. [Google Scholar] [CrossRef]
- Maynard, J.D.; Williams, E.G.; Lee, Y. Nearfield acoustic holography: I. Theory of generalized holography and the development of NAH. J. Acoust. Soc. Am. 1985, 78, 1395–1413. [Google Scholar] [CrossRef]
- Williams, E.G.; Mann, J.A. Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography. J. Acoust. Soc. Am. 2000, 108, 1373. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wu, S.F. Helmholtz equation–least-squares method for reconstructing the acoustic pressure field. J. Acoust. Soc. Am. 1997, 102, 2020–2032. [Google Scholar] [CrossRef]
- Wu, S.F. On reconstruction of acoustic pressure fields using the Helmholtz equation least squares method. J. Acoust. Soc. Am. 2000, 107, 2511–2522. [Google Scholar] [CrossRef]
- Sarkissian, A. Method of superposition applied to patch near-field acoustic holography. J. Acoust. Soc. Am. 2005, 118, 671–678. [Google Scholar] [CrossRef]
- Valdivia, N.P.; Williams, E.G. Study of the comparison of the methods of equivalent sources and boundary element methods for near-field acoustic holography. J. Acoust. Soc. Am. 2006, 120, 3694–3705. [Google Scholar] [CrossRef]
- Bi, C.-X.; Geng, L.; Zhang, X.-Z. Separation of non-stationary multi-source sound field based on the interpolated time-domain equivalent source method. Mech. Syst. Signal Process. 2016, 72–73, 745–761. [Google Scholar] [CrossRef]
- Ping, G.; Chu, Z.; Yang, Y.; Xu, Z. Wideband holography based spherical equivalent source method with rigid spherical arrays. Mech. Syst. Signal Process. 2018, 111, 303–313. [Google Scholar] [CrossRef]
- Hald, J.; Hardy, P.; Trentin, D.; Keith, G.; Mo/rkholt, J.; Bach-Andersen, M. Array based measurement of radiated and absorbed sound intensity components. J. Acoust. Soc. Am. 2008, 123, 3387. [Google Scholar] [CrossRef] [Green Version]
- Valdivia, N.P.; Williams, E.G.; Herdic, P.C. Approximations of inverse boundary element methods with partial measurements of the pressure field. J. Acoust. Soc. Am. 2008, 123, 109–120. [Google Scholar] [CrossRef]
- Valdivia, N.; Williams, E.G. Implicit methods of solution to integral formulations in boundary element method based nearfield acoustic holography. J. Acoust. Soc. Am. 2004, 116, 1559–1572. [Google Scholar] [CrossRef]
- Hald, J. Patch near-field acoustical holography using a new statistically optimal method. Proc. Inter-Noise 2003, 3, 2203–2210. [Google Scholar]
- Olsen, E.S.; Hald, J. Patch near–field acoustical holography using a new statistically optimal method. Tech. Rev. 2005, 40–50. [Google Scholar]
- Steiner, R.; Hald, J. Near-field Acoustical Holography without the Errors and Limitations Caused by the Use of Spatial DFT. Int. J. Acoust. Vib. 2001, 6, 83–89. [Google Scholar] [CrossRef]
- Jacobsen, F.; Jaud, V. Statistically optimized near field acoustic holography using an array of pressure-velocity probes. J. Acoust. Soc. Am. 2007, 121, 1550–1558. [Google Scholar] [CrossRef] [Green Version]
- Hald, J. Basic theory and properties of statistically optimized near-field acoustical holography. J. Acoust. Soc. Am. 2009, 125, 2105–2120. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Niu, Y. Improved Statistically Optimal Nearfield Acoustical Holography in subsonically moving fluid medium. J. Sound Vib. 2012, 331, 3945–3960. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhu, H.C.; Mao, R.F.; Du, X.H. Statistically optimal near-field acoustic holography for modulated sound source. J. Vib. Shock 2011, 30, 253–256–269. [Google Scholar]
- Hald, J. Scaling of plane-wave functions in statistically optimized near-field acoustic holography. J. Acoust. Soc. Am. 2014, 136, 2687–2696. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.T.; Bolton, J.S.; Hald, J. Source visualization by using statistically optimized near-field acoustical holography in cylindrical coordinates. J. Acoust. Soc. Am. 2005, 118, 2355–2364. [Google Scholar] [CrossRef] [Green Version]
- Hu, B.; Yang, D.S. Patch near-field acoustical holography study based on measurement of vector hydrophone array. J. Vib. Shock 2011, 30, 225–229. [Google Scholar]
- Wall, A.T.; Gee, K.L.; Neilsen, T.B. Modified statistically optimized near-field acoustical holography for jet noise characterization. J. Acoust. Soc. Am. 2013, 133, 3296. [Google Scholar] [CrossRef]
- Wall, A.T.; Gee, K.L.; Neilsen, T.B. Multisource statistically optimized near-field acoustical holography. J. Acoust. Soc. Am. 2015, 137, 963–975. [Google Scholar] [CrossRef] [Green Version]
- Saijyou, K. Regularization method for the application of K-space data extrapolation to near-field acoustical holography. J. Acoust. Soc. Am. 2004, 116, 396. [Google Scholar] [CrossRef]
- Pascal, J.-C.; Paillasseur, S.; Thomas, J.-H.; Li, J.-F. Patch near-field acoustic holography: Regularized extension and statistically optimized methods. J. Acoust. Soc. Am. 2009, 126, 1264–1268. [Google Scholar] [CrossRef]
- Gomes, J. A study on regularization parameter choice in Near-field Acoustical Holography. J. Acoust. Soc. Am. 2008, 123, 3385. [Google Scholar] [CrossRef] [Green Version]
- He, C.D.; Zhang, Y.B.; Bi, C.X.; Chen, X. The application of regularization technique based on partial optimization in the nearfield acoustic holography. Acta Acust. 2011, 36, 419–426. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, Z.; Lee, S.; He, Z. Source Contribution Evaluation of Mechanical Vibration Signals via Enhanced Independent Component Analysis. J. Manuf. Sci. Eng. 2012, 134, 021014. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, Z.; Lee, S.; He, Z. Investigations of denoising source separation technique and its application to source separation and identification of mechanical vibration signals. J. Vib. Control. 2013, 20, 2100–2117. [Google Scholar] [CrossRef]
- Wall, M.E.; Rechtsteiner, A.; Rocha, L.M. Singular value decomposition and principal component analysis. In A Practical Approach to Microarray Data Analysis; Springer: Boston, MA, USA, 2003; pp. 91–109. [Google Scholar]










| Contribution rate % | 1 | 2 | 3 | 4 | 5 | 7 | 10 | 15 | 25 |
| Relative error % | 12.31 | 11.81 | 11.68 | 11.39 | 11.45 | 12.34 | 12.34 | 14.42 | 16.78 |
| Name | Model | Frequency Range | Sensitivity | Range |
|---|---|---|---|---|
| Beijing SKC sound pressure sensor | MNP21 | 20~20 kHz | 50 mV/Pa | 18~136 dB |
| Methods | Cylindrical SONAH | Conical SONAH and Hald | Conical SONAH and TSVD | Conical SONAH and Combined Method |
|---|---|---|---|---|
| Relative error % | 34.70 | 24.68 | 18.32 | 11.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Ni, J.; Song, C.; Ahsan, M.M.; Chen, X.; Nie, Z.; Liu, Y. Conical Statistical Optimal Near-Field Acoustic Holography with Combined Regularization. Sensors 2021, 21, 7150. https://doi.org/10.3390/s21217150
Cheng W, Ni J, Song C, Ahsan MM, Chen X, Nie Z, Liu Y. Conical Statistical Optimal Near-Field Acoustic Holography with Combined Regularization. Sensors. 2021; 21(21):7150. https://doi.org/10.3390/s21217150
Chicago/Turabian StyleCheng, Wei, Jinglei Ni, Chao Song, Muhammad Mubashir Ahsan, Xuefeng Chen, Zelin Nie, and Yilong Liu. 2021. "Conical Statistical Optimal Near-Field Acoustic Holography with Combined Regularization" Sensors 21, no. 21: 7150. https://doi.org/10.3390/s21217150
APA StyleCheng, W., Ni, J., Song, C., Ahsan, M. M., Chen, X., Nie, Z., & Liu, Y. (2021). Conical Statistical Optimal Near-Field Acoustic Holography with Combined Regularization. Sensors, 21(21), 7150. https://doi.org/10.3390/s21217150









