An Optimal Geometry Configuration Algorithm of Hybrid Semi-Passive Location System Based on Mayfly Optimization Algorithm
Abstract
:1. Introduction
2. Time Difference of Arrival (TDOA) and Angle of Arrival (AOA) Hybrid Positioning Algorithm
2.1. TDOA Equations
2.2. AOA Equations
2.3. TDOA and AOA Hybrid Positioning
3. Geometric Dilution of Precision (GDOP) Solution Process
3.1. Cramer Rao Lower Bound (CRLB) Solution for Position Estimation
- The first part can be derived from
- 2.
- The second part can be derived from
3.2. GDOP of TDOA and AOA Hybrid Positioning
4. Mayfly Optimization Algorithm (MOA) Station Deployment for TDOA/AOA Hybrid Positioning
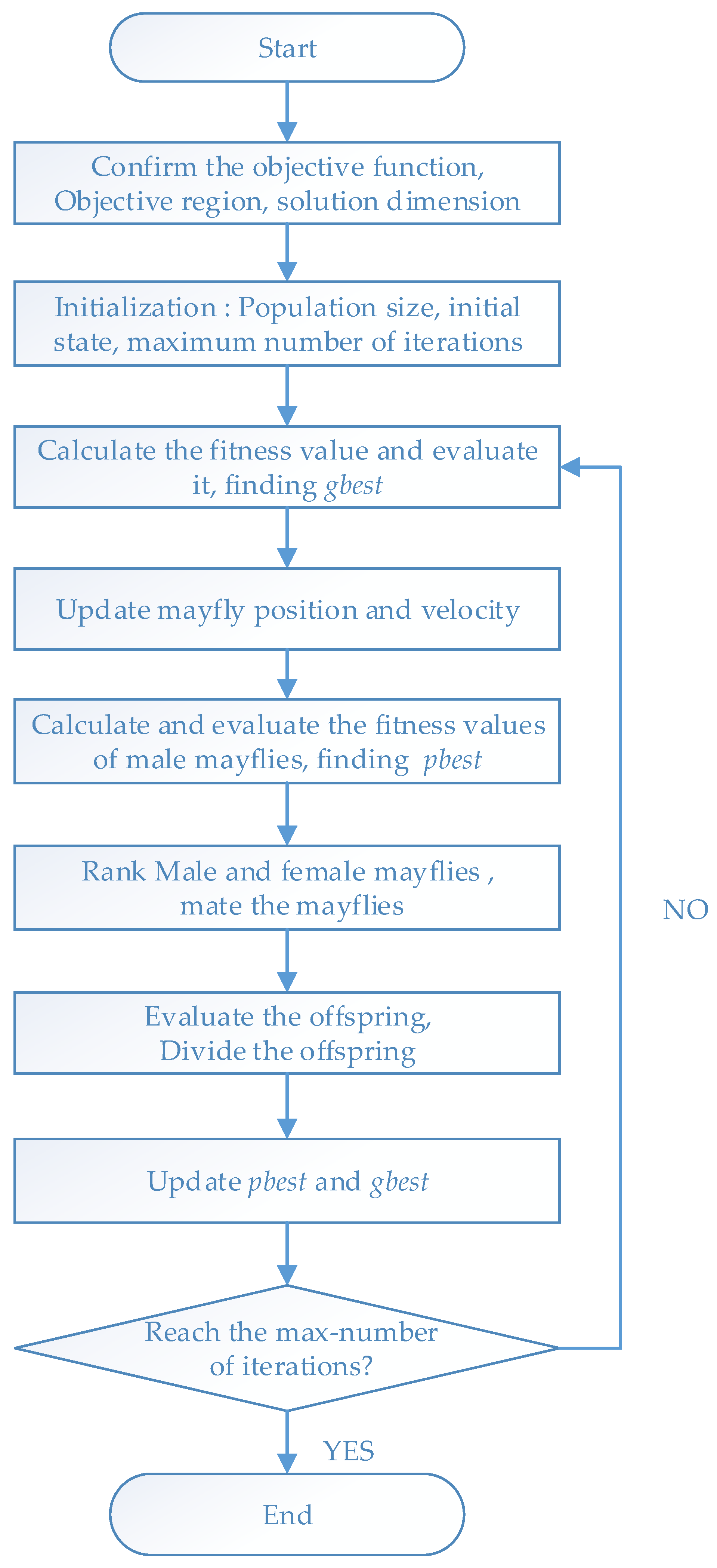
4.1. Mayfly Optimization Algorithm
- Initialize the female and male mayfly populations and set the speed parameters.
- 2.
- Calculate the fitness value and sort to obtain pbesti and gbest.
- 3.
- Update the positions of male mayflies and female mayflies in turn, and mate.
- 4.
- Calculate the fitness and update pbest and gbest;
- 5.
- Whether the stop condition is met, if it is met, exit and output the result, otherwise repeat Steps 3–5.
| Algorithm 1: Mayfly optimization algorithm. |
| Input objective function , male population size (M1), female population size (M2), visibility coefficient (), initial velocity for male mayfly (), initial velocity for female mayfly (), maximum iteration (T), a1 and a2 are positive attraction factors, solution dimension (d), population size (L) |
| Output Optimal Solution (gbest) |
|
1: begin 2: Evaluate all solutions according to the objective function 3: Find the best value from all solutions (gbest) 4: while t ≤ T 5: find pbest by (33), the best solution of each male mayfly 6: for I = 1:M2 7: for j = 1:d 8: Adjust female velocity by (32) 9: Adjust female positions by (37) 10: end for 11: end for 12: for I = 1:M2 13: for j = 1:d 14: Adjust male velocity by (31) 15: Adjust male positions by (36) 16: end for 17: Update pbest 18: end for 19: Rank male mayflies 20: Rank female mayflies 21: Mate the mayflies 22: Evaluate the offspring 23: Separate offspring to male and female randomly 24: Replace the worst solution with the best new one 25: Update pbest and gbest 26: end while 27: end |
4.2. Flow Chart of MOA Station Deployment for Hybrid Positioning
5. Simulation
5.1. Confirm the Model of Optimal Station Deployment
5.1.1. Independent Variables
5.1.2. Constraint Conditions
5.1.3. Objective Function
5.2. Simulation of Optimized Layout for the Unmanned Aerial Vehicle (UAV) Airborne Multi-Base Station
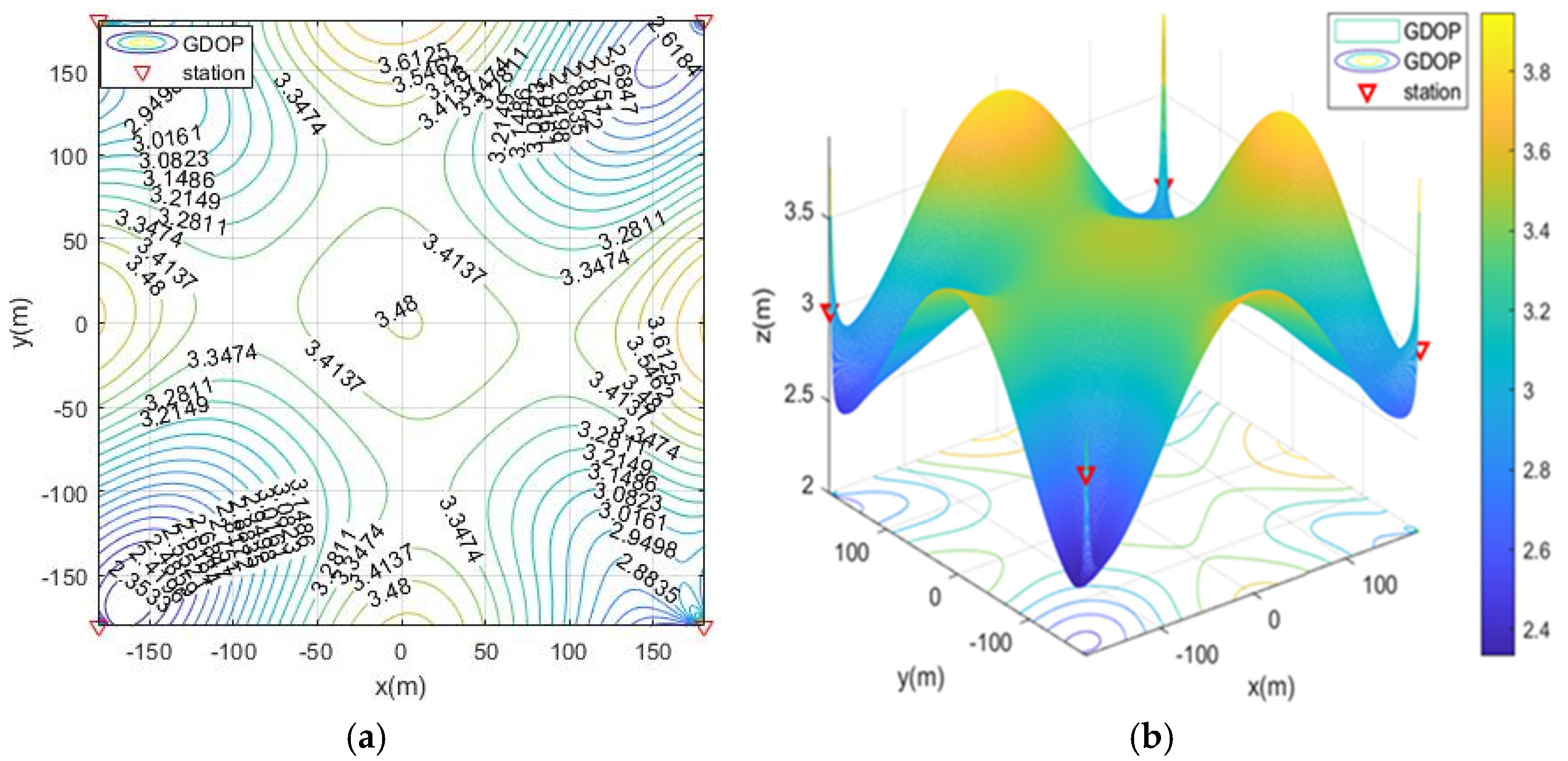
5.2.1. Simulation Scenario 1
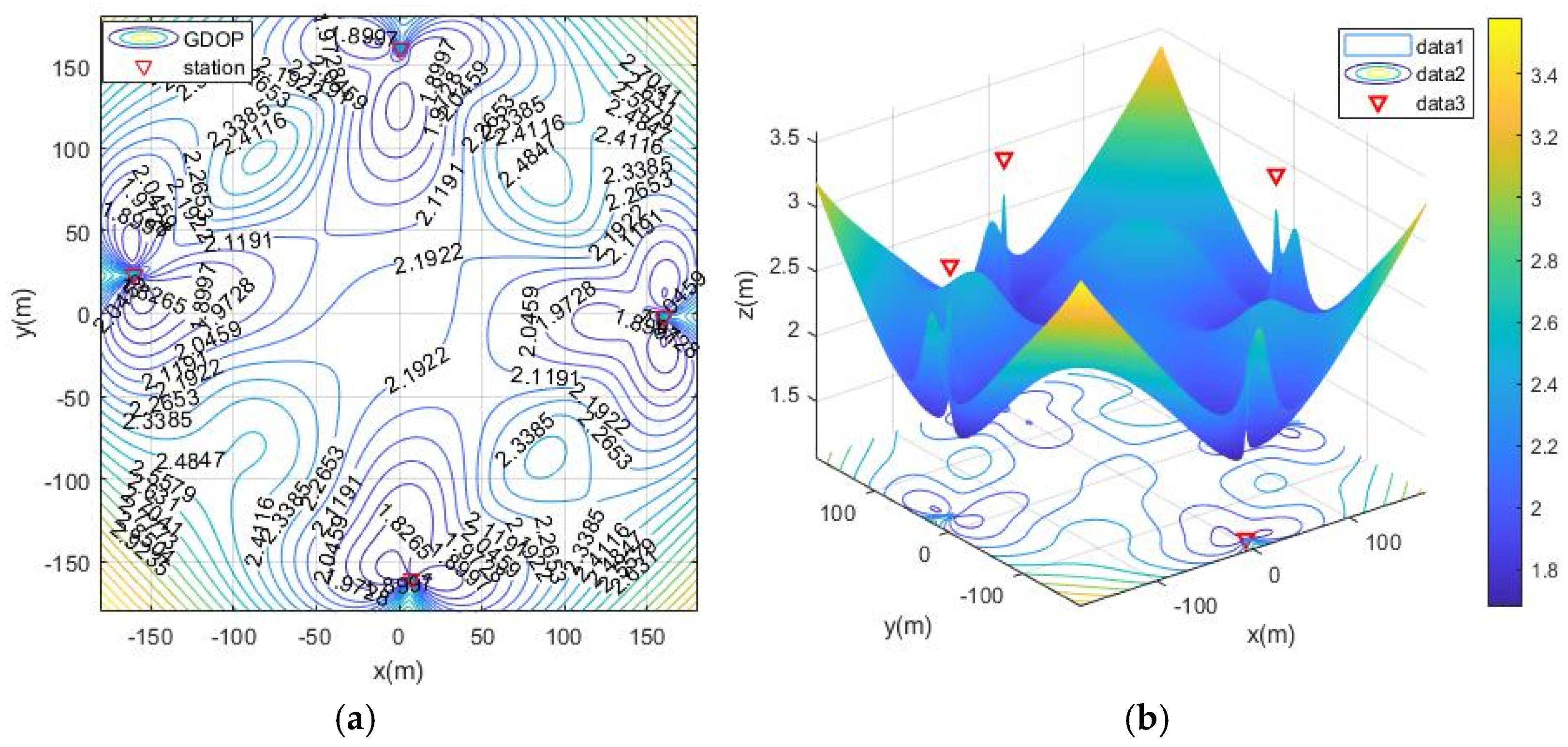
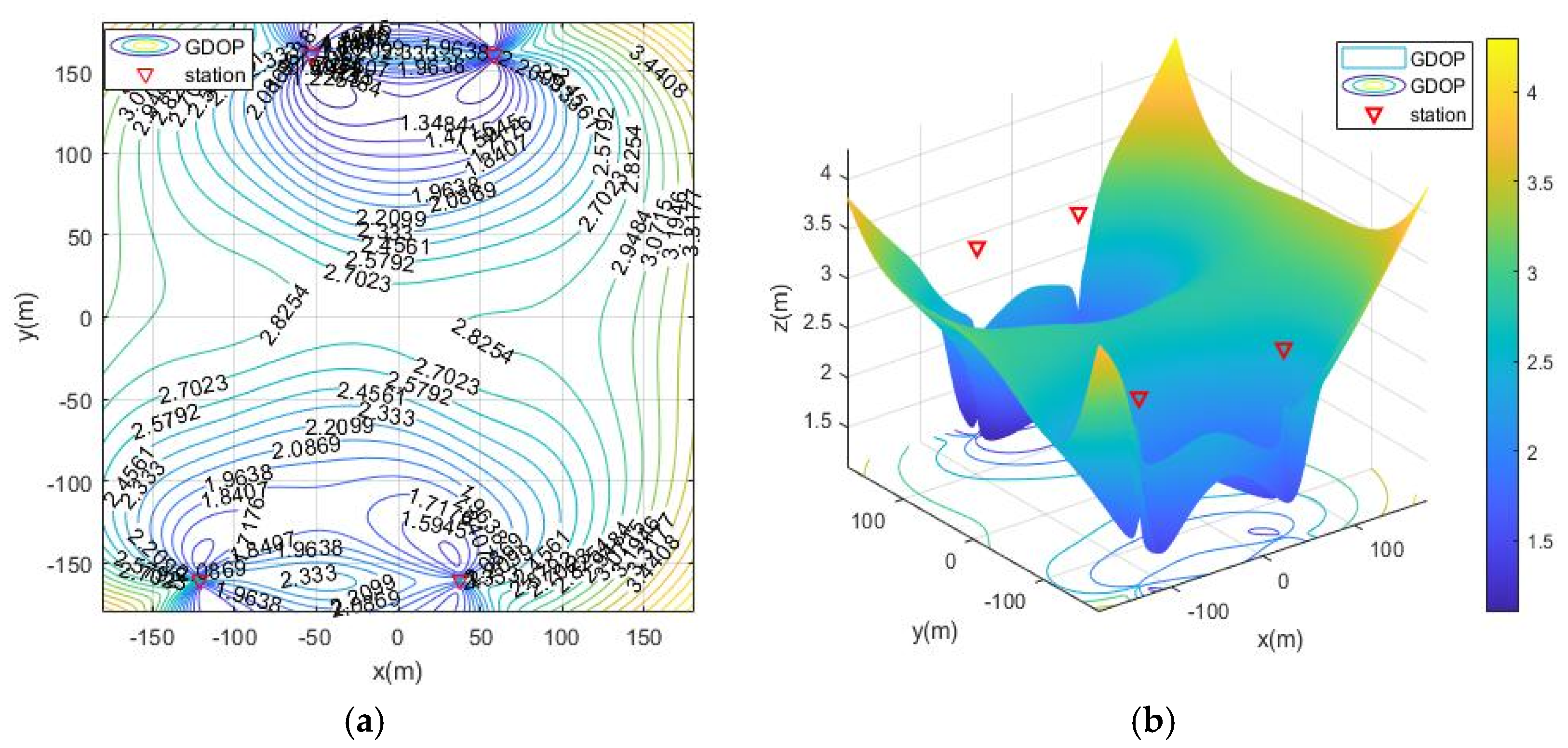
5.2.2. Simulation Scenario 2
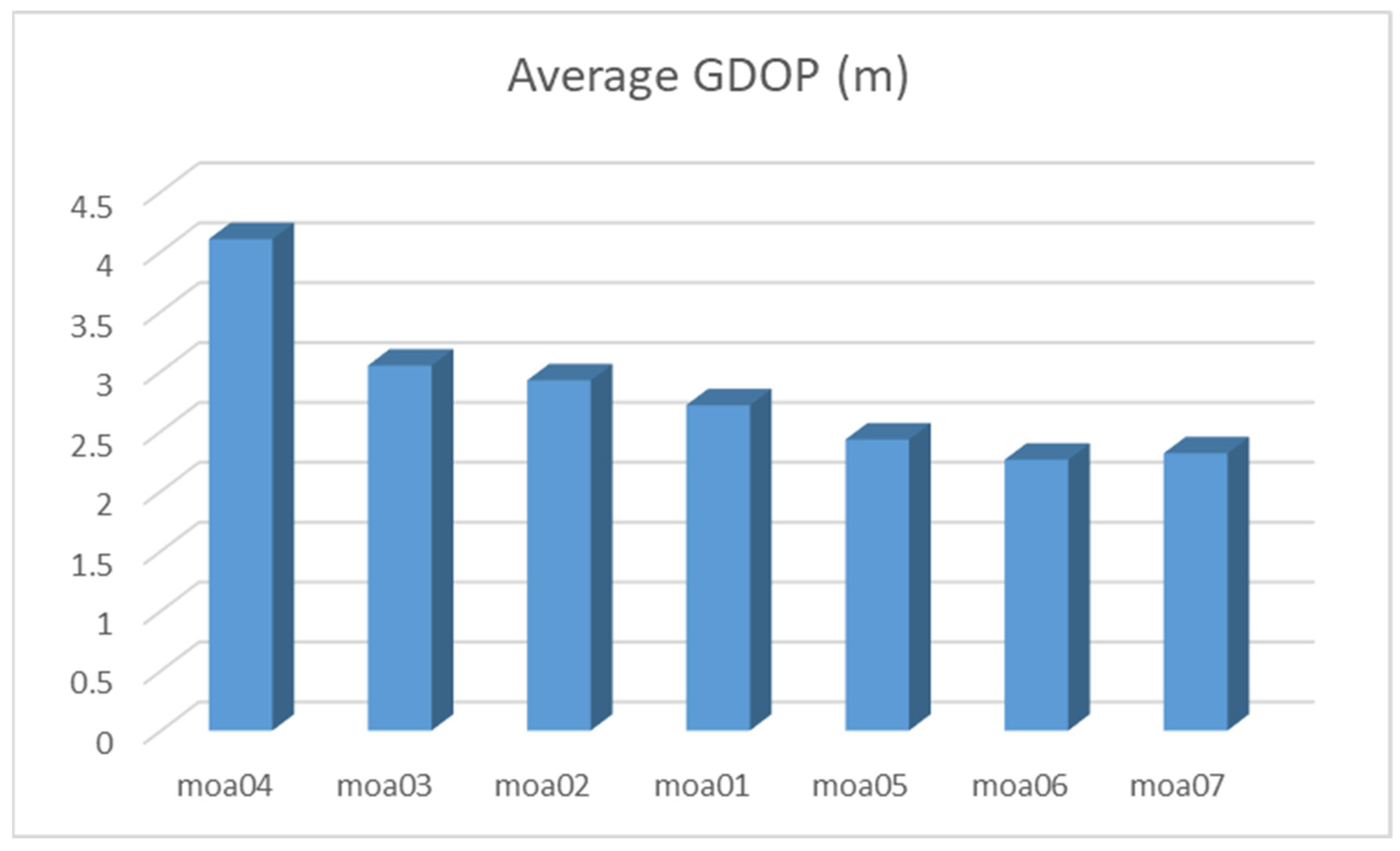
5.2.3. Positioning Simulation of Five Base Stations in Simulation Scenario 2
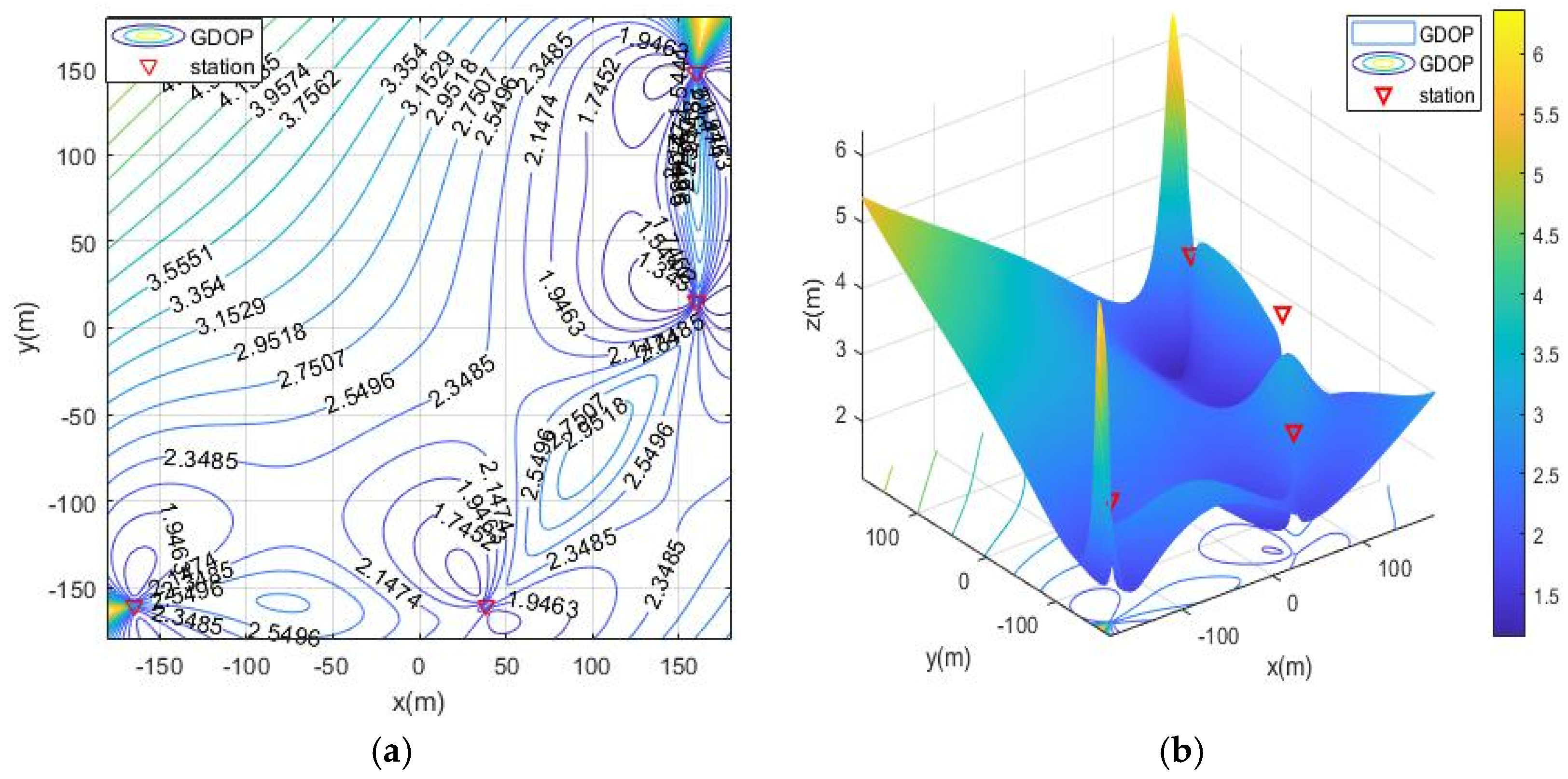
- moa01: Four stations surrounding the target region;
- moa02: Four stations are distributed on both sides of the target area;
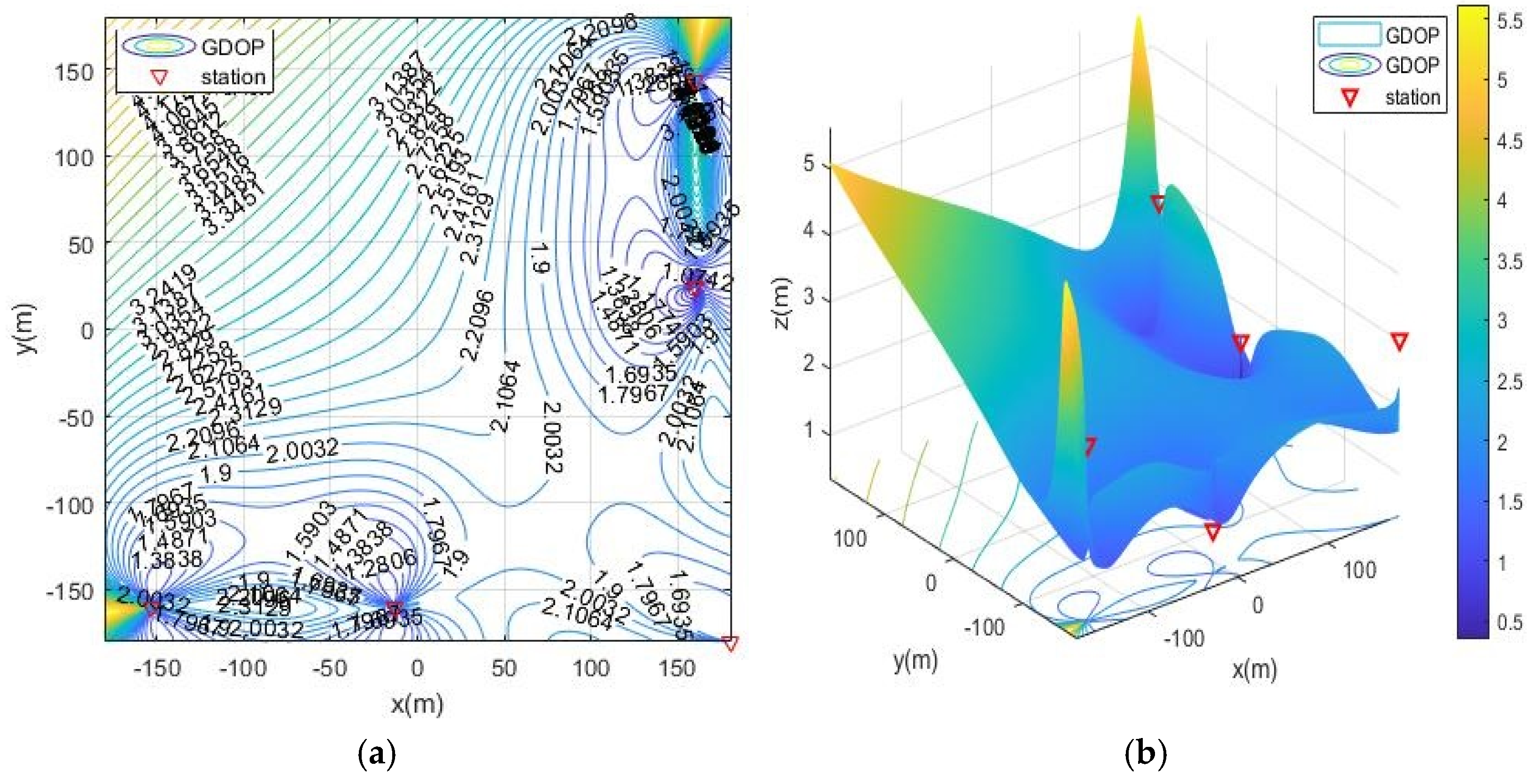
- moa03: Four stations are distributed on the vertical side of the target area;
- moa04: Four stations are distributed on single side of the target area;
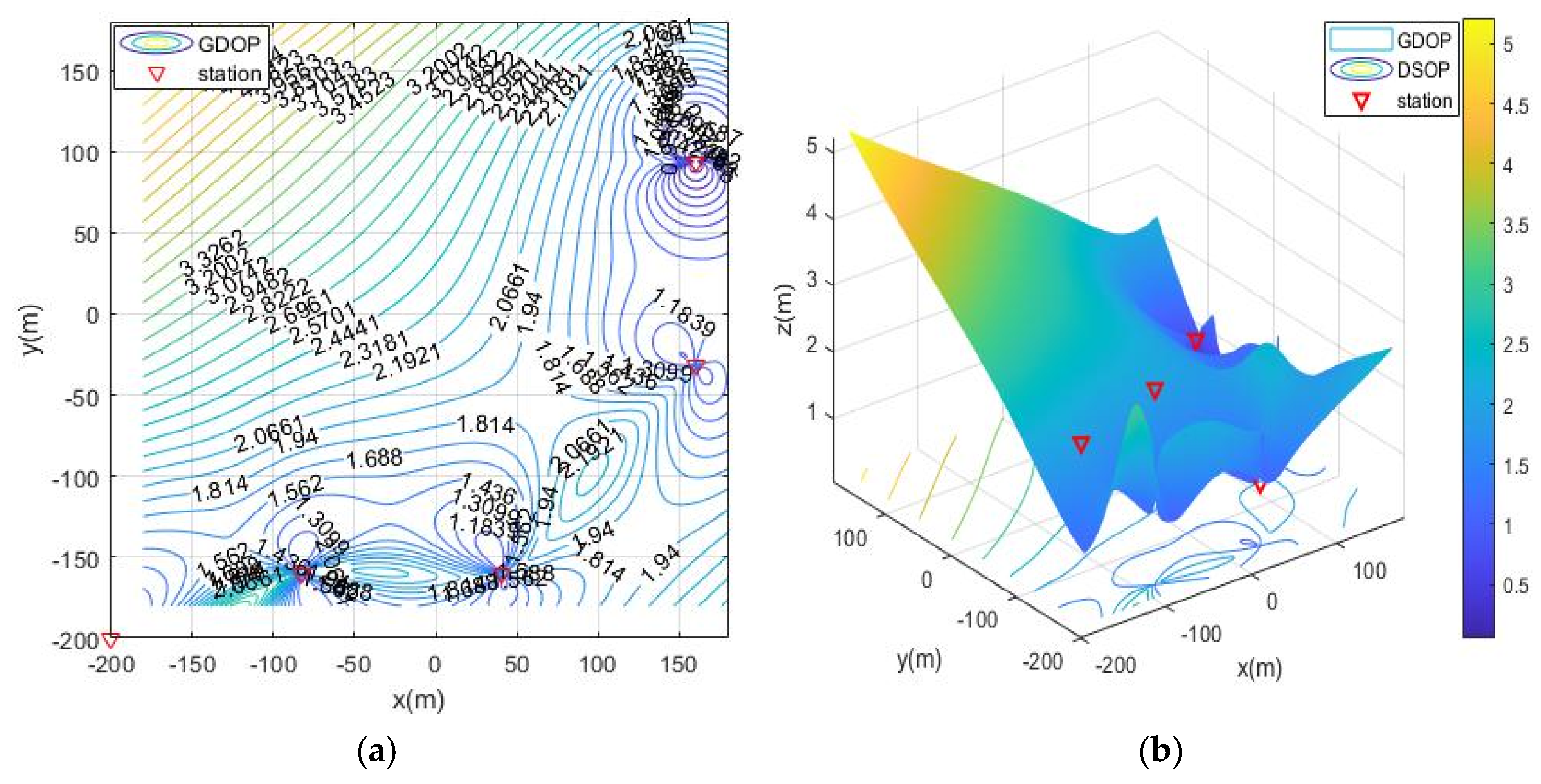
- moa05: Five base stations add station S0= (−200, 200, 3) to the distribution of moa03;
- moa06: Five base stations add station S0= (180, −180, 3) to the distribution of moa03;
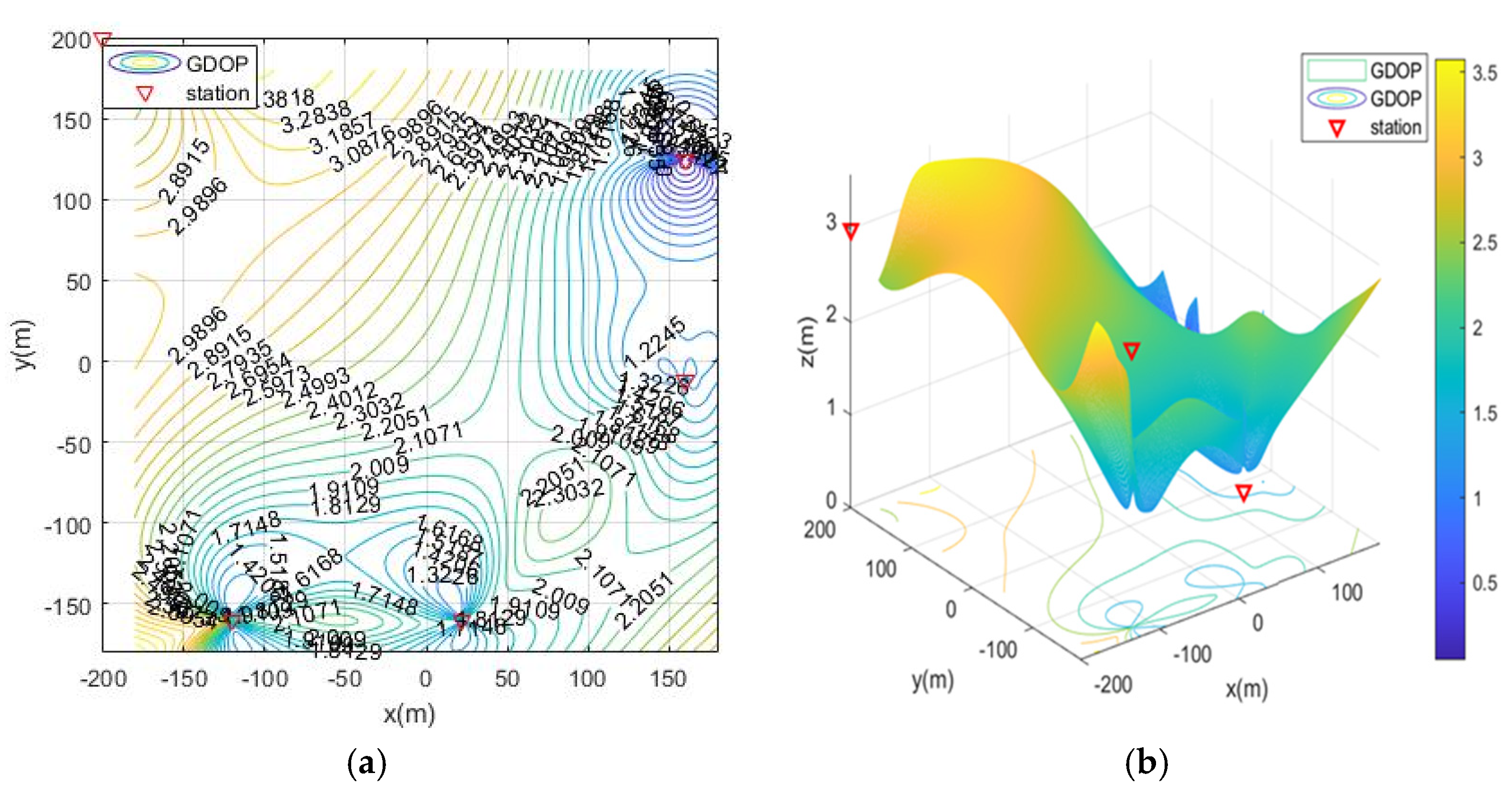
- moa07: Five base stations add station S0= (−200, −200, 3) to the distribution of moa03.
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, S. Illegal radio station localization with UAV-based Q-learning. China Commun. 2018, 15, 122–131. [Google Scholar] [CrossRef]
- Alotaibi, E.T.; Alqefari, S.S.; Koubaa, A. LSAR: Multi-UAV Collaboration for Search and Rescue Missions. IEEE Access 2019, 7, 55817–55832. [Google Scholar] [CrossRef]
- Xu, J.; Ma, M.; Law, C.L. Cooperative angle-of-arrival position localization. Measurement 2015, 59, 302–313. [Google Scholar] [CrossRef]
- Weinberg, A. The Effects of Repeater Hard-Limiting, Filter Distortion, and Noise on a Pseudo-Noise, Time-Of-Arrival Estimation System. IEEE Trans. Commun. 1979, 27, 1271–1279. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Li, Y.; Ansari, N. A Semidefinite Relaxation Method for Source Localization Using TDOA and FDOA Measurements. IEEE Trans. Veh. Technol. 2013, 62, 853–862. [Google Scholar] [CrossRef]
- Li, X. RSS-Based Location Estimation with Unknown Pathloss Model. IEEE Trans. Wireless Commun. 2006, 5, 3626–3633. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, B.M.; Lee, T.H. Optimal sensor placement for target localisation and tracking in 2D and 3D. Int. J. Control 2013, 86, 1687–1704. [Google Scholar] [CrossRef]
- Noroozi, A.; Sebt, M.A. Algebraic solution for three-dimensional TDOA/AOA localisation in multiple-input–multiple-output passive radar. IET Radar Sonar Navig. 2018, 12, 21–29. [Google Scholar] [CrossRef]
- Deng, Z.L.; Wang, H.H.; Zheng, X.Y.; Yin, L. Base Station Selection for Hybrid TDOA/RTT/DOA Positioning in Mixed LOS/NLOS Environment. Sensors 2020, 20, 4132. [Google Scholar] [CrossRef]
- Luo, J.; Walker, E.; Bhattacharya, P.; Chen, X. A new TDOA/FDOA-based recursive geolocation algorithm. In Proceedings of the 2010 42nd Southeastern Symposium on System Theory (SSST), Tyler, TX, USA, 7–9 March 2010. [Google Scholar] [CrossRef]
- Wang, W.; Bai, P.; Liang, X.; Liang, X.; Zhang, J. Optimal deployment of sensor–emitter geometries for hybrid localisation using TDOA and AOA measurements. IET Sci. Meas. Technol. 2019, 13, 622–631. [Google Scholar] [CrossRef]
- Shi, W.; Qi, X.; Li, J.; Yan, S.; Chen, L.; Yu, Y.; Feng, X. Simple solution to the optimal deployment of cooperative nodes in two-dimensional TOA-based and AOA-based localization system. Eurasip J. Wirel. Commun. Netw. 2017, 1, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Bai, P.; Wang, Y.; Liang, X.; Zhang, J. Optimal sensor deployment and velocity configuration with hybrid TDOA and FDOA measurements. IEEE Access 2019, 7, 109181–109194. [Google Scholar] [CrossRef]
- Bishop, A.N.; Jensfelt, P. An optimality analysis of sensor-target geometries for signal strength based localization. In Proceedings of the 2009 International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Melbourne, VIC, Australia, 7–10 December 2009; pp. 127–132. [Google Scholar] [CrossRef]
- Bishop, A.N.; Fidan, B.; Anderson, B.D.O. Optimality analysis of sensor target localization geometries. Automation 2010, 45, 479–492. [Google Scholar] [CrossRef]
- Bishop, A.N.; Fidan, B.; Anderson, B.D.O. Optimality analysis of sensor target geometries in passive localization: Part 1 – bearing-only localization. In Proceedings of the 2017 3rd International Conference on Intelligent Sensors Sensor Networks and Information Processing, Melbourne, VIC, Australia, 3–6 December 2007. [Google Scholar] [CrossRef]
- Bishop, A.N.; Fidan, B.; Anderson, B.D.O. Optimality analysis of sensor target geometries in passive localization: Part 2 – time-of-arrival based localization. In Proceedings of the 2017 3rd International Conference on Intelligent Sensors Sensor Networks and Information Processing, Melbourne, VIC, Australia, 3–6 December 2007. [Google Scholar] [CrossRef]
- Martínez, S.; Bullo, F. Optimal sensor placement and motion coordination for target tracking. Automation 2006, 42, 661–668. [Google Scholar] [CrossRef]
- Liang, Y.; Jia, Y. Constrained Optimal Placements of Heterogeneous Range/Bearing/RSS Sensor Networks for Source Localization with Distance-Dependent Noise. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1611–1615. [Google Scholar] [CrossRef]
- Sharp, I.; Yu, K.; Guo, Y.J. GDOP Analysis for Positioning System Design. IEEE Trans. Veh. Technol. 2009, 58, 3371–3382. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K.C. Elliptic Localization: Performance Study and Optimum Receiver Placement. IEEE Trans. Signal Process. 2014, 62, 4673–4688. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, J.F. Analytical evaluation of geometric dilution of precision for three-dimensional angle-of-arrival target localization in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2020, 16, 2000–2014. [Google Scholar] [CrossRef]
- Majid, A.S.; Joelianto, E. Optimal sensor deployment in non-convex region using Discrete Particle Swarm Optimization algorithm. In Proceedings of the 2012 IEEE Conference on Control, Systems & Industrial Informatics, Bandung, Indonesia, 23–26 September 2012. [Google Scholar] [CrossRef]
- Li, Z.; Lei, L. Sensor node deployment in wireless sensor networks based on improved particle swarm optimization. In Proceedings of the 2009 International Conference on Applied Superconductivity and Electromagnetic Devices, Chengdu, China, 25–27 September 2009. [Google Scholar] [CrossRef]
- Xiao, Z.; Yan, J.; Yan, X.; Cheng, G.; Qiang, X. A New Optimal Deployment Algorithm for Actor Node in WSAN. In Proceedings of the 2015 International Conference on Network and Information Systems for Computers, Wuhan, China, 23–25 January 2015. [CrossRef]
- Xu, S.; Doğançay, K. Optimal sensor deployment for 3D AOA target localization. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, J.; Sheng, M.; Han, S.; Shi, Y.; Valaee, S. Toward Practical Access Point Deployment for Angle-of-Arrival Based Localization. IEEE Trans. Commun. 2021, 69, 2002–2014. [Google Scholar] [CrossRef]
- Li, S.; Liu, G.; Ding, S.; Li, H.; Li, O. Finding an Optimal Geometric Configuration for TDOA Location Systems With Reinforcement Learning. IEEE Access 2021, 9, 63388–63397. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 1–23. [Google Scholar] [CrossRef]
- Shamaei, K.; Khalife, J.; Kassas, Z.M. Exploiting LTE Signals for Navigation: Theory to Implementation. IEEE Trans. Wireless Commun. 2018, 17, 2173–2189. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Ping, D.; Song, B.; Zhang, H. Optimization of Multi-Machine Passive Positioning System Based on PSO. Comp. Digital Eng. 2021, 49, 487–492. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 2, 95–99. [Google Scholar] [CrossRef]
- Yang, X.-S.; He, X. Firefly algorithm: Recent advances and applications. Int. J. Swarm Intell. 2013, 1, 36–50. [Google Scholar] [CrossRef] [Green Version]
- Durmus, A.; Kurban, R.; Karakose, E. A comparison of swarm-based optimization algorithms in linear antenna array synthesis. J. Comput. Electron. 2021, 20. [Google Scholar] [CrossRef]
- Homaifar, A.; Qi, C.X.; Lai, S.H. Constrained optimization via genetic algorithms. Simulation 1994, 62, 242–253. [Google Scholar] [CrossRef]
- Michalewicz, Z.; Dasgupta, D.; Le Riche, R.G.; Schoenauer, M. Evolutionary algorithms for constrained engineering problems. Comput. Ind. Eng. 1996, 30, 851–870. [Google Scholar] [CrossRef]
- Haspel, M. Geometric optimization of a time-of-arrival (TOA) based self-positioning terrestrial system. In Proceedings of the 2011 IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems (COMCAS 2011), Tel Aviv, Israel, 7–9 November 2011. [Google Scholar] [CrossRef]
- Dana, P. Global Positioning System Overview. Available online: http://gisweb.massey.ac.nz/topic/webreferencesites/gps/danagps/gps.html (accessed on 8 September 2021).





| Algorithm | Best Fitness (m) | Best Solution | Convergence | ||||
|---|---|---|---|---|---|---|---|
| S0 (m) | S1 (m) | S2 (m) | S3 (m) | ||||
| GA | 2.1174 | x | −11.5593 | 180.4777 | 27.4115 | −180.3046 | 22 |
| y | −186.2205 | 6.2025 | 181.0768 | 6.1282 | |||
| z | 4.7982 | 4.8517 | 3.0579 | 2.7393 | |||
| PSO | 2.096 | x | 2.1101 | 180 | −10.2916 | −180 | 56 |
| y | −180 | 6.4877 | 180 | 7.4060 | |||
| z | 3.9209 | 3.1175 | 2.1361 | 4.0180 | |||
| ABC | 2.1198 | x | 1.7987 | 180 | −3.9197 | −181.4895 | 35 |
| y | −180 | 13.9337 | 190.0083 | 22.5678 | |||
| z | 5 | 5 | 5 | 5 | |||
| MOA | 2.0914 | x | −8.9245 × 10−6 | 180.0001 | −1.7622 × 10−6 | −180 | 42 |
| y | −180 | 13.3577 | 180 | 13.3577 | |||
| z | 5 | 5 | 5 | 5 | |||
| Deployment | Best Fitness (m) | Best Solution | ||||
|---|---|---|---|---|---|---|
| S0 (m) | S1 (m) | S2 (m) | S3 (m) | |||
| Surrounding (moa01) | 2.7173 | x1 | 7.5222 | 160, | 0.9865 | −160 |
| y1 | −160 | −2.2527 | 160 | 23.6182 | ||
| z1 | 1.0603 | 3 | 2.9971 | 3 | ||
| Double-side (moa02) | 2.9254 | x2 | 37.7234 | −121.025 | 58.2313 | −53.0542 |
| y2 | −160 | −160 | 160 | 160 | ||
| z2 | 3 | 3 | 3 | 3 | ||
| Vertical Adjacent (moa03) | 3.0493 | x3 | −164.5013 | 38.5807 | 160 | 160 |
| y3 | −160 | −160 | 14.5338 | 147.1652 | ||
| z3 | 3 | 3 | 3 | 3 | ||
| Single-side (moa04) | 4.104 | x4 | −200 | 2.1497 | 128.7016 | 160 |
| y4 | −160 | −160 | −160 | −160 | ||
| z4 | 3 | 3 | 3 | 3 | ||
| S0 | Best Fitness (m) | Best Solution | ||||
|---|---|---|---|---|---|---|
| S1 (m) | S2 (m) | S3 (m) | S4 (m) | |||
| (180, −180, 3) moa05 | 2.4308 | x | −152.9574 | −12.8670, | 160 | 160 |
| y | −160 | −160 | 143.4871 | 25.0102 | ||
| z | 3 | 1 | 3 | 1.7007 | ||
| (−200, −200, 3) moa06 | 2.2625 | x | −82.6562 | 40.8520 | 160 | 160 |
| y | −160 | −160 | −31.9998 | 93.7736 | ||
| z | 3 | 1 | 1 | 1 | ||
| (−200, 200, 3) moa07 | 2.3165 | x | −120.2850 | 21.7966 | 160 | 160 |
| y | −160 | −160 | −11.6254 | 124.7243 | ||
| z | 1 | 1 | 1 | 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, A.; Deng, Z.; Yang, H.; Zhang, Y.; Gao, Y.; Zhao, D. An Optimal Geometry Configuration Algorithm of Hybrid Semi-Passive Location System Based on Mayfly Optimization Algorithm. Sensors 2021, 21, 7484. https://doi.org/10.3390/s21227484
Hu A, Deng Z, Yang H, Zhang Y, Gao Y, Zhao D. An Optimal Geometry Configuration Algorithm of Hybrid Semi-Passive Location System Based on Mayfly Optimization Algorithm. Sensors. 2021; 21(22):7484. https://doi.org/10.3390/s21227484
Chicago/Turabian StyleHu, Aihua, Zhongliang Deng, Hui Yang, Yao Zhang, Yuhui Gao, and Di Zhao. 2021. "An Optimal Geometry Configuration Algorithm of Hybrid Semi-Passive Location System Based on Mayfly Optimization Algorithm" Sensors 21, no. 22: 7484. https://doi.org/10.3390/s21227484
APA StyleHu, A., Deng, Z., Yang, H., Zhang, Y., Gao, Y., & Zhao, D. (2021). An Optimal Geometry Configuration Algorithm of Hybrid Semi-Passive Location System Based on Mayfly Optimization Algorithm. Sensors, 21(22), 7484. https://doi.org/10.3390/s21227484






