Fuzzy Logic in Aircraft Onboard Systems Reliability Evaluation—A New Approach
Abstract
1. Introduction
- Failure risk analysis and assessment.Fuzzy logic is mainly used to estimate risk and determine the probability of damage. An example research article describing this trend is a study showing the effective use of fuzzy numbers as inputs and outputs in the isobutane cylinder rupture risk analysis based on Fault Tree and Event Tree methods [10]. Other studies based on real source data of two Italian industrial plants (a tyre manufacturing company and a chemical plant) indicate that fuzzy logic can be successfully applied to quantify the risk of accidents at work [11]. Fuzzy logic was also used in aviation [12,13]. It was used to assess the risk of a helicopter crash depending on two factors: intensity of operations and the probability of a crash [14].
- Human factors leading to damage.Fuzzy logic is used to model the uncertainty associated with human error factors. Research [15] has indicated the possibility of using fuzzy logic to define quality standards for operations, maintenance, and production activities, which can significantly reduce errors made by oil refinery personnel. Fuzzy logic and expert judgement have also been successfully used to determine the probability of human error among nuclear plant operators. The research results presented in [16] demonstrate the effectiveness of using fuzzy logic to determine the significance of risk of human error. Other studies which use fuzzy logic, taking into account human error and uncertainty in failure data, aim at assessing the imprecise failure probability of level crossing systems in Morocco [17]. A further example of the application of fuzzy logic in aviation is the study of the influence of human factors on damage. It has been successfully used to assess basic event failure rates for safety-critical avionics systems [18].
- Adequate planning of maintenance, and consequently, prevention of damage.Fuzzy logic has also been successfully used for proper planning of maintenance, and thus, to prevent damage. In article [19], fuzzy logic was successfully applied to model imprecise answers in a reliability-centered maintenance (RCM) diagram to answer questions on the causes, symptoms, and types of failure. Additionally, a maintenance-oriented milling machine reliability study using fuzzy logic and comparing it with the conventional method allowed a more accurate determination of the causes and consequences of failure [20]. Fuzzy logic was also used to determine specific maintenance tasks used to make reactions in chemical plants, based on equipment operating data. Along with neural networks, fuzzy logic complemented the RCM strategy [21].
2. Research Methodology
- Analysing the available literature with a particular emphasis on the applications of fuzzy logic and the reliability issues of technical systems [9];
- Analysing available methods for estimating the systems reliability in a mathematical approach;
- Computing the reliability indicators of a selected airborne armament system, by means of a mathematical approach (based on statistical data from an IT-based aircraft reliability analysis system);
- Developing a reliability model of a selected airborne armament system by means of fuzzy logic;
- Assessing the reliability indicators of the aircraft armament system on the basis of the developed model, by means of fuzzy logic (using input signals from an IT system for the aircraft reliability analysis);
- Comparing the results obtained in the mathematical approach and the fuzzy set theory approach;
- Formulating and presenting the conclusions.
3. Object of Research
4. Scientific Approach
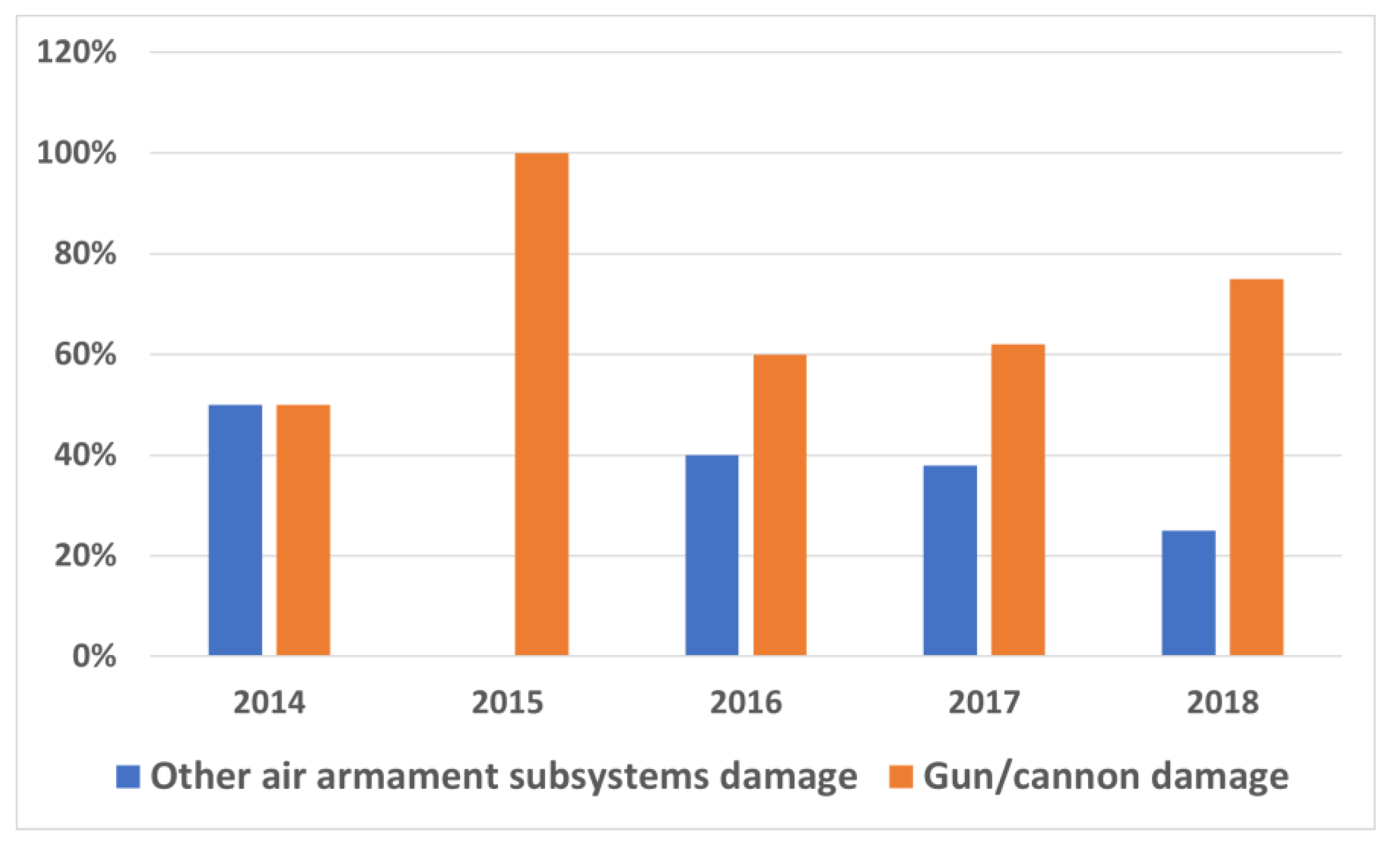
4.1. Analysis of Statistical Data
4.2. Probabilistic Model of Reliability of the Gun/Cannon Subsystem
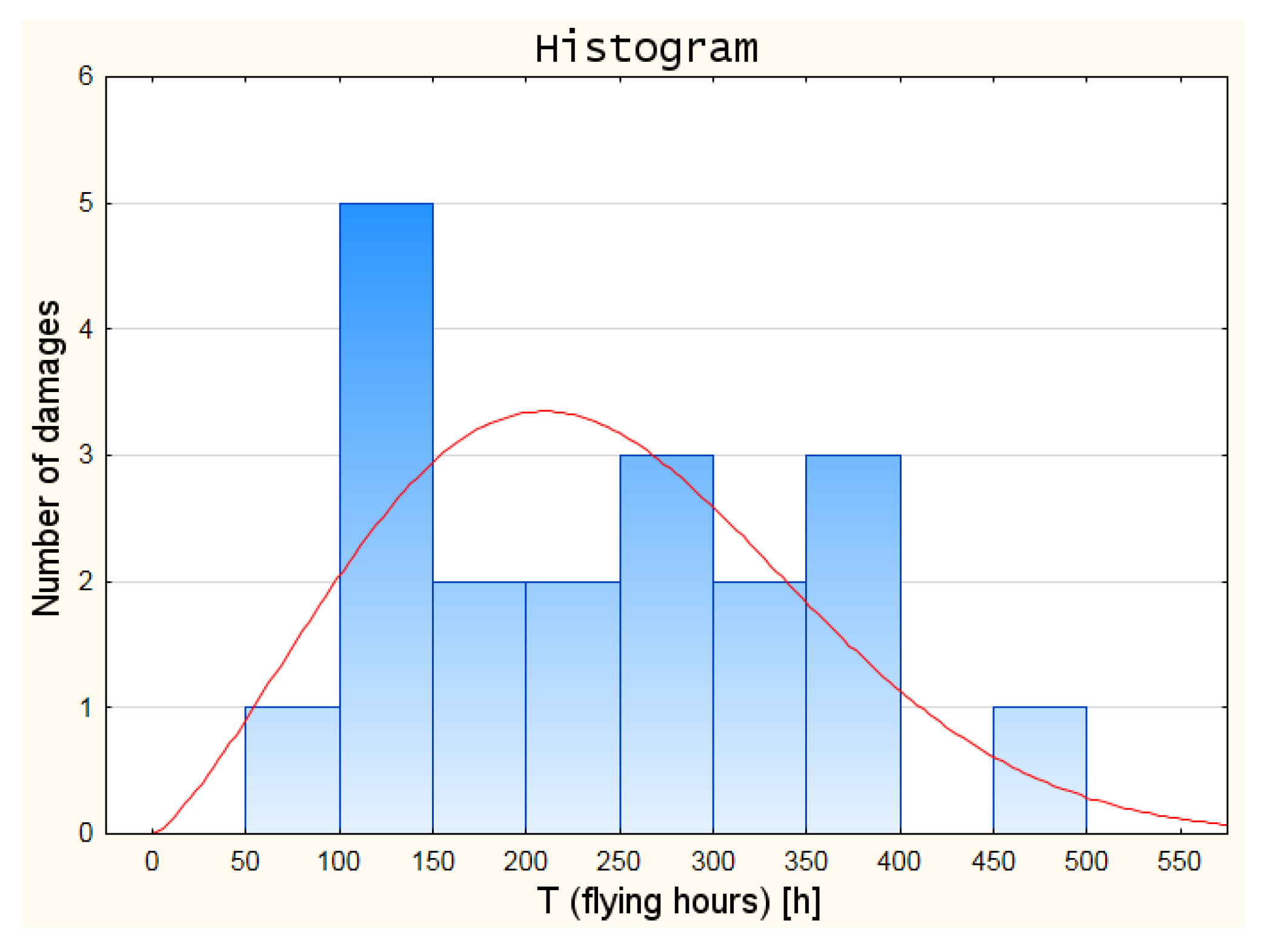
4.2.1. Alignment of Measurement Results
4.2.2. Fitting the Distribution of a Random Variable
- shape parameter α—2.2664
- scale parameter β—318.78
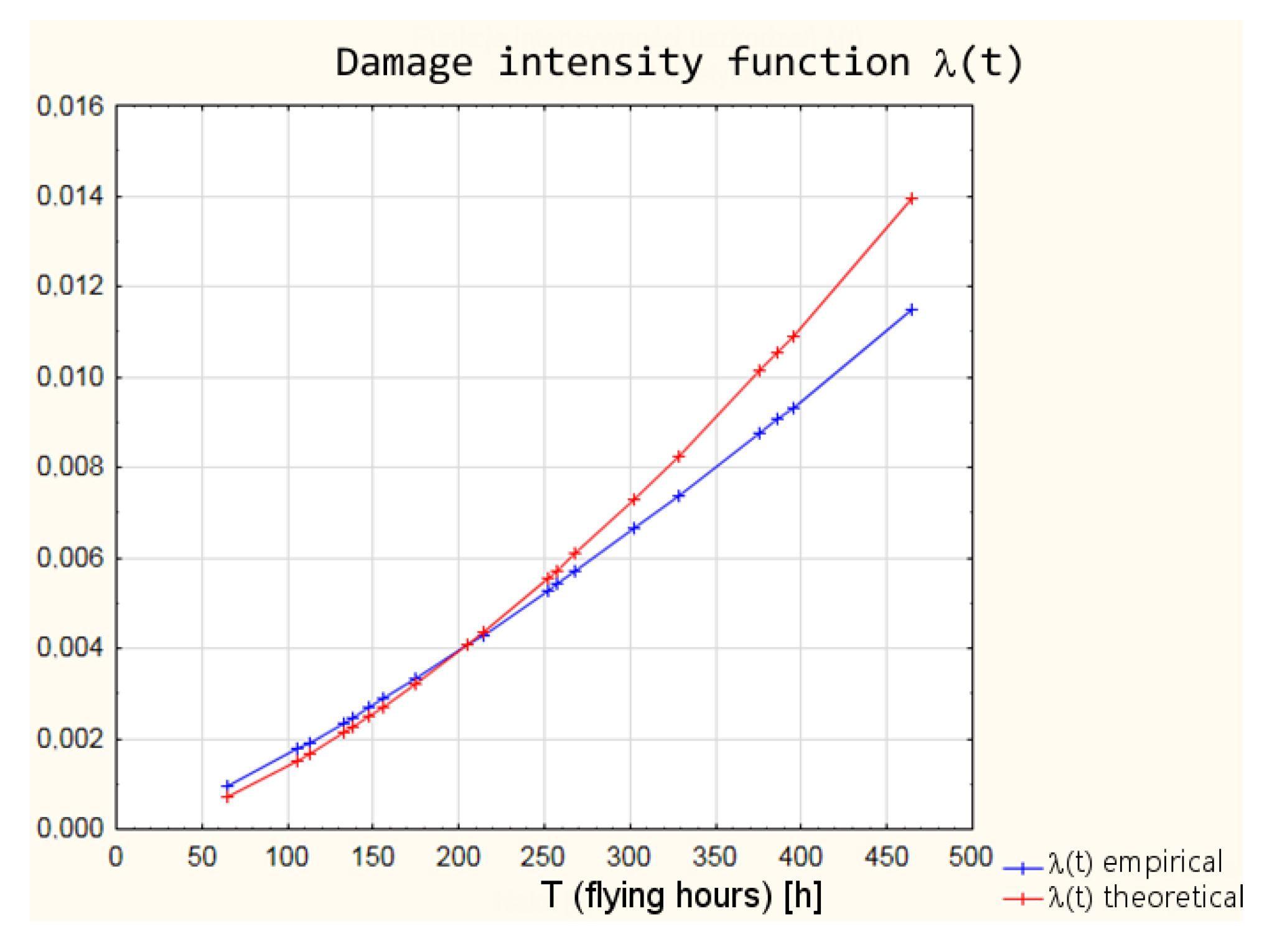
- function of the intensity of the damage λ(t)
- density distribution function f(t)
- random variable distribution F(t)
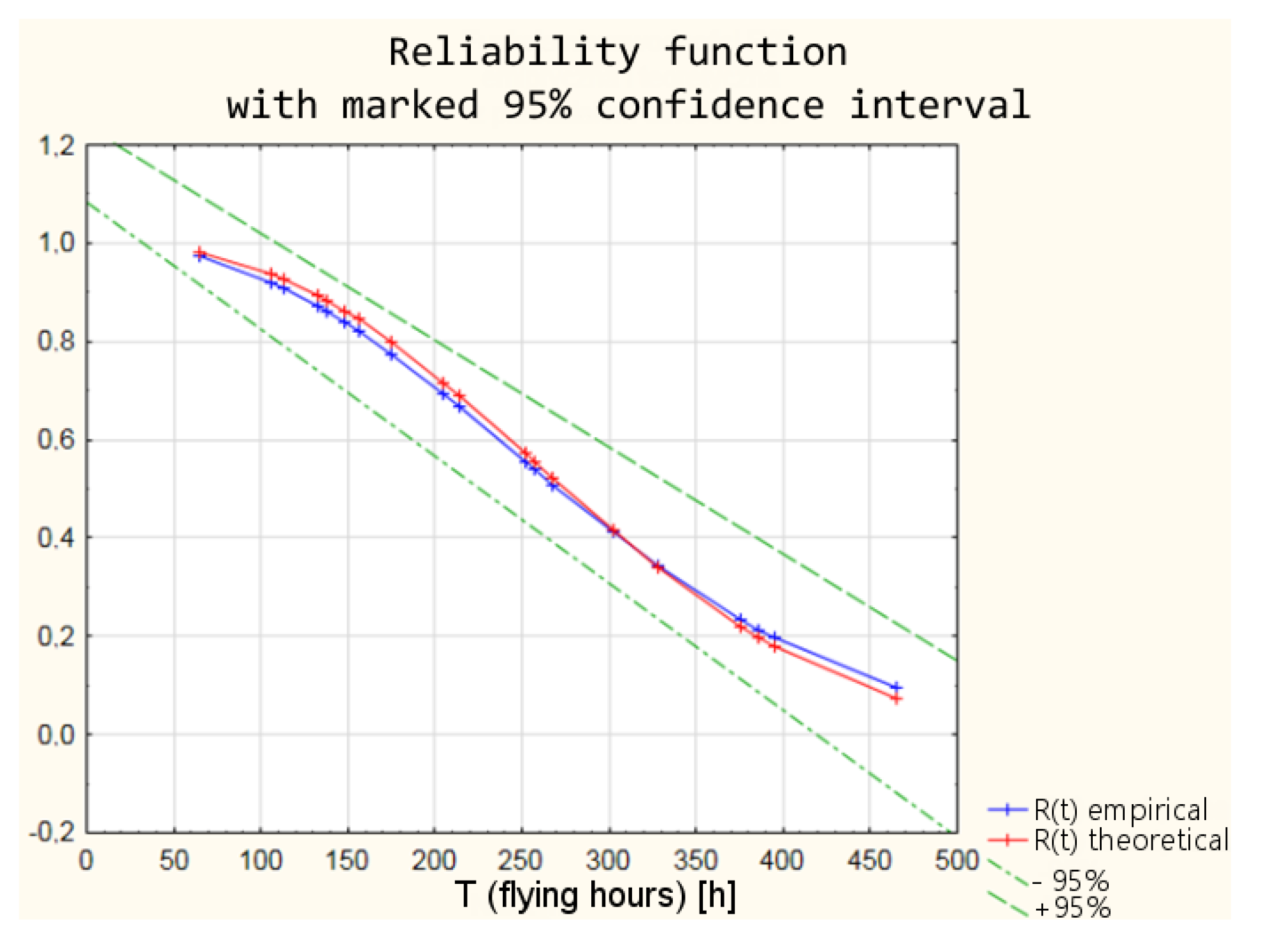
- the reliability function R(t).
4.3. Fuzzy Logic Reliability Model of a Firing Subsystem
4.4. Model Tests
4.5. Comparison of Research Findings
5. Conclusions
- Fatigue processes are an important causal group of damage to the shooting armament of the TS-11 “Iskra” aircraft.
- The differences between the parameters of empirical Weibull distribution from the operational data and the graphic method of determining the parameters, and theoretical Weibull distribution are within the 95% confidence interval, which means that with a probability of 95%, reliability indicators from both the empirical and theoretical distribution can be used in further studies on the armament reliability.
- The interpretation and comparison of the results obtained from the reliability analysis in the classical approach and the reliability analysis in the fuzzy set theory approach allowed formulating the following conclusions:
- In order to develop a reliability model using fuzzy logic, access to reliable expert knowledge is necessary.
- Fuzzy logic offers a possibility to determine reliability based on various parameters and also allows an analysis and interpretation of the relationship between input parameter values and reliability.
- The developed reliability model using fuzzy logic can be used to assess the reliability of various systems without the need for knowledge of an extensive mathematical apparatus.
- The controller pattern, designed with a fuzzy logic reliability model, can be easily upgraded by changing the membership functions (shapes and limits) and the deduction principles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kaboli, S.; Oraee, H. Reliability in Power Electronics and Electrical Machines: Industrial Applications and Performance Models; Advances in Computer and Electrical Engineering; IGI Global: Hershey, PA, USA, 2016; ISBN 978-1-4666-9429-3. [Google Scholar]
- Signoret, J.-P.; Leroy, A. Reliability Study Overview. In Reliability Assessment of Safety and Production Systems: Analysis, Modelling, Calculations and Case Studies; Signoret, J.-P., Leroy, A., Eds.; Springer Series in Reliability Engineering; Springer International Publishing: Cham, Switzerland, 2021; pp. 29–42. ISBN 978-3-030-64708-7. [Google Scholar]
- Singh, A.; Mourelatos, Z.P. Time-Dependent Reliability Estimation for Dynamic Systems Using a Random Process Approach. SAE Int. J. Mater. Manuf. 2010, 3, 339–355. [Google Scholar] [CrossRef]
- Tseng, K.-H.; Liang, J.-W.; Chang, W.; Huang, S.-C. Regression Models Using Fully Discharged Voltage and Internal Resistance for State of Health Estimation of Lithium-Ion Batteries. Energies 2015, 8, 2889–2907. [Google Scholar] [CrossRef]
- Chakrabarty, I.; Padmasali, A.N.; Kini, S. Time Series Modelling for Lifetime Estimation of Solid State Luminaires. In Proceedings of the 2nd IEEE International Conference on Recent Trends in Electronics, Information and Communication Technology, RTEICT, Piscatawa, NJ, USA, 19–20 May 2017; pp. 662–666. [Google Scholar] [CrossRef]
- Zieja, M.; Ważny, M.; Jasztal, M.; Stępień, S.; Michalski, M. The Probabilistic Method for Predicting the Reliability of Aircraft’s Commutator Devices. In Proceedings of the 29th European Safety and Reliability Conference, Hanover, Germany, 22–26 September 2019. [Google Scholar]
- An Expert System for Ensuring the Reliability of the Technological Process of Cold Sheet Metal Forming—IOPscience. Available online: https://iopscience.iop.org/article/10.1088/1757-899X/134/1/012032 (accessed on 8 October 2021).
- Using Expert Models in Human Reliability Analysis—A Dependence Assessment Method Based on Fuzzy Logic. Podofillini—2010 Risk Analysis. Wiley Online Library. Available online: https://onlinelibrary.wiley.com/doi/10.1111/j.1539-6924.2010.01425.x (accessed on 8 October 2021).
- Kuźma, K.; Grzesik, N.; Ćwiklak, J.; Zieja, M. Analysis of a Possibility of Using Fuzzy Logic to Assess the Reliability of Aircraft On-Board Systems. J. KONBiN 2019, 49, 183–198. [Google Scholar] [CrossRef]
- Markowski, A.S.; Mannan, M.S.; Bigoszewska, A. Fuzzy Logic for Process Safety Analysis. J. Loss Prev. Process Ind. 2009, 22, 695–702. [Google Scholar] [CrossRef]
- Murè, S.; Demichela, M. Fuzzy Application Procedure (FAP) for the Risk Assessment of Occupational Accidents. J. Loss Prev. Process Ind. 2009, 22, 593–599. [Google Scholar] [CrossRef]
- Ali, B.; Ashraf, M.W.; Tayyaba, S. Simulation, Fuzzy Analysis and Development of ZnO Nanostructure-Based Piezoelectric MEMS Energy Harvester. Energies 2019, 12, 807. [Google Scholar] [CrossRef]
- Zhao, H.; Zhu, Z.; Sun, H. Adaptive Robust Control and Optimal Design for Fuzzy Unmanned Helicopter Tail Reduction. Int. J. Fuzzy Syst. 2020, 22, 1400–1415. [Google Scholar] [CrossRef]
- Pokorádi, L. Application of Fuzzy Set Theory for Risk Assessment. J. KONBiN 2010, 14, 187–196. [Google Scholar] [CrossRef]
- More, J.D.; Tanscheit, R.; Vellasco, M.M.; Pacheco, M.A.; Swarcman, D.M. A Fuzzy Approach to the Study of Human Reliability in the Petroleum Industry. In Theoretical Advances and Applications of Fuzzy Logic and Soft Computing; Castillo, O., Melin, P., Ross, O.M., Sepúlveda Cruz, R., Pedrycz, W., Kacprzyk, J., Eds.; Advances in Soft Computing; Springer: Berlin/Heidelberg, Germany, 2007; pp. 415–424. ISBN 978-3-540-72434-6. [Google Scholar]
- Li, P.; Chen, G.; Dai, L.; Li, Z. Fuzzy Logic-Based Approach for Identifying the Risk Importance of Human Error. Saf. Sci. 2010, 48, 902–913. [Google Scholar] [CrossRef]
- Boudnaya, J.; Sallak, M.; Mkhida, A. Dependability Analysis of Level Crossing Systems Using a Fuzzy Dynamic Fault Tree Approach. In Proceedings of the Safety and Reliability of Complex Engineered Systems-Proceedings of the 25th European Safety and Reliability Conference, Zürich, Switzerland, 7–10 September 2015. [Google Scholar]
- Tu, J.; Cheng, R.; Tao, Q. Reliability Analysis Method of Safety-Critical Avionics System Based on Dynamic Fault Tree under Fuzzy Uncertainty. Eksploat. I Niezawodn.-Maint. Reliab. 2015, 17, 156–163. [Google Scholar] [CrossRef]
- Felecia Fuzzy Logic Reliability Centered Maintenance. J. Tek. Ind. 2014, 16, 121–126. [CrossRef]
- Gupta, G.; Mishra, R.P. A Failure Mode Effect and Criticality Analysis of Conventional Milling Machine Using Fuzzy Logic: Case Study of RCM. Qual. Reliab. Eng. Int. 2017, 33, 347–356. [Google Scholar] [CrossRef]
- Aguilar, J.; Cerrada, M.; Morillo, K. A Reliability-Based Failure Management Application Using Intelligent Hybrid Systems. IFAC Proc. Vol. 2000, 33, 201–206. [Google Scholar] [CrossRef]
- Bowles, J.B.; Pelaez, C.E. Application of Fuzzy Logic to Reliability Engineering. Proc. IEEE 1995, 83, 435–449. [Google Scholar] [CrossRef]
- Rotshtein, A.; Katielnikov, D.; Pustylnik, L. Reliability Modeling and Optimization Using Fuzzy Logic and Chaos Theory. Int. J. Qual. Stat. Reliab. 2012, 2012, 847416. [Google Scholar] [CrossRef][Green Version]
- WSK Mielec. Technical description of the TS-1. In PZL TS-11 Iskra; Ministry of the Machine Industry, WSK Mielec: Mielec, Poland, 1973. [Google Scholar]
- Grubbs, F.E. Sample Criteria for Testing Outlying Observations. Ann. Math. Stat. 1950, 21, 27–58. [Google Scholar] [CrossRef]









| Type | Data |
|---|---|
| Length | 11.15 m |
| Wingspan | 10.06 m |
| Height | 3.50 m |
| Lifting surface | 17.50 m² |
| Unloaded | 2560 kg |
| Gross weight | 3724 kg |
| Maximum take-off weight | 3840 kg |
| Engine | WSK SO-3W with a thrust of 10.80 kN (1100 kG) |
| Maximum speed | 720 km/h in 5000 m |
| Range | 1260 km |
| Operational ceiling | 11,000 m |
| Climb rate | 14.8 m/s |
| Wing loading | 213 kg/m² |
| Thrust-to-weight ratio | 1:3.4 |
| Type | Data |
|---|---|
| Calibre | 23 mm |
| Rate of fire | 500–590 rounds/min |
| Gun weight | 37.5–38.2 kg |
| Length | 1985 mm |
| Width | 164 mm |
| Height | 256 mm |
| Barrel length | 1450 mm |
| Minimum air pressure required for reloading | 30 kG/cm2 |
| No | Observation | Flying Hours from 2014 to 2018 | T (Flying Hours Until Malfunction [h]) | Censored Observations |
|---|---|---|---|---|
| 1 | O10 | 313 | 65 | complete |
| 2 | O9 | 80 | 80 | censored |
| 3 | O14 | 95 | 95 | censored |
| 4 | O5 | 249 | 106 | complete |
| 5 | O8 | 391 | 113 | complete |
| 6 | O3 | 148 | 133 | complete |
| 7 | O11 | 305 | 138 | complete |
| 8 | O1 | 296 | 148 | complete |
| 9 | O28 | 310 | 156 | complete |
| 10 | O24 | 247 | 175 | complete |
| 11 | O7 | 204 | 204 | censored |
| 12 | O21 | 410 | 205 | complete |
| 13 | O4 | 246 | 214 | complete |
| 14 | O12 | 232 | 232 | censored |
| 15 | O22 | 243 | 243 | censored |
| 16 | O26 | 251 | 251 | censored |
| 17 | O29 | 423 | 252 | complete |
| 18 | O23 | 314 | 257 | complete |
| 19 | O2 | 278 | 268 | complete |
| 20 | O25 | 278 | 278 | censored |
| 21 | O30 | 294 | 294 | censored |
| 22 | O27 | 297 | 297 | censored |
| 23 | O16 | 453 | 302 | complete |
| 24 | O6 | 307 | 307 | censored |
| 25 | O13 | 310 | 310 | censored |
| 26 | O15 | 442 | 328 | complete |
| 27 | O20 | 490 | 376 | complete |
| 28 | O18 | 448 | 386 | complete |
| 29 | O19 | 477 | 395 | complete |
| 30 | O17 | 519 | 465 | complete |
| No | Observation | Flying Hours from 2014 to 2018 | Flying Hours Until Malfunction (h) | η |
|---|---|---|---|---|
| 1 | O10 | 313 | 65 | 1.495158054 |
| 2 | O5 | 249 | 106 | 1.136449054 |
| 3 | O8 | 391 | 113 | 1.075206054 |
| 4 | O3 | 148 | 133 | 0.900226054 |
| 5 | O11 | 305 | 138 | 0.856481054 |
| 6 | O1 | 296 | 148 | 0.768991054 |
| 7 | O28 | 310 | 156 | 0.698999054 |
| 8 | O24 | 247 | 175 | 0.532768054 |
| 9 | O21 | 410 | 205 | 0.270298054 |
| 10 | O4 | 246 | 214 | 0.191557054 |
| 11 | O29 | 423 | 252 | 0.140904946 |
| 12 | O23 | 314 | 257 | 0.184649946 |
| 13 | O2 | 278 | 268 | 0.280888946 |
| 14 | O16 | 453 | 302 | 0.578354946 |
| 15 | O15 | 442 | 328 | 0.805828946 |
| 16 | O20 | 490 | 376 | 1.225780946 |
| 17 | O18 | 448 | 386 | 1.313270946 |
| 18 | O19 | 477 | 395 | 1.392011946 |
| 19 | O17 | 519 | 465 | 2.004441946 |
| d K-S | K-S p | |
|---|---|---|
| Weibull | 0.080785 | 0.980681 |
| Generalised extreme value | 0.080995 | 0.980185 |
| Normal | 0.083536 | 0.973478 |
| Gaussian mixture | 0.083917 | 0.972358 |
| Johnson SB | 0.086214 | 0.964943 |
| Rayleigh | 0.136471 | 0.584155 |
| Log-normal | 0.141784 | 0.536058 |
| Triangular | 0.161554 | 0.373656 |
| Generalised Pareto | 0.166667 | 0.337101 |
| Semi-normal | 0.240961 | 0.051135 |
| Scale (β) | Shape (α) | |
|---|---|---|
| Empirical Weibull distribution | 318.78 | 2.2664 |
| Theoretical Weibull distribution | 318.06 | 2.5030 |
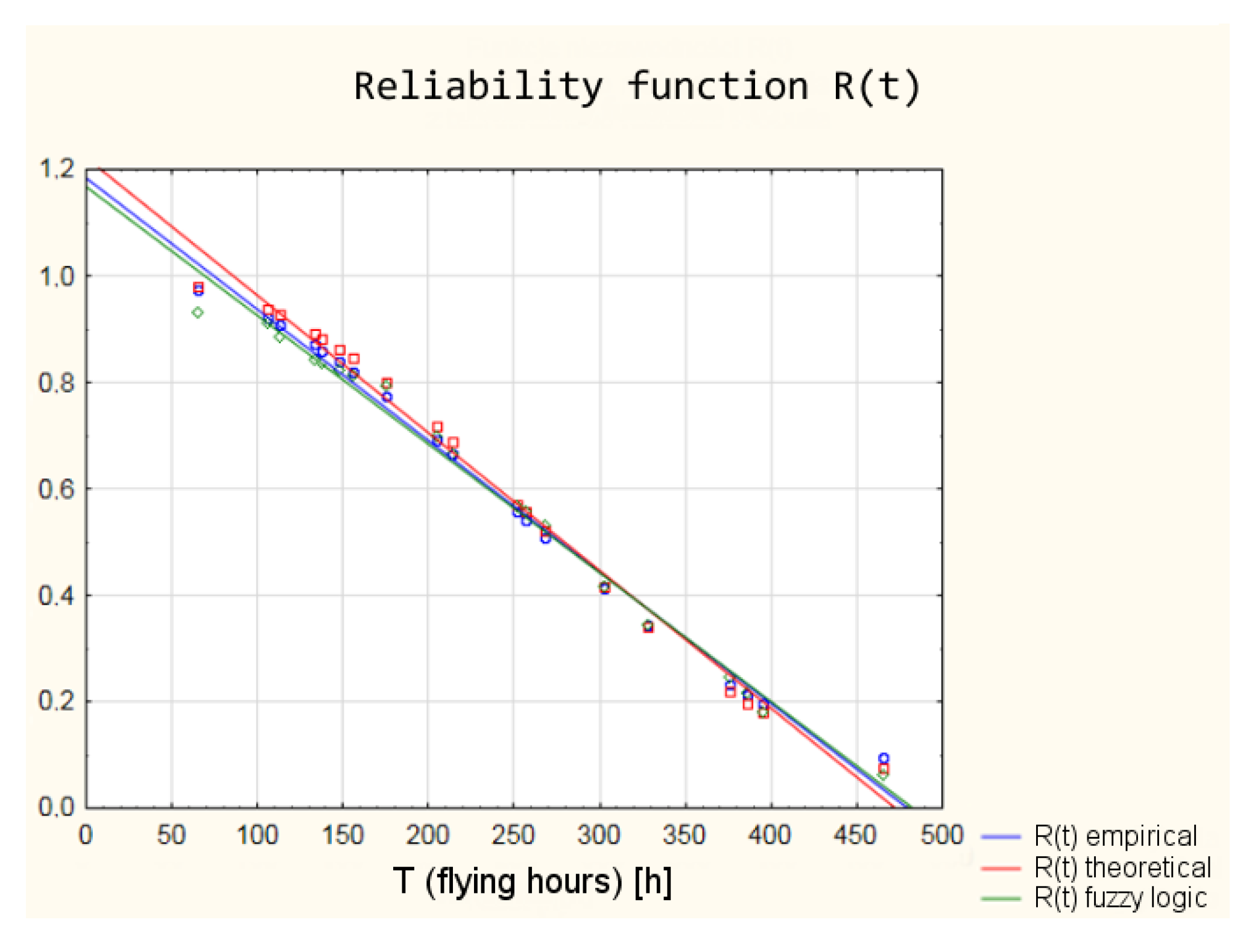
| Flying Hours Until Malfunction (h) | Empirical Density of Distribution f(t) | Theoretical Density of Distribution f(t) | Empirical Reliability R(t) | Theoretical Reliability R(t) |
|---|---|---|---|---|
| 65 | 0.00092 | 0.00071 | 0.97315 | 0.98139 |
| 106 | 0.00162 | 0.00142 | 0.92085 | 0.93809 |
| 113 | 0.00174 | 0.00154 | 0.90908 | 0.92774 |
| 133 | 0.00205 | 0.00190 | 0.87118 | 0.89335 |
| 138 | 0.00212 | 0.00198 | 0.86076 | 0.88365 |
| 148 | 0.00226 | 0.00215 | 0.83887 | 0.86298 |
| 156 | 0.00236 | 0.00228 | 0.82040 | 0.84526 |
| 175 | 0.00257 | 0.00256 | 0.77347 | 0.79919 |
| 205 | 0.00281 | 0.00292 | 0.69235 | 0.71672 |
| 214 | 0.00286 | 0.00299 | 0.66680 | 0.69012 |
| 252 | 0.00294 | 0.00317 | 0.55601 | 0.57214 |
| 257 | 0.00293 | 0.00318 | 0.54134 | 0.55626 |
| 268 | 0.00291 | 0.00317 | 0.50923 | 0.52132 |
| 302 | 0.00274 | 0.00303 | 0.41286 | 0.41546 |
| 328 | 0.00254 | 0.00280 | 0.34412 | 0.33957 |
| 376 | 0.00205 | 0.00221 | 0.23369 | 0.21866 |
| 386 | 0.00194 | 0.00208 | 0.21377 | 0.19721 |
| 395 | 0.00184 | 0.00195 | 0.19679 | 0.17909 |
| 465 | 0.00109 | 0.00105 | 0.09509 | 0.07522 |
| Input Signal | Membership Functions | |
|---|---|---|
| Flying hours [h] | VERY SMALL [0 0 105] SMALL [0 105 205] MEDIUM [105 205 305] LARGE [205 305 410] VERY LARGE [305 410 500 580] | 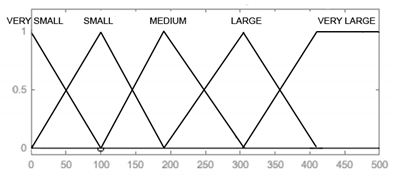 |
| Input Signal | Membership Functions | |
|---|---|---|
| Firing hours [number of shots] | VERY SMALL [0 0 400] SMALL [0 400 800] MEDIUM [400 800 1300] LARGE [800 1300 1800] VERY LARGE [1300 1800 2000 2000] |  |
| Input Signal | Membership Functions | |
|---|---|---|
| Corrosion [mm] | VERY SMALL [0 0 0.02] SMALL [0 0.02 0.04] MEDIUM [0.02 0.04 0.06] LARGE [0.04 0.06 0.075] VERY LARGE [0.06 0.075 0.1 0.1] |  |
| Output Signal | Membership Functions | |
|---|---|---|
| Reliability [P] | VERY SMALL [0 0 0.2] SMALL [0 0.2 0.4] MEDIUM [0.2 0.4 0.6] LARGE [0.4 0.6 0.8] VERY LARGE [0.6 0.8 1] OPTIMUM [0.8 1 1] | 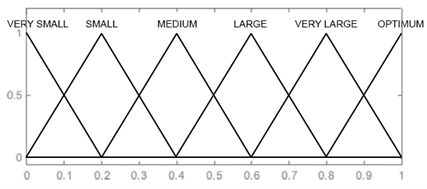 |
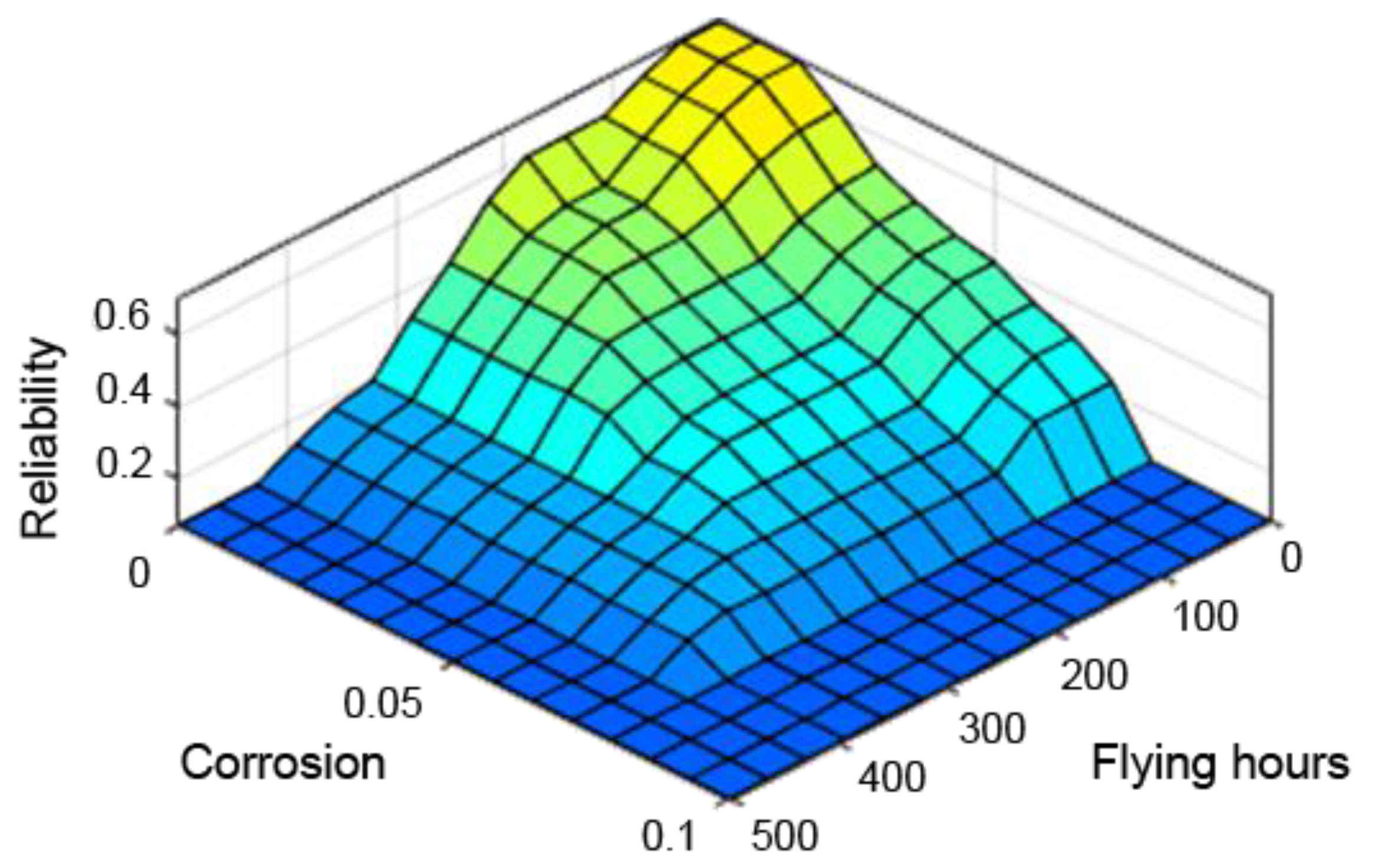
| No | Flying Hours (h) | Shots | Corrosion (mm) | R(t) |
|---|---|---|---|---|
| 1 | 65 | 0 | 0 | 0.9300 |
| 2 | 106 | 0 | 0 | 0.9100 |
| 3 | 113 | 0 | 0 | 0.8860 |
| 4 | 133 | 0 | 0 | 0.8430 |
| 5 | 138 | 0 | 0 | 0.8350 |
| 6 | 148 | 0 | 0 | 0.8220 |
| 7 | 156 | 0 | 0 | 0.8130 |
| 8 | 175 | 0 | 0 | 0.7950 |
| 9 | 205 | 0 | 0 | 0.6990 |
| 10 | 214 | 0 | 0 | 0.6650 |
| 11 | 252 | 0 | 0 | 0.5680 |
| 12 | 257 | 0 | 0 | 0.5560 |
| 13 | 268 | 0 | 0 | 0.5310 |
| 14 | 302 | 0 | 0 | 0.4160 |
| 15 | 328 | 0 | 0 | 0.3460 |
| 16 | 376 | 0 | 0 | 0.2470 |
| 17 | 386 | 0 | 0 | 0.2170 |
| 18 | 395 | 0 | 0 | 0.1790 |
| 19 | 465 | 0 | 0 | 0.0633 |
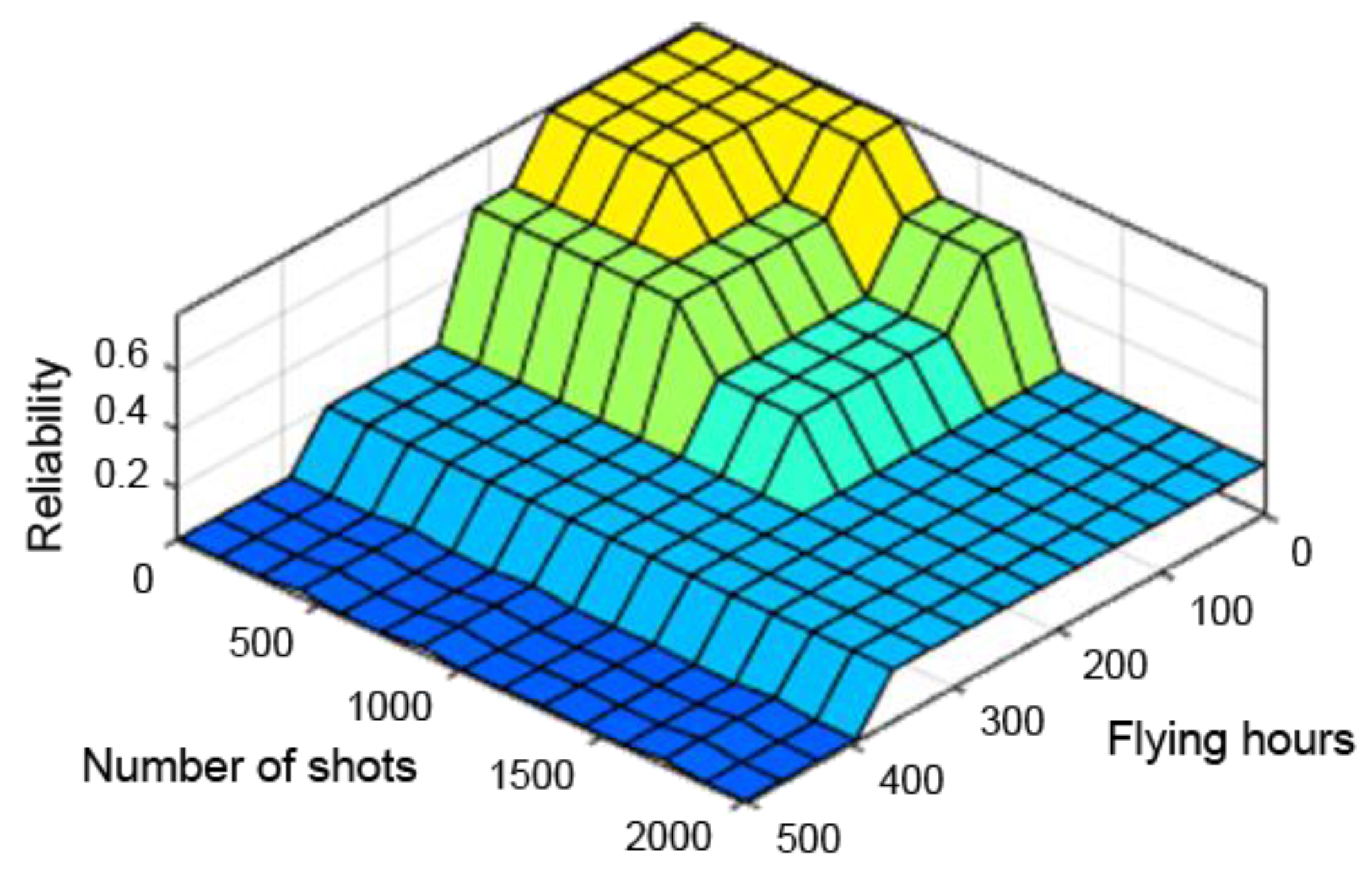
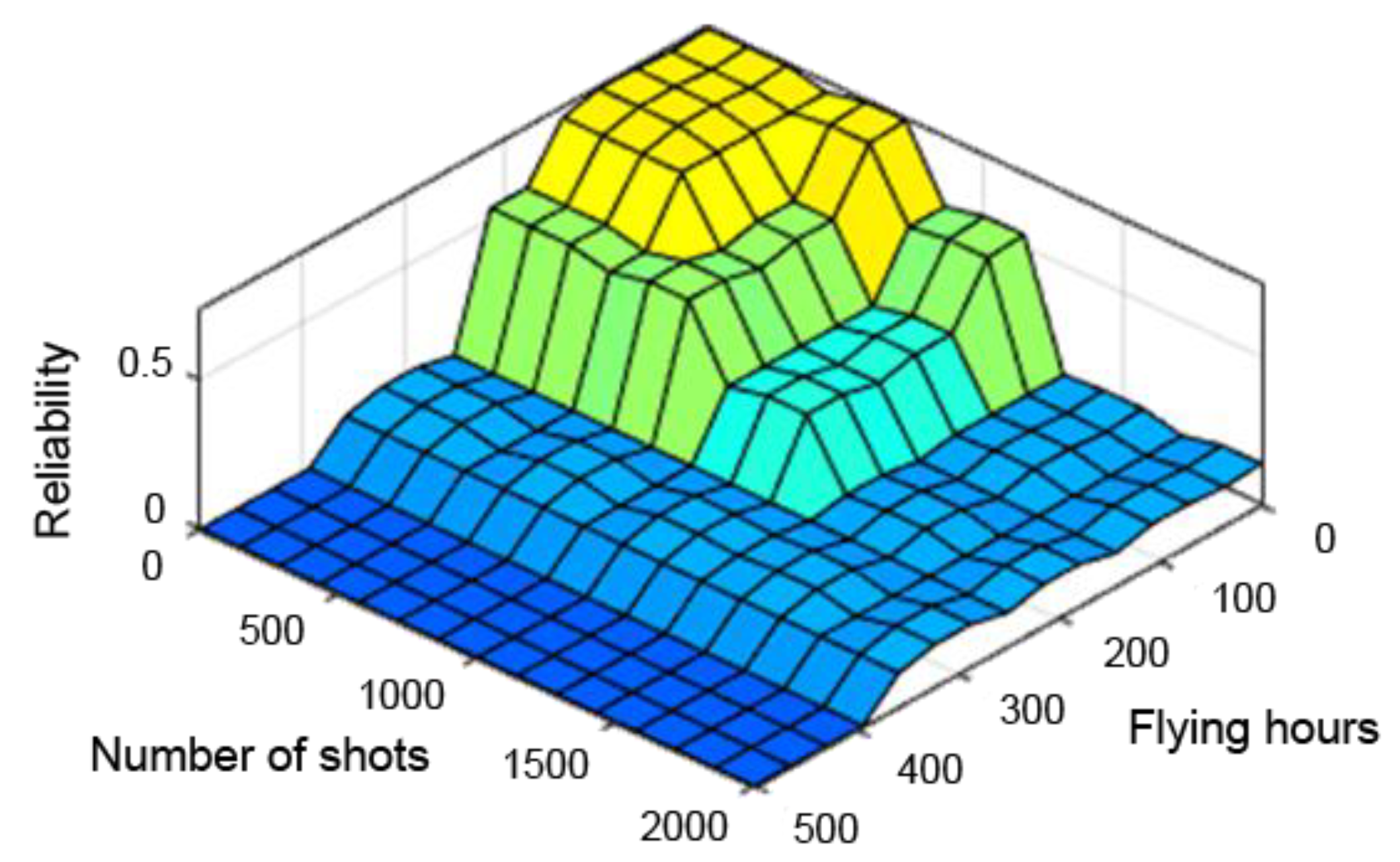
| No | Flying Hours [h] | Shots | Corrosion [mm] | R(t) Centre of Gravity Defuzzification Method | R(t) Method of Defuzzification of the Centre of Sums |
|---|---|---|---|---|---|
| 1 | 65 | 0 | 0 | 0.9300 | 0.9400 |
| 2 | 106 | 0 | 0 | 0.9100 | 0.9300 |
| 3 | 113 | 0 | 0 | 0.8860 | 0.9200 |
| 4 | 133 | 0 | 0 | 0.8430 | 0.8600 |
| 5 | 138 | 0 | 0 | 0.8350 | 0.8400 |
| 6 | 148 | 0 | 0 | 0.8220 | 0.8200 |
| 7 | 156 | 0 | 0 | 0.8130 | 0.8100 |
| 8 | 175 | 0 | 0 | 0.7950 | 0.7900 |
| 9 | 205 | 0 | 0 | 0.6990 | 0.7600 |
| 10 | 214 | 0 | 0 | 0.6650 | 0.7400 |
| 11 | 252 | 0 | 0 | 0.5680 | 0.5200 |
| 12 | 257 | 0 | 0 | 0.5560 | 0.5000 |
| 13 | 268 | 0 | 0 | 0.5310 | 0.4700 |
| 14 | 302 | 0 | 0 | 0.4160 | 0.4000 |
| 15 | 328 | 0 | 0 | 0.3460 | 0.3700 |
| 16 | 376 | 0 | 0 | 0.2470 | 0.2600 |
| 17 | 386 | 0 | 0 | 0.2170 | 0.1400 |
| 18 | 395 | 0 | 0 | 0.1790 | 0.1000 |
| 19 | 465 | 0 | 0 | 0.0633 | 0.0500 |
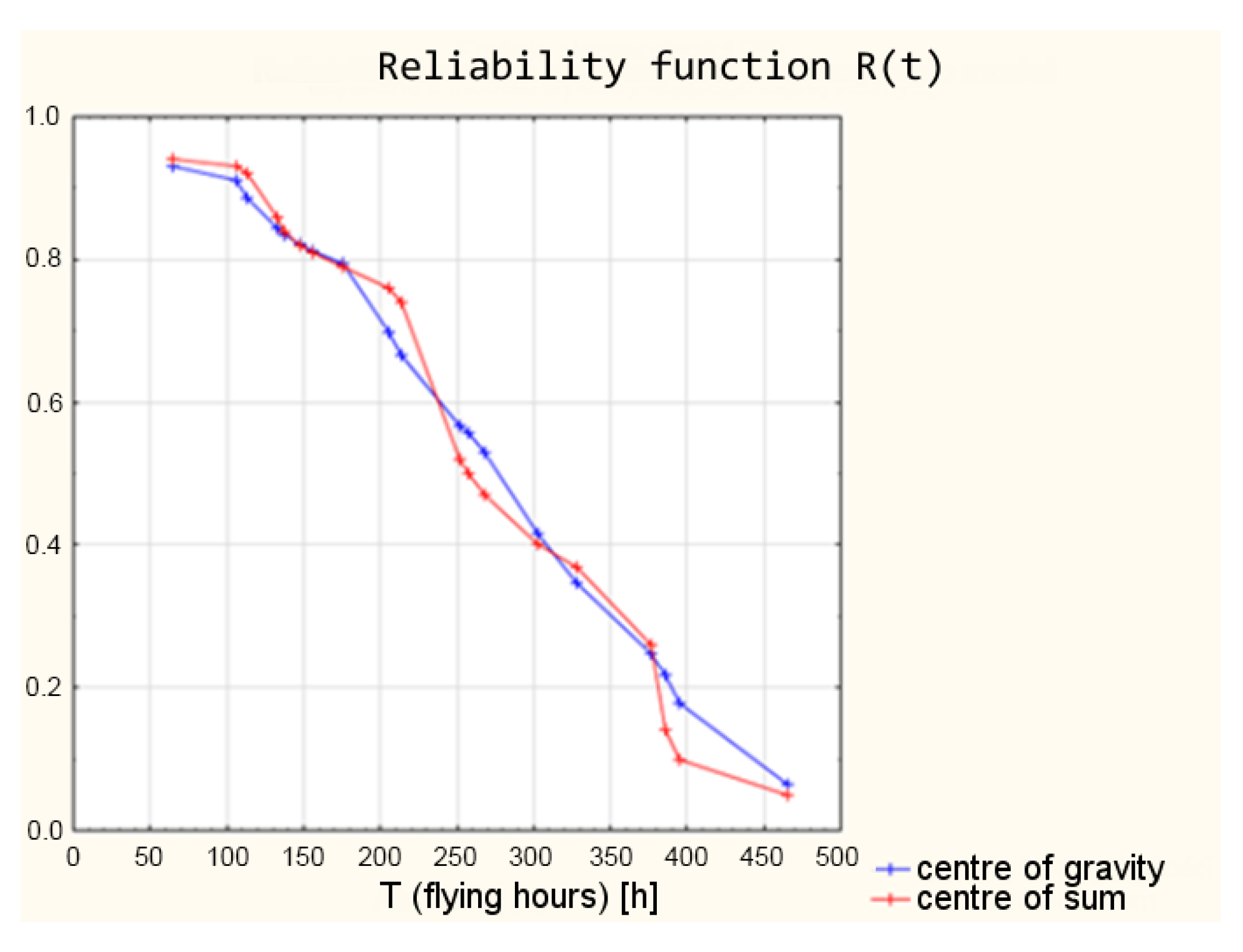
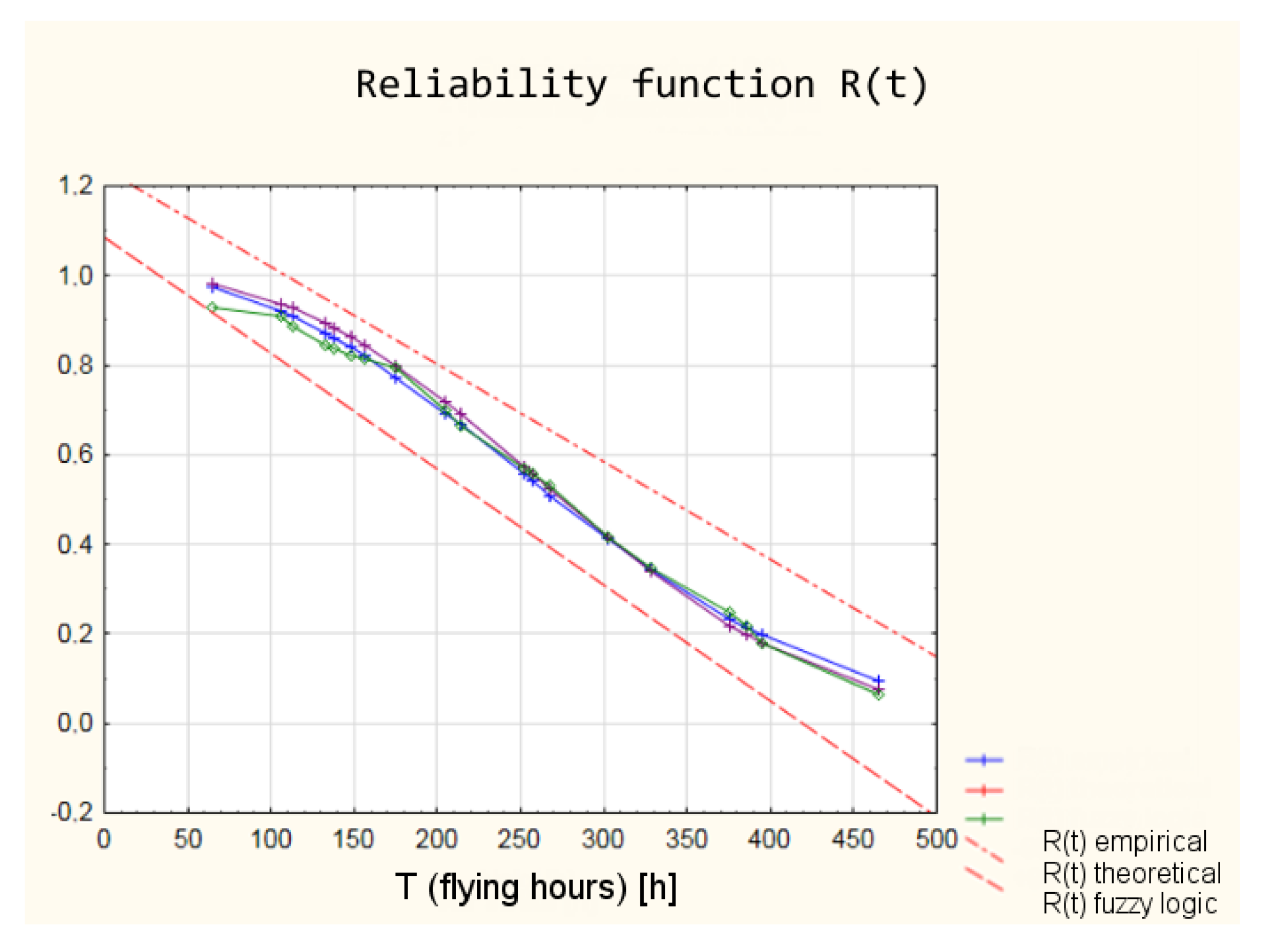
| No | Flying Hours (h) | R(t)—Classical Model (Empirical) | R(t)—Classical Model (Theoretical) | R(t)—Fuzzy Model |
|---|---|---|---|---|
| 1 | 65 | 0.97315 | 0.98139 | 0.9300 |
| 2 | 106 | 0.92085 | 0.93809 | 0.9100 |
| 3 | 113 | 0.90908 | 0.92774 | 0.8860 |
| 4 | 133 | 0.87118 | 0.89335 | 0.8430 |
| 5 | 138 | 0.86076 | 0.88365 | 0.8350 |
| 6 | 148 | 0.83887 | 0.86298 | 0.8220 |
| 7 | 156 | 0.82040 | 0.84526 | 0.8130 |
| 8 | 175 | 0.77347 | 0.79919 | 0.7950 |
| 9 | 205 | 0.69235 | 0.71672 | 0.6990 |
| 10 | 214 | 0.66680 | 0.69012 | 0.6650 |
| 11 | 252 | 0.55601 | 0.57214 | 0.5680 |
| 12 | 257 | 0.54134 | 0.55626 | 0.5560 |
| 13 | 268 | 0.50923 | 0.52132 | 0.5310 |
| 14 | 302 | 0.41286 | 0.41546 | 0.4160 |
| 15 | 328 | 0.34412 | 0.33957 | 0.3460 |
| 16 | 376 | 0.23369 | 0.21866 | 0.2470 |
| 17 | 386 | 0.21377 | 0.19721 | 0.2170 |
| 18 | 395 | 0.19679 | 0.17909 | 0.1790 |
| 19 | 465 | 0.09509 | 0.07522 | 0.0633 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żyluk, A.; Kuźma, K.; Grzesik, N.; Zieja, M.; Tomaszewska, J. Fuzzy Logic in Aircraft Onboard Systems Reliability Evaluation—A New Approach. Sensors 2021, 21, 7913. https://doi.org/10.3390/s21237913
Żyluk A, Kuźma K, Grzesik N, Zieja M, Tomaszewska J. Fuzzy Logic in Aircraft Onboard Systems Reliability Evaluation—A New Approach. Sensors. 2021; 21(23):7913. https://doi.org/10.3390/s21237913
Chicago/Turabian StyleŻyluk, Andrzej, Konrad Kuźma, Norbert Grzesik, Mariusz Zieja, and Justyna Tomaszewska. 2021. "Fuzzy Logic in Aircraft Onboard Systems Reliability Evaluation—A New Approach" Sensors 21, no. 23: 7913. https://doi.org/10.3390/s21237913
APA StyleŻyluk, A., Kuźma, K., Grzesik, N., Zieja, M., & Tomaszewska, J. (2021). Fuzzy Logic in Aircraft Onboard Systems Reliability Evaluation—A New Approach. Sensors, 21(23), 7913. https://doi.org/10.3390/s21237913







