Enhancing AlN PMUTs’ Acoustic Responsivity within a MEMS-on-CMOS Process
Abstract
:1. Introduction
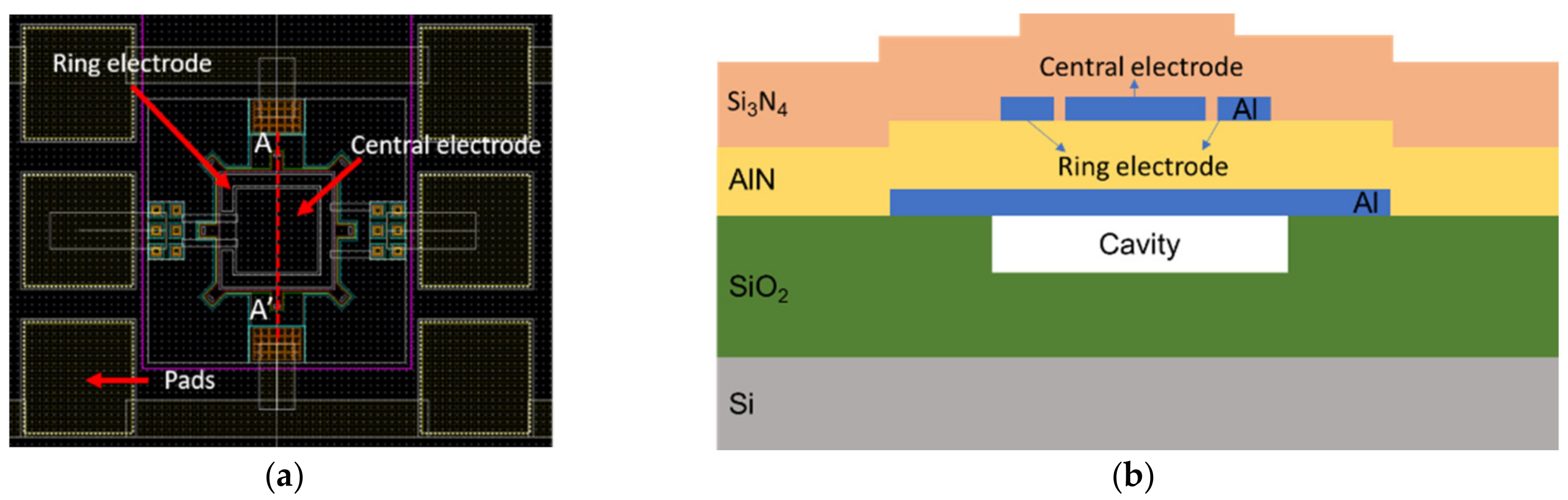
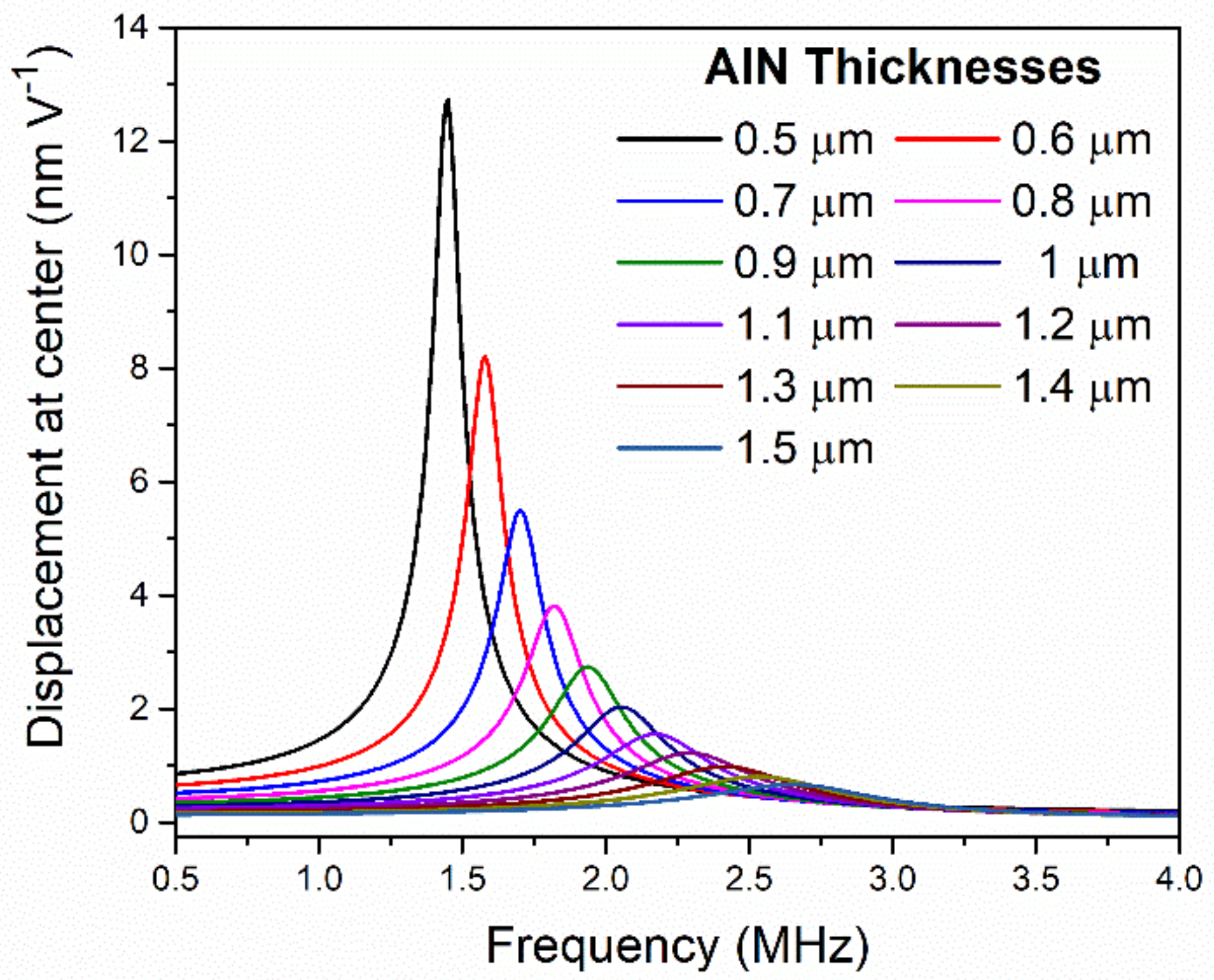
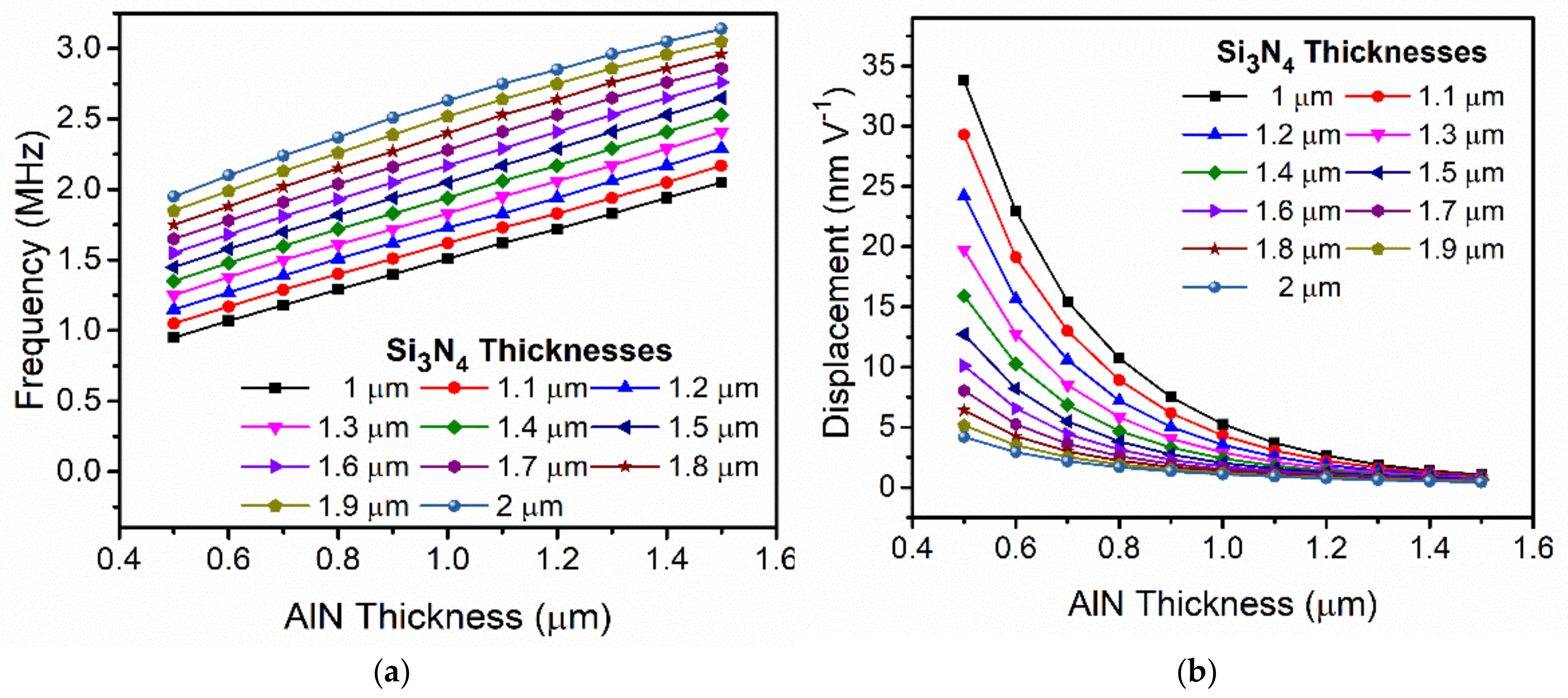
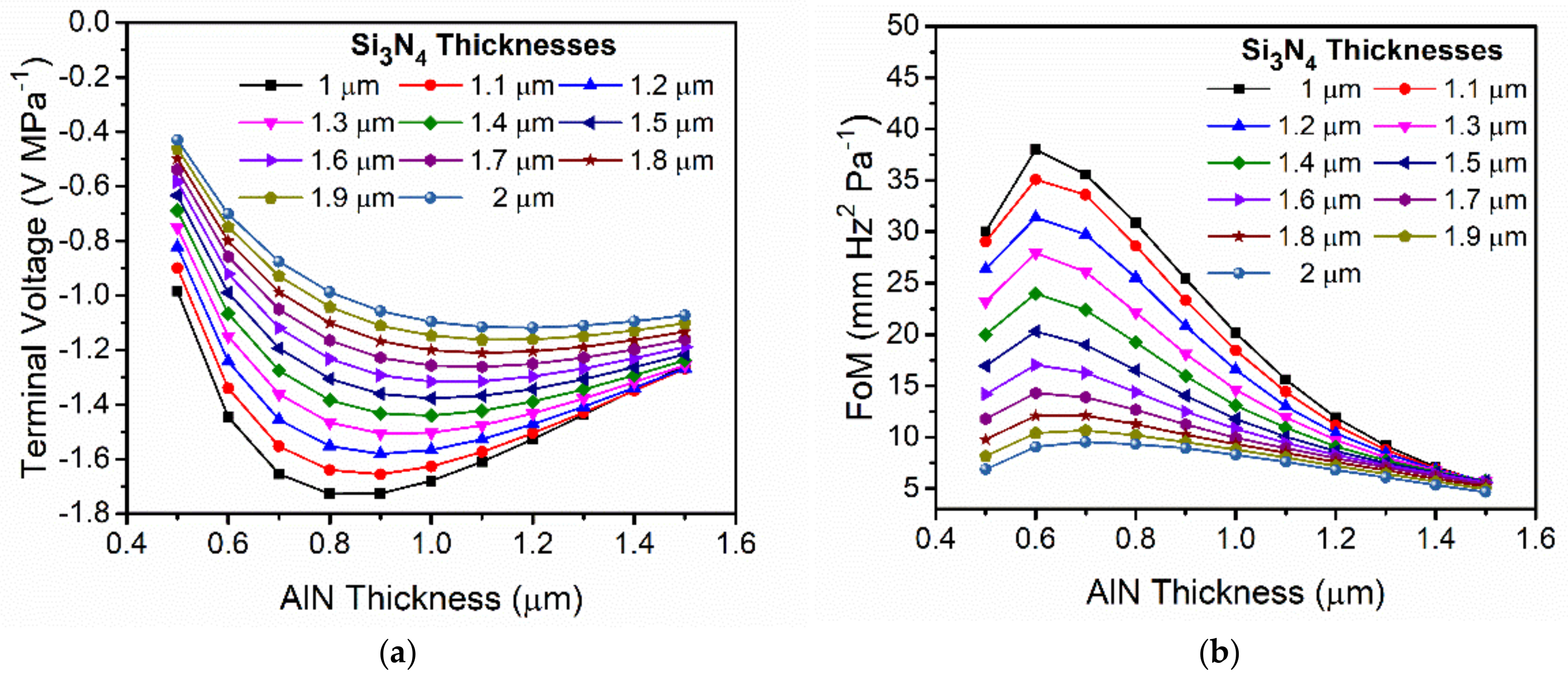
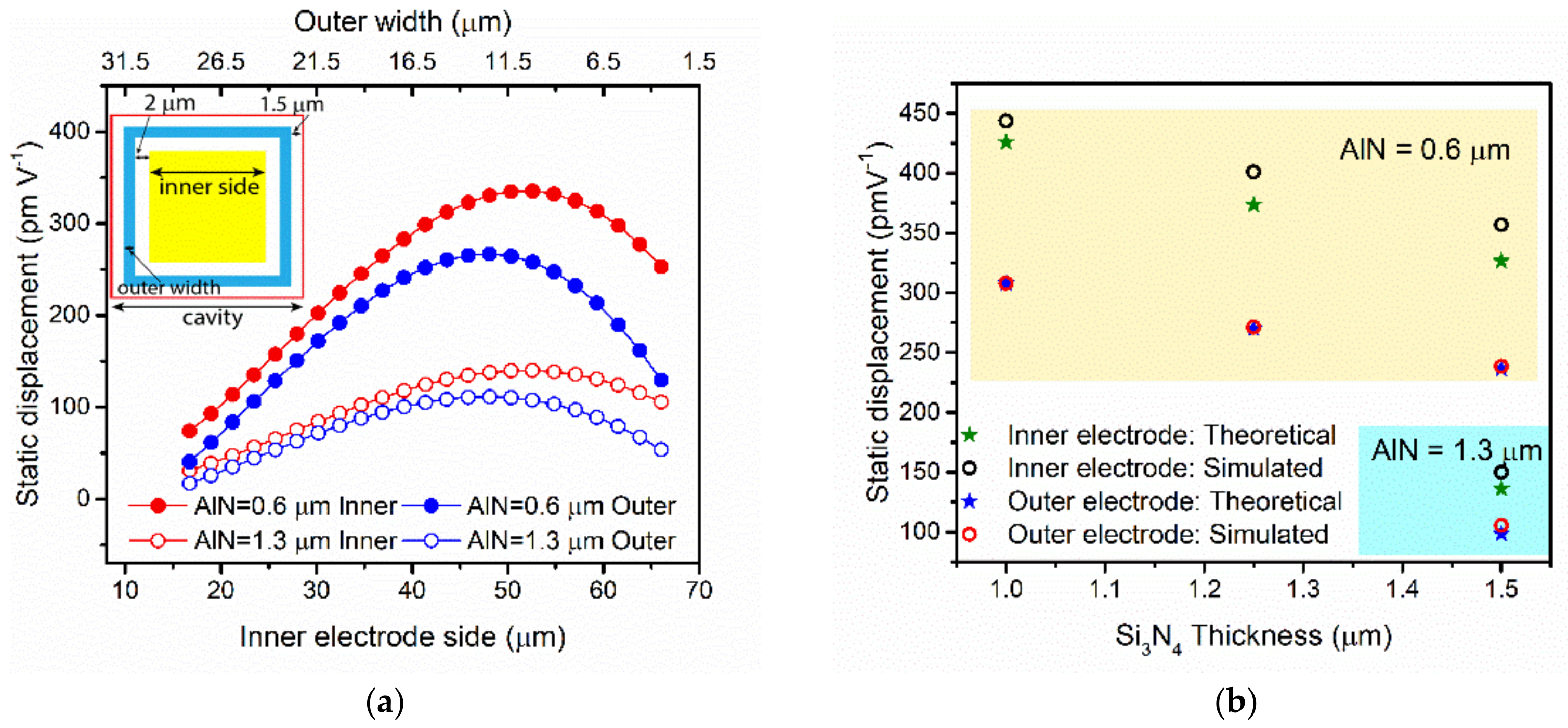
2. Materials and Methods: Optimization of PMUT Transducer
3. Experimental Results
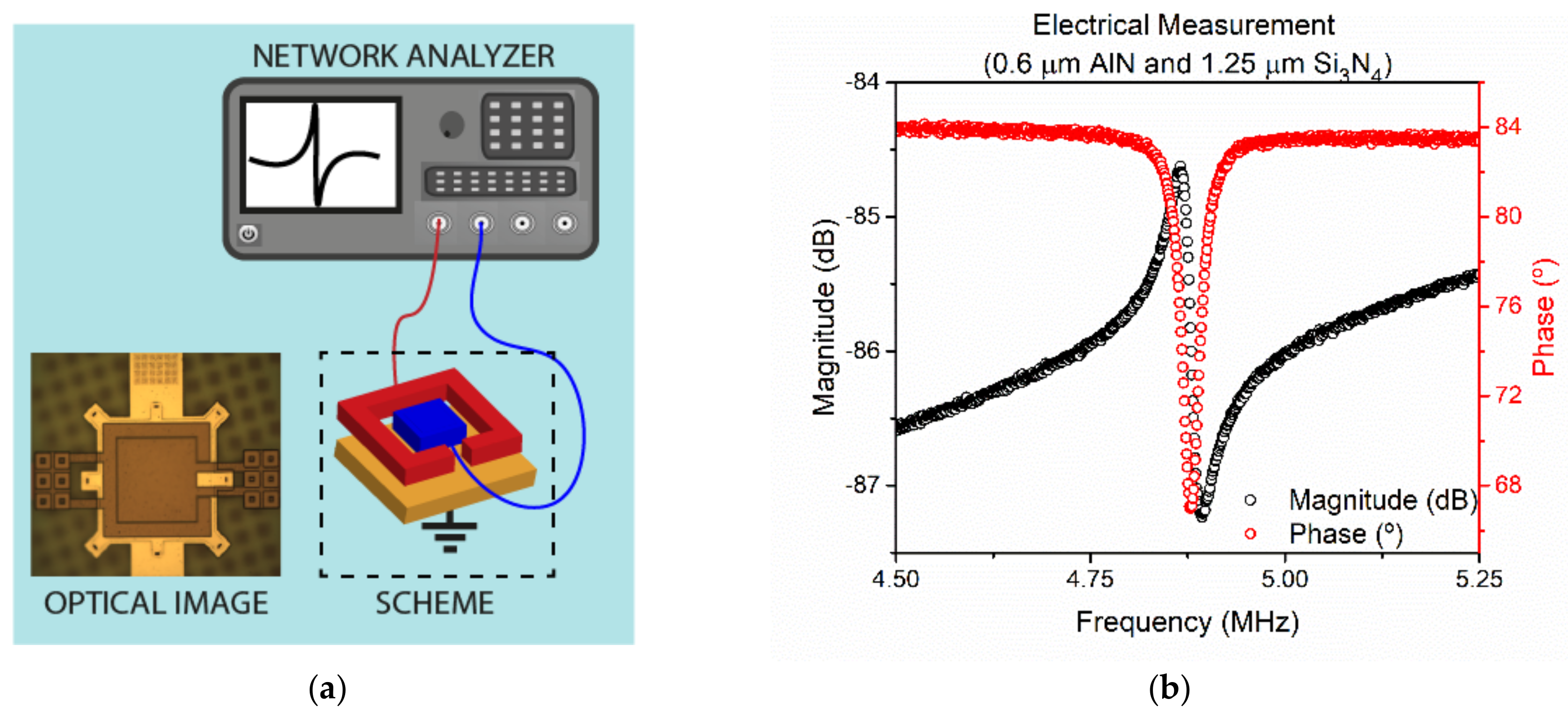
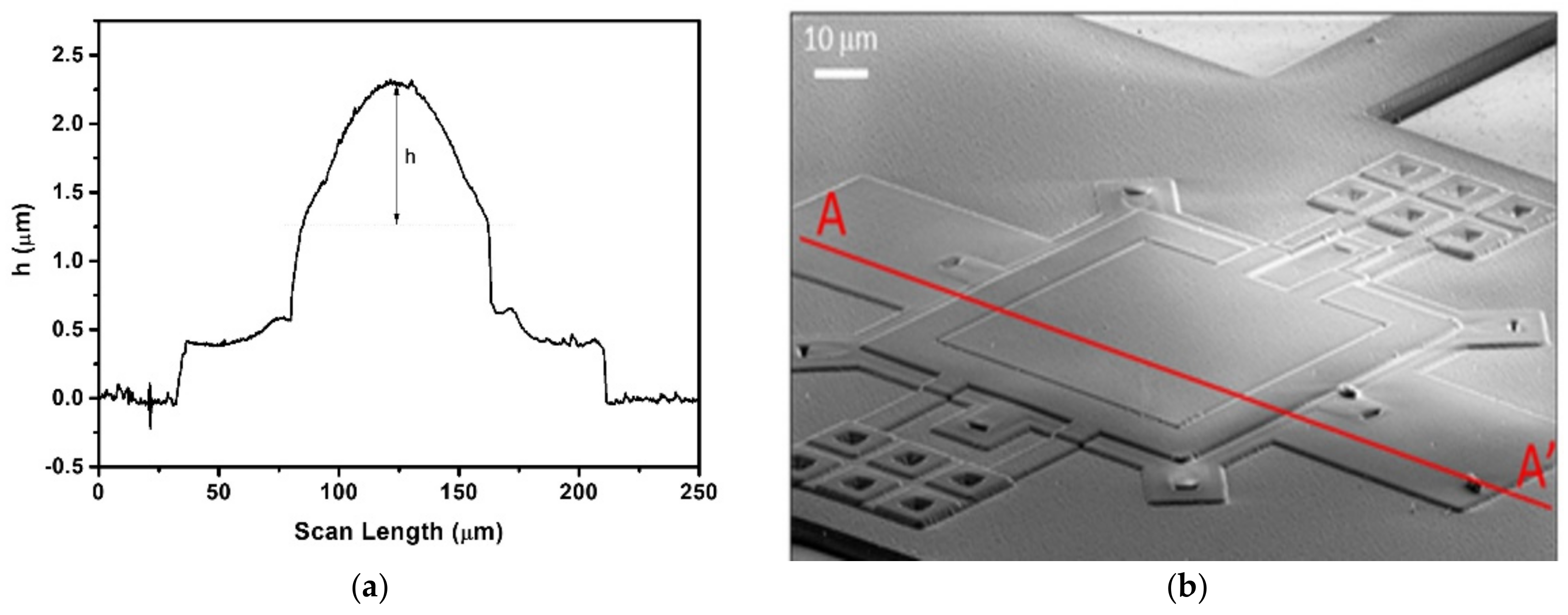
3.1. PMUTs Fabrication and Electrical Characterization
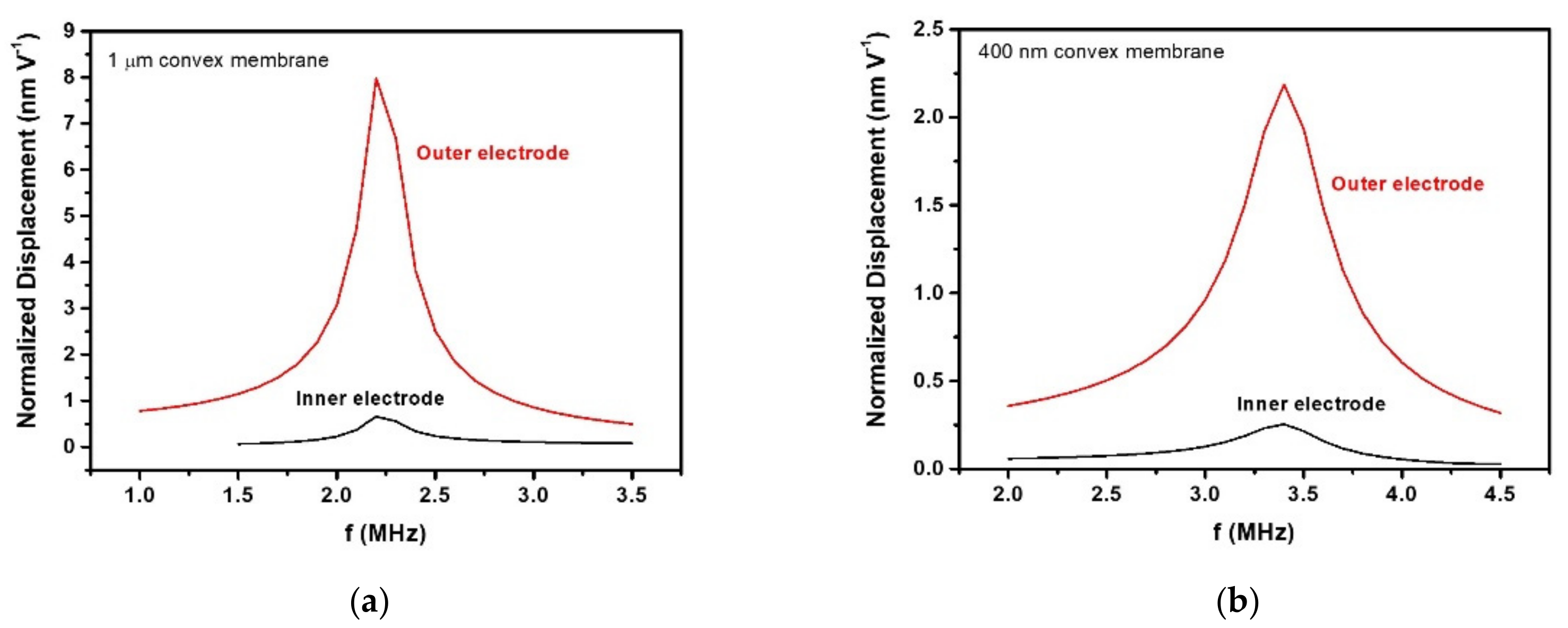
3.2. Acoustic Characterization
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Zheng, Z.; Chan, J.; Yeow, J.T.W. Capacitive micromachined ultrasound transducers for intravascular ultrasound imaging. Microsyst. Nanoeng. 2020, 6, 73. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Andino-Pavlovsky, V.; Lee, S.A.; Costa, T.; Elloian, J.; Konofagou, E.E.; Shepard, K.L. Application of a sub-0.1-mm3 implantable mote for in vivo real-time wireless temperature sensing. Sci. Adv. 2021, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.; Laursen, K.; Rashidi, A.; Mondal, T.; Corbett, B.; Moradi, F. S-MRUT: Sectored-Multiring Ultrasonic Transducer for Selective Powering of Brain Implants. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Seok, C.; Adelegan, J.O.; Biliroglu, A.O.; Yamaner, F.Y.; Oralkan, O. Wearable Ultrasonic Neurostimulator—Part II: A 2D CMUT Phased Array System with a Flip-Chip Bonded ASIC. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 705–718. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Lu, Y.; Tang, H.Y.; Tsai, J.M.; Ng, E.J.; Daneman, M.J.; Boser, B.E.; Horsley, D.A. Monolithic ultrasound fingerprint sensor. Microsyst. Nanoeng. 2017, 3, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jung, J.; Lee, W.; Kang, W.; Shin, E.; Ryu, J.; Choi, H. Review of piezoelectric micromachined ultrasonic transducers and their applications. J. Micromech. Microeng. 2017, 27, 113001. [Google Scholar] [CrossRef]
- Sun, C.; Shi, Q.; Yazici, M.C.; Kobayashi, T.; Liu, Y.; Lee, C. Investigation of Broadband Characteristics of Multi-Frequency Piezoelectric Micromachined Ultrasonic Transducer (MF-pMUT). IEEE Sens. J. 2019, 19, 860–867. [Google Scholar] [CrossRef]
- Wang, H.; Yang, H.; Jiang, H.; Chen, Z.; Feng, P.X.-L.; Xie, H. A multi-frequency PMUT array based on ceramic PZT for endoscopic photoacoustic imaging. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021. [Google Scholar] [CrossRef]
- Sadeghpour, S.; Ingram, M.; Wang, C.; D’Hooge, J.; Kraft, M. A 128x1 phased array piezoelectric micromachined ultrasound transducer (PMUT) for medical imaging. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021. [Google Scholar] [CrossRef]
- Jiang, X.; Tang, H.-Y.; Lu, Y.; Ng, E.J.; Tsai, J.M.; Boser, B.E.; Horsley, D.A. Ultrasonic Fingerprint Sensor with Transmit Beamforming Based on a PMUT Array Bonded to CMOS Circuitry. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1401–1408. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Tang, H.; Fung, S.; Wang, Q.; Tsai, J.M.; Daneman, M.; Boser, B.E.; Horsley, D.A. Ultrasonic fingerprint sensor using a piezoelectric micromachined ultrasonic transducer array integrated with complementary metal oxide semiconductor electronics. Appl. Phys. Lett. 2015, 106, 263503. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Lee, K.-R.; Eovino, B.E.; Park, J.H.; Liang, L.Y.; Lin, L.; Yoo, H.-J.; Yoo, J. A 36-Channel Auto-Calibrated Front-End ASIC for a pMUT-Based Miniaturized 3-D Ultrasound System. IEEE J. Solid-State Circuits 2021, 56, 1910–1923. [Google Scholar] [CrossRef]
- Costa, T.; Shi, C.; Tien, K.; Elloian, J.; Cardoso, F.A.; Shepard, K.L. An Integrated 2D Ultrasound Phased Array Transmitter in CMOS with Pixel Pitch-Matched Beamforming. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 731–742. [Google Scholar] [CrossRef] [PubMed]
- Zamora, I.; Ledesma, E.; Uranga, A.; Barniol, N. Monolithic Single PMUT-on-CMOS Ultrasound System with +17 dB SNR for Imaging Applications. IEEE Access 2020, 8, 142785–142794. [Google Scholar] [CrossRef]
- Ledesma, E.; Zamora, I.; Uranga, A.; Barniol, N. Monolithic PMUT on CMOS ultrasound system for single pixel acoustic imaging. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), Gainesville, FL, USA, 25–29 January 2021. [Google Scholar]
- Horsley, D.; Lu, Y.; Rozen, O. Flexural Piezoelectric Resonators. In Piezoelectric MEMS Resonators; Bhugra, H., Piazza, G., Eds.; Microsystems and Nanosystems; Springer International Publishing: Cham, Switzerland, 2017; pp. 153–167. [Google Scholar] [CrossRef]
- Wang, X.-B.; He, L.-M.; Ma, Y.-C.; Liu, W.-J.; Xu, W.-J.; Ren, J.-Y.; Riaud, A.; Zhou, J. Development of Broadband High-Frequency Piezoelectric Micromachined Ultrasonic Transducer Array. Sensors 2021, 21, 1823. [Google Scholar] [CrossRef] [PubMed]
- Ledesma, E.; Zamora, I.; Uranga, A.; Barniol, N. Tent-plate AlN PMUT with a piston-like shape under liquid operation. IEEE Sens. J. 2020, 20, 11128–11137. [Google Scholar] [CrossRef]
- Blevins, R.D. Formulas for Natural Frequency and Mode Shape. Van Nostrand Reinhold Co., Ed.; Litton Educational Publishing, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Silterra. MEMS-on-CMOS. Available online: www.silterra.com (accessed on 10 October 2021).
- Soundara Pandian, M.; Ferrer, E.M.; Tay, W.S.; Madhaven, V.; Kantimahanti, A.K.; Sobreviela, G.; Uranga, A.; Barniol, N. Thin film piezoelectric devices integrated on CMOS. In Proceedings of the 2016 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Xi’an, China, , 21–24 October 2016; pp. 167–170. [Google Scholar]
- Lu, Y.; Heidari, A.; Horsley, D.A. A High Fill-Factor Annular Array of High Frequency Piezoelectric Micromachined Ultrasonic Transducers. J. Microelectromech. Syst. 2015, 24, 904–913. [Google Scholar] [CrossRef]
- IEEE Standard on Piezoelectricity, Standard 3237638 and 176-1987; IEEE Ultrasonics and Frequency Control Society: New York, NY, USA, 1987; Available online: https://ieeexplore.ieee.org/document/26560 (accessed on 10 October 2021).
- Lu, R.; Li, M.-H.; Yang, Y.; Manzaneque, T.; Gong, S. Accurate Extraction of Large Electromechanical Coupling in Piezoelectric MEMS Resonators. J. Microelectromech. Syst. 2019, 28, 209–218. [Google Scholar] [CrossRef]
- Ledesma, E.; Zamora, I.; Uranga, A.; Barniol, N. Multielement Ring Array Based on Minute Size PMUTs for High Acoustic Pressure and Tunable Focus Depth. Sensors 2021, 21, 4786. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Lee, C. Zero-Bending Piezoelectric Micromachined Ultrasonic Transducer (pMUT) With Enhanced Transmitting Performance. J. Microelectromech. Syst. 2015, 24, 2083–2091. [Google Scholar] [CrossRef]
- Hajati, A.; Latev, D.; Gardner, D.; Hajati, A.; Imai, D.; Torrey, M.; Schoeppler, M. Three-dimensional micro electromechanical system piezoelectric ultrasound transducer. Appl. Phys. Lett. 2012, 101, 253101. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Luo, G.; Kusano, Y.; Horsley, D.A. Low thermal budget surface micromachining process for piezoelectric micromachined ultrasonic transducer arrays with in-situ vacuum sealed cavities. In Proceedings of the Hilton Head Workshop 2018: A Solid-State Sensors, Actuators and Microsystems Workshop, Hilton Head Island, SC, USA, 3–7 June 2018; pp. 245–248. [Google Scholar]
- Tan, M.; Chen, C.; Chen, Z.; Janjic, J.; Daeichin, V.; Chang, Z.-Y.; Noothout, E.; Van Soest, G.; Verweij, M.D.; De Jong, N.; et al. A front-end ASIC with high-voltage transmit switching and receive digitization for 3-D forward-looking intravascular ultrasound imaging. IEEE J. Solid-State Circuits 2018, 53, 2284–2297. [Google Scholar] [CrossRef] [Green Version]


| PMUT Layer | Properties | Geometric Dimensions | |||
|---|---|---|---|---|---|
| Mat. | Young’s Modulus (GPa) | Density (kg m−3) | Side (µm) | Thickness (µm) | |
| Substrate | SiO2 | 70 | 2200 | 100 | 2 |
| Bottom Electrode (BOT) | Al | 70 | 2700 | 86 | 0.4 |
| Piezoelectric | AlN 1 | 279 | 3230 | 100 | 0.5 to 1.5 |
| Top Electrode (CENT) | Al | 70 | 2700 | 56.6 | 0.35 |
| Top Electrode (RING) | External side: 77 Internal side: 60.6 | 0.4 | |||
| Passive | Si3N4 | 250 | 3100 | 100 | 1 to 2 |
| Si3N4 Thickness | 1 µm | 1.25 µm | 1.5 µm | |||
|---|---|---|---|---|---|---|
| Electrode | Inner | Outer | Inner | Outer | Inner | Outer |
| Frequency, f (MHz) | 1.36 | 1.58 | 1.8 | |||
| Displacement, d (pm V−1) | 2309 | 1539 | 1809 | 1175 | 1431 | 914 |
| d × f2 (m V−1 Hz2) | 4271 | 2846 | 4516 | 2933 | 4636 | 2961 |
| Terminal voltage a, Vr (V MPa−1) | 1.91 | 1.78 | 1.73 | 1.55 | 1.54 | 1.35 |
| FoM (Hz2 m kPa−1) | 8.15 | 5.06 | 7.81 | 4.55 | 7.14 | 3.99 |
| Layer Thickness | Resonance Frequency (MHz) | |||
|---|---|---|---|---|
| AlN (µm) | Si3N4 (µm) | Experimental | COMSOL | Analytical |
| 0.6 | 1 | 4.47 | 4.19 | 4.18 |
| 0.6 | 1.25 | 4.87 | 4.67 | 4.69 |
| 0.6 | 1.5 | 5.21 | 5.14 | 5.20 |
| Layer Thickness | Frequency (MHz) | Normalized Pressure @ 2 mm (Pa V−1) | P0, Normalized Surface Pressure (kPa V−1) | Vr, Received Voltage (mVpp) | FoM P0 Vr (Pa) | |
|---|---|---|---|---|---|---|
| AlN (µm) | Si3N4 (µm) | |||||
| 0.6 | 1 | 1.5 | 33.8 | 4.9 | 2.8 | 13.7 |
| 0.6 | 1.25 | 1.6 | 36.2 | 4.8 | 2.5 | 12 |
| 0.6 | 1.5 | 2 | 33.4 | 3.6 | 2 | 7.2 |
| 1.3 | 1.5 | 2.4 | 27.4 * | 2.4 | <1 | <2.4 |
| Parameters | [5] 2017 | [28] 2018 | [29] 2018 | [18] 2020 | This Work |
|---|---|---|---|---|---|
| Transducer | AlN 30 µm × 43 µm | AlN 50 µm × 50 µm | PZT 80 µm × 80 µm | AlN a 80 µm × 80 µm | AlN 80 µm × 80 µm |
| Array/single | Array 1 × 56 | Array 3 × 20 | Single | Single | Single |
| Process | Bonded-to-CMOS | CMOS compatible | Bonded-to-CMOS | MEMS-on-CMOS | MEMS-on-CMOS |
| ST (kPa V−1) | 2.95 | 2.93 | 27 b | 1.9 | 4.9 |
| SR (V MPa−1) | 2 c | 510 d | 4 e | 7.6 | 12.5 |
| FoM (×103) | 5.9 | 108 | 14.4 | 61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ledesma, E.; Zamora, I.; Uranga, A.; Torres, F.; Barniol, N. Enhancing AlN PMUTs’ Acoustic Responsivity within a MEMS-on-CMOS Process. Sensors 2021, 21, 8447. https://doi.org/10.3390/s21248447
Ledesma E, Zamora I, Uranga A, Torres F, Barniol N. Enhancing AlN PMUTs’ Acoustic Responsivity within a MEMS-on-CMOS Process. Sensors. 2021; 21(24):8447. https://doi.org/10.3390/s21248447
Chicago/Turabian StyleLedesma, Eyglis, Ivan Zamora, Arantxa Uranga, Francesc Torres, and Núria Barniol. 2021. "Enhancing AlN PMUTs’ Acoustic Responsivity within a MEMS-on-CMOS Process" Sensors 21, no. 24: 8447. https://doi.org/10.3390/s21248447
APA StyleLedesma, E., Zamora, I., Uranga, A., Torres, F., & Barniol, N. (2021). Enhancing AlN PMUTs’ Acoustic Responsivity within a MEMS-on-CMOS Process. Sensors, 21(24), 8447. https://doi.org/10.3390/s21248447








