Design of a New Seismoelectric Logging Instrument
Abstract
:1. Introduction
2. Structural Design of Seismoelectric Logging Tool
2.1. Overall Design of the Tool
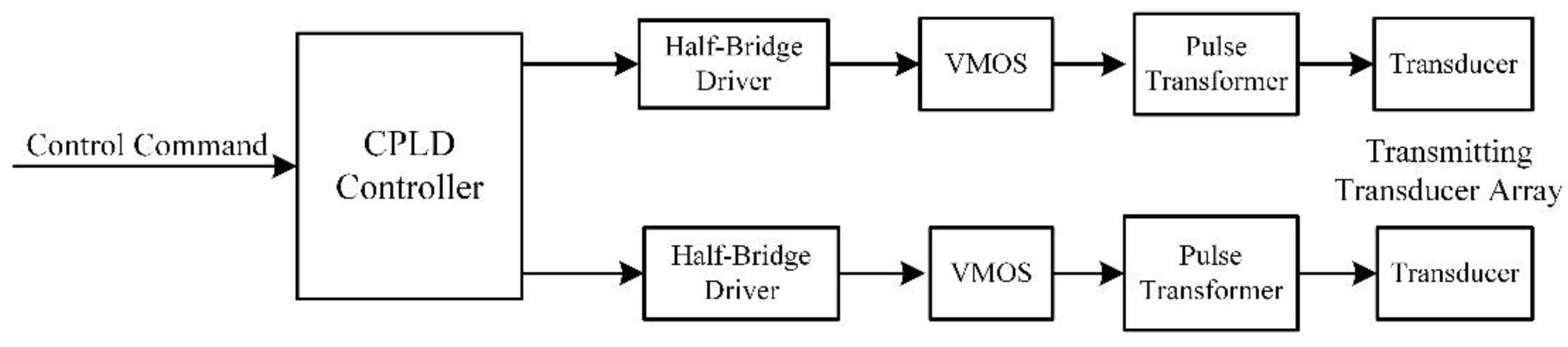
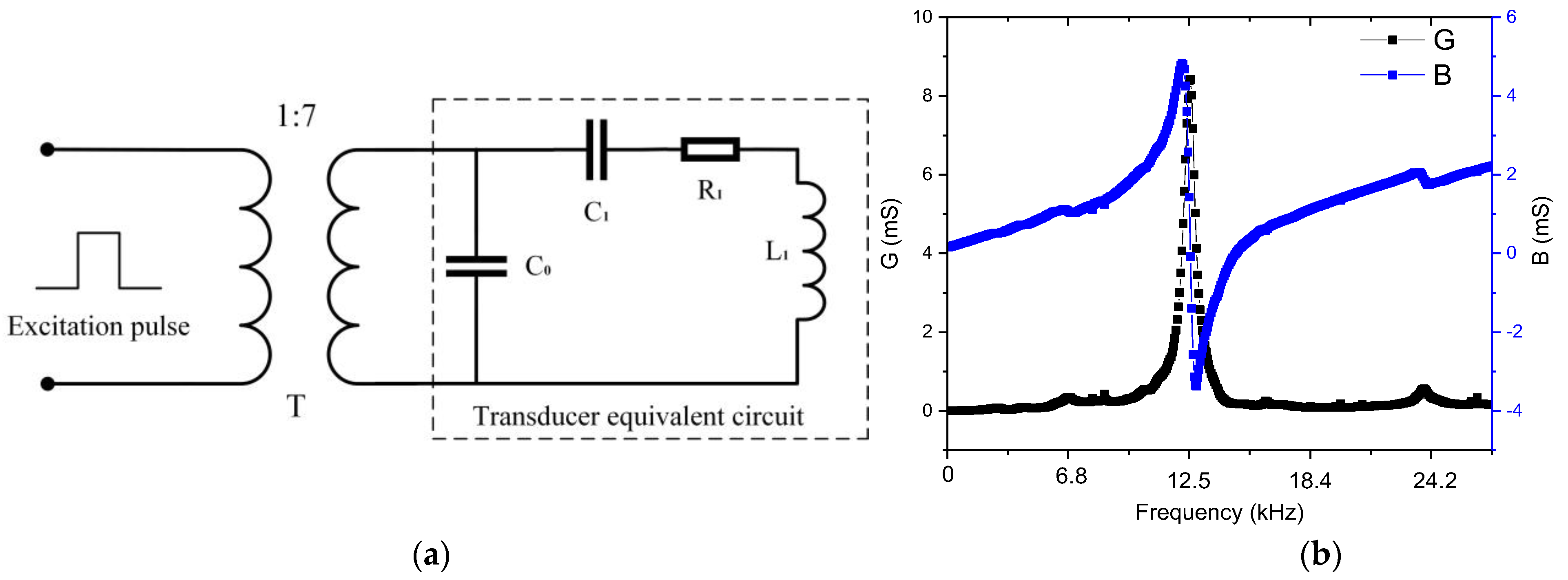
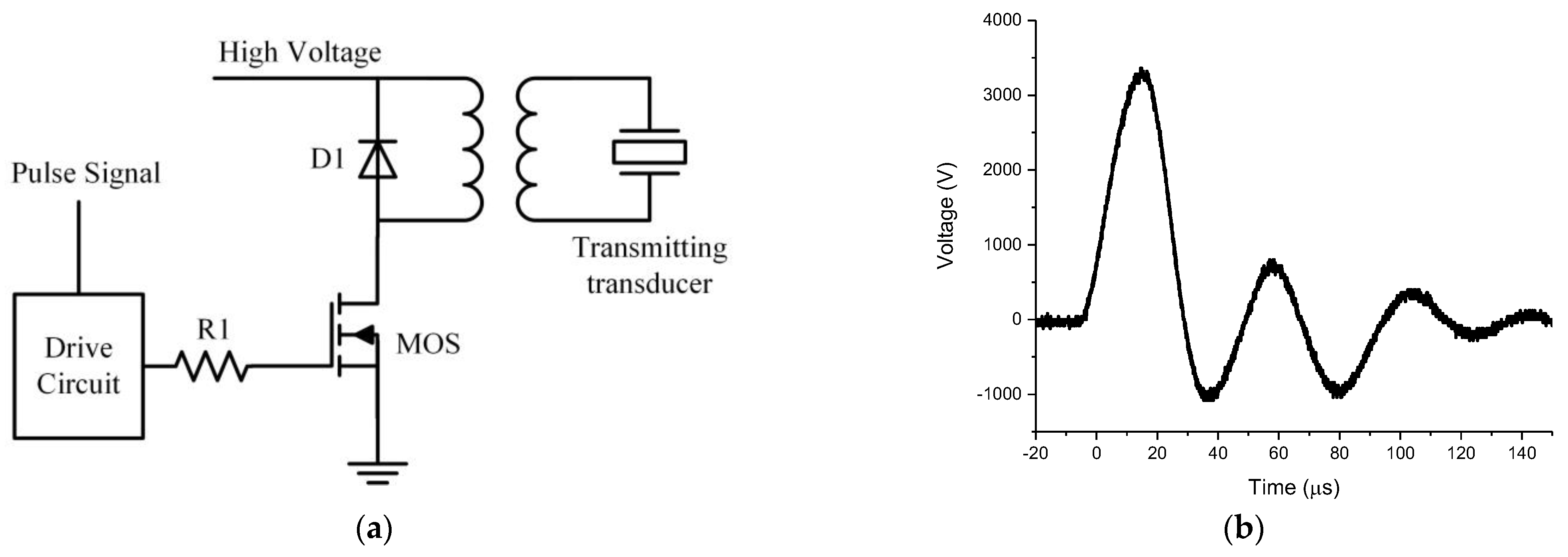
2.2. Design of the Excitation Circuit
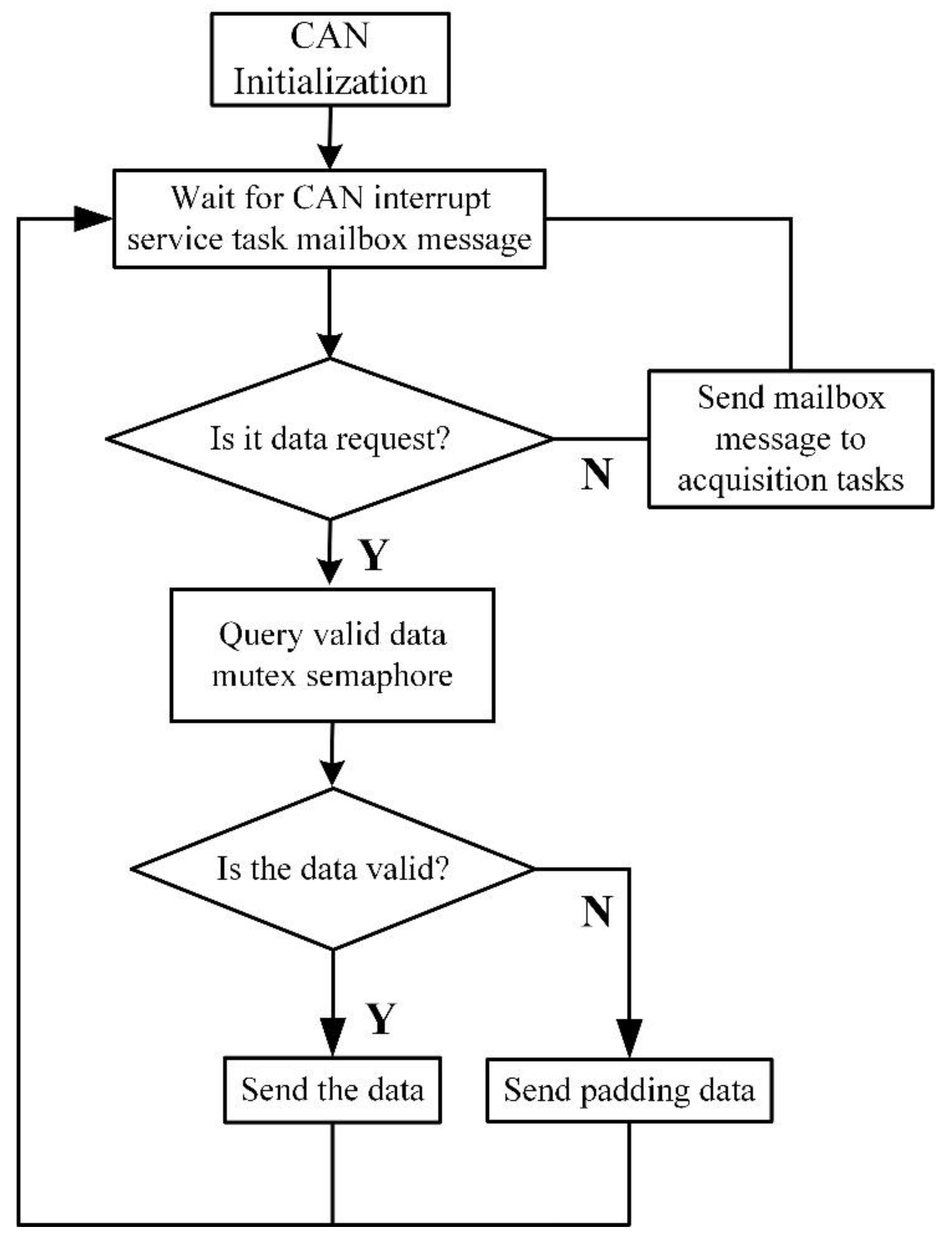
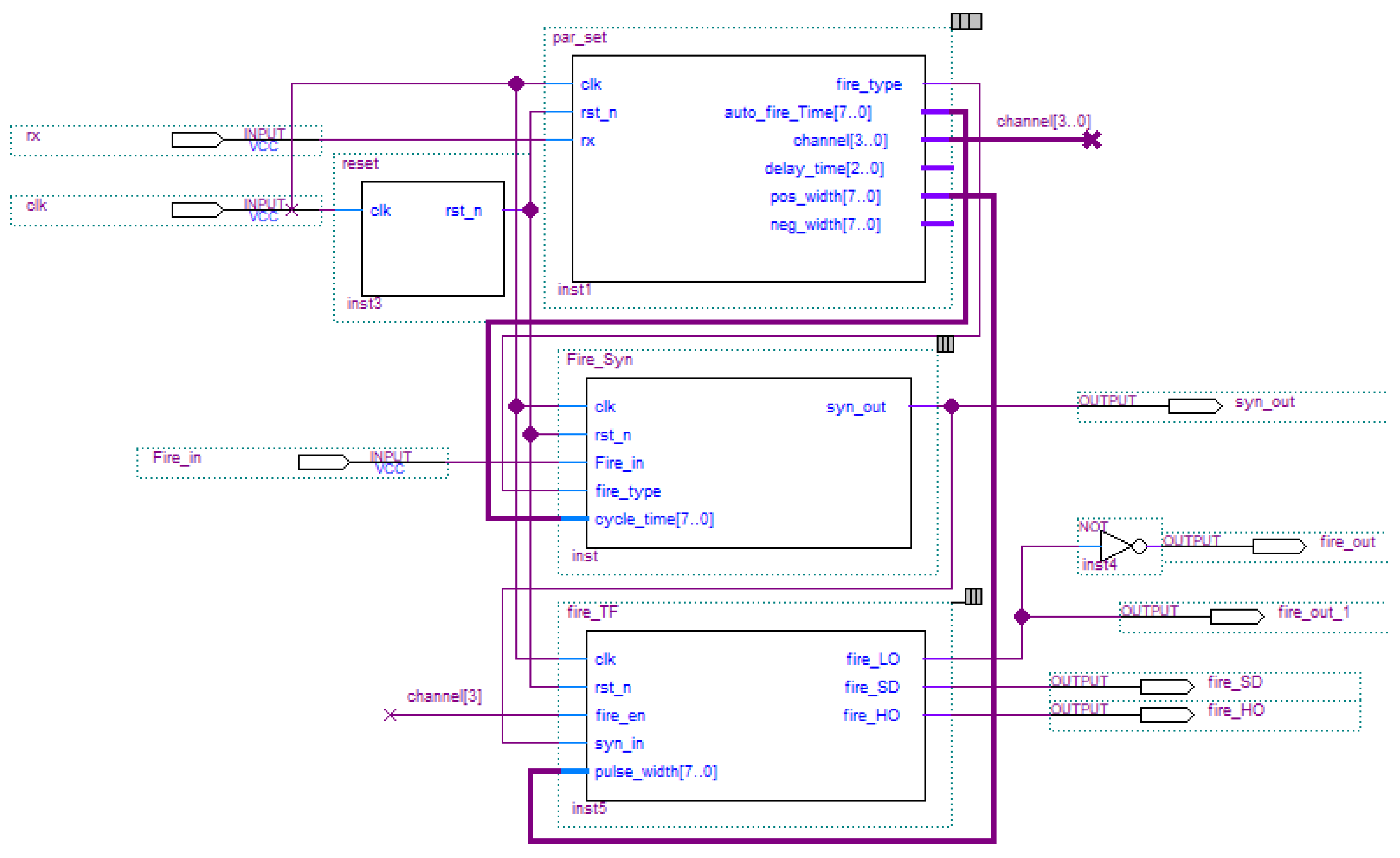
2.3. Signal Acquisition and Processing Module
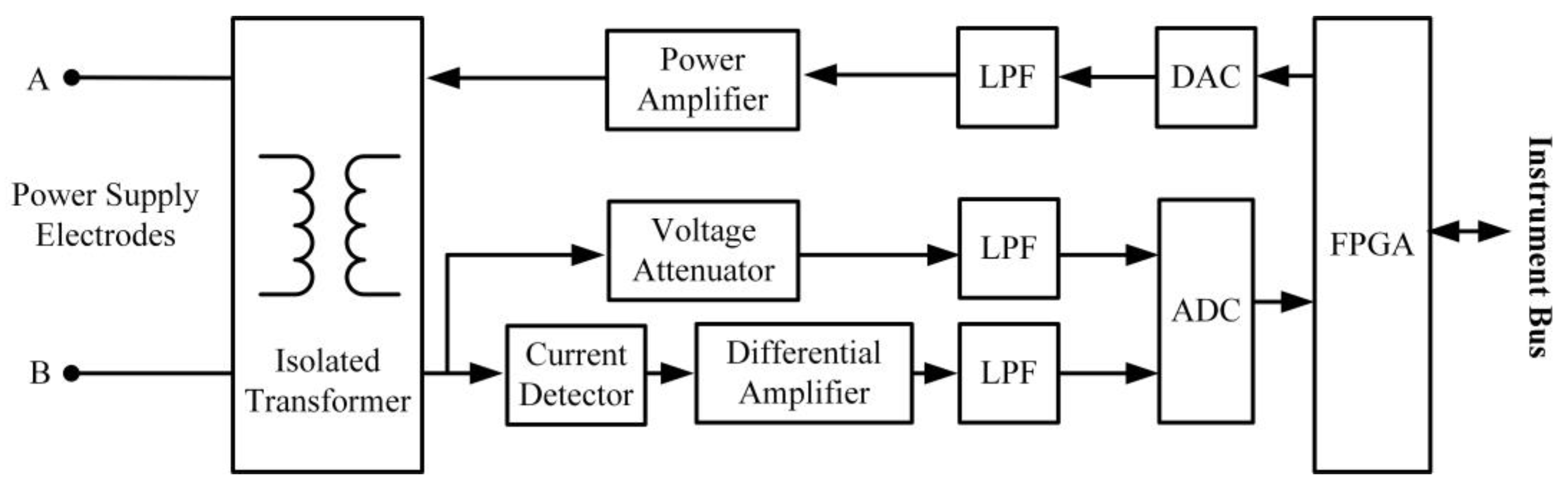
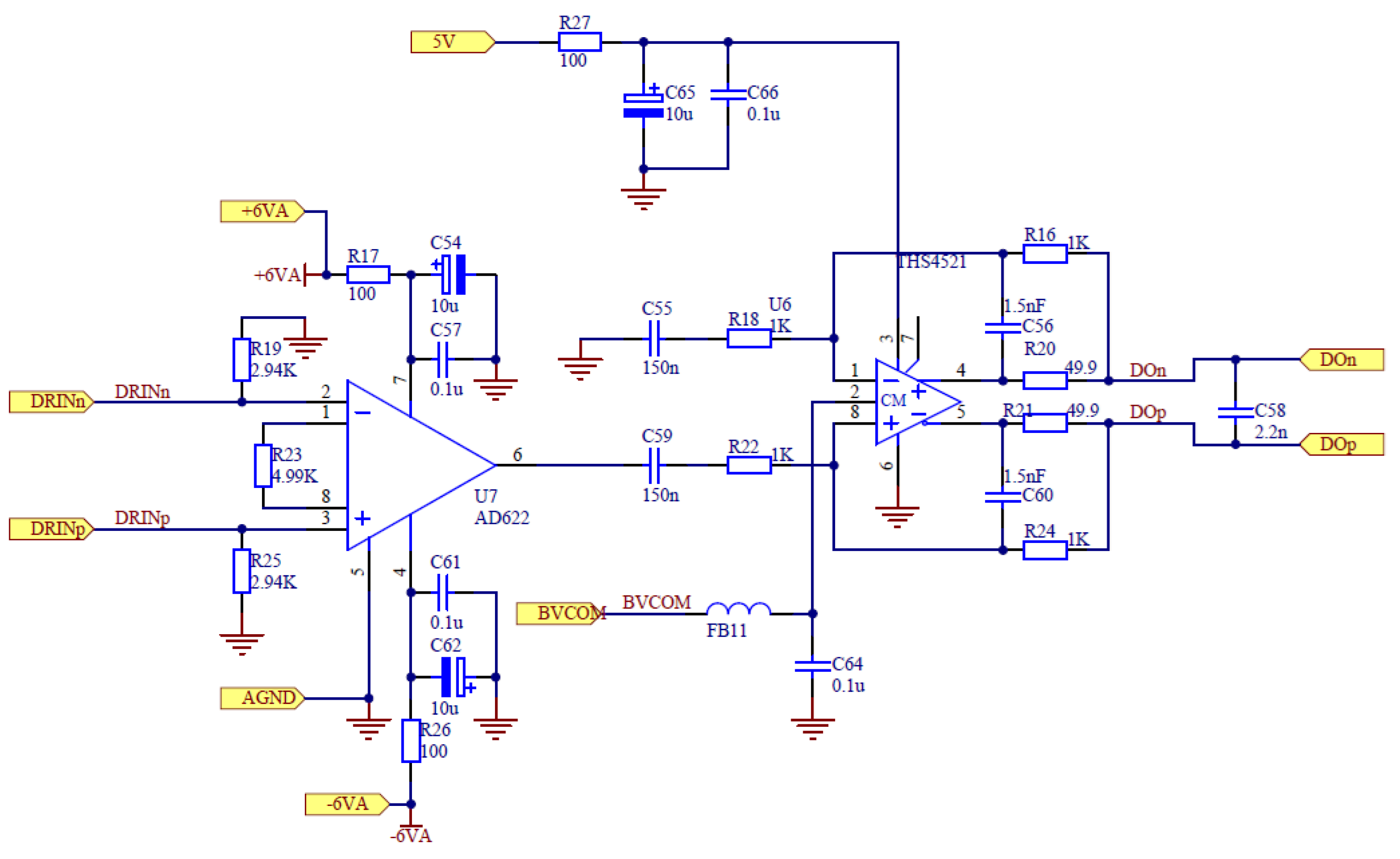
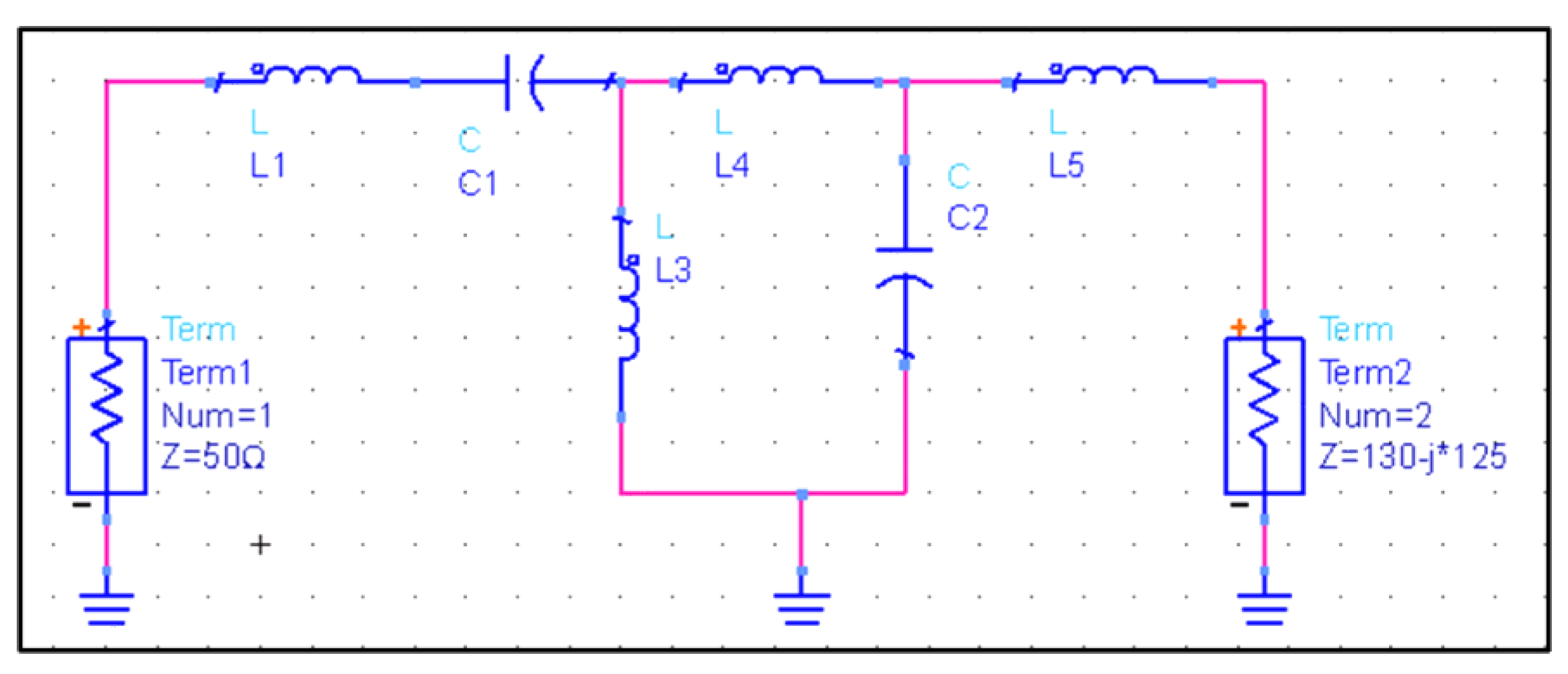
2.4. Impedance Matching Design of Transducer
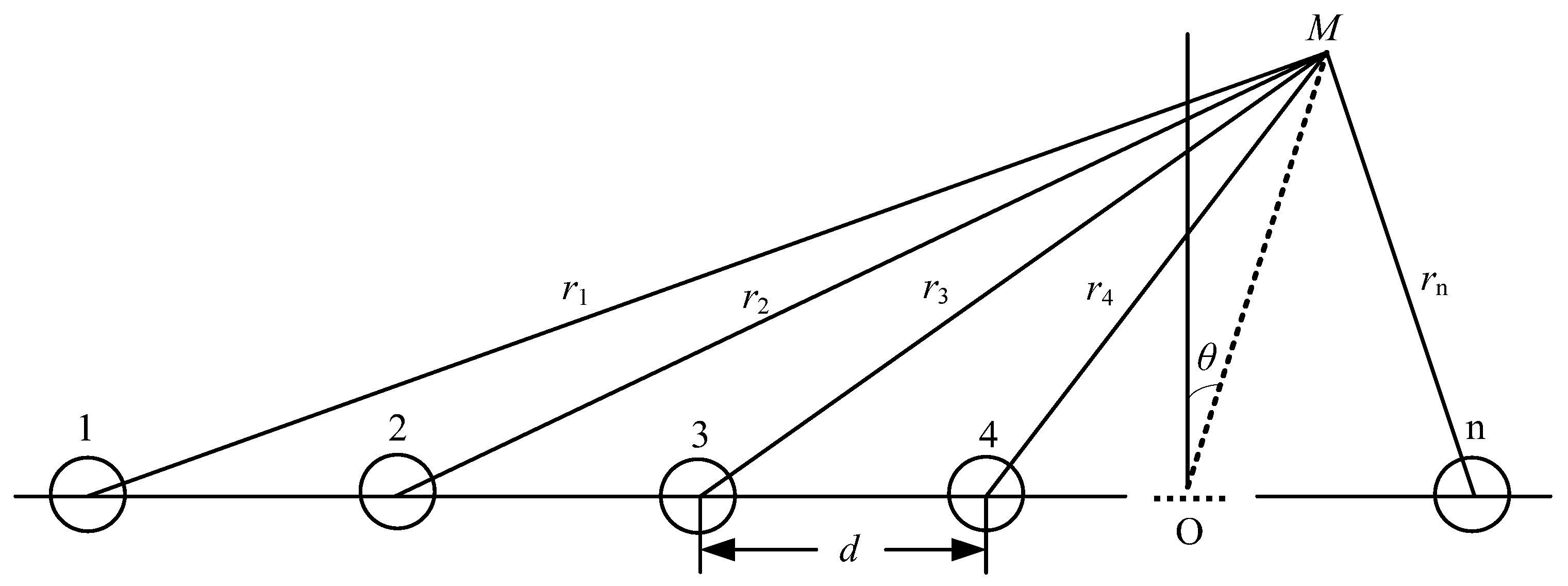
2.5. Design of Phased Array Radiator
3. Evaluation of the Performance of the Transducer of the Seismoeletric Logging Tool
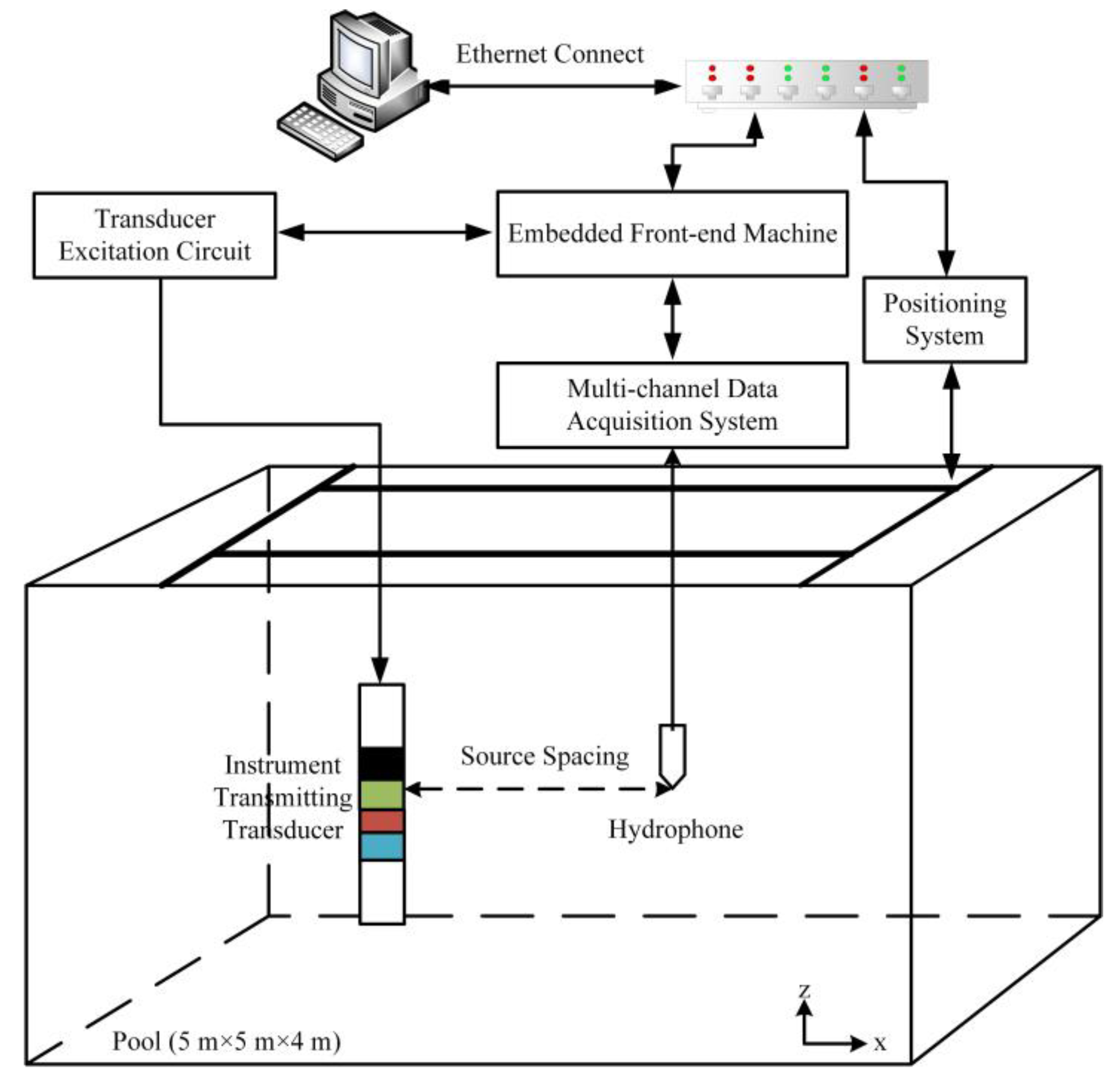
3.1. Experimental System of the Transmitting Transducer
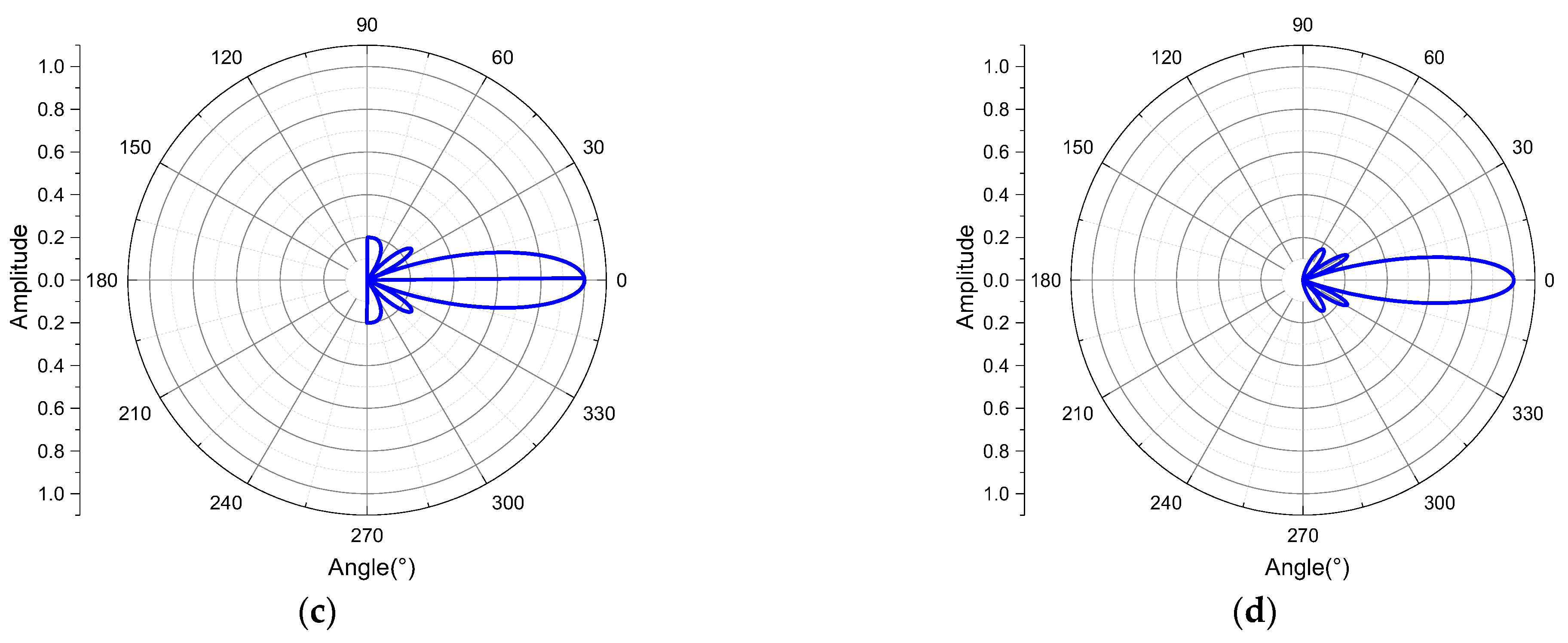
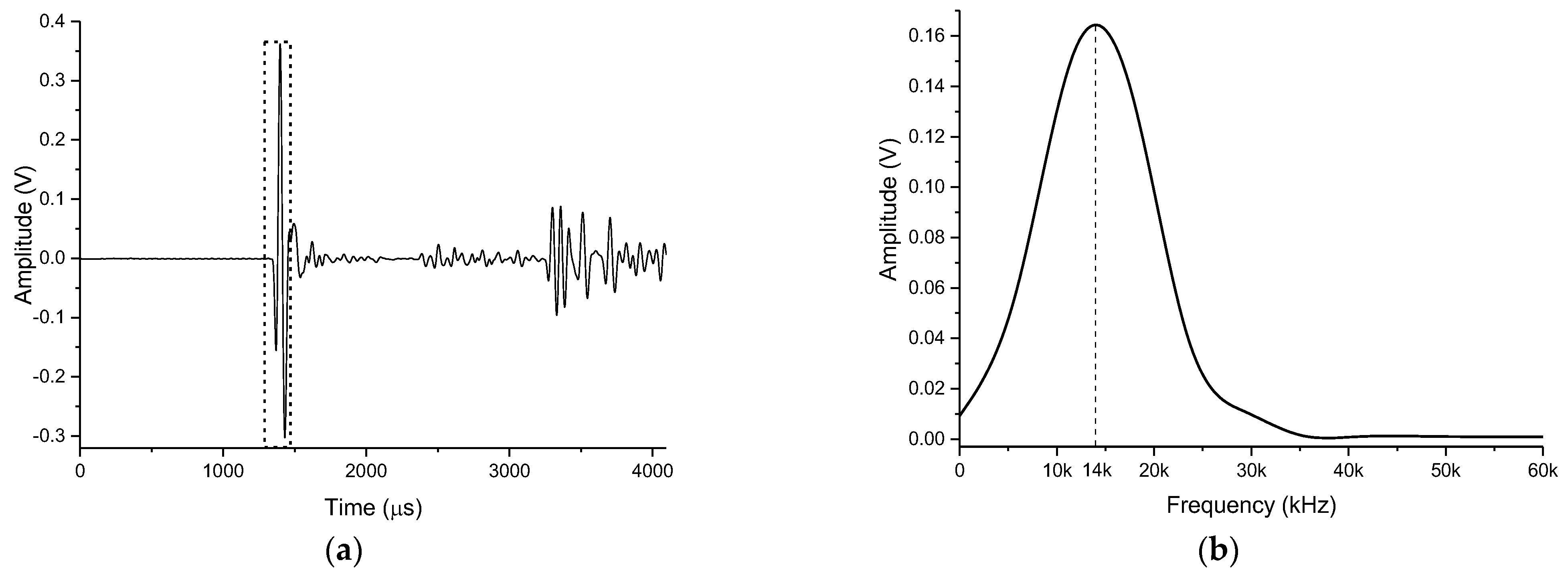
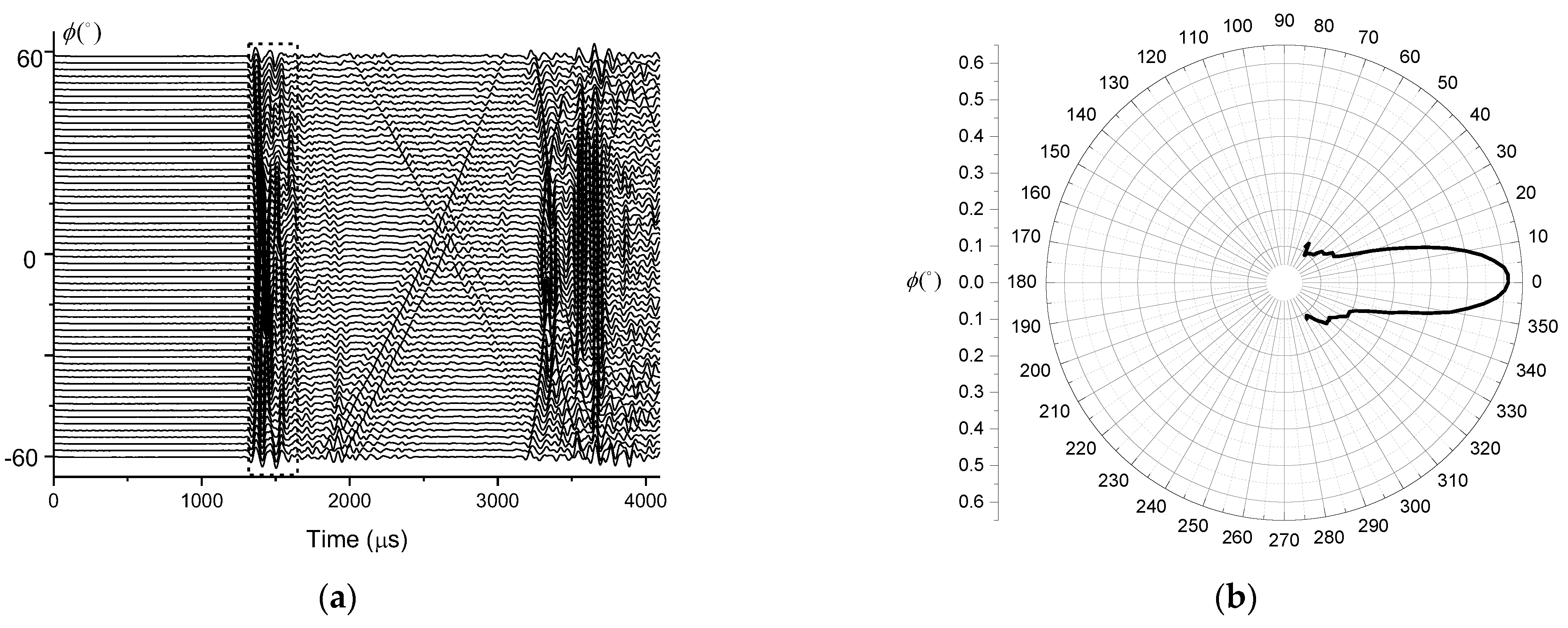
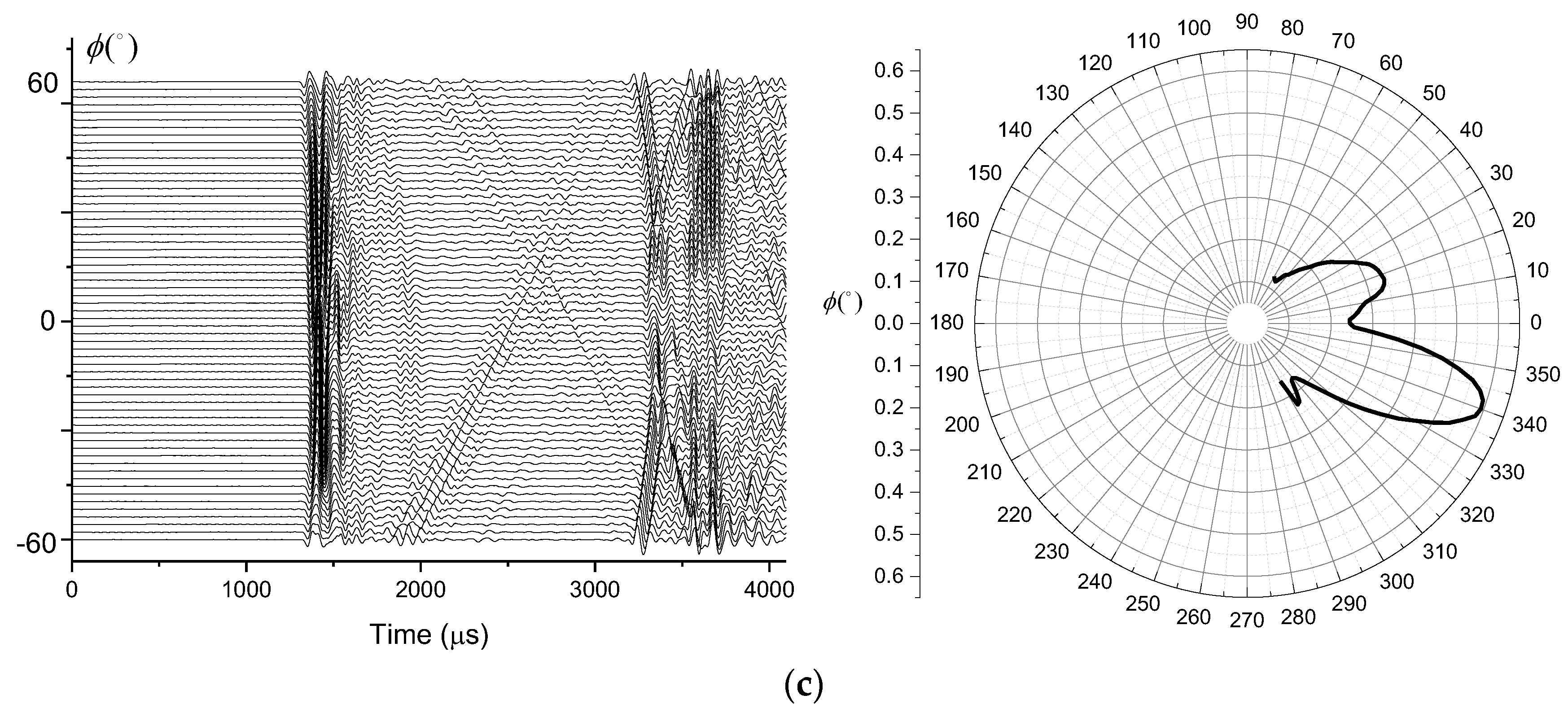
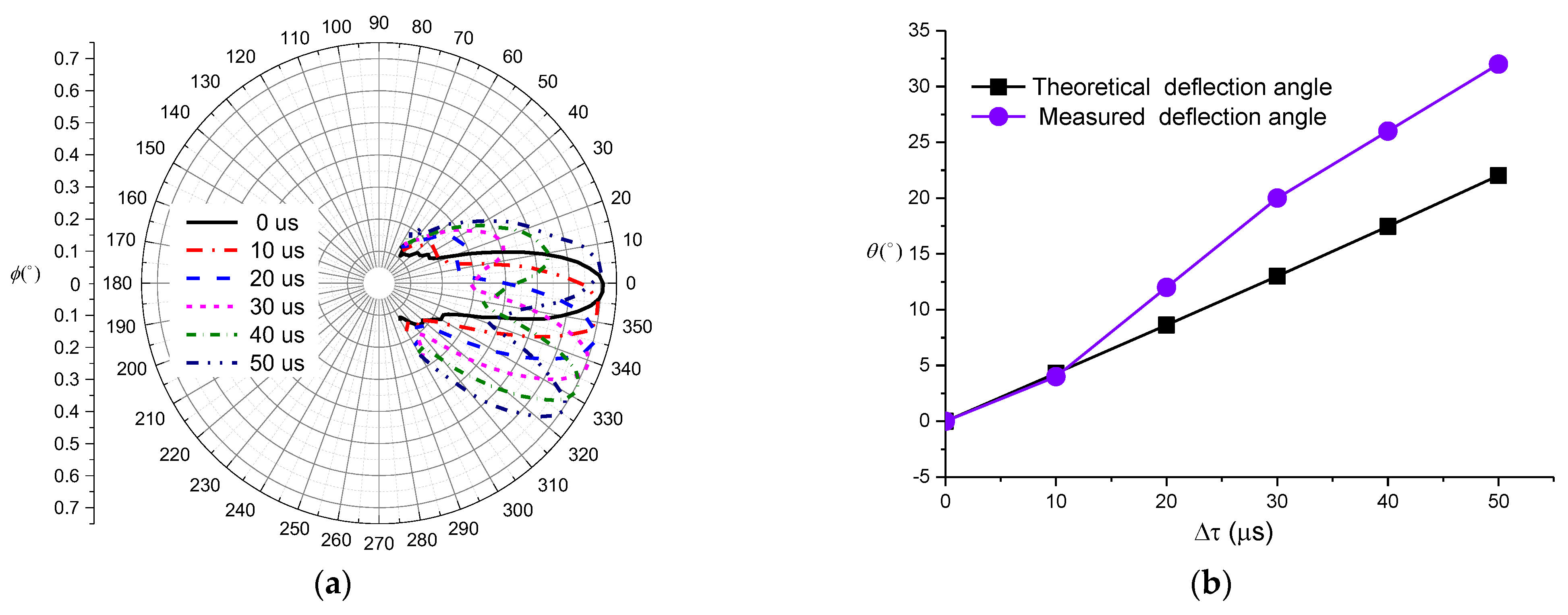
3.2. Beam Deflection Experiment of Two-Element Linear Phased Array
3.3. Evaluating the Performance of the Receiving Transducer of the Seismoelectric Logging Detector
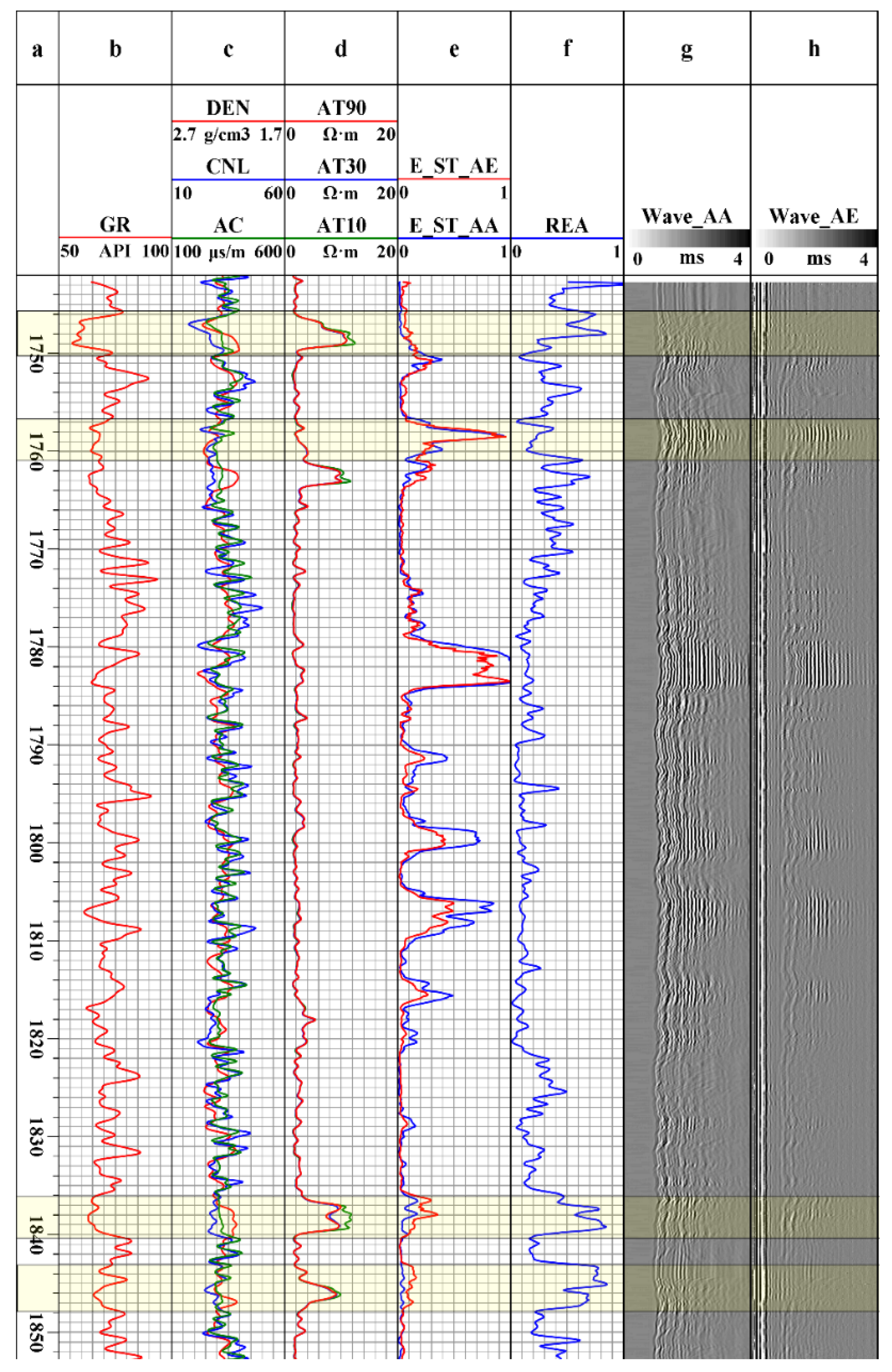
3.4. Field Test Data Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guan, W.; Chen, D.; Wang, J.; Hu, H.S. Resecrach advances of electrkinetic well logging for oil and gas reservoir. J. Appl. Acoust. 2019, 38, 142–150. [Google Scholar]
- Frenkel, J. On the theory of seismic and seismoelectric phenomena in a moist soil. J. Phys. (Soviet) 1944, 8, 230–241. [Google Scholar] [CrossRef] [Green Version]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Pride, S. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B 1994, 50, 15678–15696. [Google Scholar] [CrossRef]
- Hu, H.S.; Wang, K.X. Coupled Acoustic and Electromagnetic Waves Around A Borehole Embedded in A Porous Formation: Numerical Simulation of Acoustically Induced Fields. Well Logging Technol. 2000, 24, 3–13. [Google Scholar]
- Guan, W.; Hu, H. Finite-difference modeling of the electroseismic logging in a fluid-saturated porous formation. J. Comput. Phys. 2008, 227, 5633–5648. [Google Scholar] [CrossRef]
- Holloway, L.; Singer, J.; Stuart-Bruges, W.; Mason, G.; Saunders, J.; Stoll, J.B.; Pain, C. Electrokinetic logging has the potential to measure permeability. In Proceedings of the SPWLA 46th Annual Logging Meeting Symposium, New Orleans, LA, USA, 26–29 June 2005. [Google Scholar]
- Grobbe, N.; Slob, E.C.; Thorbecke, J.W. Comparison of eigenvectors for coupled seismo-electromagnetic layered-Earth mod-elling. Geophys. J. Int. 2016, 206, 152–190. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.E.; Savioli, G.B. A model for wave propagation in a porous solid saturated by a three-phase fluid. J. Acoust. Soc. Am. 2016, 139, 693–702. [Google Scholar] [CrossRef] [PubMed]
- Jardani, A.; Revil, A. Seismoelectric couplings in a poroelastic material containing two immiscible fluid phases. Geophys. J. Int. 2015, 202, 850–870. [Google Scholar] [CrossRef]
- Zhu, Z.; Haartsen, M.W.; Toksöz, M.N. Experimental studies of electrokinetic conversions in fluid-saturated borehole models. Geophysics 1999, 64, 1349–1356. [Google Scholar] [CrossRef]
- Zhu, Z.; Toksöz, M.N. Crosshole seismoelectric measurements in borehole models with fractures. Geophysics 2003, 68, 1519–1524. [Google Scholar] [CrossRef] [Green Version]
- Pengra, D.B.; Li, S.X.; Wong, P.-Z. Determination of rock properties by low-frequency AC electrokinetics. J. Geophys. Res. 1999, 104, 29485–29508. [Google Scholar] [CrossRef]
- Mikhailov, O.V.; Queen, J.; Toksöz, M.N. Using borehole electroseismic measurements to detect and characterize fractured (permeable) zones. Geophysics 2000, 65, 1098–1112. [Google Scholar] [CrossRef]
- Holzhauer, J.; Brito, D.; Bordes, C.; Brun, Y.; Guatarbes, B. Experimental quantification of the seismoelectric transfer function and its dependence on conductivity and saturation in loose sand. Geophys. Prospect. 2016, 65, 1097–1120. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Cui, Z.; Liu, J.; Kundu, T. Dependence of borehole shear-horizontal-wave seismoelectric response on soil textures. Geophys. Prospect. 2020, 69, 250–266. [Google Scholar] [CrossRef]
- Peng, R.; Di, B.; Wei, J.; Ding, P.; Zhao, J.; Pan, X.; Liu, Z. Experimental study of the seismoelectric interface response in wedge and cavity models. Geophys. J. Int. 2017, 210, 1703–1720. [Google Scholar] [CrossRef]
- Peng, R.; Di, B.; Glover, P.W.J.; Wei1, J.; Lorinczi, P.; Ding, P.; Liu, Z.; Zhang, Y.; Wu, M. The effect of rock permeability and porosity on seismoelectric conversion: Experiment and analytical modelling. Geophys. J. Int. 2019, 219, 328–345. [Google Scholar] [CrossRef]
- Wang, J.; Hu, H.; Guan, W. The evaluation of rock permeability with streaming current measurements. Geophys. J. Int. 2016, 206, 1563–1573. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.C.; Ju, X.D.; Lu, J.Q.; Men, B.Y. The characteristics of seismoelectric interface response measured in rock sample. In Proceedings of the 82nd EAGE Annual Conference, online, 18–21 October 2021; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Kobayashi, G.; Toshioka, T.; Takahashi, T. Development of A Practical Ekl (Electrokinetic Logging) System. In Proceedings of the Spwla Annual Logging Symposium, Oiso, Japan, 2 June 2002. [Google Scholar]
- Li, F.-B.; Ju, X.-D.; Qiao, W.-X.; Lu, J.-Q.; Men, B.-Y. Research and experimental testing of a new kind electrokinetic logging tool. Appl. Geophys. 2014, 11, 364–373. [Google Scholar] [CrossRef]
- Ju, X.D.; Zhao, H.L.; Lu, J.Q.; Men, B.Y.; Li, F.B.; Duan, W.X. Research of the Acoustoelectric Logging Tool. Well Logging Technol. 2015, 39, 323–329. [Google Scholar]
- Lu, J.; Ju, X.; Men, B.; Zhao, H.; Qiao, W.; Duan, W. An acousto-electric effect logging detector in boreholes. J. Geophys. Eng. 2017, 14, 397–407. [Google Scholar] [CrossRef]
- Hao, X.; Ju, X.; Lu, J.; Men, B.; Zhou, J. Intelligent Fault-Diagnosis System for Acoustic Logging Tool Based on Multi-Technology Fusion. Sensors 2019, 19, 3273. [Google Scholar] [CrossRef] [Green Version]
- Duan, W.X.; Ju, X.D.; Lu, J.L.; Men, B.Y.; Che, X.H.; Qiao, W.X. Field test of acoustoelectric logging signals and preliminary analysis. Pet. Sci. Bull. 2017, 01, 24–31. [Google Scholar]
- Guan, W.; Hu, H.; Wang, Z. Permeability inversion from low-frequency seismoelectric logs in fluid-saturated porous formations. Geophys. Prospect. 2012, 61, 120–133. [Google Scholar] [CrossRef]
- Guan, W.; Yin, C.G.; Hu, H.S.; Wang, J.; Cui, N.; Wang, Z. Theoretical study on the amplitude ratio of the seismoelectric field to the Stoneley wave and the formation tortuosity inversion from seismoelectric logs. Geophys. J. Int. 2015, 203, 2277–2286. [Google Scholar] [CrossRef]
- Zhang, K.; Tan, B.H.; Zhang, W.X.; Sun, Y.; Zheng, J.; Su, Y.; Liu, X.; Wu, G.; Xin, S. Design of a New Acoustic Logging While Drilling Tool. Sensors 2021, 21, 4385. [Google Scholar] [CrossRef]
- Qiao, W.-X.; Du, G.-S.; Chen, X.-L. Feasibility of Application of Linear Phased Array Acoustic Transmitters to Acoustic Well-logging. Chin. J. Geophys. 2002, 45, 755–763. [Google Scholar] [CrossRef]
- Qiao, W.X.; Chen, X.L.; Du, G.S. Laboratory simulation on acoustic well-logging with phased array transmitter. Chin. J. Acoust. 2003, 22, 33–38. [Google Scholar]
- Yang, S.; Qiao, W.; Che, X. Numerical simulation of acoustic fields in formation generated by linear phased array acoustic transmitters during logging while drilling. J. Pet. Sci. Eng. 2019, 182, 106184. [Google Scholar] [CrossRef]
- Che, X.-H.; Qiao, W.-X.; Ju, X.-D.; Wang, R.-J. Azimuthal cement evaluation with an acoustic phased-arc array transmitter: Numerical simulations and field tests. Appl. Geophys. 2016, 13, 194–202. [Google Scholar] [CrossRef]
- Wu, J.; Qiao, W.; Che, X.; Ju, X.; Lu, J.; Wu, W. Experimental study on the radiation characteristics of downhole acoustic phased combined arc array transmitter. GEOPHYSICS 2013, 78, D1–D9. [Google Scholar] [CrossRef]
- Che, X.-H.; Qiao, W.-X.; Ju, X.-D.; Lu, J.-Q.; Wu, J.-P.; Cai, M. Experimental study of the azimuthal performance of 3D acoustic transmitter stations. Pet. Sci. 2016, 13, 52–63. [Google Scholar] [CrossRef] [Green Version]
- Wooh, S.-C.; Shi, Y. Three-dimensional beam directivity of phase-steered ultrasound. J. Acoust. Soc. Am. 1999, 105, 3275–3282. [Google Scholar] [CrossRef]
- Zhang, G.; Che, X.; Qiao, W.; Ju, X.; Lu, J.; Men, B. Characteristics of the interface acoustoelectric conversion waveform in fluid-filled boreholes. J. Pet. Sci. Eng. 2021, 207, 109174. [Google Scholar] [CrossRef]
- Duan, Y.D.; Hu, H.S.; Guan, W. A study on the influence of salinity interfaces on borehole seimoelectric wavefields. Geophysics 2020, 85, D167–D180. [Google Scholar] [CrossRef]





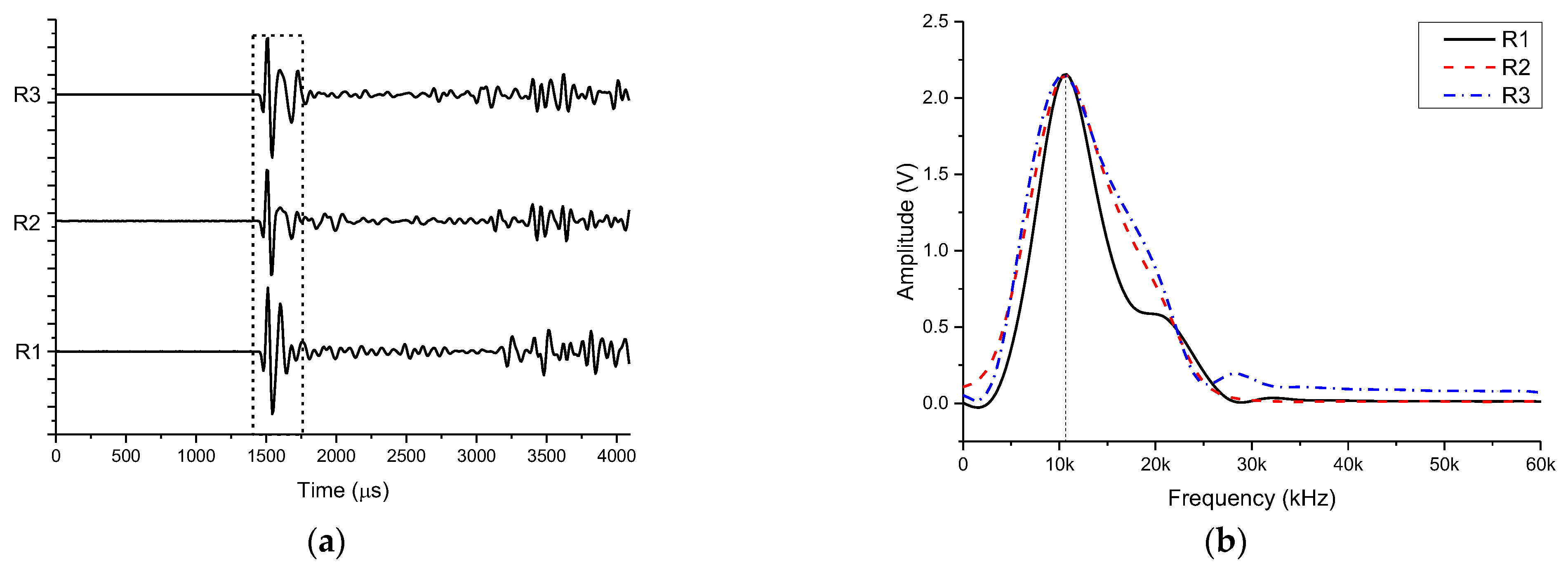
| Receiving Transducer | Peak-to-Peak Value (mV) | Normalized Value | Arrival Time of the First Wave (µs) | Dominant Frequency (kHz) |
|---|---|---|---|---|
| R1 | 834 | 0.992 | 1449 | 10.4 |
| R2 | 822 | 0.977 | 1440 | 10.4 |
| R3 | 841 | 1 | 1443 | 10.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Ju, X.; Lu, J.; Men, B.; He, W. Design of a New Seismoelectric Logging Instrument. Sensors 2021, 21, 8489. https://doi.org/10.3390/s21248489
Zhang L, Ju X, Lu J, Men B, He W. Design of a New Seismoelectric Logging Instrument. Sensors. 2021; 21(24):8489. https://doi.org/10.3390/s21248489
Chicago/Turabian StyleZhang, Liangchen, Xiaodong Ju, Junqiang Lu, Baiyong Men, and Weiliang He. 2021. "Design of a New Seismoelectric Logging Instrument" Sensors 21, no. 24: 8489. https://doi.org/10.3390/s21248489
APA StyleZhang, L., Ju, X., Lu, J., Men, B., & He, W. (2021). Design of a New Seismoelectric Logging Instrument. Sensors, 21(24), 8489. https://doi.org/10.3390/s21248489





