Using a System-Based Monitoring Paradigm to Assess Fatigue during Submaximal Static Exercise of the Elbow Extensor Muscles
Abstract
:1. Introduction
1.1. Background
1.2. Related Literature
2. Materials and Methods
2.1. Participants
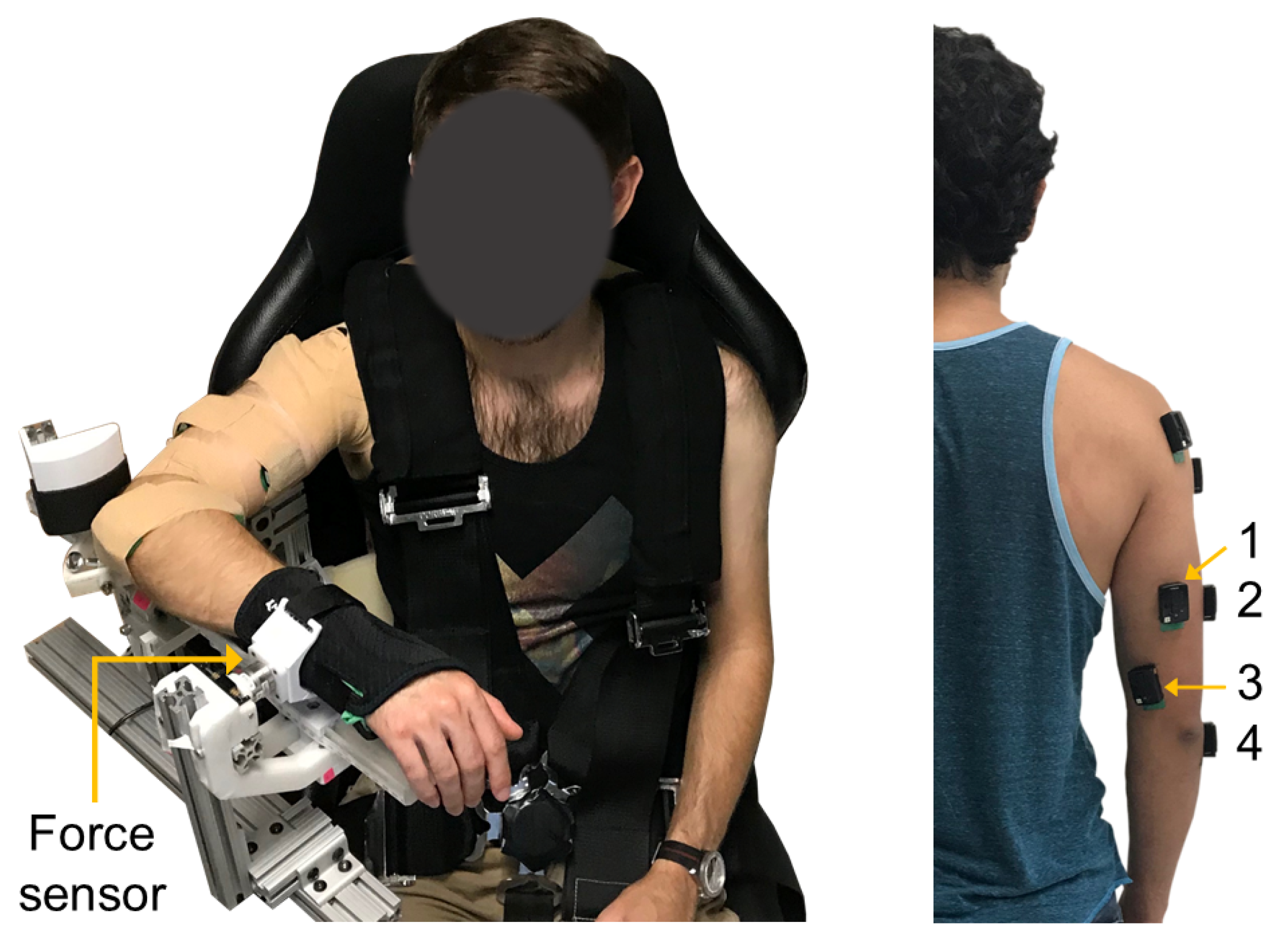
2.2. Experimental Setup
2.3. Experimental Protocol
2.4. Data Acquisition
2.5. Data Processing
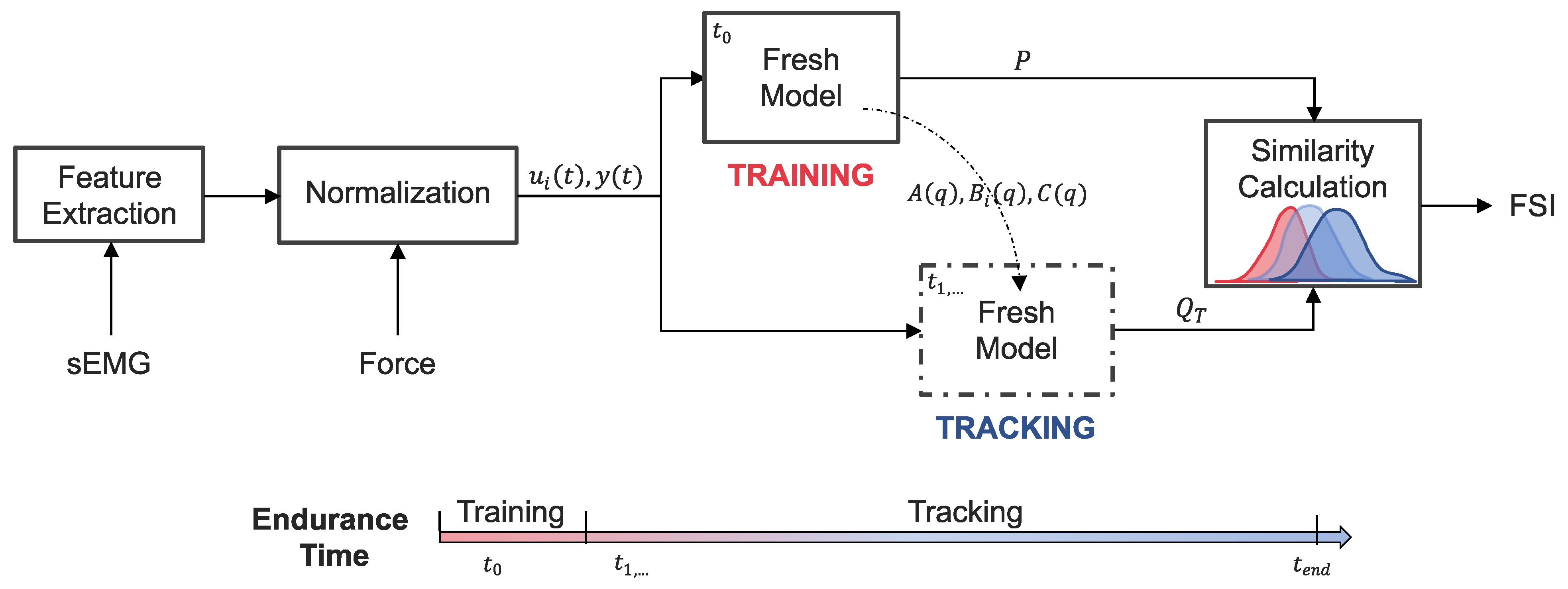
2.6. System-Based Monitoring
2.6.1. sEMG Feature Extraction
2.6.2. Normalization
2.6.3. Modeling
2.6.4. Performance Tracking
2.7. Statistical Analysis
3. Results
3.1. Confirmation of Fatigue
3.2. Evidence of Localized Muscle Fatigue
3.3. Trends in Performance Degradation
3.4. Relationship Between Measures of Performance Degradation and Fatigue
4. Discussion
4.1. Viability of a System-Based Monitoring Approach for Assessing Fatigue
4.2. Improvements to the System-Based Monitoring Paradigm
4.3. Performance of the FSI Metric
4.4. Advantages of a System-Based Monitoring Approach over Alternative Model-Based Techniques for Fatigue Monitoring
4.5. Limitations of the Study
4.6. Applications of the Study
4.7. Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| sEMG | Surface Electromyography |
| MVC | Maximum Voluntary Contraction |
| RPE | Rating of Perceived Exertion |
| FSI | Freshness Similarity Index |
| RMS | Root Mean Square |
| TFD | Time Frequency Distribution |
| ARMAX | Autoregressive Moving Average Model with Exogenous Inputs |
| RM-ANOVA | Repeated Measures Analysis of Variance |
| rmcorr | Repeated Measures Correlation |
| MU | Motor Unit |
| NMS | Neuromusculoskeletal System |
References
- Gandevia, S.C. Spinal and supraspinal factors in human muscle fatigue. Physiol. Rev. 2001, 81, 1725–1789. [Google Scholar] [CrossRef]
- De Luca, C.J. Myoelectrical manifestations of localized muscular fatigue in humans. Crit. Rev. Biomed. Eng. 1984, 11, 251–279. [Google Scholar] [PubMed]
- Carroll, T.J.; Taylor, J.L.; Gandevia, S.C. Recovery of central and peripheral neuromuscular fatigue after exercise. J. Appl. Physiol. 2017, 122, 1068–1076. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knapik, J.J.; Reynolds, K.L.; Harman, E. Soldier load carriage: Historical, physiological, biomechanical, and medical aspects. Mil. Med. 2004, 169, 45–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luttmann, A.; Jäger, M.; Laurig, W. Electromyographical indication of muscular fatigue in occupational field studies. Int. J. Ind. Ergon. 2000, 25, 645–660. [Google Scholar] [CrossRef]
- Zwarts, M.J.; Bleijenberg, G.; Van Engelen, B.G.M. Clinical neurophysiology of fatigue. Clin. Neurophysiol. 2008, 119, 2–10. [Google Scholar] [CrossRef]
- Lou, J.S.; Weiss, M.D.; Carter, G.T. Assessment and management of fatigue in neuromuscular disease. Am. J. Hosp. Palliat. Med. 2010, 27, 145–157. [Google Scholar] [CrossRef]
- Gorelick, M.; Brown, J.; Groeller, H. Short-duration fatigue alters neuromuscular coordination of trunk musculature: Implications for injury. Appl. Ergon. 2003, 34, 317–325. [Google Scholar] [CrossRef]
- Ament, W.; Verkerke, G.J. Exercise and fatigue. Sport. Med. 2009, 39, 389–422. [Google Scholar] [CrossRef]
- Mugnosso, M.; Marini, F.; Holmes, M.; Morasso, P.; Zenzeri, J. Muscle fatigue assessment during robot-mediated movements. J. Neuroeng. Rehabil. 2018, 15, 119. [Google Scholar] [CrossRef]
- Schiphof-Godart, L.; Roelands, B.; Hettinga, F.J. Drive in sports: How mental fatigue affects endurance performance. Front. Psychol. 2018, 9, 1383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borg, G. Psychophysical scaling with applications in physical work and the perception of exertion. Scand. J. Work. Environ. Health 1990, 16, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Marcora, S.M.; Staiano, W.; Manning, V. Mental fatigue impairs physical performance in humans. J. Appl. Physiol. 2009, 106, 857–864. [Google Scholar] [CrossRef] [PubMed]
- Van Cutsem, J.; Marcora, S.; De Pauw, K.; Bailey, S.; Meeusen, R.; Roelands, B. The effects of mental fatigue on physical performance: A systematic review. Sport. Med. 2017, 47, 1569–1588. [Google Scholar] [CrossRef] [Green Version]
- Vøllestad, N.K. Measurement of human muscle fatigue. J. Neurosci. Methods 1997, 74, 219–227. [Google Scholar] [CrossRef]
- Norberto, M.S.; De Arruda, T.B.; Papoti, M. A new approach to evaluate neuromuscular fatigue of extensor elbow muscles. Front. Physiol. 2020, 11, 553296. [Google Scholar] [CrossRef]
- Bigland-Ritchie, B.; Woods, J.J. Changes in muscle contractile properties and neural control during human muscular fatigue. Muscle Nerve 1984, 7, 691–699. [Google Scholar] [CrossRef]
- Merletti, R.; Knaflitz, M.; De Luca, C.J. Myoelectric manifestations of fatigue in voluntary and electrically elicited contractions. J. Appl. Physiol. 1990, 69, 1810–1820. [Google Scholar] [CrossRef] [Green Version]
- Basmajian, J.V. Muscles alive. Their functions revealed by electromyography. Acad. Med. 1962, 37, 802. [Google Scholar]
- Bonato, P.; Roy, S.H.; Knaflitz, M.; De Luca, C.J. Time-frequency parameters of the surface myoelectric signal for assessing muscle fatigue during cyclic dynamic contractions. IEEE Trans. Biomed. Eng. 2001, 48, 745–753. [Google Scholar] [CrossRef] [Green Version]
- Farina, D. Interpretation of the surface electromyogram in dynamic contractions. Exerc. Sport Sci. Rev. 2006, 34, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Cifrek, M.; Medved, V.; Tonković, S.; Ostojić, S. Surface EMG based muscle fatigue evaluation in biomechanics. Clin. Biomech. 2009, 24, 327–340. [Google Scholar] [CrossRef] [PubMed]
- González-Izal, M.; Malanda, A.; Gorostiaga, E.; Izquierdo, M. Electromyographic models to assess muscle fatigue. J. Electromyogr. Kinesiol. 2012, 22, 501–512. [Google Scholar] [CrossRef] [PubMed]
- Rampichini, S.; Vieira, T.M.; Castiglioni, P.; Merati, G. Complexity Analysis of Surface Electromyography for Assessing the Myoelectric Manifestation of Muscle Fatigue: A Review. Entropy 2020, 22, 529. [Google Scholar] [CrossRef]
- MacIsaac, D.T.; Parker, P.A.; Englehart, K.B.; Rogers, D.R. Fatigue estimation with a multivariable myoelectric mapping function. IEEE Trans. Biomed. Eng. 2006, 53, 694–700. [Google Scholar] [CrossRef]
- Rogers, D.R.; MacIsaac, D.T. Training a multivariable myoelectric mapping function to estimate fatigue. J. Electromyogr. Kinesiol. 2010, 20, 953–960. [Google Scholar] [CrossRef]
- Rogers, D.R.; MacIsaac, D.T. EMG-based muscle fatigue assessment during dynamic contractions using principal component analysis. J. Electromyogr. Kinesiol. 2011, 21, 811–818. [Google Scholar] [CrossRef]
- McDonald, A.C.; Mulla, D.M.; Keir, P.J. Using EMG amplitude and frequency to calculate a multimuscle fatigue score and evaluate global shoulder fatigue. Hum. Factors 2019, 61, 526–536. [Google Scholar] [CrossRef]
- Dideriksen, J.L.; Farina, D.; Enoka, R.M. Influence of fatigue on the simulated relation between the amplitude of the surface electromyogram and muscle force. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 2765–2781. [Google Scholar] [CrossRef] [Green Version]
- Isermann, R. Fault-Diagnosis Applications: Model-Based Condition Monitoring: Actuators, Drives, Machinery, Plants, Sensors, and Fault-Tolerant Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mussleman, M.; Gates, D.; Djurdjanovic, D. A System-Based Approach to Monitoring the Performance of a Human Neuromusculoskeletal System. Int. J. Progn. Health Manag. 2016, 7, 14. [Google Scholar]
- Xie, Y.Y.; Djurdjanovic, D. Monitoring of human neuromusculoskeletal system performance through model-based fusion of electromyogram signals and kinematic/dynamic variables. Struct. Health Monit. 2019, 1475921719848006. [Google Scholar] [CrossRef]
- Madden, K.E.; Djurdjanovic, D.; Deshpande, A.D. Monitoring human neuromusculoskeletal system performance during spacesuit glove use: A pilot study. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–10. [Google Scholar]
- Yang, K.; Nicolini, L.; Kuang, I.; Lu, N.; Djurdjanovic, D. Long-term modeling and monitoring of neuromusculoskeletal system performance using tattoo-like EMG sensors. Int. J. Progn. Health Manag. 2019, 10, 004. [Google Scholar]
- Hellmann, F.; Verdi, M.; Schlemper Junior, B.R.; Caponi, S. 50th anniversary of the Declaration of Helsinki: The double standard was introduced. Arch. Med Res. 2014, 45, 600–601. [Google Scholar] [CrossRef] [PubMed]
- Schiele, A.; van der Helm, F.C.T. Kinematic design to improve ergonomics in human machine interaction. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 456–469. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.; Bronks, R. Reproducibility and validity of the quadriceps muscle integrated electromyogram threshold during incremental cycle ergometry. Eur. J. Appl. Physiol. Occup. Physiol. 1995, 70, 252–257. [Google Scholar] [CrossRef] [PubMed]
- Ng, J.K.; Richardson, C.A. Reliability of electromyographic power spectral analysis of back muscle endurance in healthy subjects. Arch. Phys. Med. Rehabil. 1996, 77, 259–264. [Google Scholar] [CrossRef]
- Davidson, A.W.; Rice, C.L. Effect of shoulder angle on the activation pattern of the elbow extensors during a submaximal isometric fatiguing contraction. Muscle Nerve 2010, 42, 514–521. [Google Scholar] [CrossRef]
- Krogh-Lund, C.; Jørgensen, K. Changes in conduction velocity, median frequency, and root mean square-amplitude of the electromyogram during 25% maximal voluntary contraction of the triceps brachii muscle, to limit of endurance. Eur. J. Appl. Physiol. Occup. Physiol. 1991, 63, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Rogers, D.R.; MacIsaac, D.T. A comparison of EMG-based muscle fatigue assessments during dynamic contractions. J. Electromyogr. Kinesiol. 2013, 23, 1004–1011. [Google Scholar] [CrossRef]
- Hermens, H.J.; Freriks, B.; Merletti, R.; Stegeman, D.; Blok, J.; Rau, G.; Disselhorst-Klug, C.; Hägg, G. European recommendations for surface electromyography. Roessingh Res. Dev. 1999, 8, 13–54. [Google Scholar]
- Merletti, R. Standards for reporting EMG data. J. Electromyogr. Kinesiol. 1999, 9, 3–4. [Google Scholar]
- Potvin, J.; Brown, S. Less is more: High pass filtering, to remove up to 99% of the surface EMG signal power, improves EMG-based biceps brachii muscle force estimates. J. Electromyogr. Kinesiol. 2004, 14, 389–399. [Google Scholar] [CrossRef] [PubMed]
- Semmlow, J.L.; Griffel, B. Biosignal and Medical Image Processing; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Dankaerts, W.; O’Sullivan, P.B.; Burnett, A.F.; Straker, L.M.; Danneels, L.A. Reliability of EMG measurements for trunk muscles during maximal and sub-maximal voluntary isometric contractions in healthy controls and CLBP patients. J. Electromyogr. Kinesiol. 2004, 14, 333–342. [Google Scholar] [CrossRef] [PubMed]
- Bonato, P.; Gagliati, G.; Knaflitz, M. Analysis of myoelectric signals recorded during dynamic contractions. IEEE Eng. Med. Biol. Mag. 1996, 15, 102–111. [Google Scholar] [CrossRef]
- von Tscharner, V. Intensity analysis in time-frequency space of surface myoelectric signals by wavelets of specified resolution. J. Electromyogr. Kinesiol. 2000, 10, 433–445. [Google Scholar] [CrossRef]
- Boashash, B. Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, 2nd ed.; Academic Press: Oxford, UK, 2016; Chapter 16. [Google Scholar]
- Gottlieb, G.L.; Agarwal, G.C. Dynamic relationship between isometric muscle tension and the electromyogram in man. J. Appl. Physiol. 1971, 30, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Thelen, D.G.; Schultz, A.B.; Fassois, S.D.; Ashton-Miller, J.A. Identification of dynamic myoelectric signal-to-force models during isometric lumbar muscle contractions. J. Biomech. 1994, 27, 907–919. [Google Scholar] [CrossRef] [Green Version]
- Cha, S.H. Comprehensive survey on distance/similarity measures between probability density functions. Int. J. Math. Model. Methods Appl. Sci. 2007, 1, 1. [Google Scholar]
- Hernández-Rivera, E.; Coleman, S.P.; Tschopp, M.A. Using similarity metrics to quantify differences in high-throughput data sets: Application to X-ray diffraction patterns. ACS Comb. Sci. 2017, 19, 25–36. [Google Scholar] [CrossRef]
- MATLAB. Version 9.3.0 (R2017b); The MathWorks Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistics notes: Calculating correlation coefficients with repeated observations: Part 1—Correlation within subjects. BMJ 1995, 310, 446. [Google Scholar] [CrossRef] [Green Version]
- Bakdash, J.Z.; Marusich, L.R. Repeated measures correlation. Front. Psychol. 2017, 8, 456. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mukaka, M.M. A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Le Bozec, S.; Maton, B.; Cnockaert, J.C. The synergy of elbow extensor muscles during static work in man. Eur. J. Appl. Physiol. Occup. Physiol. 1980, 43, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Neumann, D.A. Kinesiology of the Musculoskeletal System; Foundation for Rehabilitation, 2nd ed.; Mosby/Elsevier: St. Louis, MO, USA, 2010; Chapter 6. [Google Scholar]
- Zhang, L.Q.; Nuber, G.W. Moment distribution among human elbow extensor muscles during isometric and submaximal extension. J. Biomech. 2000, 33, 145–154. [Google Scholar] [CrossRef]
- Elder, G.C.; Bradbury, K.; Roberts, R. Variability of fiber type distributions within human muscles. J. Appl. Physiol. 1982, 53, 1473–1480. [Google Scholar] [CrossRef]
- Le Bozec, S.; Maton, B. Differences between motor unit firing rate, twitch characteristics and fibre type composition in an agonistic muscle group in man. Eur. J. Appl. Physiol. Occup. Physiol. 1987, 56, 350–355. [Google Scholar] [CrossRef]
- Kuo, K.H.M.; Clamann, H.P. Coactivation of synergistic muscles of different fiber types in fast and slow contractions. Am. J. Phys. Med. Rehabil. 1981, 60, 219–238. [Google Scholar]
- Gonzalez-Izal, M.; Falla, D.; Izquierdo, M.; Farina, D. Predicting force loss during dynamic fatiguing exercises from non-linear mapping of features of the surface electromyogram. J. Neurosci. Methods 2010, 190, 271–278. [Google Scholar] [CrossRef]
- Merletti, R.; Conte, L.R.; Orizio, C. Indices of muscle fatigue. J. Electromyogr. Kinesiol. 1991, 1, 20–33. [Google Scholar] [CrossRef]
- Hostens, I.; Seghers, J.; Spaepen, A.; Ramon, H. Validation of the wavelet spectral estimation technique in biceps brachii and brachioradialis fatigue assessment during prolonged low-level static and dynamic contractions. J. Electromyogr. Kinesiol. 2004, 14, 205–215. [Google Scholar] [CrossRef]
- Woods, J.J.; Bigland-Ritchie, B. Linear and non-linear surface EMG/force relationships in human muscles. An anatomical/functional argument for the existence of both. Am. J. Phys. Med. 1983, 62, 287–299. [Google Scholar] [PubMed]
- Asefi, M.; Moghimi, S.; Kalani, H.; Moghimi, A. Dynamic modeling of SEMG–force relation in the presence of muscle fatigue during isometric contractions. Biomed. Signal Process. Control 2016, 28, 41–49. [Google Scholar] [CrossRef]
- Rao, G.; Berton, E.; Amarantini, D.; Vigouroux, L.; Buchanan, T.S. An EMG-driven biomechanical model that accounts for the decrease in moment generation capacity during a dynamic fatigued condition. J. Biomech. Eng. 2010, 132, 071003. [Google Scholar] [CrossRef]
- Dimitrov, G.V.; Arabadzhiev, T.I.; Mileva, K.N.; Bowtell, J.L.; Crichton, N.; Dimitrova, N.A. Muscle fatigue during dynamic contractions assessed by new spectral indices. Med. Sci. Sport. Exerc. 2006, 38, 1971–1979. [Google Scholar] [CrossRef]
- González-Izal, M.; Malanda, A.; Navarro-Amézqueta, I.; Gorostiaga, E.M.; Mallor, F.; Ibañez, J.; Izquierdo, M. EMG spectral indices and muscle power fatigue during dynamic contractions. J. Electromyogr. Kinesiol. 2010, 20, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Dearth, D.J.; Umbel, J.; Hoffman, R.L.; Russ, D.W.; Wilson, T.E.; Clark, B.C. Men and women exhibit a similar time to task failure for a sustained, submaximal elbow extensor contraction. Eur. J. Appl. Physiol. 2010, 108, 1089–1098. [Google Scholar] [CrossRef] [PubMed]
- Hunter, S.K. The relevance of sex differences in performance fatigability. Med. Sci. Sport. Exerc. 2016, 48, 2247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forkan, A.R.M.; Khalil, I. A clinical decision-making mechanism for context-aware and patient-specific remote monitoring systems using the correlations of multiple vital signs. Comput. Methods Programs Biomed. 2017, 139, 1–16. [Google Scholar] [CrossRef]
- Nordin, N.; Xie, S.Q.; Wünsche, B. Assessment of movement quality in robot-assisted upper limb rehabilitation after stroke: A review. J. Neuroeng. Rehabil. 2014, 11, 137. [Google Scholar] [CrossRef] [Green Version]
- Marchal-Crespo, L.; Reinkensmeyer, D.J. Review of control strategies for robotic movement training after neurologic injury. J. Neuroeng. Rehabil. 2009, 6, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Musselman, M.; Gates, D.; Djurdjanovic, D. System based monitoring of a neuromusculoskeletal system using divide and conquer type models. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–12. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madden, K.E.; Djurdjanovic, D.; Deshpande, A.D. Using a System-Based Monitoring Paradigm to Assess Fatigue during Submaximal Static Exercise of the Elbow Extensor Muscles. Sensors 2021, 21, 1024. https://doi.org/10.3390/s21041024
Madden KE, Djurdjanovic D, Deshpande AD. Using a System-Based Monitoring Paradigm to Assess Fatigue during Submaximal Static Exercise of the Elbow Extensor Muscles. Sensors. 2021; 21(4):1024. https://doi.org/10.3390/s21041024
Chicago/Turabian StyleMadden, Kaci E., Dragan Djurdjanovic, and Ashish D. Deshpande. 2021. "Using a System-Based Monitoring Paradigm to Assess Fatigue during Submaximal Static Exercise of the Elbow Extensor Muscles" Sensors 21, no. 4: 1024. https://doi.org/10.3390/s21041024
APA StyleMadden, K. E., Djurdjanovic, D., & Deshpande, A. D. (2021). Using a System-Based Monitoring Paradigm to Assess Fatigue during Submaximal Static Exercise of the Elbow Extensor Muscles. Sensors, 21(4), 1024. https://doi.org/10.3390/s21041024





