Sensorless Self-Excited Vibrational Viscometer with Two Hopf Bifurcations Based on a Piezoelectric Device
Abstract
:1. Introduction
2. Principle of Viscosity Measurement Based on Sensorless Self-Excited Oscillation
2.1. Theoretical Modeling of the Sensorless Viscometer System
2.1.1. Analytical Model and Governing Equations
2.1.2. Proposed Feedback Control
2.2. Dynamics of the Viscometer System
2.3. Proposed Highly Sensitive Viscosity Measurement Using the Bi-Unstable Range
2.3.1. Analysis of the Root Locus
2.3.2. Condition for the Multiple Eigenvalues
2.3.3. Derivation of the Endpoints of the Bi-Unstable Range
2.4. Summary of the Proposed Method
3. Experiment
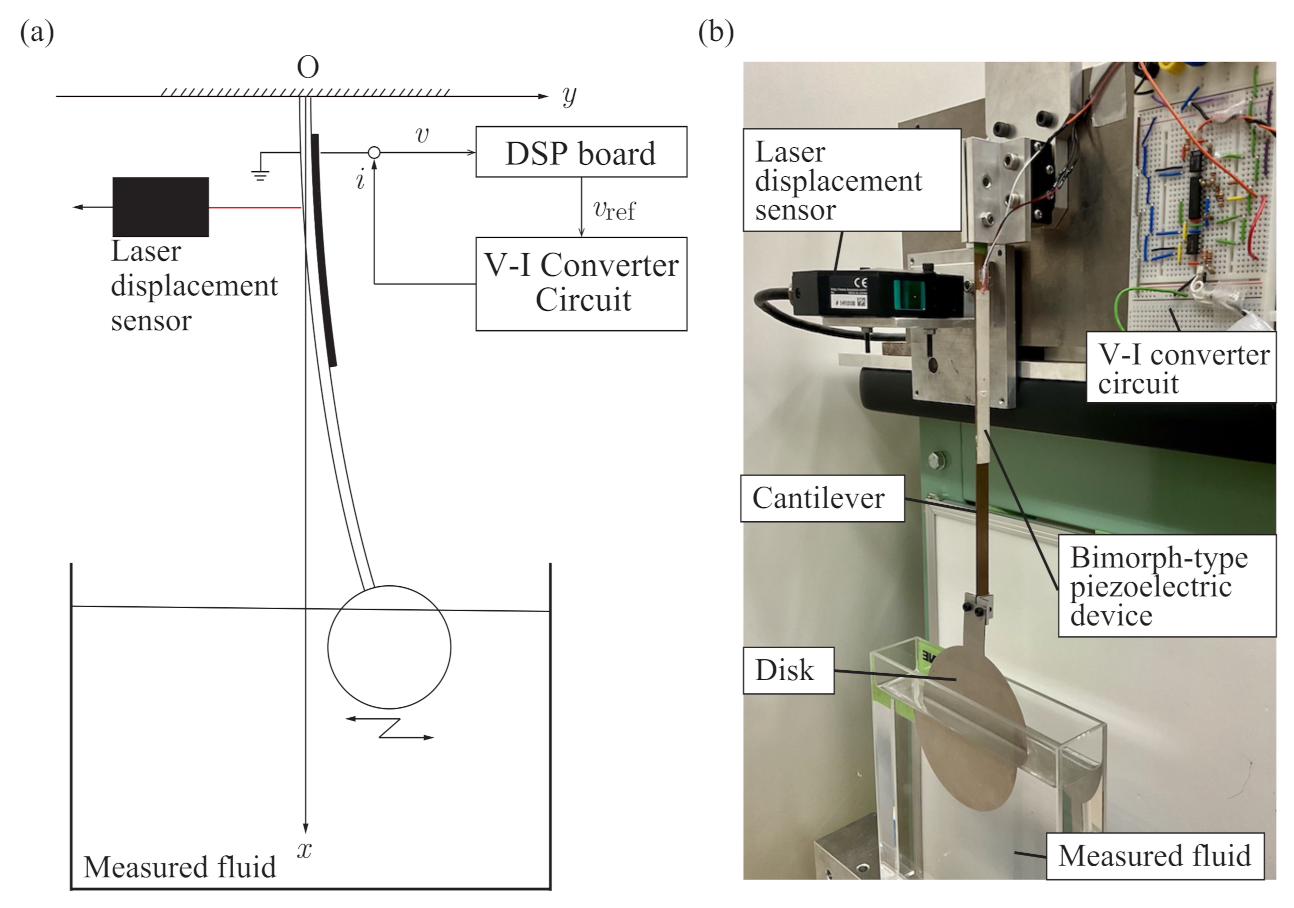
3.1. Experimental Setup and Basic Properties
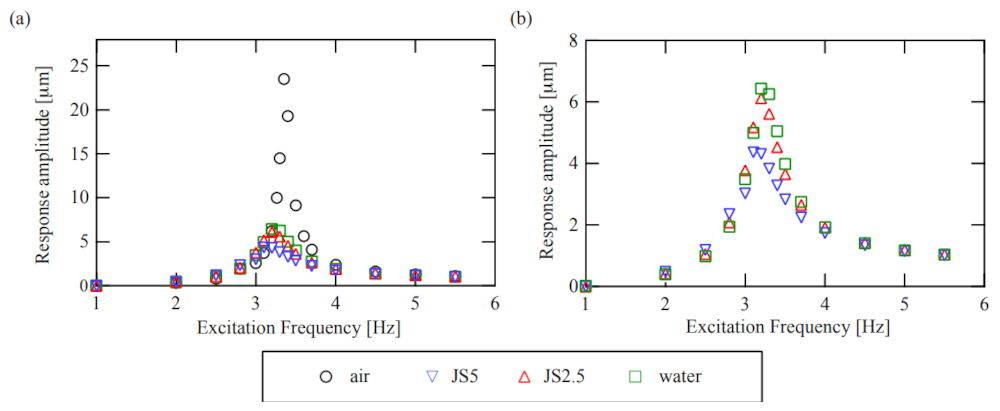
3.2. Viscosity Measurement via the Proposed Method
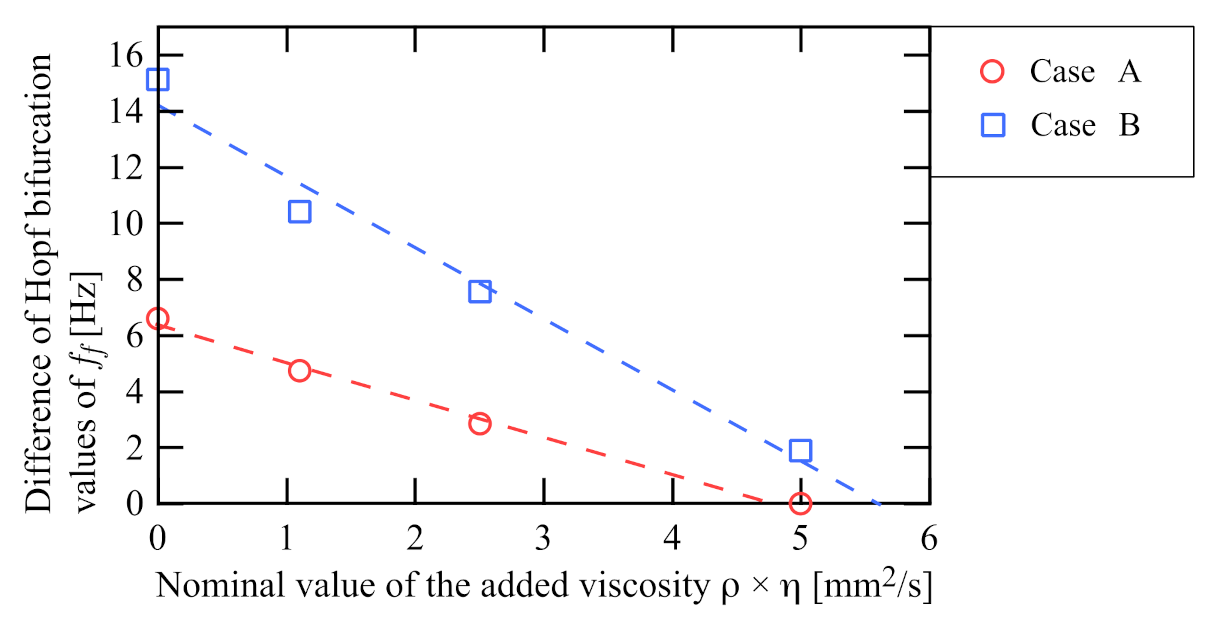
3.3. Evaluation and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Rondon, J.; Barrufet, M.A.; Falcone, G. A novel downhole sensor to determine fluid viscosity. Flow Meas. Instrum. 2012, 23, 9–18. [Google Scholar] [CrossRef]
- Antlinger, H.; Clara, S.; Beigelbeck, R.; Cerimovic, S.; Keplinger, F.; Jakoby, B. An acoustic transmission sensor for the longitudinal viscosity of fluids. Sens. Actuators A Phys. 2013, 202, 23–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woodward, J. A vibrating-plate viscometer. J. Colloid Sci. 1951, 6, 481–491. [Google Scholar] [CrossRef]
- Woodward, J.G. A Vibrating Plate Viscometer. J. Acoust. Soc. Am. 1953, 25, 147–151. [Google Scholar] [CrossRef]
- Santos, J.; Janeiro, F.M.; Ramos, P.M. Impedance frequency characterization of a vibrating wire viscosity sensor with multiharmonic signals. Measurement 2014, 55, 276–287. [Google Scholar] [CrossRef]
- Radmacher, M.; Tillamnn, R.; Fritz, M.; Gaub, H. From molecules to cells: Imaging soft samples with the atomic force microscope. Science 1992, 257, 1900–1905. [Google Scholar] [CrossRef]
- Alcaraz, J.; Buscemi, L.; Grabulosa, M.; Trepat, X.; Fabry, B.; Farre, R.; Navajas, D. Microrheology of Human Lung Epithelial Cells Measured by Atomic Force Microscopy. Biophys. J. 2003, 84, 2071–2079. [Google Scholar] [CrossRef] [Green Version]
- Cross, S.E.; Jin, Y.S.; Rao, J.; Gimzewski, J.K. Nanomechanical analysis of cells from cancer patients. Nat. Nanotechnol. 2007, 2, 780–783. [Google Scholar] [CrossRef]
- Goodwin, A.R.H.; Jakeways, C.V.; de Lara, M.M. A MEMS Vibrating Edge Supported Plate for the Simultaneous Measurement of Density and Viscosity: Results for Nitrogen, Methylbenzene, Water, 1-Propene,1,1,2,3,3,3-hexafluoro-oxidized-polymd, and Polydimethylsiloxane and Four Certified Reference Materials with Viscosities in the Range (0.038 to 275) mPa·s and Densities between (408 and 1834) kg m3 at Temperatures from (313 to 373) K and Pressures up to 60 MPa. J. Chem. Eng. Data 2008, 53, 1436–1443. [Google Scholar] [CrossRef]
- Cai, P.; Mizutani, Y.; Tsuchiya, M.; Maloney, J.M.; Fabry, B.; Van Vliet, K.J.; Okajima, T. Quantifying cell-to-cell variation in power-law rheology. Biophys. J. 2013, 105, 1093–1102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [Green Version]
- Boskovic, S.; Chon, J.W.M.; Mulvaney, P.; Sader, J.E. Rheological measurements using microcantilevers. J. Rheol. 2002, 46, 891–899. [Google Scholar] [CrossRef]
- Oden, P.I.; Chen, G.Y.; Steele, R.A.; Warmack, R.J.; Thundat, T. Viscous drag measurements utilizing microfabricated cantilevers. Appl. Phys. Lett. 1996, 68, 3814–3816. [Google Scholar] [CrossRef]
- Datar, R.; Kim, S.; Jeon, S.; Hesketh, P.; Manalis, S.; Boisen, A.; Thundat, T. Cantilever Sensors: Nanomechanical Tools for Diagnostics. MRS Bull. 2009, 34, 449–454. [Google Scholar] [CrossRef]
- Cerimovic, S.; Beigelbeck, R.; Antlinger, H.; Schalko, J.; Jakoby, B.; Keplinger, F. Sensing viscosity and density of glycerol–water mixtures utilizing a suspended plate MEMS resonator. Microsyst. Technol. 2012, 18, 1045–1056. [Google Scholar] [CrossRef] [Green Version]
- Blom, F.R.; Bouwstra, S.; Elwenspoek, M.; Fluitman, J.H.J. Dependence of the quality factor of micromachined silicon beam resonators on pressure and geometry. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 1992, 10, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Heinisch, M.; Voglhuber-Brunnmaier, T.; Reichel, E.; Dufour, I.; Jakoby, B. Reduced order models for resonant viscosity and mass density sensors. Sens. Actuators A Phys. 2014, 220, 76–84. [Google Scholar] [CrossRef] [Green Version]
- Wilson, T.L.; Campbell, G.A.; Mutharasan, R. Viscosity and density values from excitation level response of piezoelectric-excited cantilever sensors. Sens. Actuators A Phys. 2007, 138, 44–51. [Google Scholar] [CrossRef]
- Sathiya, S.; Vasuki, B. A structural tailored piezo actuated cantilever shaped 2-DOF resonators for viscosity and density sensing in liquids. Sens. Actuators A Phys. 2016, 247, 277–288. [Google Scholar] [CrossRef]
- Yabuno, H.; Higashino, K.; Kuroda, M.; Yamamoto, Y. Self-excited vibrational viscometer for high-viscosity sensing. J. Appl. Phys. 2014, 116, 124305. [Google Scholar] [CrossRef] [Green Version]
- Higashino, K.; Yabuno, H.; Aono, K.; Yamamoto, Y.; Kuroda, M. Self-Excited Vibrational Cantilever-Type Viscometer Driven by Piezo-Actuator. J. Vib. Acoust. 2015, 137, 061009. [Google Scholar] [CrossRef]
- Vidic, A.; Then, D.; Ziegler, C. A new cantilever system for gas and liquid sensing. Ultramicroscopy 2003, 97, 407–416. [Google Scholar] [CrossRef]
- Bircher, B.A.; Krenger, R.; Braun, T. Automated high-throughput viscosity and density sensor using nanomechanical resonators. Sens. Actuators B Chem. 2016, 223, 784–790. [Google Scholar] [CrossRef] [Green Version]
- Mouro, J.; Tiribilli, B.; Paoletti, P. Nonlinear behaviour of self-excited microcantilevers in viscous fluids. J. Micromech. Microeng. 2017, 27, 095008. [Google Scholar] [CrossRef]
- Mouro, J.; Tiribilli, B.; Paoletti, P. Measuring viscosity with nonlinear self-excited microcantilevers. Appl. Phys. Lett. 2017, 111, 144101. [Google Scholar] [CrossRef] [Green Version]
- Etchenique, R.; Weisz, A.D. Simultaneous determination of the mechanical moduli and mass of thin layers using nonadditive quartz crystal acoustic impedance analysis. J. Appl. Phys. 1999, 86, 1994–2000. [Google Scholar] [CrossRef] [Green Version]
- Encarnao, J.M.; Stallinga, P.; Ferreira, G.N. Influence of electrolytes in the QCM response: Discrimination and quantification of the interference to correct microgravimetric data. Biosens. Bioelectron. 2007, 22, 1351–1358. [Google Scholar] [CrossRef] [PubMed]
- Guha, A.; Sandstr, N.; Ostanin, V.P.; van der Wijngaart, W.; Klenerman, D.; Ghosh, S.K. Simple and ultrafast resonance frequency and dissipation shift measurements using a fixed frequency drive. Sens. Actuators B Chem. 2019, 281, 960–970. [Google Scholar] [CrossRef]
- Sakti, S.P.; Kamasi, D.D.; Khusnah, N.F. Stearic Acid Coating Material Loading Effect to Quartz Crystal Microbalance Sensor. Mater. Today Proc. 2019, 13, 53–58. [Google Scholar] [CrossRef]
- Wang, G.; Tan, C.; Li, F. A contact resonance viscometer based on the electromechanical impedance of a piezoelectric cantilever. Sens. Actuators A Phys. 2017, 267, 401–408. [Google Scholar] [CrossRef]
- Tanaka, Y.; Kokubun, Y.; Yabuno, H. Proposition for sensorless self-excitation by a piezoelectric device. J. Sound Vib. 2018, 419, 544–557. [Google Scholar] [CrossRef]
- Bi, Q.; Yu, P. Double Hopf Bifurcations and Chaos of a Nonlinear Vibration System. Nonlinear Dyn. 1999, 19, 313–332. [Google Scholar] [CrossRef]
- Qesmi, R.; Babram, M.A. Double Hopf bifurcation in delay differential equations. Arab J. Math. Sci. 2014, 20, 280–301. [Google Scholar] [CrossRef] [Green Version]
- Lau, W.R.; Hwang, C.A.; Brugge, H.B.; Iglesias-Silva, G.A.; Duarte-Garza, H.A.; Rogers, W.J.; Hall, K.R.; Holste, J.C.; Gammon, B.E.; Marsh, K.N. A Continuously Weighed Pycnometer for Measuring Fluid Properties. J. Chem. Eng. Data 1997, 42, 738–744. [Google Scholar] [CrossRef]







| Sample Label | JS5 | JS2.5 | Water |
|---|---|---|---|
| density [kg/m] | 8.130 | 7.728 | 1 |
| viscosity [mPa s] | 4.067 | 1.936 | 1 |
| Symbol | Value | Unit |
|---|---|---|
| 3.27 | N/V | |
| m | 4 | kg |
| 10.5 | rad/s | |
| F |
| Condition Label | Case A | Case B |
|---|---|---|
| Proportional gain [A/V] | −4.46 | −4.46 |
| Derivative gain [A/Vs] | 1.47 | 1.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urasaki, S.; Yabuno, H.; Yamamoto, Y.; Matsumoto, S. Sensorless Self-Excited Vibrational Viscometer with Two Hopf Bifurcations Based on a Piezoelectric Device. Sensors 2021, 21, 1127. https://doi.org/10.3390/s21041127
Urasaki S, Yabuno H, Yamamoto Y, Matsumoto S. Sensorless Self-Excited Vibrational Viscometer with Two Hopf Bifurcations Based on a Piezoelectric Device. Sensors. 2021; 21(4):1127. https://doi.org/10.3390/s21041127
Chicago/Turabian StyleUrasaki, Shinpachiro, Hiroshi Yabuno, Yasuyuki Yamamoto, and Sohei Matsumoto. 2021. "Sensorless Self-Excited Vibrational Viscometer with Two Hopf Bifurcations Based on a Piezoelectric Device" Sensors 21, no. 4: 1127. https://doi.org/10.3390/s21041127






