mmW Rotman Lens-Based Sensing: An Investigation Study
Abstract
:1. Introduction
2. Rotman Lens
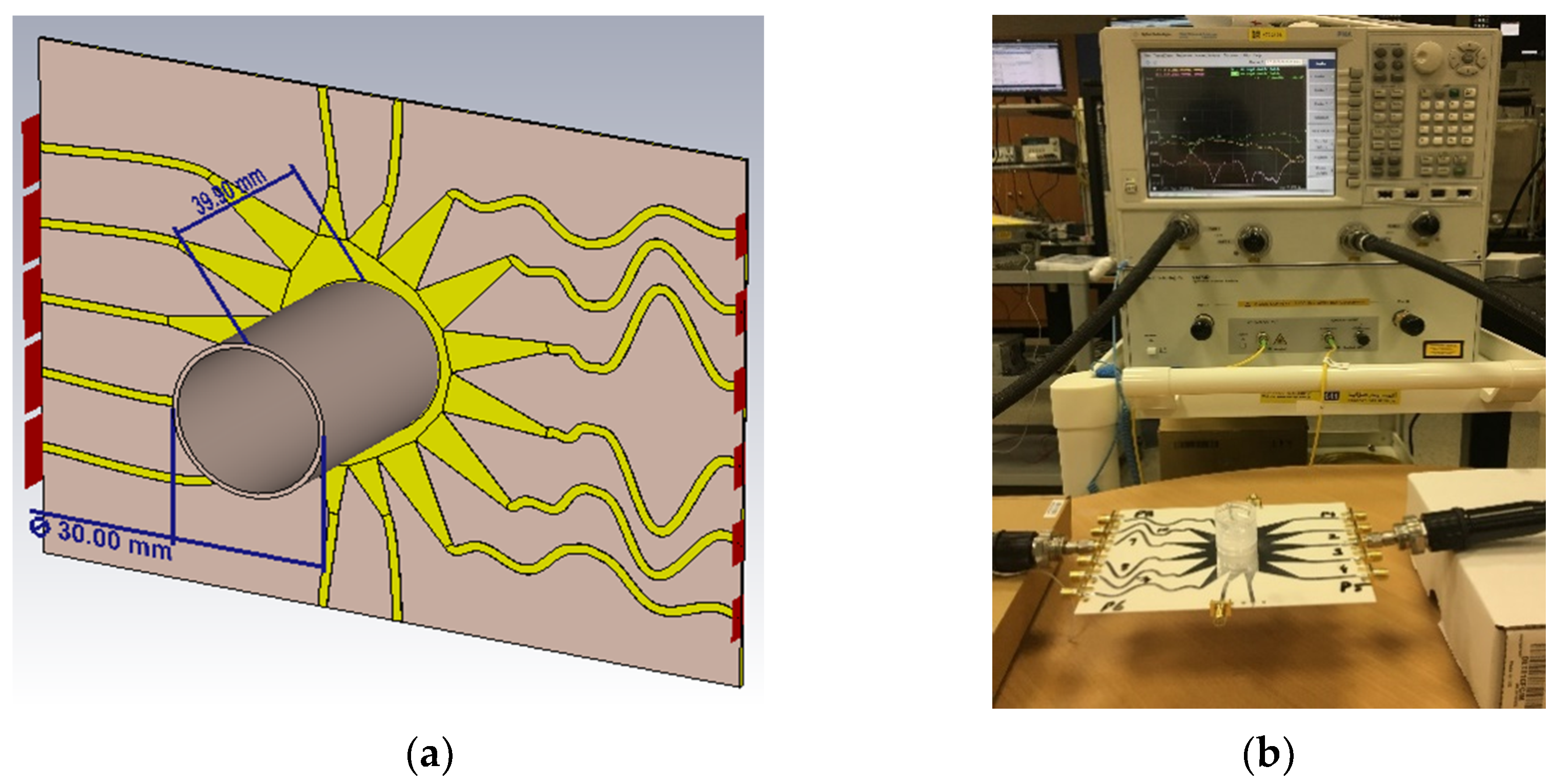
2.1. Structure
2.2. Sensor Design
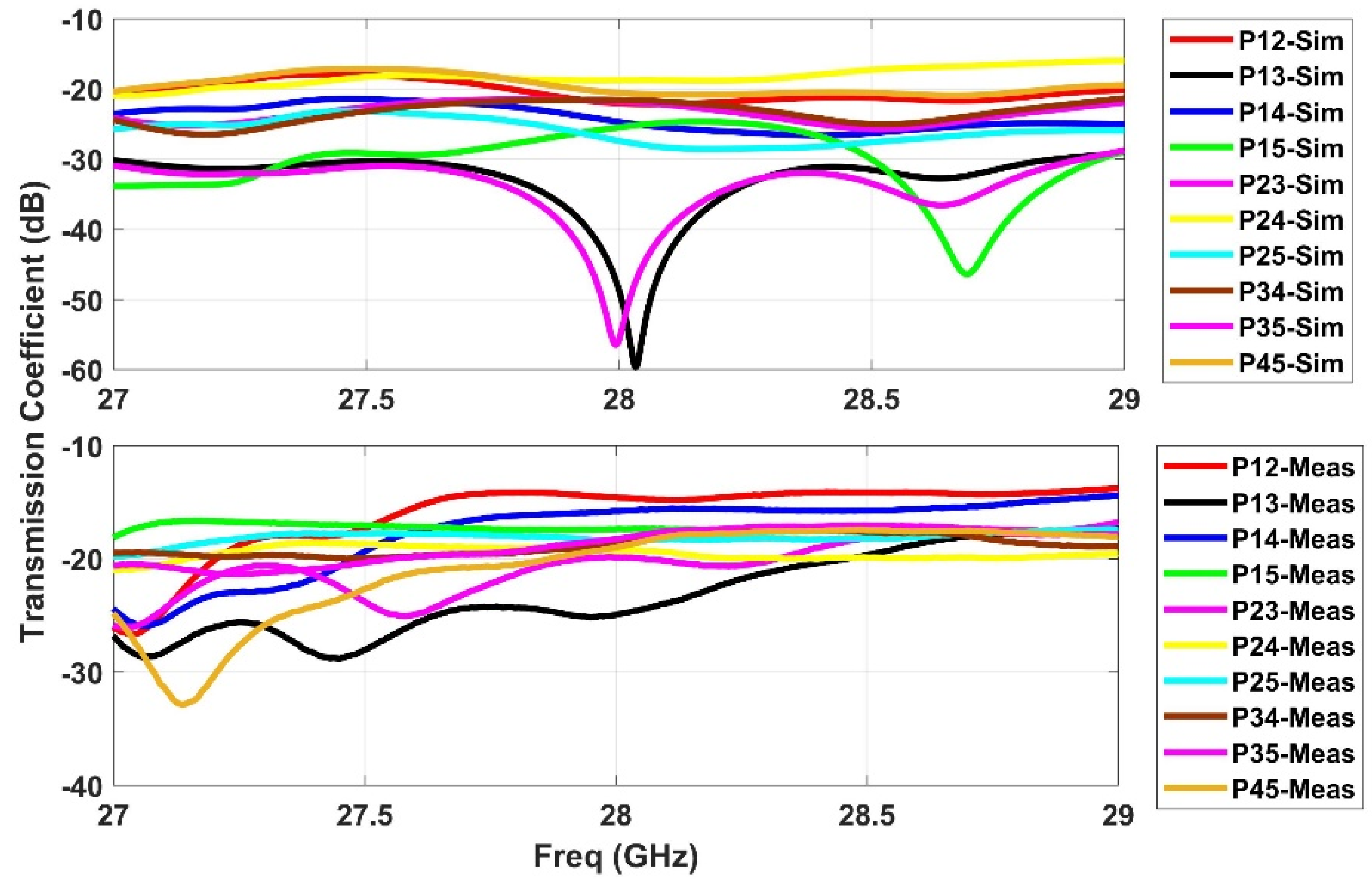
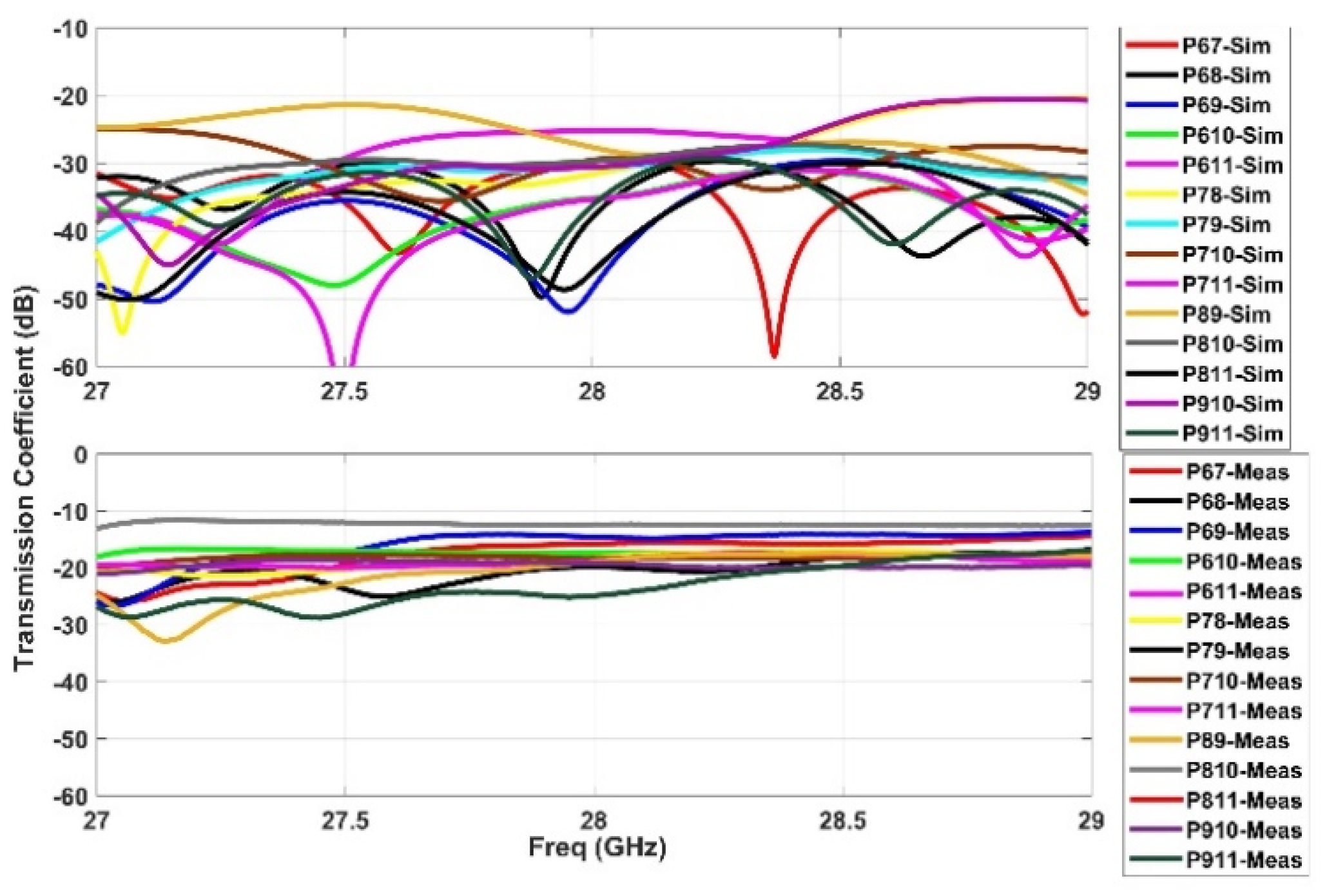
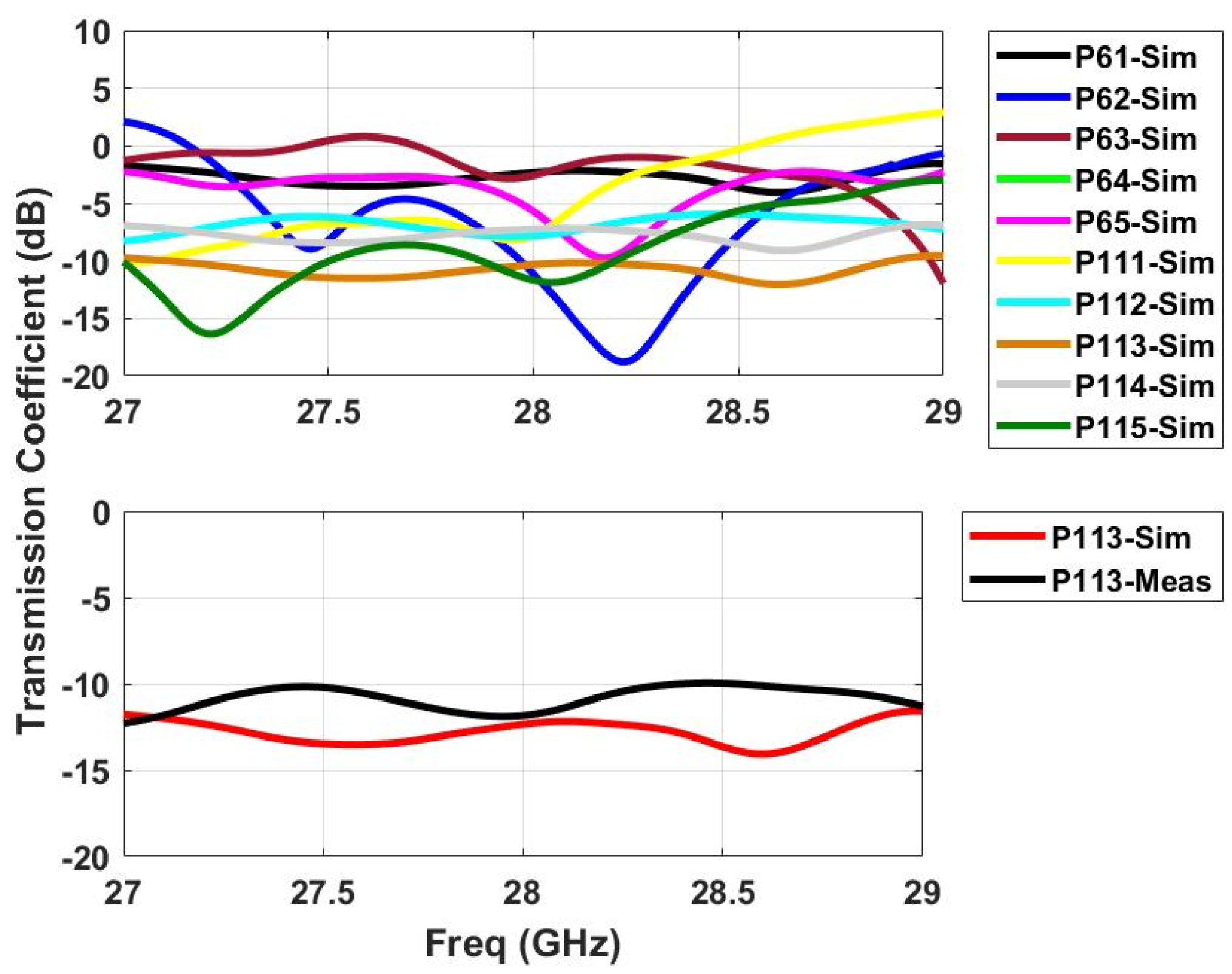
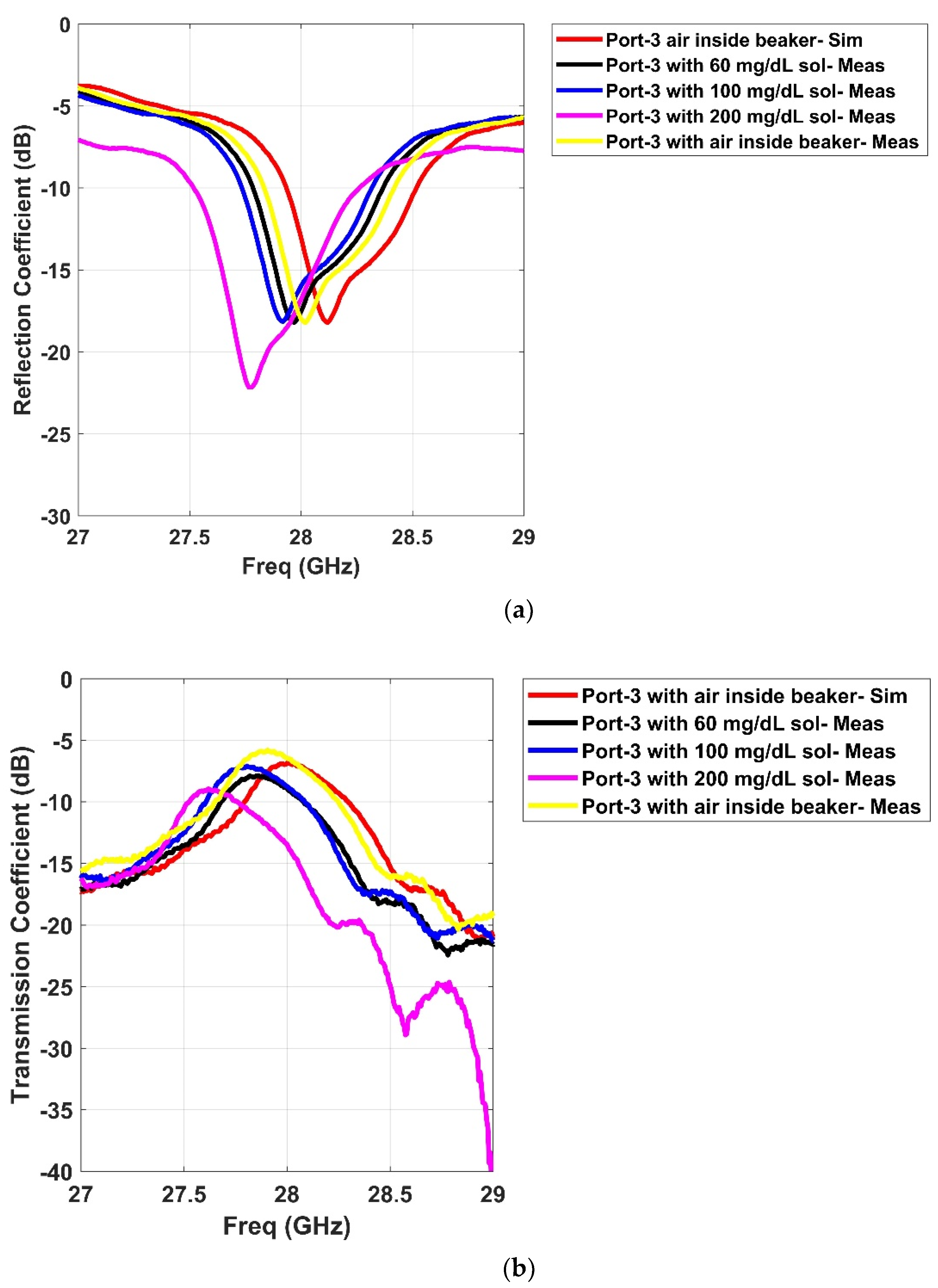
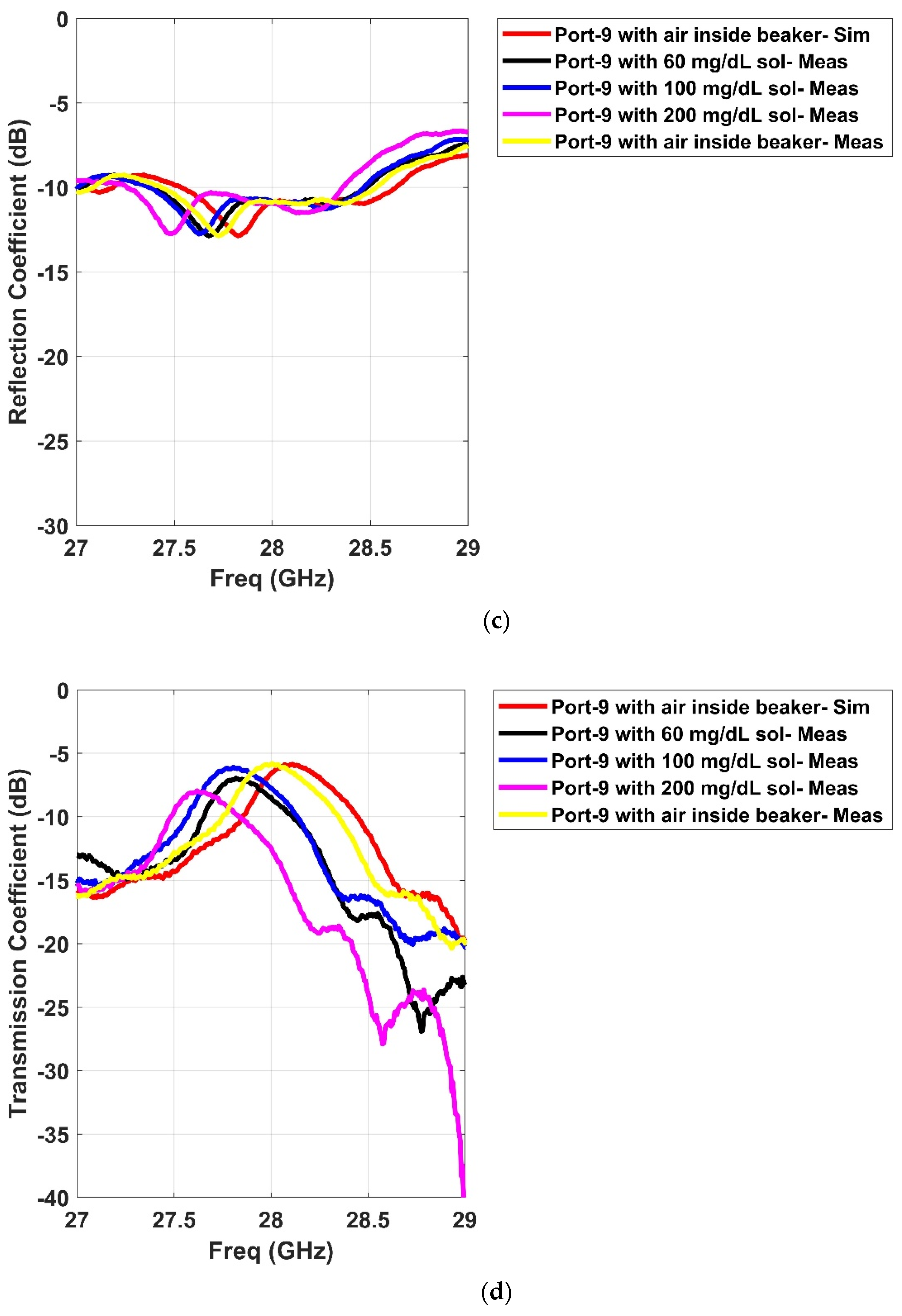
2.3. S-Parameters
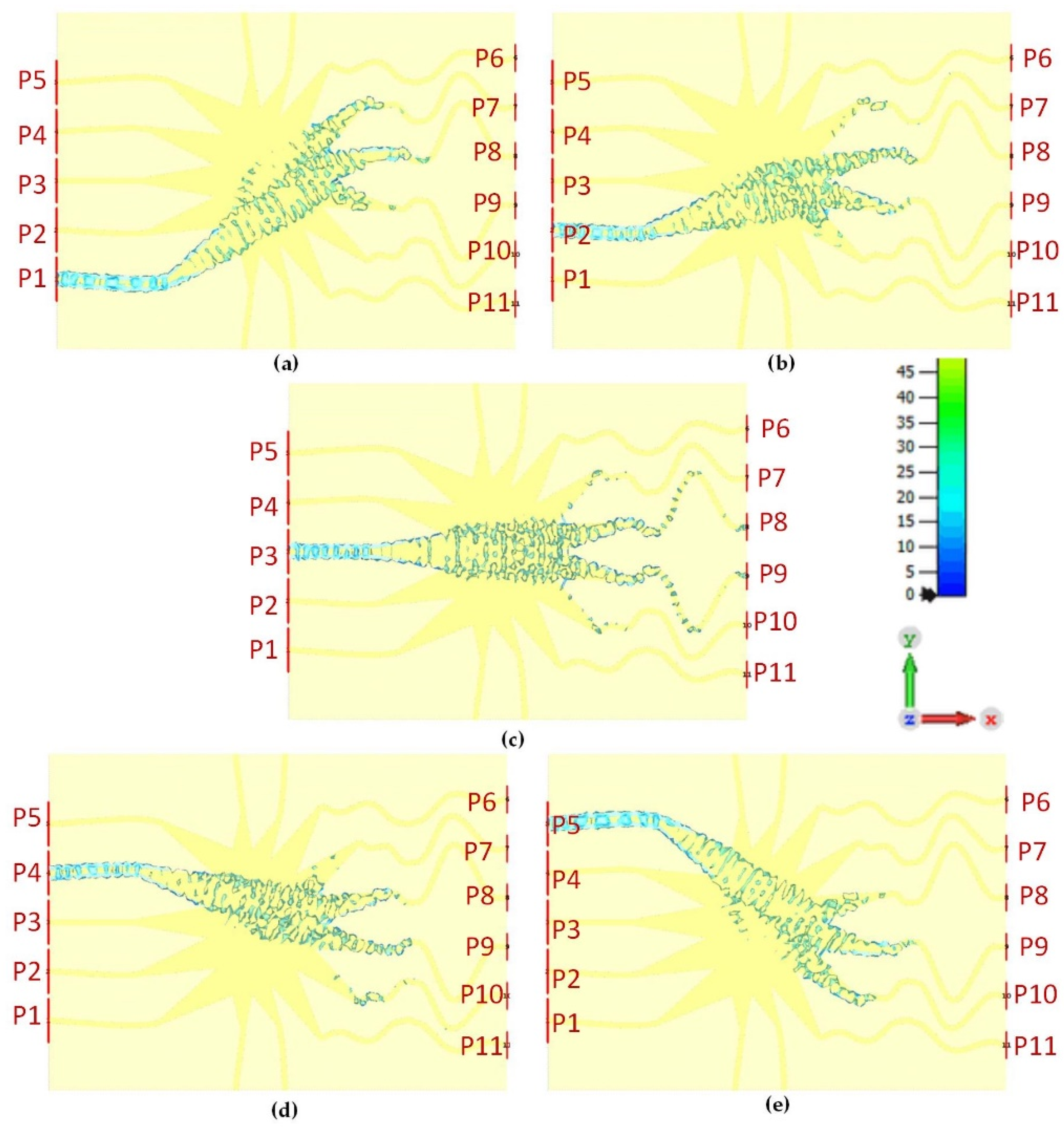
2.4. Surface Current Distributions
3. Sample Load for Testing the Sensor
3.1. Material Preparation
3.2. Sensor Validation
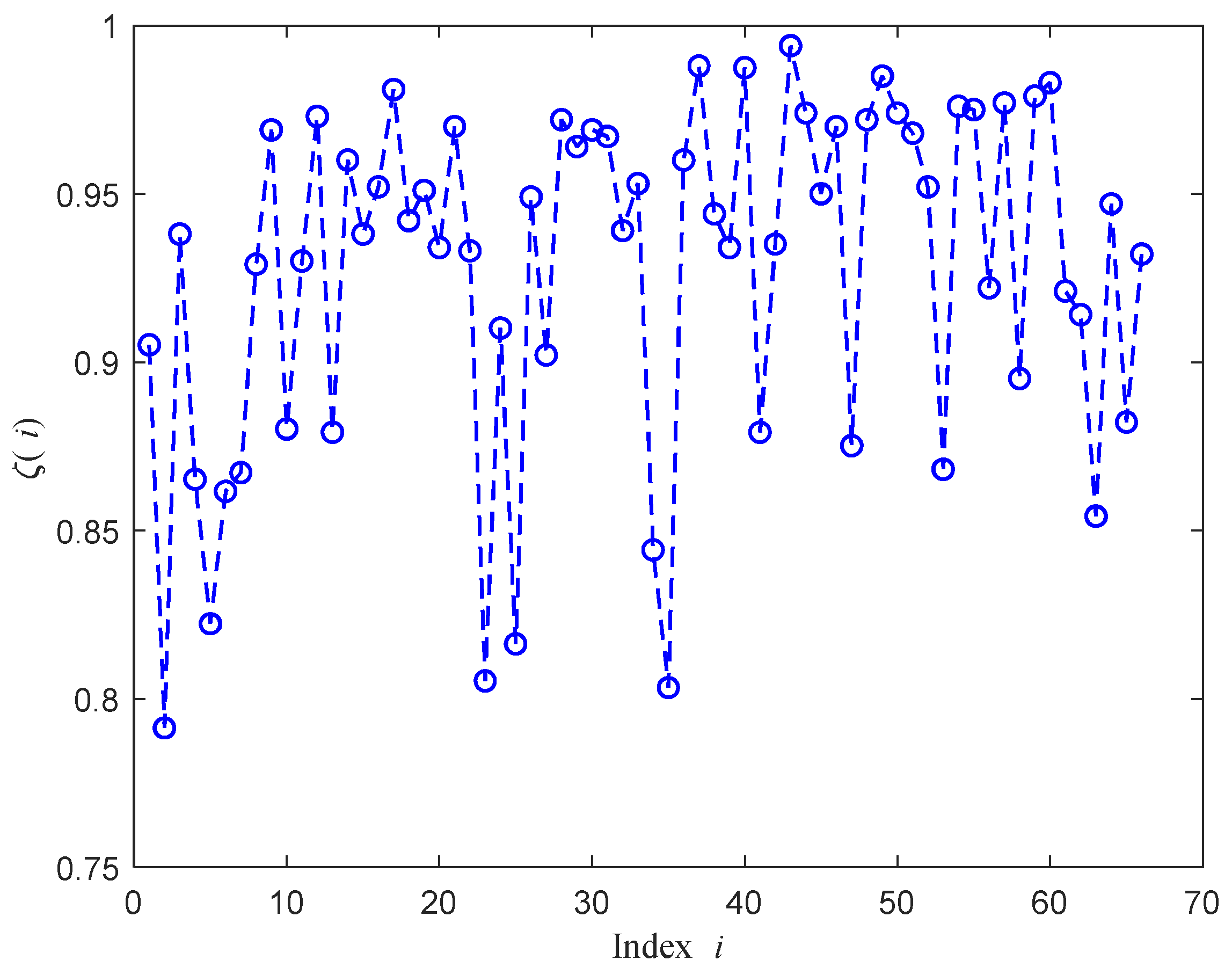
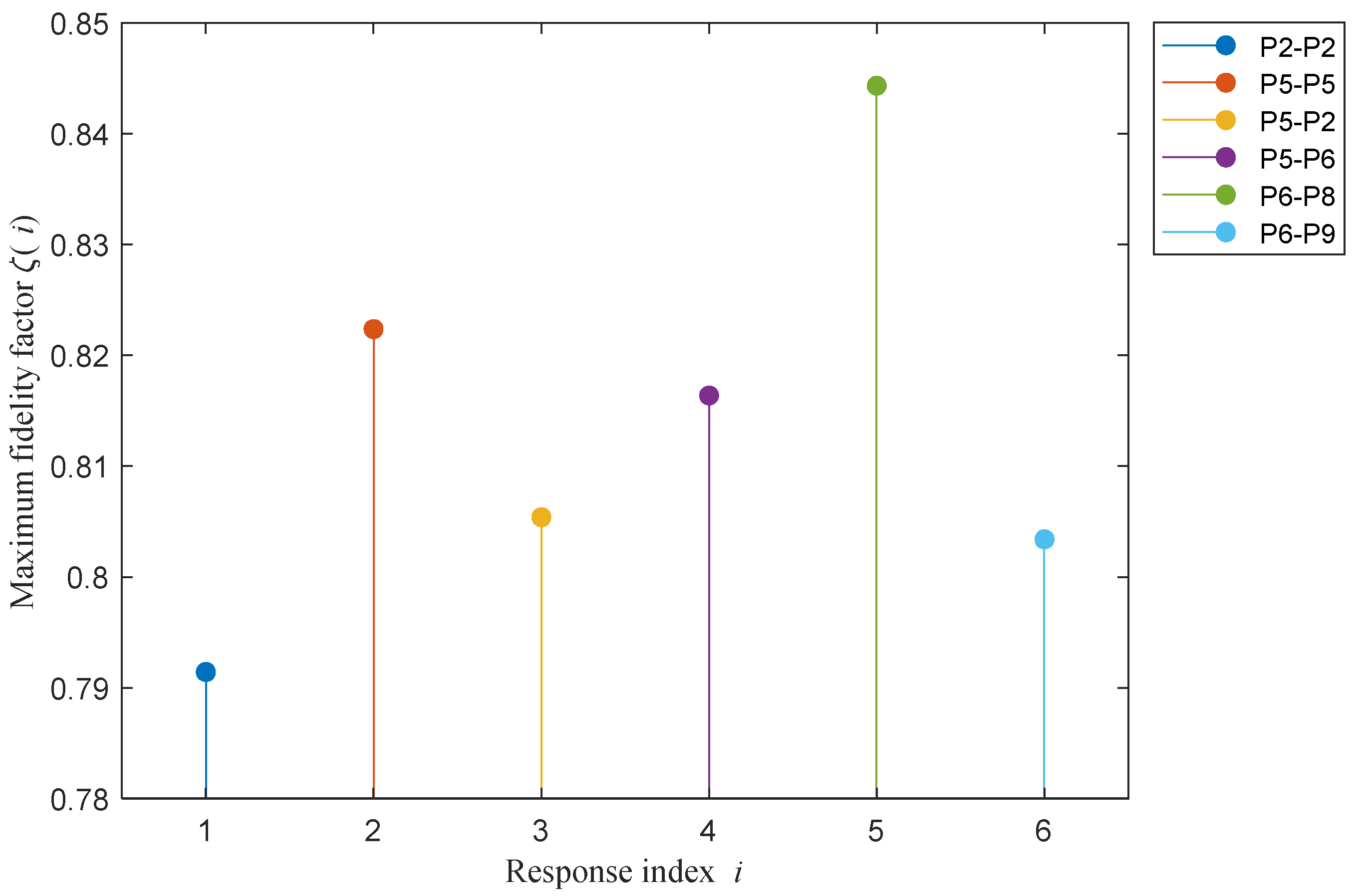
4. Port Data Analysis
- ▪
- Pre-measured responses of N solutions with different concentration values were stored in a library. Note that each solution has six responses corresponding to i = 2, 5, 23, 25, 34, and 35.
- ▪
- The fidelity factor between the response of a solution of unknown concentration and the 6N responses of N pre-stored solutions were computed.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tiefenthaler. K.; Walter. L. Optical Sensor for Selective Detection of Substances and/or for the Detection of Refractive Index Changes in Gaseous, Liquid, Solid and Porous Samples. U.S. Patent 4,815,843, 28 March 1989.
- Rodriguez, A.G.; Arias, D.N.P.; Gonzalez, S.B.E.; Sandoval, G.O.O.; Giraldo, O.O.H.; Trujillo, R.C.J.; Miriam Andrea Wilches Torres, M.A.W.; Cuautle, J.D.J.A.F. Sugar Concentration Measurement System Using Radiofrequency Sensor. Sensors 2019, 19, 2354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shah, S.A.; Fioranelli, F. RF Sensing Technologies for Assisted Daily Living in Healthcare: A Comprehensive Review. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 26–44. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, J.S.; Gymama, S. Towards a dual in-line electrochemical biosensor for the determination of glucose and hydrogen peroxide. Bioelectrochemistry 2019, 128, 56–65. [Google Scholar] [CrossRef] [PubMed]
- Yuen, J.D.; Baingane, A.; Hasan, Q.; Shriver-Lake, L.C.; Walper, S.A.; Zabetakis, D.; Breger, J.C.; Stenger, D.A.; Slaughter, G. A Fully-Flexible Solution-Processed Autonomous Glucose Indicator. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hasan, M.D.; Gymama, S. Hybrid Glucose/O2Biofuel Cell Based on as Pyroquinoline Quinone Glucose Dehydrogenase at the Bioanode. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018. [Google Scholar]
- Singh, R.; Gehlot, A.; Gupta, L.R.; Singh, B.; Tyagi, P. 7 Play with Digital Sensors. In Getting Started for Internet of Things with Launch Pad and ESP8266; River Publishers: Gistrup, Denmark, 2020; pp. 45–64. [Google Scholar]
- Rotman, W.; Turner, R. Wide-angle microwave lens for line source applications. IEEE Trans. Antennas Propag. 1963, 11, 623–632. [Google Scholar] [CrossRef]
- Iannacci, J.; Resta, G.; Bagolini, A.; Giacomozzi, F.; Bochkova, E.; Savin, E.A.; Kirtaev, R.; Tsarkov, A.; Donelli, M. RF-MEMS Monolithic K and Ka Band Multi-State Phase Shifters as Building Blocks for 5G and Internet of Things (IoT) Applications. Sensors 2020, 20, 2612. [Google Scholar] [CrossRef] [PubMed]
- Mujammami, E.H.; Islam, A.; Abdelrazik, B.S. Optimum wideband high gain analog beamforming network for 5G applications. IEEE Access 2019, 7, 52226–52237. [Google Scholar] [CrossRef]
- Heino, M.; Icheln, C.; Haarla, J.; Haneda, K. PCB-Based Design of a Beamsteerable Array with High-Gain Antennas and a Rotman Lens at 28 GHz. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1754–1758. [Google Scholar] [CrossRef]
- Sethi, W.T.; Ibrahim, A.; Khaled, I.; Albishi, A.M.; Alshebeili, S.A. A New Approach to Determining Liquid Concentration Using Multiband Annular Ring Microwave Sensor and Polarity Correlator. Electronics 2020, 9, 1616. [Google Scholar] [CrossRef]
- Vaziri, S.M.R.; Amir, R.A. An improved method of designing optimum microstrip Rotman lens based on 2D-FDTD. Int. J. RF Microw. Comput. Aided Eng. 2020, 30, e22030. [Google Scholar] [CrossRef]
- Lu, H.; Liu, Z.; Liu, J.; Wu, G.; Liu, Y.; Lv, X. Fully Metallic Anisotropic Lens Crossover-in-Antenna Based on Parallel Plate Waveguide Loaded with Uniform Posts. IEEE Trans. Antennas Propag. 2020, 68, 5061–5070. [Google Scholar] [CrossRef]
- Xie, Z.; Fan, C.; Zhu, J.; Huang, X. Robust beamforming for wideband array based on spectrum subspaces. IET Radar Sonar Navig. 2020, 14, 1319–1327. [Google Scholar] [CrossRef]
- Donelli, M.; Mohammedhusen, H.M. Design and Analysis of Antenna Feeding Networks Based on the Rotman Lens Using Interval Analysis (IA). Int. J. Antennas Propag. 2020. [Google Scholar] [CrossRef]
- Rotman Lens Designer Tool, Remcom. Available online: https://www.remcom.com/xf-rotman-lens-designer/ (accessed on 2 March 2020).
- LPKF E33 Prototyping and Etching Machine. Available online: https://www.lpkfusa.com/products/pcb_prototyp-ing/machines/protomat_e33/ (accessed on 25 July 2020).
- Computer Simulation Technology Version 2019. Available online: https://www.3ds.com/products-services/sim-ulia/products/cst-studio-suite/ (accessed on 10 June 2020).
- Vashist, S.; Luong, J.H. Non-invasive analytics for point-of-care testing of glucose. In Point-of-Care Glucose Detection for Diabetic Monitoring and Management; CRC Press: Boca Raton, FL, USA, 2017; pp. 59–84. [Google Scholar]
- Loba Chemie: Laboratory Chemicals, Laboratory Reagents, Dextrose Organic Reagents. 2018. Available online: https://www.lobachemie.com/Carbohydrates-03169/DEXTROSE-ANHYDROUS-CASNO-50-99-7.aspx?search=dextrose (accessed on 11 August 2020).
- RCT Basic. IKA. 2018. Available online: https://www.ika.com (accessed on 11 August 2020).
- Dielectric Assessment Kit from Speag. Available online: https://www.speag.com/products/dak/dielectricmeasurements/ (accessed on 15 August 2020).
- Microwave Network Analyzer N5227A. Available online: https://www.keysight.com/en/pdx-x201878-pn-N5227A/pna-microwave-network-analyzer-67-ghz?cc=PK&lc=eng (accessed on 25 May 2020).
- Ren, A.; Zahid, A.; Fan, D.; Yang, X.; Imran, M.A.; Alomainy, A.; Abbasi, Q.H. State-of-the-art in terahertz sensing for food and water security—A comprehensive review. Trends Food Sci. Technol. 2019, 85, 241–251. [Google Scholar] [CrossRef] [Green Version]

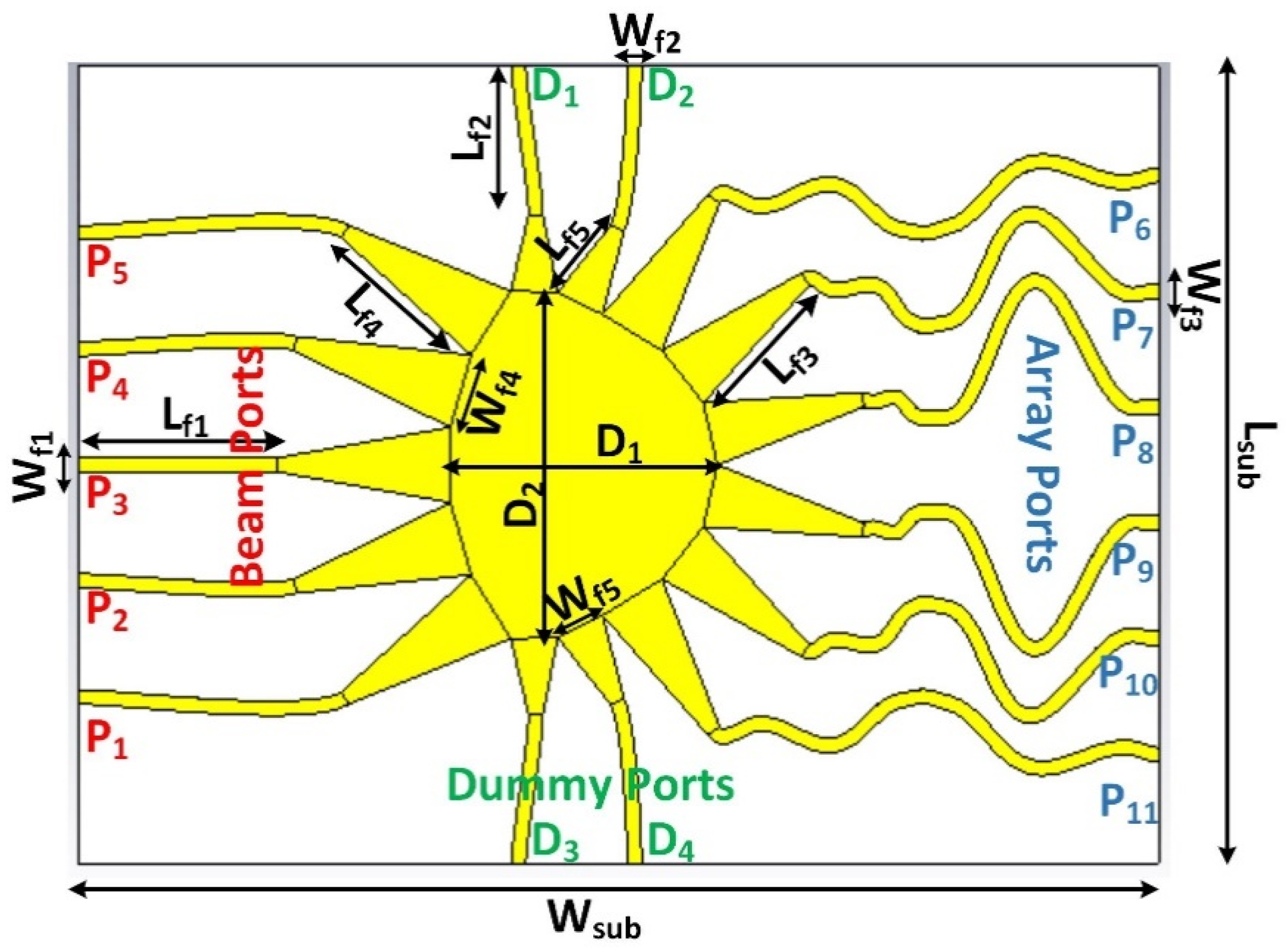






| Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|
| Lsub | 140 | Wsub | 103 |
| Lf1 | 35 | Wf1 | 1.85 |
| Lf2 | 20.54 | Wf2 | 1.85 |
| Lf3 | 20.66 | Wf3 | 1.85 |
| Lf4 | 22.67 | Wf4 | 9.73 |
| Lf5 | 10.16 | Wf5 | 6.48 |
| D1 | 34.9 | D2 | 45.22 |
| Aqueous Solutions | Nulls @ Port 3 | Aqueous Solutions | Nulls @ Port 9 |
|---|---|---|---|
| Air | 28.01 GHz | Air | 27.7 GHz |
| 60 mg/dL | 27.96 GHz | 60 mg/dL | 27.67 GHz |
| 100 mg/dL | 27.91 GHz | 100 mg/dL | 27.63 GHz |
| 200 mg/dL | 27.77 GHz | 200 mg/dL | 27.47 GHz |
| P1-P1 (1), P2-P2 (2), P3-P3 (3), P4-P4 (4), P5-P5 (5), P6-P6 (6), P7-P7 (7), P8-P8 (8), P9-P9 (9), P10-P10 (10), P11-P11 (11), P2-P1 (12), P3-P1 (13), P3-P2 (14), P4-P1 (15), P4-P2 (16), P4-P3 (17), P4-P5 (18), P4-P6 (19), P4-P7 (20), P4-P10 (21), P5-P1 (22), P5-P2 (23), P5-P3 (24), P5-P6 (25), P5-P7 (26), P5-P8 (27), P5-P9 (28), P5-P10 (29), P5-P11 (30), P6-P1 (31), P6-P2 (32), P6-P3 (33), P6-P8 (34), P6-P9 (35), P6-P10 (36), P6-P11 (37), P7-P1 (38), P7-P2 (39), P7-P3 (40), P7-P6 (41), P7-P8 (42), P8-P1 (43), P8-P2 (44), P8-P3 (45), P8-P4 (46), P8-P10 (47), P8-P11 (48), P9-P1 (49), P9-P2 (50), P9-P3 (51), P9-P4 (52), P9-P7 (53), P9-P8 (54), P9-P10 (55), P9-P11 (56), P10-P1 (57), P10-P2 (58), P10-P3 (59), P10-P7 (60), P10-P11 (61), P11-P1 (62), P11-P2 (63), P11-P3 (64), P11-P4 (65), P11-P7 (66) |
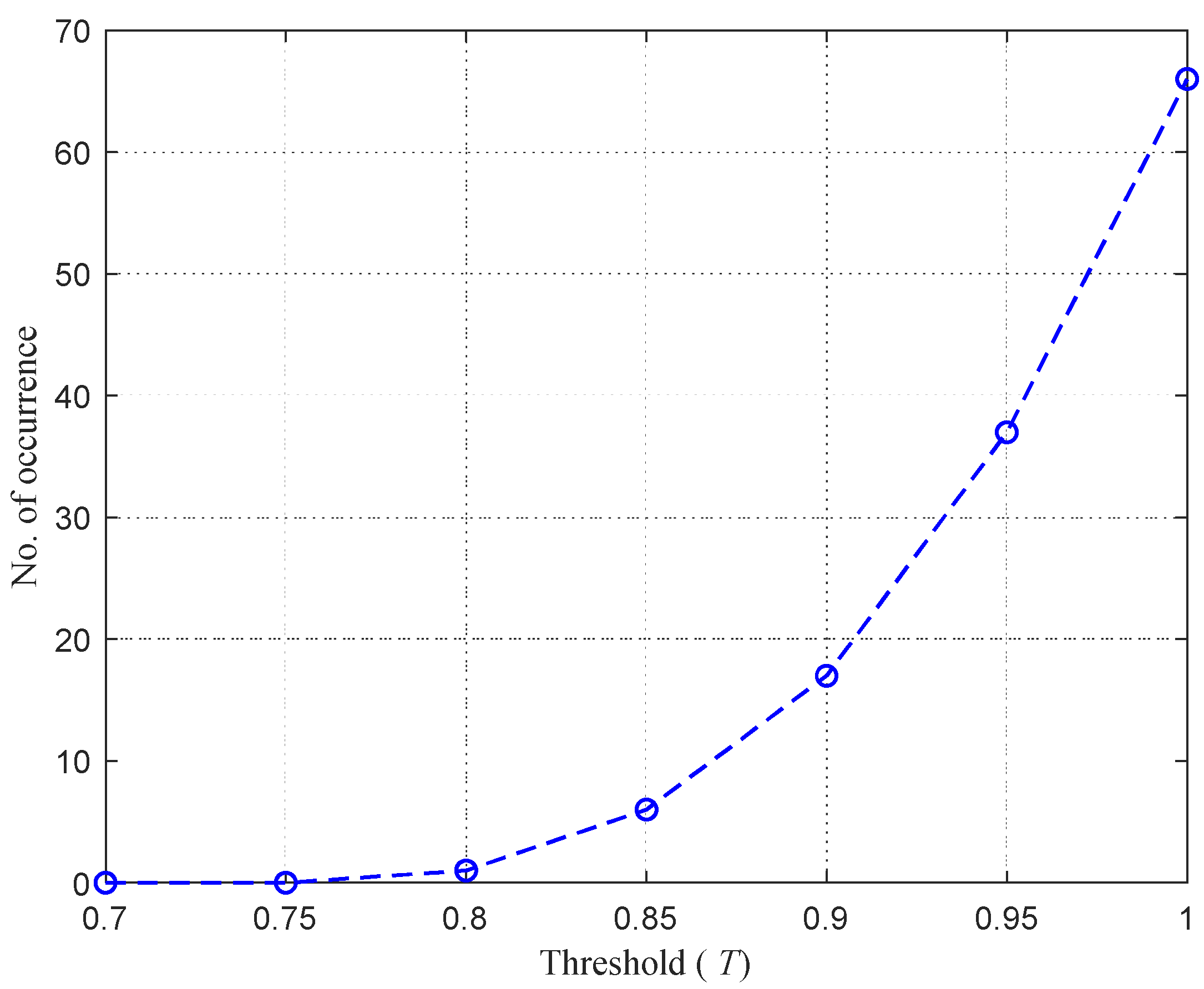
| Threshold (T) | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | 1 | ||||
| Number of responses | 0 | 1 | 6 | 17 | 37 | 66 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sethi, W.T.; Ibrahim, A.B.; Issa, K.; Alshebeili, S.A. mmW Rotman Lens-Based Sensing: An Investigation Study. Sensors 2021, 21, 1163. https://doi.org/10.3390/s21041163
Sethi WT, Ibrahim AB, Issa K, Alshebeili SA. mmW Rotman Lens-Based Sensing: An Investigation Study. Sensors. 2021; 21(4):1163. https://doi.org/10.3390/s21041163
Chicago/Turabian StyleSethi, Waleed T., Ahmed B. Ibrahim, Khaled Issa, and Saleh A. Alshebeili. 2021. "mmW Rotman Lens-Based Sensing: An Investigation Study" Sensors 21, no. 4: 1163. https://doi.org/10.3390/s21041163
APA StyleSethi, W. T., Ibrahim, A. B., Issa, K., & Alshebeili, S. A. (2021). mmW Rotman Lens-Based Sensing: An Investigation Study. Sensors, 21(4), 1163. https://doi.org/10.3390/s21041163






