Depolarization Characteristics of Different Reflective Interfaces Indicated by Indices of Polarimetric Purity (IPPs)
Abstract
1. Introduction
2. Methods
2.1. The IPPs of Material Media
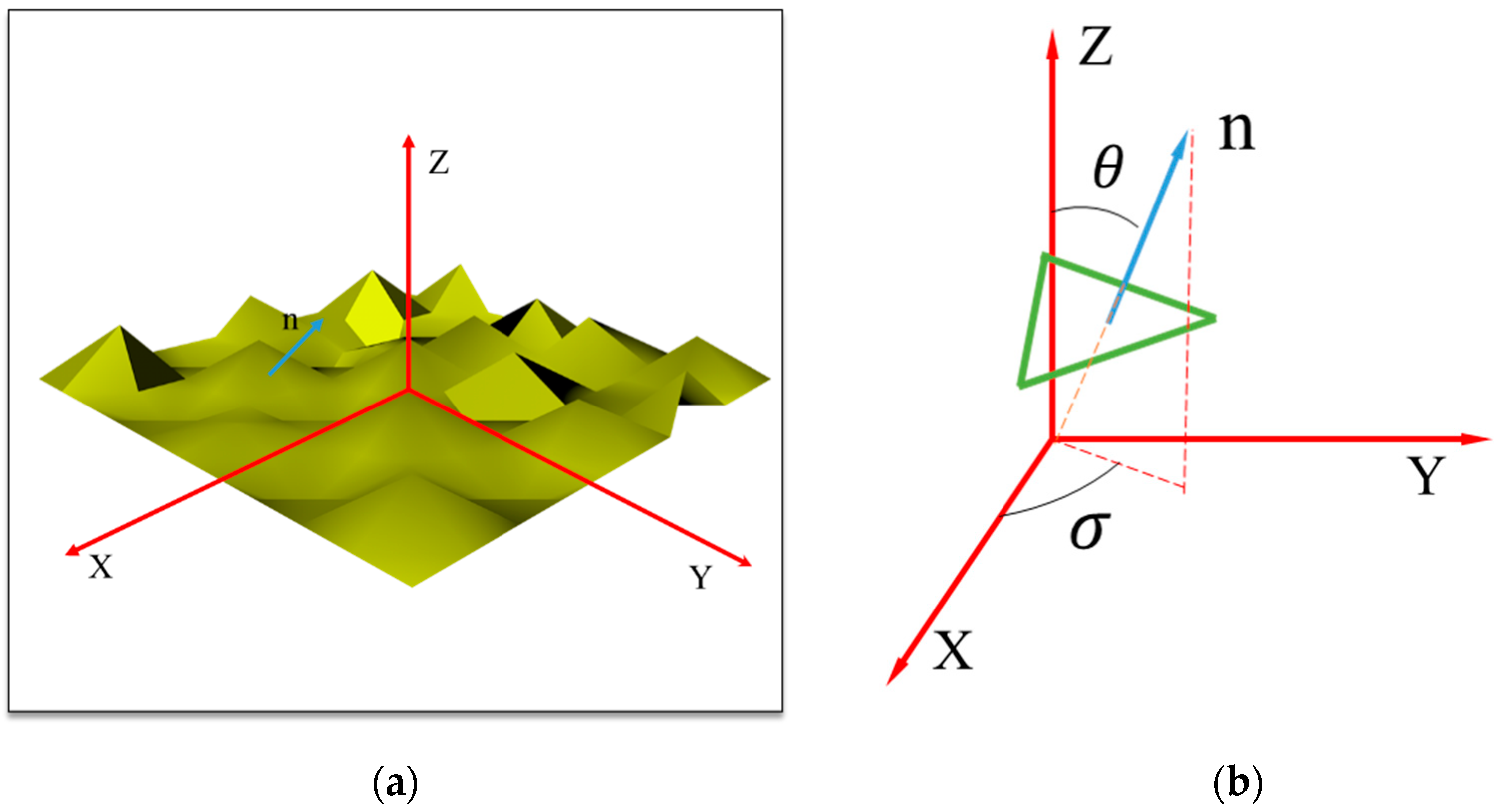
2.2. Microfacet Theory
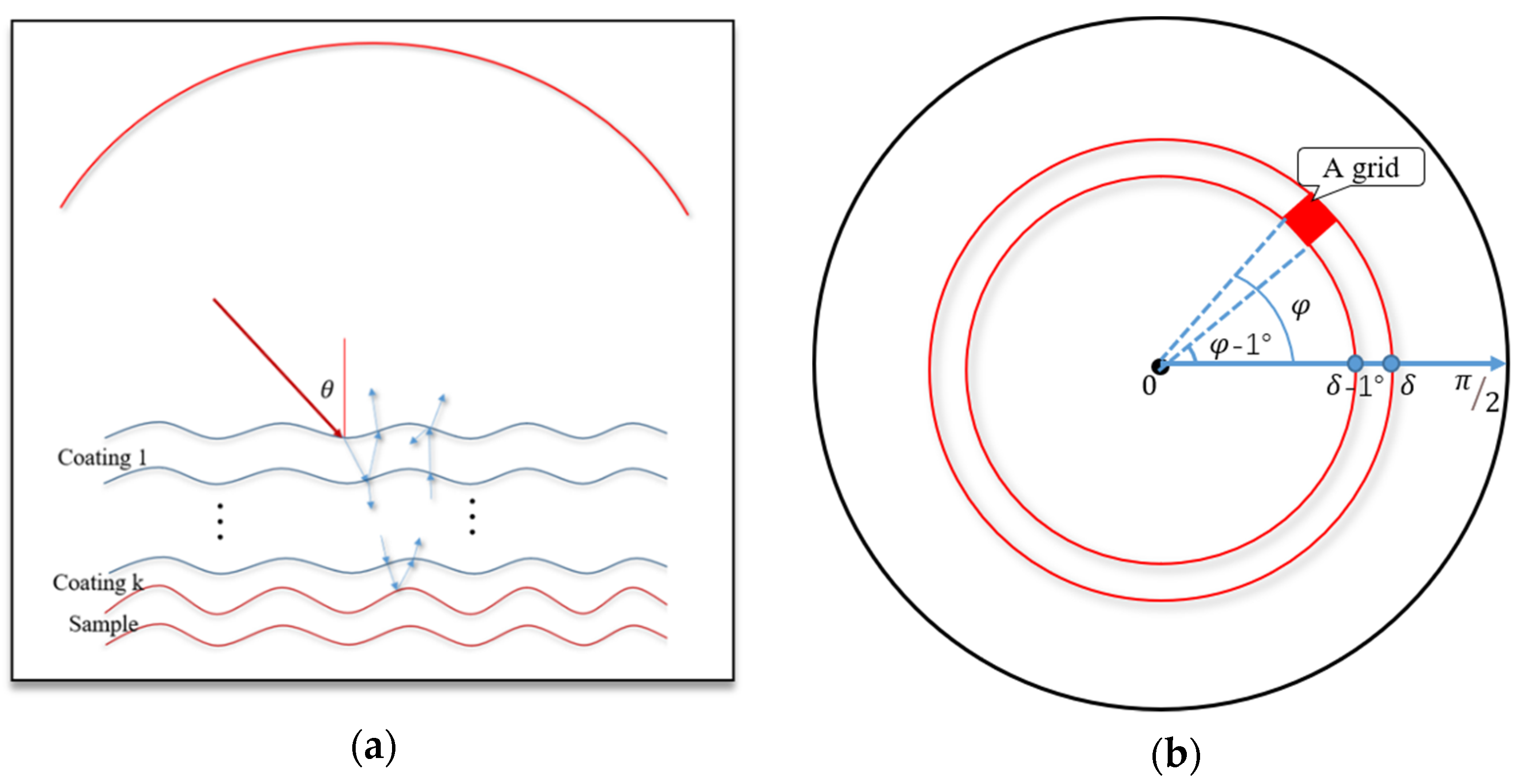
2.3. Monte Carlo Simulation
- Calculating the next layer (usually +1 or −1) to be scattered based on the number of current layer and the direction of propagation.
- Sampling the normal vector of the layer according and [34].
- Transforming polarized light from the global coordinate to the local coordinate by .
- Calculating the direction of reflected and refracted light according to the Fresnel formula and normal vector on the selected microfacet.
- Obtaining reflected and refracted light from Fresnel’s formula and MM, respectively, by , , where and are the reflective Muller matrix and the transmitting Muller matrix, respectively [34].
- Translating them from the local coordinate to the global coordinate, respectively, by ,.
- Checking whether the light has left the coating. If yes, collecting the light in the upper hemisphere. If no, back to step 1.
- Calculating MM and covariance matrix of each grid in the upper hemisphere.
- Getting the eigenvalue from the covariance matrix.
- Calculating P1, P2, P3 from .
3. Results and Discussion
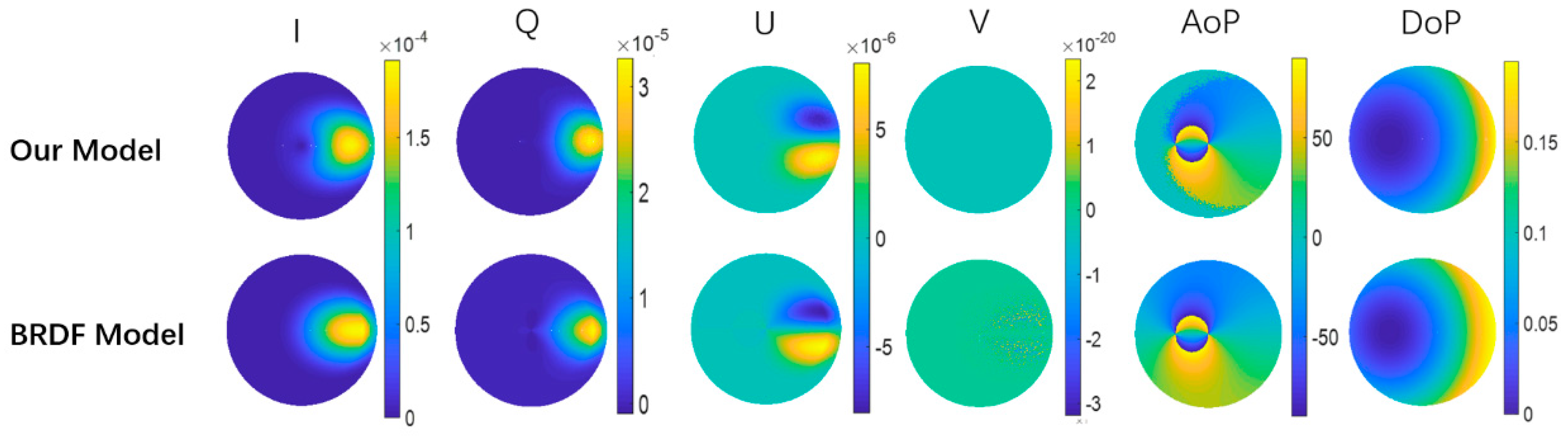
3.1. Comparing with BRDF Model
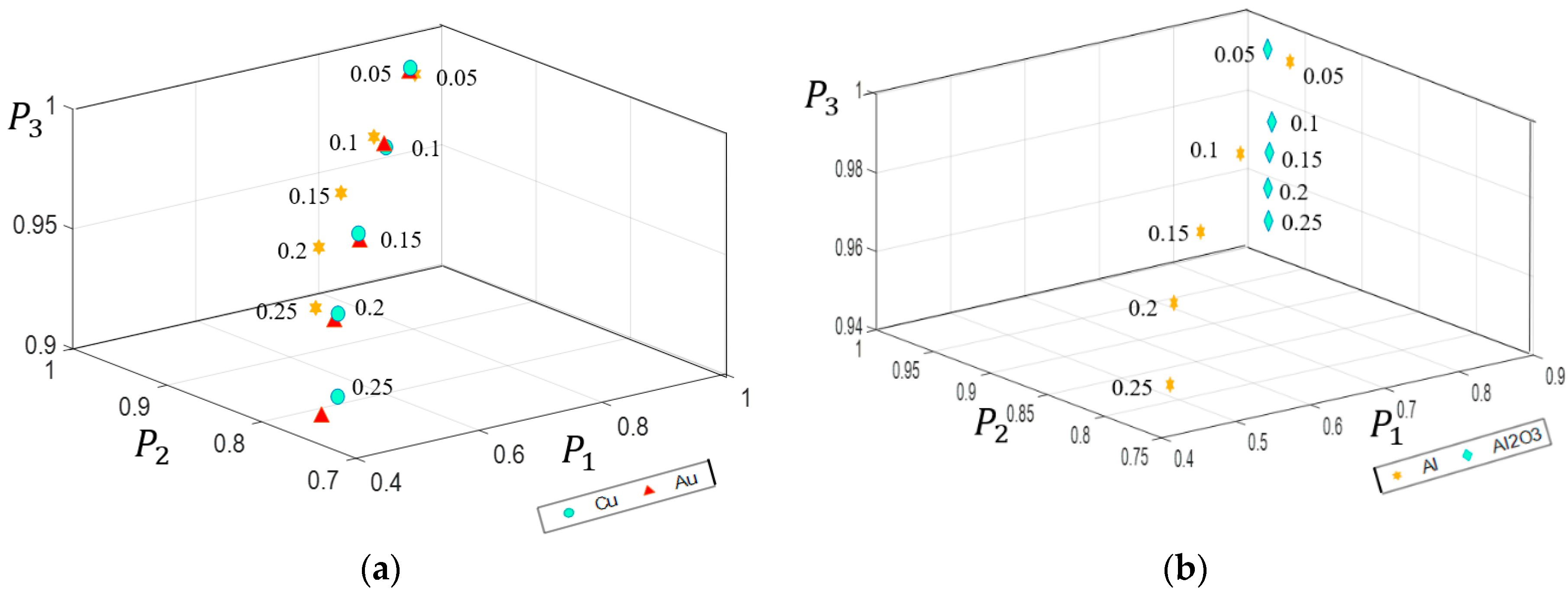
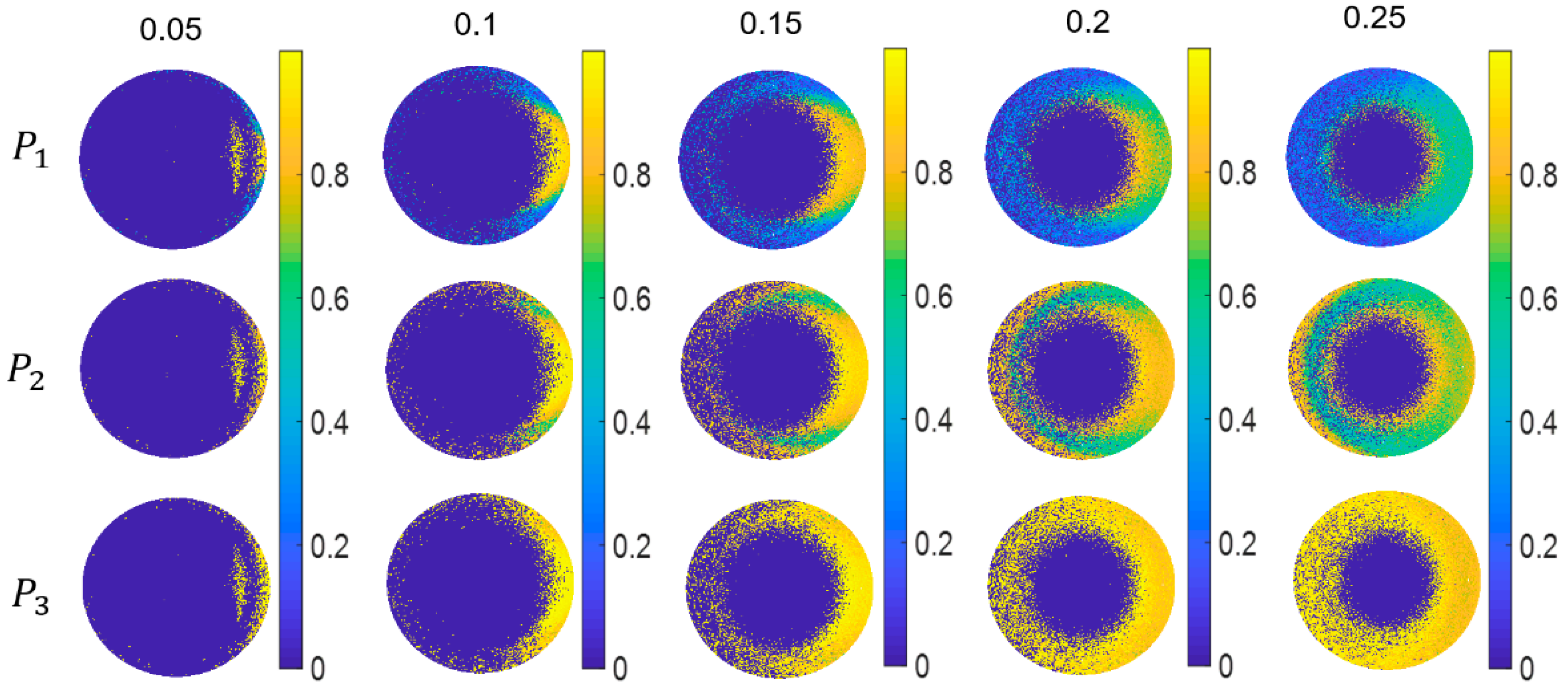
3.2. Influence of Roughness
3.3. Influence of Incident Angle
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cula, O.G.; Dana, K.J. 3D texture recognition using bidirectional feature histograms. Int. J. Comput. Vis. 2004, 59, 33–60. [Google Scholar] [CrossRef]
- Hu, J.C.; Zhang, C.C.; Li, X.; Du, X. An Electrochemical Sensor Based on Chalcogenide Molybdenum Disulfide-Gold-Silver Nanocomposite for Detection of Hydrogen Peroxide Released by Cancer Cells. Sensors 2020, 20, 6817. [Google Scholar] [CrossRef]
- Xia, J.J.; Yao, G. Angular distribution of diffuse reflectance in biological tissue. Appl. Opt. 2007, 46, 6552–6560. [Google Scholar] [CrossRef]
- Qi, H.; Zhu, B.; Wu, Z.; Liang, Y.; Li, J.; Wang, L.; Chen, T.; Lan, Y.; Zhang, L. Estimation of Peanut Leaf Area Index from Unmanned Aerial Vehicle Multispectral Images. Sensors 2020, 20, 6732. [Google Scholar] [CrossRef] [PubMed]
- Hegedus, R.; Barta, A.; Bernath, B.; Meyer-Rochow, V.B.; Horvath, G. Imaging polarimetry of forest canopies: How the azimuth direction of the sun, occluded by vegetation, can be assessed from the polarization pattern of the sunlit foliage. Appl. Opt. 2007, 46, 6019–6032. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, Y.; Tachibana, K. Mie-Scattering Ellipsometry for Analysis of Particle Behaviors in Processing Plasmas. Jpn. J. Appl. Phys. 1994, 33, L476. [Google Scholar] [CrossRef]
- Groth, S.; Greiner, F.; Tadsen, B.; Piel, A. Kinetic Mie ellipsometry to determine the time-resolved particle growth in nanodusty plasmas. J. Phys. D Appl. Phys. 2015, 46, 465203. [Google Scholar] [CrossRef]
- Kirchschlager, F.; Wolf, S.; Greiner, F.; Groth, S.; Labdon, A. In-situ analysis of optically thick nanoparticle clouds. Appl. Phys. Lett. 2017, 110, 173106. [Google Scholar] [CrossRef]
- Agnoil, G.C.; Cacciari, M.; Garutti, C.; Lenzi, P. Ship detection performance using simulated dual-polarization radarsat constellation mission data. Int. J. Remote Sens. 2015, 36, 1705–1727. [Google Scholar]
- Wang, X.Y.; Hu, T.W.; Li, D.K.; Guo, K.; Gao, J.; Guo, Z.Y. Performances of polarization-retrieve imaging in stratified dispersion media. Remote Sens. 2020, 12, 2895. [Google Scholar] [CrossRef]
- Xu, F.; Wang, H.P.; Jin, Y.Q.; Liu, X.Q.; Wang, R.; Deng, Y. Impact of cross-polarization isolation on polarimetric target decomposition and target detection. Radio Sci. 2015, 50, 327–338. [Google Scholar] [CrossRef]
- Wang, Y.T.; Ainsworth, T. Assessment of System Polarization Quality for Polarimetric SAR Imagery and Target Decomposition. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1755–1771. [Google Scholar] [CrossRef]
- Wolff, L.B. Polarization-based material classification from specular reflection. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 1059–1071. [Google Scholar] [CrossRef]
- Wolff, L.B.; Boult, T.E. Constraining object features using a polarization reflectance model. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 635–657. [Google Scholar] [CrossRef]
- Torrance, K.E.; Sparrow, E.M. Theory for off-specular reflection from roughened surfaces. J. Opt. Soc. Am. 1967, 57, 1105–1114. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Zhao, H.J.; Wang, Z.Y. Improved atmospheric effects elimination method for pBRDF models of painted surfaces. Opt. Express 2017, 25, 16458–16475. [Google Scholar] [CrossRef] [PubMed]
- Priest, R.G.; Meier, S.R. Polarimetric microfacet scattering theory with applications to absorptive and reflective surfaces. Opt. Eng. 2002, 41, 988–993. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, J.P.; Liu, H.; Du, B.Z. Expression of the degree of polarization based on the geometrical optics pBRDF model. J. Opt. Soc. Am. A 2017, 32, 259–263. [Google Scholar] [CrossRef] [PubMed]
- Wellems, D.; Ortega, S.; Bowers, D.; Boger, J.; Fetrow, M. Long wave infrared polarimetric model: Theory, measurements and parameters. J. Opt. A Pure Appl. Opt. 2006, 8, 914–925. [Google Scholar] [CrossRef]
- Renhorn, I.G.E.; Hallberg, T.; Boreman, G.D. Efficient polarimetric BRDF model. Opt. Express 2015, 23, 31253–31273. [Google Scholar] [CrossRef]
- Hyde, M.W.; Schmidt, J.D.; Havrilla, M.J. A geometrical optics polarimetric bidirectional reflectance distribution function for dielectric and metallic surfaces. Opt. Express 2009, 17, 22138–22153. [Google Scholar] [CrossRef] [PubMed]
- Ashikhmin, M.; Shirley, P. An anisotropic phong brdf model. J. Graph. Tools 2000, 5, 25–32. [Google Scholar] [CrossRef]
- Lai, Q.Z.; Liu, B.; Zhao, J.M.; Zhao, Z.W.; Tan, J.Y. BRDF characteristics of different textured fabrics in visible and near-infrared band. Opt. Express 2020, 28, 3561–3575. [Google Scholar] [CrossRef] [PubMed]
- Fields, A.P.; Cohen, A.E. Optimal tracking of a Brownian particle. Opt. Express 2012, 20, 22585–22601. [Google Scholar] [CrossRef]
- Xu, Q.; Guo, Z.; Tao, Q.; Jiao, W.; Wang, X.; Qu, S.; Gao, J. Transmitting characteristics of the polarization information under seawater. Appl. Optics. 2015, 54, 6584–6588. [Google Scholar] [CrossRef]
- Li, M.; Lu, P.F.; Yu, Z.Y.; Yan, L.; Chen, Z.H.; Yang, C.H.; Luo, X. Vector Monte Carlo simulations on atmospheric scattering of polarization qubits. J. Opt. Soc. Am. A 2013, 30, 448–454. [Google Scholar] [CrossRef]
- Garcia, R.D.M. Fresnel boundary and interface conditions for polarized radiative transfer in a multilayer medium. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 306–317. [Google Scholar] [CrossRef]
- Xu, Q.; Guo, Z.; Tao, Q.; Jiao, W.; Qu, S.; Gao, J. Multi-spectral characteristics of polarization retrieve in various atmospheric conditions. Opt. Commun. 2015, 339, 167–170. [Google Scholar] [CrossRef]
- Tao, Q.; Sun, Y.; Shen, F.; Xu, Q.; Gao, J.; Guo, Z.Y. Active imaging with the aids of polarization retrieve in turbid media system. Opt. Commun. 2016, 359, 405–410. [Google Scholar] [CrossRef]
- Kattawar, G.W.; Plass, G.N.; Guinn, J.A., Jr. Monte Carlo calculations of the polarization of radiation in the earth’s atmosphere-ocean system. J. Phys. Oceanogr. 1973, 3, 353–372. [Google Scholar] [CrossRef]
- Hu, T.; Shen, F.; Wang, K.; Guo, K.; Liu, X.; Wang, F.; Peng, Z.; Cui, Y.; Sun, R.; Ding, Z.; et al. Broad-Band Transmission Characteristics of Polarizations in Foggy Environments. Atmosphere 2019, 10, 342. [Google Scholar] [CrossRef]
- Xu, M. Electric field Monte Carlo simulation of polarized light propagation in turbid media. Opt. Express 2004, 12, 6530–6539. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.M.; Tan, J.Y.; Liu, L.H. Monte Carlo method for polarized radiative transfer in gradient-index media. J. Quant. Spectrosc. Radiat. Transf. 2014, 152, 114–126. [Google Scholar] [CrossRef]
- Wang, C.; Gao, J.; Yao, T.T.; Wang, L.M.; Sun, Y.X.; Xie, Z.; Guo, Z.Y. Acquiring reflective polarization from arbitrary multi-layer surface based on Monte Carlo simulation. Opt. Express 2016, 9, 9397–9411. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.D.; Stramski, D.; Reynolds, R.A.; Blocker, E.R. Light scattering by pure water and seawater: The depolarization ratio and its variation with salinity. Appl Opt. 2019, 58, 991–1004. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Zhang, W.H. Depolarization effect in light scattering of single gold nanosphere. Opt. Express 2020, 28, 24275–24284. [Google Scholar] [CrossRef]
- Tudor, T. On the enpolarization/depolarization effects of deterministic devices. Opt. Lett. 2018, 43, 5234–5237. [Google Scholar] [CrossRef]
- Sato, K.; Okamoto, H.; Ishimoto, H. Modeling the depolarization of space-borne lidar signals. Opt. Express 2019, 27, A117–A132. [Google Scholar] [CrossRef]
- Bi, L.; Lin, W.H.; Liu, D.; Zhang, K.J. Assessing the depolarization capabilities of nonspherical particles in a super-ellipsoidal shape space. Opt. Express 2018, 26, 1726–1742. [Google Scholar] [CrossRef]
- Thomas, A. Evolution of transmitted depolarization in diffusely scattering media. J. Opt. Soc. Am. A 2020, 37, 980–987. [Google Scholar]
- Callum, M. Characterizing the depolarization of circularly polarized light in turbid scattering media. J. Opt. Soc. Am. A 2018, 35, 2104–2110. [Google Scholar]
- Pierangelo, A.; Nazac, A.; Benali, A.; Validire, P.; Cohen, H.; Novikova, T.; Ibrahim, B.H.; Manhas, S.; Fallet, C.; Antonelli, M.R.; et al. Polarimetric imaging of uterine cervix: A case study. Opt. Express 2013, 21, 14120–14130. [Google Scholar] [CrossRef]
- Shen, F.; Zhang, M.; Guo, K.; Zhou, H.P.; Peng, Z.Y.; Cui, Y.M.; Wang, F.; Guo, Z.Y. The depolarization performances of scattering systems based on the Indices of Polarimetric Purity. Opt. Express 2019, 27, 28337–28349. [Google Scholar] [CrossRef]
- José, I.S.; Gil, J.J. Invariant indices of polarimetric purity: Generalized indices of purity for n× n covariance matrices. Opt. Commun. 2011, 284, 38–47. [Google Scholar] [CrossRef]
- Gil, J.J. Components of purity of a three-dimensional polarization state. J. Opt. Soc. Am. A 2016, 33, 40–43. [Google Scholar] [CrossRef] [PubMed]
- Tariq, A.; He, H.H.; Li, P.C.; Ma, H. Purity-depolarization relations and the components of purity of a Mueller matrix. Opt. Express 2019, 27, 22645–22662. [Google Scholar] [CrossRef] [PubMed]
- Gil, J.J.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Goldstein, D. Polarized Light (Second Edition); Marcel Dekker Inc.: New York, NY, USA, 2003. [Google Scholar]
- Michael, B.; Decusatis, C.M.; Enoch, J.; MacDonald, C. Handbook of Optics; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Germer, T. SCATMECH v 7.0: Polarized Light Scattering C++ Class Library; NIST: Gaithersburg, MD, USA, 2017. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Guo, K.; Sun, Y.; Bi, X.; Gao, J.; Guo, Z. Depolarization Characteristics of Different Reflective Interfaces Indicated by Indices of Polarimetric Purity (IPPs). Sensors 2021, 21, 1221. https://doi.org/10.3390/s21041221
Li D, Guo K, Sun Y, Bi X, Gao J, Guo Z. Depolarization Characteristics of Different Reflective Interfaces Indicated by Indices of Polarimetric Purity (IPPs). Sensors. 2021; 21(4):1221. https://doi.org/10.3390/s21041221
Chicago/Turabian StyleLi, Dekui, Kai Guo, Yongxuan Sun, Xiang Bi, Jun Gao, and Zhongyi Guo. 2021. "Depolarization Characteristics of Different Reflective Interfaces Indicated by Indices of Polarimetric Purity (IPPs)" Sensors 21, no. 4: 1221. https://doi.org/10.3390/s21041221
APA StyleLi, D., Guo, K., Sun, Y., Bi, X., Gao, J., & Guo, Z. (2021). Depolarization Characteristics of Different Reflective Interfaces Indicated by Indices of Polarimetric Purity (IPPs). Sensors, 21(4), 1221. https://doi.org/10.3390/s21041221






