Design and Implementation of a Novel Interferometric Microwave Radiometer for Human Body Temperature Measurement
Abstract
:1. Introduction
2. Microwave Radiometer Temperature Measurement Scheme
3. Design of Novel Interferometric Microwave Radiometer for Human Body Temperature Measurement
3.1. Hardware Design of Interferometric Microwave Thermometer Radiometer
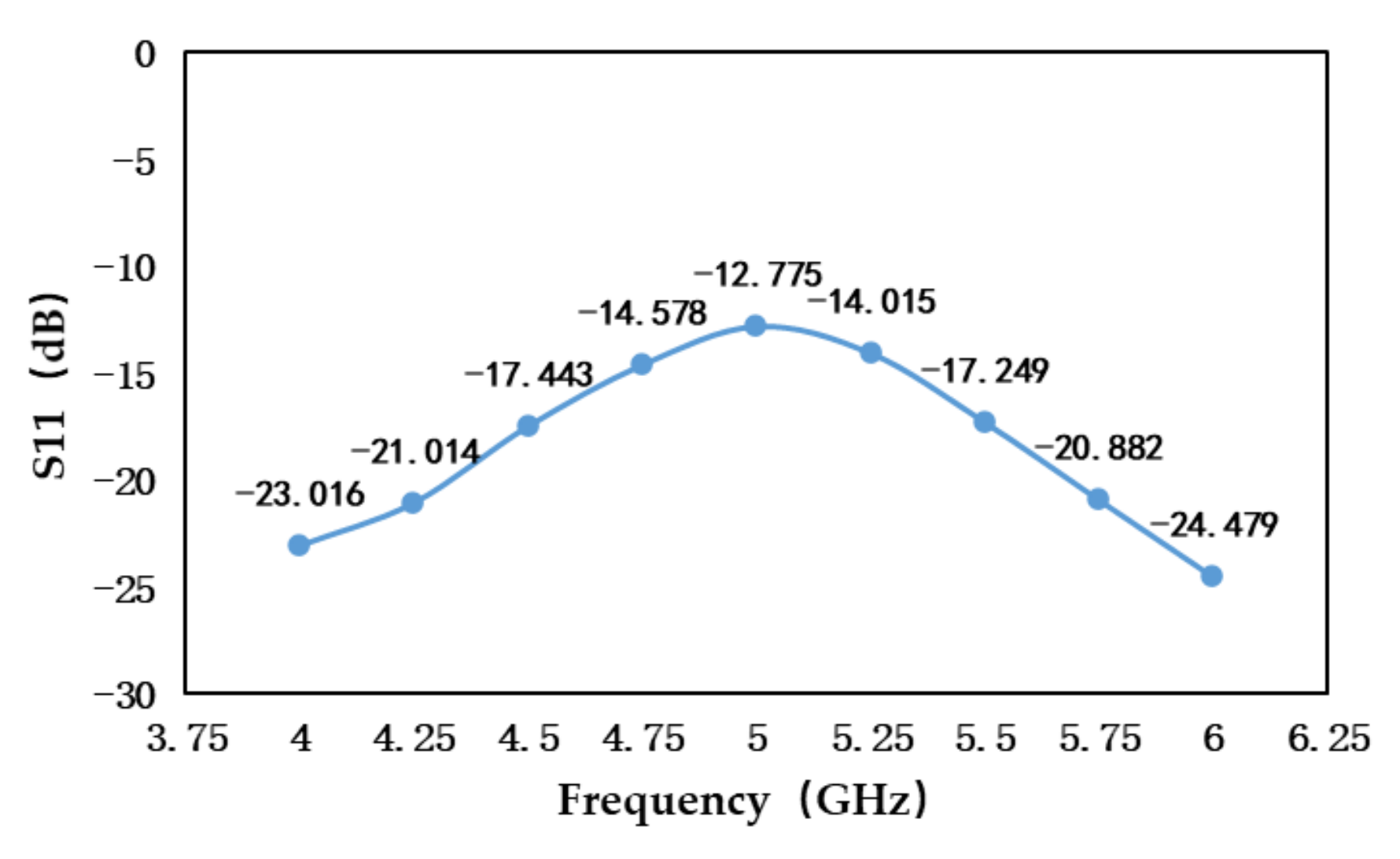
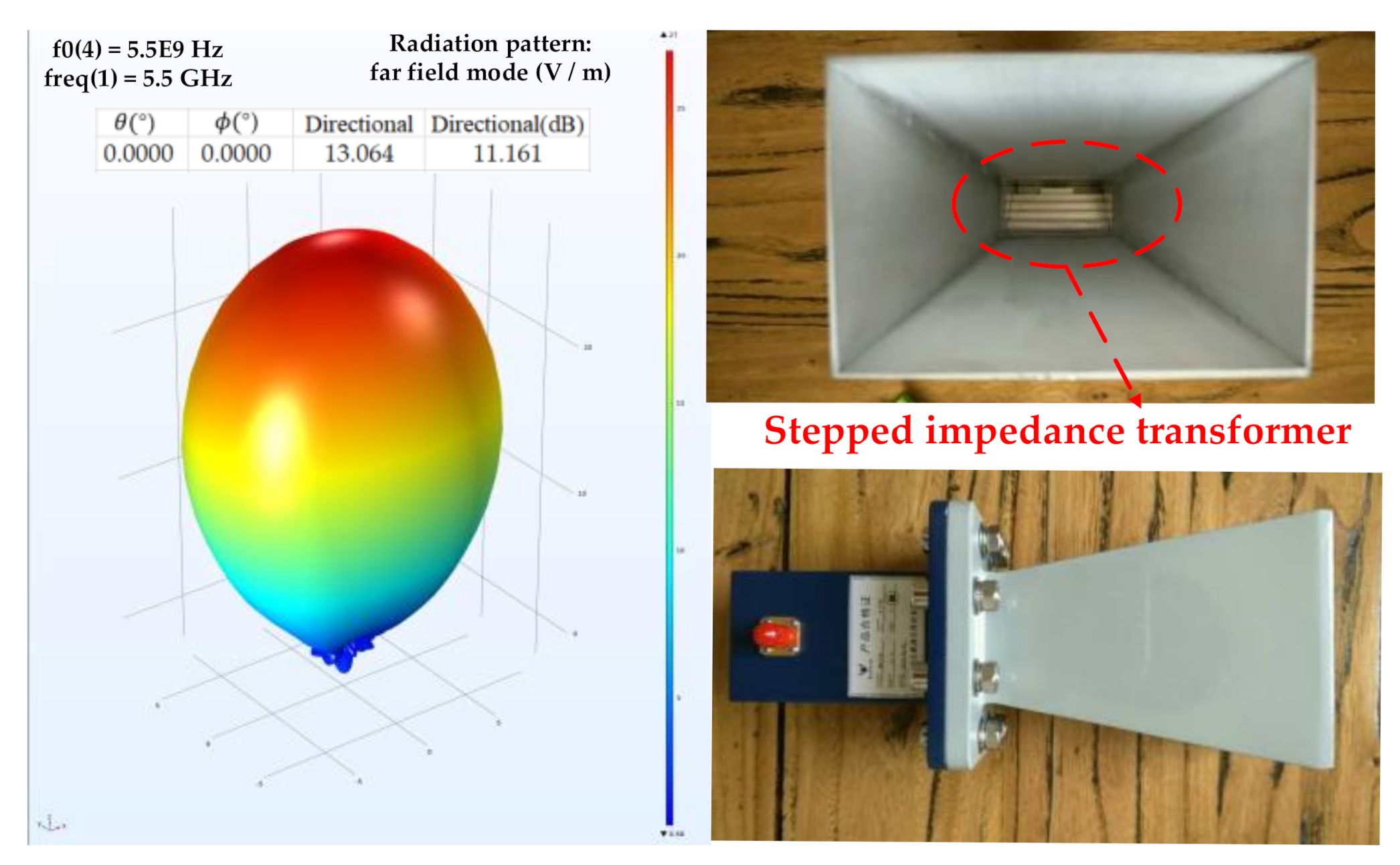
3.1.1. Design of High Directivity Temperature Measurement Antenna
3.1.2. Design of Interferometric Analog Complex Correlator
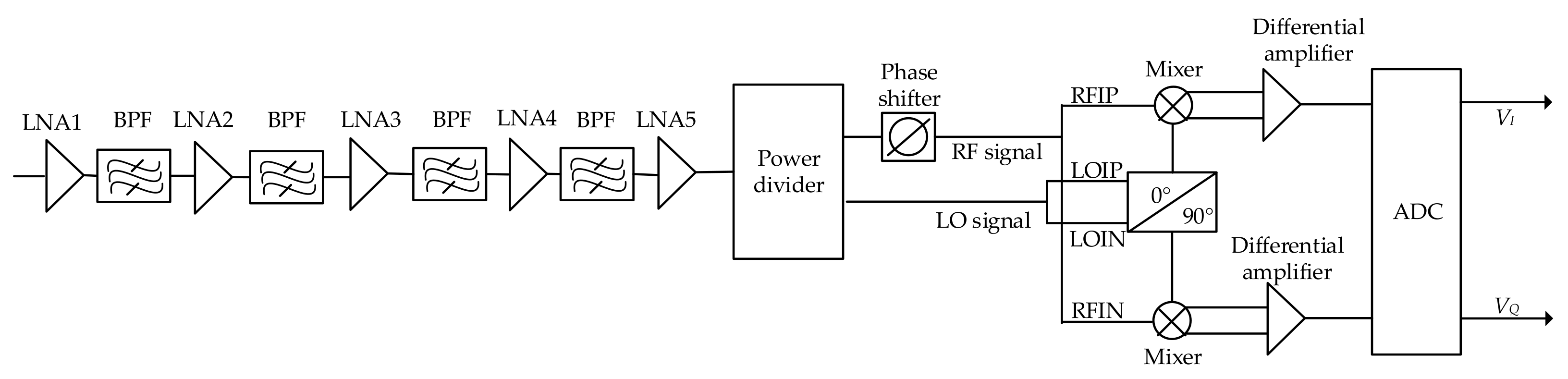
3.1.3. RF Front End Circuit Design of Microwave Radiometer
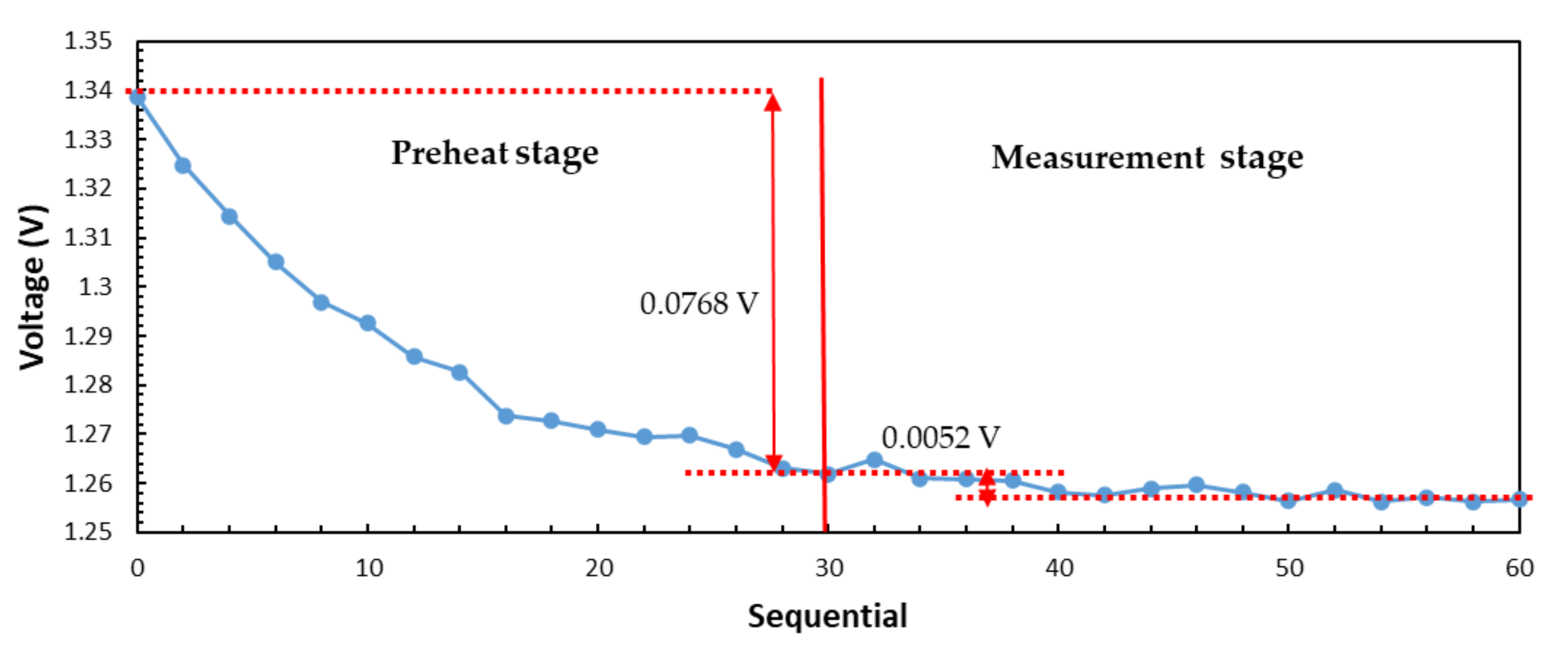
3.2. Collection and Processing of Water Temperature Data
3.3. Design of Temperature Measurement Software for Microwave Radiometer
3.3.1. Microwave Radiometer Offset Error Correction Algorithm
3.3.2. Design of Calibration Mechanism for Microwave Radiometer
3.3.3. Water Temperature Inversion Algorithm in Near Field
4. Discussion
5. Conclusions
- (1)
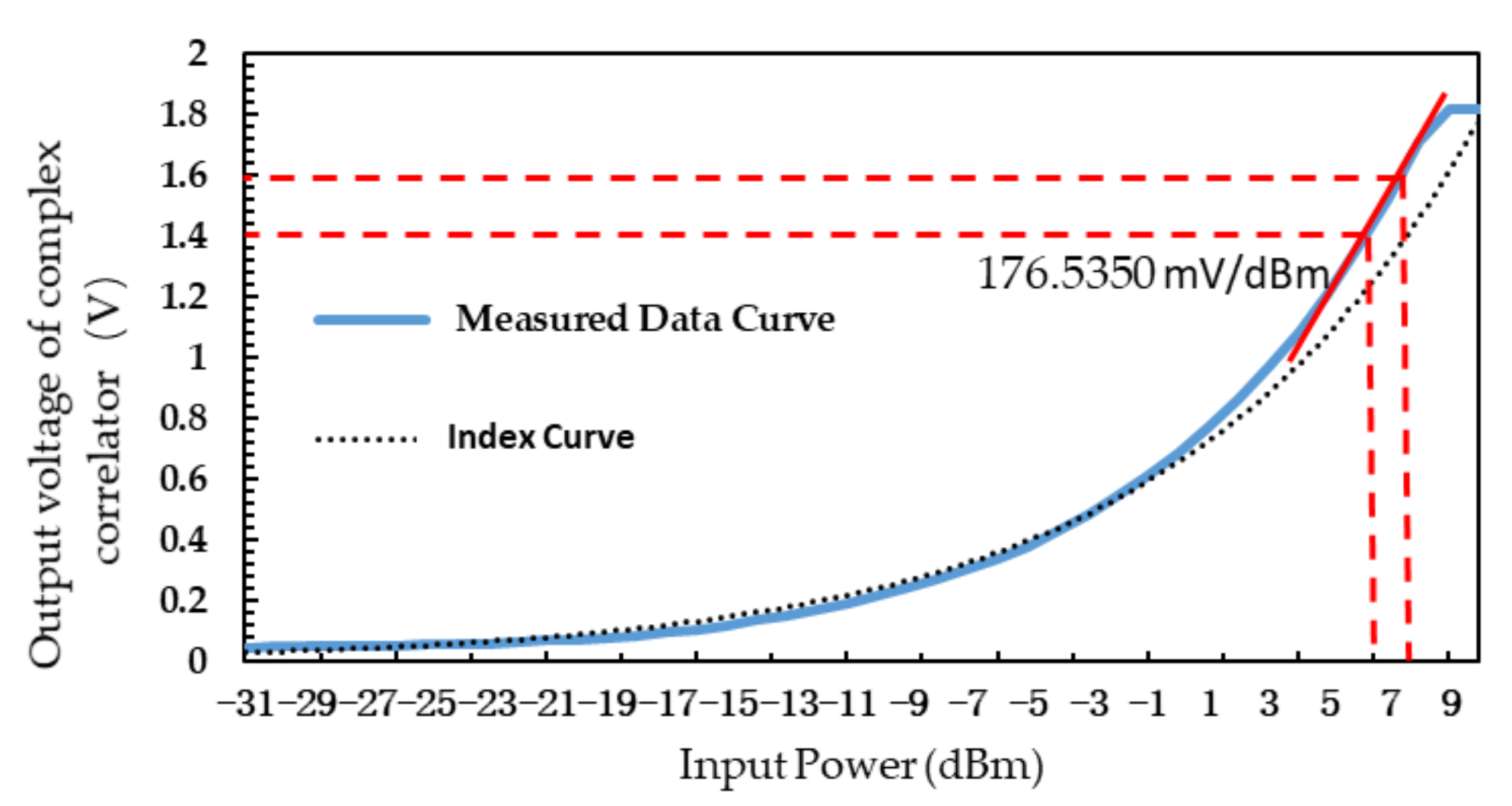
- This paper innovatively uses 500–6000 MHz broadband quadrature demodulator to design the interferometric microwave thermometer radiometer. Compared with the traditional total power microwave radiometer, the detection sensitivity increases by 3.48 times. In addition, the detection bandwidth is 2 GHz and the circuit structure is simple. The maximum sensitivity of the microwave radiometer can reach 176.54 mV/dBm when the input point frequency signal power is 7 dBm. It can be concluded that the sensitivity of temperature measurement can reach ± °C/mV when the body temperature is 35–45 °C.
- (2)
- The noise power is about −80.70 to −80.56 dBm when human body temperature ranges from 35 to 45 °C. In this paper, a multi-stage low noise amplifier is used in the RF front-end to make the total gain about 90 dBm, at this time, the microwave radiometer reaches the working point of the maximum sensitivity near 7 dBm, which ensures that the microwave radiometer has a higher detection sensitivity.
- (3)
- At this time, the multi-correlator reaches the maximum sensitivity operating point near 7 dBm to ensure that the radiometer has a higher detection sensitivity.
- (4)
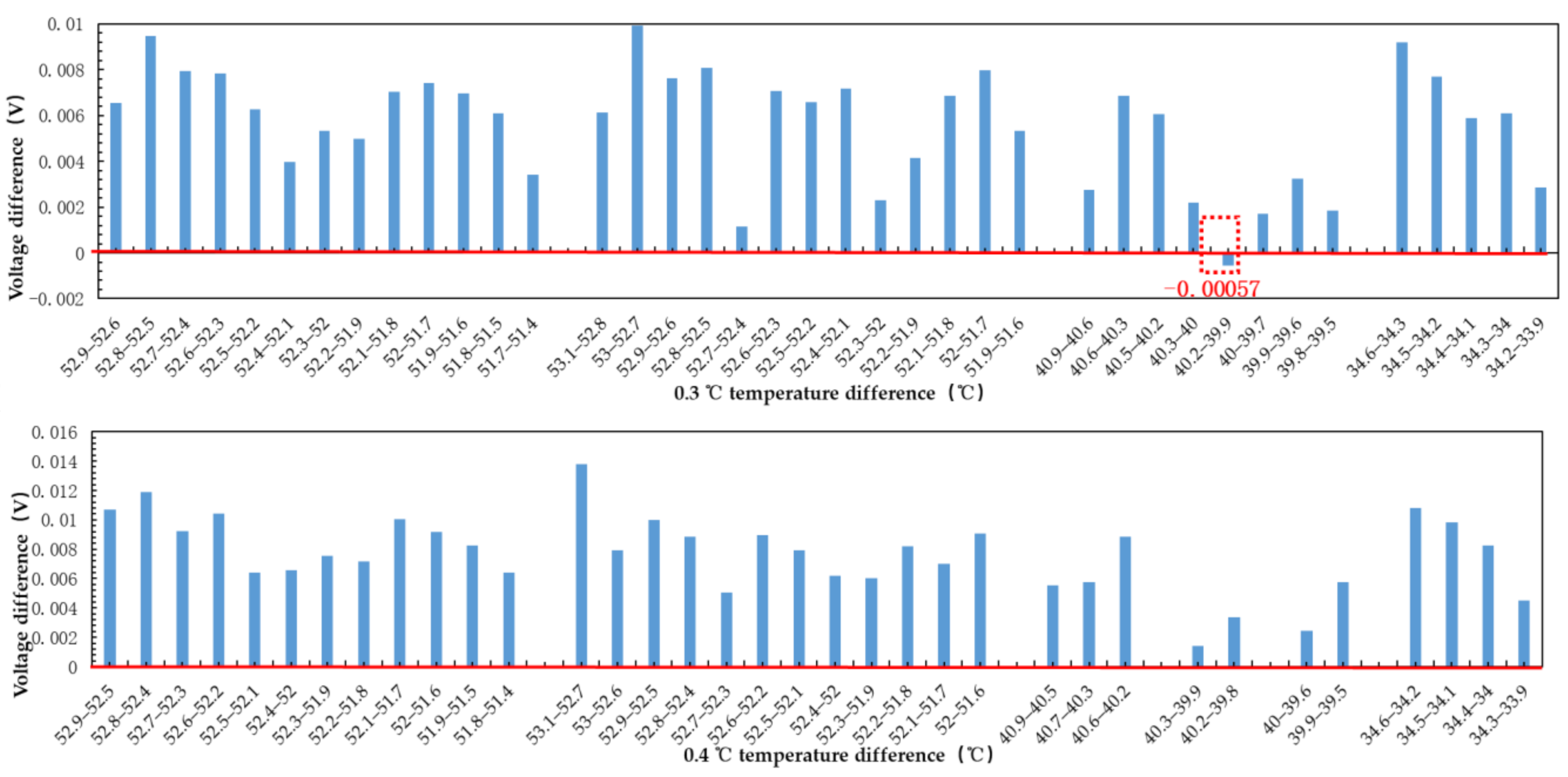
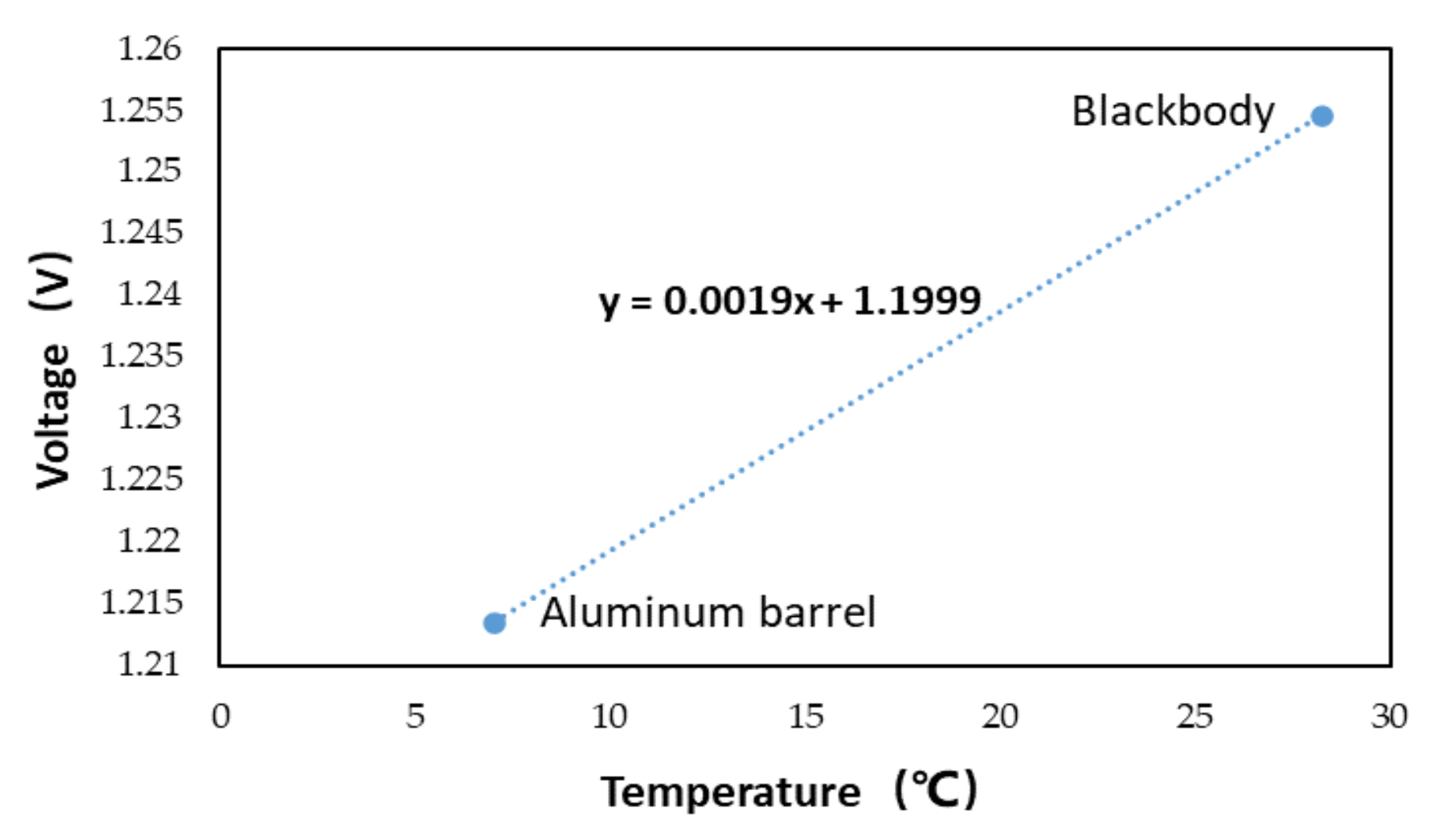
- To reduce the influence of phase error, gain error and offset error of microwave radiometer on temperature measurement accuracy and sensitivity, the phase shift value of phase shifter is controlled to correct the system phase error and the gain error and offset error are corrected by using linear fitting algorithm. After correction, the phase error reduces from 40° to 1.4° and the voltage amplitude changes obviously when the temperature changes 0.1 °C.
- (5)
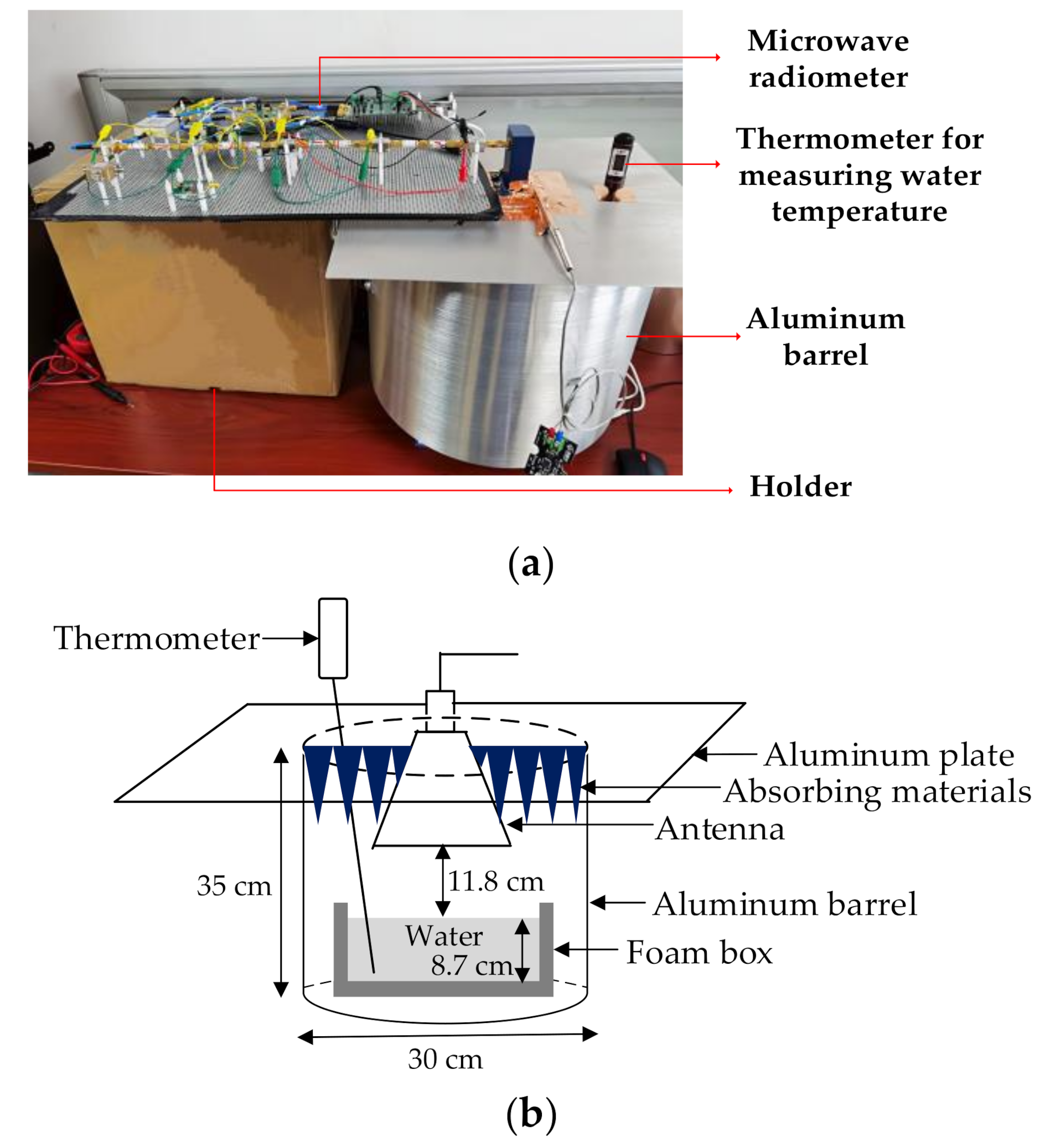
- The microwave radiometer is calibrated by step-by-step calibration scheme and overall calibration scheme respectively. In the step-by-step calibration, the microwave radiometer is calibrated by microwave load with different resistance, the antenna is calibrated according to the antenna efficiency and the antenna physical temperature. In the overall calibration, aluminum plates and absorbing materials with different emissivity are selected to calibrate the whole system. The results show that the overall calibration result is consistent with the emissivity relationship of the measured object, and the step-by-step calibration can evaluate the change of calibration curve caused by the temperature rise of the microwave radiometer at any time.
- (6)
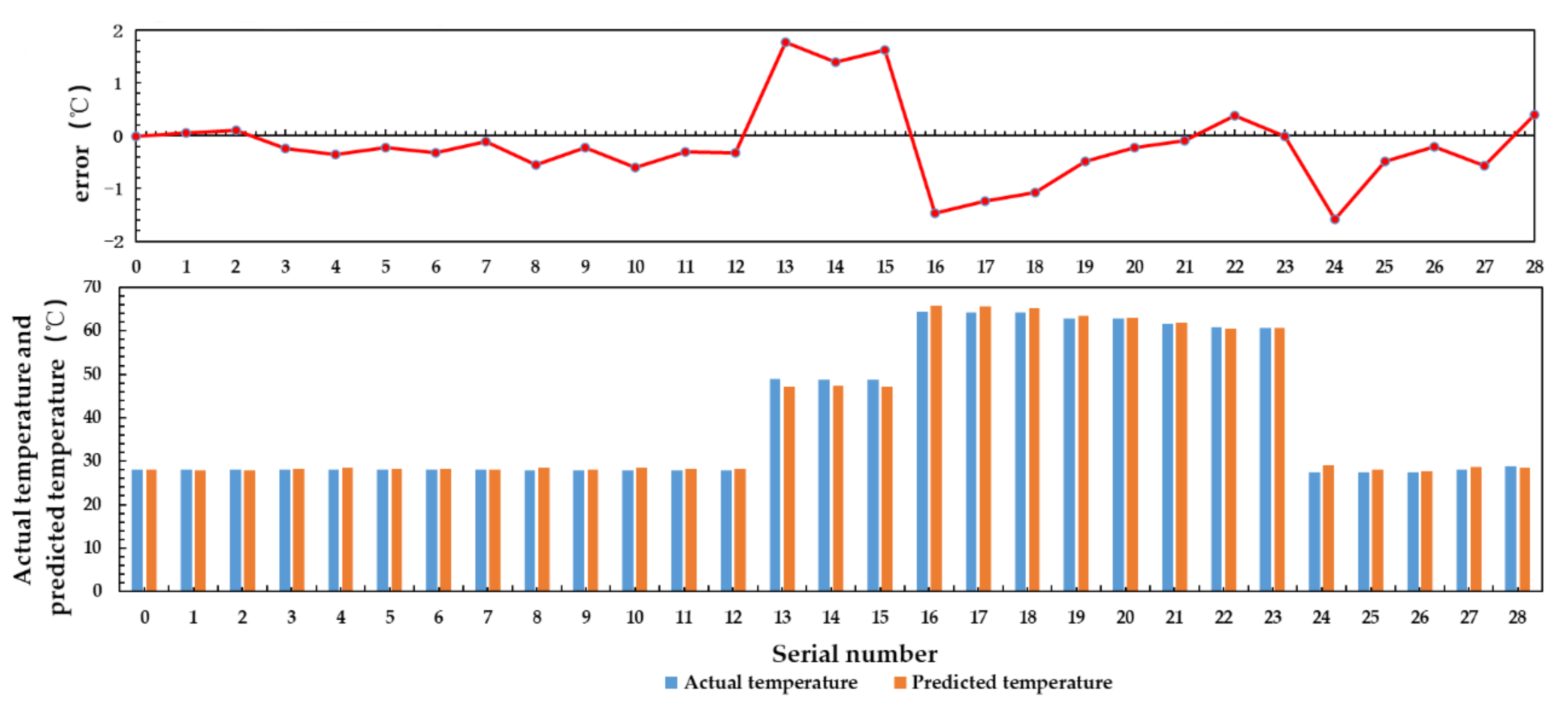
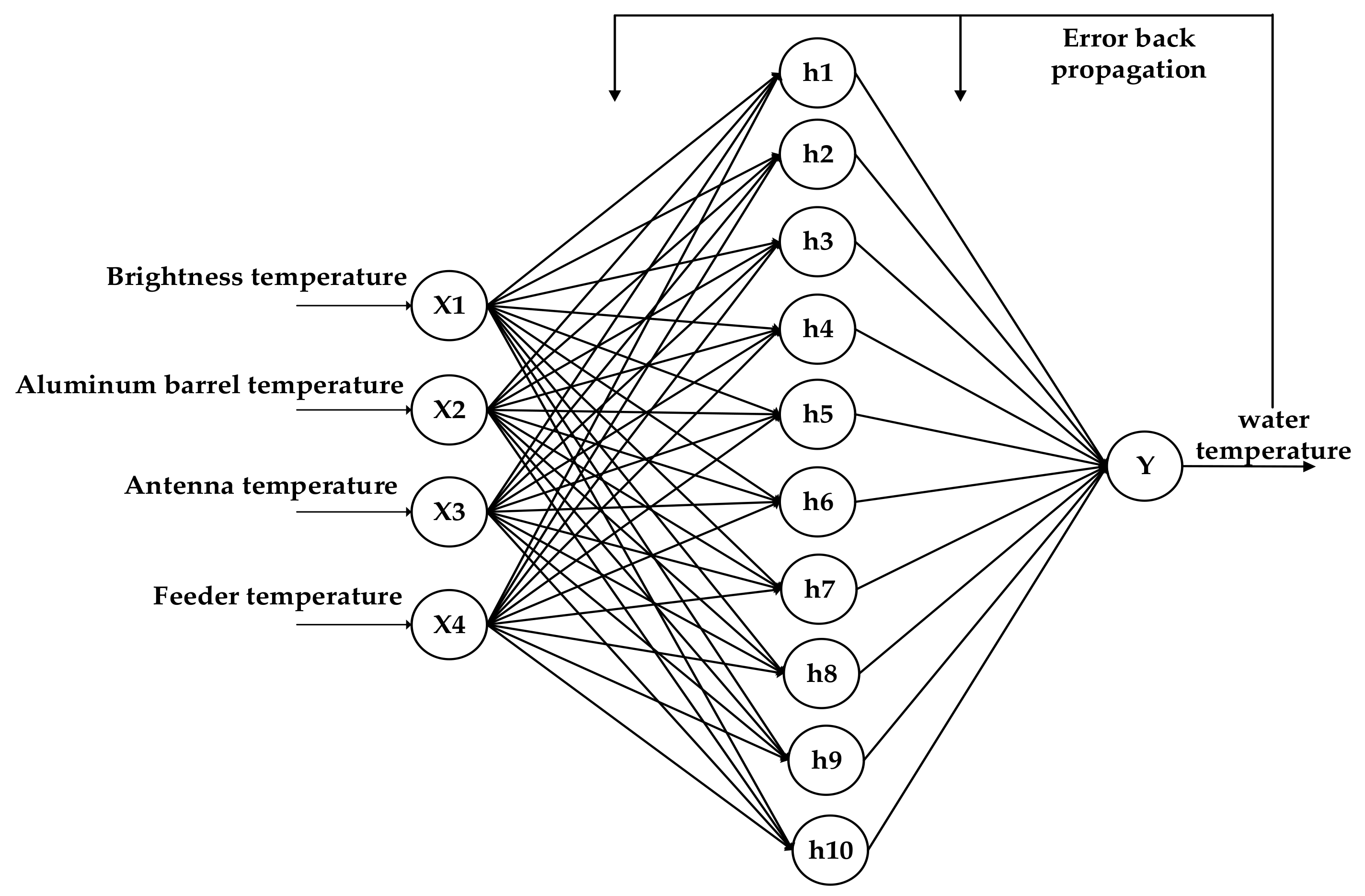
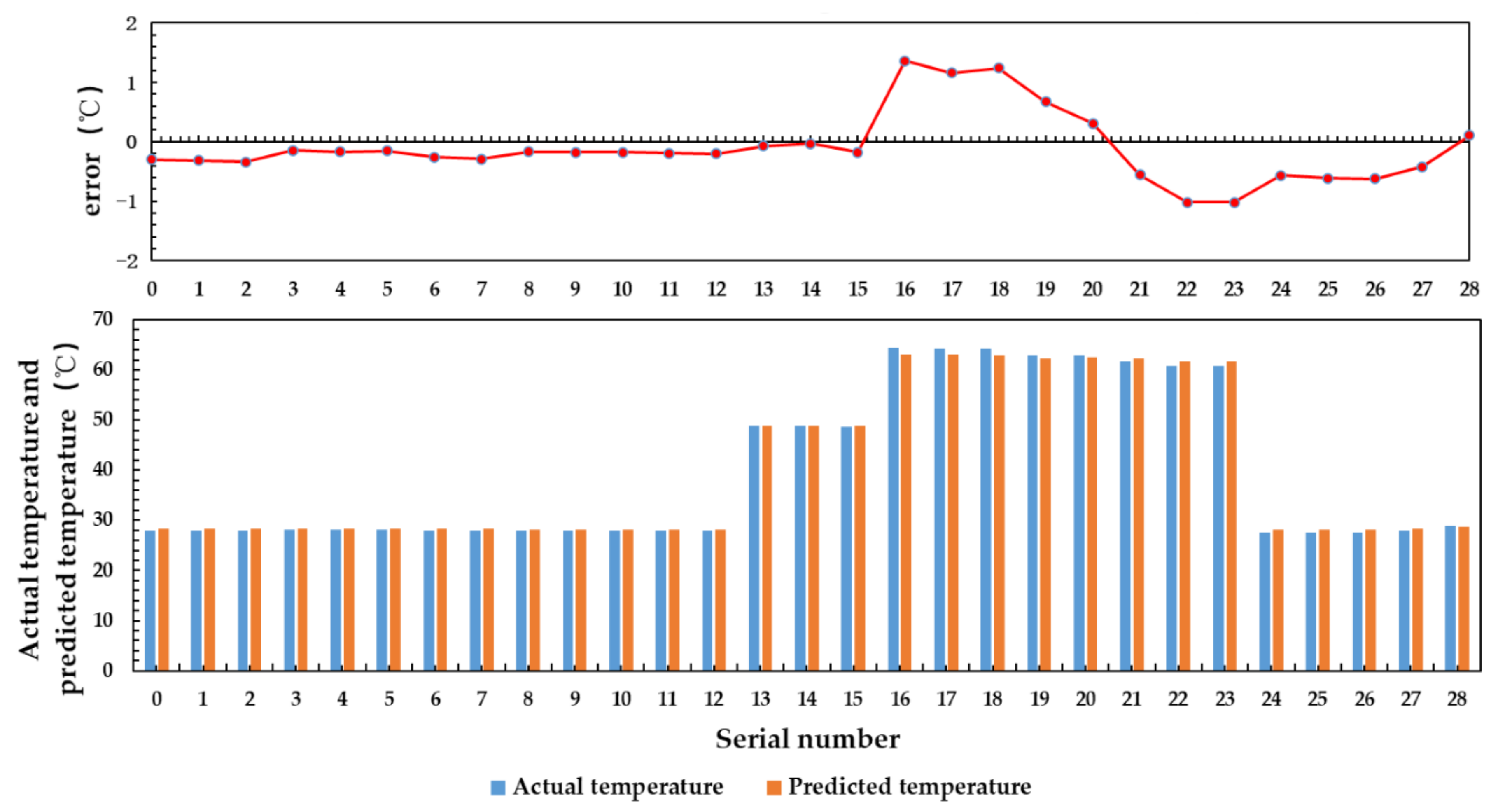
- In order to evaluate the impacts of aluminum plate temperature, antenna temperature and feeder temperature on the output result, this paper accounts these factors in the inversion algorithm. Multiple linear regression algorithm and BP neural network algorithm are used to carry out inversion operation. The results show that the mean square error of multiple linear regression algorithm is 0.607 and that of BP neural network algorithm is 0.334. The inversion accuracy can be improved by reducing the temperature range. In the follow-up work, the accuracy of temperature measurement will be further improved by increasing the amount of sampling data and selecting better inversion algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bonds, Q.; Weller, T.; Roeder, B. A total power radiometer (TPR) and measurement test bed for non-contact biomedical sensing applications. In Proceedings of the 2009 IEEE 10th Annual Wireless and Microwave Technology Conference, Clearwater, FL, USA, 20–21 April 2009. [Google Scholar]
- Bonds, Q. A Microwave Radiometer for Close Proximity Core Body Temperature Monitoring: Design, Development, and Experimentation; University of South Florida: Tampa, FL, USA, 2010. [Google Scholar]
- Bonds, Q.; Weller, T.; Roeder, B. A tunable Cavity Backed Slot Antenna (CBSA) for close proximity biomedical sensing applications. In Proceedings of the 2009 IEEE International Conference on Microwaves, Communications, Antennas and Electronics Systems, Tel Aviv, Israel, 9–11 November 2009. [Google Scholar]
- Bonds, Q.; Gerig, J.; Weller, T.M. Towards core body temperature measurement via close proximity radiometric sensing. IEEE Sens. J. 2012, 12, 3. [Google Scholar] [CrossRef]
- Pi, Z. Research on Microwave Radiometer Antenna for Human Body Temperature Measurement; Huazhong University of Science and Technology: Wuhan, China, 2015. [Google Scholar]
- Park, W.; Jeong, J. Total Power Radiometer for Medical Sensor Applications Using Matched and Mismatched Noise Sources. Sensors 2017, 17, 2105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kashif, M.; Hu, A.; Miao, J. Design and Implementation of an Analog Complex Correlator for Passive Millimeter Wave Imaging System. In Proceedings of the International Bhurban Conference on Applied Sciences & Technology, Islamabad, Pakistan, 12–16 January 2016. [Google Scholar]
- Wang, C.; Xin, X.; Kashif, M.; Miao, J. A Compact Analog Complex Cross-Correlator for Passive Millimeter-Wave Imager. IEEE Trans. Instrum. Meas. J. 2017, 66, 2997–3006. [Google Scholar] [CrossRef]
- Wang, C.; Ye, X. A 3.5–8 GHz Analog Complex Cross-correlator for Interferometric Passive Millimeter-wave Security Imaging Systems. In Proceedings of the 2018 Progress In Electromagnetics Research Symposium (PIERS-Toyama), Toyama, Japan, 1–4 August 2018. [Google Scholar]
- Shi, J.; Xie, Y.; Wu, L. Brief introduction of calibration method for fully polarized microwave radiometer. J. Microw. Sci. 2014, S1, 608–611. [Google Scholar]
- He, F. Research on Inversion Method of Microwave Nondestructive Measurement of Human Body Internal Temperature; Huazhong University of Science and Technology: Wuhan, China, 2015. [Google Scholar]
- Dong, S.; Wang, Z.; Wang, X. Study on a variable temperature calibration source for Microwave Radiometer Based on polarization grid. Acta Electron. Sin. J. 2018, 46, 185–189. [Google Scholar]
- Li, Z.; Liu, S. Study on the principle of periodic two-point calibration microwave radiometer. Electromagn. Field Microw. 2006, 36, 45–47. [Google Scholar]
- Scheeler, R.P. A Microwave Radiometer for Internal Body Temperature Measurement; University of Colorado at Boulder: Boulder, CO, USA, 2013. [Google Scholar]
- Gu, Z. Study on Radiation Characteristics of Millimeter Wave Stealth Coating; Nanjing University of technology: Nanjing, China, 2004. [Google Scholar]
- Ying, G.; Zhou, C.; Chen, H. Microwave Radiometer; Ocean Press: Beijing, China, 1992; pp. 1–250. [Google Scholar]
- Wu, Q.; Qu, D.; Qin, Y. Millimeter Wave Medical Technology and Its Clinical Application; China Science and Technology Press: Beijing, China, 2010; pp. 1–250. [Google Scholar]
- Jeong, J.; Park, K.; Lee, C. Design of Cavity-Backed Bow-Tie Antenna with Matching Layer for Human Body Application. Sensors 2019, 19, 4015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xin, C.; Hu, A.; Liu, K.; Miao, J. Real time elimination of analog correlation bias using vector modulator. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 2489–2495. [Google Scholar]
- Li, N.; Ye, N.; Su, R. Fast inversion algorithm of magnetic nano temperature based on Gaussian Newton method. J. Huazhong Univ. Sci. Technol. 2018, 46, 105–109. [Google Scholar]
- Wang, C.; Xin, X.; Liang, B.; Li, Z.; Miao, J. Quadrature Errors and DC Offsets Calibration of Analog Complex Cross-Correlator for Interferometric Passive Millimeter-Wave Imaging Applications. Sensors 2018, 18, 677. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karabetsos, S.; Koulouras, G.; Charamis, P.; Adamidis, G.; Vardiambasis, I.O.; Nassiopoulos, A. Development of the RF Front-end of a Multi-Channel Microwave Radiometer for Internal Body Temperature Measurements. J. Physics: Conf. Ser. 2015, 637, 012010. [Google Scholar] [CrossRef] [Green Version]
- Vaks, V.L.; Gaikovich, K.P.; Reznik, A.N. Thermal near field and the possibilities of its use for in-depth temperature diagnostics of media. Radiophys. Quantum Electron. 2002, 45, 7–22. [Google Scholar] [CrossRef]
- Popovic, Z.; Momenroodaki, P.; Scheeler, R. Toward wearable wireless thermometers for internal body temperature measurements. IEEE Commun. Mag. 2014, 52, 118–125. [Google Scholar] [CrossRef]
- Ai, W.; Feng, M.; Chen, G.; Lu, W. Research on sea surface temperature retrieval by the one-dimensional synthetic aperture microwave radiometer, 1D-SAMR. Acta Oceanol. Sin. 2020, 39, 115–122. [Google Scholar] [CrossRef]
- Zhang, Z. Microwave Radiometer Front-End and Its Wide-IF Super-Heterodyne Model and Application; School of Electronic Science and Engineering: Sichuan, China, 2019. [Google Scholar]
- Chen, Q. Research on Key Technologies of the Frontend of W-Band Focal Plane Array Passive Imaging System; School of Electronic Engineering: Sichuan, China, 2016. [Google Scholar]
- Xie, Y. Sensitivity analysis of a periodically calibrated Dicke radiometer. Electron. Meas. Technol. 2009, 32, 8–10. [Google Scholar]
- Wang, B. Research on the Calibration and Error Analysis of AC Radiometer System; Huazhong University of Science and Technology: Wuhan, China, 2013. [Google Scholar]
- Li, X. Research on Temperature Control of Blackbody Emitter Based on PID Algorithm of Neural Network; Tianjin University of Technology: Tianjin, China, 2018. [Google Scholar]
- Yadav, R.K.; Anubhav. GA and PSO hybrid algorithm for ANN training with application in Medical Diagnosis. In Proceedings of the 2019 Third International Conference on Intelligent Computing in Data Sciences (ICDS), Marrakech, Morocco, 28–30 October 2019; pp. 1–5. [Google Scholar]
- Ling, Z.W. Magnetic nano temperature inversion algorithm based on PSO. Electron. World 2019, 11, 5–8. [Google Scholar]
- Zhu, Z.; Sun, G.L.; He, C.; Liu, A. Prediction of the tensile force applied on surface-hardened steel rods based on a CDIF and PSO-optimized neural network. Meas. Sci. Technol. 2018, 29, 1–21. [Google Scholar] [CrossRef]
- Li, Y.L.; Liang, Y.; Song, W.; Liu, Q.; Qin, X.Y. Vegetable Price Prediction Based on PSO-BP Neural Network. In Proceedings of the 2015 8th International Conference on Intelligent Computation Technology and Automation (ICICTA), Nanchang, China, 14–15 June 2015. [Google Scholar]







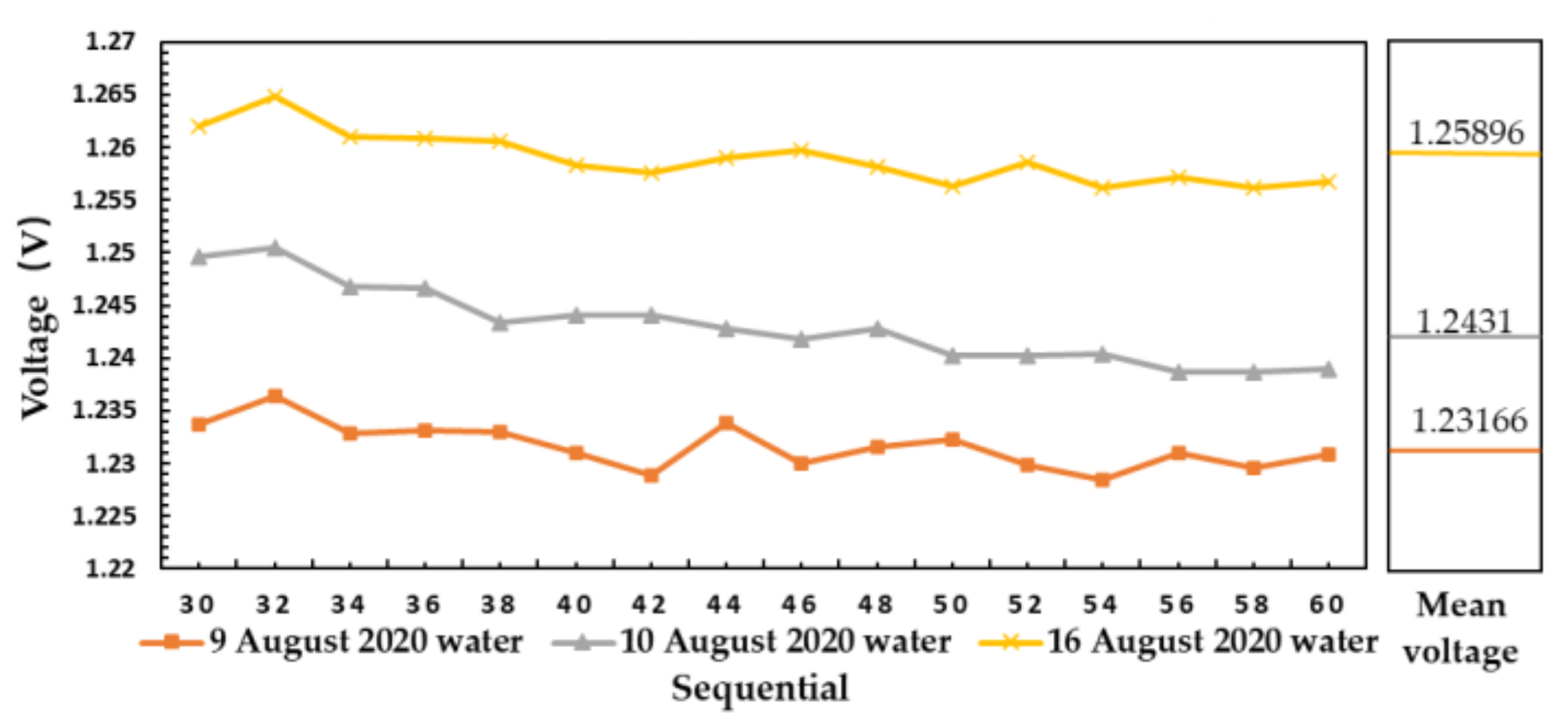
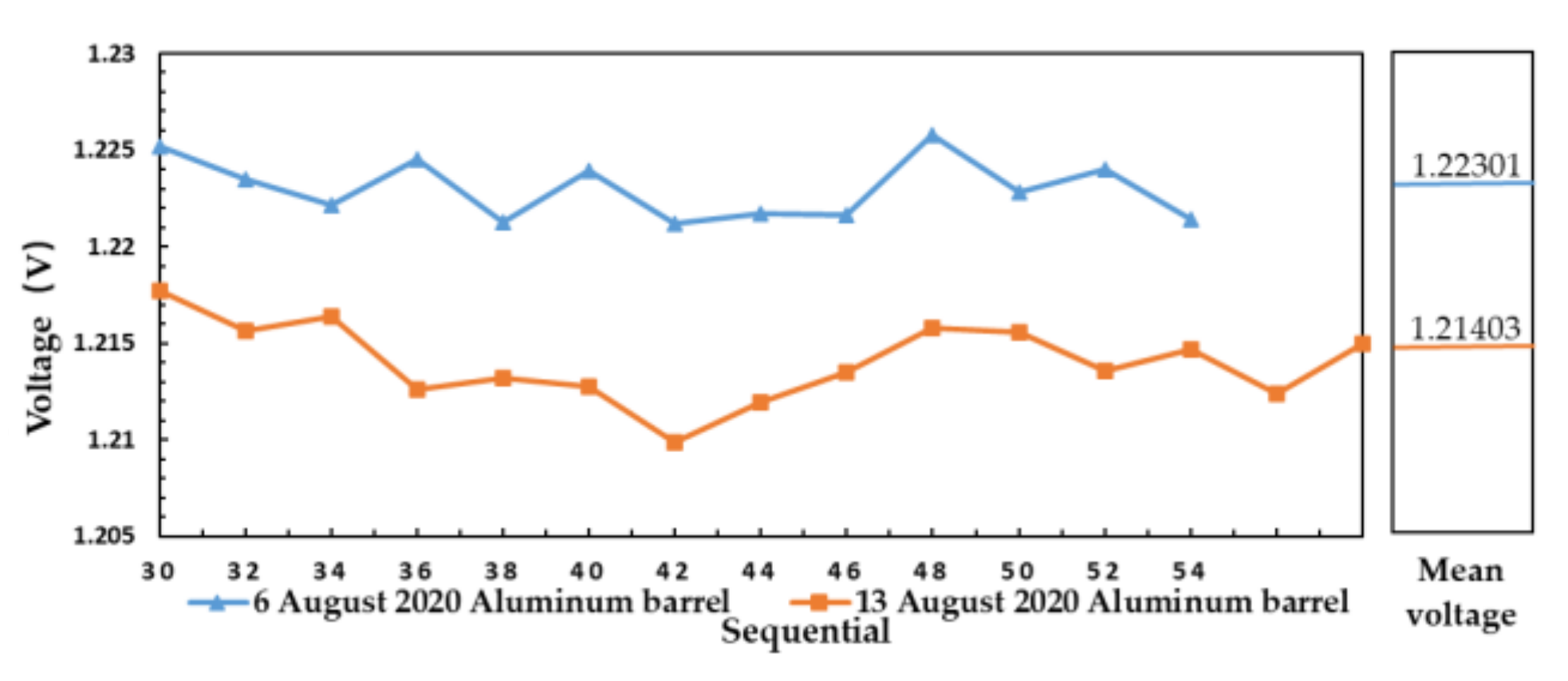
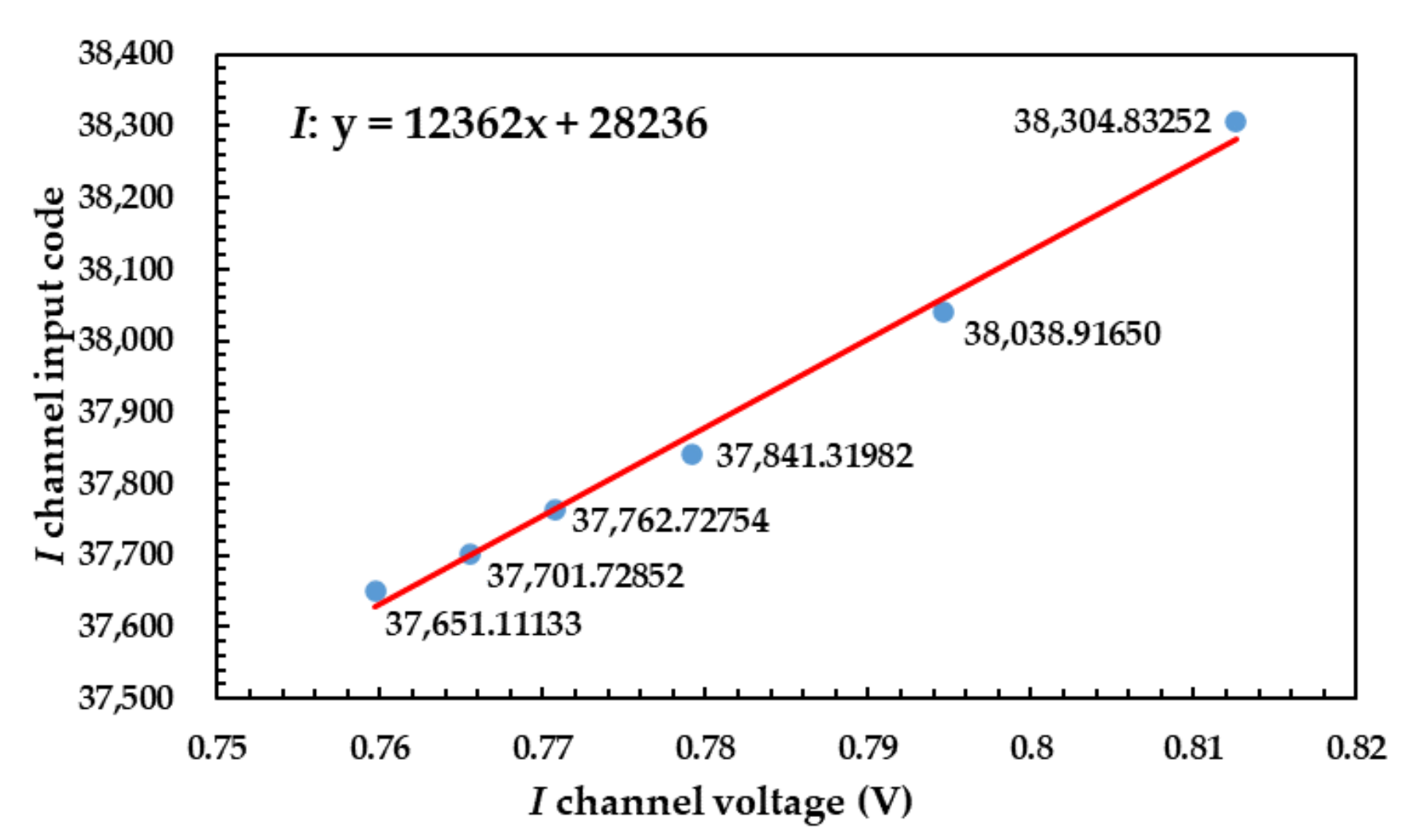





| Date | 6 August 2020 | |||||||||||||||
| Temperature (°C) | 52.9 | 52.8 | 52.7 | 52.6 | 52.5 | 52.4 | 52.3 | 52.2 | 52.1 | 52 | 51.9 | 51.8 | 51.7 | 51.6 | 51.5 | 51.4 |
| Voltage (V) | 1.266 | 1.265 | 1.261 | 1.260 | 1.256 | 1.253 | 1.252 | 1.249 | 1.249 | 1.247 | 1.244 | 1.242 | 1.239 | 1.237 | 1.236 | 1.236 |
| Date | 8 August 2020 | |||||||||||||||
| Temperature (°C) | 53.1 | 53 | 52.9 | 52.8 | 52.7 | 52.6 | 52.5 | 52.4 | 52.3 | 52.2 | 52.1 | 52 | 51.9 | 51.8 | 51.7 | 51.6 |
| Voltage (V) | 1.297 | 1.293 | 1.292 | 1.290 | 1.283 | 1.285 | 1.282 | 1.282 | 1.278 | 1.276 | 1.274 | 1.275 | 1.272 | 1.268 | 1.267 | 1.266 |
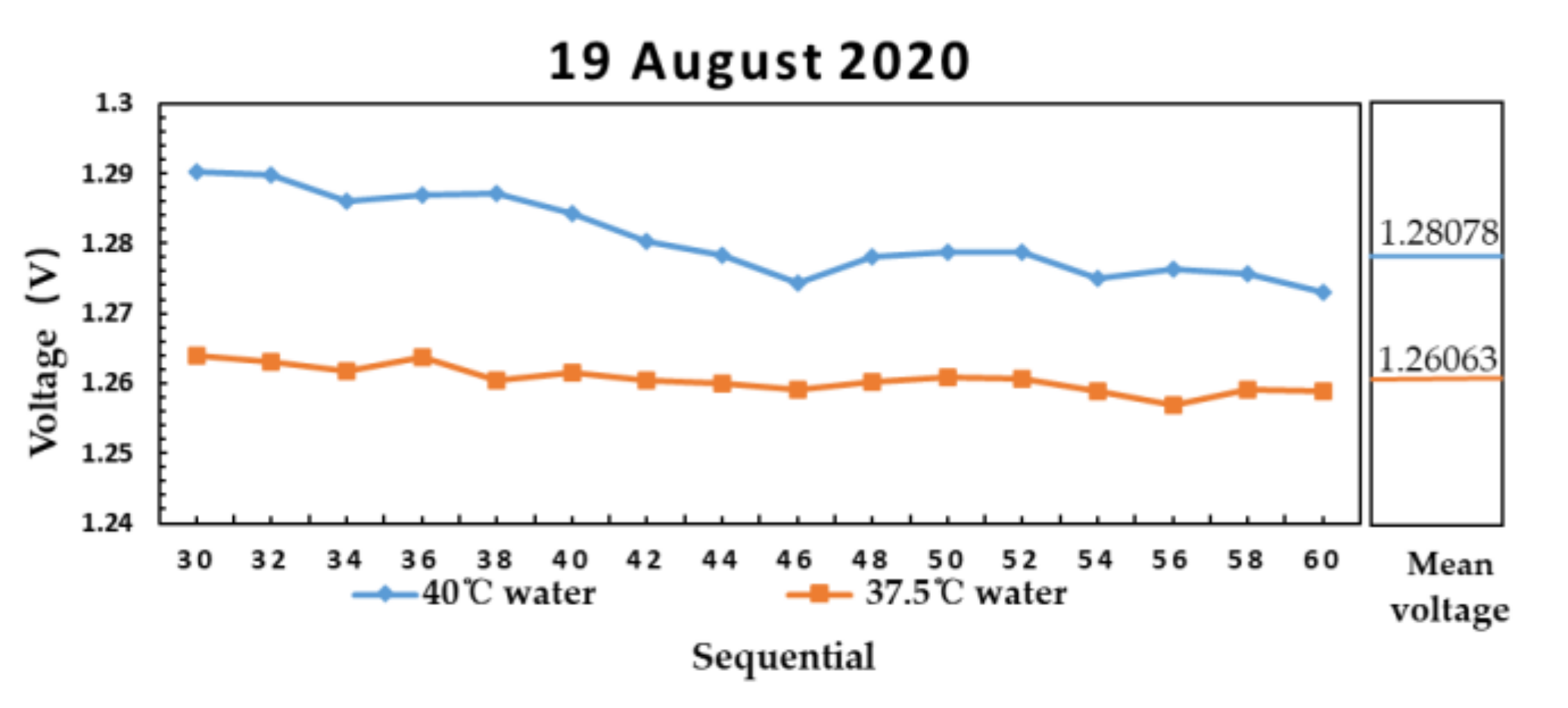
| Date | 19 August 2020 | |||||||||||||||
| Temperature (°C) | 41 | 40.9 | 40.7 | 40.6 | 40.5 | 40.3 | 40.2 | 40 | 39.9 | 39.8 | 39.7 | 39.6 | 39.5 | |||
| Voltage (V) | 1.290 | 1.290 | 1.286 | 1.287 | 1.284 | 1.280 | 1.278 | 1.278 | 1.279 | 1.275 | 1.276 | 1.276 | 1.273 | |||
| Date | 20 August 2020 | |||||||||||||||
| Temperature (°C) | 34.6 | 34.5 | 34.4 | 34.3 | 34.2 | 34.1 | 34 | 33.9 | ||||||||
| Voltage (V) | 1.293 | 1.290 | 1.286 | 1.284 | 1.283 | 1.280 | 1.278 | 1.280 | ||||||||
| 6 August 2020 | 13 August 2020 | |||
|---|---|---|---|---|
| Physical Temperature | Brightness Temperature | Physical temperature | Brightness temperature | |
| Aluminum plate | 28.8 °C | 7.488 °C | 27 °C | 7.02 °C |
| Different Types of Microwave Radiometers | Temperature Resolution (K) |
|---|---|
| Total power microwave radiometer [6] | 0.62 |
| Dicke microwave radiometer [5] | 0.11 |
| The one-dimensional synthetic aperture microwave radiometer [25] | 0.7106 |
| Ka-band direct detection radiometer [26] | 0.41 |
| W-band direct detection radiometer [27] | 0.5 |
| Dicke microwave radiometer [28] | Aperiodic calibration 1.35 Periodic calibration 0.62 Thermostat 0.17 |
| Ka-band AC radiometer [29] | 0.47 |
| Interferometric microwave radiometer designed in this paper | 0.4 |
| Temperature (°C) | Voltage (V) | Phase (°) |
|---|---|---|
| 38 | 1.286 | 49.068 |
| 37.9 | 1.257 | 50.377 |
| 37.8 | 1.233 | 51.242 |
| 37.7 | 1.220 | 51.468 |
| 37.6 | 1.212 | 51.711 |
| 37.5 | 1.203 | 51.824 |
| Temperature (°C) | Voltage (V) | Phase error (°) |
|---|---|---|
| 38 | 1.279 | 1.131 |
| 37.9 | 1.260 | 1.317 |
| 37.8 | 1.237 | 1.433 |
| 37.7 | 1.219 | 1.458 |
| 37.6 | 1.209 | 1.489 |
| 37.5 | 1.196 | 1.500 |
| Measured Object | Temperature (°C) | Emissivity | Emission Temperature | Corrected Voltage (V) |
|---|---|---|---|---|
| Absorbing materials | 28.3 | 0.995 | 28.1585 | 1.254 |
| Measured Object | Temperature (°C) | Emissivity | Emission Temperature | Corrected Voltage (V) |
|---|---|---|---|---|
| Aluminum plate | 27 | 0.26 | 7.02 | 1.213 |
| Absorbing material | 28.4 | 0.995 | 28.258 | 1.255 |
| Large Temperature Range (27.5–64.5 °C) | Small Temperature Range (27.5–28.9 °C) | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean square error | Mean Error | Max error | Mini error | Mean square error | Mean error | Max error | Mini error | |
| Multiple linear regression algorithm | 0.607 | 0.759 | 1.777 | 0.018 | 0.070 | 0.223 | 0.508 | 0.007 |
| BP neural network algorithm | 0.334 | 0.575 | 1.358 | 0.033 | 0.059 | 0.202 | 0.525 | 0.006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, G.; Ma, P.; Liu, J.; Shi, C.; Ma, J.; Peng, L. Design and Implementation of a Novel Interferometric Microwave Radiometer for Human Body Temperature Measurement. Sensors 2021, 21, 1619. https://doi.org/10.3390/s21051619
Sun G, Ma P, Liu J, Shi C, Ma J, Peng L. Design and Implementation of a Novel Interferometric Microwave Radiometer for Human Body Temperature Measurement. Sensors. 2021; 21(5):1619. https://doi.org/10.3390/s21051619
Chicago/Turabian StyleSun, Guangmin, Pan Ma, Jie Liu, Chong Shi, Jingyan Ma, and Li Peng. 2021. "Design and Implementation of a Novel Interferometric Microwave Radiometer for Human Body Temperature Measurement" Sensors 21, no. 5: 1619. https://doi.org/10.3390/s21051619
APA StyleSun, G., Ma, P., Liu, J., Shi, C., Ma, J., & Peng, L. (2021). Design and Implementation of a Novel Interferometric Microwave Radiometer for Human Body Temperature Measurement. Sensors, 21(5), 1619. https://doi.org/10.3390/s21051619








