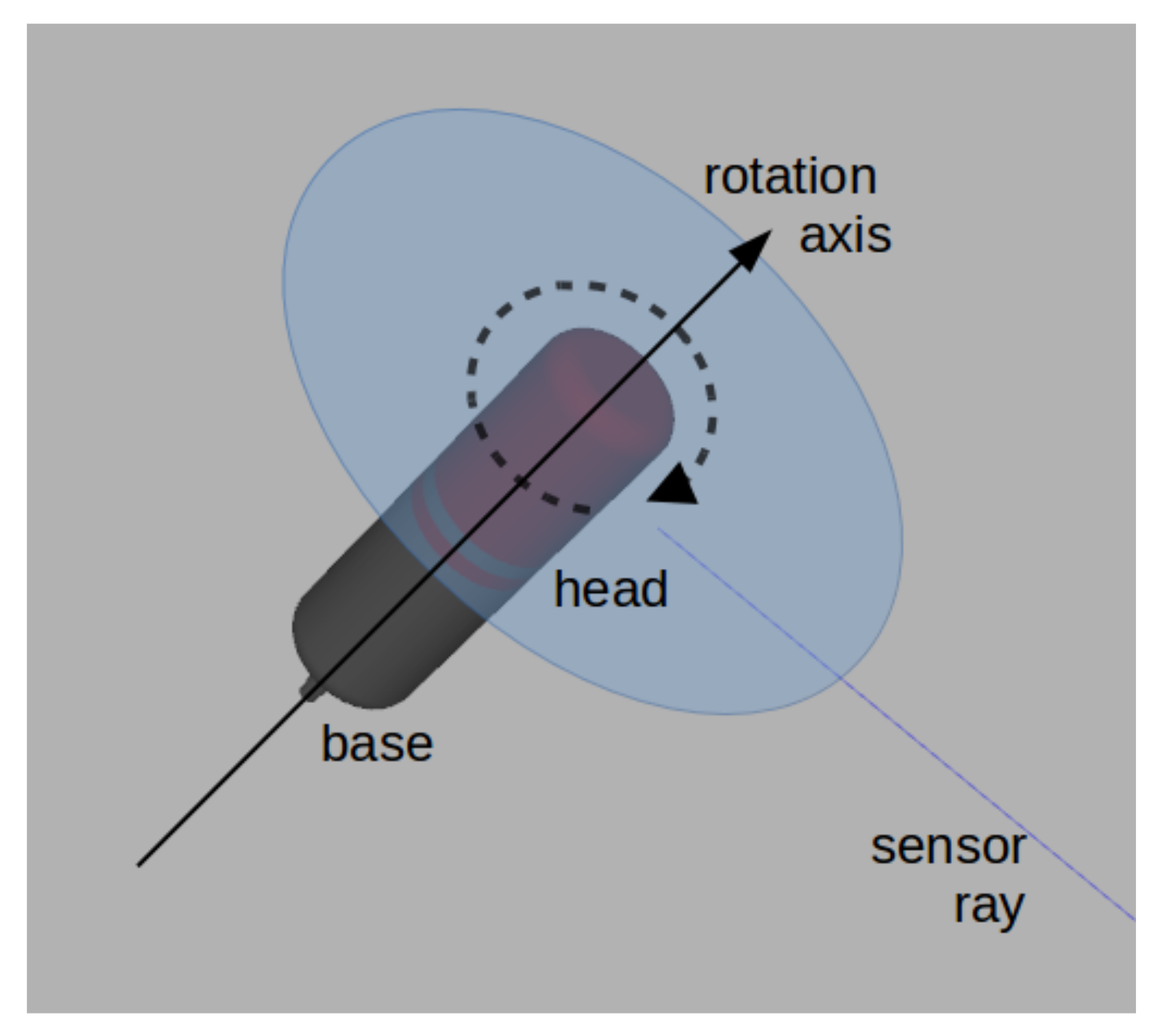
In this section we mathematically describe an ideal robot designed to perform mapping of a partially structured man-made tunnel and its ideal mapping sensor used to formalize the problem of mapping for one sensor connected to a robot, as the latter moves with constant velocity, .
The sensor is mounted in a UUV with normalized heading vector,
, matching
r, such that
. In addition, we position the UUV at a point,
, centered at the entrance of a tunnel with cross-section shown in
Figure 2, where
a is the tunnel width,
b is the tunnel height, and
,
and
form the basis of the coordinate frame of the tunnel. We assume the tunnel is straight and, as the robot moves, it is always at a point
inside the tunnel, where
and
l is the tunnel length along
. The robot heading,
is co-directed with
, making every sensor ray co-planar with a plane represented by point
and its normal
, where a cross-section along the tunnel length lies.
We then start to study the resolution of 3D maps of tunnels. We break the problem into parts. First we consider the cross-section and then the whole map as the robot moves along the length of the tunnel with constant velocity. Lastly, we study the behavior of multiple sensors working in tandem.
The Sampling Period over Cross-Sections
When our ideal point-wise robot is stopped, we can disregard the effect of the robot motion over
and simply analyze the behavior of the sensor as it rotates. Therefore, we can devise a function
g representing the cross-section of the tunnel in cylindrical coordinates as
where at any time
t,
x is the value that designates the point
where the robot is stopped,
is the distance from the center of the cross-section to the internal surface of the tunnel at angle
, all on the plane with normal
, regardless of
x. This way,
conveniently represents the sensor range reading, while
represents the current angle of the head of the sensor—assuming the robot and sensor are centered at the cross-section (see
Figure 2).
If using Cartesian coordinates, the function
can be written as
Even if there are no occlusions blocking the sensor field of view, sensors do not have infinitely small step angles. The number of angular steps for a full rotation of the sensor,
n, is finite and given by
where
, the sensor step angle, is often small (typically around one degree), depending on sensor configuration and quality.
Since the profiling sensor offers a single range measurement of the tunnel cross-section at each angular position,
and
are only available at time instants
, where
and
,
is the sampling time (time interval between successive samples), and
and
are respectively the starting angle and the angular velocity of the sensor head. Consequently, only a sampled version of the function
can be acquired in practice.
Angular sampling in our case produces evenly spaced angles, but spatial samples are usually not evenly spaced. The distance between samples in space will only be equal if the robot is mapping an ideal duct, pipe or tunnel with the shape of a cylinder. In this case, the cross-section of the environment is a circle and the space between samples is guaranteed to be the same. For our tunnel, if , the ceiling respects such condition; still, at the floor and vertical walls, it is not. Moreover, the reconstruction, simply put as a Fourier transform used to reconstruct a signal, would also rely on base functions of different frequencies, but such frequencies represent changes in the terrain or cross-section, measured by the rate of change of , in meters. The information between such samples can be lost if the features at the surface are not salient enough or are smaller than twice the distance between samples—which is a consequence of the sampling theorem. Therefore, we can lose data with our ideal sensor.
In order to analyze the sensor while it is mapping the floor, we keep the initial angular position with the sensor pointing down to
(see
Figure 3). The distance between samples,
, when the sensor rotates clockwise one step angle,
, is trivial and given by
This is the spatial sampling interval along the cross-section with the smallest distance between the sensor and the floor. Besides, the distance between samples on the floor is proportional to the tangent of the angular position of the head,
, and the angular step,
. On the other extreme, assuming the sensor moved
steps clockwise, conveniently reaching the corner which connects the floor and side wall (see
Figure 3), the sampling interval is given by
where
. It represents the distance between samples with the largest distance between the sensor and the floor—
when
m reaches the corner. Nevertheless, Equation (
6) also describes all the distances between consecutive samples on the floor by changing the value of
m. In fact, it reduces to
5 when
. Now we can write Theorem 1 (see proof in
Appendix A).
Theorem 1. When a single point sensor rotates around an axis to perform the sampling of a flat region, sampling with uniform angular steps results in non-uniform spatial sampling. In particular, if we assume the angular sampling starts at forming a vector which is perpendicular to the flat region, any pair of samples on the floor, obtained by stepping from to , will display a smaller spatial distance between samples than the next pair obtained at the next step—that is, going from to .
Thus, we can infer the best and worst cases of spatial sampling over the cross-section at flat regions with direct impact on sampling, knowing exactly where poor sampling will occur. That is, corresponds to the smallest distance between samples on the flat region, while , when the sensor ray hits the corner, is the largest. In other words, the best resolution obtained while sampling the floor would occur at the center of the tunnel, degrading as sampling approaches the corners
Once the robot moves sideways, the distance to the farthest corner is increased in the same amount. While such displacement to the sides can be small, its resulting effect in the tangent function may not be negligible, depending on the size of the tunnel under consideration and . Similarly, once the robot moves vertically towards the floor, the distance between adjacent samples will decrease when the ray is nearly perpendicular to the floor. However, it will increase near the corners, increasing drastically as the ray approaches parallelism with the floor. Finally, if the robot does not keep its heading aligned with the length of the tunnel, the difference in the yaw angle from the correct heading will also result in an increased distance from the farthest wall. As a consequence, the values of and are affected by the robot displacement and attitude.
Sidewalls can be compared applying the same strategy, if they are flat. Then, the last step is to study the ceiling. For tunnels with a rectangular cross-section, there is nothing else to do but comparing such regions. However, for the cross-section with the circular shaped ceiling of
Figure 2, the spatial distance between samples is given by
in the specific case where the center of the cross-section, matches both the robot position and the center of the half-circle which forms the ceiling, that is,
. The distance between samples in this case is always smaller at the ceiling than the floor. That is, as long as the profile of the ceiling presents a convex shape and the ceiling curvature does not go beyond the center of the cross-section,
. The intuition behind it is this: if the ceiling is convex, every time the sensor spins one step angle, the ceiling curvature keeps the measurement
constant or smaller than the distance of a purely flat ceiling parallel to the floor (see
Appendix B). Besides, the equation for the ceiling is bounded by the sine function, which can only grow up to 1, while the tangent function which defines
can grow to infinity.
Therefore, the sampling quality along the plane belonging to the cross-section is constrained by corners. Such sampling period is given by . and , can both be used to as best case scenarios of sampling along . However, calculation varies with ceiling shape and distance, since the ceiling often has specific constructions which do not match our design. Thus, using the simple floor equation may be a reasonable approximation.
Note, that such distances also depend on the robot position, and small changes to the sides lead to changes in minima and maxima. Also, man-made constructions often have sharp corners where the derivative of the function representing the surface is not defined. Such sharp corners demand infinite samples, previous knowledge about the terrain or some sort of heuristic for reasonable reconstruction. Such discontinuities usually are detected by sudden increases in the distance between adjacent samples, which change maxima values. Discontinuities in the surface will also reflect on minima, since a salient object, for example, a rock, may lead to the reduction of the distance between the sensor and the feature.
We can also compute the mean distance of consecutive samples on the floor. One way to compute it is using Equation (
6) in the form of a sum, which for the first quadrant is:
Note that Equation (
8) is a telescopic sum which can be directly reduced to:
Since we have a symmetry, both sides of the flat region reduces to the same equation.
Moreover, we can estimate the mean distance between samples over the entire cross-section as
where
p is the perimeter of the cross-section and
n is the number of angular steps given by the sonar in one revolution of the sensor (see proof in
Appendix C). Note that only
is independent of the position of the sensor over the cross-section.
Together, , (or ) can be used to estimate the size of features which can be detected over the cross-section. Still, the robot forward motion affects sampling in important ways.