Investigation of Magnetoelectric Sensor Requirements for Deep Brain Stimulation Electrode Localization and Rotational Orientation Detection
Abstract
:1. Introduction
- Bipolar non-directional electrode configuration (ring stimulation) with the activation of contacts at different electrode heights for electrode localization and
- bipolar directional electrode configuration with the activation of the tip of the electrode against an individual segmented contact for electrode orientation detection.
2. Materials and Methods
2.1. Experimental Design
2.2. Data Acquisition
2.3. Signal Processing
3. Results
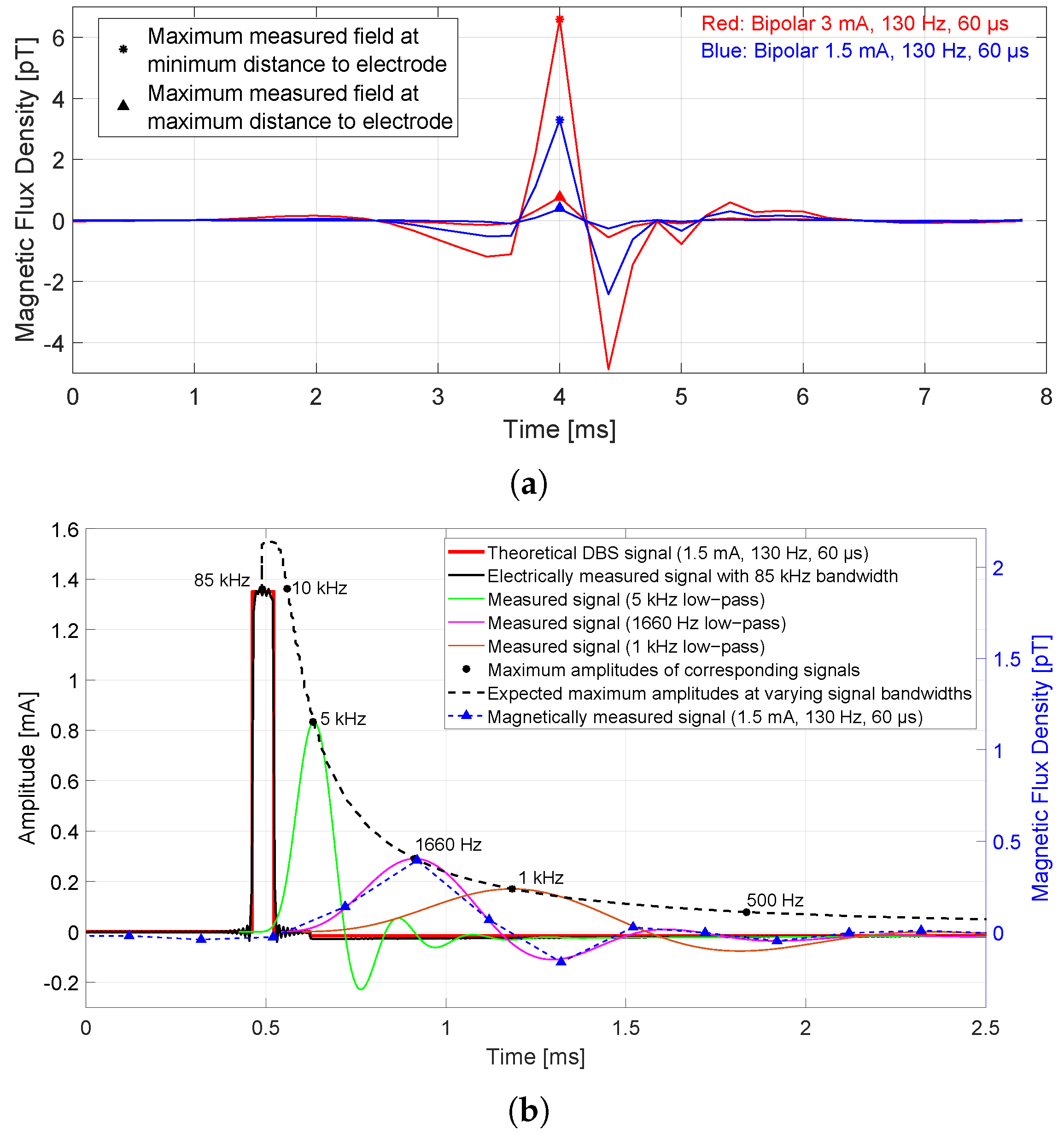
3.1. Presence of Magnetic Flux Densities in the Time Domain
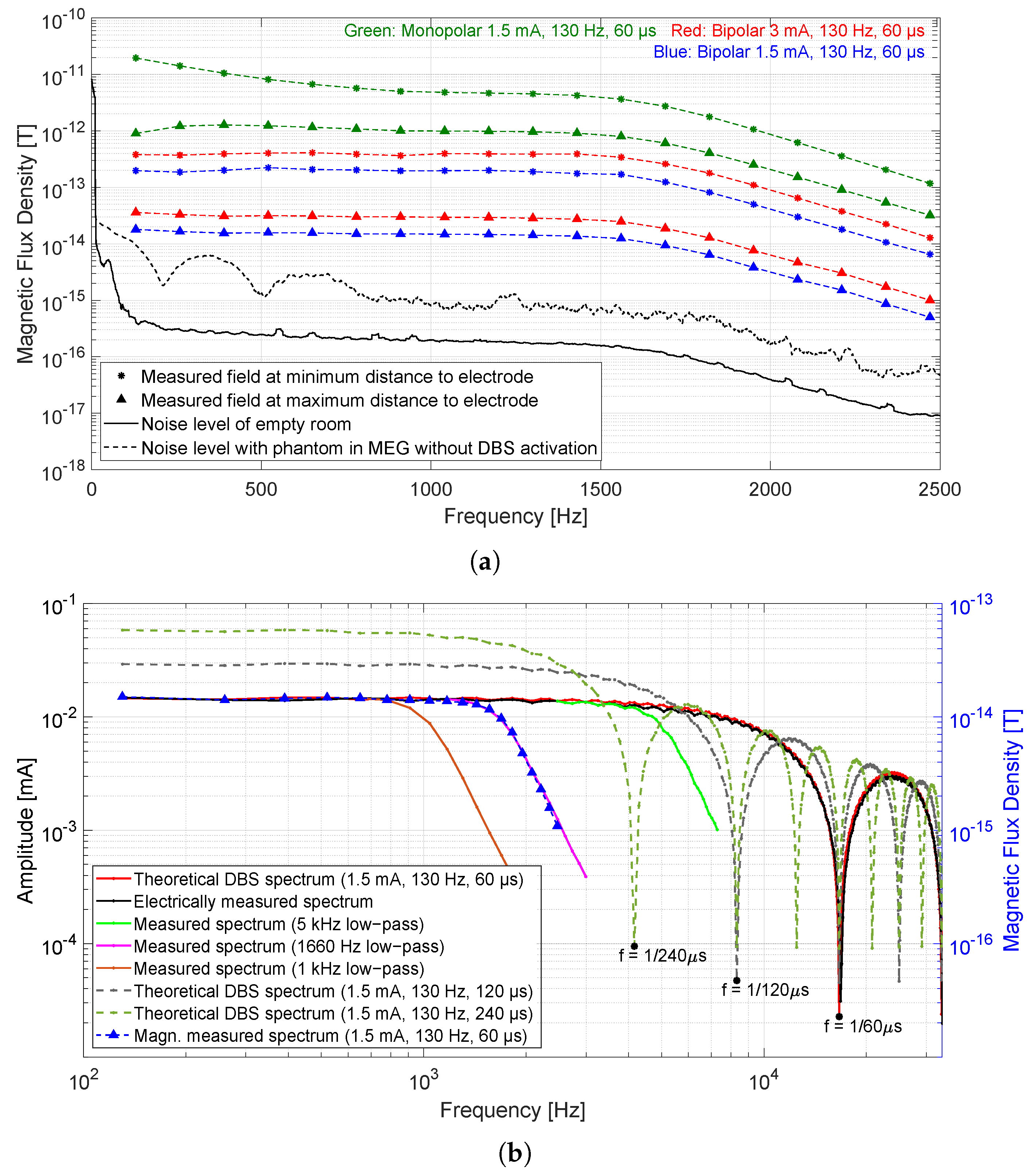
3.2. Presence of Magnetic Flux Densities in the Frequency Domain
3.3. The Required Frequency Bandwidth of Magnetic Sensor
3.4. The Required Limit of Detection
4. Discussion
- For 1.5 mA, 130 Hz, and 60 s bipolar mode, the maximum measured field in the time domain at the sensor closest to the electrode (7 cm) was 3.3 pT and the maximum measured field at the farthest sensor (15 cm) was 0.4 pT. The measured amplitude in the frequency domain at the stimulation frequency was 0.2 pT for the sensor closest to the electrode and the spectral value at the sensor farthest away was 18 fT.
- An increase in the stimulation amplitude from 1.5 to 3 mA (with pulse width and frequency remaining the same) leads to a proportional increase in the magnetic field amplitude in both the time and frequency domain.
- The maximum amplitude of the magnetic field in the time domain (that is generated by the broadband stimulus signal) depends on the given frequency bandwidth of the sensor or system. Since the SQUID sensor acts like a low-pass filter due to the system frequency bandwidth (0–1660 Hz limited by the MEG system), the maximum amplitude is attenuated by −13 dB (20% amplitude compared to a broadband amplitude).
- Measured magnetic field amplitudes in the frequency domain at the stimulation frequency and at its harmonics up to 1660 Hz are approximately equal in height. The spectral values decrease due to the system bandwidth of 1660 Hz.
- An increase in the stimulation pulse width from 60 to 120 s (amplitude and frequency remain the same) results in an increase in spectral values at lower frequencies (even doubling up to 1 kHz), while the main magnitude loop in the spectrum comes closer to the origin and higher. The maximum amplitude in the time domain also increases with increasing stimulation pulse width. The same behavior applies to the maximum amplitude in the time domain.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Limousin, P.; Foltynie, T. Long-term outcomes of deep brain stimulation in Parkinson disease. Nat. Rev. Neurol. 2019, 15, 234–242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schuepbach, W.M.M.; Rau, J.; Knudsen, K.; Volkmann, J.; Krack, P.; Timmermann, L.; Hälbig, T.D.; Hesekamp, H.; Navarro, S.M.; Meier, N.; et al. Neurostimulation for Parkinson’s disease with early motor complications. N. Engl. J. Med. 2013, 368, 610–622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krack, P.; Volkmann, J.; Tinkhauser, G.; Deuschl, G. Deep Brain Stimulation in Movement Disorders: From Experimental Surgery to Evidence-Based Therapy. Mov. Disord. 2019, 34, 1795–1810. [Google Scholar] [CrossRef] [PubMed]
- Lozano, A.M.; Lipsman, N.; Bergman, H.; Brown, P.; Chabardes, S.; Chang, J.W.; Matthews, K.; McIntyre, C.C.; Schlaepfer, T.E.; Schulder, M.; et al. Deep brain stimulation: Current challenges and future directions. Nat. Rev. Neurol. 2019, 15, 148–160. [Google Scholar] [CrossRef] [PubMed]
- Wagle Shukla, A.; Zeilman, P.; Fernandez, H.; Bajwa, J.A.; Mehanna, R. DBS Programming: An Evolving Approach for Patients with Parkinson’s Disease. Parkinsons Dis. 2017, 2017, 8492619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Volkmann, J.; Herzog, J.; Kopper, F.; Deuschl, G. Introduction to the programming of deep brain stimulators. Mov. Disord. 2002, 17 (Suppl. S3), S181–S187. [Google Scholar] [CrossRef] [PubMed]
- Picillo, M.; Lozano, A.M.; Kou, N.; Munhoz, R.P.; Fasano, A. Programming Deep Brain Stimulation for Tremor and Dystonia: The Toronto Western Hospital Algorithms. Brain Stimul. 2016, 9, 438–452. [Google Scholar] [CrossRef]
- Muthuraman, M.; Bange, M.; Koirala, N.; Ciolac, D.; Pintea, B.; Glaser, M.; Tinkhauser, G.; Brown, P.; Deuschl, G.; Groppa, S. Cross-frequency coupling between gamma oscillations and deep brain stimulation frequency in Parkinson’s disease. Brain 2020, 143, 3393–3407. [Google Scholar] [CrossRef]
- Stoker, V.; Krack, P.; Tonder, L.; Barnett, G.; Durand-Zaleski, I.; Schnitzler, A.; Houeto, J.L.; Timmermann, L.; Rau, J.; Schade-Brittinger, C.; et al. Deep Brain Stimulation Impact on Social and Occupational Functioning in Parkinson’s Disease with Early Motor Complications. Mov. Disord. Clin. Pract. 2020, 7, 672–680. [Google Scholar] [CrossRef]
- Steigerwald, F.; Matthies, C.; Volkmann, J. Directional Deep Brain Stimulation. Neurotherapeutics 2019, 16, 100–104. [Google Scholar] [CrossRef] [Green Version]
- Merola, A.; Romagnolo, A.; Krishna, V.; Pallavaram, S.; Carcieri, S.; Goetz, S.; Mandybur, G.; Duker, A.P.; Dalm, B.; Rolston, J.D.; et al. Current Directions in Deep Brain Stimulation for Parkinson’s Disease—Directing Current to Maximize Clinical Benefit. Neurol. Ther. 2020, 9, 25–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kramme, J.; Dembek, T.A.; Treuer, H.; Dafsari, H.S.; Barbe, M.T.; Wirths, J.; Visser-Vandewalle, V. Potentials and Limitations of Directional Deep Brain Stimulation: A Simulation Approach. Stereotact. Funct. Neurosurg. 2021, 99, 65–74. [Google Scholar] [CrossRef] [PubMed]
- Engelhardt, J.; Guehl, D.; Damon-Perrière, N.; Branchard, O.; Burbaud, P.; Cuny, E. Localization of Deep Brain Stimulation Electrode by Image Registration Is Software Dependent: A Comparative Study between Four Widely Used Software Programs. Stereotact. Funct. Neurosurg. 2018, 96, 364–369. [Google Scholar] [CrossRef] [PubMed]
- Ellenbogen, J.; Tuura, R.; Ashkan, K. Localisation of DBS Electrodes Post-Implantation, to CT or MRI? Which Is the Best Option? Stereotact. Funct. Neurosurg. 2018, 96, 347–348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lange, F.; Steigerwald, F.; Engel, D.; Malzacher, T.; Neun, T.; Fricke, P.; Volkmann, J.; Matthies, C.; Capetian, P. Longitudinal Assessment of Rotation Angles after Implantation of Directional Deep Brain Stimulation Leads. Stereotact. Funct. Neurosurg. 2020. [Google Scholar] [CrossRef] [PubMed]
- Hunsche, S.; Neudorfer, C.; Majdoub, F.E.; Maarouf, M.; Sauner, D. Determining the Rotational Orientation of Directional Deep Brain Stimulation Leads Employing Flat-Panel Computed Tomography. Oper. Neurosurg. 2019, 16, 465–470. [Google Scholar] [CrossRef] [PubMed]
- Reinacher, P.C.; Krüger, M.T.; Coenen, V.A.; Shah, M.; Roelz, R.; Jenkner, C.; Egger, K. Determining the Orientation of Directional Deep Brain Stimulation Electrodes Using 3D Rotational Fluoroscopy. AJNR Am. J. Neuroradiol. 2017, 38, 1111–1116. [Google Scholar] [CrossRef] [Green Version]
- Yalaz, M.; Teplyuk, A.; Deuschl, G.; Höft, M. Dipole Fit Localization of the Deep Brain Stimulation Electrode Using 3D Magnetic Field Measurements. IEEE Sens. J. 2020, 20, 9550–9557. [Google Scholar] [CrossRef]
- Yalaz, M.; Noor, S.; McIntyre, C.; Butz, M.; Schnitzler, A.; Deuschl, G.; Höft, M. DBS electrode localization and rotational orientation detection using SQUID-based magnetoencephalography. J. Neural. Eng. 2021. [Google Scholar] [CrossRef]
- Yalaz, M.; Teplyuk, A.; Muthuraman, M.; Deuschl, G.; Höft, M. The Magnetic Properties of Electrical Pulses Delivered by Deep-Brain Stimulation Systems. IEEE Trans. Instrum. Meas. 2020, 69, 4303–4313. [Google Scholar] [CrossRef]
- Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Muñoz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S.; et al. Moving magnetoencephalography towards real-world applications with a wearable system. Nature 2018, 555, 657–661. [Google Scholar] [CrossRef] [PubMed]
- Hill, R.M.; Boto, E.; Rea, M.; Holmes, N.; Leggett, J.; Coles, L.A.; Papastavrou, M.; Everton, S.K.; Hunt, B.A.; Sims, D.; et al. Multi-channel whole-head OPM-MEG: Helmet design and a comparison with a conventional system. NeuroImage 2020, 219, 116995. [Google Scholar] [CrossRef] [PubMed]
- Tierney, T.M.; Holmes, N.; Mellor, S.; López, J.D.; Roberts, G.; Hill, R.M.; Boto, E.; Leggett, J.; Shah, V.; Brookes, M.J.; et al. Optically pumped magnetometers: From quantum origins to multi-channel magnetoencephalography. NeuroImage 2019, 199, 598–608. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Niekiel, F.; Fichtner, S.; Kirchhof, C.; Meyners, D.; Quandt, E.; Wagner, B.; Lofink, F. Frequency Tunable Resonant Magnetoelectric Sensors for the Detection of Weak Magnetic Field. J. Micromech. Microeng. 2020, 30. [Google Scholar] [CrossRef]
- Salzer, S.; Jahns, R.; Piorra, A.; Teliban, I.; Reermann, J.; Höft, M.; Quandt, E.; Knöchel, R. Tuning fork for noise suppression in magnetoelectric sensors. Sens. Actuators A Phys. 2016, 237, 91–95. [Google Scholar] [CrossRef]
- Su, J.; Niekiel, F.; Fichtner, S.; Thormaehlen, L.; Kirchhof, C.; Meyners, D.; Quandt, E.; Wagner, B.; Lofink, F. AlScN-based MEMS magnetoelectric sensor. Appl. Phys. Lett. 2020, 117, 132903. [Google Scholar] [CrossRef]
- Kittmann, A.; Durdaut, P.; Zabel, S.; Reermann, J.; Schmalz, J.; Spetzler, B.; Meyners, D.; Sun, N.X.; McCord, J.; Gerken, M.; et al. Wide Band Low Noise Love Wave Magnetic Field Sensor System. Sci. Rep. 2018, 8, 278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oostenveld, R.; Fries, P.; Maris, E.; Schoffelen, J.M. Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 2011, 156869. [Google Scholar] [CrossRef]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Heinzel, G.; Rüdiger, A.; Schilling, R. Spectrum and Spectral Density Estimation by the Discrete Fourier transform (DFT), Including a Comprehensive List of Window Functions and Some New Flat-Top Windows; Max-Planck-Institut für Gravitationsphysik (Albert-Einstein-Institut): Hannover, Germany. Available online: http://hdl.handle.net/11858/00-001M-0000-0013-557A-5 (accessed on 15 February 2002).
- Wu, N. Using a Matched Filter to Improve SNR of Radio Maps. Astron. Data Anal. Softw. Syst. 1992, 25, 291. [Google Scholar]
- Sun, Y.; Farzan, F.; Dominguez, L.G.; Barr, M.S.; Giacobbe, P.; Lozano, A.M.; Wong, W.; Daskalakis, Z.J. A novel method for removal of deep brain stimulation artifact from electroencephalography. J. Neurosci. Methods 2014, 237, 33–40. [Google Scholar] [CrossRef] [PubMed]
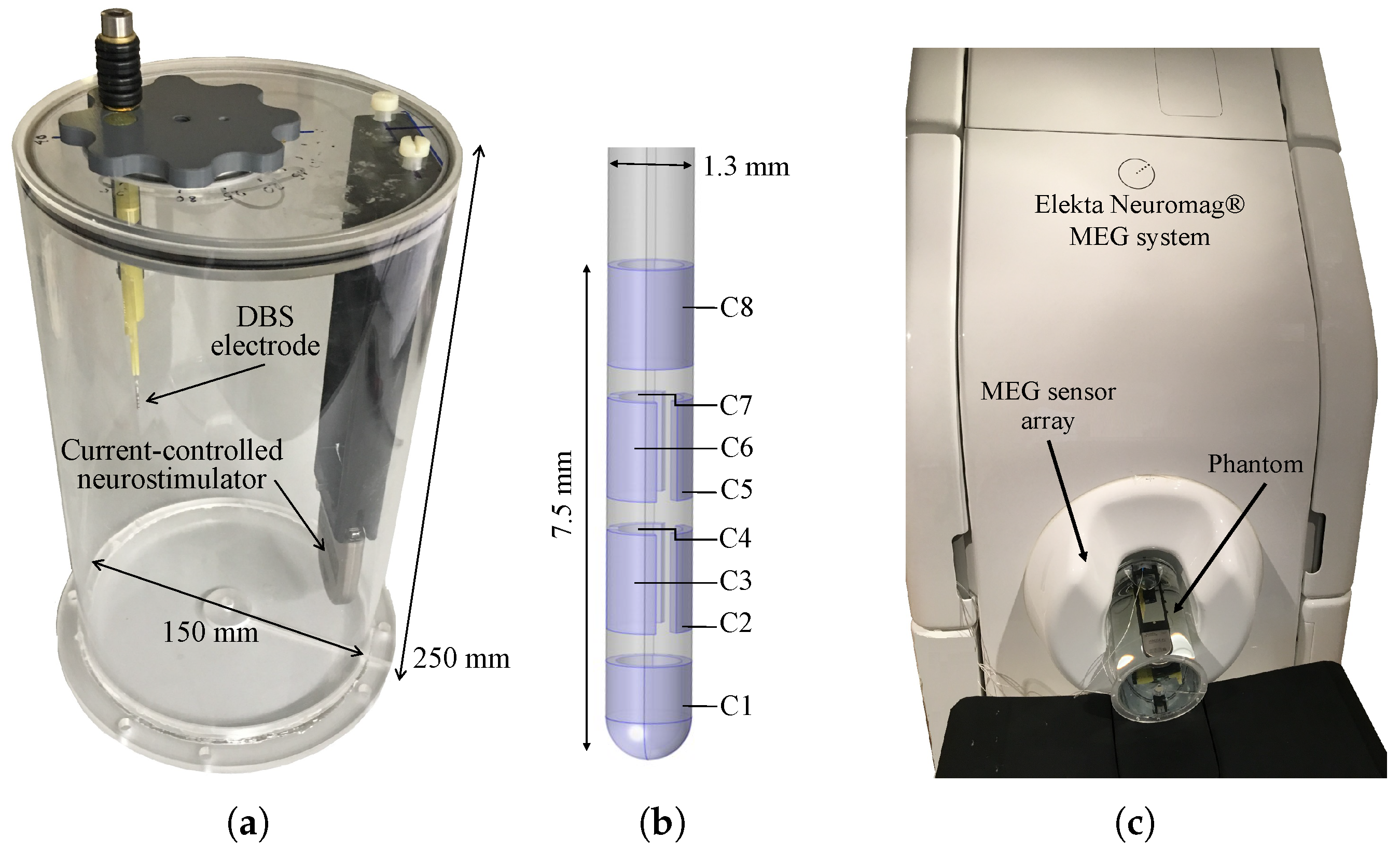



| Num. | Configuration | Contacts: (−) vs. (+) | Amplitude [mA] | Pulse [s] | Frequency [Hz] |
|---|---|---|---|---|---|
| 1 | Bipolar | 1 vs. 234 | 3 | 60 | 130 |
| 2 | Bipolar | 234 vs. 567 | 3 | 60 | 130 |
| 3 | Bipolar | 567 vs. 8 | 3 | 60 | 130 |
| 4 | Bipolar | 1 vs. 234 | 1.5 | 60 | 130 |
| 5 | Bipolar | 234 vs. 567 | 1.5 | 60 | 130 |
| 6 | Bipolar | 567 vs. 8 | 1.5 | 60 | 130 |
| 7 | Monopolar | 1 vs. Case | 1.5 | 60 | 130 |
| 8 | Monopolar | 234 vs. Case | 1.5 | 60 | 130 |
| 9 | Monopolar | 8 vs. Case | 1.5 | 60 | 130 |
| Config. | Ampl. [mA], Pulse [s], Freq. [Hz] | Available Magnetic Flux Densities [pT] within Bandwidth | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0–10 kHz | 0–1660 Hz | 0–1 kHz | 130 Hz | ||||||
| Min | Max | Min | Max | Min | Max | Min | Max | ||
| Bipolar | 3.0, 60, 130 | 3.8 | 30 | 0.8 | 6.6 | 0.5 | 3.9 | 0.036 | 0.38 |
| 1.5, 60, 130 | 1.9 | 15 | 0.4 | 3.3 | 1.9 | 10 | 0.018 | 0.19 | |
| Monopolar | 1.5, 60, 130 | - | - | 5 | 195 | - | - | 1 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yalaz, M.; Deuschl, G.; Butz, M.; Schnitzler, A.; Helmers, A.-K.; Höft, M. Investigation of Magnetoelectric Sensor Requirements for Deep Brain Stimulation Electrode Localization and Rotational Orientation Detection. Sensors 2021, 21, 2527. https://doi.org/10.3390/s21072527
Yalaz M, Deuschl G, Butz M, Schnitzler A, Helmers A-K, Höft M. Investigation of Magnetoelectric Sensor Requirements for Deep Brain Stimulation Electrode Localization and Rotational Orientation Detection. Sensors. 2021; 21(7):2527. https://doi.org/10.3390/s21072527
Chicago/Turabian StyleYalaz, Mevlüt, Günther Deuschl, Markus Butz, Alfons Schnitzler, Ann-Kristin Helmers, and Michael Höft. 2021. "Investigation of Magnetoelectric Sensor Requirements for Deep Brain Stimulation Electrode Localization and Rotational Orientation Detection" Sensors 21, no. 7: 2527. https://doi.org/10.3390/s21072527
APA StyleYalaz, M., Deuschl, G., Butz, M., Schnitzler, A., Helmers, A.-K., & Höft, M. (2021). Investigation of Magnetoelectric Sensor Requirements for Deep Brain Stimulation Electrode Localization and Rotational Orientation Detection. Sensors, 21(7), 2527. https://doi.org/10.3390/s21072527






