Magnetoelastic Coupling and Delta-E Effect in Magnetoelectric Torsion Mode Resonators
Abstract
:1. Introduction
2. MEMS Torsion Mode Sensors
3. Sensitivity
3.1. Definition of the Sensitivity
3.2. Magnetic Sensitivity of Arbitrary Resonance Modes
4. Sensor Modelling
4.1. Electromechanical Model
4.2. Magnetoelastic Model
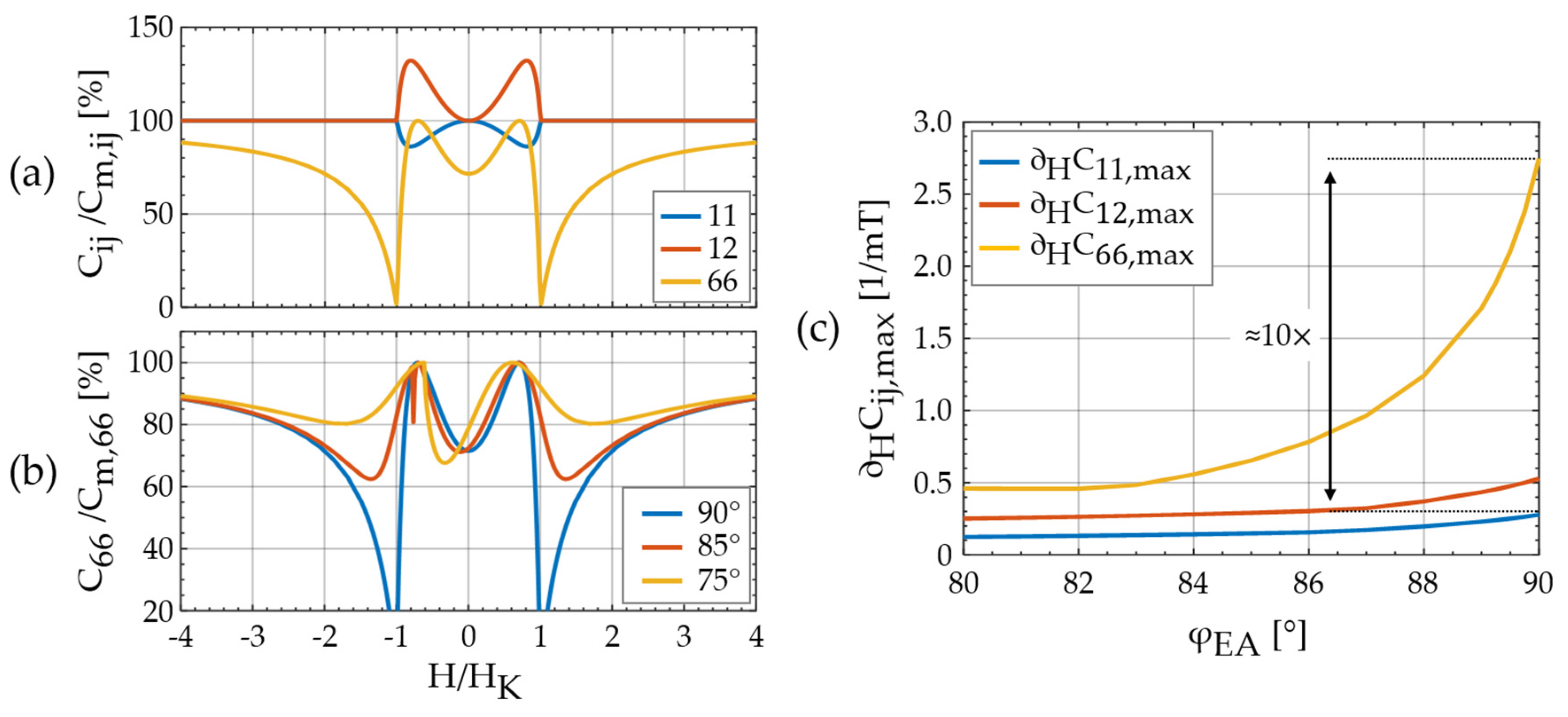
5. Implications of the Magnetic Model
6. Results
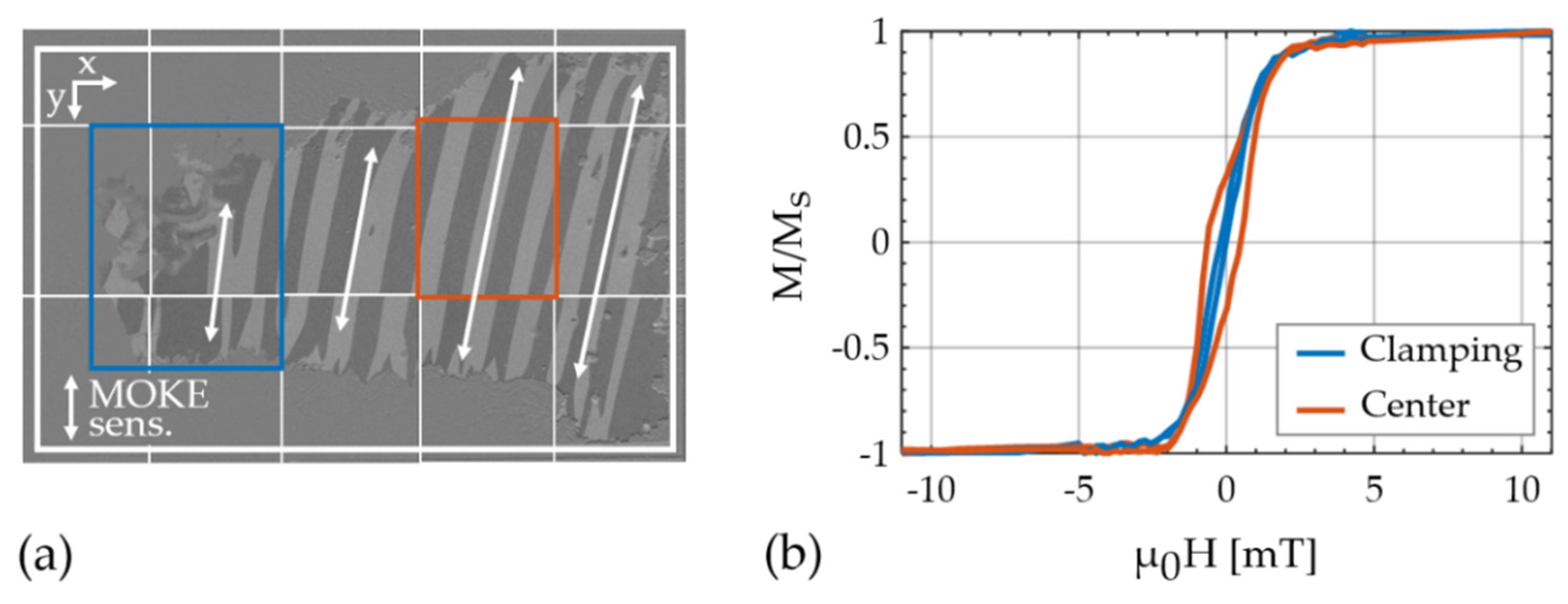
6.1. Magnetization Measurements
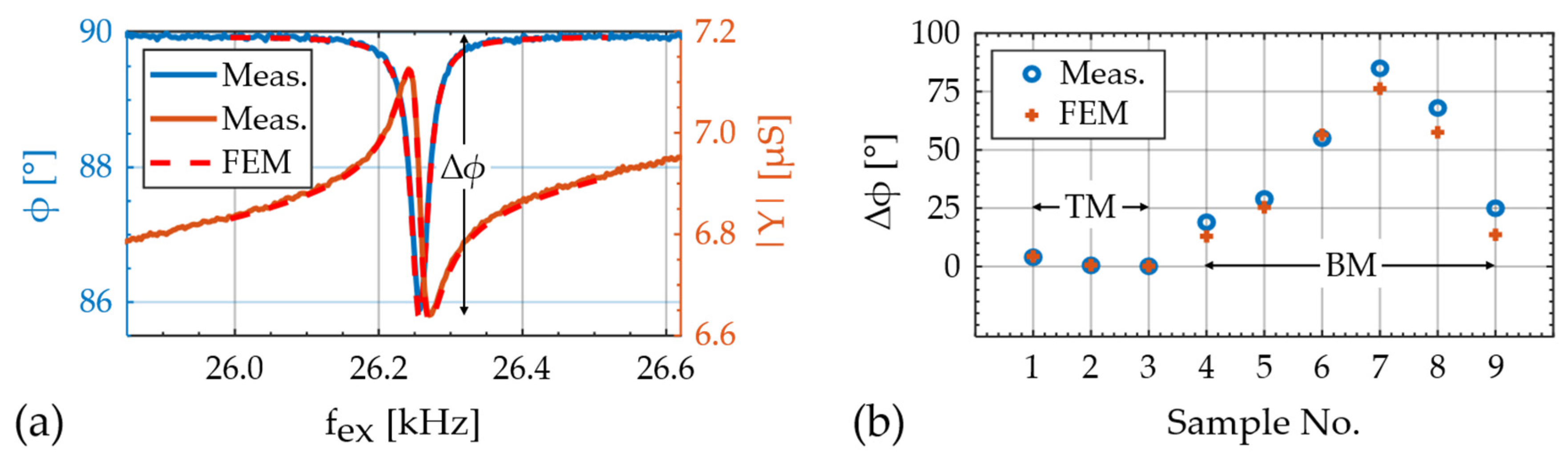
6.2. Electromechanical Properties
6.3. Delta-E Effect and Sensitivities
6.4. Resonance Frequency Simulations
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Magnetoelastic Model
A.1. Definition of Vectors
A.2. General Expression for
A.3. Derivatives of the Energy Density Functional
Appendix B. Resonance Frequencies and Sensitivities
| Mode | |||||||
|---|---|---|---|---|---|---|---|
| TM1 | 26.26 | 26.26 | 900 | 330 | 12.6 | 4780 | 850 |
| TM2 | 87.48 | 88.20 | 700 | 837 | 9.5 | 59 | 27.5 |
| TM3 | 175.15 | 179.20 | 280 | 542 | 3.0 | 115 | 95 |
| BM1 | 7.65 | 7.80 | 300 | 26.7 | 3.5 | 2550 | 150 |
| BM2 | 47.18 | 48.55 | 300 | 432 | 9.2 | 220 | 70 |
| BM3 | 121.40 | 116.20 | 300 | 811 | 6.7 | 18 | 42 |
Appendix C. Geometry and Material Parameters
C.1. Geometry
C.2. Substrate (Poly-Si)
C.3. Magnetic Material (FeCoSiB)
C.4. Piezoelectric Material (AlN)
References
- Reermann, J.; Durdaut, P.; Salzer, S.; Demming, T.; Piorra, A.; Quandt, E.; Frey, N.; Höft, M.; Schmidt, G. Evaluation of magnetoelectric sensor systems for cardiological applications. Meas. J. Int. Meas. Confed. 2018, 116, 230–238. [Google Scholar] [CrossRef]
- Zuo, S.; Schmalz, J.; Ozden, M.-O.; Gerken, M.; Su, J.; Niekiel, F.; Lofink, F.; Nazarpour, K.; Heidari, H. Ultrasensitive Magnetoelectric Sensing System for pico-Tesla MagnetoMyoGraphy. IEEE Trans. Biomed. Circuits Syst. 2020, 1. [Google Scholar] [CrossRef]
- Kwong, J.S.W.; Leithäuser, B.; Park, J.W.; Yu, C.M. Diagnostic value of magnetocardiography in coronary artery disease and cardiac arrhythmias: A review of clinical data. Int. J. Cardiol. 2013, 167, 1835–1842. [Google Scholar] [CrossRef] [PubMed]
- Röbisch, V.; Salzer, S.; Urs, N.O.; Reermann, J.; Yarar, E.; Piorra, A.; Kirchhof, C.; Lage, E.; Höft, M.; Schmidt, G.U.; et al. Pushing the detection limit of thin film magnetoelectric heterostructures. J. Mater. Res. 2017, 32, 1009–1019. [Google Scholar] [CrossRef]
- Kneller, E. Ferromagnetismus; Springer: Berlin/Heidelberg, Germany, 1962; ISBN 9783642866951. [Google Scholar]
- Livingston, J.D. Magnetomechanical properties of amorphous metals. Phys. Status Solidi A 1982, 70, 591–596. [Google Scholar] [CrossRef]
- Lee, E.W. Magnetostriction and Magnetomechanical Effects. Rep. Prog. Phys. 1955, 18, 184–229. [Google Scholar] [CrossRef]
- De Lacheisserie, T. Theory and Application of Magnetoelasticity; CRC Press: Boca Raton, FL, USA, 1993; ISBN 9780849369346. [Google Scholar]
- Bou Matar, O.; Robillard, J.F.; Vasseur, J.O.; Hladky-Hennion, A.C.; Deymier, P.A.; Pernod, P.; Preobrazhensky, V. Band gap tunability of magneto-elastic phononic crystal. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef] [Green Version]
- Mazzamurro, A.; Dusch, Y.; Pernod, P.; Matar, O.B.; Addad, A.; Talbi, A.; Tiercelin, N. Giant magnetoelastic coupling in Love acoustic waveguide based on uniaxial multilayered TbCo2/FeCo nanostructured thin film on Quartz ST-cut. Phys. Rev. Appl. 2020, 13. [Google Scholar] [CrossRef] [Green Version]
- Del Moral, A. Magnetostriction and magnetoelasticity theory: A modern view. In Handbook of Magnetism and Advanced Magnetic Materials; Kronmüller, H., Parkin, S., Eds.; Wiley-Interscience: Hoboken, NJ, USA, 2007; Volume 1, ISBN 9780470022177. [Google Scholar]
- Atkinson, D.; Squire, P.T.; Gibbs, M.R.J.; Atalay, S.; Lord, D.G. The effect of annealing and crystallization on the magnetoelastic properties of Fe-Si-B amorphous wire. J. Appl. Phys. 1993, 73, 3411–3417. [Google Scholar] [CrossRef]
- Barandiarán, J.M.; Gutiérrez, J.; García-Arribas, A.; Squire, P.T.; Hogsdon, S.N.; Atkinson, D. Comparison of magnetoelastic resonance and vibrating reed measurements of the large delta-E effect in amorphous alloys. J. Magn. Magn. Mater. 1995, 140–144, 273–274. [Google Scholar] [CrossRef]
- Squire, P.T. Domain model for magnetoelastic behaviour of uniaxial ferromagnets. J. Magn. Magn. Mater. 1995, 140–144, 1829–1830. [Google Scholar] [CrossRef]
- Gutiérrez, J.; García-Arribas, A.; Garitaonaindia, J.S.; Barandiarán, J.M.; Squire, P.T. ΔE effect and anisotropy distribution in metallic glasses with oblique easy axis induced by field annealing. J. Magn. Magn. Mater. 1996, 157–158, 543–544. [Google Scholar] [CrossRef]
- Squire, P.T.; Atalay, S.; Chiriac, H. ΔE effect in amorphous glass covered wires. IEEE Trans. Magn. 2000, 36, 3433–3435. [Google Scholar] [CrossRef]
- Ludwig, A.; Quandt, E. Optimization of the delta-E effect in thin films and multilayers by magnetic field annealing. IEEE Trans. Magn. 2002, 38, 2829–2831. [Google Scholar] [CrossRef]
- Dong, C.; Li, M.; Liang, X.; Chen, H.; Zhou, H.; Wang, X.; Gao, Y.; McConney, M.E.; Jones, J.G.; Brown, G.J.; et al. Characterization of magnetomechanical properties in FeGaB thin films. Appl. Phys. Lett. 2018, 113, 262401. [Google Scholar] [CrossRef]
- Yoshizawa, N.; Yamamoto, I.; Shimada, Y. Magnetic field sensing by an electrostrictive/magnetostrictive composite resonator. IEEE Trans. Magn. 2005, 41, 4359–4361. [Google Scholar] [CrossRef]
- Nan, T.; Hui, Y.; Rinaldi, M.; Sun, N.X. Self-biased 215 MHz magnetoelectric NEMS resonator for ultra-sensitive DC magnetic field detection. Sci. Rep. 2013, 3, 1985. [Google Scholar] [CrossRef] [Green Version]
- Hui, Y.; Nan, T.; Sun, N.X.; Rinaldi, M. High resolution magnetometer based on a high frequency magnetoelectric MEMS-CMOS oscillator. J. Microelectromech. Syst. 2015, 24, 134–143. [Google Scholar] [CrossRef]
- Li, M.; Matyushov, A.; Dong, C.; Chen, H.; Lin, H.; Nan, T.; Qian, Z.; Rinaldi, M.; Lin, Y.; Sun, N.X. Ultra-sensitive NEMS magnetoelectric sensor for picotesla DC magnetic field detection. Appl. Phys. Lett. 2017, 110, 143510. [Google Scholar] [CrossRef]
- Osiander, R.; Ecelberger, S.A.; Givens, R.B.; Wickenden, D.K.; Murphy, J.C.; Kistenmacher, T.J. A microlectromechanical-based magnetostrictive magnetometer. Appl. Phys. Lett. 1996, 69, 2930–2931. [Google Scholar] [CrossRef]
- Gojdka, B.; Jahns, R.; Meurisch, K.; Greve, H.; Adelung, R.; Quandt, E.; Knöchel, R.; Faupel, F. Fully integrable magnetic field sensor based on delta-E effect. Appl. Phys. Lett. 2011, 99, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Kiser, J.; Finkel, P.; Gao, J.; Dolabdjian, C.; Li, J.; Viehland, D. Stress reconfigurable tunable magnetoelectric resonators as magnetic sensors. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef] [Green Version]
- Jahns, R.; Zabel, S.; Marauska, S.; Gojdka, B.; Wagner, B.; Knöchel, R.; Adelung, R.; Faupel, F. Microelectromechanical magnetic field sensor based on the delta-E effect. Appl. Phys. Lett. 2014, 105, 2012–2015. [Google Scholar] [CrossRef]
- Zabel, S.; Kirchhof, C.; Yarar, E.; Meyners, D.; Quandt, E.; Faupel, F. Phase modulated magnetoelectric delta-E effect sensor for sub-nano tesla magnetic fields. Appl. Phys. Lett. 2015, 107. [Google Scholar] [CrossRef]
- Zabel, S.; Reermann, J.; Fichtner, S.; Kirchhof, C.; Quandt, E.; Wagner, B.; Schmidt, G.; Faupel, F. Multimode delta-E effect magnetic field sensors with adapted electrodes. Appl. Phys. Lett. 2016, 108, 222401. [Google Scholar] [CrossRef]
- Bian, L.; Wen, Y.; Li, P.; Wu, Y.; Zhang, X.; Li, M. Magnetostrictive stress induced frequency shift in resonator for magnetic field sensor. Sens. Actuators A Phys. 2016, 247, 453–458. [Google Scholar] [CrossRef] [Green Version]
- Bennett, S.P.; Baldwin, J.W.; Staruch, M.; Matis, B.R.; Lacomb, J.; Van ’T Erve, O.M.J.; Bussmann, K.; Metzler, M.; Gottron, N.; Zappone, W.; et al. Magnetic field response of doubly clamped magnetoelectric microelectromechanical AlN-FeCo resonators. Appl. Phys. Lett. 2017, 111. [Google Scholar] [CrossRef]
- Staruch, M.; Yang, M.-T.; Li, J.F.; Dolabdjian, C.; Viehland, D.; Finkel, P. Frequency reconfigurable phase modulated magnetoelectric sensors using ΔE effect. Appl. Phys. Lett. 2017, 111, 2–6. [Google Scholar] [CrossRef] [Green Version]
- Bian, L.; Wen, Y.; Wu, Y.; Li, P.; Wu, Z.; Jia, Y.; Zhu, Z. A Resonant Magnetic Field Sensor with High Quality Factor Based on Quartz Crystal Resonator and Magnetostrictive Stress Coupling. IEEE Trans. Electron Devices 2018, 65, 2585–2591. [Google Scholar] [CrossRef]
- Lukat, N.; Friedrich, R.M.; Spetzler, B.; Kirchhof, C.; Arndt, C.; Thormählen, L.; Faupel, F.; Selhuber-Unkel, C. Mapping of magnetic nanoparticles and cells using thin film magnetoelectric sensors based on the delta-E effect. Sens. Actuators A Phys. 2020, 309, 1–8. [Google Scholar] [CrossRef]
- Spetzler, B.; Bald, C.; Durdaut, P.; Reermann, J.; Kirchhof, C.; Teplyuk, A.; Meyners, D. Exchange biased delta—E effect enables the detection of low frequency pT magnetic fields with simultaneous localization. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef]
- Becker, R.; Döring, W. Ferromagnetismus; Springer: Berlin/Heidelberg, Germany, 1939; ISBN 9783642471124. [Google Scholar]
- Atalay, S.; Squire, P.T. Magnetomechanical damping in FeSiB amorphous wires. J. Appl. Phys. 1993, 73, 871–875. [Google Scholar] [CrossRef]
- Squire, P. Magnetostrictive materials for sensors and actuators. Ferroelectrics 1999, 228, 305–319. [Google Scholar] [CrossRef]
- Charles, F.K. Development of the Shear Wave; Magnetometer; University of Bath: Bath, UK, 1992. [Google Scholar]
- Kittmann, A.; Durdaut, P.; Zabel, S.; Reermann, J.; Schmalz, J.; Spetzler, B.; Meyners, D.; Sun, N.X.; McCord, J.; Gerken, M.; et al. Wide Band Low Noise Love Wave Magnetic Field Sensor System. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Schmalz, J.; Spetzler, B.; Faupel, F.; Gerken, M. Love Wave Magnetic Field Sensor Modeling—From 1D to 3D Model. In Proceedings of the 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 9–13 September 2019; pp. 765–769. [Google Scholar]
- Schell, V.; Müller, C.; Durdaut, P.; Kittmann, A.; Thormählen, L.; Lofink, F.; Meyners, D.; Höft, M.; McCord, J.; Quandt, E. Magnetic anisotropy controlled FeCoSiB thin films for surface acoustic wave magnetic field sensors. Appl. Phys. Lett. 2020, 116. [Google Scholar] [CrossRef]
- Schmalz, J.; Kittmann, A.; Durdaut, P.; Spetzler, B.; Faupel, F.; Höft, M.; Quandt, E.; Gerken, M. Multi-mode love-wave SAW magnetic-field sensors. Sensors 2020, 20, 3421. [Google Scholar] [CrossRef]
- Sárközi, Z.; Mackay, K.; Peuzin, J.C. Elastic properties of magnetostrictive thin films using bending and torsion resonances of a bimorph. J. Appl. Phys. 2000, 88, 5827–5832. [Google Scholar] [CrossRef]
- Staruch, M.; Matis, B.R.; Baldwin, J.W.; Bennett, S.P.; van ’t Erve, O.; Lofland, S.; Bussmann, K.; Finkel, P. Large non-saturating shift of the torsional resonance in a doubly clamped magnetoelastic resonator. Appl. Phys. Lett. 2020, 116, 232407. [Google Scholar] [CrossRef]
- Yarar, E.; Hrkac, V.; Zamponi, C.; Piorra, A.; Kienle, L.; Quandt, E. Low temperature aluminum nitride thin films for sensory applications. AIP Adv. 2016, 6, 075115. [Google Scholar] [CrossRef]
- Durdaut, P.; Höft, M.; Friedt, J.-M.; Rubiola, E. Equivalence of Open-Loop and Closed-Loop Operation of SAW Resonators and Delay Lines. Sensors 2019, 19, 185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spetzler, B.; Kirchhof, C.; Reermann, J.; Durdaut, P.; Höft, M.; Schmidt, G.; Quandt, E.; Faupel, F. Influence of the quality factor on the signal to noise ratio of magnetoelectric sensors based on the delta-E effect. Appl. Phys. Lett. 2019, 114, 183504. [Google Scholar] [CrossRef]
- Durdaut, P.; Rubiola, E.; Friedt, J.; Muller, C.; Spetzler, B.; Kirchhof, C.; Meyners, D.; Quandt, E.; Faupel, F.; McCord, J.; et al. Fundamental Noise Limits and Sensitivity of Piezoelectrically Driven Magnetoelastic Cantilevers. J. Microelectromech. Syst. 2020, 1–15. [Google Scholar] [CrossRef]
- Spetzler, B.; Kirchhof, C.; Quandt, E.; McCord, J.; Faupel, F. Magnetic Sensitivity of Bending-Mode Delta-E-Effect Sensors. Phys. Rev. Appl. 2019, 12, 1. [Google Scholar] [CrossRef]
- Kittel, C. On the theory of ferromagnetic resonance absorption. Phys. Rev. 1948, 73, 155–161. [Google Scholar] [CrossRef]
- Spetzler, B.; Golubeva, E.V.; Müller, C.; McCord, J.; Faupel, F. Frequency Dependency of the Delta-E Effect and the Sensitivity of Delta-E Effect Magnetic Field Sensors. Sensors 2019, 19, 4769. [Google Scholar] [CrossRef] [Green Version]
- Gebert, A.; McCord, J.; Schmutz, C.; Quandt, E. Permeability and Magnetic Properties of Ferromagnetic NiFe/FeCoBSi Bilayers for High-Frequency Applications. IEEE Trans. Magn. 2007, 43, 2624–2626. [Google Scholar]
- Avdiaj, S.; Setina, J.; Syla, N. Modeling of the piezoelectric effect using the finite-element method (FEM). Mater. Technol. 2009, 43, 283–291. [Google Scholar]
- Yang, J. An Introduction to the theory of piezoelectricity. In Advances in Mechanics and Mathematics, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2018; Volume 9, ISBN 9783030031367. [Google Scholar]
- IEEE Standards Board. IEEE Standard on Magnetostrictive Materials: Piezomagnetic Nomenclature. IEEE Trans. Sonics Ultrason. 1973, 20, 67–77. [Google Scholar] [CrossRef]
- COMSOL AB. Structural Mechanics Module User’s Guide, COMSOL Multiphysics (TM) v. 5.4; COMSOL AB: Stockholm, Sweden, 2018. [Google Scholar]
- Mudivarthi, C.; Datta, S.; Atulasimha, J.; Evans, P.G.; Dapino, M.J.; Flatau, A.B. Anisotropy of constrained magnetostrictive materials. J. Magn. Magn. Mater. 2010, 322, 3028–3034. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Muto, V.; Squire, P.T. Induced anisotropy and magnetoelastic properties in Fe-rich metallic glasses. J. Non. Cryst. Solids 2001, 287, 417–420. [Google Scholar] [CrossRef]
- McCord, J. Progress in magnetic domain observation by advanced magneto-optical microscopy. J. Phys. D. Appl. Phys. 2015, 48, 333001. [Google Scholar] [CrossRef]
- Aharoni, A. Demagnetizing factors for rectangular ferromagnetic prisms. J. Appl. Phys. 1998, 83, 3432–3434. [Google Scholar] [CrossRef]
- Varadan, V.K.; Vinoy, K.J.; Gopalakrishnan, S. Smart Material Systems and MEMS: Design and Development Methodologies; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 0470093617. [Google Scholar]
- Krey, M.; Hähnlein, B.; Tonisch, K.; Krischok, S.; Töpfer, H. Automated parameter extraction of ScALN MEMS devices using an extended euler–bernoulli beam theory. Sensors 2020, 20, 1001. [Google Scholar] [CrossRef] [Green Version]
- Akiyama, M.; Umeda, K.; Honda, A.; Nagase, T. Influence of scandium concentration on power generation figure of merit of scandium aluminum nitride thin films. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef]
- Fichtner, S.; Wolff, N.; Krishnamurthy, G.; Petraru, A.; Bohse, S.; Lofink, F.; Chemnitz, S.; Kohlstedt, H.; Kienle, L.; Wagner, B. Identifying and overcoming the interface originating c-axis instability in highly Sc enhanced AlN for piezoelectric micro-electromechanical systems. J. Appl. Phys. 2017, 122. [Google Scholar] [CrossRef]
- Su, J.; Niekiel, F.; Fichtner, S.; Thormaehlen, L.; Kirchhof, C.; Meyners, D.; Quandt, E.; Wagner, B.; Lofink, F. AlScN-based MEMS magnetoelectric sensor. Appl. Phys. Lett. 2020, 117, 132903. [Google Scholar] [CrossRef]
- Sharpe, W.N.; Turner, K.T.; Edwards, R.L. Tensile testing of polysilicon. Exp. Mech. 1999, 39, 162–170. [Google Scholar] [CrossRef]
- Sharpe, W.N.; Yuan, B.; Vaidyanathan, R.; Edwards, R.L. Measurements of Young’s modulus, Poisson’s ratio, and tensile strength of polysilicon. Proc. IEEE Micro Electro Mech. Syst. 1997, 424–429. [Google Scholar] [CrossRef]
- Marc, J. Madou Fundamentals of Microfabrication: The Science of Miniaturization, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2002; ISBN 0849308267. [Google Scholar]
- Caro, M.A.; Zhang, S.; Riekkinen, T.; Ylilammi, M.; Moram, M.A.; Lopez-Acevedo, O.; Molarius, J.; Laurila, T. Piezoelectric coefficients and spontaneous polarization of ScAlN. J. Phys. Condens. Matter 2015, 27, 245901. [Google Scholar] [CrossRef] [PubMed]




| Resonance Mode | TM1 | TM2 | TM3 | BM1 | BM2 | BM3 |
|---|---|---|---|---|---|---|
| 0.010 | 0.017 | 0.029 | 0.060 | 0.056 | 0.052 | |
| 0.034 | 0.026 | 0.016 | 0 | 0 | 0 | |
| 0 | 0 | 0 | −0.003 | −0.006 | −0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spetzler, B.; Golubeva, E.V.; Friedrich, R.-M.; Zabel, S.; Kirchhof, C.; Meyners, D.; McCord, J.; Faupel, F. Magnetoelastic Coupling and Delta-E Effect in Magnetoelectric Torsion Mode Resonators. Sensors 2021, 21, 2022. https://doi.org/10.3390/s21062022
Spetzler B, Golubeva EV, Friedrich R-M, Zabel S, Kirchhof C, Meyners D, McCord J, Faupel F. Magnetoelastic Coupling and Delta-E Effect in Magnetoelectric Torsion Mode Resonators. Sensors. 2021; 21(6):2022. https://doi.org/10.3390/s21062022
Chicago/Turabian StyleSpetzler, Benjamin, Elizaveta V. Golubeva, Ron-Marco Friedrich, Sebastian Zabel, Christine Kirchhof, Dirk Meyners, Jeffrey McCord, and Franz Faupel. 2021. "Magnetoelastic Coupling and Delta-E Effect in Magnetoelectric Torsion Mode Resonators" Sensors 21, no. 6: 2022. https://doi.org/10.3390/s21062022






