1. Introduction
The Brillouin-enhanced four-wave mixing induced by counter-propagating pump lights and one probe light produces backward Stokes light at every location in an optical fiber under test [
1], which is assumed to be the reflection of the probe light by the acoustic wave or Brillouin dynamic grating generated in the fiber by the two pump lights. Optical time-domain reflectometry (OTDR) has been used to detect the power of the Stokes light as a function of distance while changing the frequency difference between the pump lights to obtain the Brillouin spectrum distribution in the optical fiber [
2,
3,
4,
5,
6]. A micrometer-scale spatial resolution is indispensable for diagnosing planar lightwave circuits (PLCs) [
7] with the same four-wave mixing technique. Since the spatial resolution of the OTDR is determined by the temporal width of the employed optical pulses, a picosecond optical pulse should be launched into the optical fiber and detect return pulses without deformation by using a high-speed optical detector. Such an attempt to increase the spatial resolution often resulted in increased electrical noise due to the ultra-wide detection bandwidth over 10 GHz, and this degraded the signal-to-noise ratio (S/N). To our knowledge, therefore, there have been no reports on Brillouin dynamic grating measurement with a micrometer-scale spatial resolution using the OTDR method.
To overcome the S/N degradation, we have proposed Brillouin grating-based coherent frequency-modulated continuous-wave (FMCW) reflectometry [
8], which is the frequency-domain counterpart of optical low coherence reflectometry (OLCR) [
9] and it detects the power of the Stokes light by utilizing its interference with local oscillator (LO) light at a detection bandwidth of less than 1 MHz. We have succeeded in incorporating a fiber loop mechanism in conventional coherent FMCW reflectometry to generate the Stokes light [
10,
11,
12]. Since the distance to the fiber segment where the Stokes light is generated is derived from the beat frequency, we do not have to use a mechanical stage such as that used in OLCR and thus we can extend the available distance range much further than can be achieved by the translation of the stage. Hereafter in this paper, the distribution of the Stokes light power along a fiber is referred to simply as a reflectogram from the fiber. Once we acquire reflectograms at various frequency differences, the Brillouin spectrum distribution along the optical fiber is obtained by changing the horizontal grid from equal distances to equal frequency intervals in the two-dimensional power data, which provides us with the strain distribution of the fiber.
Although we succeeded in demonstrating reflection measurement from a Brillouin dynamic grating with coherent FMCW reflectometry, we found signal-dependent multiplicative noise [
13] to be the dominant noise, which meant that we could not improve the S/N merely by increasing the powers of the tunable laser output and pump lights and/or by narrowing the detection bandwidth. Hereafter in this paper, for convenience such multiplicative noise is referred to as speckle-like noise. Since the reflectograms that we derived from different measurements or made at different times had unavoidable speckle-like noise, we had no choice but to repetitively sweep the tunable laser source and add them to obtain a smoothed profile at every frequency difference. That is, we could obtain the desired Brillouin spectrum distribution and thus the strain distribution only after making a vast number of the repetitive sweeps over a long period of time. Therefore, to reduce the number of sweeps and the measurement time it was indispensable that we clarify the origin of the speckle-like noise and reduce it greatly.
This paper shows theoretically and experimentally that the speckle-like noise was generated by frequency fluctuations contained in the output light wave from the distributed feedback laser diode (DFB LD) used as the pump light source. Since the current from the employed current source injected into the LD had components that fluctuated with time, or technical noise, the resultant instantaneous frequency of the light output also fluctuated, and this generated the speckle-like noise in the reflectogram. First, we describe the experimental setup we employed for the coherent FMCW reflectometry system. Since silica-based PLC chips are usually between few millimeters and several tens of centimeters long, we adjusted the length of the optical fiber under test to be around 1 m. We constructed an unbalanced Mach-Zehnder interferometer (MZI) to obtain the power spectral density of the frequency fluctuations [
14]. We employed two commercially available current sources from different manufacturers to drive the same LD, which had different power spectral density distributions. We used the density data to calculate the theoretical S/N and compared it with the experimental result.
Next, we theoretically derive the S/N dependence on the power spectral density of the frequency fluctuations on the condition that the absolute value of the complex amplitude of the acoustic wave or Brillouin dynamic grating was constant along the fiber. We calculated the second and fourth-order terms of the variance of the fluctuating Stokes light signal, which depended on the moments of the instantaneous frequency deviation of the pump light wave, and we derived the latter term as the correction of the former. Then, we compare the theoretical results with the experimental data obtained from a 1.35 m long optical fiber to confirm that the speckle-like noise was generated by the frequency fluctuations of the pump light waves. We showed that the second-order term provided us with the correct values for the S/N ranging from 10 to 190 when the coherence effect of the pump light wave was negligible. Then we measured the S/N distributions for 10 and 40 m long optical fibers. As the fiber length approached the coherence length of the pump light, the S/N values calculated with both the second and fourth-order terms no longer agreed with the measured value. Finally, we introduced the coherence function of the pump light wave into the second and fourth-order terms of the variance to explain the coherent effect and compared the calculated results with the data.
3. Calculation
In this section we derive the mean level and standard deviation of the fluctuating power of the Stokes light signal to obtain the S/N of the reflection measurement. We assume that the frequency of the tunable laser output sweeps from the start frequency
ω1 sufficiently linearly with time to meet
ω(
t) =
βt with a constant
β. To simplify the calculation of the Fourier inverse transform of Equation (2) with respect to
ω(
t), we introduce a new variable
ῶ, which is defined by
ω1 +
ω(
t) −
ωp =
ῶ, so that
t is a function of
ῶ represented by
t =(
ῶ +
ωp −
ω1)/
β. By expanding the exponential function in the integrand of
I(
t) in power series up to the fourth order,
I(
t) is approximated as:
The Fourier inverse transform of
I(
t) with respect to
ῶ is then written as:
where
X(0) =
r(
τ) and:
and where
t1 = (
ῶ1 +
ωp −
ω1)/
β. Hereafter we abbreviate
r(
τ) as
r when there is no confusion.
X(0) =
r(
τ) is independent of the random process, whereas
X(k) (
k ≥ 1) is a random variable that contains the
kth power of Δ(
t) in the integrand. From Equation (4) the absolute square is given by:
which provides the mean value of
Z as:
when we decompose
Z into <
Z> +
δZ, the variance
σ2 of
Z is <(
δZ)
2 >, which is represented by:
The calculations for deriving Equations (7) and (8) are detailed in
Appendix A, where the summands in Equation (8) are defined by Equations (A5) to (A10). The superscript
k in
Y(k) denotes that
Y(k) contains the
kth power of Δ(
t) in the integral.
In accordance with the Wiener–Khinchin theorem [
20,
21], we introduce the power spectral density
G(
χ) of Δ(
t), which is defined by:
where
G(
χ) should be a real-valued and even function of the angular frequency
χ. By letting Δ(
t) = 2
πδν(
t) and
χ = 2π
f, Equation (9) is changed to <
δν(
t1)
δν(
t2) > = (1/2π)∫
−∞ +∞ G(2
πf)exp[−2π
if(
t1 −
t2)]
df, where
δν(
t) is the instantaneous frequency deviation of the pump light and
f is frequency, and thus we find the relational expression of
G(
χ) = 2
πH(
χ/2
π) between
G(
χ) and the power spectral density
H(
f) of
δν(
t). It is noted that each plot in
Figure 5 shows
H(
f) measured when we drove the LD with either current source A or current source B. The mean square value of
δν(
t), which we denote as
δνrms2, is represented by the infinite integral of
H(
f) with respect to
f. Actually, however, the detection bandwidth for the Stokes light signal was limited to
fu =
βτe/2
π so that
δνrms2 must be evaluated by taking the finite integral over (−
fu,
fu), which is changed to the integral over (0,
fu) as:
because
H(
f) is an even function of
f. Equation (10) means that
δνrms depends on the length of the fiber under test and is related to Δ
rms, which is the root mean square value of Δ(
t) via Δ
rms = 2
πδνrms.
To express <
Z> using
G(
χ), we must calculate the following double integral at
k = 2 and 4:
By assuming that Δ(
t) is a zero-mean Gaussian random variable, we obtain <Δ
4(
t)> = 3Δ
rms4 with Δ
rms2 = <Δ
2(
t)> according to the moment theorem [
21,
22,
23]. In the double integral in Equation (11), first we take the iterated integral with respect to
ῶ1 to obtain 2
πδ(
τ −
τ1), where
δ(
τ) is the delta function. Then we integrate the resultant integrand including the delta function with respect to
τ1 to obtain <
X(2) > = −
r(
τ)Δ
rms2(
τc −
τ)
2/2 and <
X(4)> =
r(
τ)Δ
rms4(
τc −
τ)
4/8. When we neglect the last two terms <|
X(1)|
2> + <|
X(2)|
2> in Equation (7), we have <
Z> ≈ |
r(
τ)|
2[1 − Δ
rms2(
τc −
τ)
2 + Δ
rms4(
τc −
τ)
4/4], which is approximated by the Gaussian function as:
It is noted that the actual third terms of the power series expansion of the Gaussian function should be Δrms4(τc − τ)4/2.
From Equation (8),
σ2 is expanded to <
Y(1)2> + 2 <
Y(1)(
Y1(2) +
Y2(2))> + 2 <
Y(1)Y(3)> + <(
Y1(2) +
Y2(2))
2> + higher-order terms, where the second term vanishes because the integrand of it contains the third-order moment of Δ(
t). Then the variance is approximated by adding the second-order term
σ(2) and fourth-order term
σ(4) as:
where:
σ(4) is considered to be a correction term when we estimate the variance from Equation (14).
We calculated
σ(2) and
σ(4) by assuming that Δ(
t) obeys a Gaussian random process as described in
Appendix B and
Appendix C, respectively. Because |
σ(4)| < <
σ(2) as long as we measure the 1.35 m long optical fiber as will be shown in
Section 4, here we describe the result of
σ(2) only:
In general, the variance depends on the distribution
r(
τ), which changes along the fiber in an actual field application, and this means that it would be rather difficult to calculate the integrals in Equation (16). Since our aim in this paper is to clarify the origin of the speckle-like noise that we observed in the reflection measurement, we assume that the fiber under test is uniform and tension-free throughout the fiber and thus
r(
τ) is a constant function of
τ, or
r(
τ) =
r0 in the range
τi ≤
τ≤
τe and
r(
τ) = 0 elsewhere. The integrands of the first and second terms in Equation (16) contain the functions of
r(
τ −
χ/
β) and
r(
τ −
χ/
β)
r(
τ +
χ/
β), which are finite only when the variable
χ satisfies the conditions of
τi ≤
τ−
χ/
β ≤
τe, and
τi ≤
τ ±
χ/
β ≤
τe, respectively. Then <
Z> and √
σ(2) are calculated to be proportional to |
r0|
2, which is dropped when taking the ratio of <
Z> to √
σ(2) to obtain S/N. For this reason, we redefined
σ(2) as the one which is obtained by letting |
r0| = 1 in the original expression. The explicit forms of
σ(2) for
τi <
τ < (
τi +
τe)/2 and (
τi +
τe)/2 <
τ <
τe are given by Equations (A42) and (A43), respectively, in
Appendix D. The S/N including the fourth-order term
σ(4) is calculated in
Appendix E.
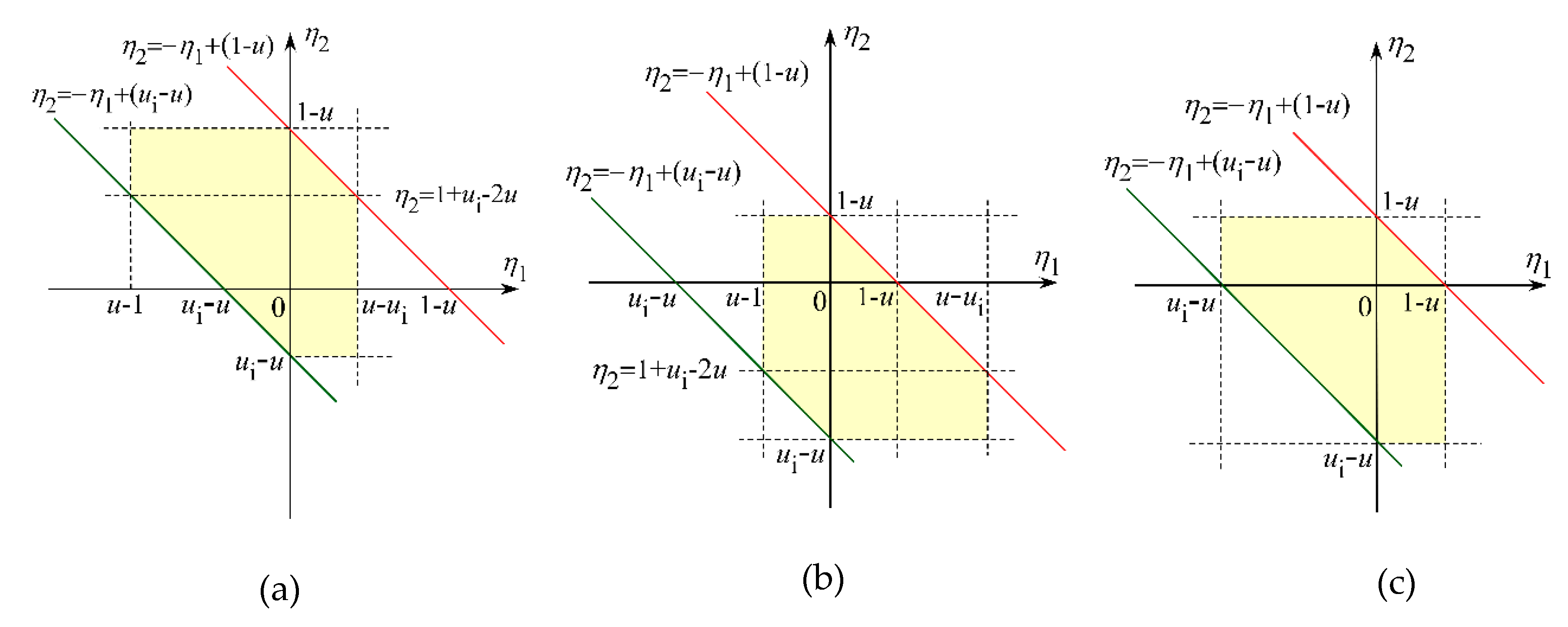
By introducing the variable
u and parameters
uc and
ui, which are defined as
u =
τ/
τe,
uc =
τc/
τe and
ui =
τi/
τe, the ranges of
τ for
τi <
τ < (
τi +
τe)/2 and (
τi +
τe)/2 <
τ <
τe are changed to those of
u for
ui <
u < (
ui + 1)/2, and (
ui + 1)/2 <
u < 1, respectively. Then the mean signal level described by Equation (12) is rewritten as:
By letting |
r(
τ)| = 1 and thus S/N for
ui <
u < (
ui + 1)/2 is described with the variance as:
where:
and where
η =
χ/(
βτe) =
f/
fu,
fu =
βτe/2
π and
G(
βτeη) = 2
πH(
f). To obtain the expression for (
ui + 1)/2 <
u < 1, in Equation (19) we should change the interval of the first integral to (1 −
u,
u −
ui) and that of the second integral to (0, 1 −
u), and change the sign of the variable
η in the integrand of the first term.
Since the power spectral density
H(
f) of the frequency fluctuations had a vast number of peaks due to the technical noise from the current sources, as shown in
Figure 5, to evaluate Δ
rms and
σ(2) we should calculate Equation (19) numerically using the measured power spectral density. In
Appendix F, we calculated
σ(2) analytically on the assumption that the noise was concentrated on a narrow region expressed by a Gaussian function
G(
χ) =
G0exp[− (
χ/
δχe)
2] using
δχe for the spectral half width at 1/
e maximum and that the fiber under test was sufficiently long for the fiber input end and the center of pumping to be
τi ≈ 0 and
τc ≈
τe/2, respectively, so that we can let
ui = 0 and
uc = 1/2. S/N at an arbitrary value of
α =
βτe/
δχe is obtained by substituting
σ(2) represented by Equation (A78) into Equation (18) for 0 <
u < 1/2, or by substituting that represented by Equation (A80) into Equation (18) for 1/2 <
u < 1.
Although the analytical solution to
σ(2) had a complicated form, we could approximate it as represented by Equation (A83) and it is valid that:
at
α ≥
αmin = 8 within a calculation error of around 20%, as will be shown numerically in
Section 4. In Equation (20),
fh and
γ, respectively, are the spectral half width at a half maximum of the Gaussian spectrum defined by
fh =
δχe(√ln2)/2
π, and the sweep rate of the tunable laser output defined by
γ =
β/2
π.
α is denoted as (√ln2)
γτe/
fh, which should be less than
αmin so that the approximation of Equation (20) holds. To meet the condition, the range allowed for
fh should be:
Because 0 <
u < 1, the numerator in Equation (20) takes
γ at
u =
uc = 1/2 and decreases to
γexp[− (Δ
rmsτe/2)
2] at both ends, which is written as
γexp[− (
πδνrmsτe)
2] using the relational expression Δ
rms = 2
πδνrms. Thus, we impose the second condition:
to regard the numerator as the constant
γ so that the mean signal level is kept constant throughout the fiber. Then, (
S/
N)
∞ is simplified to √(ln2/2)
γ/(2
πfhδνrms), which should be equal to or greater than the target value of (
S/
N)
tgt, and so we found that
δνrms and
fh must satisfy the third condition:
at given values of
γ and (
S/
N)
tgt.
4. Experimental Results
We fixed the up-conversion frequency of the pump light wave at 10.861 GHz, which was the center frequency of the Brillouin spectrum of the 1.35 m long optical fiber under test. The parameters
ui and
uc were originally defined by
ui =
τi/
τe and
uc =
τc/
τe and were rewritten as
ui =
zi/
ze and
uc =
zc/
ze because of the linearity between the propagation time and distance, or
τi = 2
nzi/
c,
τc = 2
nzc/
c and
τe = 2
nze/
c. We calculated the mean reflectogram from the 30 reflectograms shown in
Figure 2a and measured the distances to the points where the Stokes signal raised and fell to give
zi = 4.11 cm and
ze = 139.8 cm. With these values, we obtained
ui = 0.0294. To locate the center of pumping, we launched a picosecond optical pulse from another input port of fiber coupler CP3 into the optical fiber loop and measured the propagation times during which the counter-propagating optical pulses reached the two angled-polished end faces of the optical fiber under test. Since the center of pumping was defined by the position where the optical path lengths of the counter-propagating pump lights were equal in the fiber loop, the distance
zc to the center of pumping could be determined by the difference between the propagation times of the pulses. Since the distance increased by connecting a longer optical fiber delay line between polarizer #2 and optical circulator CL2, we precisely increased the length of the fiber delay line to shift the center of pumping to
uc = −0.042, 0.45 and 0.93 in sequence while measuring the time differences between the counter-propagating optical pulses.
We drove the DFB LD with current source A. At each
uc value, we swept the tunable laser source at a rate of 0.5 nm/s 30 times and derived the magnitude of the Stokes light signal as a function of
z. We calculated the mean value and standard deviation at every distance from the 30 reflectograms and plotted the distribution of the S/N in
Figure 6 after changing the grids of the horizontal axis from
z to
u, which was defined as
u =
z/
ze.
Figure 6a–c show the S/N distributions obtained when we set
uc at −0.042, 0.45 and 0.93, respectively. Here it is noted that the Stokes light signals at the two spliced points and at one mated point of the APC connectors decreased so rapidly that the resultant S/N values were changed. The best S/N we achieved was only 36 at
u = 0.16 and
uc = 0.45, where the fluctuations of the Stokes light signal were within 7% with respect to its mean level as shown in
Figure 2a. The most values of S/N that we obtained by setting
uc at −0.042 and 0.93 ranged from 10 to 20.
Assuming that statistically independent random noise was superimposed on the Stokes light signal, we could increase the S/N by √
N by calculating the mean value of
N individual signals [
24]. Therefore, we should acquire at least 30 beat signal waveforms by sweeping the tunable laser 30 times and calculate the mean reflectogram of the individual reflectograms to achieve an S/N of the order of 200 at every up-conversion frequency. We measured the S/N as a function of
u when the DFB LD was driven with current source B.
The results are shown in
Figure 7a–c when we set
uc at −0.042, 0.45 and 0.93, respectively. By comparing each pair in
Figure 6 and
Figure 7, e.g.,
Figure 6a and
Figure 7a, it was clear that we could greatly increase the S/N merely by changing the current source from A to B. For example, the best S/N was increased to 190 at
u = 0.18 and
uc = 0.45. This meant that a single sweep was sufficient to obtain a smooth reflectogram, which could be obtained only after sweeping the laser 30 times when we used current source A.
For comparison with the measured values, we calculated S/N as a function of
u numerically using Equations (18) and (19). The theoretical S/N was given by the ratio of the Gaussian function to the square root of the variance
σ(2), where the Gaussian function could be regarded as unity when we tested the 1.35 m long optical fiber. This was concluded by calculating the value of
δνrms as follows.
δνrms was given by integrating
H(
f) over the interval (0,
fu) with respect to
f as described in Equation (10). Here we had already measured the power spectral density
H(
f) as shown in
Figure 5a, where the sampling interval was Δ
f = 0.0853 Hz and each sampling frequency was represented by
fk =
kΔ
f (
k = 0,1,2,…). The upper limit of integration was
fu, which was the detection bandwidth and given by
fu =
τeβ/2π. We obtained
τe = 13.5 ns by substituting
ze = 139.8 cm and
n = 1.45 into the relational expression of
τe = 2
nze/
c. Since we set the sweep speed of the tunable laser source at 0.5 nm/s at 1.55 μm, we obtained
β/2π = 62.5 GHz/s. With these values we found that the upper limit of integration was
fu = 844 Hz.
We performed the numerical integration to obtain the value of δνrms by approximating the integral of H(f) with respect to f as the sum of the areas HkΔf of the equally-spaced rectangles under the curve H(f) for all values of k satisfying fL < fk < fu, where the value of H(f) taken at fk is denoted as Hk. In addition, we introduced the lower limit of integration at fL = 1 Hz to avoid the effect of the environmental perturbations. Following the numerical calculation, we obtained δνrms = 2.17 MHz and therefore we had Δrms = 1.36 × 107 rad/s from the relational expression of Δrms = 2πδνrms. With the values of τe and Δrms, we had Δrmsτe = 0.184 and thus we found that [Δrmsτe(uc − u)]2 < 0.0368 for all values of u and uc. The result meant that we could consider the Gaussian function as unity when we tested the 1.35 m long optical fiber.
We calculated
σ(2) as a function of
u ranging from 0 to 1 in steps of 0.01, where
βτe3 = 9.66 × 10
−13 s,
ui = 0.0294 and the value of
G(
χ) at
χ was obtained from that of 2
πH(
f) at
f =
χ/2π. That is, at each value of
u for
ui <
u < (
ui + 1)/2 and
ui = 0.0294, we approximated the first integral in Equation (19) as the sum of 2π(
uc –
u −
ηk)
2HkΔ
η for all values of
k satisfying max{
fL,(
u −
ui)
fu} <
fk < (1 −
u)
fu, where
ηk =
fk/
fu, Δ
η = Δ
f/
fu and max{,} returns the greater of two values. Similarly, the second integral in Equation (19) was approximated as the sum of 2π
ηk2HkΔ
η for all values of
k satisfying
fL <
fk < (
u −
ui)
fu. With the two numerical integrations we calculated the value of
σ(2) and the resultant S/N according to Equation (18), where the numerator was approximated as unity. At each value of
u for (
ui + 1)/2 <
u < 1, we performed the same numerical calculation of the integrals in Equation (A45) in
Appendix D to obtain
σ(2) and thus S/N as a function of
u.
By repeating these series of numerical integrations at
uc = −0.042, 0.45 and 0.93, we obtained S/N as a function of
u as shown in
Figure 6a–c, respectively. Similarly, we calculated S/N as a function of
u when the DFB LD was driven with current source B. The results are shown in
Figure 7a–c when we set
uc at
uc = −0.042, 0.45 and 0.93, respectively. The calculation showed that when we set
uc at 0.45 or near the center of the optical fiber under test, the distribution of S/N had peaks on both sides of the center, whereas one or both peaks were suppressed at
uc = −0.042 and 0.93, which was consistent with the measurement result obtained using either current source A or current source B. We should set
uc close to 0.5 to avoid the suppression of the peaks and achieve a higher S/N throughout the fiber. It is noted that the value of
uc automatically approaches 0.5 as the length of the optical fiber under test is increased to 10 m or more. This is because the distance to the center of the optical fiber is much longer than the distance to the original center of pumping which is located if we connect the input end directly to the output end of the fiber.
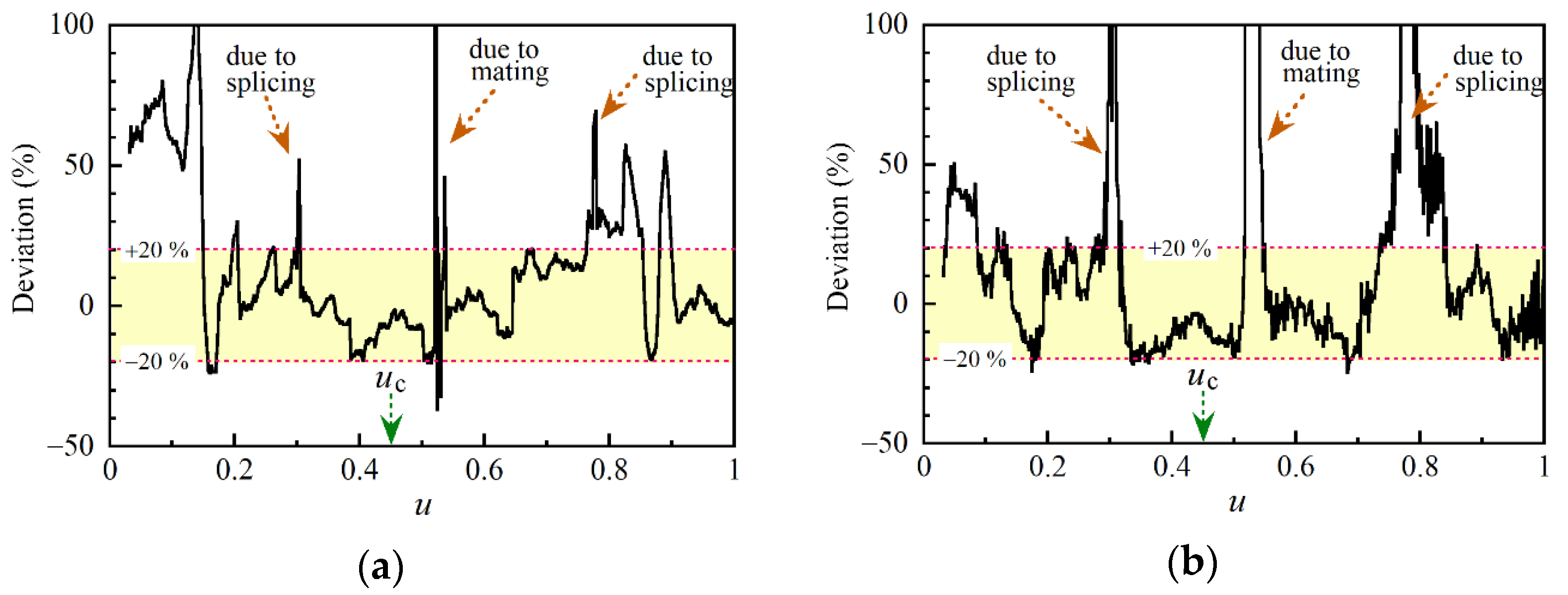
We plotted the difference between the calculated and measured S/N values in percent as a function of
u in
Figure 8, where (a) and (b) show the distributions calculated from the data shown in
Figure 6b and
Figure 7b, respectively. The optical fiber under test consisted of four pieces of the single-mode fiber which were fusion spliced at
u = 0.31 and 0.78 and mated with APC connectors at 0.53, where the Stokes light signal decreased and thus the deviation changed rapidly. Excluding these parts, however, the differences were limited to within 20% in most parts of the fiber as highlighted in yellow in each figure. We derived the theoretical expression for S/N by imposing a condition whereby the absolute value of the complex amplitude of the acoustic wave was constant along the fiber, whereas its temporal phase was modulated by the frequency fluctuations of the pump light. In spite of the fact that we could not experimentally generate the Brillouin dynamic grating uniformly throughout the fiber, the calculated values were in good agreement with those measured in the 10 to 190 range as shown in
Figure 6 and
Figure 7. Therefore, we confirmed that the theoretical expression we derived could represent the actual S/N of the reflection measurement and that the main source which substantially determined the S/N in our experiment was technical noise from the current source used to drive the DFB LD. Although S/N fell rapidly to 70 at both ends of the fiber as shown in
Figure 7b even when we used current source B, we will be able to increase it to the same level as the peak by using a different current source with much reduced technical noise.
Since the calculated values did not exactly agree with the measured ones obtained with either current source A or current source B, we calculated the correction term
σ(4) when using current source A at
uc = 0.45 by numerically calculating the constituent terms
A through
H, which are defined by Equations (A59) to (A66), while using the power spectral density shown in
Figure 5a. The calculated values of
σ(2) and
σ(4) as a function of
u are plotted in
Figure 9 together with the change in each term.
σ(2) had a minimum value of 10
−3 on both sides of the center of pumping, whereas
σ(4) had a maximum value of 3 × 10
−5 at 0.1 <
u < 0.9. Thus, we found that the correction term was at best 3% of
σ(2), and we could not bring the calculated values very much closer to the measured ones. The theoretical expressions for
σ(2) and
σ(4) were based on the expansion of the exponential function in the integrand of
I(
t) in a power series of Δ(
t). The result showed that
σ(4) was negligibly smaller than
σ(2), and the first-order expansion was sufficient to calculate S/N as far as the reflection measurement of the 1.35 m long optical fiber was concerned.
Since the phases of the counter-propagating pump light waves always coincide with each other at the center of pumping, the temporal phase of the acoustic wave generated at the center is independent of the frequency fluctuations of the pump light waves. Considering that the phase of the Stokes light that was generated there was also unaffected by the fluctuations, it appears that the variance due to the frequency fluctuations become negligibly small and the resultant S/N should be at its maximum exactly at the center. Actually, however, when the center was located at uc = 0.45, the S/N value was not at its maximum at the center and had noticeable peaks on both sides. The reflectometry method we employed decomposed the beat signal waveform into components with different frequencies and distributed the powers of the decomposed components along the fiber. When the frequency distribution of the beat signal waveform overlapped that of Δ(t), as in our experiment, the Stokes lights generated on either side of the center had components with the same frequency as that produced at the center via up and down frequency conversions by the phase modulation, which were superimposed on and recognized as the Stokes light generated at the center. This meant that even the signal detected at the center had larger fluctuations than we expected.
Planar lightwave circuits (PLCs) such as an 8 × 8 optical matrix switch and an arrayed-waveguide grating [
7] have fiber pigtails several meters long, which are connected to their input and output ends with adhesive for practical applications. To investigate the possibility of using our reflectometer to diagnose them by means of strain distribution, we tested a 5 m long polarization-maintaining (PM) fiber. To excite the fast and slow axes of the PM fiber with the probe light and the counter-propagating pump lights, respectively, we spliced 250 µm buffered single-mode fibers with APC connectors to both ends of the PM fiber with a mechanical fusion splicer and mated the APC connectors to those of the fiber pigtails, which were attached to optical circulators CL1 and CL2. We inserted each 250 µm buffered single-mode fiber into an in-line polarization controller with a rotatable fiber squeezer mechanism to adjust the SOPs of the probe and pump lights propagating through the fiber.
After setting the up-conversion frequency at 10.881 GHz and changing to current source B, we measured 30 reflectograms from the 5 m long PM fiber and calculated the S/N distribution along the fiber as shown in
Figure 10. As a result of the measurement range being extended from 1 to 5 m, the S/N was degraded to the 20 to 45 range. Considering that except around the center of pumping at
zc = 3.8 m the measured and calculated values agreed, we concluded that we needed to use a current source with greatly reduced noise to increase the S/N. Although not shown in this paper, we observed a background component in the beat signal waveform that undulated periodically during the frequency sweep and which we did not observe when we tested the 1.35 m long single-mode fiber. We changed to another PM fiber with a different cutoff wavelength, but we still observed such a component. Therefore, we believe that some fraction of the launched probe and pump lights propagated without being attenuated through the fiber in the cladding modes such as the modes in the stress-applying parts or between it and the core. There was a probability that the periodic change in the S/N that we observed around the center was produced by the light component, which propagated in the cladding modes and entered the balanced mixer to produce the fluctuated components by interference between it and the LO light.
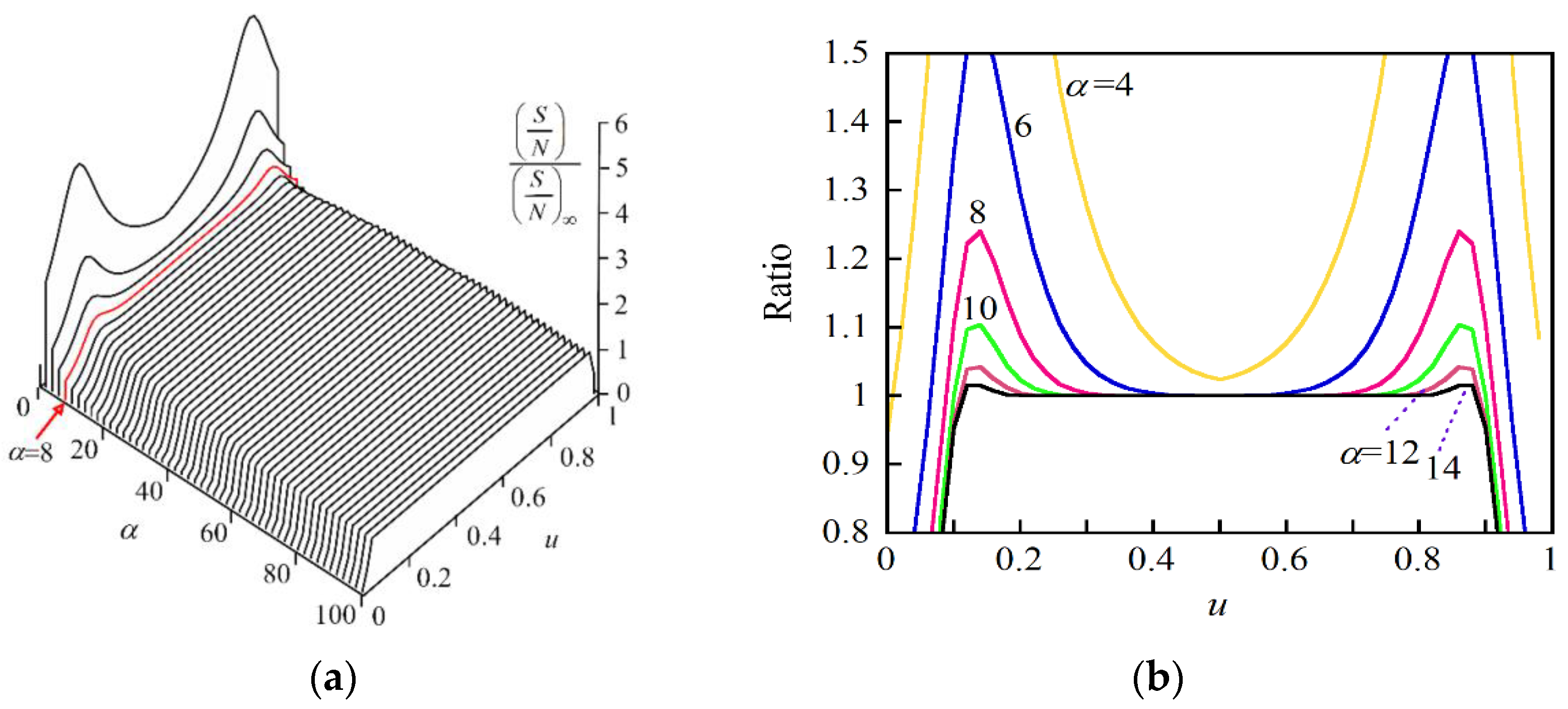
We investigated the specifications of the pump light wave required for achieving the S/N at 200 even when we tested a 5 m long PM fiber. When the power spectral density was a Gaussian function, we obtained the analytical solution to
σ(2), as detailed in
Appendix F. We calculated the ratio of S/N to (S/N)
∞ as functions of α and
u using Equations (A81) and (A82) in
Appendix F and plotted the result in
Figure 11a. When
α was close to 0, the ratio had the same two peaks as in
Figure 6b and
Figure 7b and then approached unity for almost all values of
u as
α increased. To observe the precise change in the ratio around
α = 10, we plotted the ratio as a function of
u by setting
α at 4 to 14 in steps of 2 in
Figure 11b. It was clear from the figure that at
α = 8 the maximum deviation of the ratio from unity was only 23% in the 0.1 <
u < 0.9 range and the deviation decreased rapidly as
α increased from 8. Since a difference of around 20% was unavoidable between the calculated and measured data, as observed in
Figure 8, we confirmed that we could regard the ratio as unity as long as
α ≥ 8, where we could use the simple expression given by Equation (20).
In the relational expressions of (21) and (22),
τe was the round-trip time from the origin to the output end of the fiber under test and was given by
τe =2
nL/
c, where we assumed that the fiber was long enough to allow
zi = 0. With the values
L = 5 m and
n = 1.45, we estimated
τe to be 48.4 ns. By substituting
τe = 48.4 ns and
γ = 62.5 GHz (or 0.5 nm/s) into the right-hand sides of expressions (21) and (22), we obtained upper limits for
fh and
δνrms of 0.315 kHz and 3.3 MHz, respectively. In
Figure 12 we plot red and green dotted lines, which are upper boundaries defined by
fh = 0.315 kHz and
δνrms = 3.3 MHz, respectively, in two-dimensional space with a (
fh,
δνrms) coordinate system. By substituting
γ = 62.5 GHz and (
S/
N)
tgt = 200 into the right-hand side of the relational expression (23), we found that the point (
fh,
δνrms) should be included in the domain located below the red solid line, which was the boundary curve defined by
δνrms = 0.0293/
fh and was plotted in a log-log scale, where the units of
fh and
δνrms are kHz and MHz, respectively. Therefore, when we sweep the laser at the rate of
γ = 62.5 GHz, the point (
fh,
δνrms) should be included in the allowable domain surrounded by the three lines highlighted in yellow in
Figure 12 to achieve (
S/
N)
tgt = 200.
For example, when the spectral half width is reduced to fh = 50 Hz by installing a low pass filter in the current source circuit, the rms frequency fluctuations should be equal to or lower than δνrms = 0.59 MHz. This is determined by drawing a vertical line at fh = 50 Hz and finding the coordinate of the point A, which is the intersection between the vertical line and the red solid line. When the spectral half width is much wider due to the potential difficulty involved in installing such a low pass filter, one way to achieve (S/N)tgt is to sweep the tunable laser faster in such a way that the point (fh, δνrms) is included in the extended domain determined by the new sweep rate. For example, by letting γ = 625 GHz or 5 nm/s, the domain highlighted in blue is added as the allowable one so that the range of the spectral half width becomes ten times wider.
5. Discussion
This section describes the effect of the coherence time of the pump light on the S/N of the reflection measurement. When the counter-propagating pump light waves collided at z along the 1.35 m long optical fiber, the difference between the propagation times of the two pump light waves was given by |τc − τ| where τc = 2nzc/c and τ = 2nz/c, whose upper limit was τe = 13.5 ns for all possible combinations of (τc, τ) satisfying 0 < τc < τe and 0 < τ < τe. According to the data supplied by the manufacturer of the LD, the nominal spectral linewidth was of the order of 1 MHz, and so the coherence time of the pump light waves was estimated to be a few microseconds. That is, the coherence time was much longer than any possible values of the time differences between the pump light waves, and they were considered to be coherent with each other anywhere along the 1.35 m long optical fiber. In the frequency domain, the individual spectral components in the pump light waves should receive the same phase modulation from the technical noise and generate the same acoustic wave along the entire length of the fiber.
To observe the change in the Stokes light signal level as the fiber length increased, we spliced 250 µm buffered single-mode fibers with APC connectors to both ends of a 10 m long PM fiber and installed it as the DUT in the reflectometer. After testing the 10 m long PM fiber, we prepared a 40 m long PM fiber as the DUT and tested it again. Here we increased the carrier frequency for detecting the beat signal waveform to 300 kHz by driving the phase modulators PM1 and PM3 at f0 = 500 kHz and f1 = 800 kHz, respectively. This was because the maximum frequency of the beat signal waveform was increased to 25 kHz. In accordance with the higher detection frequency, we increased the carrier frequency of the unbalanced MZI, which we used to measure the power spectral density, to the same frequency at 300 kHz. As the fiber length increased, unfortunately the number of data needed for the numerical integration also increased, and this resulted in a longer calculation time and a fatal memory overflow. To avoid such results, we reduced the record length of the beat signal waveform to one-tenth and increased the sampling interval of the power spectral density to 0.853 Hz.
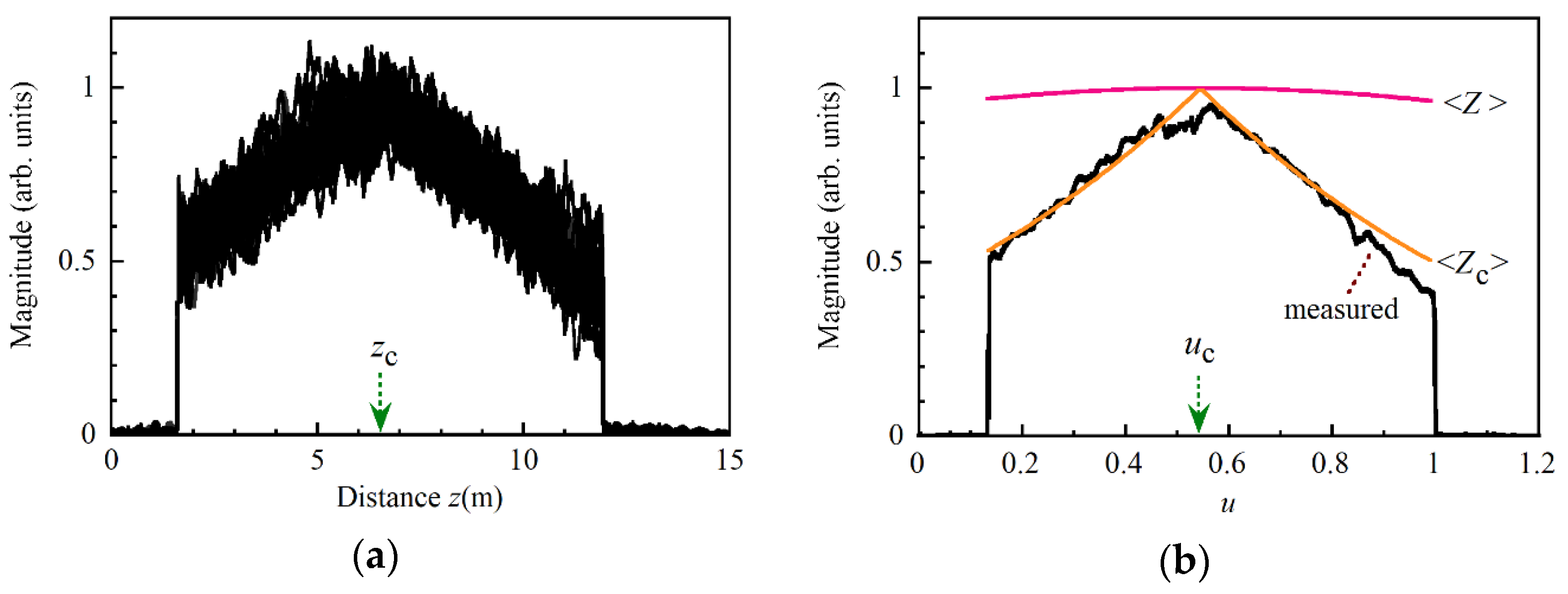
We obtained 30 reflectograms from the 10 m long PM fiber and plotted them all and their mean reflectogram in
Figure 13a,b, respectively. It was clear from the figures that all these reflectograms had peaks at the center of pumping and decayed as the position deviated from the center. In the first place, the mean Stokes light signal level <
Z> should decrease due to the technical noise according to the Gaussian function as given by Equation (17).
We numerically integrated
H(
f) with respect to
f using Equation (10) and obtained
δνrms = 0.60 MHz and thus Δ
rms = 3.74 × 10
6 rad/s. With the value of Δ
rms,
τe = 115 ns and
uc = 0.545, we calculated <
Z> as a function of
u as drawn by the red solid curve in
Figure 13b and found that the decay induced by the technical noise was too small to fit the measured signal change. We employed an external-cavity tunable laser source and a DFB LD source in our experiment and both light sources were capable of causing the signal decay. If the finite coherence time of the output light from the former laser was the dominant origin of the decay, each waveform in
Figure 13a,b should have a peak at
z = 0 and decay as the distance increases. This was because the optical path length difference between the LO light and the Stokes light generated at
z = 0 was zero and increased with distance. Actually, we observed the peak at the center of pumping, which was consistent with the fact that the optical path length difference between the counter-propagating pump light waves was zero at the center and increased as the position deviated from it. Therefore, it was clear that the decay we observed was caused by the finite coherence time of the pump light waves.
Since we measured the frequency fluctuations due to the technical noise by using an unbalanced MZI with a short delay of
τMZI = 8.912 ns, we considered that the individual spectral components of the pump light passed through the MZI coherently and produced the same signal change with time, and thus the resultant power spectral density did not contain the effect of the finite coherence time. In
Section 2, we denoted the amplitude of the electric field of the LD output as
A(
t) =
A0exp(−
iϕ(
t)), where
A0 was a constant and
ϕ(
t) represented the phase change due to the technical noise. To introduce the effect of the finite coherence time, we express the amplitude as
A(
t) =
A0Ã(
t)exp(−
iϕ(
t)) and let
Ã(
t) be the amplitude fluctuation caused by the finite coherence time while keeping <|
Ã(
t)|
2> = 1. Then the analytic signal represented by Equation (2) should be changed to
Ic(
t) as follows:
where
t = (
ῶ +
ωp −
ω1)/
β.
Considering that the fluctuation
Ã(
t) was statistically independent of the frequency fluctuations Δ(
t) due to the technical noise, a simple way to incorporate the coherence effect into the reflection measurement is to approximate the fluctuating product
Ã(
t −
τ1/2)
à *(
t −
τc +
τ1/2) in the integrand of Equation (24) by the ensemble average <
Ã(
t −
τ1/2)
à *(
t −
τc +
τ1/2)>, which is denoted as
V(
τc −
τ1) using the coherence function
V(
τ) defined by:
Gp(
ωp +
ῶ) was the optical power spectrum of the pump light, and we assumed that the spectrum was normalized in such a way that ∫
−∞ +∞Gp(
ωp +
ῶ)
dῶ = 1. Then the analytic signal
Ic(
t) was approximated by:
Equation (26) means that the mean signal level <
Zc>, the variance
σc(2) and the correction term
σc(4) including the coherence effect are obtained by replacing
r(
τ) with
r(
τ)
V(
τc −
τ) in Equations (12), (16), and (A31)–(A38) in
Appendix C, respectively.
Supposing that the pump light has a Lorentzian spectrum with a full width at half maximum of
δνL, we obtain a real function of
V(
τ) = exp(−
πδνL|
τ|). By introducing a new function
U(
u) which is defined by:
<
Zc> and
σc(2) for
u1 <
u < (
u1 + 1)/2 are denoted as:
To obtain the expression for (
ui + 1)/2 <
u <1, in Equation (29) we should change the interval of the first integral to (1 −
u,
u −
ui) and that of the second integral to (0, 1 −
u), and change the sign of the variable
η in the integrands. We estimated the
δνL of the employed LD to be 2.0 MHz by fitting the theoretical curve defined by Equation (28) with the measured mean reflectogram, as shown by an orange curve in
Figure 13b.
We calculated the S/N as a function of
u from 30 reflectograms which are shown in
Figure 13a and plotted the result in
Figure 14a. The distribution had rapidly varying components, but the overall profile had a peak at the center of the pumping and decayed as the distance from the center increased. We calculated
σc(2) and
σc(4) as a function of
u numerically by using Equation (29) and Equations (A67) to (A74) in
Appendix E, respectively. Then we plotted the two distributions of S/N, which we obtained by substituting
σc(2) and
σc(2) +
σc(4) into the denominator of Equation (18), as shown by the red and blue lines, respectively, in
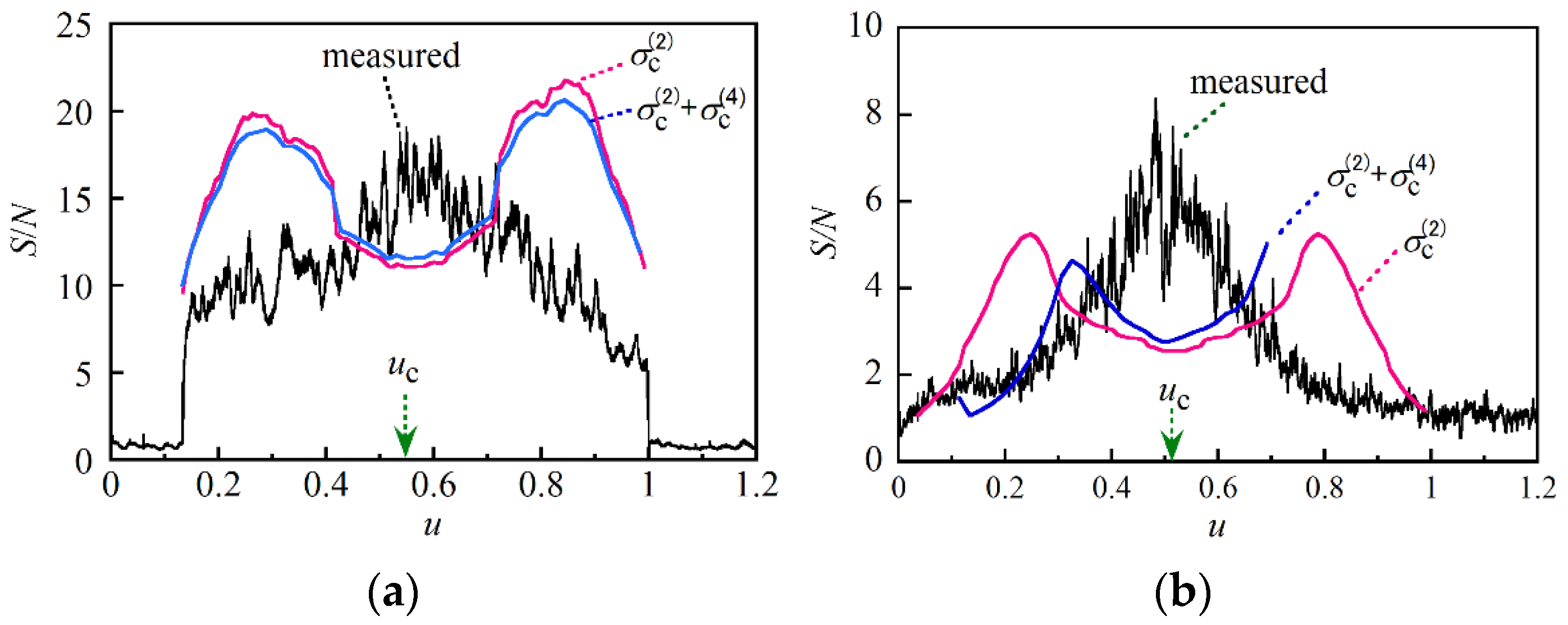
Figure 14a. Since the calculated values differed from the measured values by a factor of up to 2, it was clear that we could obtain the approximate S/N value by using the theoretical expression even when the length of the optical fiber approached the coherence length of the pump light and the resultant S/N was degraded. However, they still had peaks on both sides of the center of pumping and there was a noticeable discrepancy between the calculated and measured reflection profiles. Then we measured the reflectograms from the 40 m long PM fiber and plotted the S/N distribution together with those which we calculated using
σc(2) and
σc(2) +
σc(4) in
Figure 14b. The best S/N value was further degraded to 8, and the calculated distribution had still the same two peaks.
Since the correction term σc(4) did not lead to a fundamental solution for suppressing the side peaks, we concluded that the discrepancy was not caused by the approximation of the factor exp{− iΔ(t)(τc−τ)} in the integrand of <Ic(t)> as the power series expansion. In deriving the expressions for σc(2) and σc(2) + σc(4), we made one more approximation such that ϕ(t − τ/2) − ϕ(t − τc + τ/2) ≈ Δ(t)(τc − τ), where we theoretically showed that the approximation error was of the order of π2fuδνrmsτe2/2. When we tested the 40 m long PM fiber, we had fu = 25 kHz, δνrms = Δrms/2π = 0.9 MHz and τe = 402 ns, and with these values we estimated the approximation error to be around 0.018 rad, and this meant that the approximation was still valid. Therefore, the origin of the noticeable discrepancy that we observed resulted not from the error due to the two kinds of approximations that we employed but from the simple method we introduced as an effect of the finite coherence time.
Returning to the basics of statistical averaging, therefore, we should calculate the mean value and variance of the absolute square of the Fourier inverse transform with two different kinds of statistically independent random processes such as Gaussian noise due to technical noise and AM and phase noise inherent in the laser diode [
25,
26]. If our reflectometry technique is to be applied to mid and long-range distributed strain sensing, the employed optical fiber will range in length from hundreds of meters to several kilometers. As described in our experiment, S/N will be degraded both by frequency fluctuations due to technical noise and by the finite coherence time unless we use an excellent DFB LD as the pump light source. Once we succeed in deriving the theoretical formula for S/N including the finite coherence time, we will be able to obtain the detailed specifications for the pump light source needed to achieve a high S/N even when we test an optical fiber several kilometers in length.