A Novel Method of Fault Detection and Identification in a Tightly Coupled, INS/GNSS-Integrated System
Abstract
:1. Introduction
2. Background
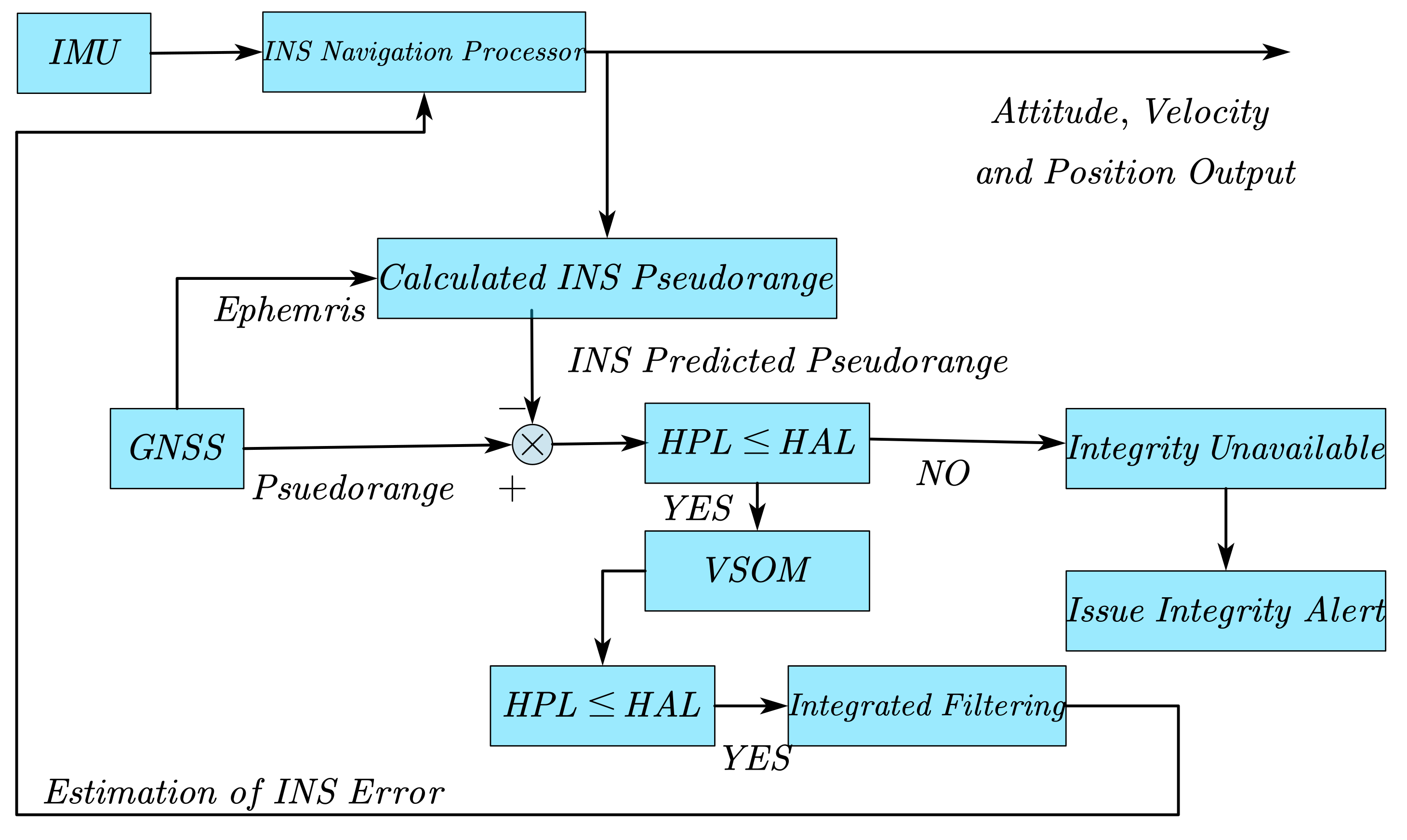
2.1. Mathematical Model of a Tightly Coupled, INS/GNSS-Integrated Navigation System
2.2. Variance Shift Outlier Model
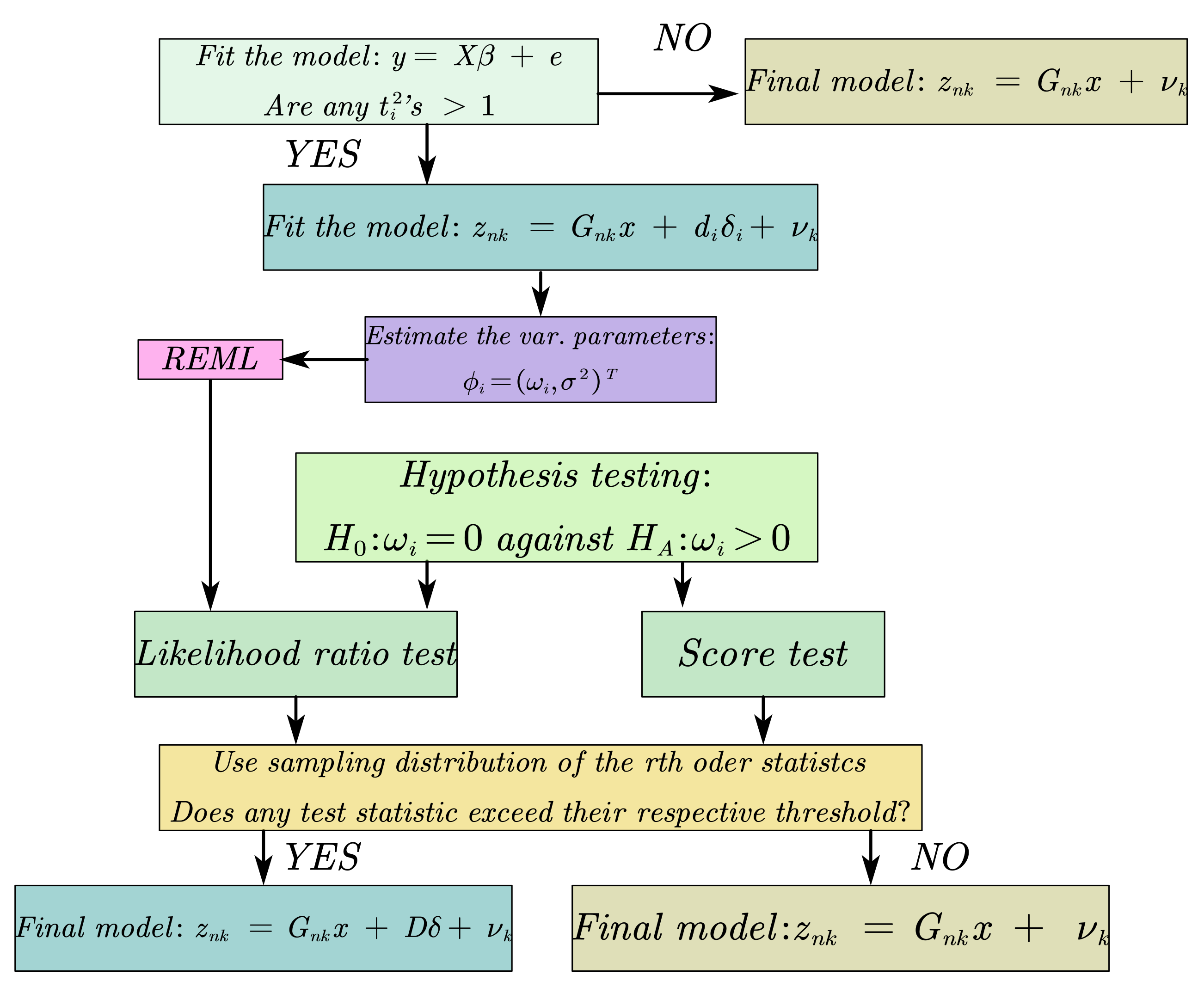
3. Methodology
3.1. Establishment of Test Statistics
3.1.1. Likelihood Ratio Test Statistics
3.1.2. Score Test Statistics
3.2. Significance and Multiple Testing
- S1:
- Estimate (23) under the null hypothesis, obtaining parameter estimates and .
- S2:
- Generate new measurementswhere is simulated as .
- S3:
- Fit the null hypothesis (23) and obtain bootstrap LR test statistic and score test statistics . Obtain the order statistics from each set.
- S4:
- Step 2 and step 3 are required to be repeated B times, for B is reasonably large. An empirical distribution(ED) of size B for each order statistic is generated.
- S5:
- Calculate the th percentile for each order statistic for the required , where is the significance level.
3.3. Down-Weighting
3.4. Horizontal Protection Level Computation
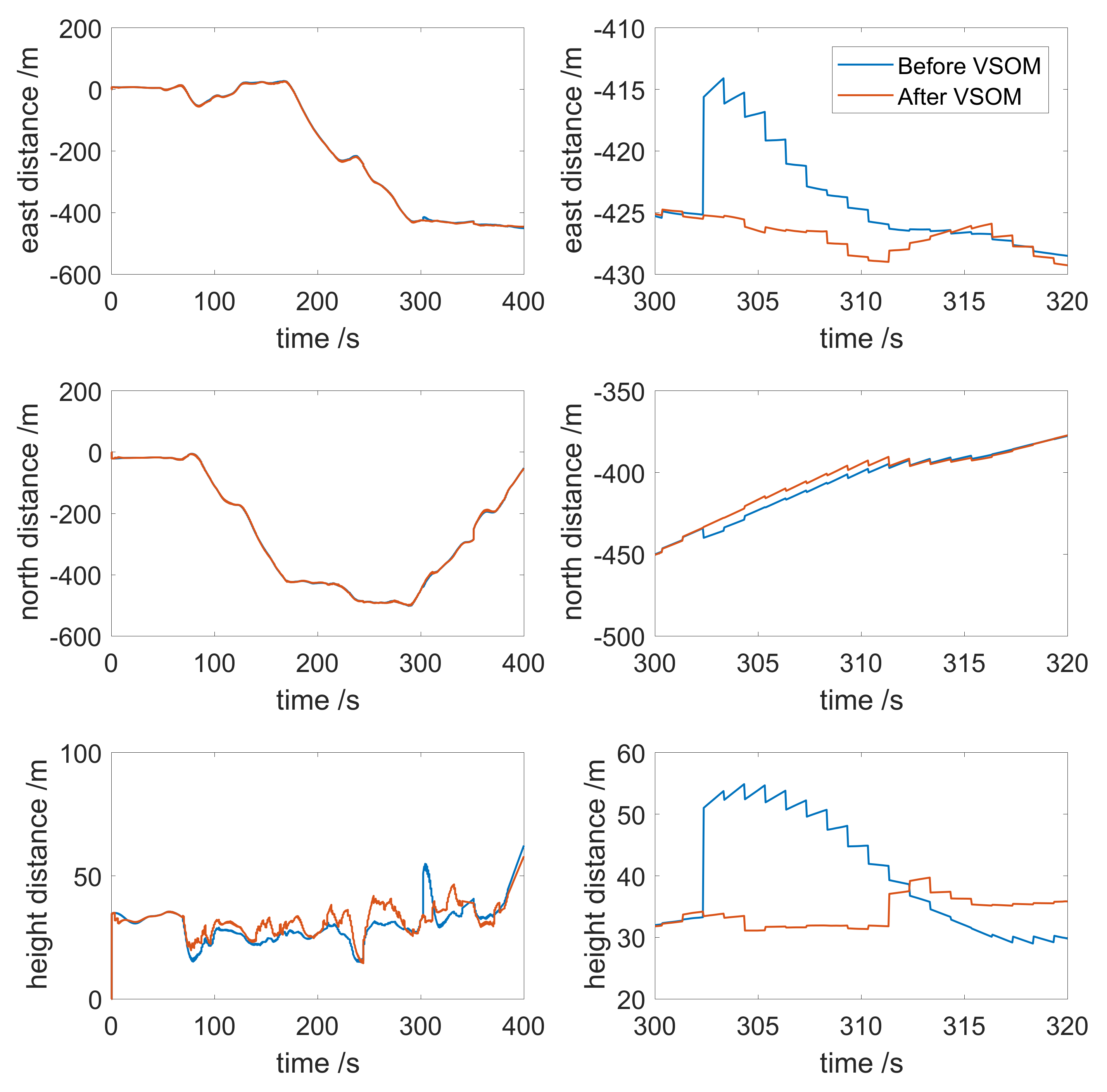
4. Field Test
4.1. Static Test
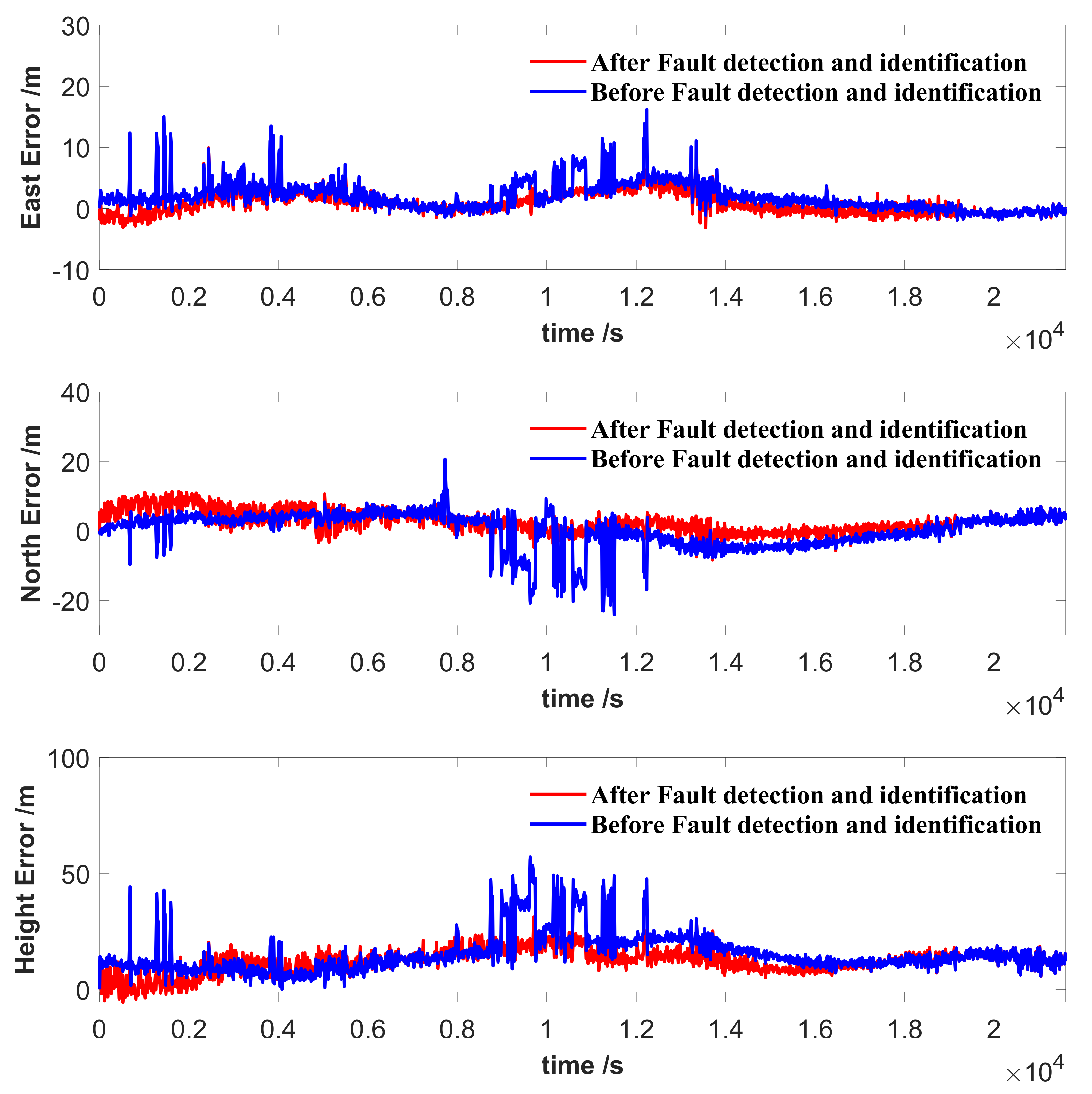
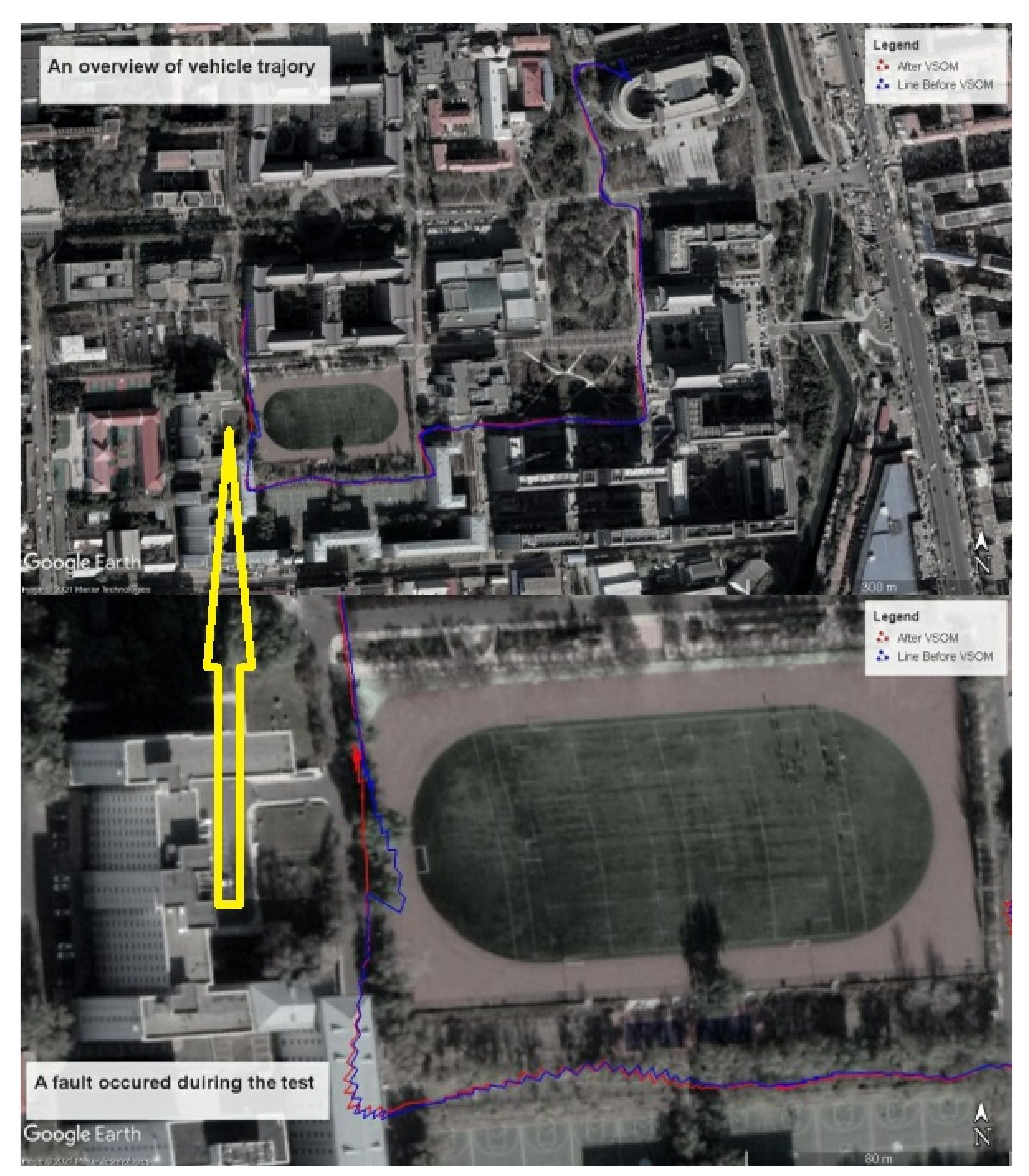
4.2. Dynamic Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Farrell, J. Aided Navigation: GPS with High Rate Sensors; McGraw-Hill: New York City, NY, USA, 2008. [Google Scholar]
- Stepanov, O.A. Optimal and Suboptimal Filtering in Integrated Navigation Systems. In Aerospace Navigation Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; Chapter 8; pp. 244–298. [Google Scholar] [CrossRef]
- Zhao, Y. Performance evaluation of Cubature Kalman filter in a GPS/IMU tightly-coupled navigation system. Signal Process. Off. Publ. Eur. Assoc. Signal Process. (EURASIP) 2016, 119, 67–79. [Google Scholar] [CrossRef]
- Hu, G.; Gao, S.; Zhong, Y. A derivative UKF for tightly coupled INS/GPS integrated navigation. ISA Trans. 2015, 56, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Shaheen, E.M. Mathematical Analysis for the GPS Carrier Tracking Loop Phase Jitter in Presence of Different Types of Interference Signals. Gyroscopy Navig. 2018, 9, 267–276. [Google Scholar] [CrossRef]
- Gautier, J.D.; Parkinson, B.W. Using the GPS/INS generalized evaluation tool (GIGET) for the comparison of loosely coupled, tightly coupled and ultra-tightly coupled integrated navigation systems. In Proceedings of the 59th Annual Meeting of The Institute of Navigation and CIGTF 22nd Guidance Test Symposium (2003), Albuquerque, NM, USA, 2003 June 23–25; pp. 65–76. [Google Scholar]
- Sukkarieh, S.; Nebot, E.M.; Durrant-Whyte, H.F. A high integrity IMU/GPS navigation loop for autonomous land vehicle applications. IEEE Trans. Robot. Autom. 1999, 15, 572–578. [Google Scholar] [CrossRef] [Green Version]
- Sturza, M.A. Navigation system integrity monitoring using redundant measurements. Navigation 1988, 35, 483–501. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Quality control in integrated navigation systems. IEEE Position Locat. Navig. Symp. 1990, 5, 35–41. [Google Scholar]
- Diesel, J.; Luu, S. GPS/IRS AIME: Calculation of thresholds and protection radius using Chi-square methods. In Proceedings of the 8th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1995), Salt Lake City, UT, USA, 19–22 September 2000; pp. 1959–1964. [Google Scholar]
- Hewitson, S.; Wang, J. Extended receiver autonomous integrity monitoring (e raim) for gnss/ins integration. J. Surv. Eng. 2010, 136, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Zhan, X.; Zhai, Y.; Liu, B. Fault Detection and Exclusion for Tightly Coupled GNSS/INS System Considering Fault in State Prediction. Sensors 2020, 20, 590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gandhi, M.A.; Mili, L. Robust Kalman filter based on a generalized maximum-likelihood-type estimator. IEEE Trans. Signal Process. 2009, 58, 2509–2520. [Google Scholar] [CrossRef]
- Roysdon, P.F.; Farrell, J.A. Robust GPS-INS outlier accommodation: A Soft-Thresholded optimal estimator. IFAC Pap. 2017, 50, 3574–3579. [Google Scholar] [CrossRef]
- Stromberg, A.J. Computing the exact least median of squares estimate and stability diagnostics in multiple linear regression. SIAM J. Sci. Comput. 1993, 14, 1289–1299. [Google Scholar] [CrossRef]
- Crespillo, O.G.; Medina, D.; Skaloud, J.; Meurer, M. Tightly coupled GNSS/INS integration based on robust M-estimators. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 1554–1561. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, X.; Pang, C.; Wang, Y.; Zhang, L.; Feng, B. Improved Fault Detection Method Based on Robust Estimation and Sliding Window Test for INS/GNSS Integration. J. Navig. 2020, 73, 776–796. [Google Scholar] [CrossRef]
- Sun, R.; Cheng, Q.; Wang, G.; Ochieng, W.Y. A Novel Online Data-Driven Algorithm for Detecting UAV Navigation Sensor Faults. Sensors 2017, 17, 2243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, Y.; Cheng, X.; Wang, L. A Novel Fault Detection Method for an Integrated Navigation System using Gaussian Process Regression. J. Navig. 2016, 69, 905–919. [Google Scholar] [CrossRef] [Green Version]
- Gumedze, F.N. A Variance Shift Model for Outlier Detection Andestimation in Linear and Linear Mixed Models. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 2009. [Google Scholar]
- Grove, P.D. Principles of GNSS, Inertial and Multi-Sensor Integrated Navigation Systems; Artech House: Norwood, MA, USA, 2012. [Google Scholar]
- Gumedze, F.N.; Welham, S.J.; Gogel, B.J.; Thompson, R. A variance shift model for detection of outliers in the linear mixed model. Comput. Stat. Data Anal. 2010, 54, 2128–2144. [Google Scholar] [CrossRef]
- Gumedze, F.N. Use of likelihood ratio tests to detect outliers under the variance shift outlier model. J. Appl. Stat. 2019, 46, 598–620. [Google Scholar] [CrossRef]
- Thompson, R. A Note on Restricted Maximum Likelihood Estimation with an Alternative Outlier Model. J. R. Stat. Soc. Ser. B (Methodol.) 1985, 47, 53–55. [Google Scholar] [CrossRef]
- Atkinson, A.C. Transformation and Regression; Clarendon Press: Oxford, UK, 1985. [Google Scholar]
- Gleason, S.; Gebreegziabher, D. GNSS Applications and Methods; Artech House: Norwood, MA, USA, 2009. [Google Scholar]
- Joerger, M.; Pervan, B. Integrity risk of Kalman filter-based RAIM. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 21–24 September 2011; pp. 3856–3867. [Google Scholar]
- Sun, R.; Zhang, W.; Zheng, J.; Ochieng, W.Y. GNSS/INS Integration with Integrity Monitoring for UAV No-fly Zone Management. Remote Sens. 2020, 12, 524. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.C.; O’Laughlin, D.G. Performance Analysis of a Tightly Coupled GPS/Inertial System for Two Integrity Monitoring Methods1. Navigation 2000, 47, 175–189. [Google Scholar] [CrossRef]
- Feng, S.; Ochieng, W.; Moore, T.; Hill, C.; Hide, C. Carrier phase-based integrity monitoring for high-accuracy positioning. GPS Solut. 2009, 13, 13–22. [Google Scholar] [CrossRef]
- Mackinnon, J. Bootstrap Hypothesis Testing. In Handbook of Computational Econometrics; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef] [Green Version]



| Gyroscope | Accelerometer | |
|---|---|---|
| Bias | h | 100 μg |
| Bias Instability | h | 100 μg |
| Random Walk | 10 μg/ |
| LRT | Score Test | |
|---|---|---|
| 1.6132 | 0.1568 (4.9503) | 0.2089 (12.3899) |
| 0.5216 | 0 | 0 |
| 0.8932 | 0 | 0 |
| 2.4981 | 0.7231 (4.2108) | 1.2489 (10.3595) |
| 0.0043 | 0 | 0 |
| 0.0554 | 0 | 0 |
| 0.3930 | 0 | 0 |
| 6.9031 | 7.7 (3.4822) | 19.2598 (8.3406) |
| 0.0985 | 0 | 0 |
| 0.8244 | 0 | 0 |
| 0.0815 | 0 | 0 |
| 0.1435 | 0 | 0 |
| 0.0027 | 0 | 0 |
| 0.9772 | 0 | 0 |
| 1.3200 | 0.04821 (4.3286) | 0.0569 (10.6851) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Wang, Y.; Gao, Y. A Novel Method of Fault Detection and Identification in a Tightly Coupled, INS/GNSS-Integrated System. Sensors 2021, 21, 2922. https://doi.org/10.3390/s21092922
Zhang F, Wang Y, Gao Y. A Novel Method of Fault Detection and Identification in a Tightly Coupled, INS/GNSS-Integrated System. Sensors. 2021; 21(9):2922. https://doi.org/10.3390/s21092922
Chicago/Turabian StyleZhang, Fan, Ye Wang, and Yanbin Gao. 2021. "A Novel Method of Fault Detection and Identification in a Tightly Coupled, INS/GNSS-Integrated System" Sensors 21, no. 9: 2922. https://doi.org/10.3390/s21092922
APA StyleZhang, F., Wang, Y., & Gao, Y. (2021). A Novel Method of Fault Detection and Identification in a Tightly Coupled, INS/GNSS-Integrated System. Sensors, 21(9), 2922. https://doi.org/10.3390/s21092922





