Mathematical Analysis and Micro-Spacing Implementation of Acoustic Sensor Based on Bio-Inspired Intermembrane Bridge Structure
Abstract
:1. Introduction
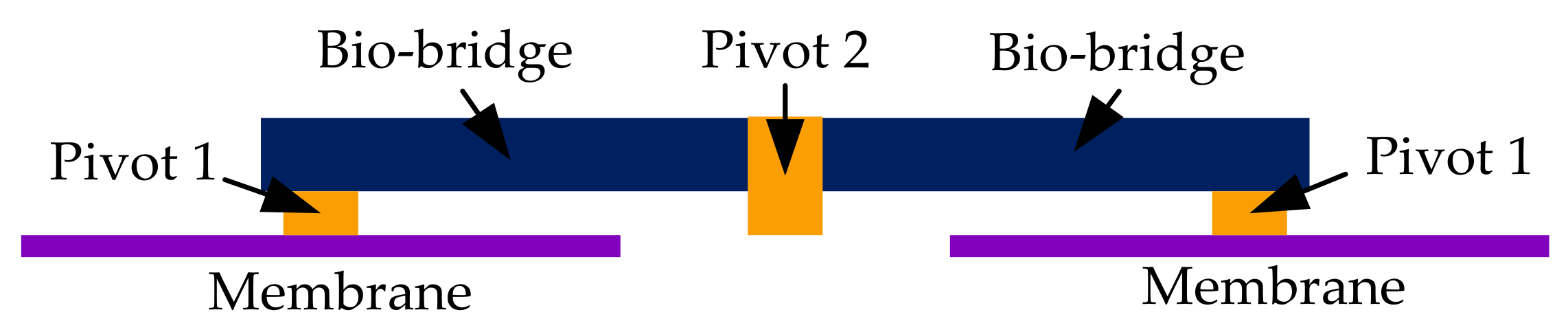
2. Mathematical Analysis of the Intermembrane Bridge Bionic Structure
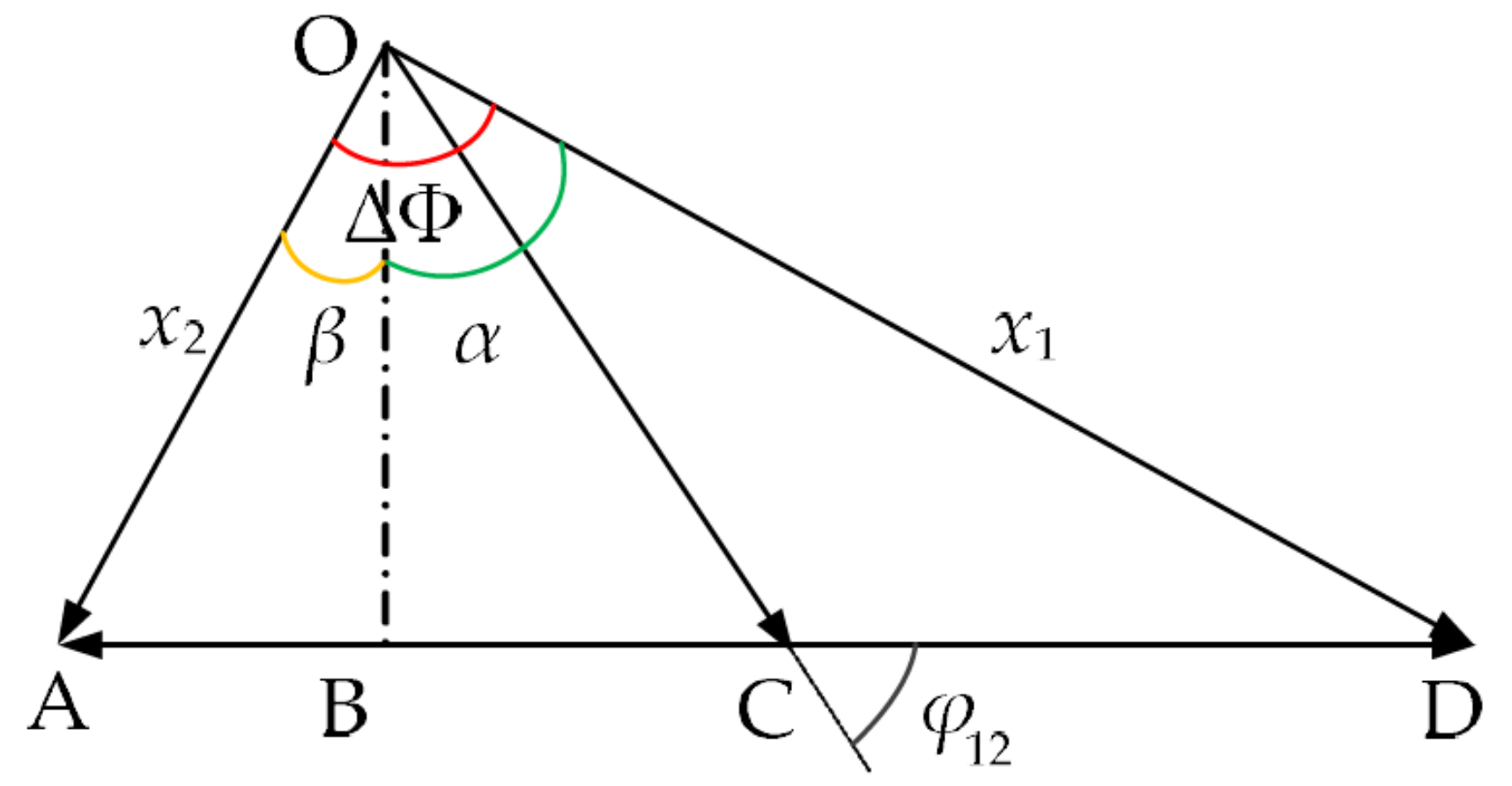
2.1. Establishment of the Mechanical Dynamics Model
2.2. Modal Analysis of the Mechanical Dynamics Model
3. Simulation Analysis of the Intermembrane Bridge Bionic Structure
3.1. Mathematical Simulation Analysis
3.2. Structural Simulation Analysis
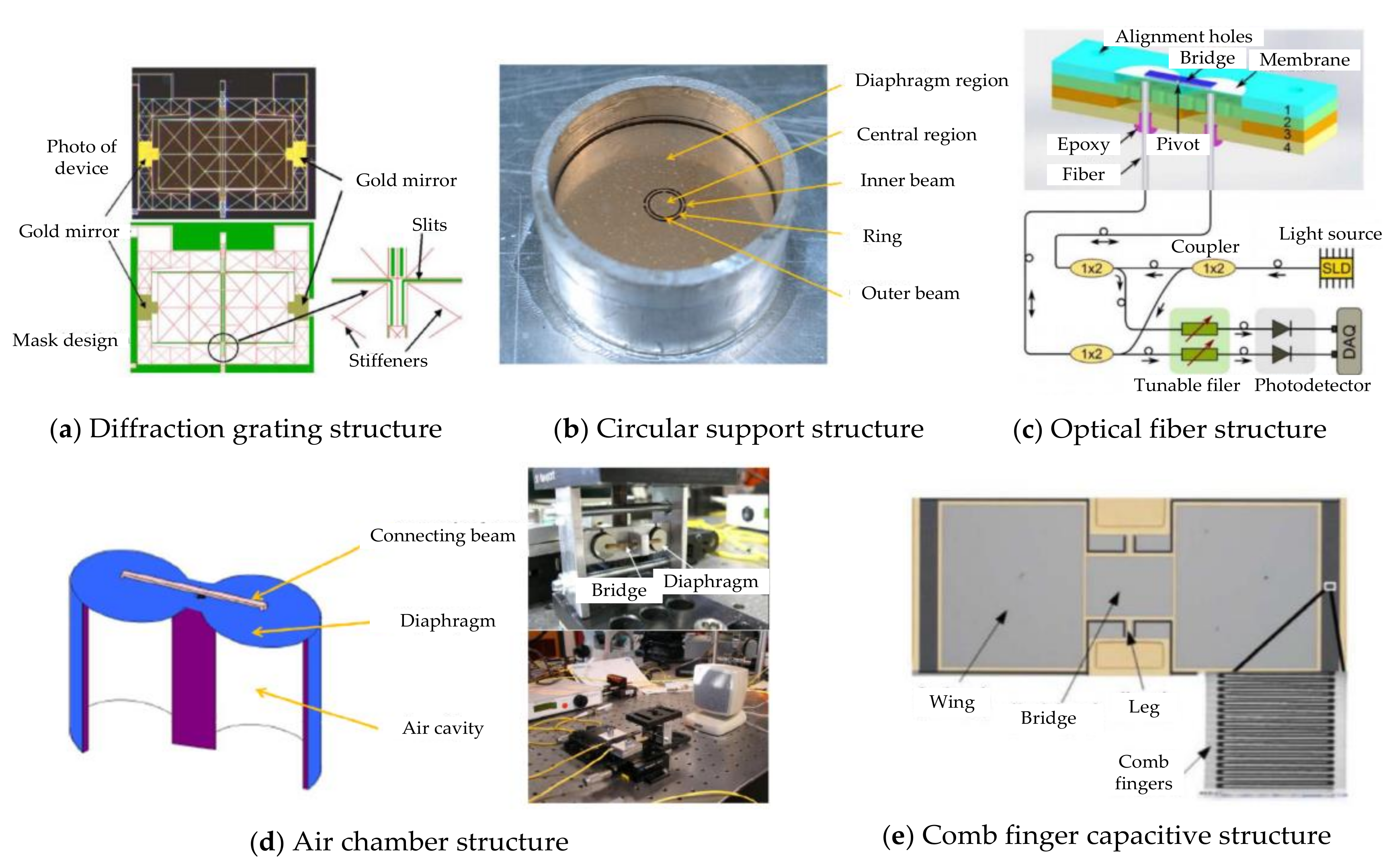
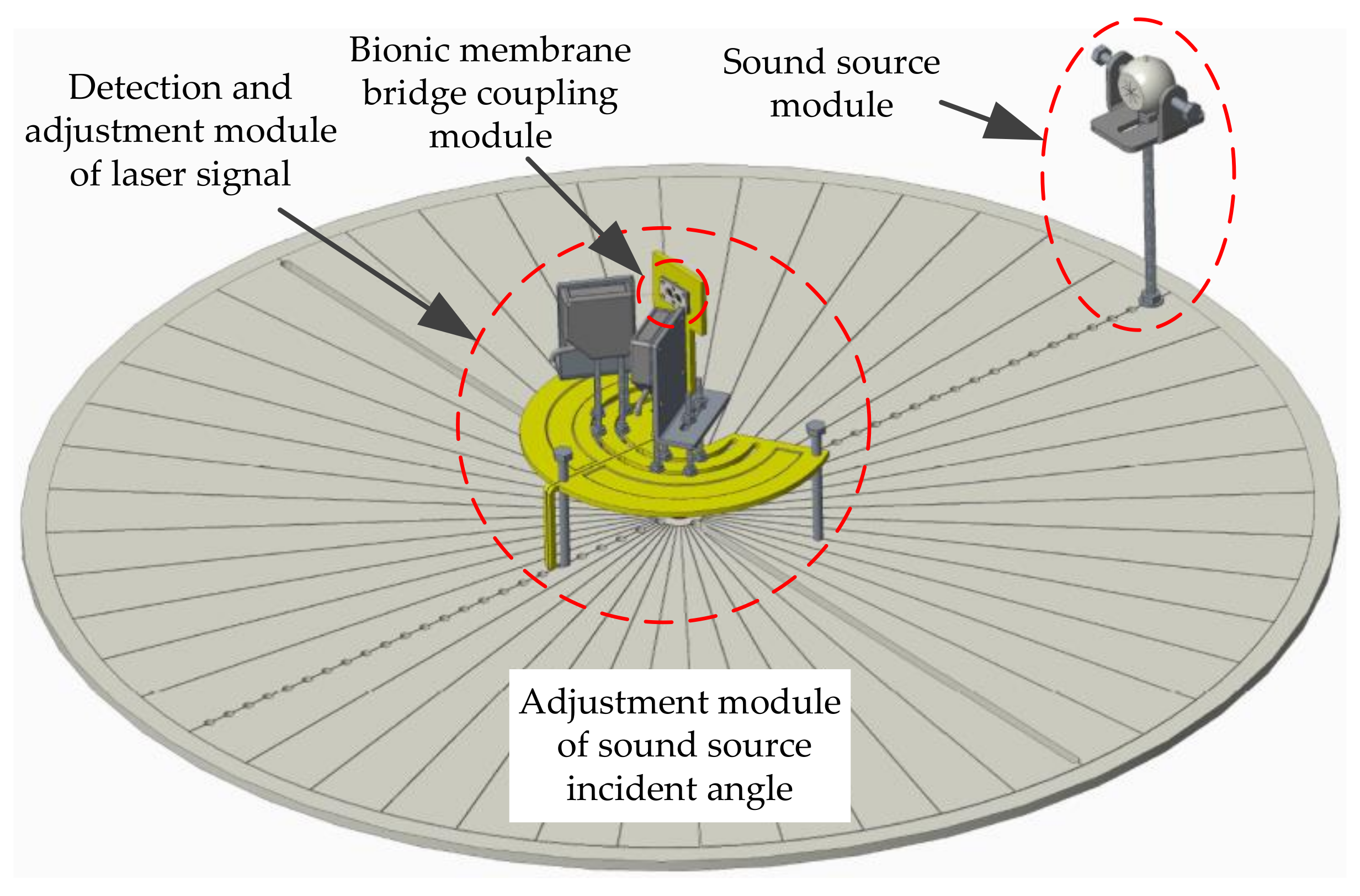
4. Microscale Implementation of the Intermembrane Bridge Bionic Structure
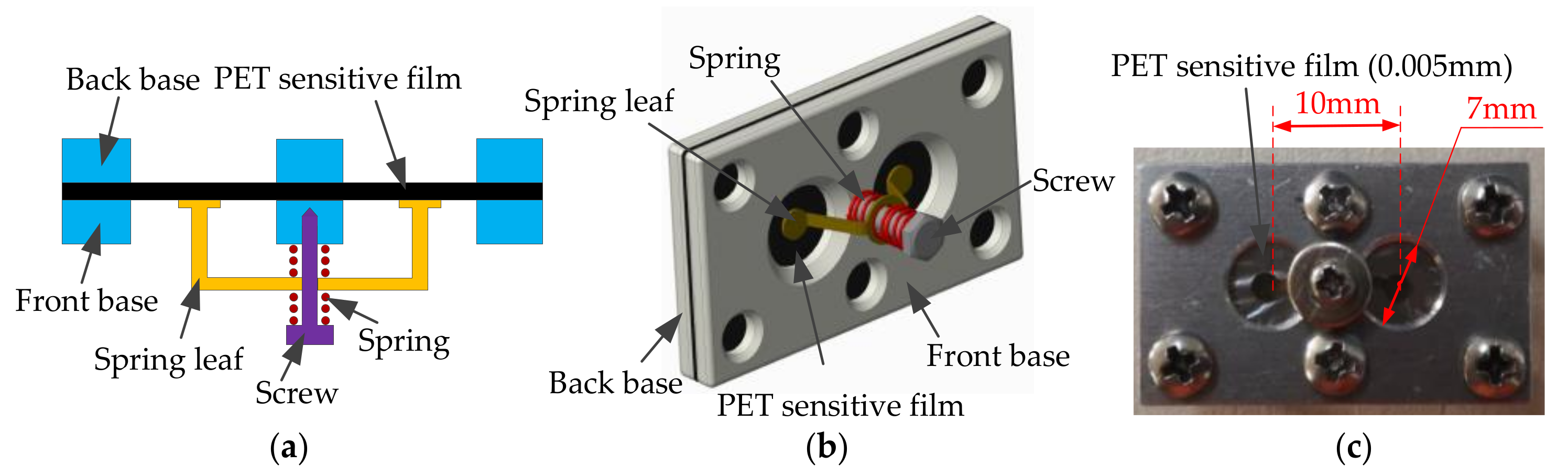
4.1. Design and Fabrication
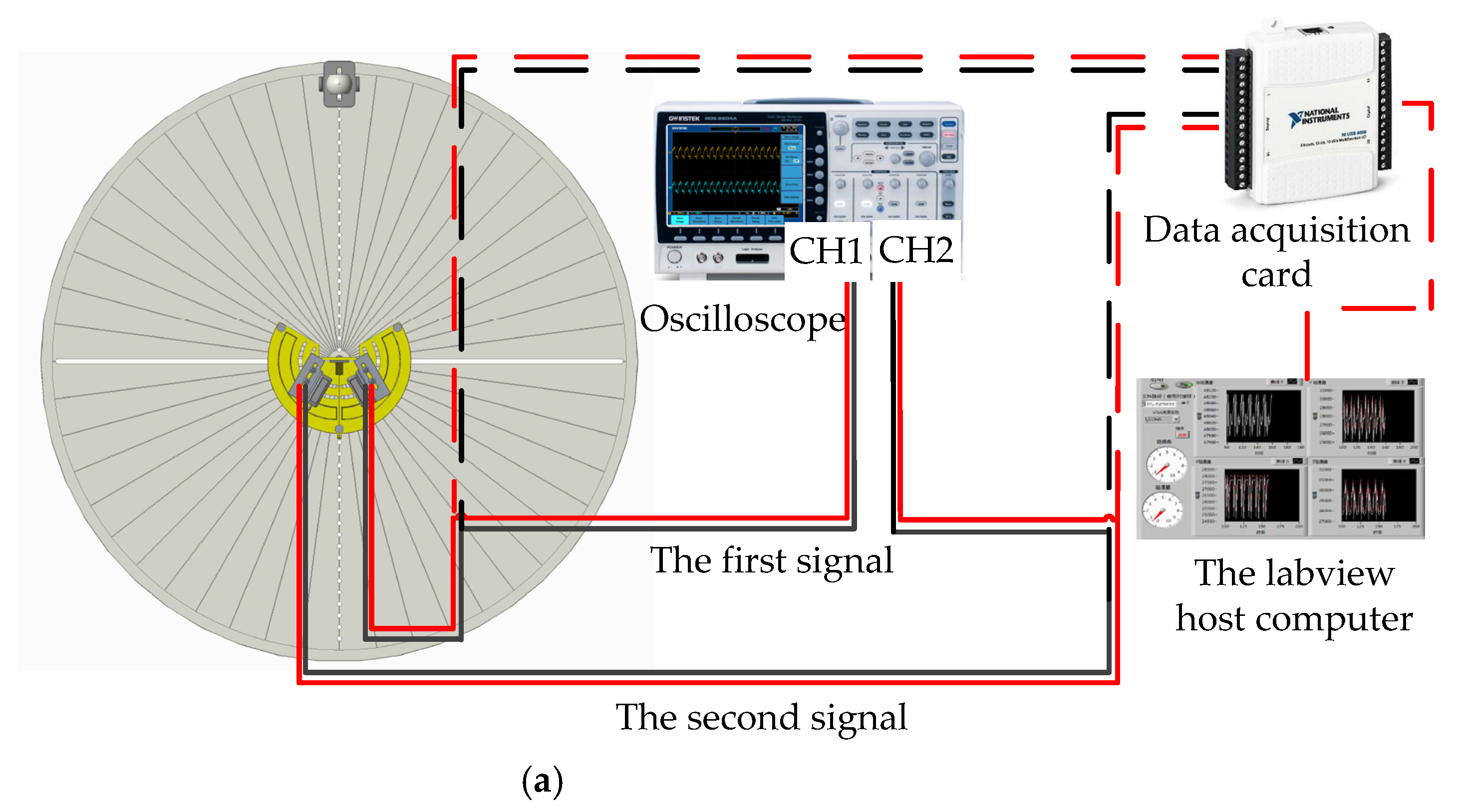
4.2. Experiment Analysis of Acoustic Signal Characteristics
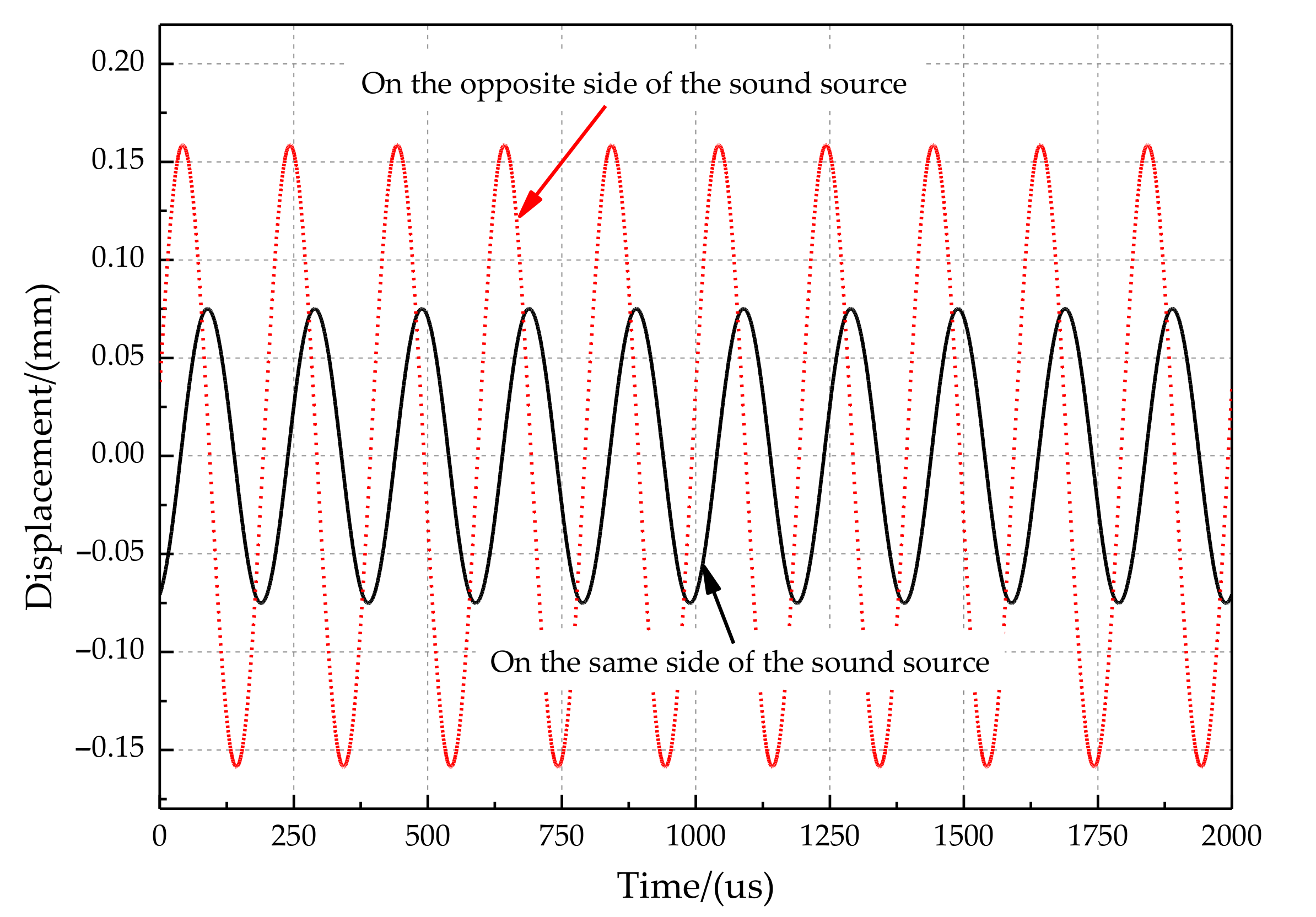
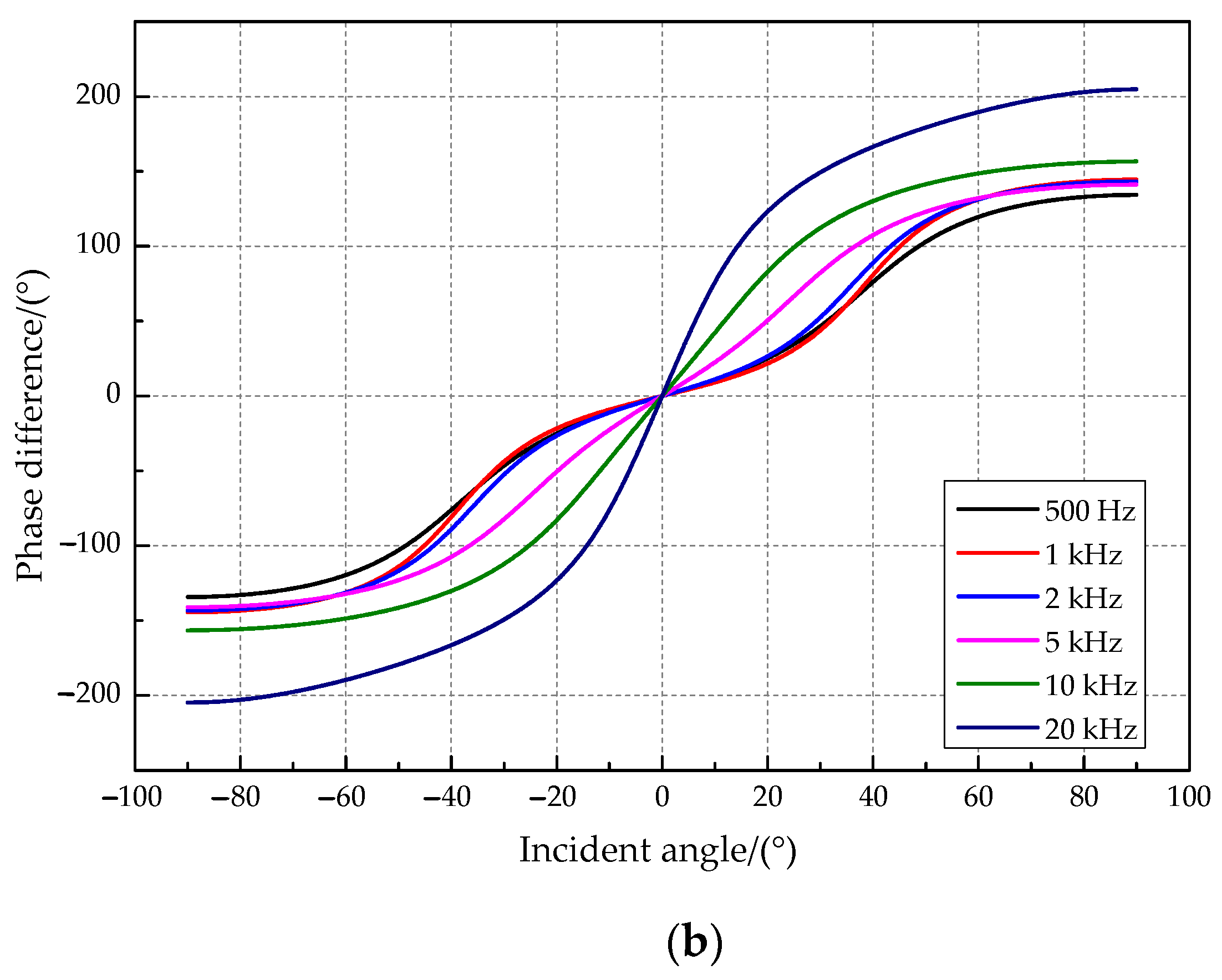
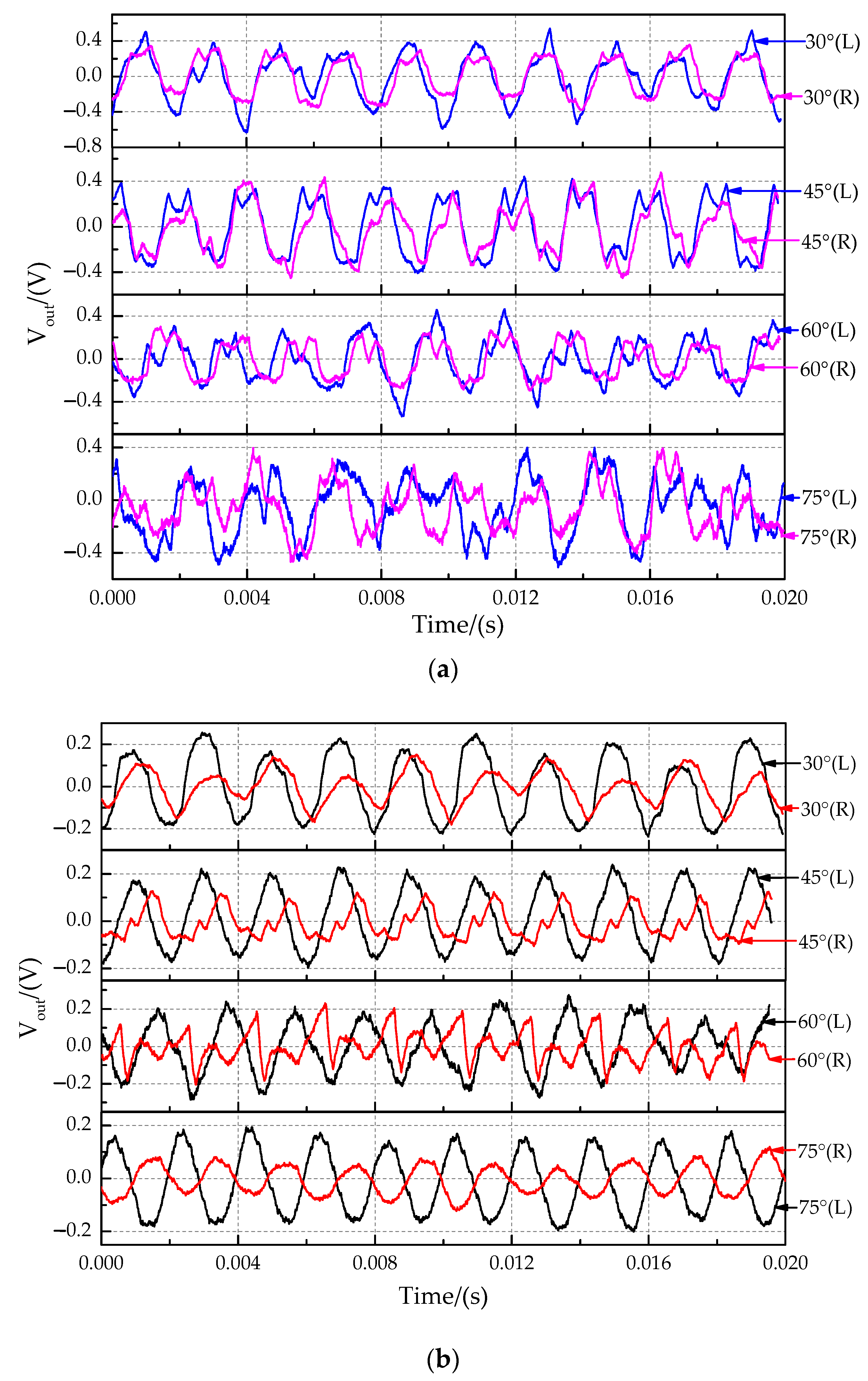
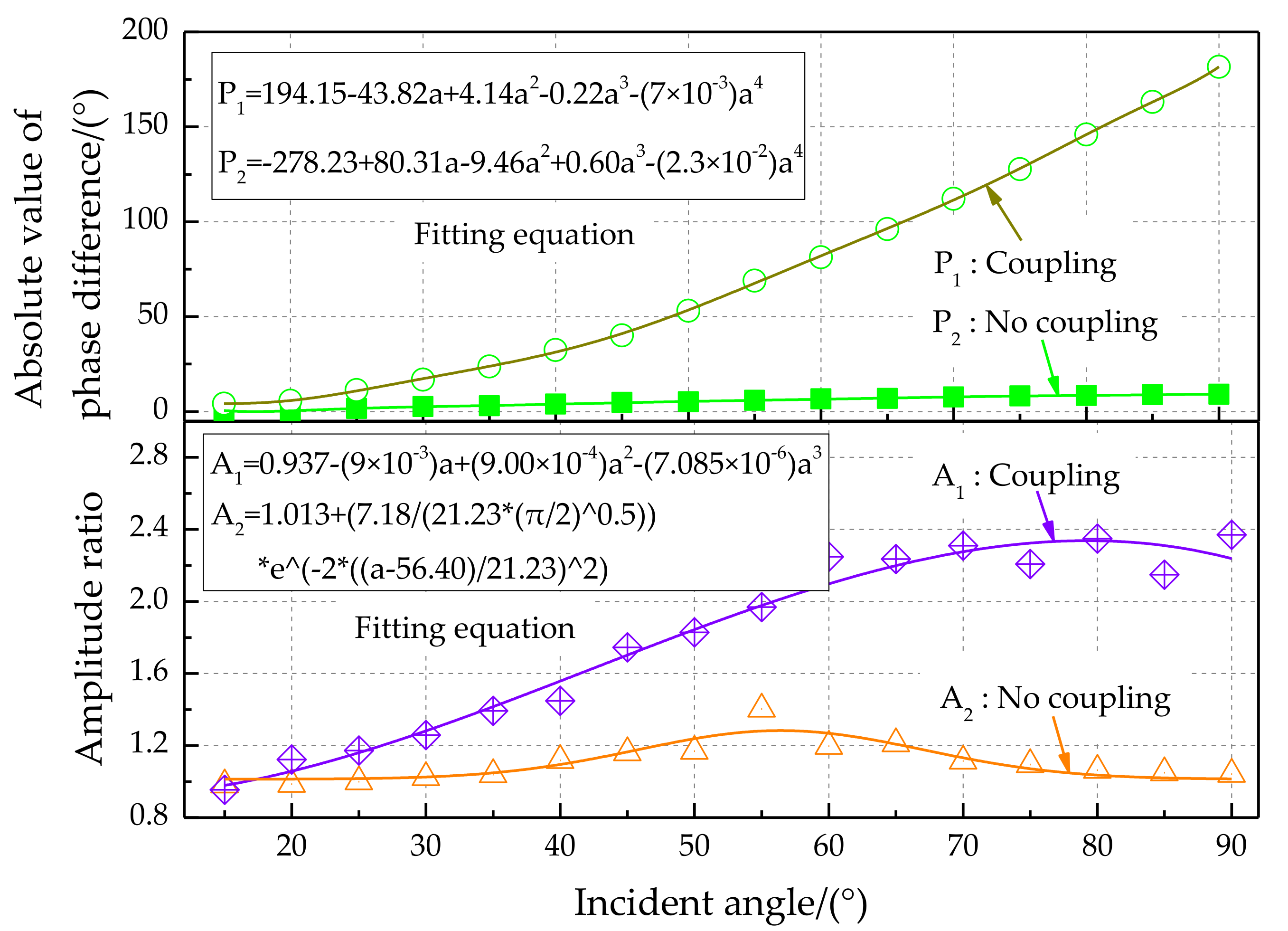
4.2.1. Analysis of the Sound Source Incident Angle Characteristic
- The frequency of the sound source was 500 Hz;
- The distance between the front surface of the speaker and the midpoint of the two diaphragms was 100 mm;
- The sound pressure level of the sound source on the front surface of the speaker was 90 dB.
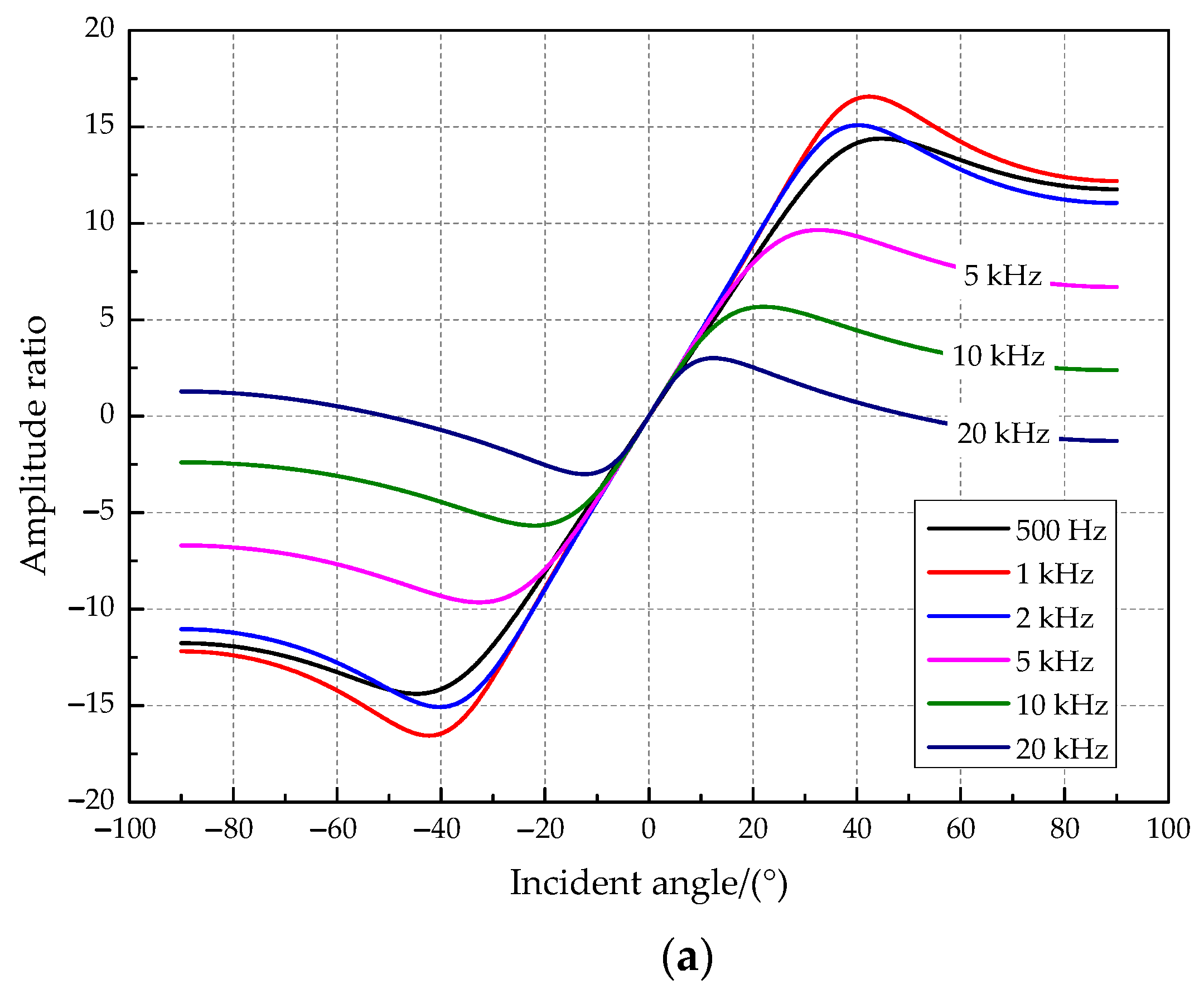
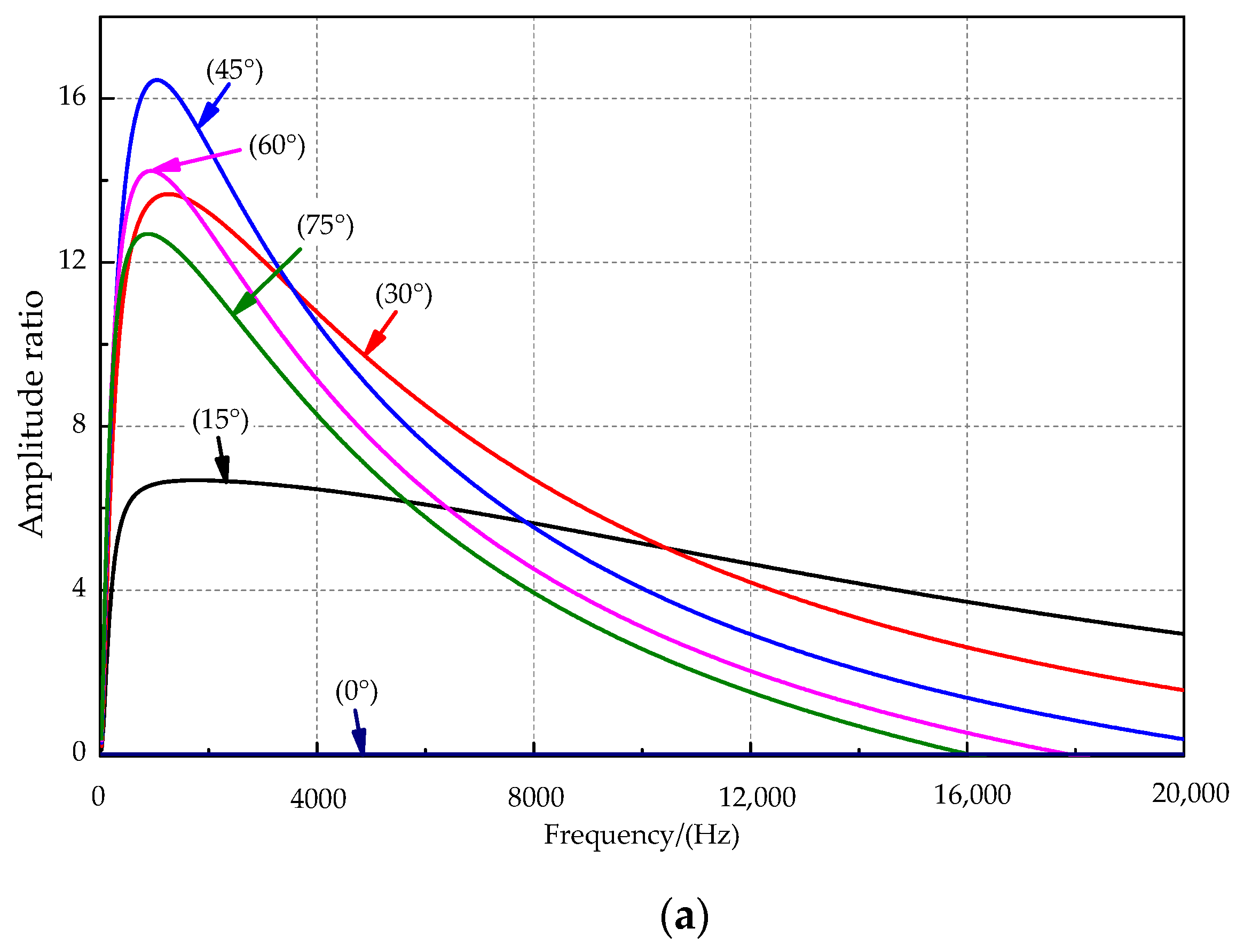
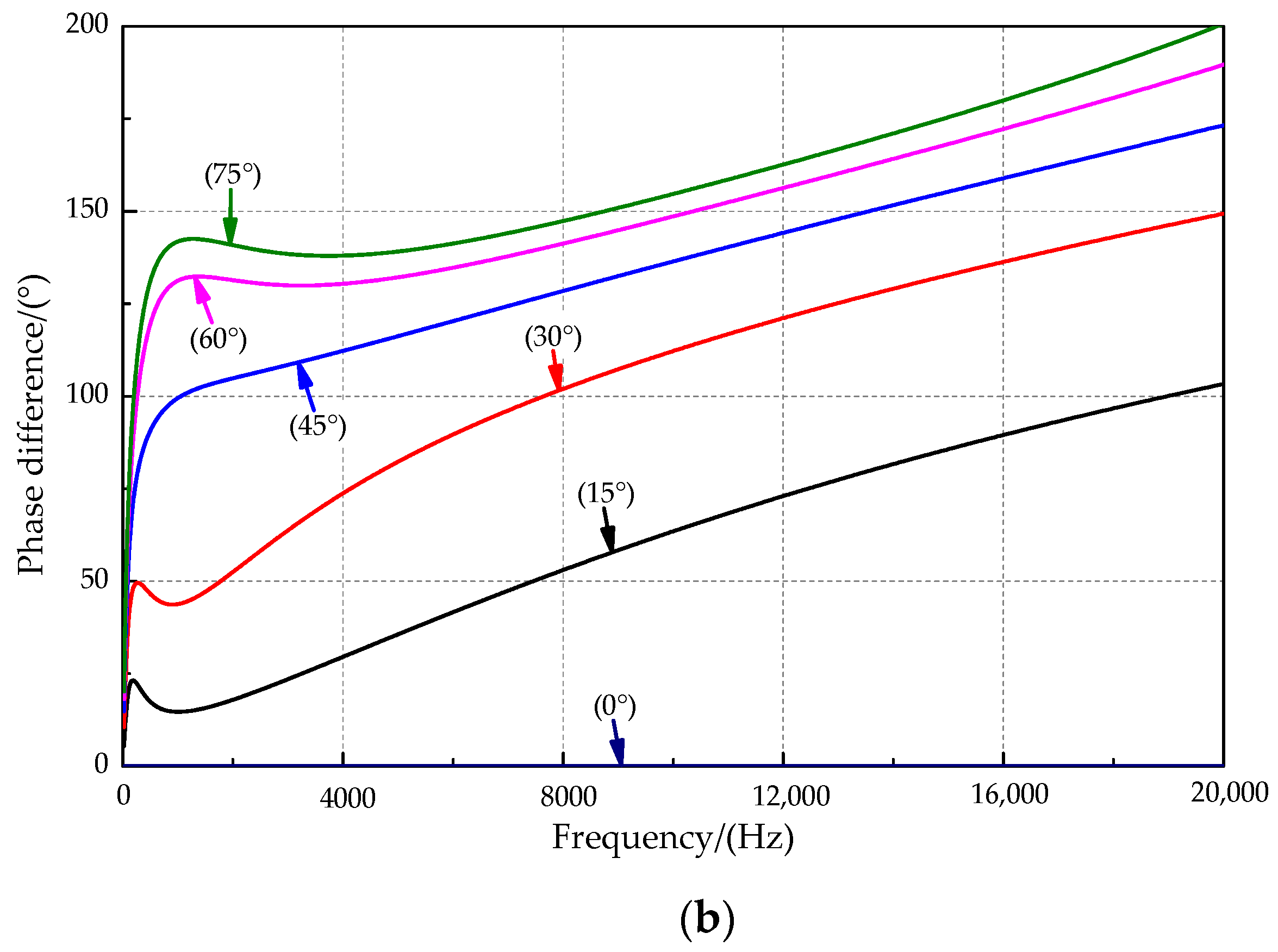
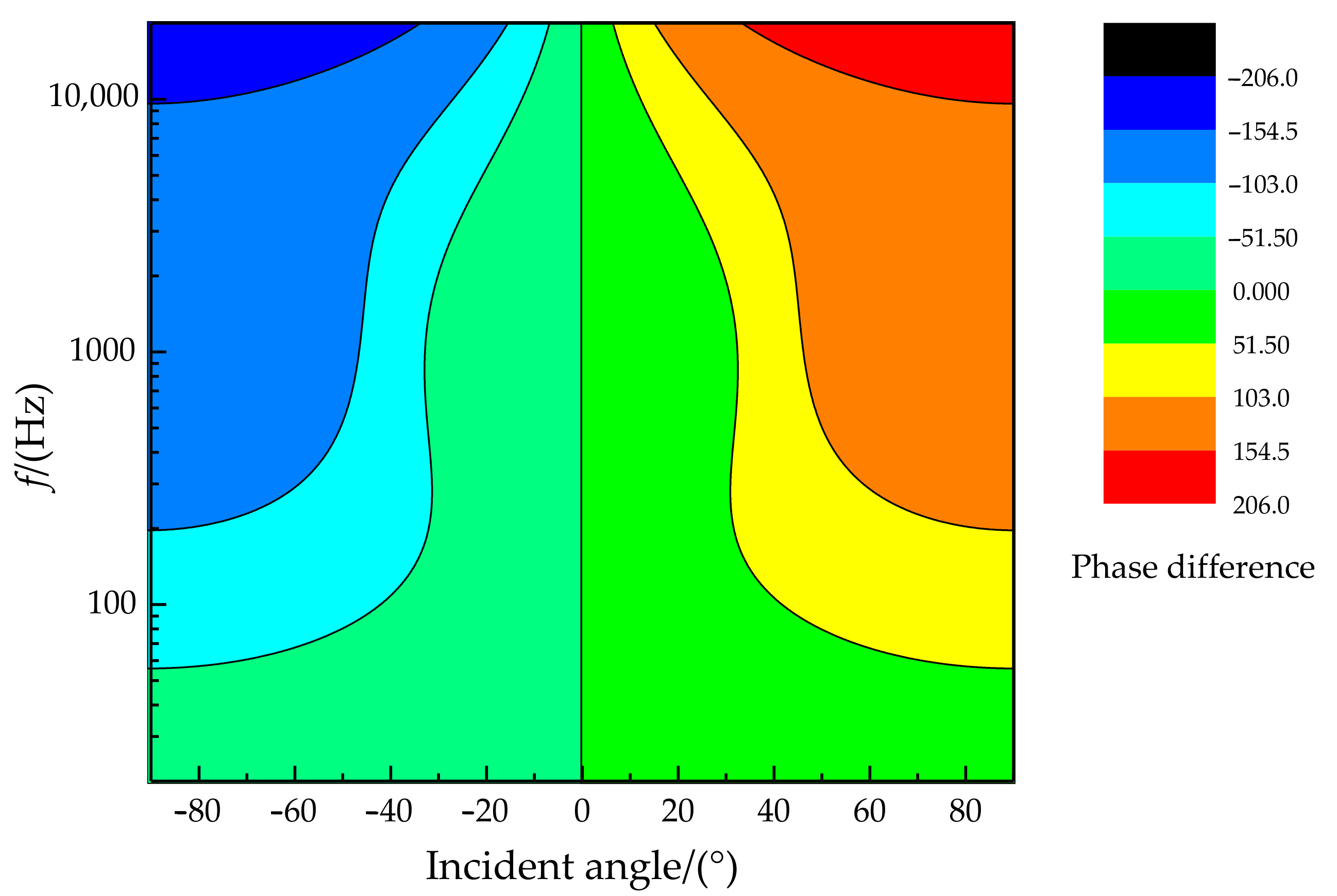
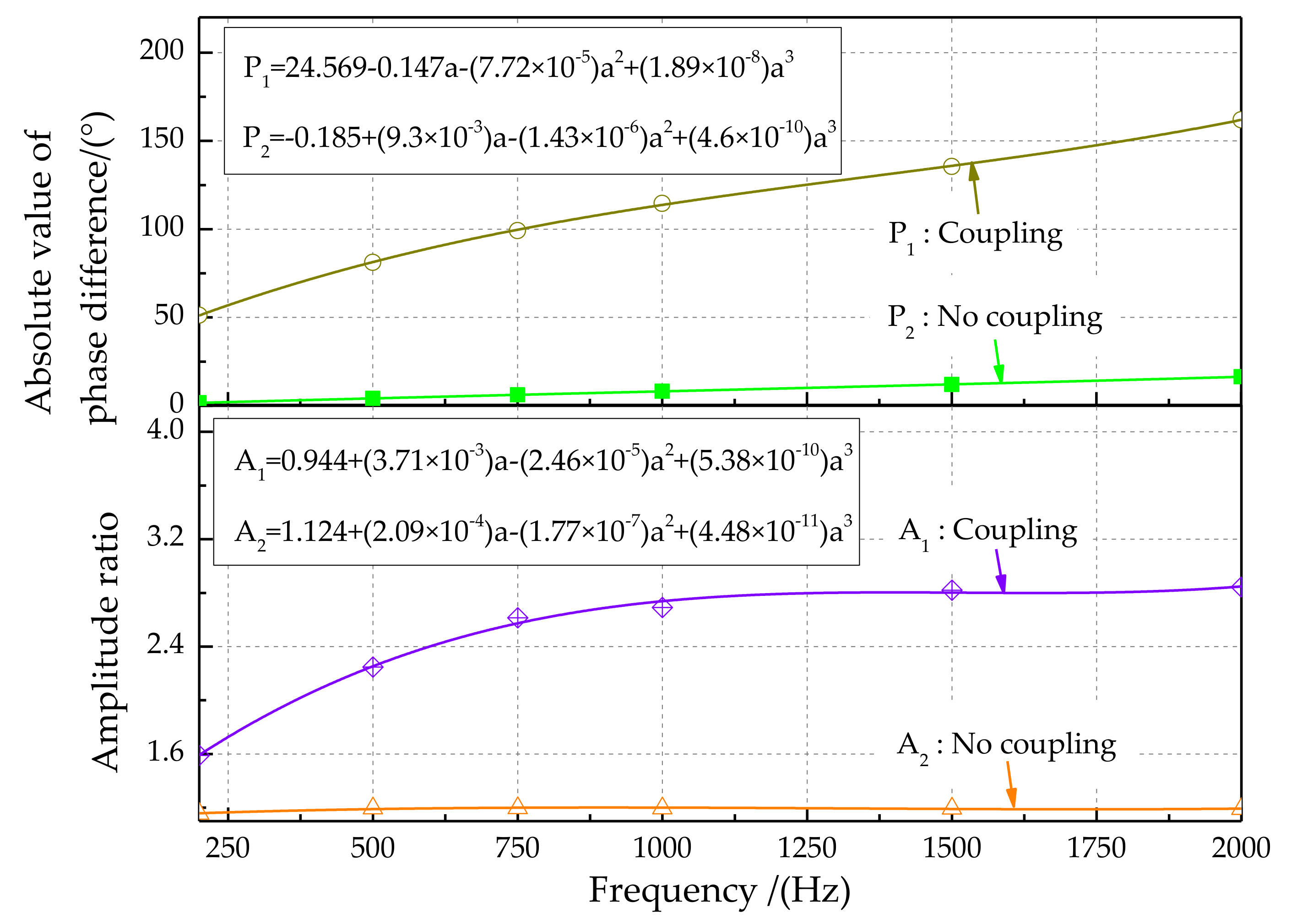
4.2.2. Analysis of the Sound Source Frequency Characteristic
4.3. Recognition Experiment of the Direction Angle
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| O. ochracea | Ormia ochracea |
| PET | Polyester |
| OSC | Oscilloscope |
| DAQ | Data acquisition |
| RMS | Root-mean-square |
| De | Decibel |
| Di | Distance from sound source |
| DOF | Degrees of freedom |
References
- Keyrouz, F. Advanced Binaural Sound Localization in 3-D for Humanoid Robots. IEEE Trans. Instrum. Meas. 2014, 63, 2098–2107. [Google Scholar] [CrossRef]
- Walker, T.J. Phonotaxis in female Ormia ochracea (Diptera, Tachinidae), a parasitoid of field crickets. J. Insect. Behav. 1993, 6, 389–410. [Google Scholar] [CrossRef]
- Cade, W.H.; Ciceran, M.; Murray, A.M. Temporal patterns of parasitoid fly (Ormia ochracea) attraction to field cricket song (Gryllus integer). Can. J. Zool. 1996, 74, 393–395. [Google Scholar] [CrossRef]
- Robert, D.; Miles, R.N.; Hoy, R.R. Tympanal mechanics in the parasitoid fly Ormia ochracea: Intertympanal coupling during mechanical vibration. J. Comp. Physiol. 1998, 183, 443–452. [Google Scholar] [CrossRef]
- Miles, R.N.; Robert, D.; Hoy, R.R. Mechanically coupled ears for directional hearing in the parasitoid fly Ormia ochracea. J. Acoust. Soc. Amer. 1995, 98, 3059–3070. [Google Scholar] [CrossRef] [PubMed]
- Miles, R.N.; Su, Q.; Cui, W.; Shetye, M.; Degertekin, F.L.; Bicen, B.; Hall, N. A low-noise differential microphone inspired by the ears of the parasitoid fly Ormia ochracea. J. Acoust. Soc. Amer. 2009, 125, 2013–2026. [Google Scholar] [CrossRef] [Green Version]
- Miles, R.N.; Cui, W.; Su, Q.T.; Homentcovschi, D. A MEMS low-noise sound pressure gradient microphone with capacitive sensing. J. Microelectromech. Syst. 2015, 24, 241–248. [Google Scholar] [CrossRef]
- Kuntzman, M.L.; Hall, N.A. Sound source localization inspired by the ears of the Ormia ochracea. Appl. Phys. Lett. 2014, 105, 33701. [Google Scholar] [CrossRef]
- Liu, H.; Currano, L.; Gee, D.; Helms, T.; Yu, M. Understanding and mimicking the dual optimality of the fly ear. Sci. Rep. 2013, 3, 2489. [Google Scholar] [CrossRef] [Green Version]
- Mackie, D.J.; Jackson, J.C.; Brown, J.G.; Uttamchandani, D.; Charles Windmill, J.F. Directional acoustic response of a silicon disc-based microelectromechanical systems structure. IET Micro Nano Lett. 2014, 9, 276–279. [Google Scholar] [CrossRef] [Green Version]
- Ishfaque, A.; Kim, B. Squeeze film damping analysis of biomimetic micromachined microphone for sound source localization. Sens. Actuators A Phys. 2016, 250, 60–70. [Google Scholar] [CrossRef]
- Touse, M.; Sinibaldi, J.; Simsek, K.; Catterlin, J.; Harrison, S.; Karunasiri, G. Fabrication of a microelectromechanical directional sound sensor with electronic readout using comb fingers. Appl. Phys. Lett. 2010, 96, 173701. [Google Scholar] [CrossRef]
- Ishfaque, A.; Kim, B. Analytical modeling of squeeze air film damping of biomimetic MEMS directional microphone. J. Sound Vib. 2016, 375, 422–435. [Google Scholar] [CrossRef]
- Chen, C.C.; Cheng, Y.T. Physical analysis of a biomimetic microphone with a central-supported (C-S) circular diaphragm for sound source localization. IEEE Sens. J. 2012, 12, 1504–1512. [Google Scholar] [CrossRef]
- Miles, R.N.; Degertekin, F.L.; Cui, W.; Su, Q.; Homentcovschi, D.; Banser, F. A biologically inspired silicon differential microphone with active Q control and optical sensing. Proc. Meet. Acoust. 2013, 19, 030031. [Google Scholar]
- Rahaman, A.; Kim, B. Sound source localization by Ormia ochracea inspired low–noise piezoelectric MEMS directional micro-phone. Sci. Rep. 2020, 10, 9545. [Google Scholar] [CrossRef] [PubMed]
- Wilmott, D.; Alves, F.; Karunasiri, G. Bio-inspired miniature direction finding acoustic sensor. Sci. Rep. 2016, 6, 29957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.J.; Yu, M.; Zhang, X.M. Biomimetic optical directional microphone with structurally coupled diaphragms. Appl. Phys. Lett. 2008, 93, 243902. [Google Scholar] [CrossRef]
- Kuntzman, M.L.; Lee, J.G.; Hewa-Kasakarage, N.; Kim, D.; Hall, N.A. Micromachined piezoelectric microphones with in-plane directivity. Appl. Phys. Lett. 2013, 102, 54109. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Bauer, R.; Windmill, J.F.C.; Uttamchandani, D. Multiband asymmetric piezoelectric MEMS microphone inspired by the Ormia ochracea. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016; pp. 1114–1117. [Google Scholar]
- Hall, N.A.; Kuntzman, M.; Kim, D. A biologically inspired piezoelectric microphone. J. Acoust. Soc. Amer. 2017, 141, 3794. [Google Scholar] [CrossRef]
- Chen, H.; Ballal, T.; Muqaibel, A.H.; Zhang, X.; Al-Naffouri, T.Y. Air Writing via Receiver Array-Based Ultrasonic Source Lo-calization. IEEE Trans. Instrum. Meas. 2020, 69, 8088–8101. [Google Scholar]
- Cui, X.; Yu, K.; Zhang, S.; Wang, H. Azimuth-Only Estimation for TDOA-Based Direction Finding With 3-D Acoustic Array. IEEE Trans. Instrum. Meas. 2020, 69, 985–994. [Google Scholar] [CrossRef]
- Downey, R.H.; Karunasiri, G. Reduced residual stress curvature and branched comb fingers increase sensitivity of MEMS acoustic sensor. J. Microelectromech. Syst. 2014, 23, 417–423. [Google Scholar] [CrossRef]
- Kuntzman, M.L.; Hewa-Kasakarage, N.N.; Rocha, A.; Kim, D.; Hall, N.A. Micromachined in-plane pressure-gradient piezoe-lectric microphones. IEEE Sens. J. 2015, 15, 1347–1357. [Google Scholar] [CrossRef]
- Rahaman, A.; Ishfaque, A.; Kim, B. Effect of torsional beam length on acoustic functionalities of bio-inspired piezoelectric MEMS directional microphone. IEEE Sens. J. 2019, 19, 6046–6055. [Google Scholar] [CrossRef]
- Seo, Y.; Corona, D.; Hall, N.A. On the theoretical maximum achievable signal-to-noise ratio (SNR) of piezoelectric microphones. Sens. Actuators A Phys. 2017, 264, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Calero, D.; Paul, S.; Gesing, A.; Alves, F.; Cordioli, J.A. A technical review and evaluation of implantable sensors for hearing devices. BioMed Eng OnLine. 2018, 17, 23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Reid, A.; Windmill, J.F.C. Insect-inspired acoustic micro-sensors. Curr. Opin. Insect Sci. 2018, 30, 33–38. [Google Scholar] [CrossRef]
- Kishor Bhaskarrao, N.; Sreekantan, A.C.; Dutta, P.K. Analysis of a Linearizing Direct Digitizer With Phase-Error Compensation for TMR Angular Position Sensor. IEEE Trans. Instrum. Meas. 2018, 67, 1795–1803. [Google Scholar] [CrossRef]
- Hu, G.; Wang, K.; Liu, L. Underwater Acoustic Target Recognition Based on Depthwise Separable Convolution Neural Networks. Sensors 2021, 21, 1429. [Google Scholar] [CrossRef]
- Fu, J.; Yin, S.; Cui, Z.; Kundu, T. Experimental Research on Rapid Localization of Acoustic Source in a Cylindrical Shell Structure without Knowledge of the Velocity Profile. Sensors 2021, 21, 511. [Google Scholar] [CrossRef] [PubMed]
- Jafari, N.; Azhari, M. Free vibration analysis of viscoelastic plates with simultaneous calculation of natural frequency and viscous damping. Math. Comput. Simulat. 2021, 185, 646–659. [Google Scholar] [CrossRef]








| Membrane | Bio-Bridge | Pivot 1 | Pivot 2 | |
|---|---|---|---|---|
| Equivalent Elastic modulus/(MPa) | 4000 | 97,000 | 2590 | 2880 |
| Poisson ratio | 0.3 | 0.32 | 0.3 | 0.3 |
| Density/(kg/mm3) | 1.38 × 10−9 | 8.65 × 10−9 | 1.55 × 10−9 | 1.55 × 10−9 |
| Size/(mm) | Φ7 × 0.005 | 11 × 2 × 0.05 | 0.2 × 0.2 × 0.2 | 2 × 0.2 × 0.2 |
| Stiffness damping/(N∙s/mm) | 1.15 × 10−8 | 2.88 × 10−8 |
| Actual Value | Calculated Value by Phase Difference Amplification Identification | Maximum Error | Calculated Value by Amplitude Ratio Amplification Identification | Maximum Error |
|---|---|---|---|---|
| 36° | 42.209° | +6.209° | 39.177° | +3.177° |
| 42° | 36.413° | −5.587° | 44.185° | +2.185° |
| 48° | 44.561° | −3.439° | 43.204° | −4.796° |
| 54° | 49.339° | −4.661° | 51.460° | −2.540° |
| Mean of Absolute Value of Error | 4.974° | 3.1745° | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Zhao, L.; Xu, J.; Yao, X. Mathematical Analysis and Micro-Spacing Implementation of Acoustic Sensor Based on Bio-Inspired Intermembrane Bridge Structure. Sensors 2021, 21, 3168. https://doi.org/10.3390/s21093168
Shen X, Zhao L, Xu J, Yao X. Mathematical Analysis and Micro-Spacing Implementation of Acoustic Sensor Based on Bio-Inspired Intermembrane Bridge Structure. Sensors. 2021; 21(9):3168. https://doi.org/10.3390/s21093168
Chicago/Turabian StyleShen, Xiang, Liye Zhao, Jiawen Xu, and Xuwei Yao. 2021. "Mathematical Analysis and Micro-Spacing Implementation of Acoustic Sensor Based on Bio-Inspired Intermembrane Bridge Structure" Sensors 21, no. 9: 3168. https://doi.org/10.3390/s21093168
APA StyleShen, X., Zhao, L., Xu, J., & Yao, X. (2021). Mathematical Analysis and Micro-Spacing Implementation of Acoustic Sensor Based on Bio-Inspired Intermembrane Bridge Structure. Sensors, 21(9), 3168. https://doi.org/10.3390/s21093168






