Intelligent Trajectory Tracking Behavior of a Multi-Joint Robotic Arm via Genetic–Swarm Optimization for the Inverse Kinematic Solution
Abstract
:1. Introduction
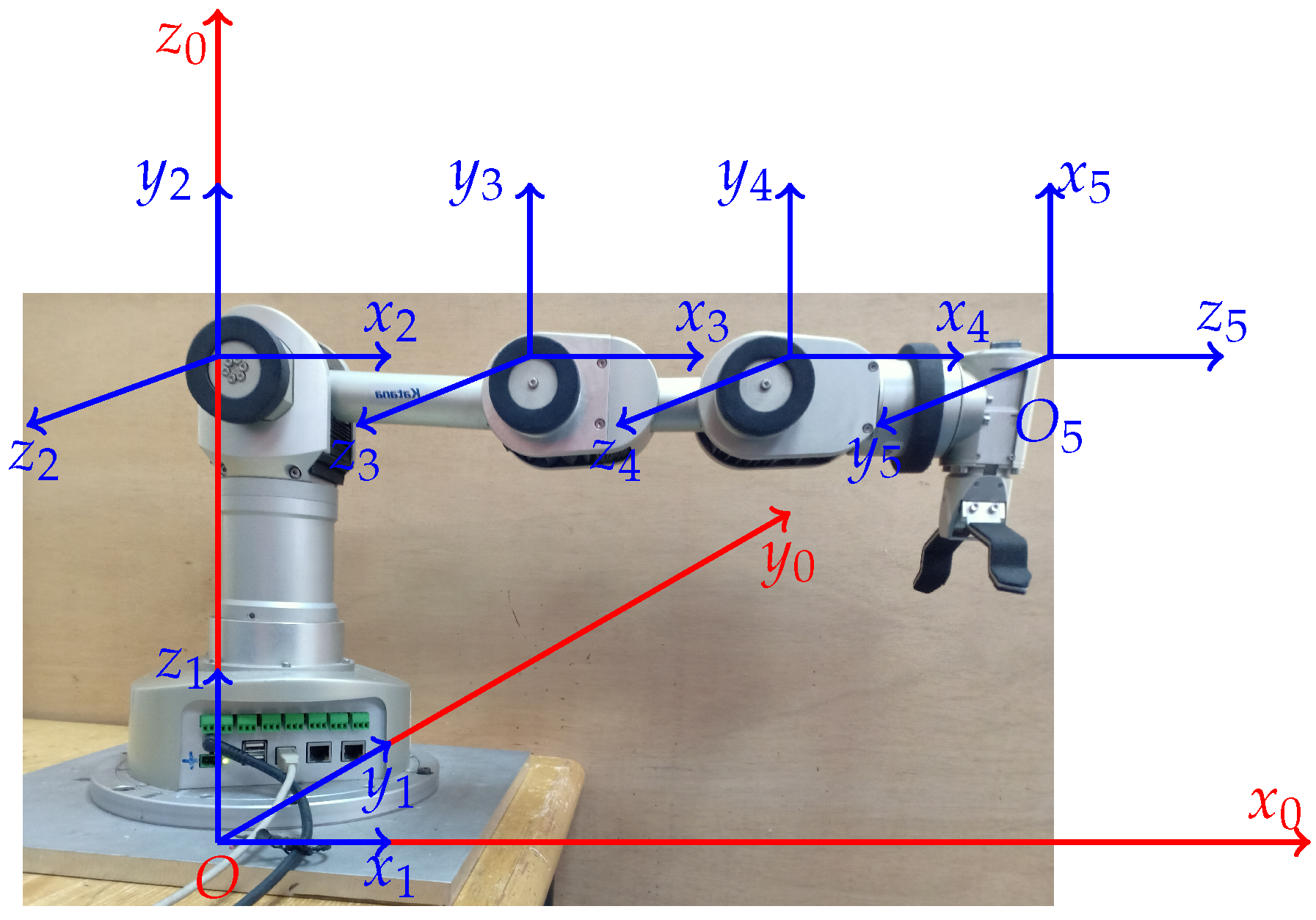
2. Dynamic and Kinematic Model
3. Optimal Inverse Kinematic
| Algorithm 1 Pseudo code of GSO |
|
4. Control System and Tuning
5. Results and Discussion
- For GA, : crossover = 0.9, mutation = 0.1, population = 40 and generation = 400; : crossover = 0.8, mutation = 0.2, population = 40, and generation = 400; : crossover = 0.7, mutation = 0.3, population = 40 and generation = 400;
- For PSO, : particles = 20, and generation = 200; : particles = 30 and generation = 300; : particles = 40 and generation = 400;
- For GSO, : crossover = 0.9, mutation = 0.1, population of GA and particles of PSO = 40, generation of GA = 300 iteration of PSO = 100, : crossover = 0.8, mutation = 0.2, population of GA and particles of PSO = 40, generation of GA = 200 iteration of PSO = 200, : crossover = 0.7, mutation = 0.3, population of GA and particles of PSO = 40, generation of GA = 100 and iteration of PSO = 300.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jahnavi, K.; Sivraj, P. Teaching and Learning Robotic Arm Model. In Proceedings of the International Conference on Intelligent Computing, Instrumentation and Control Technologies, Kerala, India, 6–7 July 2017; pp. 1570–1575. [Google Scholar] [CrossRef]
- Quiros, A.R.F.; Abad, A.C.; Dadios, E.P. Object Locator and Collector Robotic Arm using Artificial Neural Networks. In Proceedings of the International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management, HNICEM, Cebu, Philippines, 9–12 December 2016; pp. 200–203. [Google Scholar] [CrossRef]
- Pavlovčič, U.; Arko, P.; Jezeršek, M. Simultaneous hand–eye and intrinsic calibration of a laser profilometer mounted on a robot arm. Sensors 2021, 21, 1037. [Google Scholar] [CrossRef]
- Shah, S.K.; Mishra, R.; Ray, L.S. Solution and Validation of Inverse Kinematics using Deep Artificial Neural Network. Mater. Today Proc. 2020, 26, 1250–1254. [Google Scholar] [CrossRef]
- Shirafuji, S.; Ota, J. Kinematic Synthesis of a Serial Robotic Manipulator by Using Generalized Differential Inverse Kinematics. IEEE Trans. Robot. 2019, 35, 1047–1054. [Google Scholar] [CrossRef]
- Sun, P.; Li, Y.B.; Wang, Z.; Chen, K.; Chen, B.; Zeng, X.; Zhao, J.; Yue, Y. Inverse displacement analysis of a novel hybrid humanoid robotic arm. Mech. Mach. Theory 2020, 147, 103743. [Google Scholar] [CrossRef]
- Megalingam, R.K.; Boddupalli, S.; Apuroop, K.G.S. Robotic Arm Control through Mimicking of Miniature Robotic Arm. In Proceedings of the 4th International Conference on Advanced Computing and Communication Systems, ICACCS, Coimbatore, India, 6–7 January 2017; pp. 4–10. [Google Scholar] [CrossRef]
- Xu, Y.; Ding, C.; Shu, X.; Gui, K.; Bezsudnova, Y.; Sheng, X.; Zhang, D. Shared control of a robotic arm using non-invasive brain–computer interface and computer vision guidance. Robot. Auton. Syst. 2019, 115, 121–129. [Google Scholar] [CrossRef]
- Fang, B.; Ma, X.; Wang, J.; Sun, F. Vision-based posture-consistent teleoperation of robotic arm using multi-stage deep neural network. Robot. Auton. Syst. 2020, 131, 103592. [Google Scholar] [CrossRef]
- Narayan, J.; Mishra, S.; Jaiswal, G.; Dwivedy, S.K. Novel design and kinematic analysis of a 5-DOFs robotic arm with three-fingered gripper for physical therapy. Mater. Today Proc. 2020, 28, 2121–2132. [Google Scholar] [CrossRef]
- Ye, H.; Wang, D.; Wu, J.; Yue, Y.; Zhou, Y. Forward and inverse kinematics of a 5-DOF hybrid robot for composite material machining. Robot. Comput. Integr. Manuf. 2020, 65, 101961. [Google Scholar] [CrossRef]
- Wei, H.; Bu, Y.; Zhu, Z. Robotic arm controlling based on a spiking neural circuit and synaptic plasticity. Biomed. Signal Process. Control 2020, 55, 101640. [Google Scholar] [CrossRef]
- Ren, H.; Ben-Tzvi, P. Learning Inverse Kinematics and Dynamics of a Robotic Manipulator using Generative Adversarial Networks. Robot. Auton. Syst. 2020, 124, 103386. [Google Scholar] [CrossRef]
- Kang, M.; Shin, H.; Kim, D.; Yoon, S.E. TORM: Fast and accurate trajectory optimization of redundant manipulator given an end-effector path. IEEE Int. Conf. Intell. Robot. Syst. 2020. [Google Scholar] [CrossRef]
- Jin, M.; Liu, Q.; Wang, B.; Liu, H. An Efficient and Accurate Inverse Kinematics for 7-DOF Redundant Manipulators Based on a Hybrid of Analytical and Numerical Method. IEEE Access 2020, 8, 16316–16330. [Google Scholar] [CrossRef]
- Cao, Y.; Gan, Y.; Dai, X. Kinematic Optimization of Redundant Manipulators to Improve the Fault-Tolerant Control. In Proceedings of the 31st Chinese Control and Decision Conference, Nanchang, China, 3–5 June 2019. [Google Scholar] [CrossRef]
- Starke, S.; Hendrich, N.; Zhang, J. Memetic Evolution for Generic Full-Body Inverse Kinematics in Robotics and Animation. IEEE Trans. Evol. Comput. 2019, 23, 406–420. [Google Scholar] [CrossRef]
- Jamali, B.; Rasekh, M.; Jamadi, F.; Gandomkar, R.; Makiabadi, F. Using PSO-GA algorithm for training artificial neural network to forecast solar space heating system parameters. Appl. Therm. Eng. 2019, 147, 647–660. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, Y.; Jiang, W. Genetic particle swarm optimization–based feature selection for very-high-resolution remotely sensed imagery object change detection. Sensors 2016, 16, 1024. [Google Scholar] [CrossRef] [Green Version]
- Ajmi, N.; Helali, A.; Lorenz, P.; Mghaieth, R. MWCSGA—Multi Weight Chicken Swarm Based Genetic Algorithm for Energy Efficient Clustered Wireless Sensor Network. Sensors 2021, 21, 791. [Google Scholar] [CrossRef]
- Dziwinski, P.; Bartczuk, L. A New Hybrid Particle Swarm Optimization and Genetic Algorithm Method Controlled by Fuzzy Logic. IEEE Trans. Fuzzy Syst. 2020, 28, 1140–1154. [Google Scholar] [CrossRef]
- Farnad, B.; Jafarian, A.; Baleanu, D. A new hybrid algorithm for continuous optimization problem. Appl. Math. Model. 2018, 55, 652–673. [Google Scholar] [CrossRef]
- Mahmud, M.; Motakabber, S.; Zahirul Alam, A.H.; Nordin, A.N. Adaptive PID Controller Using for Speed Control of the BLDC Motor. In Proceedings of the IEEE International Conference on Semiconductor Electronics, Kuala Lumpur, Malaysia,, 28–29 July 2020; pp. 168–171. [Google Scholar] [CrossRef]
- Misaghi, M.; Yaghoobi, M. Improved invasive weed optimization algorithm (IWO) based on chaos theory for optimal design of PID controller. J. Comput. Des. Eng. 2019, 6, 284–295. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ramli, R.; Ibrahim, M.F. Initialized Model Reference Adaptive Control for Lower Limb Exoskeleton. IEEE Access 2019, 7, 167210–167220. [Google Scholar] [CrossRef]
- Castillo-Zamora, J.J.; Camarillo-GóMez, K.A.; Perez-Soto, G.I.; Rodriguez-Resendiz, J. Comparison of PD, PID and Sliding-Mode Position Controllers for V-Tail Quadcopter Stability. IEEE Access 2018, 6, 38086–38096. [Google Scholar] [CrossRef]
- Demirel, B.; Ghadimi, E.; Quevedo, D.Q.; Johansson, M. Optimal Control of Linear Systems with Limited Control Actions: Threshold-Based Event-Triggered Control. IEEE Trans. Control. Netw. Syst. 2018, 5, 1275–1286. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Yan, Z.; Shaltout, M.L.; Chen, D. Optimal Real-Time Control of Wind Turbine During Partial Load Operation. IEEE Trans. Control. Syst. Technol. 2015, 23, 2216–2226. [Google Scholar] [CrossRef]
- Belkadi, A.; Oulhadj, H.; Touati, Y.; Khan, S.A.; Daachi, B. On the robust PID adaptive controller for exoskeletons: A particle swarm optimization based approach. Appl. Soft Comput. 2017, 60, 87–100. [Google Scholar] [CrossRef]
- Phu, D.X.; Mien, V.; Tu, P.H.T.; Nguyen, N.P.; Choi, S.B. A New Optimal Sliding Mode Controller with Adjustable Gains based on Bolza-Meyer Criterion for Vibration Control. J. Sound Vib. 2020, 485, 115542. [Google Scholar] [CrossRef]
- Suhaimin, S.C.; Azmi, N.L.; Rahman, M.M.; Yusof, H.M. Analysis of Point-to-Point Robotic Arm Control using PID Controller. In Proceedings of the 7th International Conference on Mechatronics Engineering, ICOM, Putrajaya, Malaysia, 30–31 October 2019; pp. 5–10. [Google Scholar] [CrossRef]
- Kang, S.; Chou, W. Kinematic Analysis, Simulation and Manipulating of a 5-DOF Robotic Manipulator for Service Robot. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 4–7 August 2019; pp. 643–649. [Google Scholar] [CrossRef]
- Mukherjee, S.; Goswami, D.; Chatterjee, S. A Lagrangian Approach to Modeling and Analysis of a Crowd Dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 865–876. [Google Scholar] [CrossRef]
- Wu, J.; Gao, J.; Song, R.; Li, R.; Li, Y.; Jiang, L. The design and control of a 3DOF lower limb rehabilitation robot. Mechatronics 2016, 33, 13–22. [Google Scholar] [CrossRef]
- Sun, J.D.; Cao, G.Z.; Li, W.B.; Liang, Y.X.; Huang, S.D. Analytical inverse kinematic solution using the D-H method for a 6-DOF robot. In Proceedings of the 14th International Conference on Ubiquitous Robots and Ambient Intelligence, Jeju, Korea, 28 June–1 July 2017; pp. 714–716. [Google Scholar] [CrossRef]
- Al-Oqaily, A.T.; Shakah, G. Solving Non-Linear Optimization Problems Using Parallel Genetic Algorithm. In Proceedings of the 8th International Conference on Computer Science and Information Technology, Amman, Jordan, 11–12 July 2018; pp. 103–106. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ramli, R.; Ibrahim, M.F. Optimal parameter estimation for a DC motor using genetic algorithm. Int. J. Power Electron. Drive Syst. (IJPEDS) 2020, 11, 1047–1054. [Google Scholar] [CrossRef]
- Xu, S. Predicted Residual Error Sum of Squares of Mixed Models: An Application for Genomic Prediction. G3 Genes Genomes Genet. 2017, 7, 895–909. [Google Scholar] [CrossRef] [Green Version]
- Rayno, J.; Iskander, M.F.; Kobayashi, M.H. Hybrid Genetic Programming with Accelerating Genetic Algorithm Optimizer for 3-D Metamaterial Design. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1743–1746. [Google Scholar] [CrossRef]
- Cheng, Y.F.; Shao, W.; Zhang, S.J.; Li, Y.P. An Improved Multi-Objective Genetic Algorithm for Large Planar Array Thinning. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ramli, R.; Ibrahim, M.F. Genetically optimized parameter estimation of mathematical model for multi-joints hip–knee exoskeleton. Robot. Auton. Syst. 2020, 125, 103425. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ramli, R.; Ibrahim, M.F. Hybrid design of PID controller for four DoF lower limb exoskeleton. Appl. Math. Model. 2019, 72, 17–27. [Google Scholar] [CrossRef]
- Sumathi, S.; Paneerselvam, S. Computational Intelligence Paradigms Theory and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ramli, R.; Ibrahim, M.F.; Wahab, D.A.; Aliman, N. Adaptive Particle Swarm Optimization of PID Gain Tuning for Lower-Limb Human Exoskeleton in Virtual Environment. Mathematics 2020, 8, 2040. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ramli, R.; Tarmizi, M.A.A.; Ibrahim, M.F.; Danesh Narooei, K. Simulation and Control of a Six Degree of Freedom Lower Limb Exoskeleton. J. Kejuruter. 2020, 32, 197–204. [Google Scholar] [CrossRef]









| link | |||||
|---|---|---|---|---|---|
| 0.3 | 0.15 | 0.748 | 0.0013 | 0.72 | |
| 0.19 | 0.095 | 0.8020 | 0.0043 | 0.83 | |
| 0.14 | 0.07 | 0.792 | 0.0023 | 0.95 | |
| 0.075 | 0.691 | 0.0015 | 1.88 | ||
| 0.02 | 0.2562 | 0.00012 | 0.83 |
| Joints | ||||
|---|---|---|---|---|
| One | 0 | 0 | 0 | |
| Two | 0 | |||
| Three | 0 | 0 | ||
| Four | 0 | 0 | ||
| Five | 0 |
| Runs | ||||
|---|---|---|---|---|
| GA | 1 | 4.33 | 1.87 | 6.12 |
| 2 | 0.0013 | 4.43 | 1.6 | |
| 3 | 1.24 | 1.99 | 5.23 | |
| 4 | 1.7 | 2.05 | 2.96 | |
| 5 | 4.25 | 2.0 | 1.76 | |
| 6 | 2.43 | 6.38 | 3.6 | |
| 7 | 3.913 | 8.19 | 7.5 | |
| 8 | 3.74 | 6.27 | 6.65 | |
| 9 | 3.95 | 3.95 | 1.75 | |
| 10 | 1.13 | 1.13 | 6.96 | |
| Mean | 1.54 | 3.83 | 2.83 | |
| Max | 1.3 | 8.19 | 7.5 | |
| variance | 1.61 | 5.87 | 9.69 | |
| H-value | 0.03 | |||
| Runs | ||||
| PSO | 1 | 1.14 | 1.45 | 6.20 |
| 2 | 5.43 | 2.2 | 9.41 | |
| 3 | 0.14 | 6.79 | 6.79 | |
| 4 | 8.57 | 2.44 | 1.99 | |
| 5 | 2.63 | 6.2 | 6.2 | |
| 6 | 2.5 | 1.01 | 6.2 | |
| 7 | 3.33 | 9.9 | 1.0 | |
| 8 | 7.28 | 6.24 | 5.66 | |
| 9 | 3.79 | 5.42 | 6.2 | |
| 10 | 3.68 | 2.81 | 6.2 | |
| Mean | 2.89 | 2.2 | 6.8 | |
| Max | 2.63 | 2.2 | 5.66 | |
| Variance | 6.79 | 4.83 | 3.14 | |
| H-value | 16.07 | |||
| Runs | ||||
| GSO | 1 | 8.34 | 6.2 | 6.2 |
| 2 | 1.74 | 3.03 | 2.37 | |
| 3 | 2.7 | 2.45 | 1.54 | |
| 4 | 1.71 | 1 | 6.2 | |
| 5 | 7.59 | 7.85 | 2.02 | |
| 6 | 7.19 | 6.79 | 6.2 | |
| 7 | 8.1 | 5.43 | 2.02 | |
| 8 | 6.2 | 7.76 | 5.49 | |
| 9 | 3.14 | 6.2 | 2.67 | |
| 10 | 2.87 | 7.63 | 4.99 | |
| Mean | 9.97 | 2.94 | 7.9 | |
| Max | 8.1 | 2.45 | 4.99 | |
| Variance | 7.13 | 5.98 | 2.86 | |
| H-value | 15.84 |
| Runs | GA | PSO | GSO |
|---|---|---|---|
| 1 | 8.35 (s) | 2.46 (s) | 3.87 (s) |
| 2 | 8.18 (s) | 2.41 (s) | 3.81 (s) |
| 3 | 8.01 (s) | 2.35 (s) | 3.83 (s) |
| 4 | 8.11 (s) | 2.40 (s) | 3.77 (s) |
| 5 | 8.09(s) | 2.41 (s) | 3.45 (s) |
| 6 | 8.33 (s) | 2.36 (s) | 3.80 (s) |
| 7 | 8.26 (s) | 2.39 (s) | 3.86 (s) |
| 8 | 8.26 (s) | 2.35 (s) | 3.54 (s) |
| 9 | 8.13 (s) | 2.37 (s) | 3.88 (s) |
| 10 | 8.38 (s) | 2.43 (s) | 3.84 (s) |
| Mean | 8.21 (s) | 2.39 (s) | 3.76 (s) |
| Positions | Angles | ||||
|---|---|---|---|---|---|
| Points | Coordinates | ||||
| A | (0.11,0.25,0.14) | 2.41 | 1.26 | 1.705 | −0.83 |
| B | (0.21,0.32,0.22) | 2.35 | 1.37 | 0.63 | −0.029 |
| C | (0.12,0.14,0.12) | 2.11 | 1.17 | 1.21 | 0.75 |
| D | (0.19,0.14,0.05) | 2.08 | 1.58 | 1.36 | −0.95 |
| E | (0.19,−0.1,0.5) | 1.25 | 0.3 | 0.59 | 1.04 |
| F | (0.21,−0.16,0.7) | 1.13 | 0.72 | 0.07 | −1.17 |
| G | (0.15,0.1,0.3) | 1.94 | 0.45 | 1.35 | 0.93 |
| H | (0.14,−0.11,0.14) | 1.16 | 1.49 | 0.34 | 1.67 |
| I | (0.12,0.15,0.05) | 2.15 | 1.44 | 1.49 | −0.17 |
| PSO | GA | GSO | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Joint 1 | 15.35 | 34.3233 | 2.8305 | 51.2684 | 175.3676 | 0.2106 | 36.2147 | 295.5165 | 0.2556 |
| Joint 2 | 26.8257 | 25.2366 | 7.8637 | 59.9833 | 173.4063 | 8.6907 | 39.5278 | 242.1184 | 8.4769 |
| Joint 3 | 13.3082 | 15.4017 | 3.3305 | 76.2230 | 160.6402 | 3.0397 | 83.4758 | 175.8795 | 3.3379 |
| Joint 4 | 5.4971 | 6.4876 | 3.4602 | 83.6052 | 189.7420 | 7.7188 | 68.0942 | 183.7764 | 4.1200 |
| Joint 1 | 0.0561 | 0.05871 | 0.5407 |
| Joint 2 | 0.0348 | 0.0313 | 0.0304 |
| Joint 3 | 0.0728 | 0.0794 | 0.0675 |
| Joint 4 | 0.0621 | 0.0605 | 0.0488 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soleimani Amiri, M.; Ramli, R. Intelligent Trajectory Tracking Behavior of a Multi-Joint Robotic Arm via Genetic–Swarm Optimization for the Inverse Kinematic Solution. Sensors 2021, 21, 3171. https://doi.org/10.3390/s21093171
Soleimani Amiri M, Ramli R. Intelligent Trajectory Tracking Behavior of a Multi-Joint Robotic Arm via Genetic–Swarm Optimization for the Inverse Kinematic Solution. Sensors. 2021; 21(9):3171. https://doi.org/10.3390/s21093171
Chicago/Turabian StyleSoleimani Amiri, Mohammad, and Rizauddin Ramli. 2021. "Intelligent Trajectory Tracking Behavior of a Multi-Joint Robotic Arm via Genetic–Swarm Optimization for the Inverse Kinematic Solution" Sensors 21, no. 9: 3171. https://doi.org/10.3390/s21093171
APA StyleSoleimani Amiri, M., & Ramli, R. (2021). Intelligent Trajectory Tracking Behavior of a Multi-Joint Robotic Arm via Genetic–Swarm Optimization for the Inverse Kinematic Solution. Sensors, 21(9), 3171. https://doi.org/10.3390/s21093171





