Robust Output Feedback Control of Single-Link Flexible-Joint Robot Manipulator with Matched Disturbances Using High Gain Observer
Abstract
:1. Introduction
2. Dynamical Model and Problem Statement
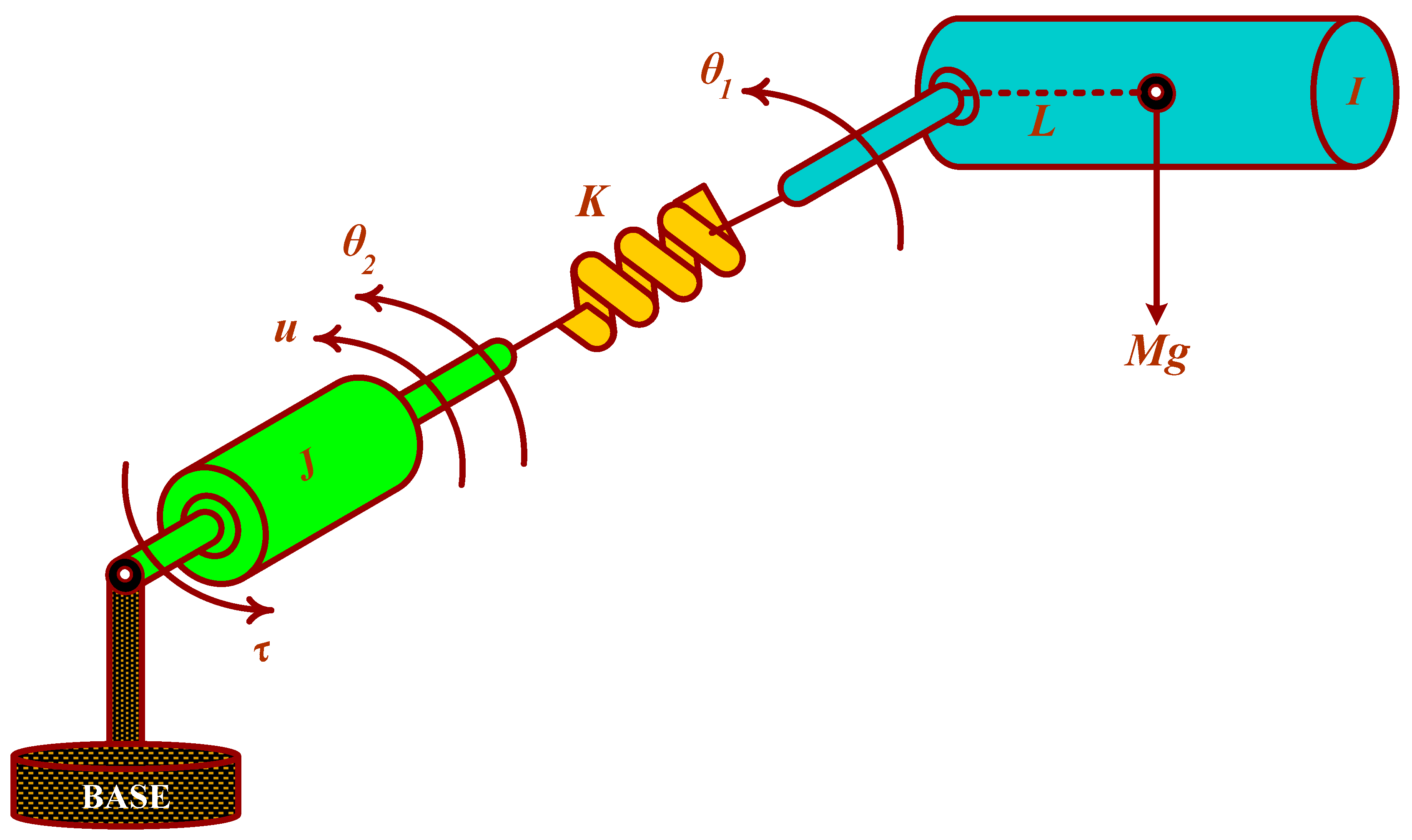
2.1. Dynamical Model of SFJRM
2.2. Problem Statement and Preliminaries
- (i)
- Sensing device is available only to measure the output i.e., position of SFJRM
- (ii)
- The parametric values of the system (, and ) are not exactly known
- (iii)
- The angular rate of the actuator is subjected to unknown bounded disturbances.
- (i)
- and for in the neighborhood of
- (ii)
- .
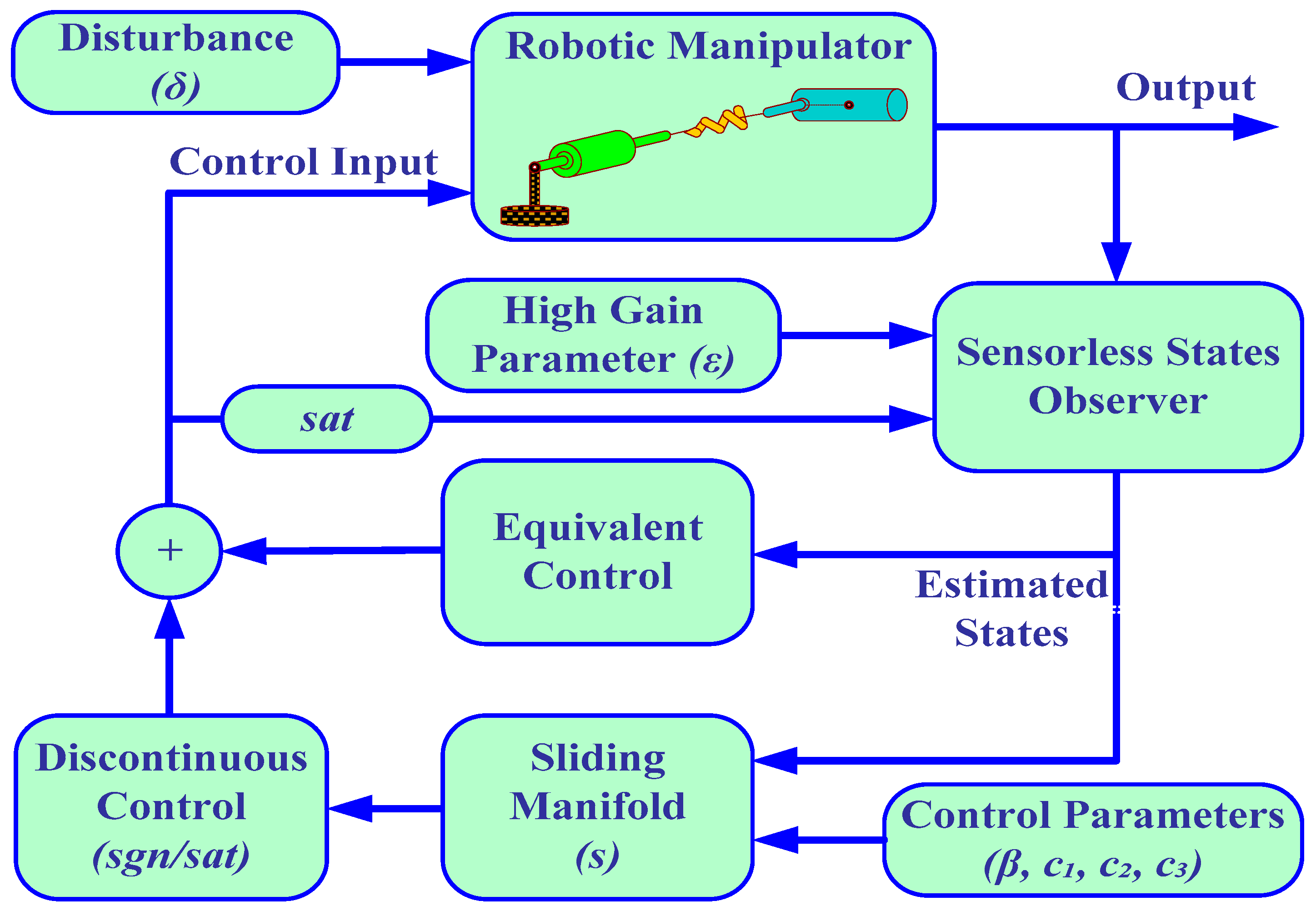
3. Sliding Mode Control Design
- Design of sliding surface
- Design of a discontinuous control to establish the sliding mode
4. High-Gain Observer Design
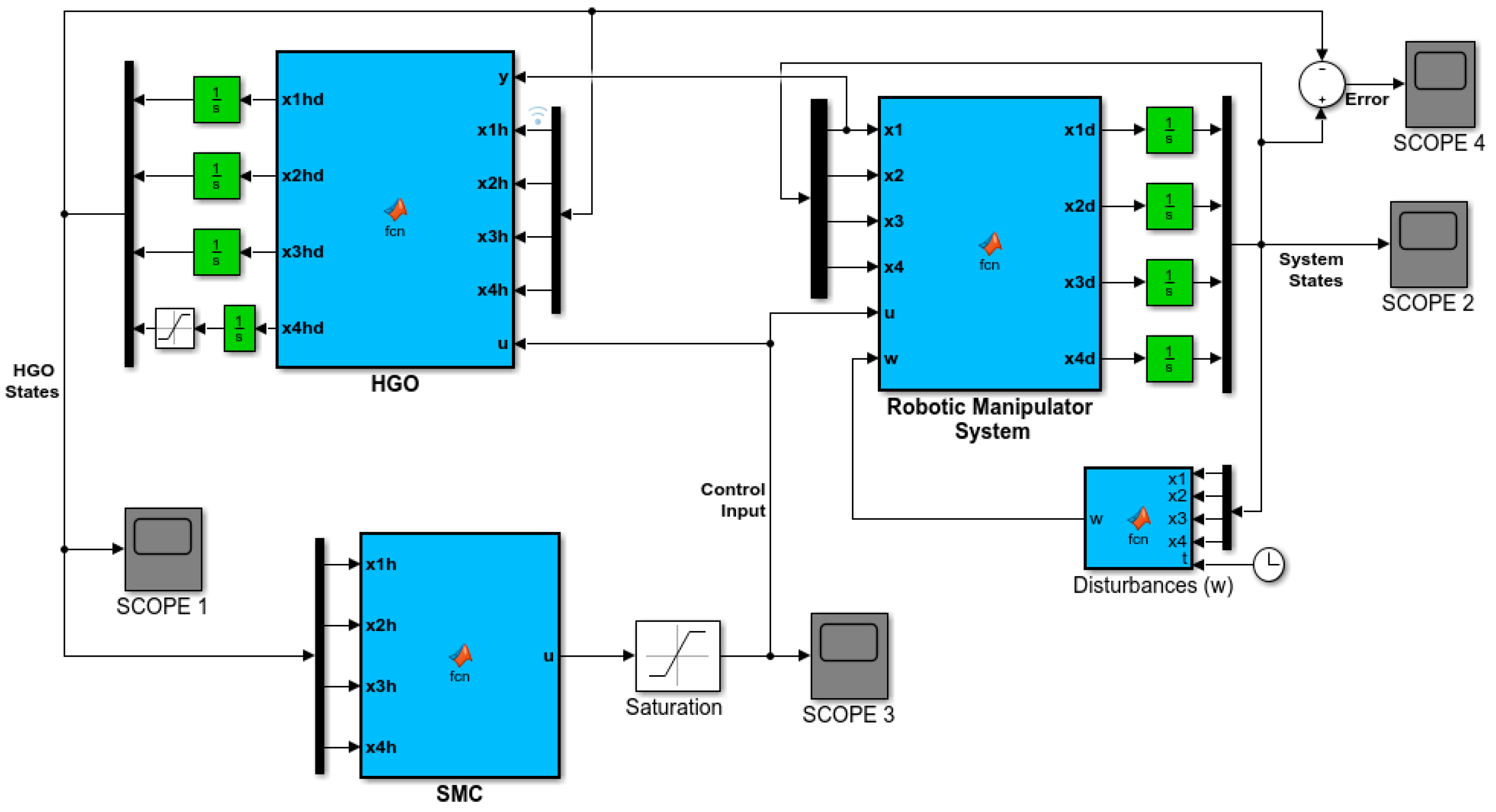
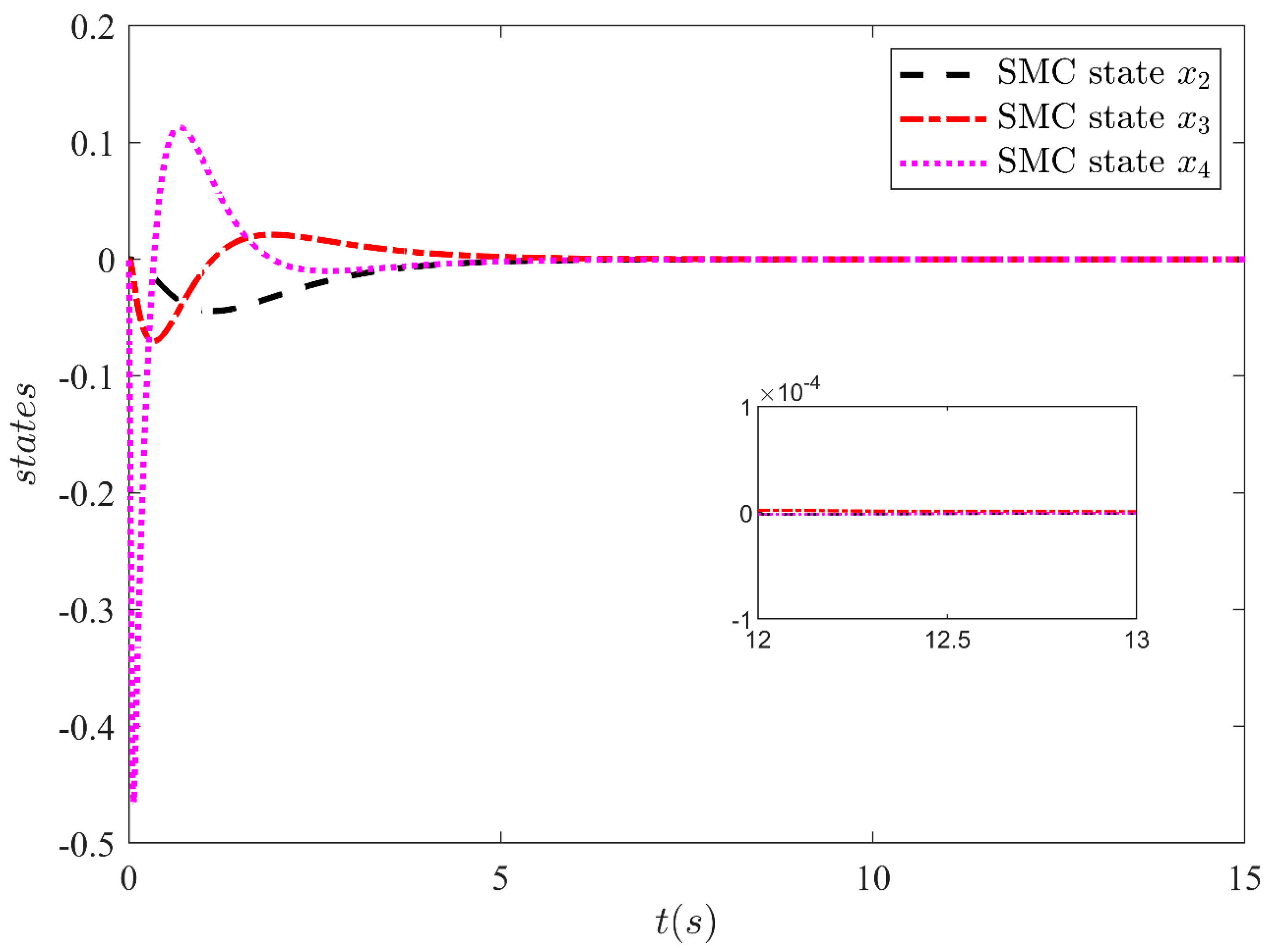
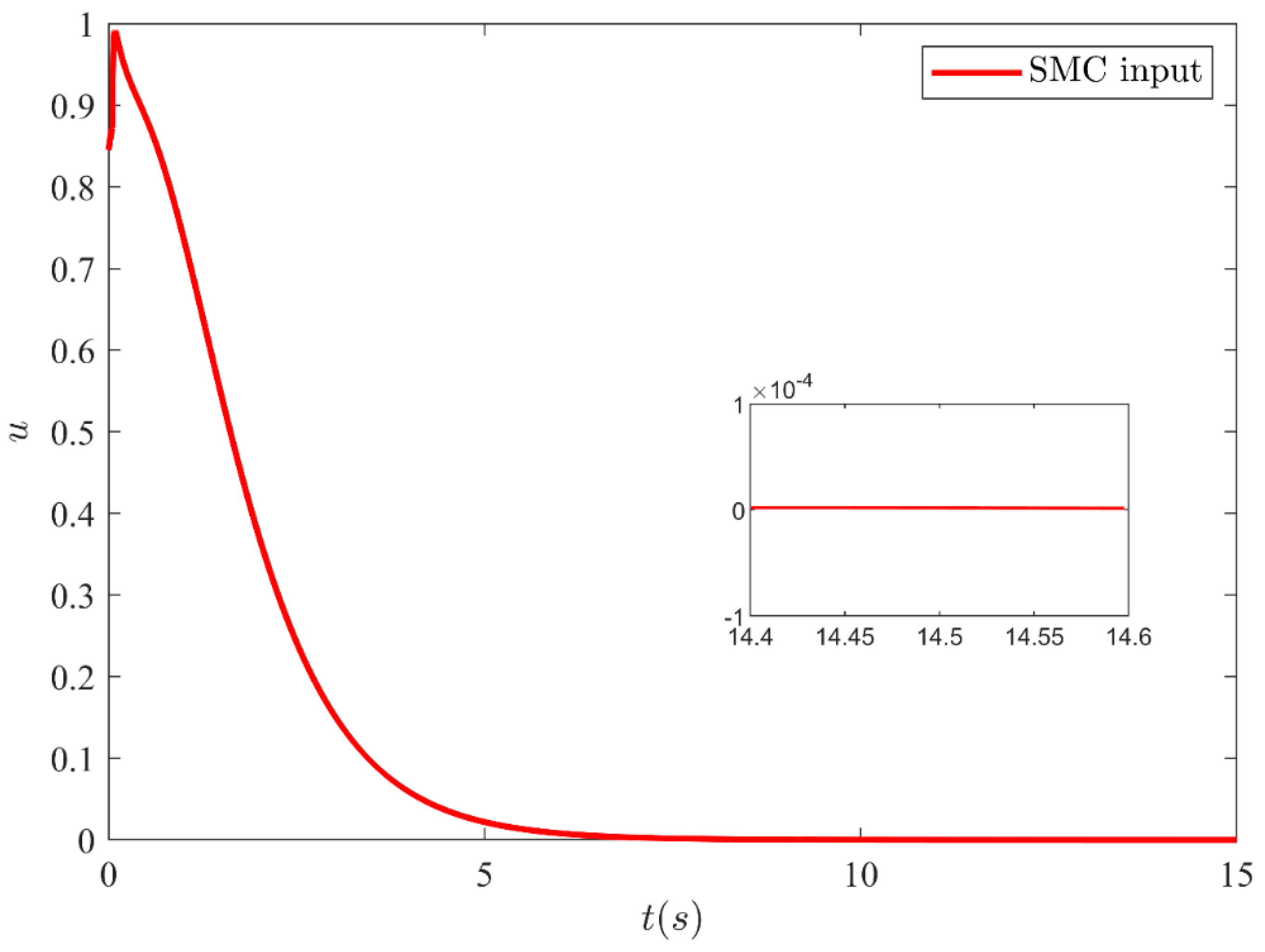
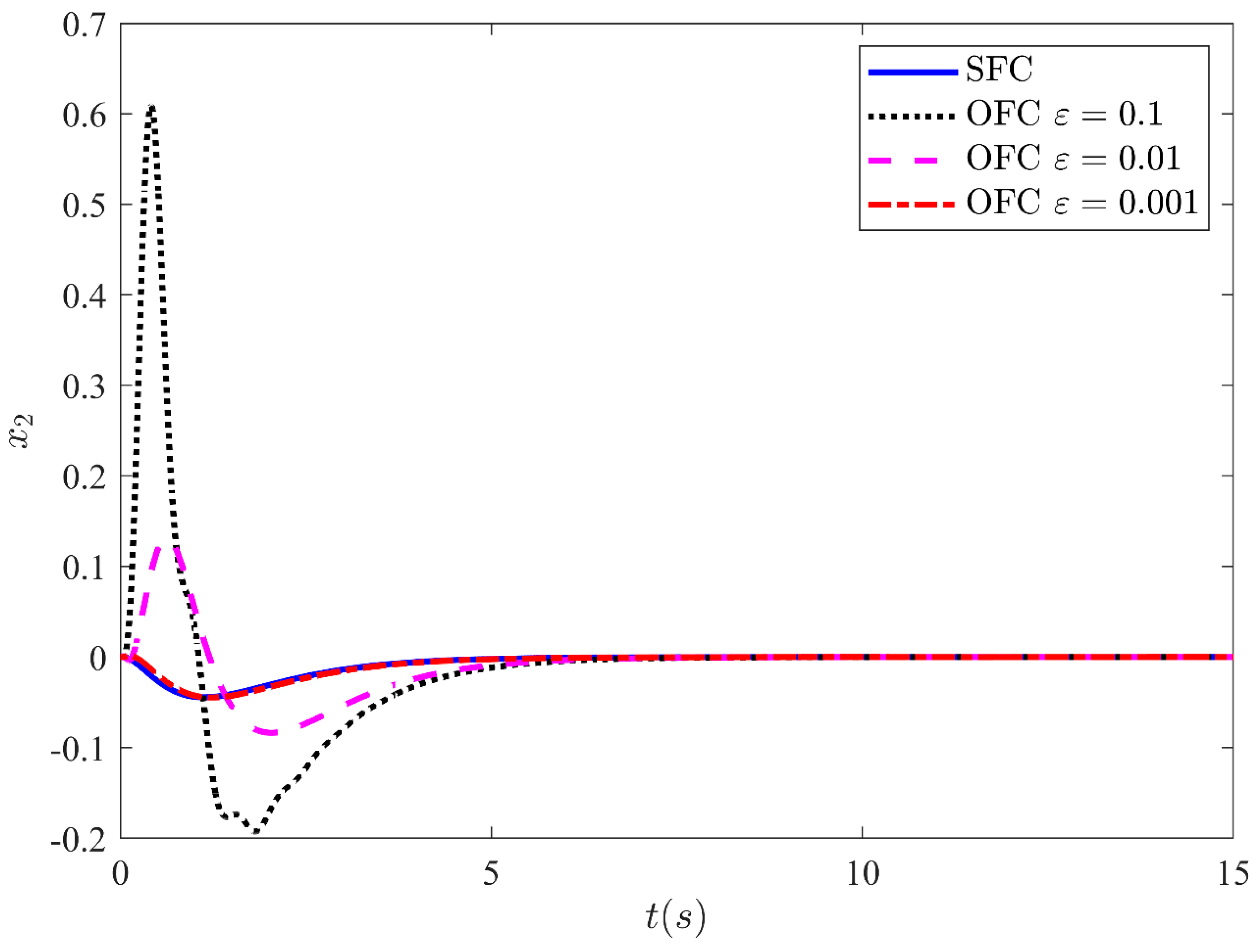
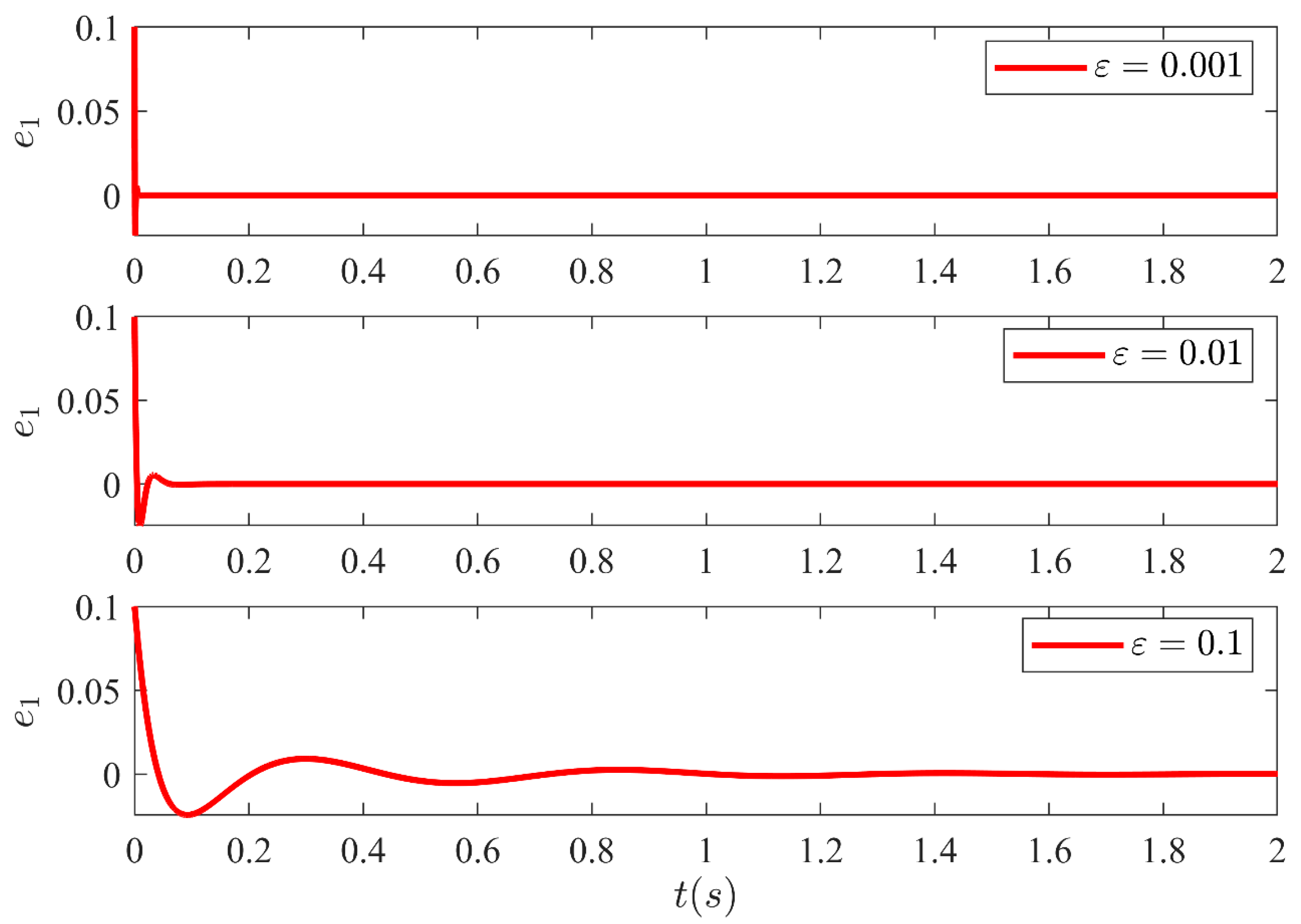
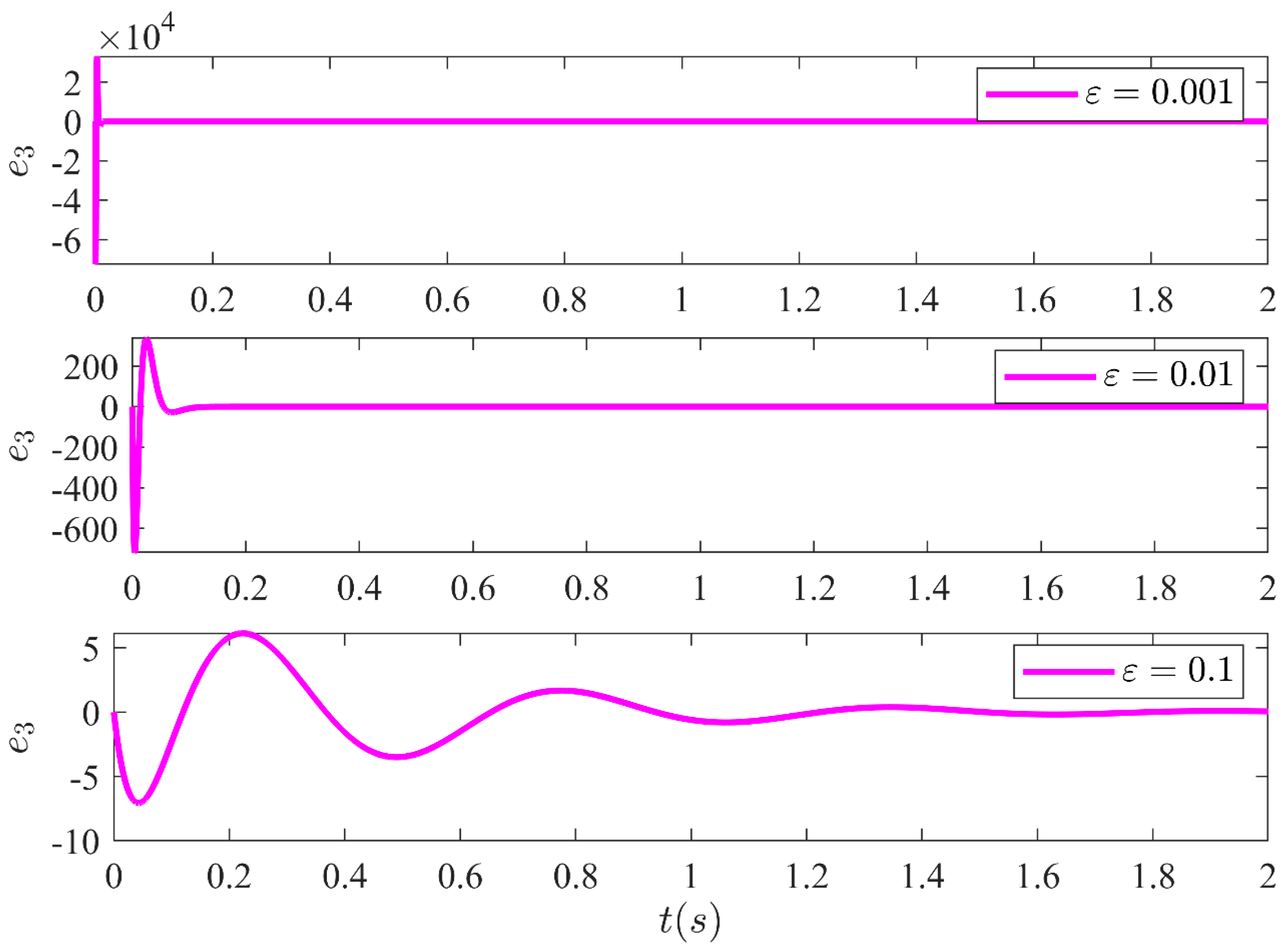
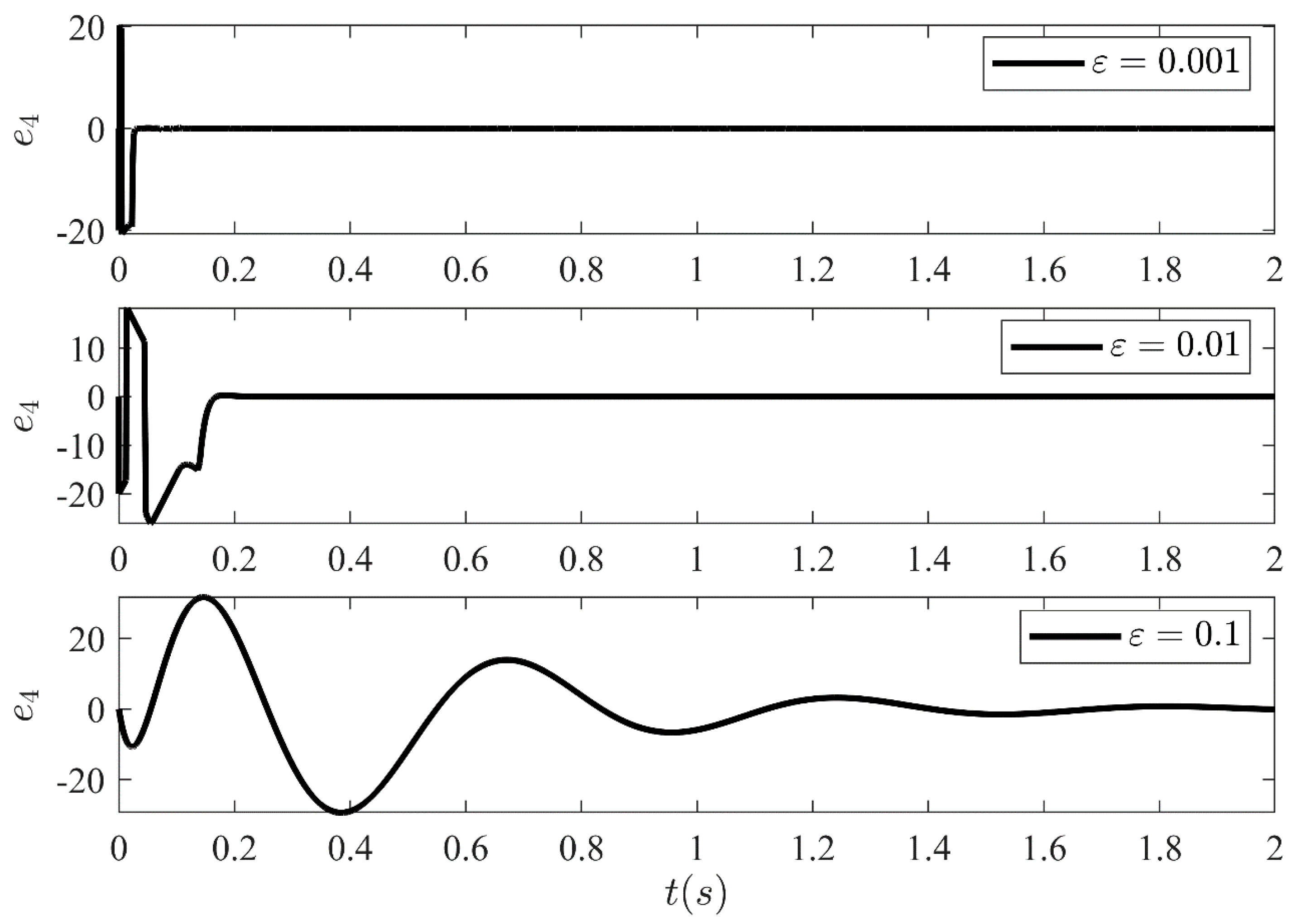
5. Simulation Results and Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ulrich, S.; Sasiadek, J.Z.; Barkana, I. Nonlinear adaptive output feedback control of flexible-joint space manipulators with joint stiffness uncertainties. J. Guid. Control Dyn. 2014, 37, 1961–1975. [Google Scholar] [CrossRef] [Green Version]
- Qiao, L.; Zhang, W. Adaptive non-singular integral terminal sliding mode tracking control for autonomous underwater vehicles. IET Control Theory Appl. 2017, 11, 1293–1306. [Google Scholar] [CrossRef]
- Suprem, A.; Mahalik, N.; Kim, K. A review on application of technology systems, standards and interfaces for agriculture and food sector. Comput. Stand. Interfaces 2013, 35, 355–364. [Google Scholar] [CrossRef]
- Yang, C.; Teng, T.; Xu, B.; Li, Z.; Na, J.; Su, C.-Y. Global adaptive tracking control of robot manipulators using neural networks with finite-time learning convergence. Int. J. Control Autom. Syst. 2017, 15, 1916–1924. [Google Scholar] [CrossRef]
- Bottin, M.; Cocuzza, S.; Comand, N.; Doria, A. Modeling and identification of an industrial robot with a selective modal approach. Appl. Sci. 2020, 10, 4619. [Google Scholar] [CrossRef]
- Yang, C.; Huang, K.; Cheng, H.; Li, Y.; Su, C.-Y. Haptic identification by ELM-controlled uncertain manipulator. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 239409. [Google Scholar] [CrossRef] [Green Version]
- Burgner-Kahrs, J.; Rucker, D.C.; Choset, H. Continuum robots for medical applications: A survey. IEEE Trans. Robot. 2015, 31, 126280. [Google Scholar] [CrossRef]
- Mosayebi, M.; Ghayour, M.; Sadigh, M.J. A nonlinear high gain observer based input–output control of flexible link manipulator. Mech. Res. Commun. 2012, 45, 34–41. [Google Scholar] [CrossRef]
- Rahimi, H.; Nazemizadeh, M. Dynamic analysis and intelligent control techniques for flexible manipulators: A review. Adv. Robot. 2014, 28, 63–76. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, M.; Zou, Y. Dynamic learning from adaptive neural control for flexible joint robot with tracking error constraints using high-gain observer. Syst. Sci. Control Eng. 2018, 6, 177–190. [Google Scholar] [CrossRef] [Green Version]
- Dwivedy, S.K.; Eberhard, P. Dynamic analysis of flexible manipulators, a literature review. Mech. Mach. Theory 2006, 41, 749–777. [Google Scholar] [CrossRef]
- Feliu-Talegon, D.; Feliu-Batlle, V.; Tejado, I.; Vinagre, B.M.; HosseinNia, S.H. Stable force control and contact transition of a single link flexible robot using a fractional-order controller. ISA Trans. 2019, 89, 139–157. [Google Scholar] [CrossRef] [PubMed]
- Wei, K.; Ren, B. A method on dynamic path planning for robotic manipulator autonomous obstacle avoidance based on an improved RRT algorithm. Sensors 2018, 18, 571. [Google Scholar] [CrossRef] [Green Version]
- Meng, Q.-X.; Lai, X.-Z.; Wang, Y.-W.; Wu, M. A fast stable control strategy based on system energy for a planar single-link flexible manipulator. Nonlinear Dyn. 2018, 94, 615–626. [Google Scholar] [CrossRef]
- Arteaga, M.A.; Siciliano, B. On tracking control of flexible robot arms. IEEE Trans. Autom. Control 2000, 45, 520–527. [Google Scholar] [CrossRef]
- Huang, A.-C.; Chen, Y.-C. Adaptive sliding control for single-link flexible-joint robot with mismatched uncertainties. IEEE Trans. Control Syst. Technol. 2004, 12, 770–775. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, B. Sliding mode fault tolerant tracking control for a single-link flexible joint manipulator system. IEEE Access 2019, 7, 83046–83057. [Google Scholar] [CrossRef]
- Singh, J.P.; Lochan, K.; Kuznetsov, N.V.; Roy, B. Coexistence of single-and multi-scroll chaotic orbits in a single-link flexible joint robot manipulator with stable spiral and index-4 spiral repellor types of equilibria. Nonlinear Dyn. 2017, 90, 1277–1299. [Google Scholar] [CrossRef]
- Pham, M.N.; Ahn, H.-J. Experimental optimization of a hybrid foil–magnetic bearing to support a flexible rotor. Mech. Systems Signal Process. 2014, 46, 361–372. [Google Scholar] [CrossRef]
- Nanos, K.; Papadopoulos, E.G. On the dynamics and control of flexible joint space manipulators. Control Eng. Pract. 2015, 45, 230–243. [Google Scholar] [CrossRef]
- Castillo-Berrio, C.F.; Feliu-Batlle, V. Vibration-free position control for a two degrees of freedom flexible-beam sensor. Mechatronics 2015, 27, 1–12. [Google Scholar] [CrossRef]
- Pan, Y.; Li, X.; Yu, H. Efficient PID tracking control of robotic manipulators driven by compliant actuators. IEEE Trans. Control Syst. Technol. 2018, 27, 915–922. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Chen, B.-S.; Lee, T.-C. Tracking control of flexible joint manipulators using only position measurements. Int. J. Control 1996, 64, 567–593. [Google Scholar] [CrossRef]
- Hernandez, J.; Barbot, J.-P. Sliding observer-based feedback control for flexible joints manipulator. Automatica 1996, 32, 1243–1254. [Google Scholar] [CrossRef]
- Ibrir, S.; Xie, W.F.; Su, C.-Y. Observer-based control of discrete-time Lipschitzian non-linear systems: Application to one-link flexible joint robot. Int. J. Control 2005, 78, 385–395. [Google Scholar] [CrossRef]
- Tomei, P. A simple PD controller for robots with elastic joints. IEEE Trans. Autom. Control 1991, 36, 1208–1213. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Sanchez, T.; Nuño, E.; Moreno, J.A. Lyapunov-based finite-time control of robot manipulators. Int. J. Robust Nonlinear Control 2021. [Google Scholar] [CrossRef]
- Hu, J.-L.; Sun, X.-X.; He, L.; Liu, R.; Deng, X.-F. Adaptive output feedback formation tracking for a class of multiagent systems with quantized input signals. Front. Inf. Technol. Electron. Eng. 2018, 19, 1086–1097. [Google Scholar] [CrossRef]
- Le-Tien, L.; Albu-Schäffer, A. Robust adaptive tracking control based on state feedback controller with integrator terms for elastic joint robots with uncertain parameters. IEEE Trans. Control Syst. Technol. 2017, 26, 2259–2267. [Google Scholar] [CrossRef]
- Korayem, M.H.; Nekoo, S. Finite-time state-dependent Riccati equation for time-varying nonaffine systems: Rigid and flexible joint manipulator control. ISA Trans. 2015, 54, 125–144. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Croft, E.A. Full-state tracking control for flexible joint robots with singular perturbation techniques. IEEE Trans. Control Syst. Technol. 2017, 27, 63–73. [Google Scholar] [CrossRef]
- Jin, H.; Liu, Z.; Zhang, H.; Liu, Y.; Zhao, J. A dynamic parameter identification method for flexible joints based on adaptive control. IEEE/ASME Trans. Mechatron. 2018, 23, 2896–2908. [Google Scholar] [CrossRef]
- He, W.; Yan, Z.; Sun, Y.; Ou, Y.; Sun, C. Neural-learning-based control for a constrained robotic manipulator with flexible joints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5993–6003. [Google Scholar] [CrossRef]
- Chen, S.; Xue, W.; Huang, Y. Analytical design of active disturbance rejection control for nonlinear uncertain systems with delay. Control Eng. Pract. 2019, 84, 323–336. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Y.; Li, D.; Lee, K.Y. Tuning of Active Disturbance Rejection Control with application to power plant furnace regulation. Control Eng. Pract. 2019, 92, 104122. [Google Scholar] [CrossRef]
- Wei, W.; Xue, W.; Li, D. On disturbance rejection in magnetic levitation. Control Eng. Pract. 2019, 82, 24–35. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, X.; Zhang, L.; Tang, M. Disturbance rejection for nonlinear systems with mismatched disturbances based on disturbance observer. J. Frankl. Inst. 2017, 354, 4404–4424. [Google Scholar] [CrossRef]
- Cao, P.; Gan, Y.; Dai, X. Finite-time disturbance observer for robotic manipulators. Sensors 2019, 19, 1943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Talole, S.E.; Kolhe, J.P.; Phadke, S.B. Extended-state-observer-based control of flexible-joint system with experimental validation. IEEE Trans. Ind. Electron. 2009, 57, 1411–1419. [Google Scholar] [CrossRef]
- Raza, A.; Malik, F.M.; Mazhar, N.; Khan, R.; Ullah, H. Feedback Linearization using High Gain Observer for Nonlinear Electromechanical Actuator. In Proceedings of the 22nd International Multitopic Conference (INMIC), Islamabad, Pakisan, 29–30 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Raza, A.; Malik, F.M.; Khan, R.; Mazhar, N.; Ullah, H. Robust output feedback control of fixed-wing aircraft. Aircr. Eng. Aerosp. Technol. 2020, 92, 1263–1273. [Google Scholar] [CrossRef]
- Farza, M.; M’Saad, M.; Triki, M.; Maatoug, T. High gain observer for a class of non-triangular systems. Syst. Control Lett. 2011, 60, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Sanfelice, R.G.; Praly, L. Convergence of Nonlinear Observers on ℝⁿ With a Riemannian Metric (Part I). IEEE Trans. Autom. Control 2011, 57, 1709–1722. [Google Scholar] [CrossRef] [Green Version]
- Khalil, H.K.; Praly, L. High-gain observers in nonlinear feedback control. Int. J. Robust Nonlinear Control 2014, 24, 993–1015. [Google Scholar] [CrossRef]
- Khalil, H.K. High-Gain Observers in Nonlinear Feedback Control; SIAM: Philadelphia, PA, USA, 2017. [Google Scholar]
- Ahmad, I.; Liaquat, M.; Malik, F.M.; Ullah, H.; Ali, U. Variants of the Sliding Mode Control in Presence of External Disturbance for Quadrotor. IEEE Access 2020, 8, 227810–227824. [Google Scholar] [CrossRef]
- Raza, A.; Malik, F.M.; Mazhar, N.; Ullah, H.; Khan, R. Finite-Time Trajectory Tracking Control of Output-Constrained Uncertain Quadrotor. IEEE Access 2020, 8, 215603–215612. [Google Scholar] [CrossRef]
- Zaare, S.; Soltanpour, M.R.; Moattari, M. Voltage based sliding mode control of flexible joint robot manipulators in presence of uncertainties. Robot. Auton. Syst. 2019, 118, 204–219. [Google Scholar] [CrossRef]
- Zhao, H.; Niu, Y. Finite-time sliding mode control of switched systems with one-sided Lipschitz nonlinearity. J. Frankl. Inst. 2020, 357, 11171–11188. [Google Scholar] [CrossRef]
- Zaare, S.; Soltanpour, M.R.; Moattari, M. Adaptive slidig mode cotrol of n flexible-joit robot maipulators in the presece of structured and ustructured ucertaities. Multibody Syst. Dyn. 2019, 47, 397–434. [Google Scholar] [CrossRef]
- Veysi, M.; Soltanpour, M.R.; Khooban, M.H. A novel self-adaptive modified bat fuzzy sliding mode control of robot manipulator in presence of uncertainties in task space. Robotica 2015, 33, 2045–2064. [Google Scholar] [CrossRef]
- Narang-Siddarth, A.; Valasek, J. Nonlinear Time Scale Systems in Standard and Nonstandard Forms: Analysis and Control; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Marchetti, D.H.; Conti, W.R. Singular Perturbation of Nonlinear Systems with Regular Singularity. Discret. Dyn. Nat. Soc. 2018, 2018. [Google Scholar] [CrossRef]
- Isidori, A. Nonlinear Control Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]







| Symbol | Description | Value (Unit) |
|---|---|---|
| Mass of the link | ||
| Length of the mass location from the center | ||
| Spring stiffness | ||
| Inertia of the link | ||
| Inertia of the actuator | ||
| Gravitational acceleration |
| SMC Parameter | Value | HGO Parameter | Value |
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, H.; Malik, F.M.; Raza, A.; Mazhar, N.; Khan, R.; Saeed, A.; Ahmad, I. Robust Output Feedback Control of Single-Link Flexible-Joint Robot Manipulator with Matched Disturbances Using High Gain Observer. Sensors 2021, 21, 3252. https://doi.org/10.3390/s21093252
Ullah H, Malik FM, Raza A, Mazhar N, Khan R, Saeed A, Ahmad I. Robust Output Feedback Control of Single-Link Flexible-Joint Robot Manipulator with Matched Disturbances Using High Gain Observer. Sensors. 2021; 21(9):3252. https://doi.org/10.3390/s21093252
Chicago/Turabian StyleUllah, Hameed, Fahad Mumtaz Malik, Abid Raza, Naveed Mazhar, Rameez Khan, Anjum Saeed, and Irfan Ahmad. 2021. "Robust Output Feedback Control of Single-Link Flexible-Joint Robot Manipulator with Matched Disturbances Using High Gain Observer" Sensors 21, no. 9: 3252. https://doi.org/10.3390/s21093252
APA StyleUllah, H., Malik, F. M., Raza, A., Mazhar, N., Khan, R., Saeed, A., & Ahmad, I. (2021). Robust Output Feedback Control of Single-Link Flexible-Joint Robot Manipulator with Matched Disturbances Using High Gain Observer. Sensors, 21(9), 3252. https://doi.org/10.3390/s21093252






