A New Stochastic Model Updating Method Based on Improved Cross-Model Cross-Mode Technique
Abstract
:1. Introduction
2. Theoretical Background
2.1. The ICMCM Method
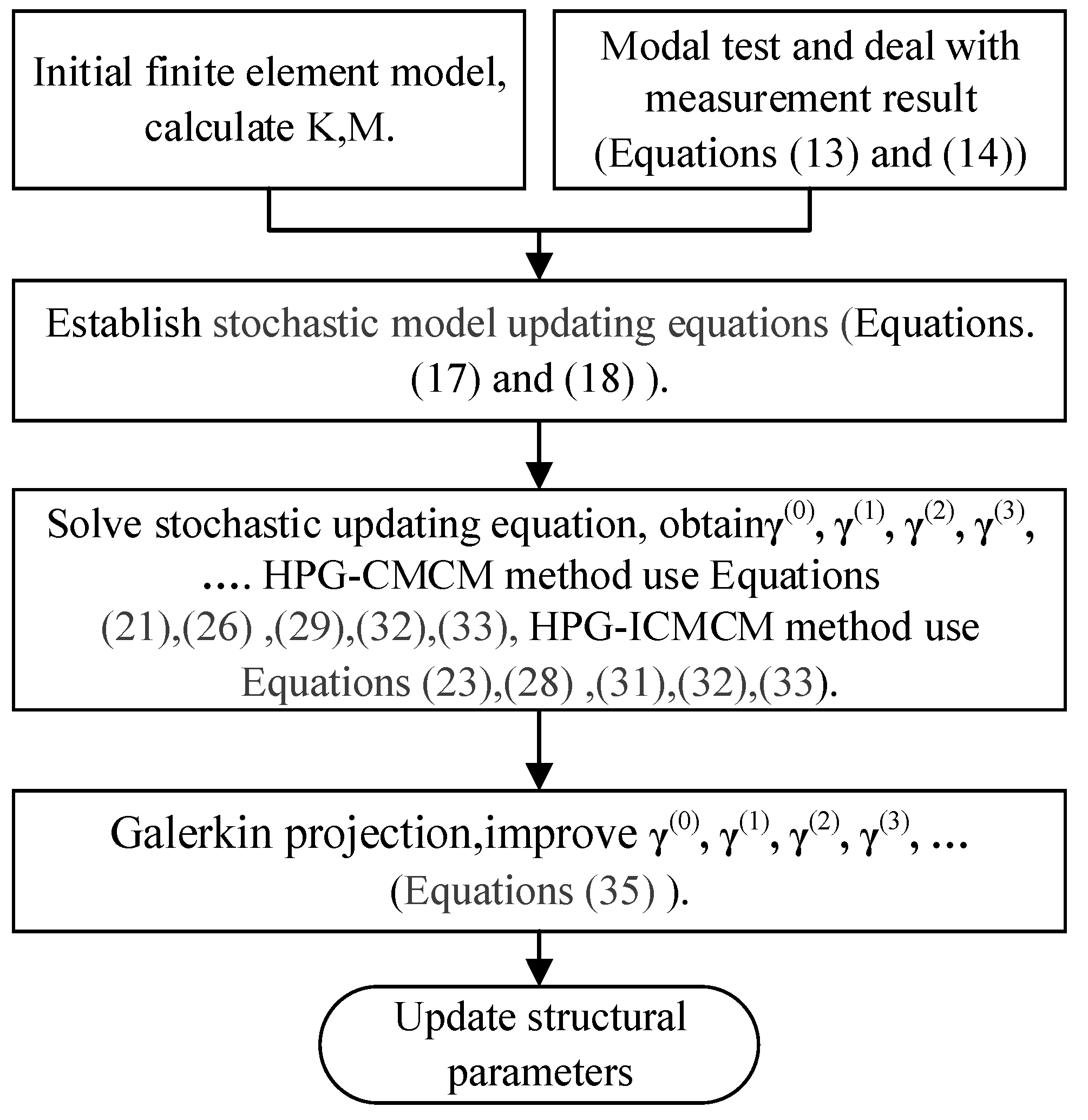
2.2. The Stochastic ICMCM Method
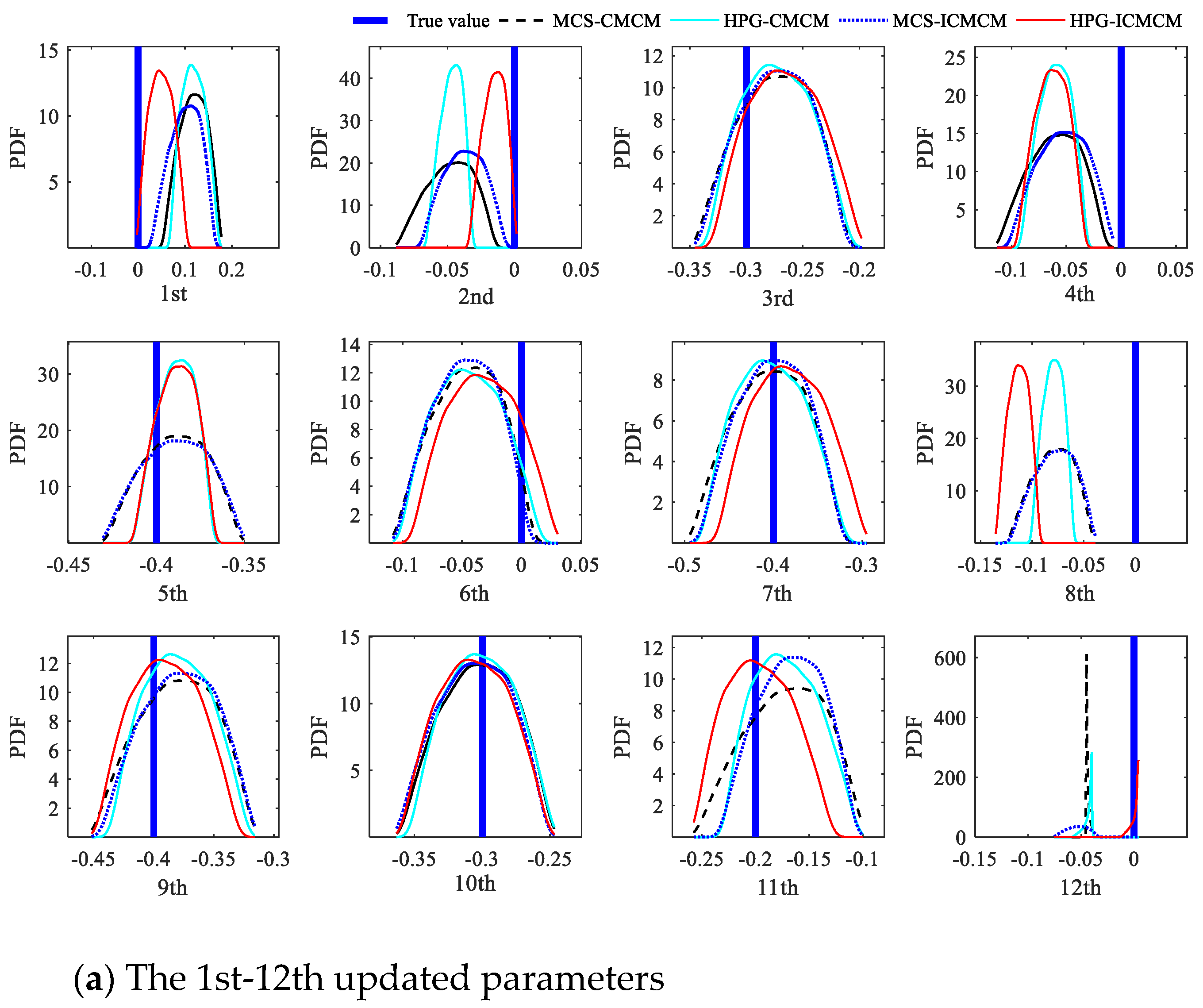
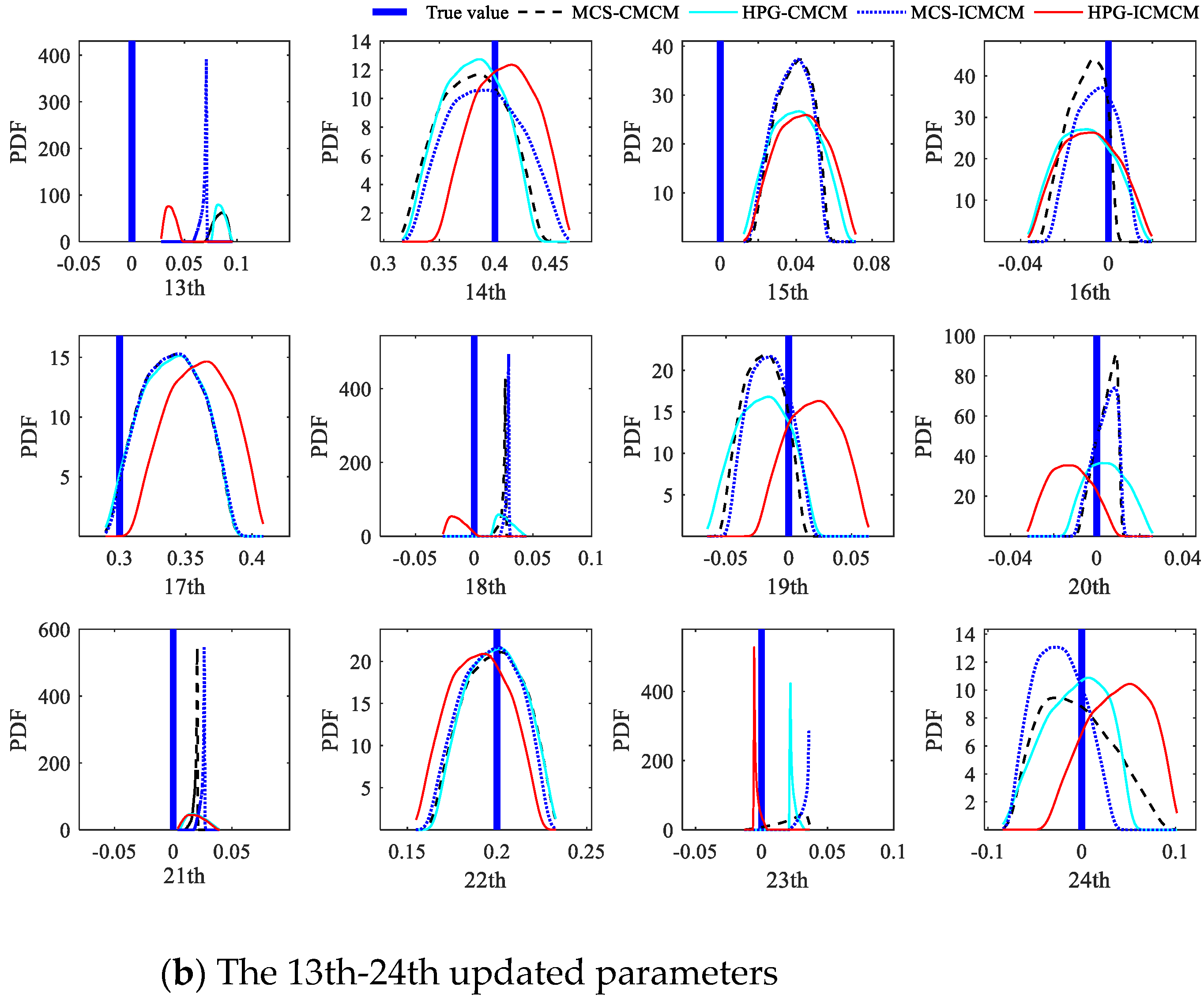
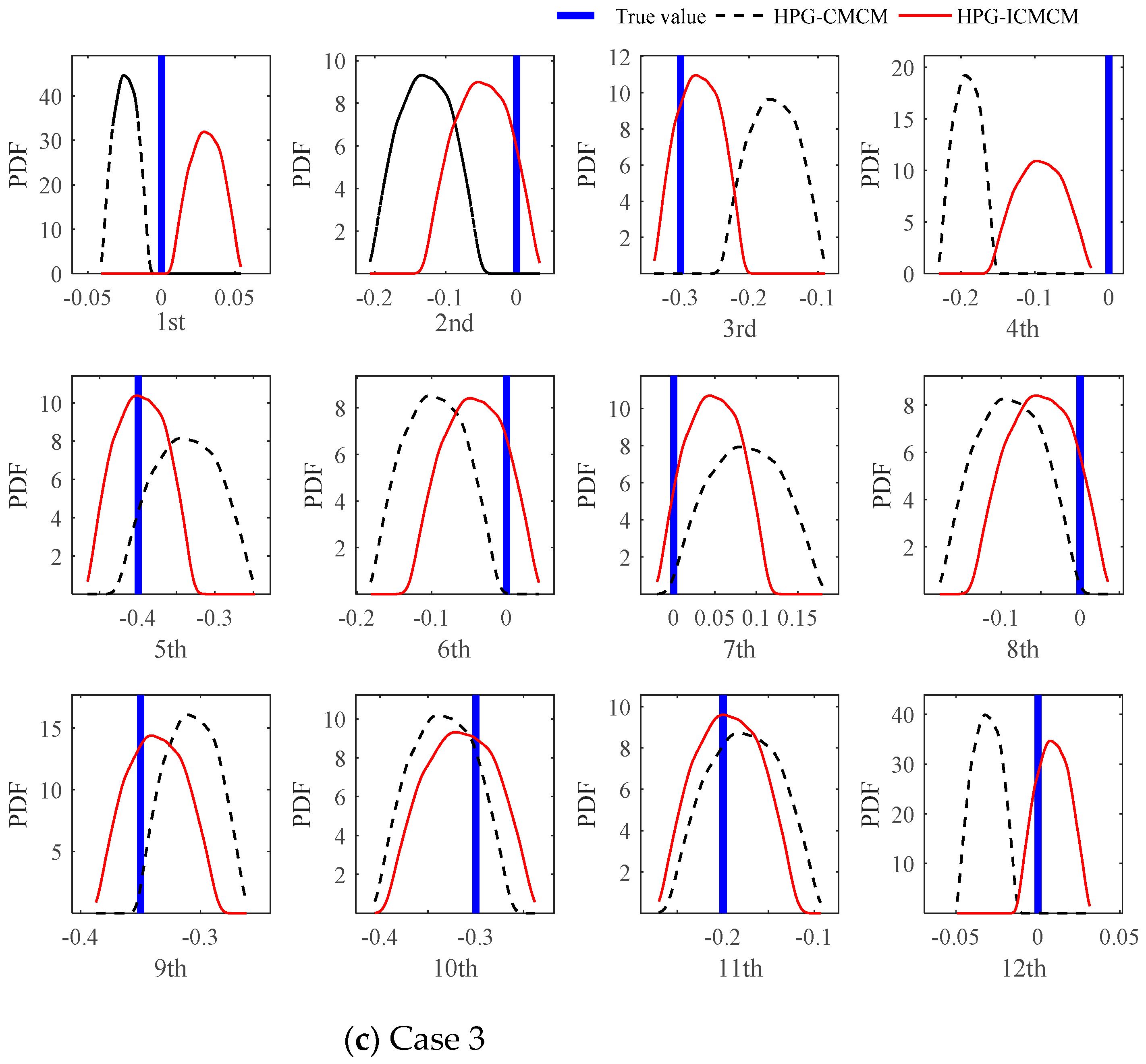
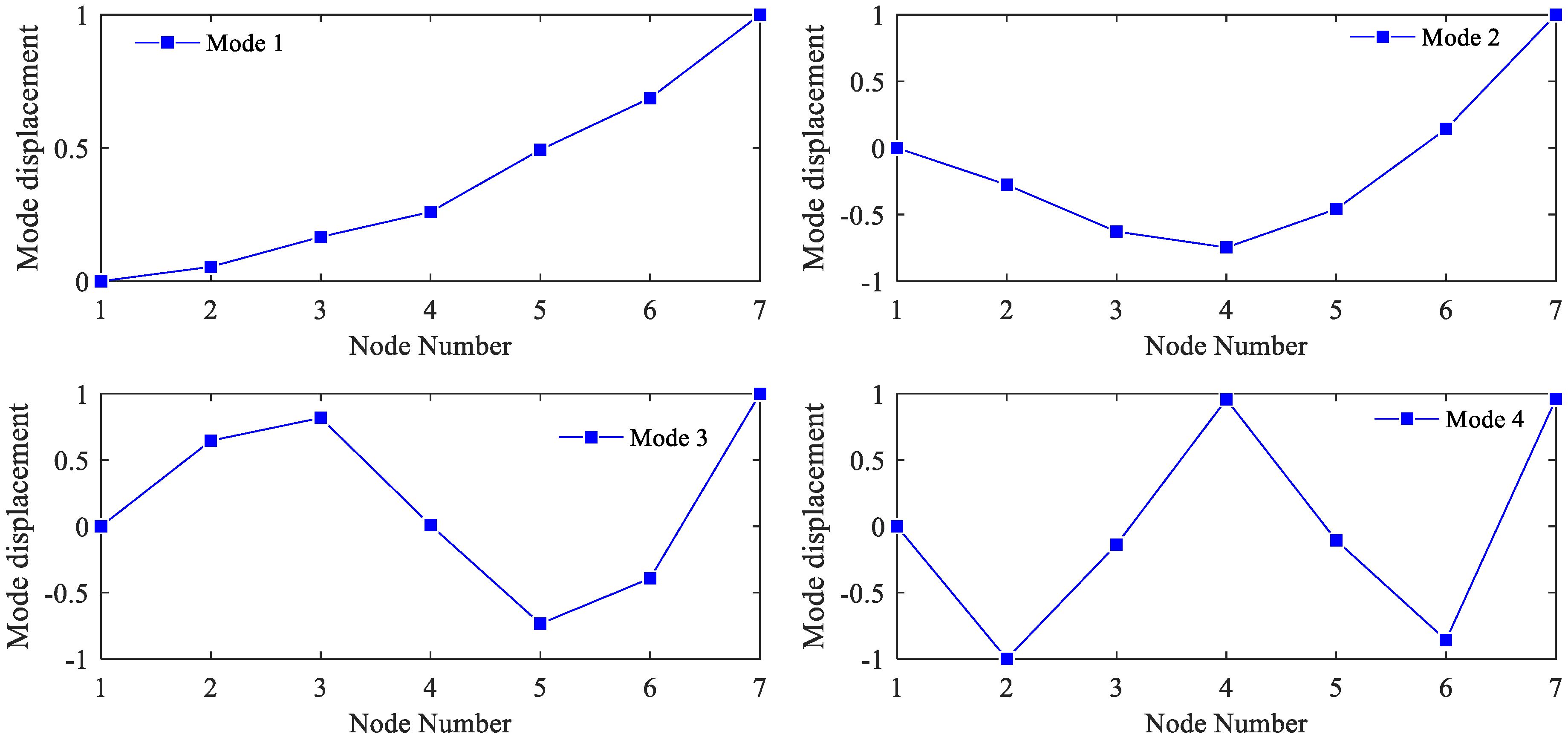
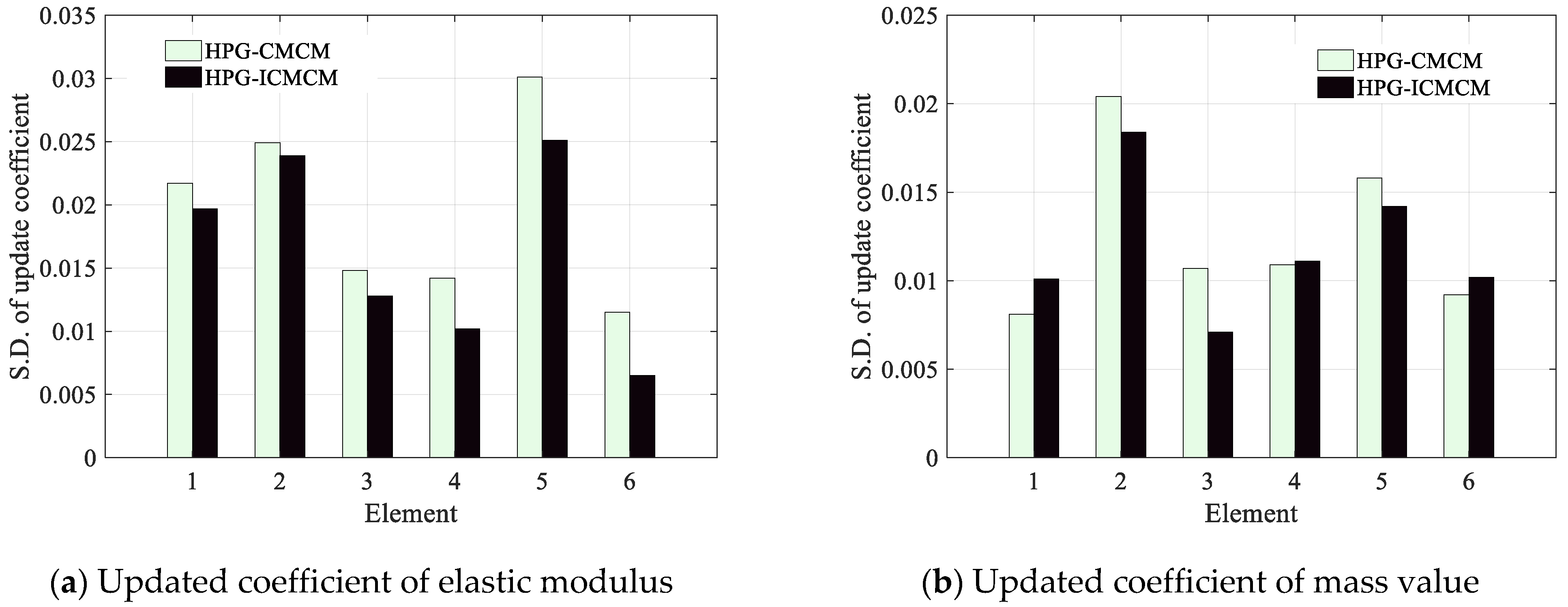
3. Numerical Study: A Two-Span Continuous Beam
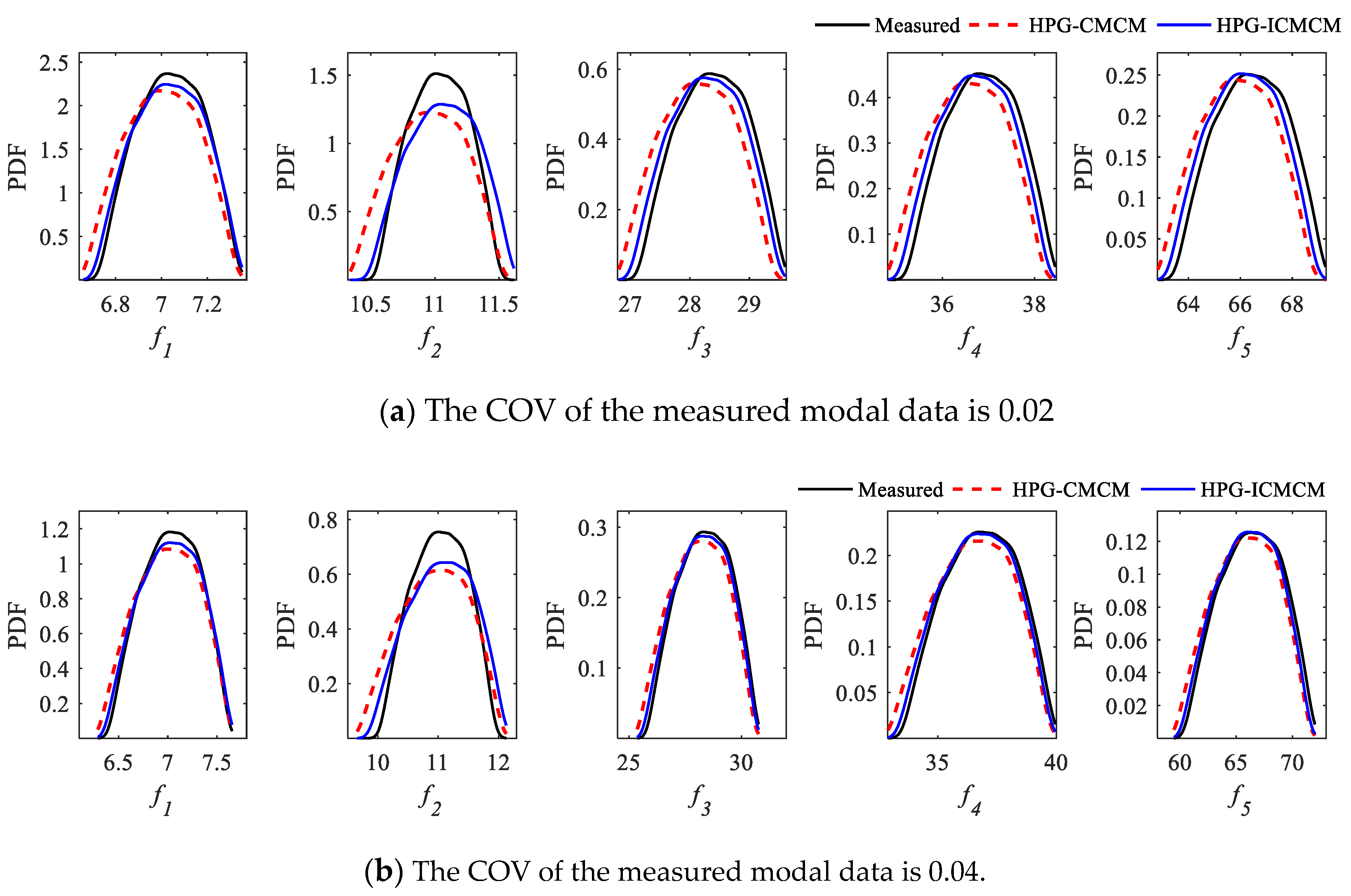
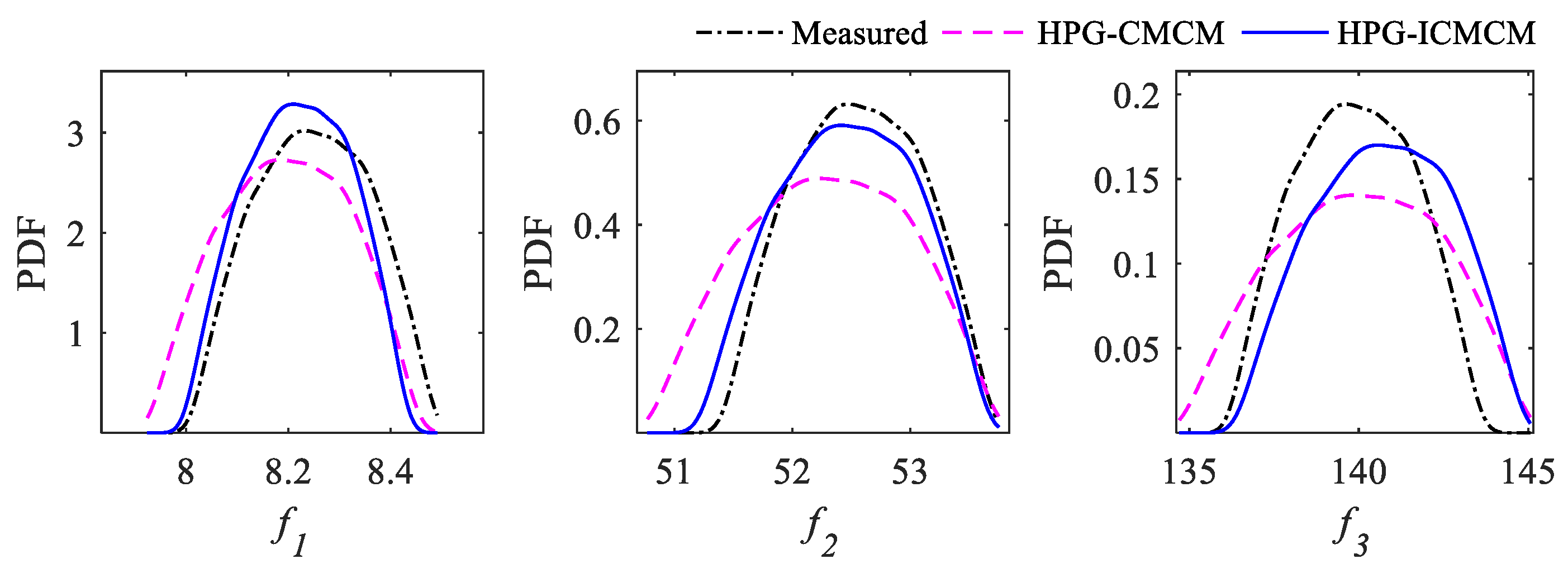
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, K.; Xu, Y.-L.; Lu, X.; Guan, Z.; Li, J. Cluster computing-aided model updating for a high-fidelity finite element model of a long-span cable-stayed bridge. Earthq. Eng. Struct. Dyn. 2020, 49, 904–923. [Google Scholar] [CrossRef]
- Hua, X.G.; Ni, Y.Q.; Chen, Z.Q.; Ko, J.M. An improved perturbation method for stochastic finite element model updating. Int. J. Numer. Methods Eng. 2008, 73, 1845–1864. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y.; Zhou, X. Structural damage detection based on l1 regularization using natural frequencies and mode shapes. Struct. Control. Health Monit. 2018, 25, e2107. [Google Scholar] [CrossRef]
- Huang, M.; Cheng, X.; Lei, Y. Structural damage identification based on substructure method and improved whale optimization algorithm. J. Civ. Struct. Health Monit. 2021, 11, 351–380. [Google Scholar] [CrossRef]
- Huang, M.; Li, X.; Lei, Y.; Gu, J. Structural damage identification based on modal frequency strain energy assurance criterion and flexibility using enhanced Moth-Flame optimization. Structures 2020, 28, 1119–1136. [Google Scholar] [CrossRef]
- Huang, M.S.; Cheng, S.X.; Zhang, H.Y.; Gul, M.; Lu, H. Structural damage identification under temperature variations based on PSO-CS hybrid algorithm. Int. J. Struct. Stab. Dyn. 2019, 19, 1950139. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.-S.; Gül, M.; Zhu, H.-P. Vibration-Based Structural Damage Identification under Varying Temperature Effects. J. Aerosp. Eng. 2018, 31, 04018014. [Google Scholar] [CrossRef]
- Ren, W.-X.; De Roeck, G. Structural Damage Identification using Modal Data. II: Test Verification. J. Struct. Eng. 2002, 128, 96–104. [Google Scholar] [CrossRef]
- Hu, S.J.; Li, H.; Wang, S. Cross-model cross-mode method for model updating. Mech. Syst. Signal Process. 2007, 21, 1690–1703. [Google Scholar] [CrossRef]
- Yan, W.-J.; Ren, W.-X. Closed-form modal flexibility sensitivity and its application to structural damage detection without modal truncation error. J. Vib. Control. 2014, 20, 1816–1830. [Google Scholar] [CrossRef]
- Yang, Q. A new damage identification method based on structural flexibility disassembly. J. Vib. Control. 2011, 17, 1000–1008. [Google Scholar] [CrossRef]
- Huang, B.; Chen, H. A new approach for stochastic model updating using the hybrid perturbation-Galerkin method. Mech. Syst. Signal Process. 2019, 129, 1–19. [Google Scholar] [CrossRef]
- Hasançebi, O.; Dumlupınar, T. Linear and nonlinear model updating of reinforced concrete T-beam bridges using artificial neural networks. Comput. Struct. 2013, 119, 1–11. [Google Scholar] [CrossRef]
- Deng, Z.; Guo, Z.; Zhang, X. Interval model updating using perturbation method and Radial Basis Function neural networks. Mech. Syst. Signal Process. 2017, 84, 699–716. [Google Scholar] [CrossRef]
- Huang, M.; Lei, Y.; Li, X. Structural Damage Identification Based on l1Regularization and Bare Bones Particle Swarm Optimization with Double Jump Strategy. Math. Probl. Eng. 2019, 2019, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Sehgal, S.; Kumar, H. Structural Dynamic Model Updating Techniques: A State of the Art Review. Arch. Comput. Methods Eng. 2015, 23, 515–533. [Google Scholar] [CrossRef]
- Fang, S.-E.; Perera, R. Damage identification by response surface based model updating using D-optimal design. Mech. Syst. Signal Process. 2011, 25, 717–733. [Google Scholar] [CrossRef]
- Jacquelin, E.; Adhikari, S.; Friswell, M. A second-moment approach for direct probabilistic model updating in structural dynamics. Mech. Syst. Signal Process. 2012, 29, 262–283. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Hu, S.-L.J. Using incomplete modal data for damage detection in offshore jacket structures. Ocean Eng. 2008, 35, 1793–1799. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Li, H. Structural model updating of an offshore platform using the cross model cross mode method: An experimental study. Ocean Eng. 2015, 97, 57–64. [Google Scholar] [CrossRef]
- Liu, K.; Yan, R.-J.; Soares, C.G. An improved model updating technique based on modal data. Ocean Eng. 2018, 154, 277–287. [Google Scholar] [CrossRef]
- Schuëller, G.I.; Calvi, A.; Pellissetti, M.F.; Pradlwarter, H.J.; Fransen, S.H.J.A.; Kreis, A. Uncertainty Analysis of a Large-Scale Satellite Finite Element Model. J. Spacecr. Rocket. 2009, 46, 191–202. [Google Scholar] [CrossRef]
- Hua, X.G.; Ni, Y.Q.; Chen, Z.Q.; He, X.H. Monte Carlo Study of the Effect of Measurement Noise in Model Updating with Regularization. J. Eng. Mech. 2012, 138, 71–81. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties—I: Bayesian statistical framework. J. Eng. Mech. 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Katafygiotis, L.S.; Beck, J.L. Updating models and their uncertainties—II: Model identifiability. J. Eng. Mech. 1998, 124, 463–467. [Google Scholar] [CrossRef]
- Lam, H.-F.; Yang, J.-H.; Au, S.-K. Markov chain Monte Carlo-based Bayesian method for structural model updating and damage detection. Struct. Control. Health Monit. 2018, 25, e2140. [Google Scholar] [CrossRef]
- Wan, H.P.; Ren, W.X. Stochastic model updating utilizing Bayesian approach and Gaussian process model. Mech. Syst. Signal Process. 2016, 70, 245–268. [Google Scholar] [CrossRef]
- Fang, S.E.; Chen, S.; Lin, Y.Q.; Dong, Z.L. Probabilistic damage identification incorporating approximate Bayesian computation with stochastic response surface. Mech. Syst. Signal Process. 2019, 128, 229–243. [Google Scholar] [CrossRef]
- Li, Y.-J.; Huang, B.; Li, C.-Q. Hybrid perturbation-Galerkin methods for structural reliability analysis. Probab. Eng. Mech. 2017, 48, 59–67. [Google Scholar] [CrossRef]
- Peeters, B.; Abdel Wahab, M.; De Roeck, G.; De Visscher, J.; De Wilde, W.P.; Ndambi, M.; Vantomme, J. Evaluation of structural damage by dynamic system identification. In Proceedings of the ISMA 21, the 21th International Seminar on Modal Analysis, Katholieke Universiteit Leuven, Leuven, Belgium, 18–20 September 1996; pp. 1349–1361. [Google Scholar]




| Case No. | Number of Modes | Method | Rank | Number of Updating Equations |
|---|---|---|---|---|
| Case 1 | Nc = 6, Nm = 4 | CMCM | = 12 | 24 |
| ICMCM | = 12 | 40 | ||
| Case 2 | Nc = 3, Nm = 3 | CMCM | = 9 | 9 |
| ICMCM | = 12 | 18 | ||
| Case 3 | Nc = 4, Nm = 2 | CMCM | = 8 | 8 |
| ICMCM | = 12 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Huang, B.; Tee, K.F.; Lu, B. A New Stochastic Model Updating Method Based on Improved Cross-Model Cross-Mode Technique. Sensors 2021, 21, 3290. https://doi.org/10.3390/s21093290
Chen H, Huang B, Tee KF, Lu B. A New Stochastic Model Updating Method Based on Improved Cross-Model Cross-Mode Technique. Sensors. 2021; 21(9):3290. https://doi.org/10.3390/s21093290
Chicago/Turabian StyleChen, Hui, Bin Huang, Kong Fah Tee, and Bo Lu. 2021. "A New Stochastic Model Updating Method Based on Improved Cross-Model Cross-Mode Technique" Sensors 21, no. 9: 3290. https://doi.org/10.3390/s21093290
APA StyleChen, H., Huang, B., Tee, K. F., & Lu, B. (2021). A New Stochastic Model Updating Method Based on Improved Cross-Model Cross-Mode Technique. Sensors, 21(9), 3290. https://doi.org/10.3390/s21093290






