Intelligent Fault Diagnosis Framework for Modular Multilevel Converters in HVDC Transmission
Abstract
:1. Introduction
- The proposed intelligent fault diagnosis framework utilises only current sensor data for fault diagnosis. This study achieves high accuracy of fault diagnosis using only current sensors and AI-based techniques.
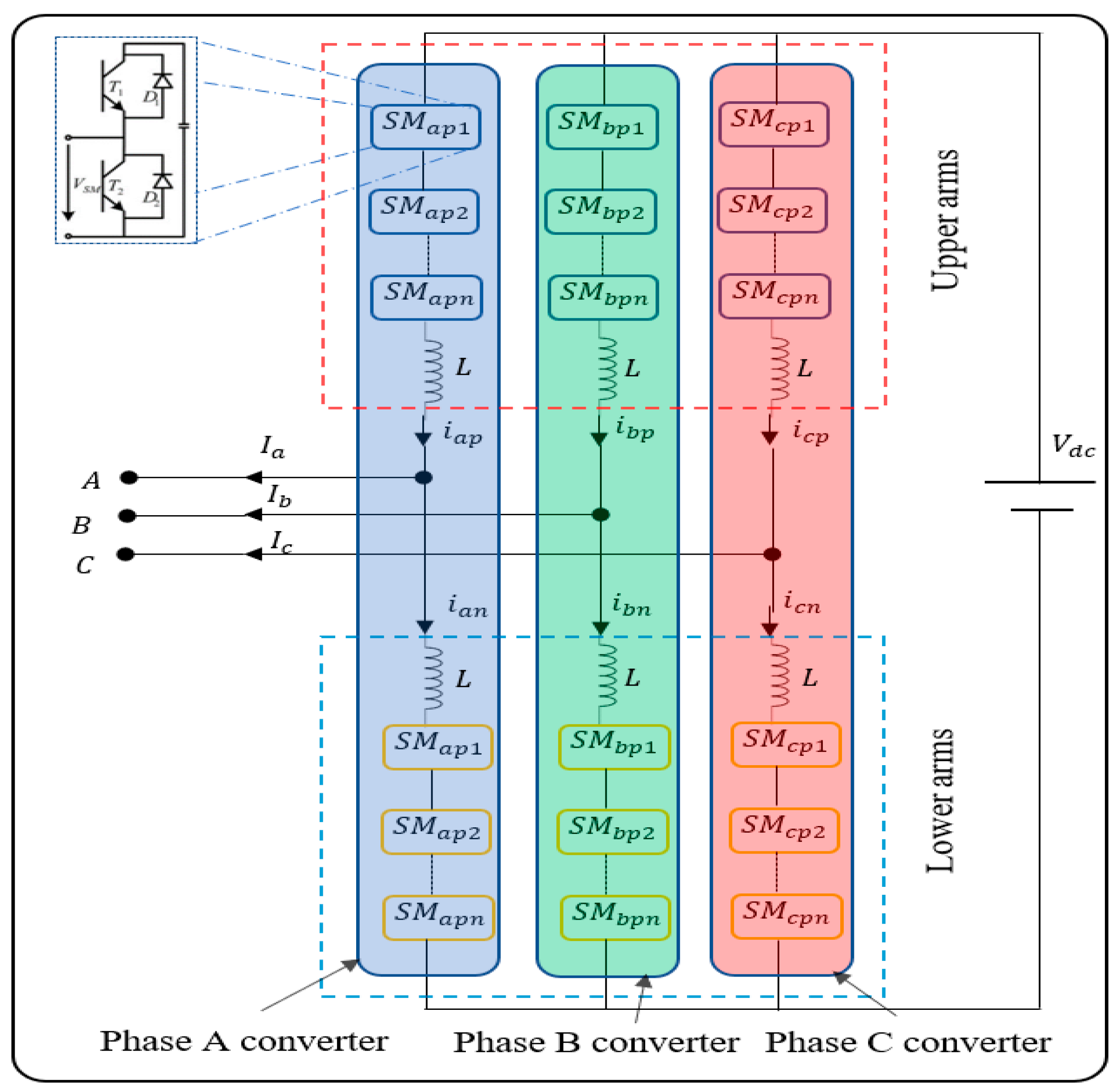
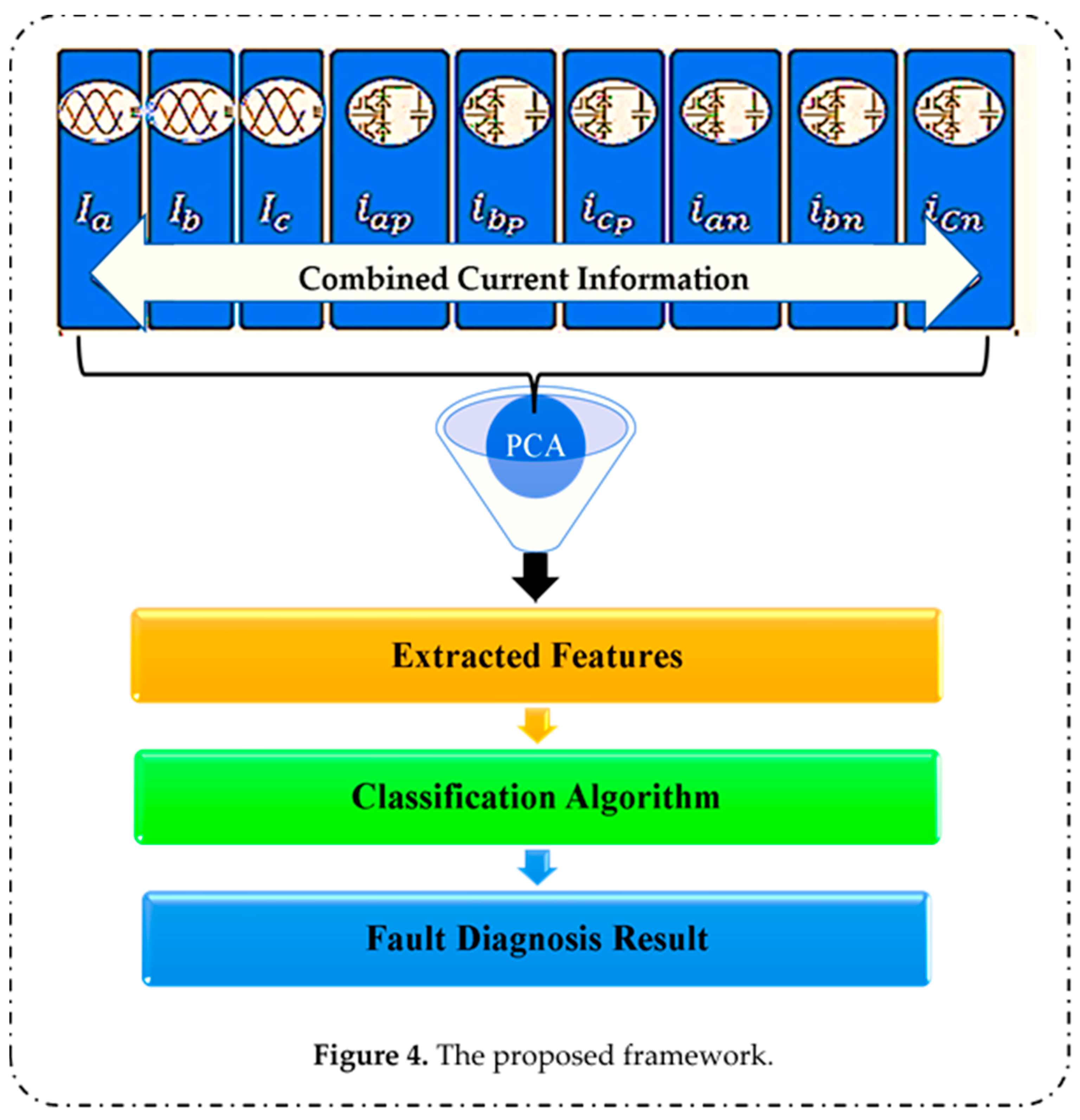
- We combine the measured current data of the AC-side three-phase current and of the upper bridge and lower bridge of each three phases to form a vector of features that represent the current health condition of MMCs.
- Our proposed framework reduces measured current data using PCA that linearly maps the current data into a lower-dimensional space of principal components.
- For fault classification, multiclass SVM based on error-correcting output codes (ECOC) and multinomial logistic regression (MLR) algorithms are used with the learned feature vector to achieve improved classification accuracy and reduced computation time.
- Compared to recently published results that are based on machine learning techniques, our proposed method is faster and yet achieves competitive, if not better, classification accuracies of open-circuit failures of IGBT fault diagnosis in MMC-HVDC transmission.
- The high reduction in the computational time comes from two elements of our proposed method: (i) using a minimum number of only current sensors; (ii) using the PCA method to select fewer features that can be used for training the classification algorithm—i.e., SVM and MLRC algorithms—and for classifying MMC-HVDC health conditions using the trained classification models.
- Being able to obtain high classification accuracy while highly reducing the computational time, our proposed method can be used in real implementations of MMC-HVDC fault diagnosis systems.
2. Proposed Framework
2.1. Data Modeling
2.2. Description of the Proposed Framework
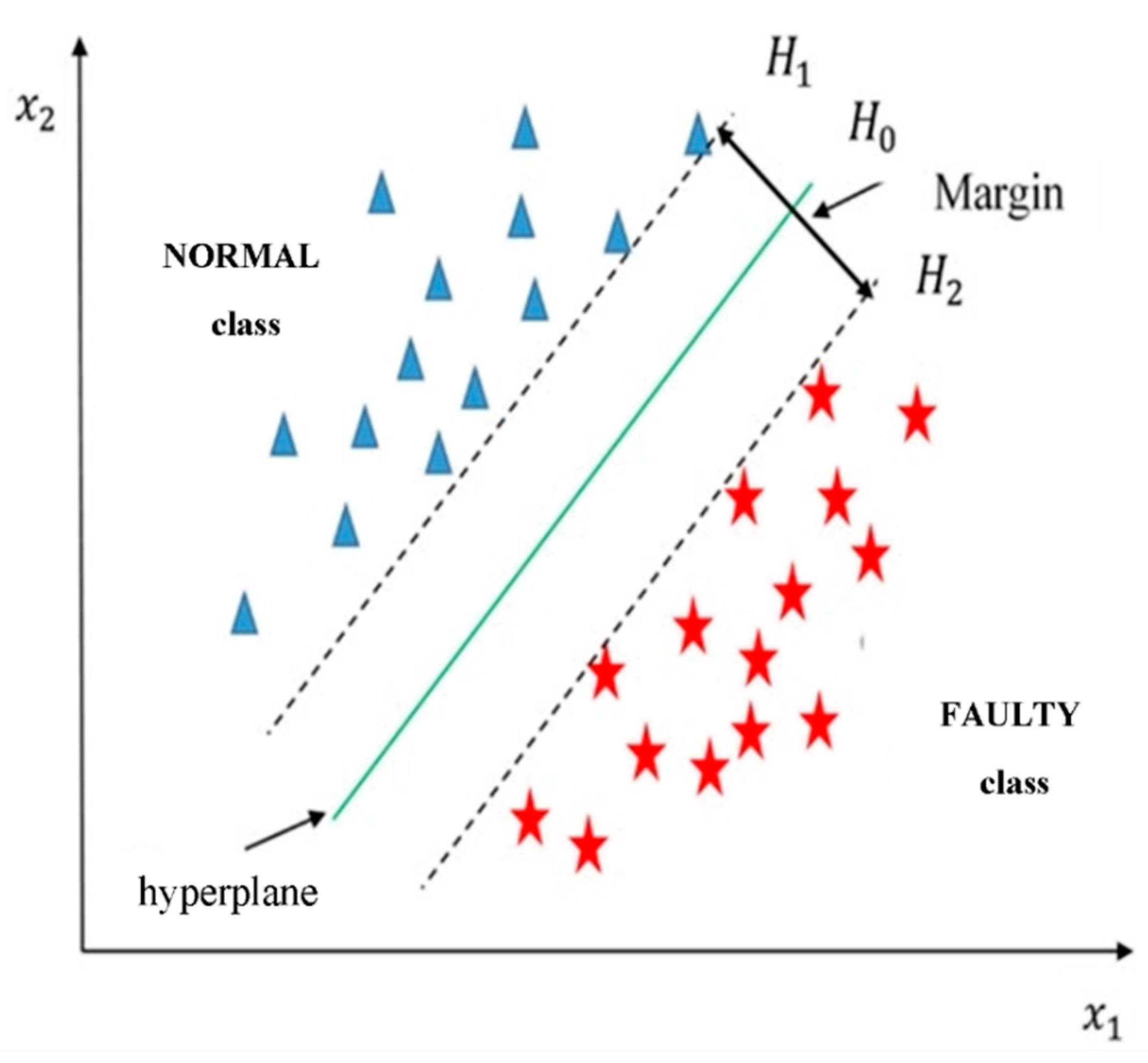
2.2.1. SVM-Based ECOC
2.2.2. MLR
3. Experimental Study
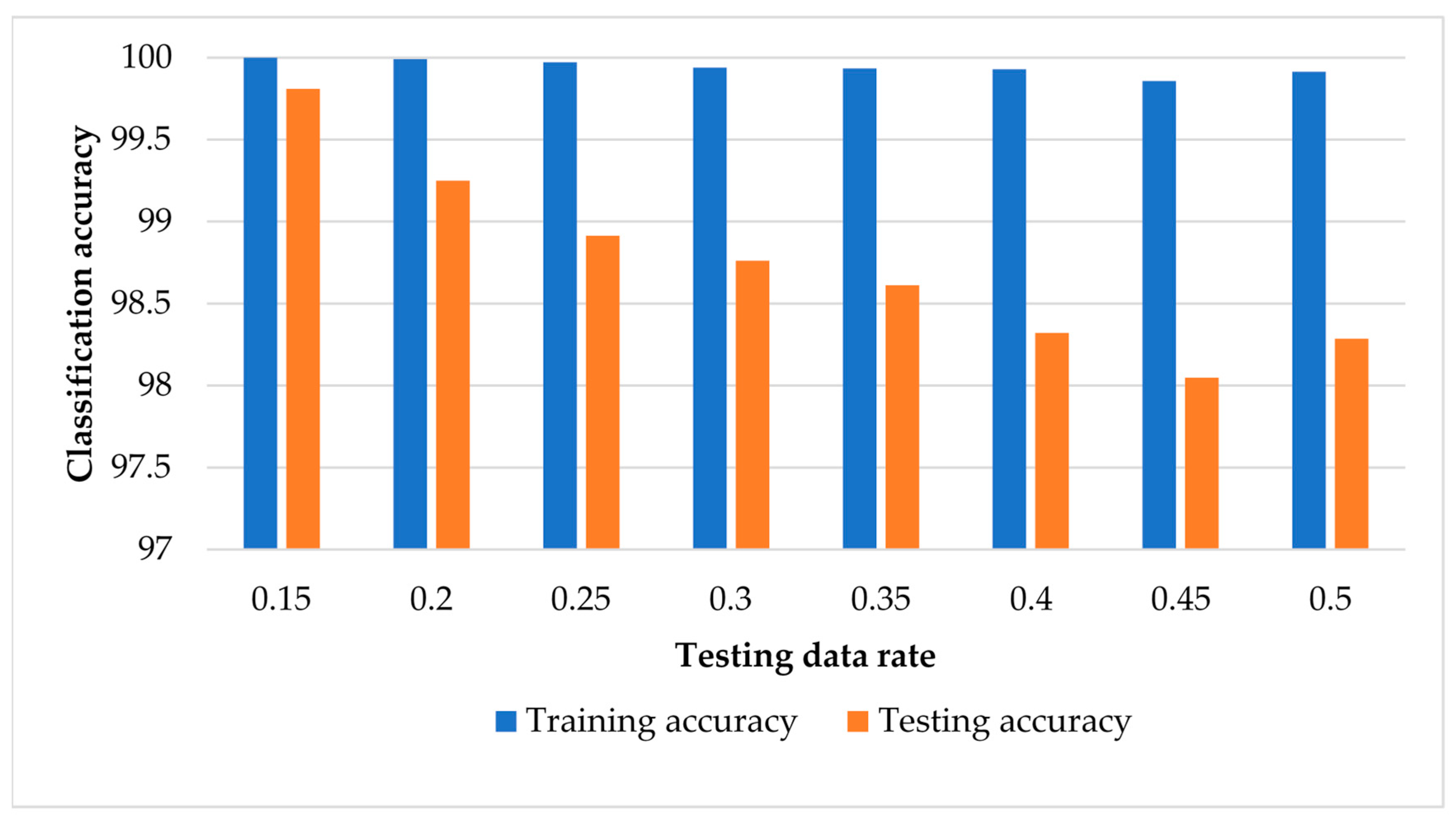
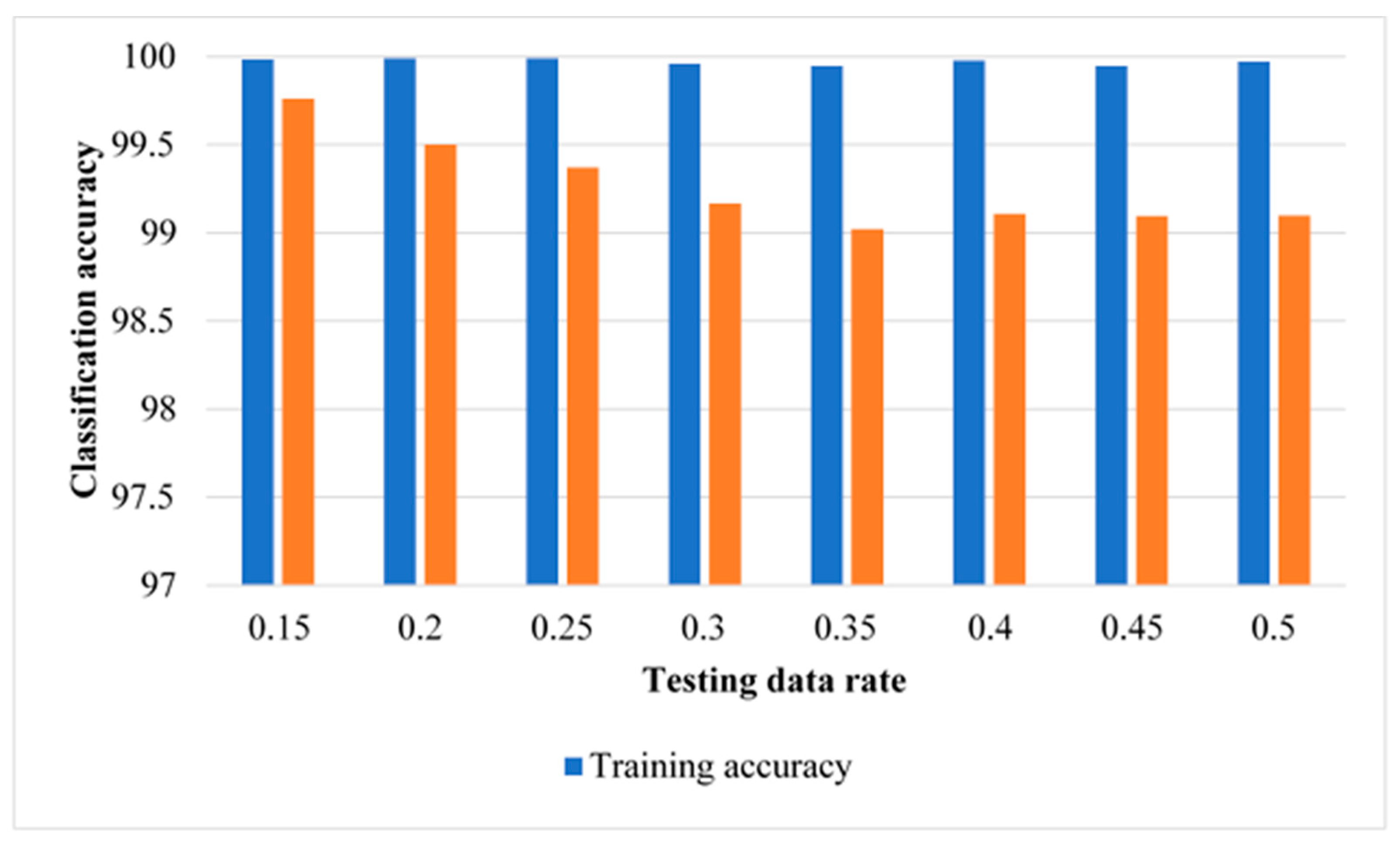
3.1. Results of SVM-Based ECOC without Data Normalisation
3.2. Results of SVM-Based ECOC with Data Normalisation
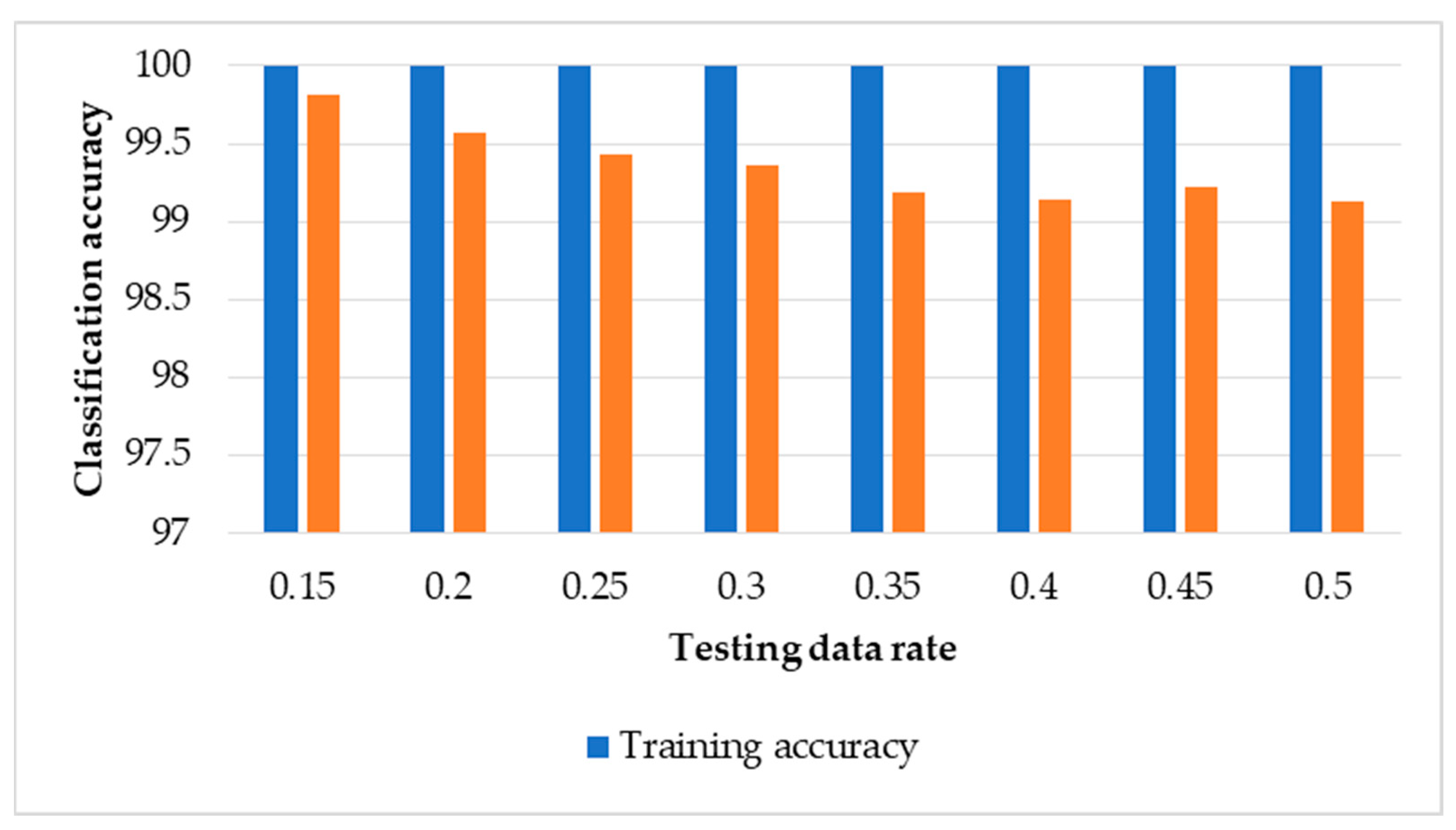
3.3. Results of MLR without Data Normalisation
3.4. Results of MLR with Data Normalisation
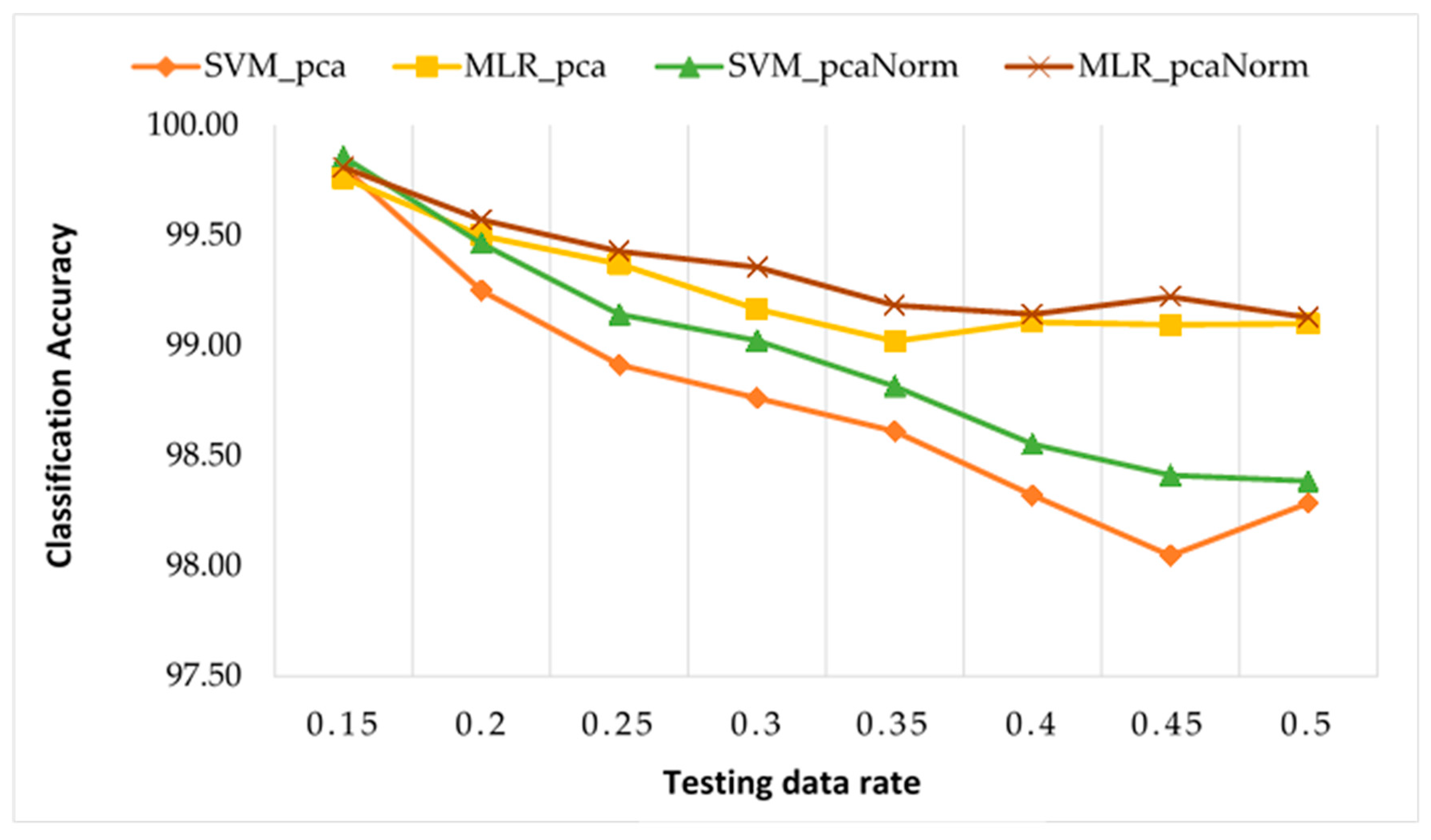
4. Comparisons of Results
4.1. Comparisons of Testing Classifications
4.2. Comparisons with Recently Published Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Pérez, M.A.; Leon, J.I. Recent advances and industrial applications of multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Saeedifard, M.; Iravani, R.; Pou, J. A space vector modulation strategy for a back–to back five-level HVDC converter system. IEEE Trans. Ind. Electron. 2009, 56, 452–466. [Google Scholar] [CrossRef]
- Gnanarathna, U.N.; Gole, A.M.; Jayasinghe, R.P. Efficient modeling of modular Multi-level HVDC converters (MMC) on electromagnetic transient simulation programs. IEEE Trans. Power Deliv. 2014, 26, 316–324. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, R. Stromrichterschaltungen Mit Verteilten Energiespeichern. German Patent DE10103031A1, 24 January 2001. [Google Scholar]
- Sharifabadi, K.; Harnefors, L.; Nee, H.P.; Norrga, S.; Teodorescu, R. Design, Control, and Application of Modular Multilevel Converters for HVDC Transmission Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, Y.; Ahmed, H.O.; Darwish, M.; Nandi, A.K. Fault detection and classification in MMC-HVDC systems using learning methods. Sensors 2020, 20, 4438. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An industry-based survey of reliability in power electronic converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Lu, B.; Sharma, S.K. A literature review of IGBT fault diagnostic and protection methods for power inverters. IEEE Trans. Ind. Appl. 2009, 45, 1770–1777. [Google Scholar] [CrossRef]
- Ciappa, M. Selected failure mechanisms of modern power modules. Microelectron. Reliab. 2002, 42, 653–667. [Google Scholar] [CrossRef]
- Nuutinen, P.; Peltoniemi, P.; Silventoinen, P. Short-circuit protection in a converter-fed low-voltage distribution network. IEEE Trans. Power Electron. 2012, 28, 1587–1597. [Google Scholar] [CrossRef]
- Abdallah, M.M.; Hamad, M.S.; Helal, A.A. Fault detection and isolation of MMC under submodule open circuit fault. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 1195–1200. [Google Scholar] [CrossRef]
- Estima, J.O.; Cardoso, A.J.M. A new algorithm for real-time multiple open-circuit fault diagnosis in voltage-fed PWM motor drives by the reference current errors. IEEE Trans. Ind. Electron. 2012, 60, 3496–3505. [Google Scholar] [CrossRef]
- Liu, H.; Ma, K.; Wang, C.; Blaabjerg, F. Fault diagnosis and fault-tolerant control of modular multi-level converter high-voltage DC system: A review. Electric Power Compon. Syst. 2016, 44, 16–1759. [Google Scholar] [CrossRef]
- Liu, H.; Loh, P.C.; Blaabjerg, F. Review of fault diagnosis and fault-tolerant control for modular multilevel converter of HVDC. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 1242–1247. [Google Scholar] [CrossRef]
- Sen, M.; Alaraj, M.; Park, J.D. Open circuit fault detection and localization in modular multilevel converter. In Proceedings of the North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Khomfoi, S.; Tolbert, L.M. Fault diagnosis and reconfiguration for multilevel inverter drive using AI-based techniques. IEEE Trans. Ind. Electron. 2007, 54, 2954–2968. [Google Scholar] [CrossRef]
- Song, W.; Huang, A.Q. Fault-tolerant design and control strategy for cascaded H-bridge multilevel converter-based STATCOM. IEEE Trans. Ind. Electron. 2009, 57, 2700–2708. [Google Scholar] [CrossRef]
- Sedghi, S.; Dastfan, A.; Ahmadyfard, A. Fault detection of a seven level modular multilevel inverter via voltage histogram and neural network. In Proceedings of the IEEE 8th International Conference on Power Electronics-ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 1005–1012. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, C.; Li, Y.P.; Wang, M. Fault detection and remedy of multilevel inverter based on BP neural network. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Lezana, P.; Aguilera, R.; Rodríguez, J. Fault detection on multicell converter based on output voltage frequency analysis. IEEE Trans. Ind. Electron. 2009, 56, 2275–2283. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, A.; Sepahvand, H.; Crow, M.L.; Ferdowsi, M. Fault detection and mitigation in multilevel converter STATCOMs. IEEE Trans. Ind. Electron. 2010, 58, 1307–1315. [Google Scholar] [CrossRef]
- Wang, T.; Xu, H.; Han, J.; Elbouchikhi, E.; Benbouzid, M.E.H. Cascaded H-bridge multilevel inverter system fault diagnosis using a PCA and multiclass relevance vector machine approach. IEEE Trans. Power Electron. 2015, 30, 7006–7018. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, J.; Xu, S.; Deng, F. Detection and location of open-circuit fault for modular multilevel converter. Int. J. Electr. Power Energy Syst. 2020, 115, 105425. [Google Scholar] [CrossRef]
- Shao, S.; Wheeler, P.W.; Clare, J.C.; Watson, A.J. Fault detection for modular multilevel converters based on sliding mode observer. IEEE Trans. Power Electron. 2013, 28, 4867–4872. [Google Scholar] [CrossRef] [Green Version]
- Shao, S.; Watson, A.J.; Clare, J.C.; Wheeler, P.W. Robustness analysis and experimental validation of a fault detection and isolation method for the modular multilevel converter. IEEE Trans. Power Electron. 2015, 31, 3794–3805. [Google Scholar] [CrossRef] [Green Version]
- Pu, L.I.N.; ZHANG, Z.; ZHANG, Z.; Kang, L.; Wang, X. Open-circuit Fault Diagnosis for Modular Multilevel Converter Using Wavelet Neural Network. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 250–255. [Google Scholar] [CrossRef]
- Jiao, W.; Liu, Z.; Zhang, Y. Fault Diagnosis of Modular Multilevel Converter with FA-SVM Algorithm. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 5093–5098. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Gastli, A.; Ben-Brahim, L.; Al-Emadi, N.; Gabbouj, M. Real-time fault detection and identification for MMC using 1-D convolutional neural networks. IEEE Trans. Ind. Electron. 2018, 66, 8760–8771. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Zhang, Y.; Chai, L.; Xu, B. Diagnosis and location of the open-circuit fault in modular multilevel converters: An improved machine learning method. Neurocomputing 2019, 28, 58–66. [Google Scholar] [CrossRef]
- Chen, H.; Wang, J.; Liu, J.; Rehman, B.; Qian, F.; Liu, C. Validation Method for Simulation Model of Internet of Things-Aided Power System. IEEE Access 2019, 8, 1185–1192. [Google Scholar] [CrossRef]
- Yang, Q.; Qin, J.; Saeedifard, M. Analysis, detection, and location of open-switch submodule failures in a modular multilevel converter. IEEE Trans. Power Deliv. 2015, 31, 155–164. [Google Scholar] [CrossRef]
- Huai, Q.; Liu, K.; Hooshyar, A.; Ding, H.; Chen, K.; Liang, Q. Single-ended line fault location method for multi-terminal HVDC system based on optimized variational mode decomposition. Electr. Power Syst. Res. 2021, 194, 107054. [Google Scholar] [CrossRef]
- Han, Y.; Qi, W.; Ding, N.; Geng, Z. Short-time wavelet entropy integrating improved LSTM for fault diagnosis of modular multilevel converter. IEEE Trans. Cybern. 2021, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Xing, W.; Yang, H.; Sheng, J.; Chang, X.; Li, W.; He, X. Open-circuit Fault Detection and Location in MMCs with Multivariate Gaussian Distribution. In Proceedings of the 2020 4th IEEE International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020; pp. 555–559. [Google Scholar] [CrossRef]
- Ye, X.; Lan, S.; Xiao, S.J.; Yuan, Y. Single Pole-to-Ground Fault Location Method for MMC-HVDC System Using Wavelet Decomposition and DBN. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 238–247. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, T.; Amirat, Y.; Chen, G. IGBT Open-Circuit Fault Diagnosis for MMC Submodules Based on Weighted-Amplitude Permutation Entropy and DS Evidence Fusion Theory. Machines 2021, 9, 317. [Google Scholar] [CrossRef]
- Ke, L.; Zhang, Y.; Yang, B.; Luo, Z.; Liu, Z. Fault diagnosis with synchrosqueezing transform and optimized deep convolutional neural network: An application in modular multilevel converters. Neurocomputing 2021, 21, 24–33. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, X.; Li, J.; Li, G. Fault diagnosis of modular multilevel converter based on adaptive chirp mode decomposition and temporal convolutional network. Eng. Appl. Artif. Intell. 2022, 107, 104544. [Google Scholar] [CrossRef]
- Reddy, G.A.; Shukla, A. Arm current sensor-less control of MMC for Circulating current suppression. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6905–6910. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Deng, Z.; Song, S.; Ouyang, S. IGBT Open-Circuit Fault Diagnosis for Modular Multilevel Converter With Reduced-Number of Voltage Sensor Measuring Technique. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 47–50. [Google Scholar] [CrossRef]
- Xu, K.; Xie, S.; Yan, Y.; Zhang, Z.; Zhang, B.; Qian, Q. A fast fault diagnosis method for submodule failures in modular multilevel converters. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 1125–1130. [Google Scholar] [CrossRef]
- Li, B.; Shi, S.; Wang, B.; Wang, G.; Wang, W.; Xu, D. Fault diagnosis and tolerant control of single IGBT open-circuit failure in modular multilevel converters. IEEE Trans. Power Electron. 2015, 31, 3165–3176. [Google Scholar] [CrossRef]
- Yang, S.; Tang, Y.; Wang, P. Seamless fault-tolerant operation of a modular multilevel converter with switch open-circuit fault diagnosis in a distributed control architecture. IEEE Trans. Power Electron. 2018, 33, 7058–7070. [Google Scholar] [CrossRef]
- Deng, F.; Chen, Z.; Khan, M.R.; Zhu, R. Fault detection and localization method for modular multilevel converters. IEEE Trans. Power Electron. 2014, 30, 2721–2732. [Google Scholar] [CrossRef]
- Shao, S.; Wheeler, P.W.; Clare, J.C.; Watson, A.J. Open-circuit fault detection and isolation for modular multilevel converter based on sliding mode observer. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE)-IEEE, Lille, France, 2–6 September 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, Y.; Ahmed, H.O.; Darwish, M.; Nandi, A.K. Open-Circuit Fault Detection and Classification of Modular Multilevel Converters in High Voltage Direct Current Systems (MMC-HVDC) with Long Short-Term Memory (LSTM) Method. Sensors 2021, 21, 4159. [Google Scholar] [CrossRef] [PubMed]
- Anaya-Lara, O.; Acha, E. Modeling and analysis of custom power systems by PSCAD/EMTDC. IEEE Trans. Power Deliv. 2002, 17, 266–272. [Google Scholar] [CrossRef]
- Pearson, K. LIII: On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Gunn, S.R. Support vector machines for classification and regression. ISIS Tech. Rep. 1998, 14, 5–16. [Google Scholar]
- Mathworks.com. Fit Multiclass Models for Support Vector Machines or Other Classifiers—MATLAB Fitcecoc. 2017. Available online: http://uk.mathworks.com/help/stats-/fitcecoc.html (accessed on 25 July 2021).
- Ahmed, H.; Nandi, A.K. Compressive sampling and feature ranking framework for bearing fault classification with vibration signals. IEEE Access 2018, 6, 44731–44746. [Google Scholar] [CrossRef]
- Ahmed, H.O.; Nandi, A.K. Three-stage hybrid fault diagnosis for rolling bearings with compressively sampled data and subspace learning techniques. IEEE Trans. Ind. Electron. 2018, 66, 5516–5524. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.O.A.; Wong, M.L.D.; Nandi, A.K. Intelligent condition monitoring method for bearing faults from highly compressed measurements using sparse over-complete features. Mech. Syst. Signal Processing 2018, 99, 459–477. [Google Scholar] [CrossRef]
- Ahmed, H.O.; Nandi, A.K. Condition Monitoring with Vibration Signals: Compressive Sampling and Learning Algorithms for Rotating Machines; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Wang, J.; Zheng, X.; Tai, N. DC Fault Detection and Classification Approach of MMC-HVDC Based on Convolutional Neural Network. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Qu, X.; Duan, B.; Yin, Q.; Shen, M.; Yan, Y. Deep Convolution Neural Network Based Fault Detection and Identification for Modular Multilevel Converters. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]



| Ref. | Approach Used | Detection Threshold Parameters | Localisation Threshold Parameters |
|---|---|---|---|
| [24] | Fault detection: The comparison between the observed using Sliding Mode Observer (SMO) and measured the current of the upper arm ip. Fault localisation The comparison between the observed and measured lower arm current, and ip, and the capacitor voltages, and Vci of the assumed faulty SM. | Threshold parameters: Ith, and 700 time-steps (2 µs per step) Usage: If and it lasts for 700 time-steps (2 µs per step) then an open-circuit fault has occurred. | Threshold parameters: Ith, Vthi, and 100 ms. Usage: If and and it lasts for 100 ms, then the SM is faulty. |
| [42] | Fault detection: The detection is achieved using a state observer to estimate the ideal circulating current and the output current using the state models of the MMC and the variables already available from the main control system. Fault localisation The comparison between the SM capacitor voltage Vci and a threshold value Uth. | Threshold parameters: Ith, and ΔT1. Usage: If and it lasts for ΔT1, then an open-circuit fault has occurred. | Threshold parameters: Uth, and ΔT2. Usage: If and it lasts for ΔT2, then this SM is located to be faulty. |
| [44] | Fault detection: The comparison between measured inner difference current idiff and the estimated inner difference current through Kalman Filter (KF). Fault localisation Each capacitor voltage (Vc,p,N) of the upper and lower arms of the targeted phase, i.e., the phase with a detected fault, is compared with the minimum capacitor voltage value (Vc(t),min) for a given time instant. | Threshold parameters: Δidiff and Δti. Usage: If and it lasts for a period of Δti, then a fault is assumed in this phase of the MMC. | Threshold parameters: ΔVc and Δtv. Usage: If and it lasts for a period of Δtv, then it indicates this SM is faulty. |
| [45] | Fault detection: The comparison between the measured current of the lower arm current iN and observed arm current , which is based on Sliding Mode Observer (SMO), and one of the capacitor voltages, and Vc. Fault localisation The comparison between the observed and measured lower arm current, and iN, and the capacitor voltages, and Vci of the assumed faulty SM. | Threshold parameters: Ith and Vth. Usage: If and and it lasts for 500 μs (50 time-steps, 10 μs per step), then an open-circuit fault has occurred. | Threshold parameters: Ith and Vthi. Usage: If , and and it lasts for 80 ms, then the SM is faulty. |
| Parameters | Value |
|---|---|
| Number of SMs per arm | 9 |
| SM capacitor | 3000 μF |
| Arm inductance | 0.05 ohm |
| AC frequency | 50 Hz |
| Faulty Bridge | Label Value |
|---|---|
| Normal | 1 |
| A-phase lower SMs | 2 |
| A-phase upper SMs | 3 |
| B-phase lower SMs | 4 |
| B-phase upper SMs | 5 |
| C-phase lower SMs | 6 |
| C-phase upper SMs | 7 |
| Testing Data = 15% | |||||||
| Normal | A-Phase Lower SMs | A-Phase Upper SMs | B-Phase Lower SMs | B-Phase Upper SMs | C-Phase Lower SMs | C-Phase Upper SMs | |
| Normal | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| A-Phase Lower SMs | 0 | 99.7 | 0 | 0 | 0 | 1 | 0 |
| A-Phase Upper SMs | 0 | 0 | 100 | 0 | 0 | 0 | 0 |
| B-Phase Lower SMs | 0 | 0 | 0 | 100 | 0 | 0 | 0 |
| B-Phase Upper SMs | 0 | 0 | 0 | 0 | 100 | 0 | 0 |
| C-Phase Lower SMs | 0 | 0.3 | 0 | 0 | 0 | 99.0 | 0 |
| C-Phase Upper SMs | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| Testing Data = 40% | |||||||
| Normal | A-Phase Lower SMs | A-Phase Upper SMs | B-Phase Lower SMs | B-Phase Upper SMs | C-Phase Lower SMs | C-Phase Upper SMs | |
| Normal | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| A-Phase Lower SMs | 0 | 98.8 | 0 | 0.4 | 1.5 | 1.8 | 0.5 |
| A-Phase Upper SMs | 0 | 0 | 98.8 | 0 | 0.8 | 0 | 0 |
| B-Phase Lower SMs | 0 | 0.6 | 0 | 99.1 | 0 | 0.4 | 0 |
| B-Phase Upper SMs | 0 | 0 | 0.5 | 0 | 96.6 | 0 | 1.9 |
| C-Phase Lower SMs | 0 | 0.4 | 0.7 | 0.5 | 0 | 97.4 | 0 |
| C-Phase Upper SMs | 0 | 0.2 | 0 | 0 | 1.1 | 0.5 | 97.6 |
| Testing Data = 15% | |||||||
| Normal | A-Phase Lower SMs | A-Phase Upper SMs | B-Phase Lower SMs | B-Phase Upper SMs | C-Phase Lower SMs | C-Phase Upper SMs | |
| Normal | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| A-Phase Lower SMs | 0 | 99.7 | 0 | 0 | 0 | 0.7 | 0 |
| A-Phase Upper SMs | 0 | 0 | 100 | 0 | 0 | 0 | 0 |
| B-Phase Lower SMs | 0 | 0 | 0 | 100 | 0 | 0 | 0 |
| B-Phase Upper SMs | 0 | 0 | 0 | 0 | 100 | 0 | 0 |
| C-Phase Lower SMs | 0 | 0.3 | 0 | 0 | 0 | 99.3 | 0 |
| C-Phase Upper SMs | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| Testing Data = 40% | |||||||
| Normal | A-Phase Lower SMs | A-Phase Upper SMs | B-Phase Lower SMs | B-Phase Upper SMs | C-Phase Lower SMs | C-Phase Upper SMs | |
| Normal | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| A-Phase Lower SMs | 0 | 98.5 | 0 | 0.8 | 1.5 | 1.5 | 0.6 |
| A-Phase Upper SMs | 0 | 0 | 98.9 | 0 | 0.8 | 0 | 0 |
| B-Phase Lower SMs | 0 | 0.9 | 0 | 99.1 | 0 | 0.4 | 0 |
| B-Phase Upper SMs | 0 | 0 | 0.5 | 0 | 97.0 | 0 | 0.5 |
| C-Phase Lower SMs | 0 | 0.4 | 0.6 | 0.1 | 0 | 97.5 | 0 |
| C-Phase Upper SMs | 0 | 0.3 | 0 | 0 | 0.8 | 0.6 | 98.9 |
| Testing Data = 15% | |||||||
| Normal | A-Phase Lower SMs | A-Phase Upper SMs | B-Phase Lower SMs | B-Phase Upper SMs | C-Phase Lower SMs | C-Phase Upper SMs | |
| Normal | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| A-Phase Lower SMs | 0 | 99.7 | 0 | 0 | 0 | 1 | 0 |
| A-Phase Upper SMs | 0 | 0 | 100 | 0 | 0 | 0 | 0 |
| B-Phase Lower SMs | 0 | 0 | 0 | 100 | 0 | 0 | 0 |
| B-Phase Upper SMs | 0 | 0 | 0 | 0 | 100 | 0 | 0.3 |
| C-Phase Lower SMs | 0 | 0.3 | 0 | 0 | 0 | 99.0 | 0 |
| C-Phase Upper SMs | 0 | 0 | 0 | 0 | 0 | 0 | 99.7 |
| Testing Data = 40% | |||||||
| Normal | A-Phase Lower SMs | A-Phase Upper SMs | B-Phase Lower SMs | B-Phase Upper SMs | C-Phase Lower SMs | C-Phase Upper SMs | |
| Normal | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| A-Phase Lower SMs | 0 | 99.4 | 0 | 0.4 | 0 | 2 | 0.5 |
| A-Phase Upper SMs | 0 | 0 | 99.5 | 0 | 0 | 0 | 0 |
| B-Phase Lower SMs | 0 | 0 | 0 | 99.1 | 0 | 0.4 | 0 |
| B-Phase Upper SMs | 0 | 0 | 0.5 | 0 | 100 | 0 | 0.9 |
| C-Phase Lower SMs | 0 | 0.4 | 0 | 0.5 | 0 | 97.1 | 0 |
| C-Phase Upper SMs | 0 | 0.2 | 0 | 0 | 0 | 0.5 | 98.6 |
| Testing Data = 15% | |||||||
| Normal | A-Phase Lower SMs | A-Phase Upper SMs | B-Phase Lower SMs | B-Phase Upper SMs | C-Phase Lower SMs | C-Phase Upper SMs | |
| Normal | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| A-Phase Lower SMs | 0 | 99.7 | 0 | 0 | 0 | 1 | 0 |
| A-Phase Upper SMs | 0 | 0 | 100 | 0 | 0 | 0 | 0 |
| B-Phase Lower SMs | 0 | 0 | 0 | 100 | 0 | 0 | 0 |
| B-Phase Upper SMs | 0 | 0 | 0 | 0 | 100 | 0 | 0 |
| C-Phase Lower SMs | 0 | 0.3 | 0 | 0 | 0 | 99.0 | 0 |
| C-Phase Upper SMs | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| Testing Data = 40% | |||||||
| Normal | A-Phase Lower SMs | A-Phase Upper SMs | B-Phase Lower SMs | B-Phase Upper SMs | C-Phase Lower SMs | C-Phase Upper SMs | |
| Normal | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| A-Phase Lower SMs | 0 | 99.4 | 0 | 0.4 | 0 | 2 | 0.5 |
| A-Phase Upper SMs | 0 | 0 | 99.5 | 0 | 0.2 | 0 | 0 |
| B-Phase Lower SMs | 0 | 0 | 0 | 99.1 | 0 | 0.4 | 0 |
| B-Phase Upper SMs | 0 | 0 | 0.5 | 0 | 99.8 | 0 | 0.4 |
| C-Phase Lower SMs | 0 | 0.4 | 0 | 0.5 | 0 | 97.1 | 0 |
| C-Phase Upper SMs | 0 | 0.2 | 0 | 0 | 0 | 0.5 | 99.1 |
| Ref. | Type of Measurement | No. of Measured Parameters | Classification Accuracy | Testing Time |
|---|---|---|---|---|
| [27] | Capacitor voltage Circulating current | 5000 × 7 5 × 9 | 98.9% | 80 ms |
| [56] | DC current | -- | 92.8% | - |
| [57] | Capacitor’s voltages in all SMs | 800 × 72 | 98.2% | -- |
| [6] | Current signals CNN AE-DNN | 5001 × 9 40% testing rate | 97.0% 97.5% | 400 ms 1500 ms |
| [46] | Current signals LSTM BiLSTM | 5001 × 9 40% testing rate | 97.4% 97.0% | 1290 ms 2630 ms |
| Proposed framework at 15% testing rate using PCA in all cases | Current signals and their phases | 5001 × 9 100 × 7 | ||
| SVM, no norm | 99.8% | 62 ms | ||
| SVM, with norm | 99.9% | 59 ms | ||
| MLR, no norm | 99.8% | 4 ms | ||
| MLR, with norm | 99.8% | 4 ms | ||
| at 40% testing rate using PCA in all cases | SVM, no norm | 98.3% | 106 ms | |
| SVM, with norm | 98.6% | 96 ms | ||
| MLR, no norm | 99.1% | 8 ms | ||
| MLR, with norm | 99.2% | 7 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.O.A.; Yu, Y.; Wang, Q.; Darwish, M.; Nandi, A.K. Intelligent Fault Diagnosis Framework for Modular Multilevel Converters in HVDC Transmission. Sensors 2022, 22, 362. https://doi.org/10.3390/s22010362
Ahmed HOA, Yu Y, Wang Q, Darwish M, Nandi AK. Intelligent Fault Diagnosis Framework for Modular Multilevel Converters in HVDC Transmission. Sensors. 2022; 22(1):362. https://doi.org/10.3390/s22010362
Chicago/Turabian StyleAhmed, Hosameldin O. A., Yuexiao Yu, Qinghua Wang, Mohamed Darwish, and Asoke K. Nandi. 2022. "Intelligent Fault Diagnosis Framework for Modular Multilevel Converters in HVDC Transmission" Sensors 22, no. 1: 362. https://doi.org/10.3390/s22010362
APA StyleAhmed, H. O. A., Yu, Y., Wang, Q., Darwish, M., & Nandi, A. K. (2022). Intelligent Fault Diagnosis Framework for Modular Multilevel Converters in HVDC Transmission. Sensors, 22(1), 362. https://doi.org/10.3390/s22010362








