Determination of the Geometric Parameters of Electrode Systems for Electrical Impedance Myography: A Preliminary Study
Abstract
:1. Introduction
2. An Acceptable Model of Electrical Impedance Myography Based on Numerical Simulation Determination
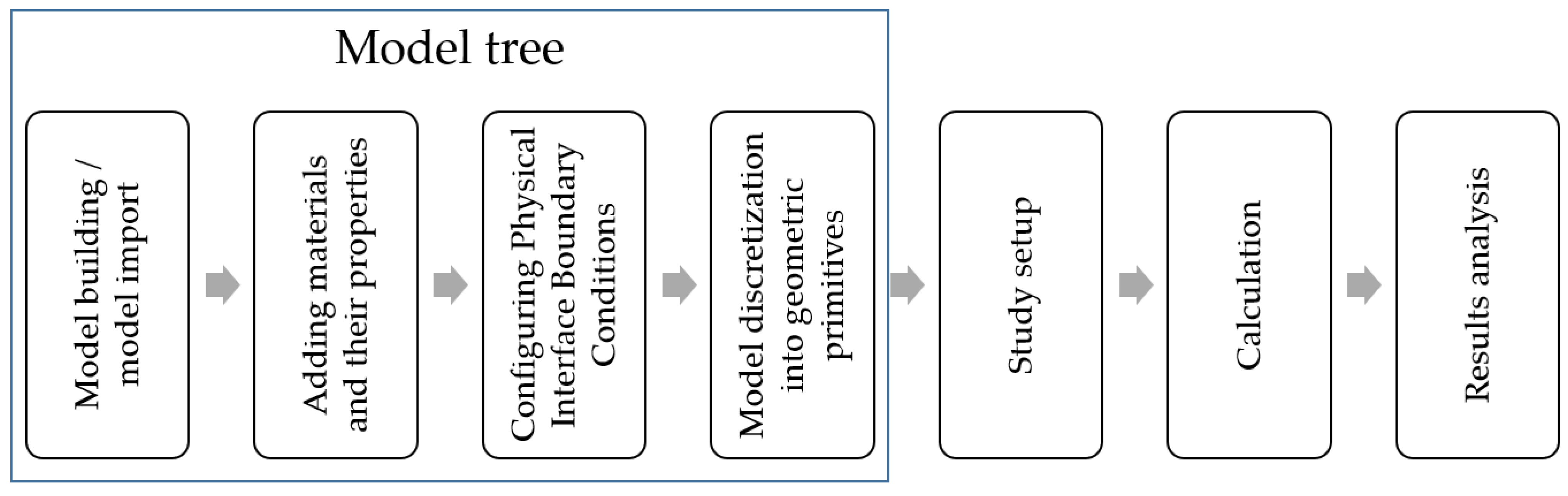
2.1. Software
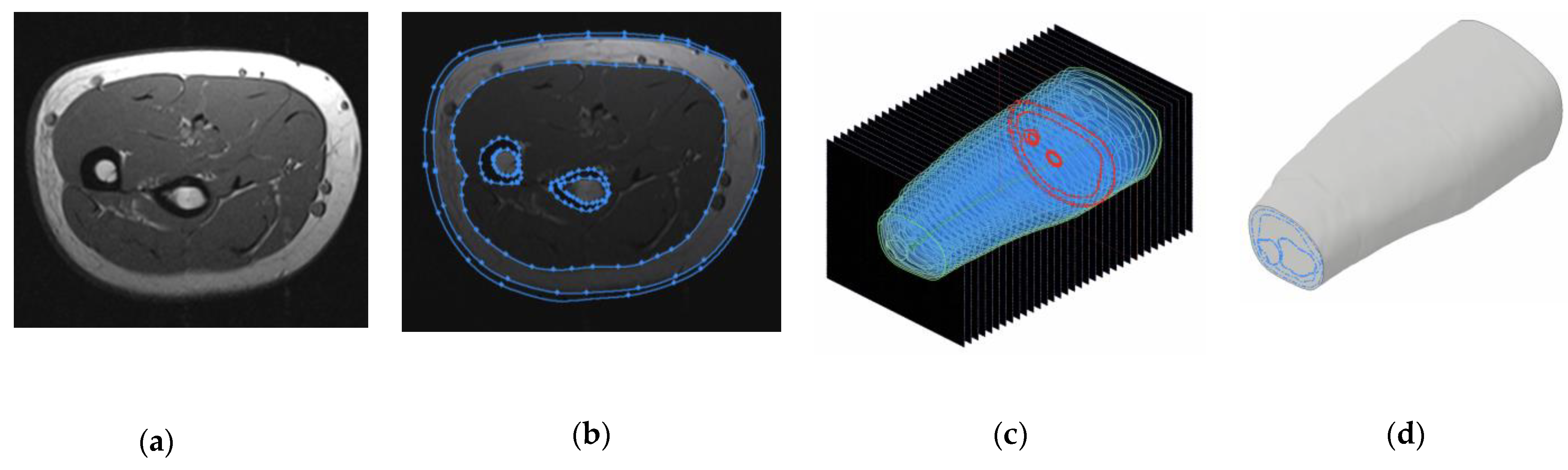
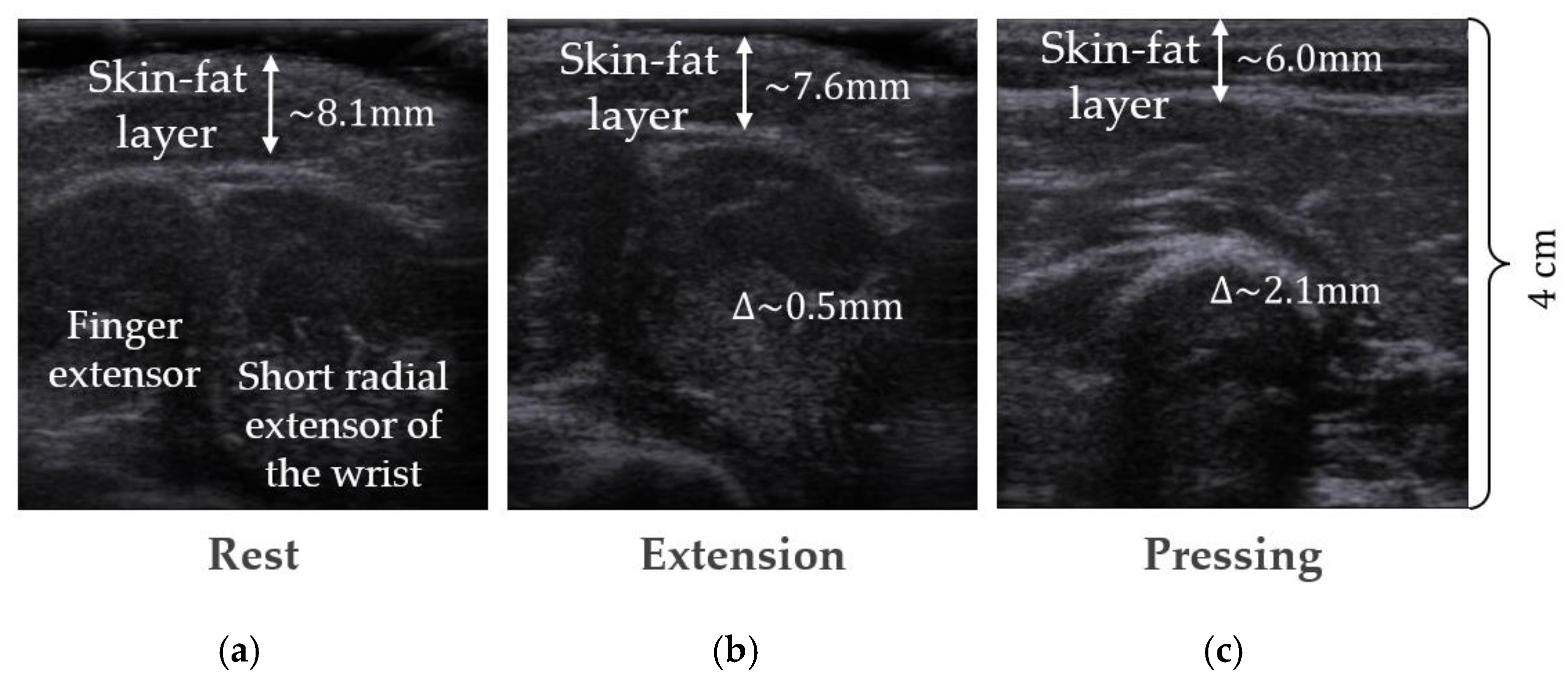
2.2. Volunteer MRI Forearm Anatomical Models
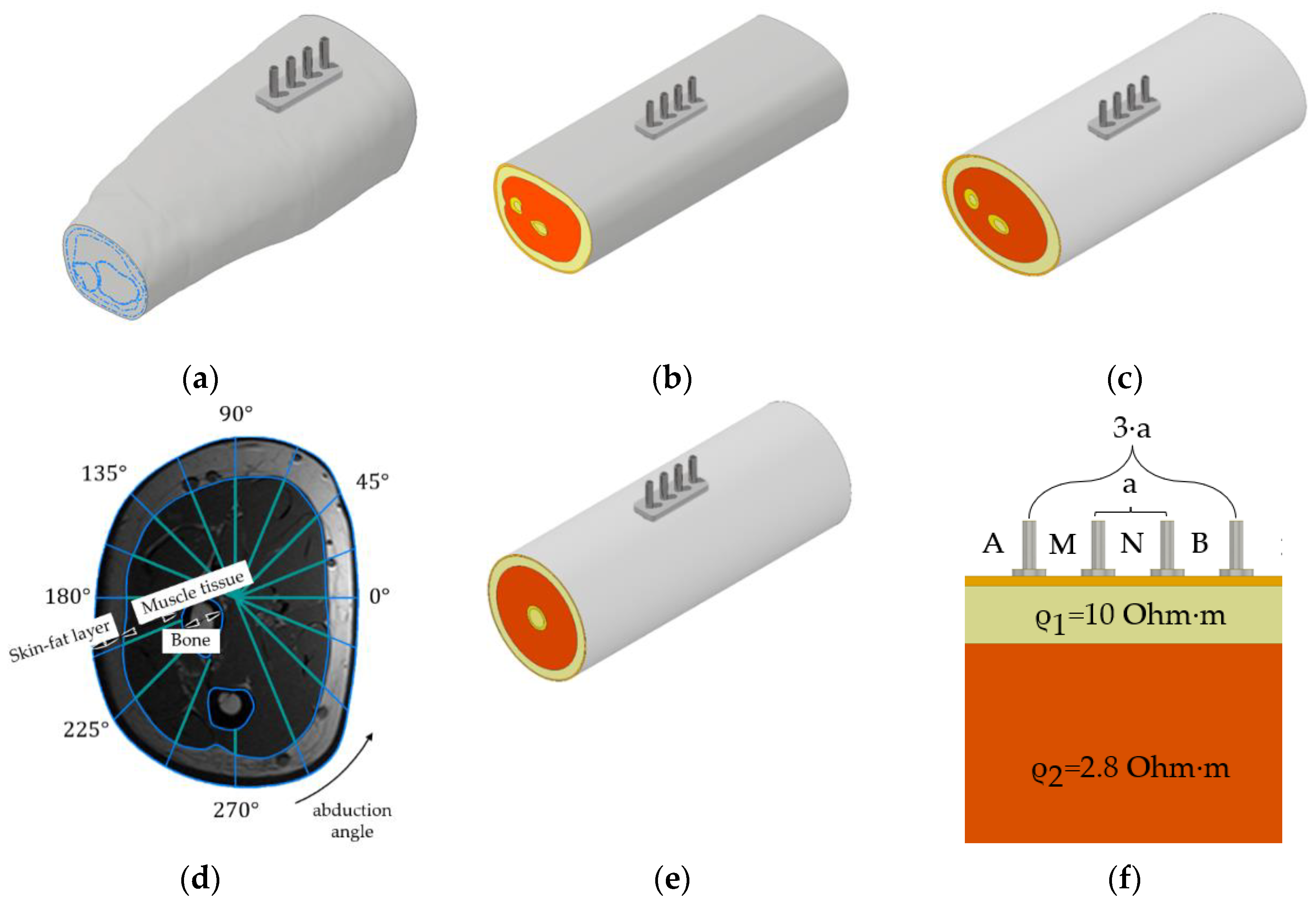
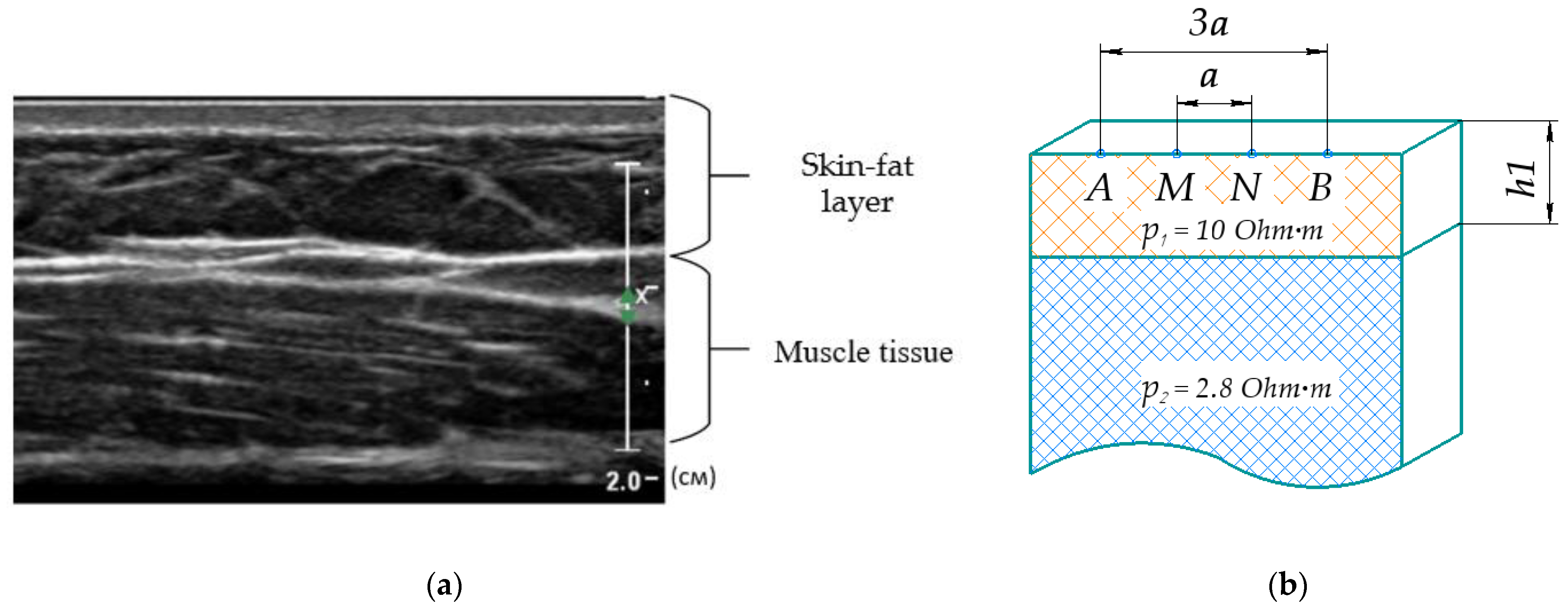
2.3. Forearm Models Simplification
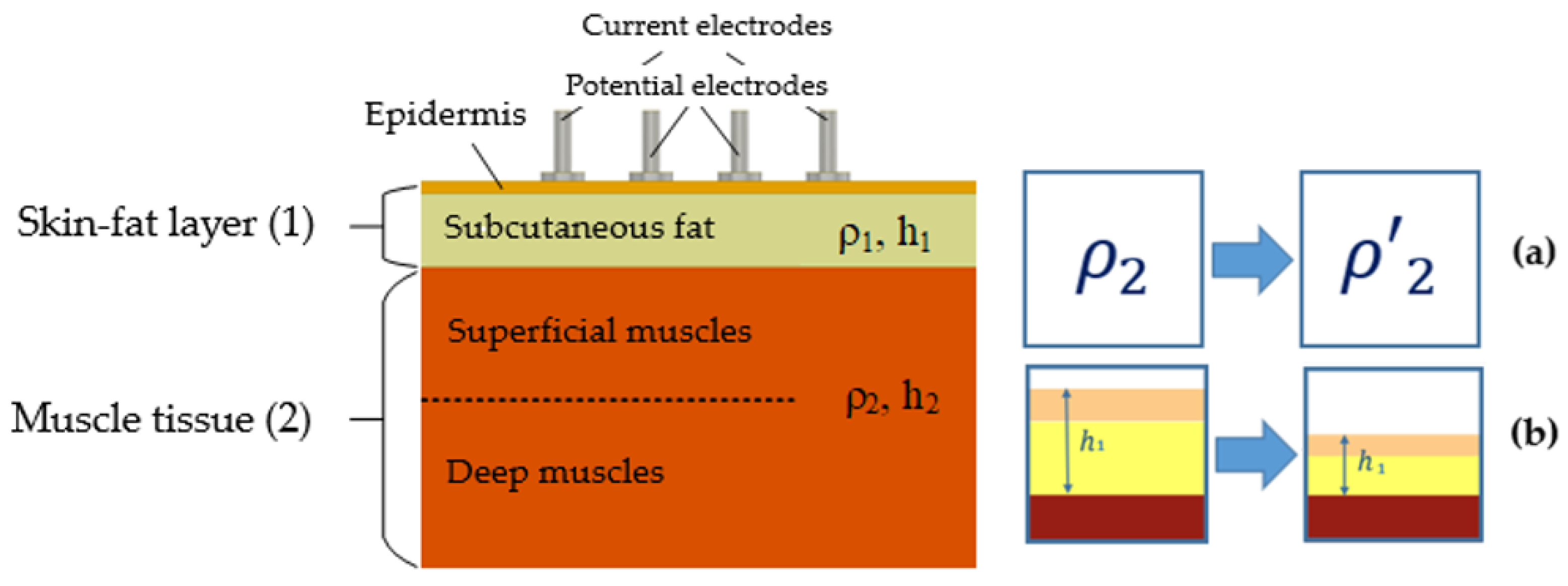
2.4. Model Parameters and Assumptions
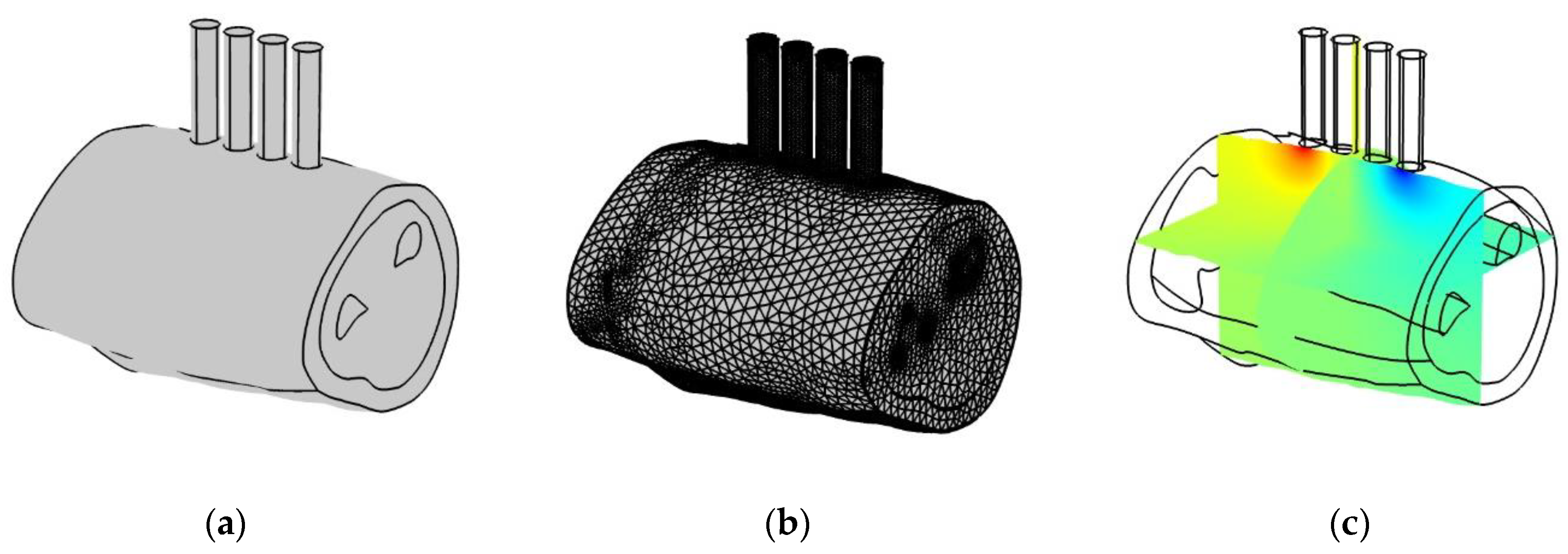
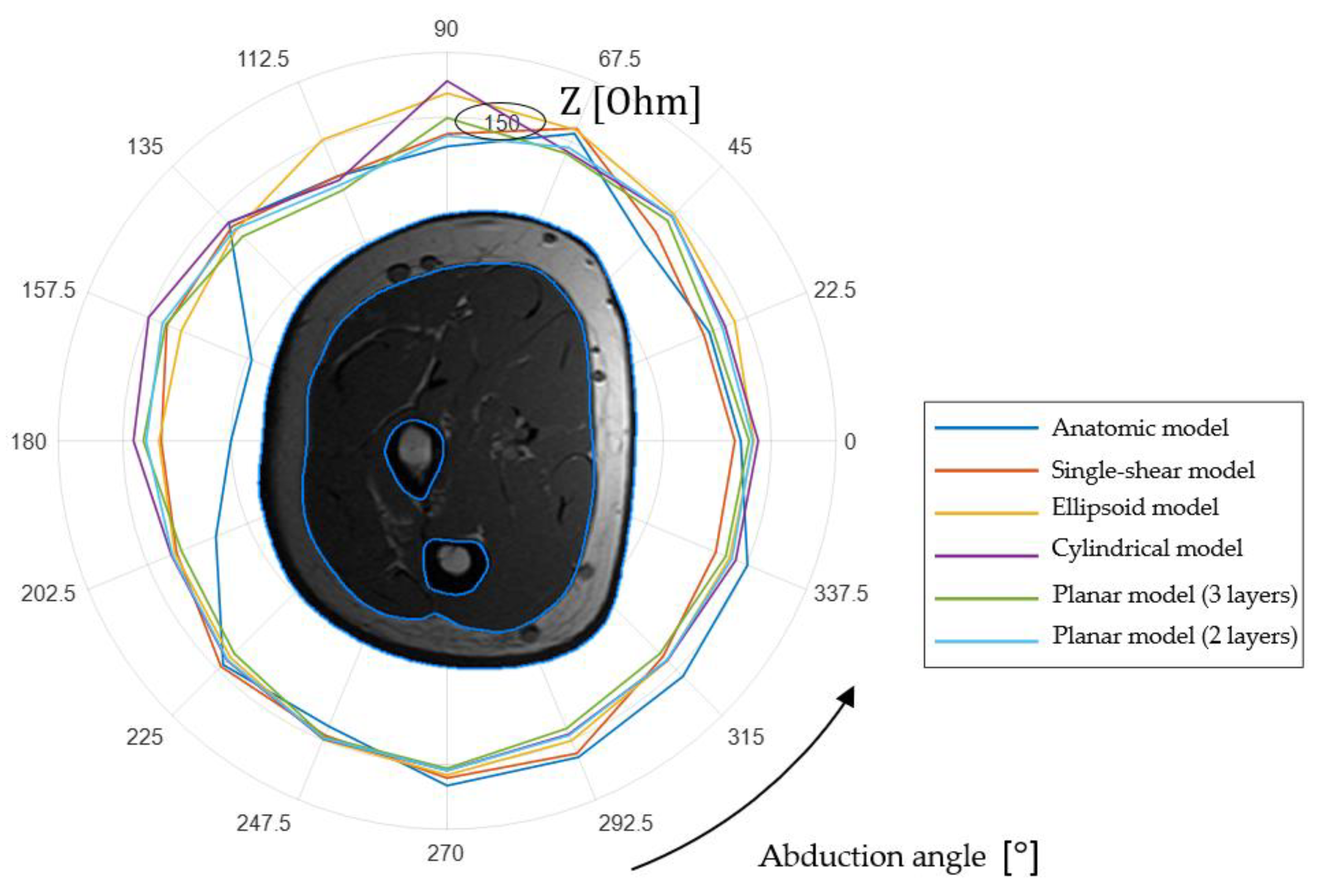
2.5. Finite Element Simulation Results
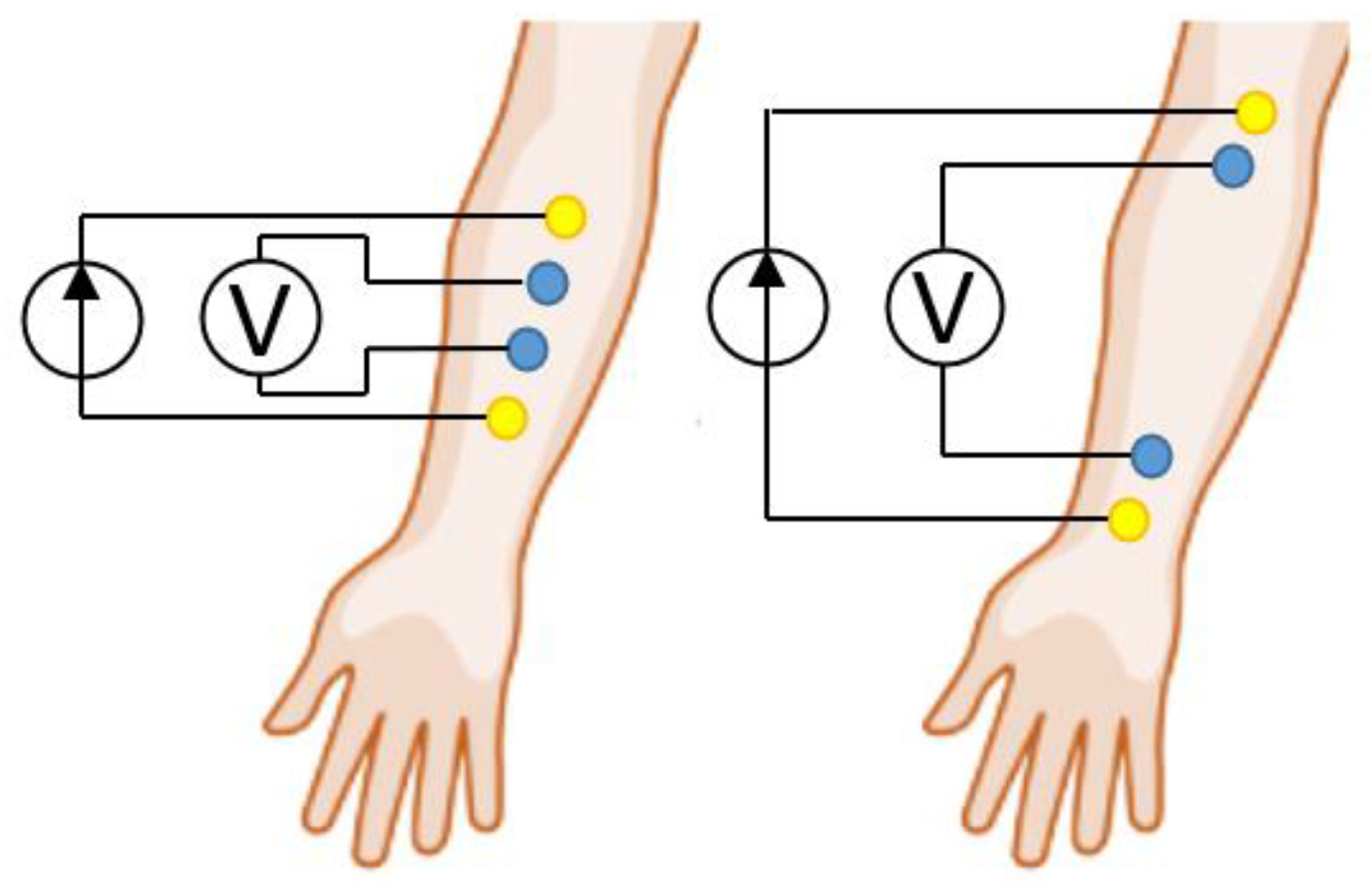
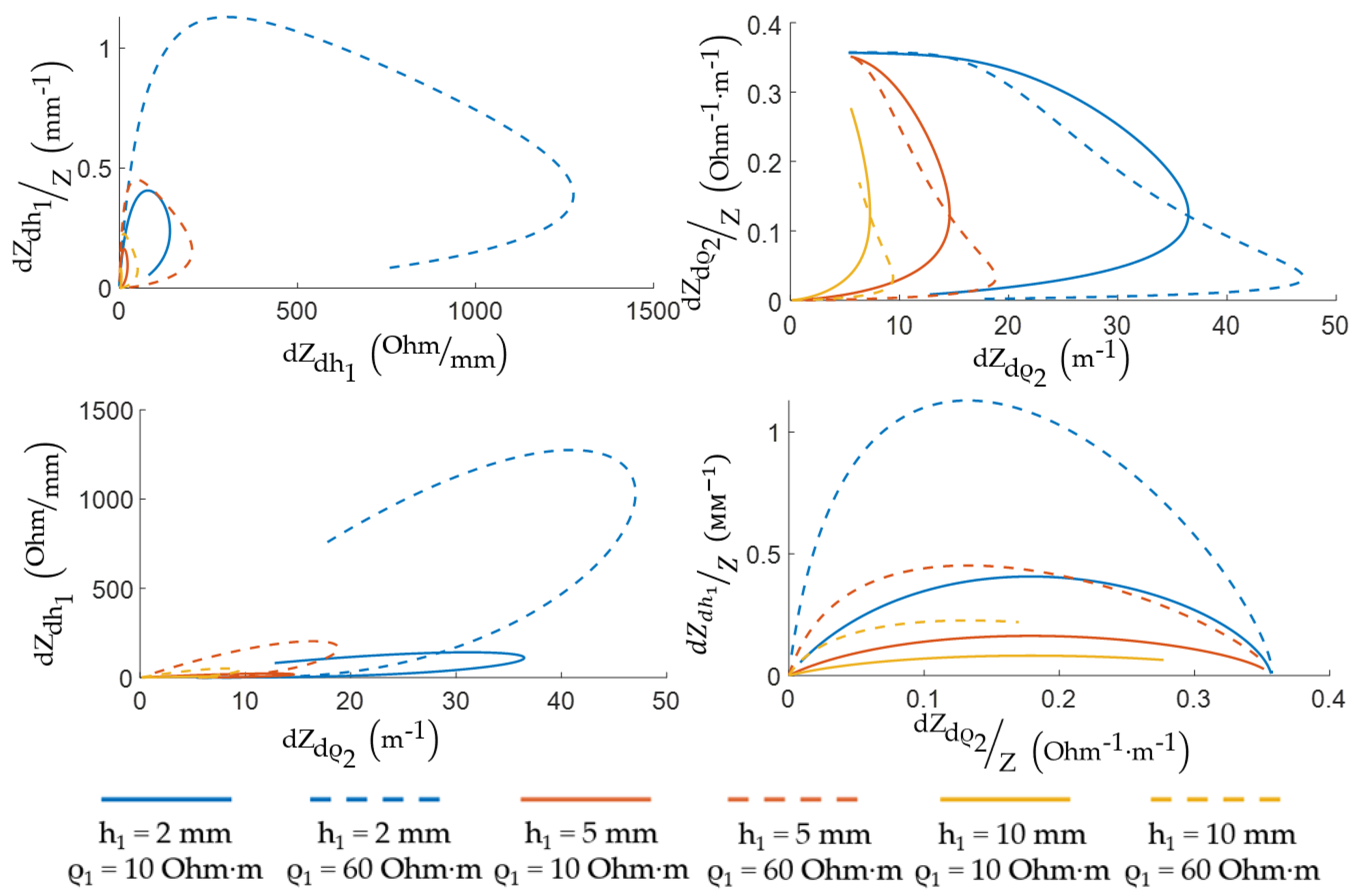
3. Methodology for Selecting ES Geometric Dimensions for EI Myography
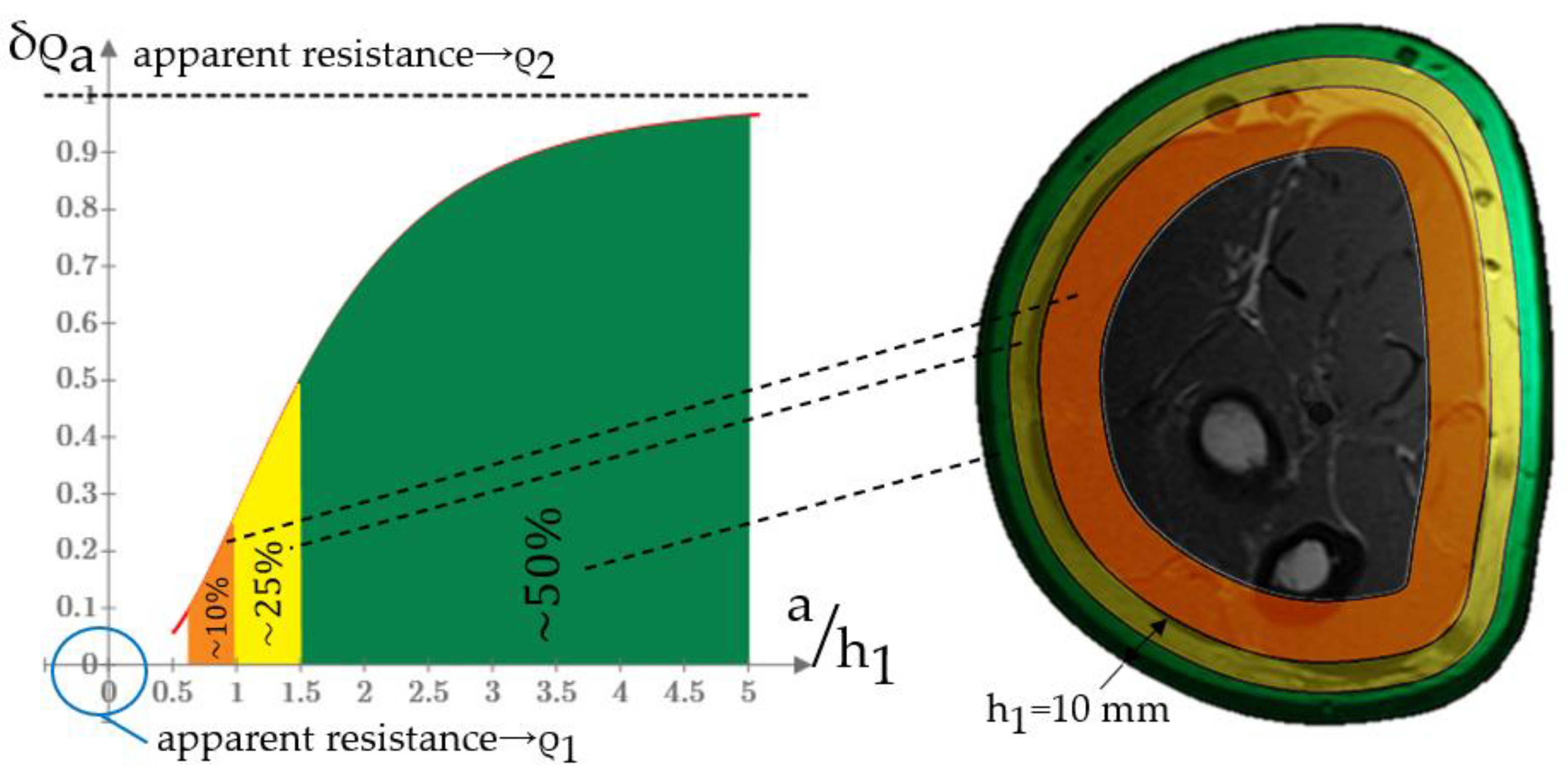
3.1. Acceptable ES Sizes Criteria
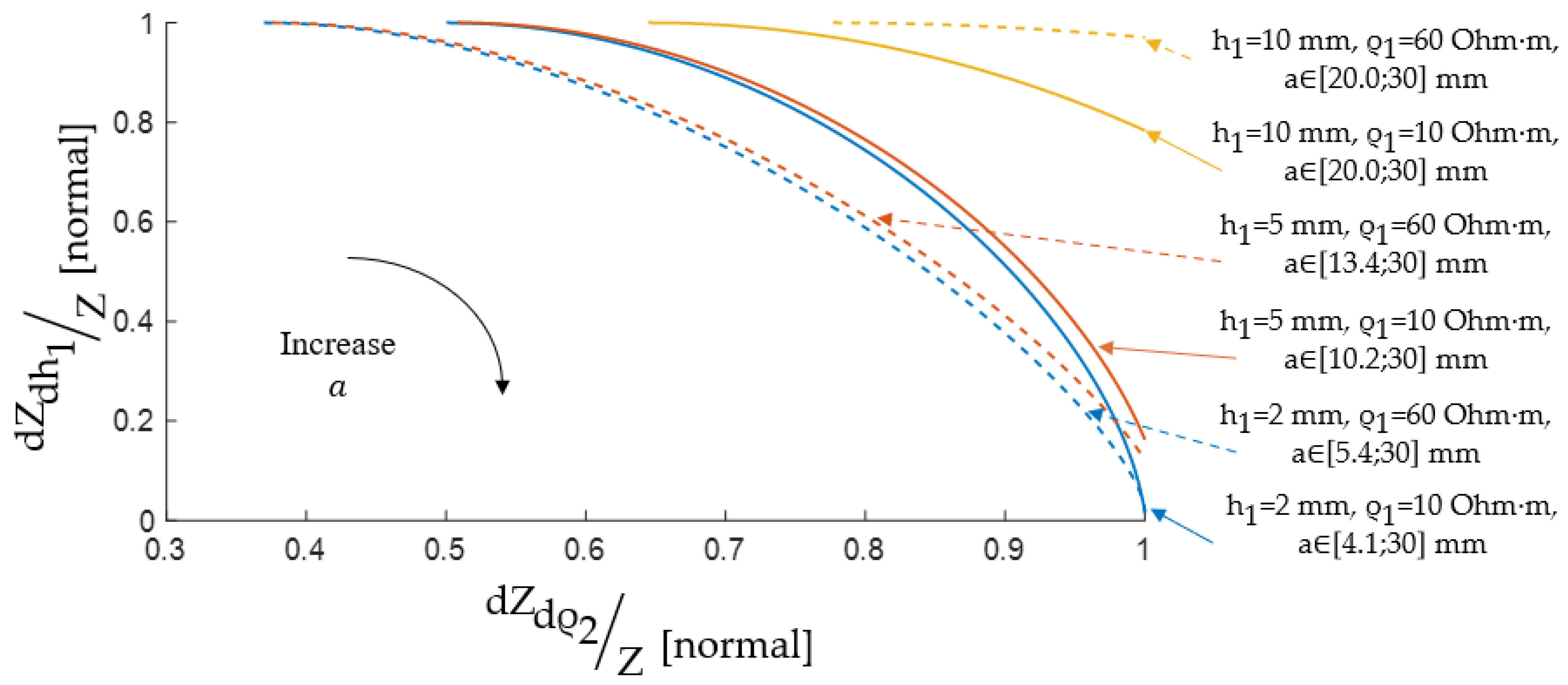
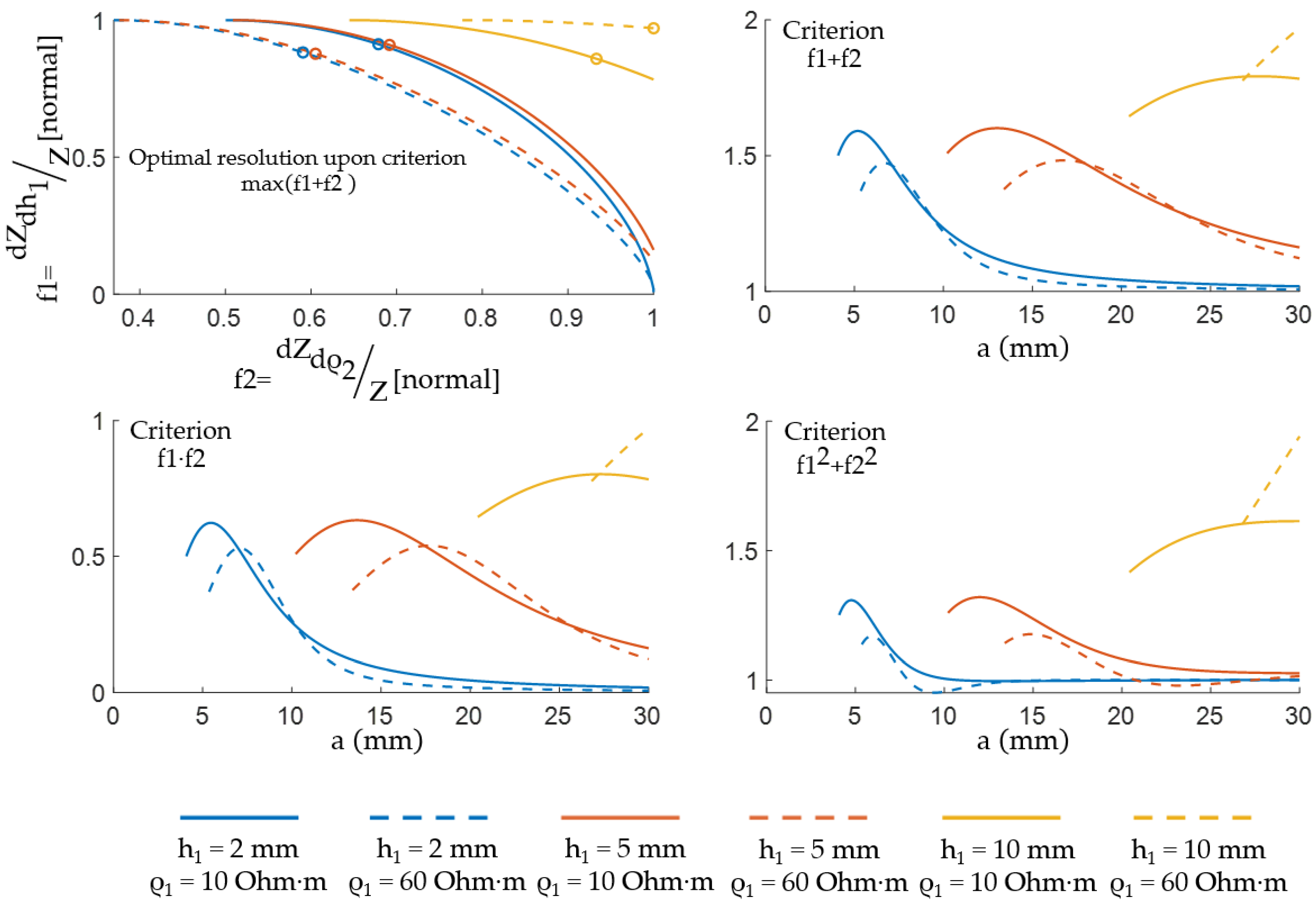
3.2. ES Size Selection by Pareto Optimality
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
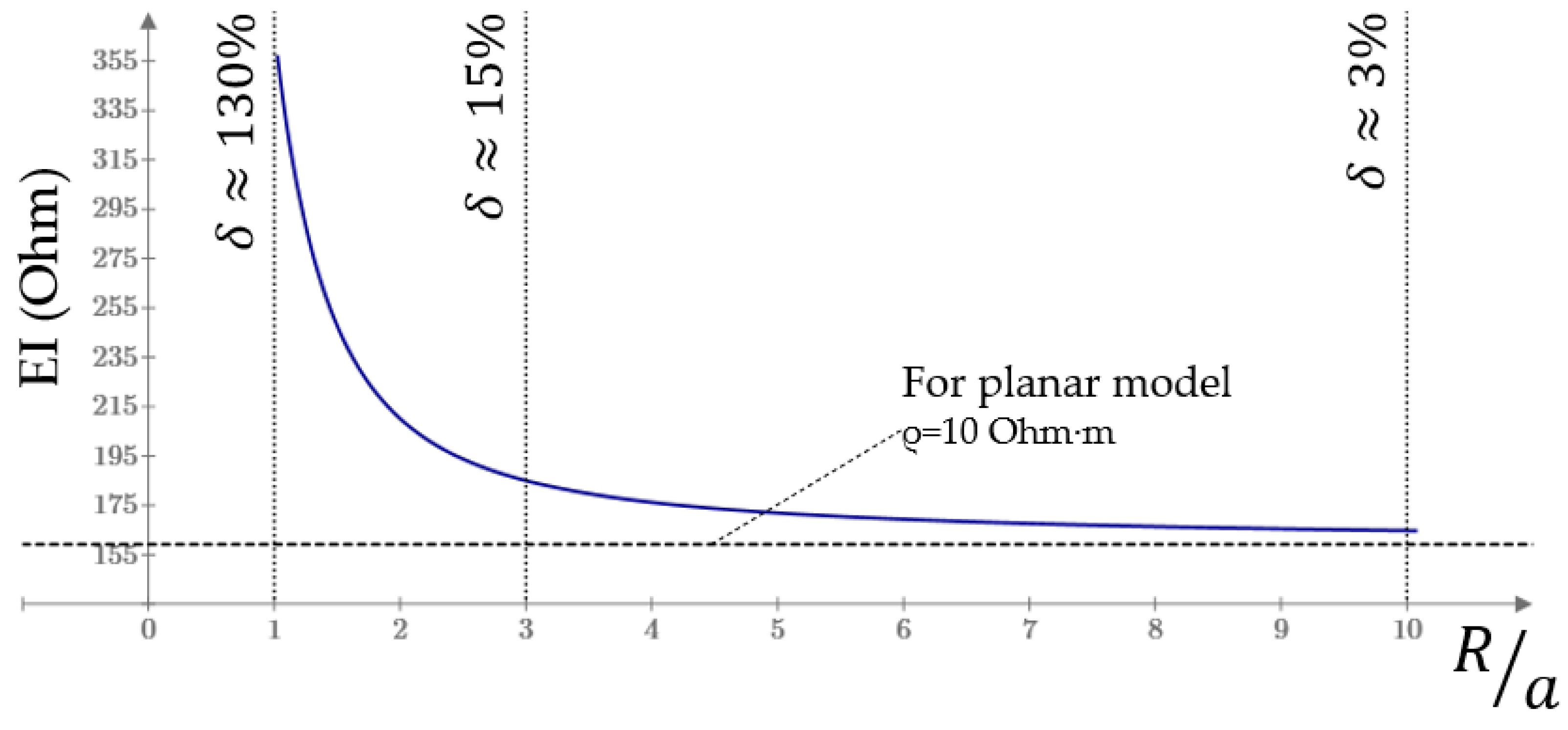
Appendix A. EI Model Acceptable Size Determination
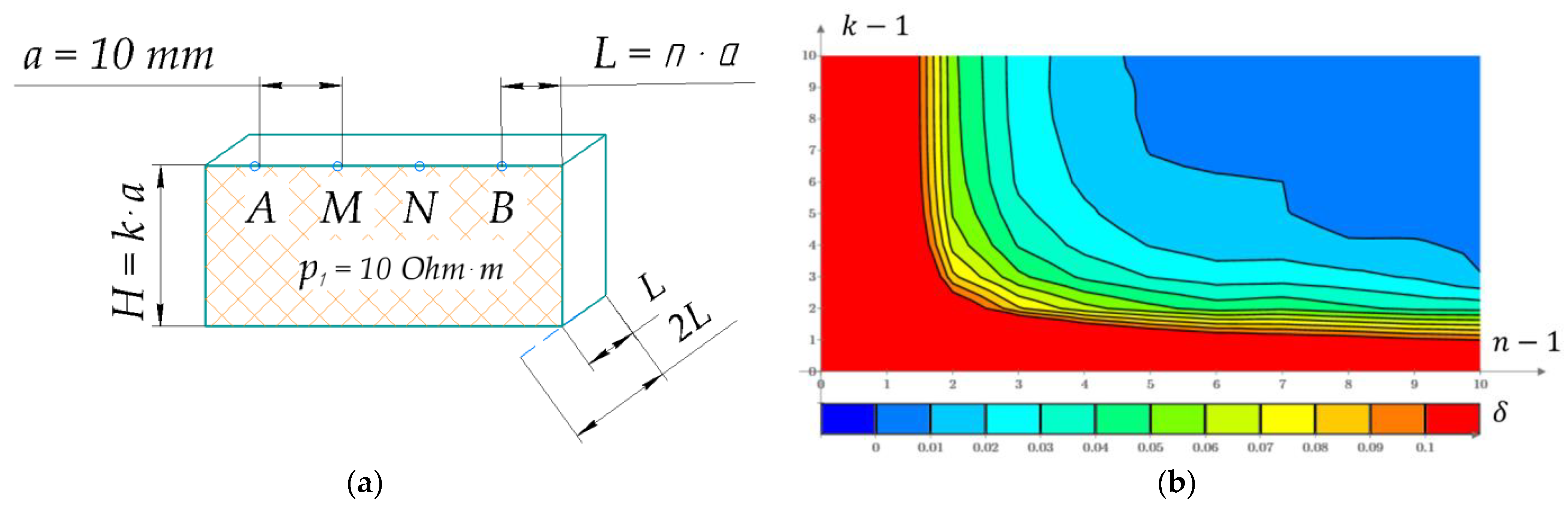
Appendix B. Computational Model Grid Type Dividing Substantiation
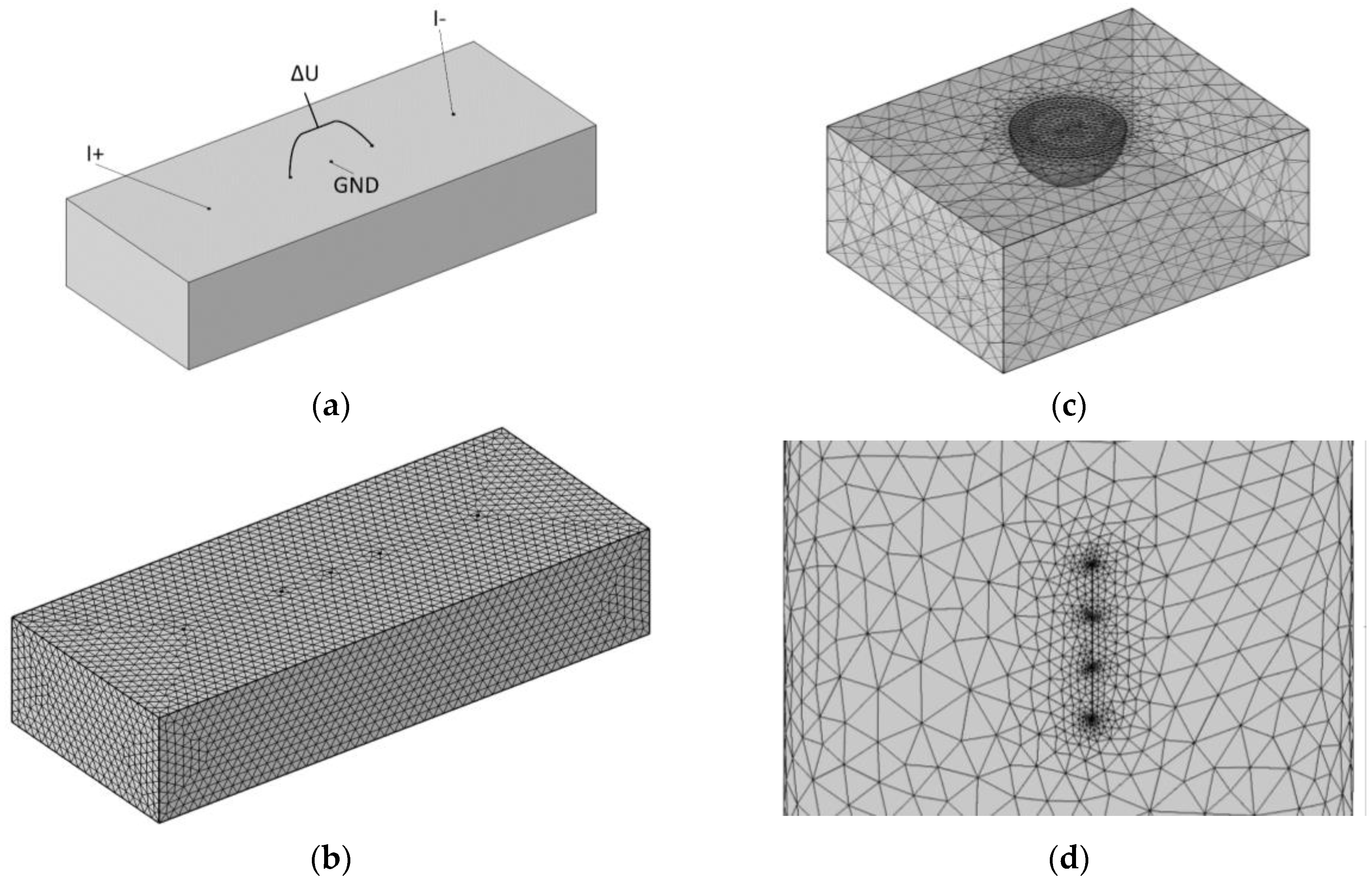
| Elements’ Parameters | Elements Distribution | ||
|---|---|---|---|
| Maximum size | 10 mm | Quantity | 10 |
| Minimum size | 0.01 mm | Ratio | 10 |
| Rate of increase | 1.4 | Ascending formula | Arithmetic |
| Curve factor | 0.4 | Symmetric distribution | Yes |
| Narrow regions resolution | 0.7 | ||
| Element type | Tetrahedron |
Appendix C. Computational Model Type of Grid Division Substantiation

References
- Kobelev, A.V.; Shchukin, S.I. Anthropomorphic prosthesis control based on the electrical impedance signals analysis. In 2018 Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT); IEEE: New York, NY, USA, 2018; pp. 33–36. [Google Scholar] [CrossRef]
- Lo, H.S.; Xie, S.Q. Exoskeleton robots for upper-limb rehabilitation: State of the art and future prospects. Med. Eng. Phys. 2012, 34, 261–268. [Google Scholar] [CrossRef] [PubMed]
- Cordella, F.; Ciancio, A.L.; Sacchetti, R.; Davalli, A.; Cutti, A.G.; Guglielmelli, E.; Zollo, L. Literature review on needs of upper limb prosthesis users. Front. Neurosci. 2016, 10, 209. [Google Scholar] [CrossRef] [PubMed]
- Osborn, L.E.; Iskarous, M.M.; Thakor, N.V. Sensing and control for prosthetic hands in clinical and research applications. In Wearable Robotics; Elsevier: Amsterdam, The Netherlands, 2020; pp. 445–468. [Google Scholar] [CrossRef]
- Mooney, L.M.; Rouse, E.J.; Herr, H.M. Autonomous exoskeleton reduces metabolic cost of human walking during load carriage. J. Neuroeng. Rehabil. 2014, 11, 80. [Google Scholar] [CrossRef] [Green Version]
- Scott, R.N.; Parker, P.A. Myoelectric prostheses: State of the art. J. Med Eng. Technol. 1988, 12, 143–151. [Google Scholar] [CrossRef]
- Micera, S.; Carpaneto, J.; Raspopovic, S. Control of hand prostheses using peripheral information. IEEE Rev. Biomed. Eng. 2010, 3, 48–68. [Google Scholar] [CrossRef] [Green Version]
- Žagar, T.; Krizaj, D. Electrical impedance of relaxed and contracted skeletal muscle. In Proceedings of the 13th International Conference on Electrical Bioimpedance and the 8th Conference on Electrical Impedance Tomography, Graz, Austria, 29 August–2 September 2007; pp. 711–714. [Google Scholar] [CrossRef]
- Rutkove, S.B. Electrical impedance myography: Background, current state, and future directions. Muscle Nerve Off. J. Am. Assoc. Electrodiagn. Med. 2009, 40, 936–946. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, B.; Rutkove, S.B. Electrical impedance myography and its applications in neuromuscular disorders. Neurotherapeutics 2016, 14, 107–118. [Google Scholar] [CrossRef] [PubMed]
- Schwan, H.P. Electrode polarization impedance and measurements in biological materials. Ann. N. Y. Acad. Sci. 1968, 148, 191–209. [Google Scholar] [CrossRef] [PubMed]
- Kobelev, A.; Shchukin, S.I.; Leonhardt, S. Application of tetrapolar electrode systems in electrical impedance measurements. Biomed. Eng. 2019, 52, 383–386. [Google Scholar] [CrossRef]
- Sanchez, B.; Li, J.; Geisbush, T.; Bardia, R.B.; Rutkove, S. Impedance alterations in healthy and diseased mice during electrically induced muscle contraction. IEEE Trans. Biomed. Eng. 2014, 63, 1602–1612. [Google Scholar] [CrossRef] [PubMed]
- Tarulli, A.W.; Duggal, N.; Esper, G.J.; Garmirian, L.P.; Fogerson, P.M.; Lin, C.H.; Rutkove, S.B. Electrical impedance myography in the assessment of disuse atrophy. Arch. Phys. Med. Rehabil. 2009, 90, 1806–1810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Harosh, M.B.; Shchukin, S. Peripheral vein detection using electrical impedance method. J. Electr. Bioimpedance 2017, 8, 79–83. [Google Scholar] [CrossRef] [Green Version]
- Kudashov, I.A.; Shchukin, S.; Al-Harosh, M.B. The study of needle electrode characteristics for venipuncture electrical impedance controlling system. In EMBEC & NBC 2017; Springer: Singapore, 2017; pp. 350–353. [Google Scholar] [CrossRef]
- Malakhov, A.; Tikhomirov, A.; Shchookin, S.I.; Kaplunova, V.Y. The precordial electrical impedance methods possibilities in the evaluation of local heart chambers contractility. In EMBEC & NBC 2017; Springer: Singapore, 2017; pp. 759–762. [Google Scholar] [CrossRef]
- McClendon, J.F. The increased permeability of striated muscle to ions during contraction. Am. J. Physiol. Content 1912, 29, 302–305. [Google Scholar] [CrossRef]
- Dubuisson, M. Recherches sur les modifications qui survien-nent dans la conductibilité électrique du muscle au cours de la contraction. Arch. Int. Physiol. 1933, 37, 35–57. [Google Scholar] [CrossRef]
- Shiffman, C.A.; Aaron, R.; Rutkove, S.B. Electrical impedance of muscle during isometric contraction. Physiol. Meas. 2003, 24, 213–234. [Google Scholar] [CrossRef]
- Sanchez, B.; Pacheck, A.; Rutkove, S. Guidelines to electrode positioning for human and animal electrical impedance myography research. Sci. Rep. 2016, 6, 32615. [Google Scholar] [CrossRef] [Green Version]
- Anand, G.; Yu, Y.; Lowe, A.; Kalra, A. Bioimpedance analysis as a tool for hemodynamic monitoring: Overview, methods and challenges. Physiol. Meas. 2021, 42, 03TR01. [Google Scholar] [CrossRef]
- Barnes, R.; Pliquett, U.; Barthel, A. Simultaneous measurement of action potentials and bioimpedance during muscle movement. In Proceedings of the 15th International Conference on Electrical Bio-Impedance, Heilbad Heiligenstadt, Germany, 22–25 April 2013. [Google Scholar] [CrossRef]
- Fatt, P. An analysis of the transverse electrical impedance of striated muscle. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1964, 159, 606–651. [Google Scholar] [CrossRef]
- Epstein, B.R.; Foster, K.R. Anisotropy in the dielectric properties of skeletal muscle. Med. Biol. Eng. Comput. 1983, 21, 51–55. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Tang, L.; Bronlund, J.E. Surface EMG signal amplification and filtering. Int. J. Comput. Appl. 2013, 82, 15–22. [Google Scholar] [CrossRef]
- Mobley, B.A.; Leung, J.; Eisenberg, R.S. Longitudinal impedance of single frog muscle fibers. J. Gen. Physiol. 1975, 65, 97–113. [Google Scholar] [CrossRef] [Green Version]
- Mobley, B.A.; Eidt, G. Transverse impedance of single frog skeletal muscle fibers. Biophys. J. 1982, 40, 51–59. [Google Scholar] [CrossRef] [Green Version]
- Pryor, R.W. Multiphysics Modeling Using COMSOL®: A First-Principles Approach; Jones & Bartlett Learning: Burlington, MA, USA, 2009. [Google Scholar]
- Pettersen, F.-J.; Høgetveit, J.O. From 3D tissue data to impedance using Simpleware ScanFE+ IP and COMSOL Multiphysics—A tutorial. J. Electr. Bioimpedance 2011, 2, 13–32. [Google Scholar] [CrossRef] [Green Version]
- “COMSOL Multiphysics 5.4 Introduction”. 2018. Available online: www.comsol.ru (accessed on 10 December 2021).
- Malmivuo, J.; Plonsey, R. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields; Oxford University Press: Oxford, UK, 1995. [Google Scholar] [CrossRef]
- Grimnes, S.; Martinsen, O.G. Bioimpedance and Bioelectricity Basics; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Faes, T.J.C.; Van Der Meij, H.A.; De Munck, J.C.; Heethaar, R.M. The electric resistivity of human tissues (100 Hz–10 MHz): A meta-analysis of review studies. Physiol. Meas. 1999, 20, R1–R10. [Google Scholar] [CrossRef]
- Schooling, C.N.; Healey, T.J.; McDonough, H.E.; French, S.J.; McDermott, C.J.; Shaw, P.J.; Kadirkamanathan, V.; Alix, J.J.P. Modelling and analysis of electrical impedance myography of the lateral tongue. Physiol. Meas. 2020, 41, 125008. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Balaguera, E.; López-Dolado, E.; Polo, J.L. Obtaining electrical equivalent circuits of biological tissues using the current interruption method, circuit theory and fractional calculus. RSC Adv. 2016, 6, 22312–22319. [Google Scholar] [CrossRef]
- Hernández-Balaguera, E.; López-Dolado, E.; Polo, J.L. In vivo rat spinal cord and striated muscle monitoring using the current interruption method and bioimpedance measurements. J. Electrochem. Soc. 2018, 165, G3099–G3103. [Google Scholar] [CrossRef]
- Briko, A.; Parnovskaya, A.; Larionova, M.; Dyachencova, S.; Gulyaev, Y. Influence of Electrodes Shape on Electrical Impedance Registration in Solving Bionic Control Problems. In 2020 Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT); IEEE: New York, NY, USA, 2020; pp. 73–76. [Google Scholar] [CrossRef]
- Zaborovsky, A.I. Electrical Prospecting; Gostoptekhizdat: Moscow, Russia, 1963; p. 423. [Google Scholar]
- Seleznev, N.V.; Briko, A.N.; Deshin, I.A.; Tikhomirov, A. Electrode system sensitivity evaluation at longitudinal-transverse precardiac impedance heart mapping. AIP Conf. Proc. 2019, 2140, 020065. [Google Scholar] [CrossRef]
- Bozler, E.; Cole, K.S. Electric impedance and phase angle of muscle in rigor. J. Cell. Comp. Physiol. 1935, 6, 229–241. [Google Scholar] [CrossRef]
- Bozler, E. The change of alternating current impedance of muscle produced by contraction. J. Cell. Comp. Physiol. 1935, 6, 217–228. [Google Scholar] [CrossRef]
- Briko, A.N.; Parnovskaya, A.D.; Kapravchuk, V.V.; Dyachenkova, S.I.; Shchukin, S.I.; Kobelev, A.V.; Vasiliev, Y.A.; Petryaikin, A.V. Раrаmеtriс assessment of morphological changes in forеаrm tissues when performing basic actions with а hand based on MRI: Methodological aspects. Biomed. Radioeleкronika Biomed. Radioeng. 2021, 24, 6–16. [Google Scholar] [CrossRef]
- Podinovskiy, V.V.; Nogin, V.D. Pareto-Optimal Solutions of Multicriteria Problems; Fizmatlit: Moscow, Russia, 2007. [Google Scholar]
- Shchukin, S.I.; Kobelev, A.V.; Lipich, Y.N.; Ngo, C.; Gulyaev, Y.V.; Briko, A.N.; Hülkenberg, A.; Leonhardt, S. Fusion of Electromyogram and Bioimpedance (Electrical Impedance Myography) for Force-Moment Control in Medical Assisted Devices. Russ. Found. Basic Res. J. 2021, 112–125. [Google Scholar] [CrossRef]



| Single Cut | Ellipsoidal | Cylindrical | Planar 3 Layers | Planar 2 Layers | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a (mm) | S (Ohm) | S/Z | S (Ohm) | S/Z | S (Ohm) | S/Z | S (Ohm) | S/Z | S (Ohm) | S/Z |
| 5 | 4.93 | 0.02 | 7.59 | 0.02 | 8.16 | 0.03 | 6.28 | 0.02 | 6.07 | 0.02 |
| 10 | 14.97 | 0.14 | 9.60 | 0.07 | 9.34 | 0.07 | 6.99 | 0.05 | 6.17 | 0.04 |
| 15 | 9.56 | 0.16 | 8.45 | 0.10 | 10.43 | 0.14 | 7.19 | 0.09 | 5.69 | 0.07 |
| 20 | 5.72 | 0.14 | 6.32 | 0.12 | 11.93 | 0.21 | 8.24 | 0.16 | 5.01 | 0.10 |
| Parameters | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 2 | 4.0 | 203.7 | 41.2 | 5.0 | 8.3 | 5.3 | 123.2 | 20.0 | 4.3 | 4.7 |
| 10 | 5 | 10.1 | 80.0 | 6.5 | 2.0 | 3.3 | 13.3 | 49.0 | 3.4 | 1.7 | 2.0 |
| 10 | 10 | 20.0 | 40.7 | 1.7 | 1.0 | 1.7 | 20.0 | 40.7 | 1.7 | 1.0 | 1.7 |
| 60 | 2 | 5.3 | 277.3 | 126.9 | 5.0 | 25.4 | 7.3 | 103.0 | 30.4 | 3.5 | 8.6 |
| 60 | 5 | 13.4 | 106.9 | 22.5 | 2.0 | 11.4 | 18.4 | 40.3 | 6.0 | 1.4 | 4.2 |
| 60 | 10 | 20.0 | 134.4 | 13.1 | 1.2 | 10.7 | 20.0 | 134.4 | 13.1 | 1.2 | 10.7 |
| Parameters | ||||
|---|---|---|---|---|
| 10 | 2 | 5.2 | 5.5 | 4.8 |
| 10 | 5 | 13.0 | 13.6 | 12.0 |
| 10 | 10 | 27.7 | 27.3 | 29.9 |
| 60 | 2 | 6.7 | 7.1 | 5.9 |
| 60 | 5 | 16.8 | 17.7 | 14.9 |
| 60 | 10 | 30.0 | 30.0 | 30.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Briko, A.; Kapravchuk, V.; Kobelev, A.; Tikhomirov, A.; Hammoud, A.; Al-Harosh, M.; Leonhardt, S.; Ngo, C.; Gulyaev, Y.; Shchukin, S. Determination of the Geometric Parameters of Electrode Systems for Electrical Impedance Myography: A Preliminary Study. Sensors 2022, 22, 97. https://doi.org/10.3390/s22010097
Briko A, Kapravchuk V, Kobelev A, Tikhomirov A, Hammoud A, Al-Harosh M, Leonhardt S, Ngo C, Gulyaev Y, Shchukin S. Determination of the Geometric Parameters of Electrode Systems for Electrical Impedance Myography: A Preliminary Study. Sensors. 2022; 22(1):97. https://doi.org/10.3390/s22010097
Chicago/Turabian StyleBriko, Andrey, Vladislava Kapravchuk, Alexander Kobelev, Alexey Tikhomirov, Ahmad Hammoud, Mugeb Al-Harosh, Steffen Leonhardt, Chuong Ngo, Yury Gulyaev, and Sergey Shchukin. 2022. "Determination of the Geometric Parameters of Electrode Systems for Electrical Impedance Myography: A Preliminary Study" Sensors 22, no. 1: 97. https://doi.org/10.3390/s22010097
APA StyleBriko, A., Kapravchuk, V., Kobelev, A., Tikhomirov, A., Hammoud, A., Al-Harosh, M., Leonhardt, S., Ngo, C., Gulyaev, Y., & Shchukin, S. (2022). Determination of the Geometric Parameters of Electrode Systems for Electrical Impedance Myography: A Preliminary Study. Sensors, 22(1), 97. https://doi.org/10.3390/s22010097








