A Real-Time Monitoring Method for Civil Aircraft Take-Off and Landing Based on Synthetic Aperture Microwave Radiation Technology
Abstract
:1. Introduction
2. Materials and Methods
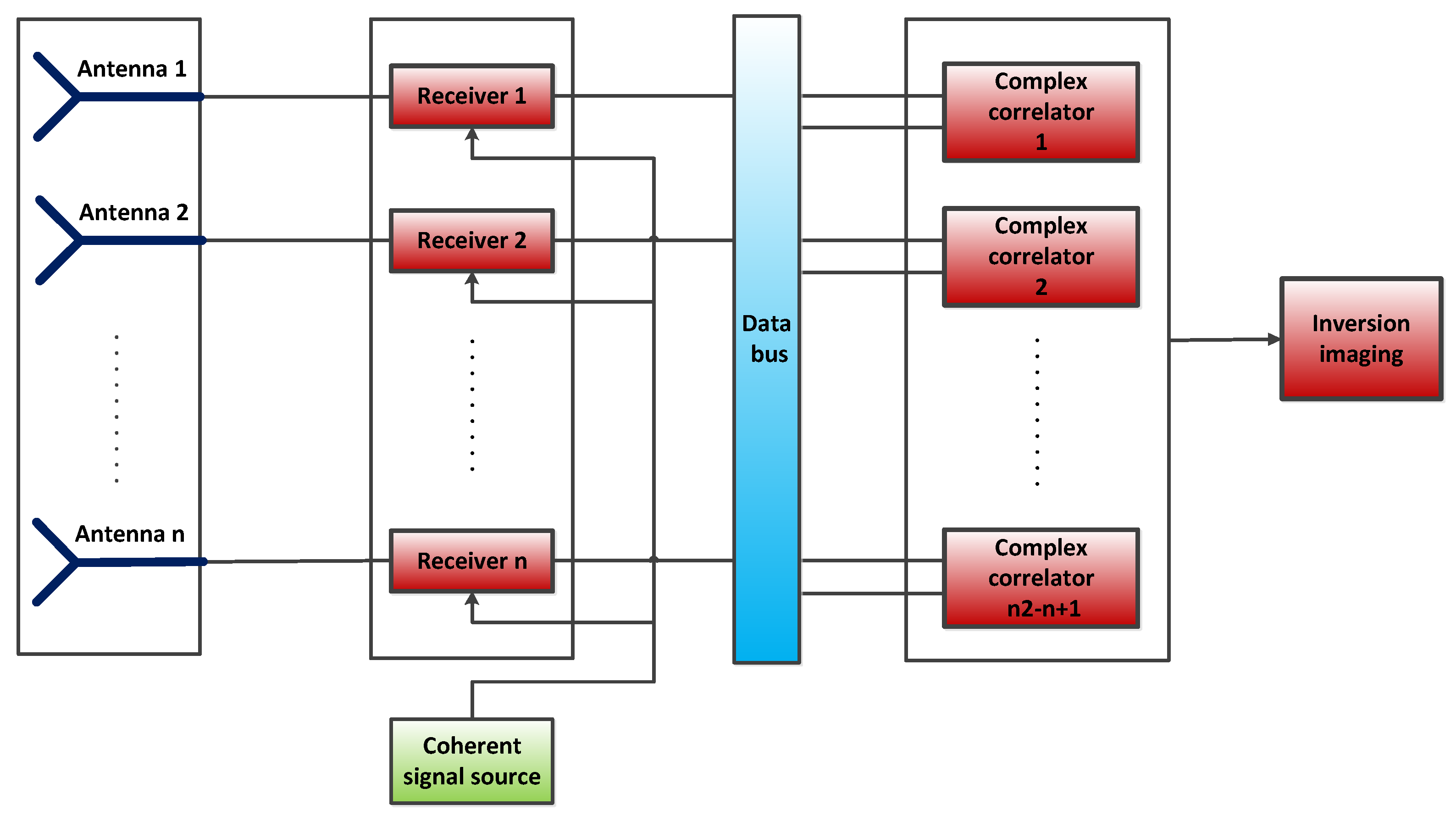
2.1. System Design
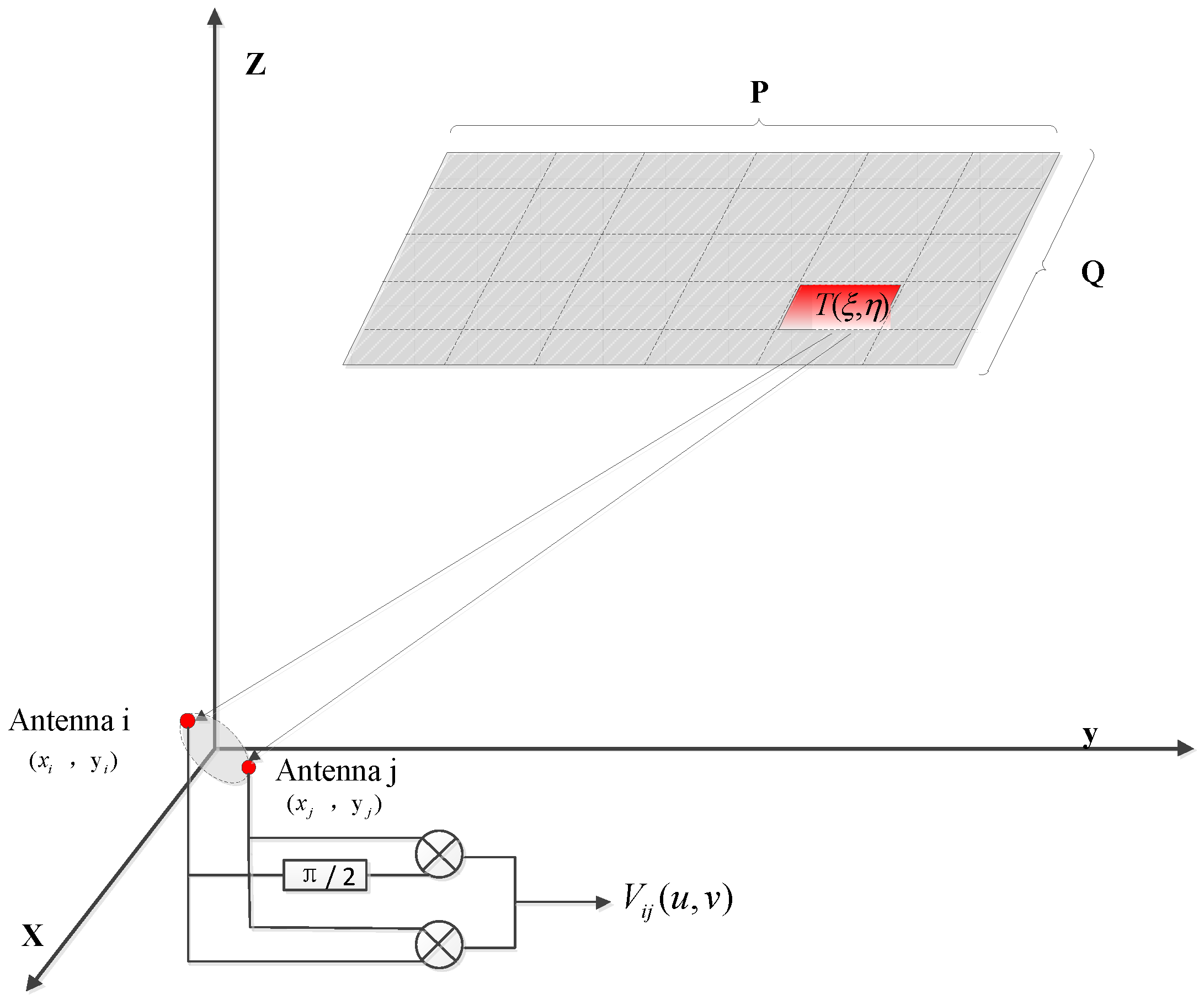
2.2. Inversion Imaging Algorithms
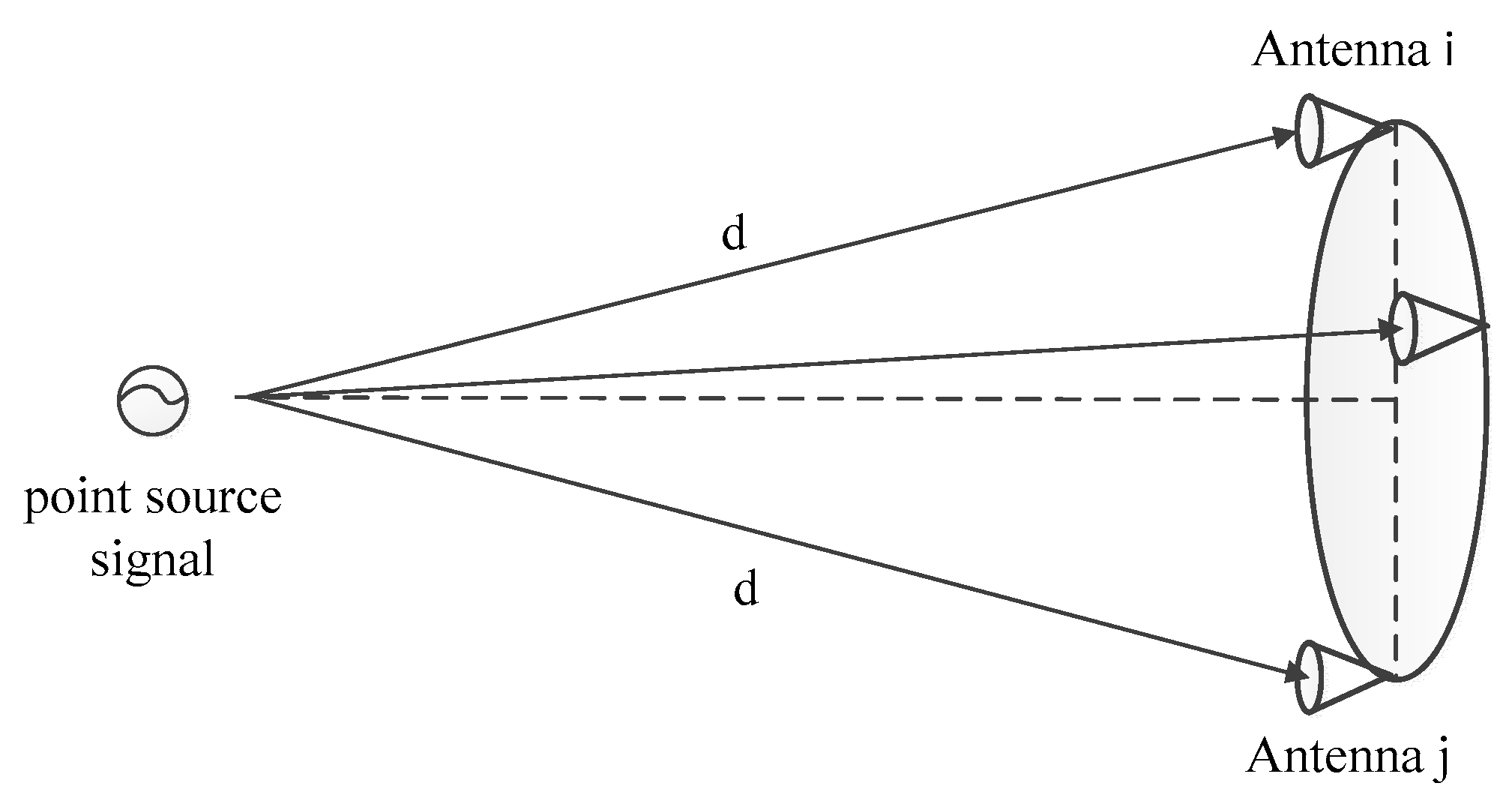
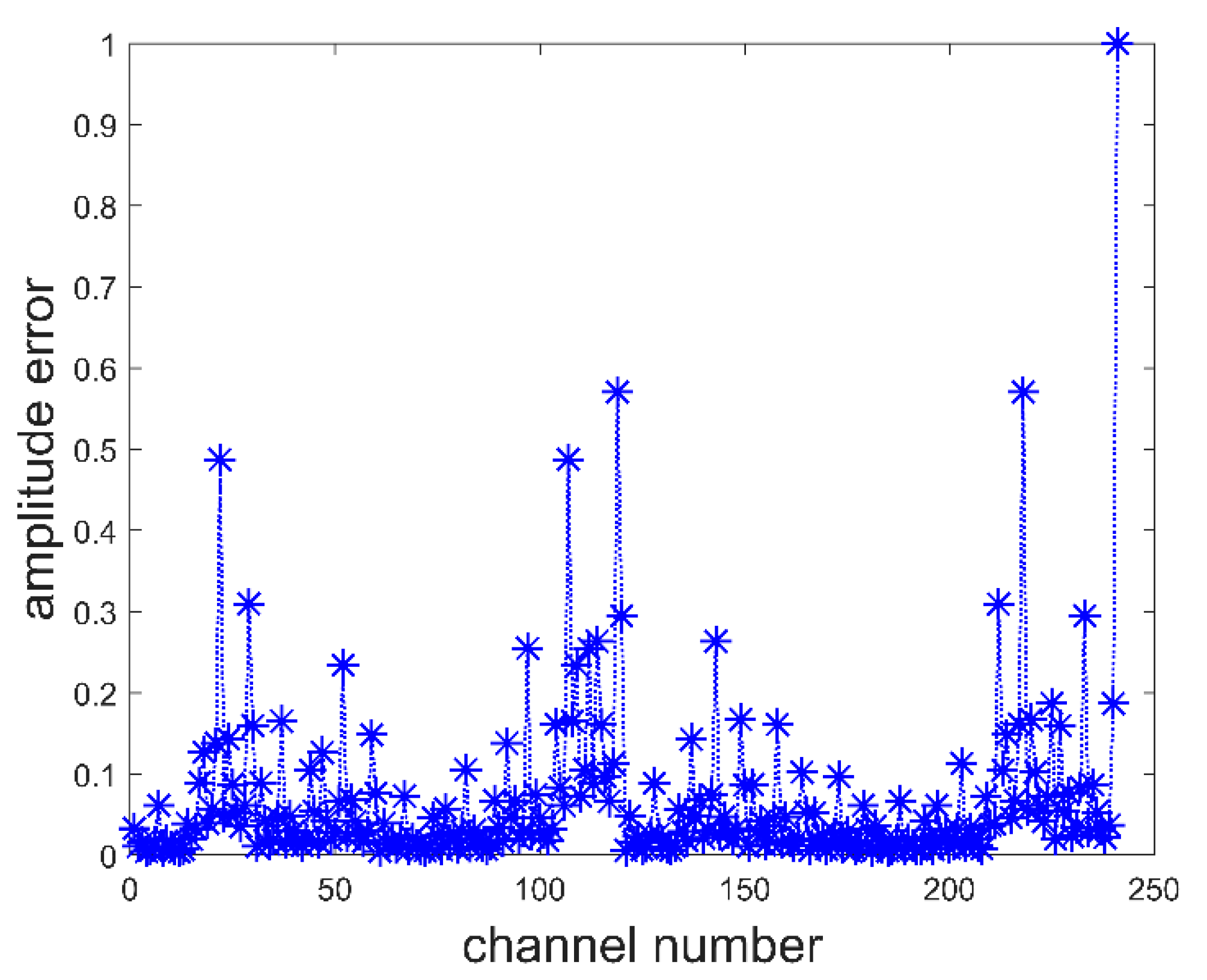
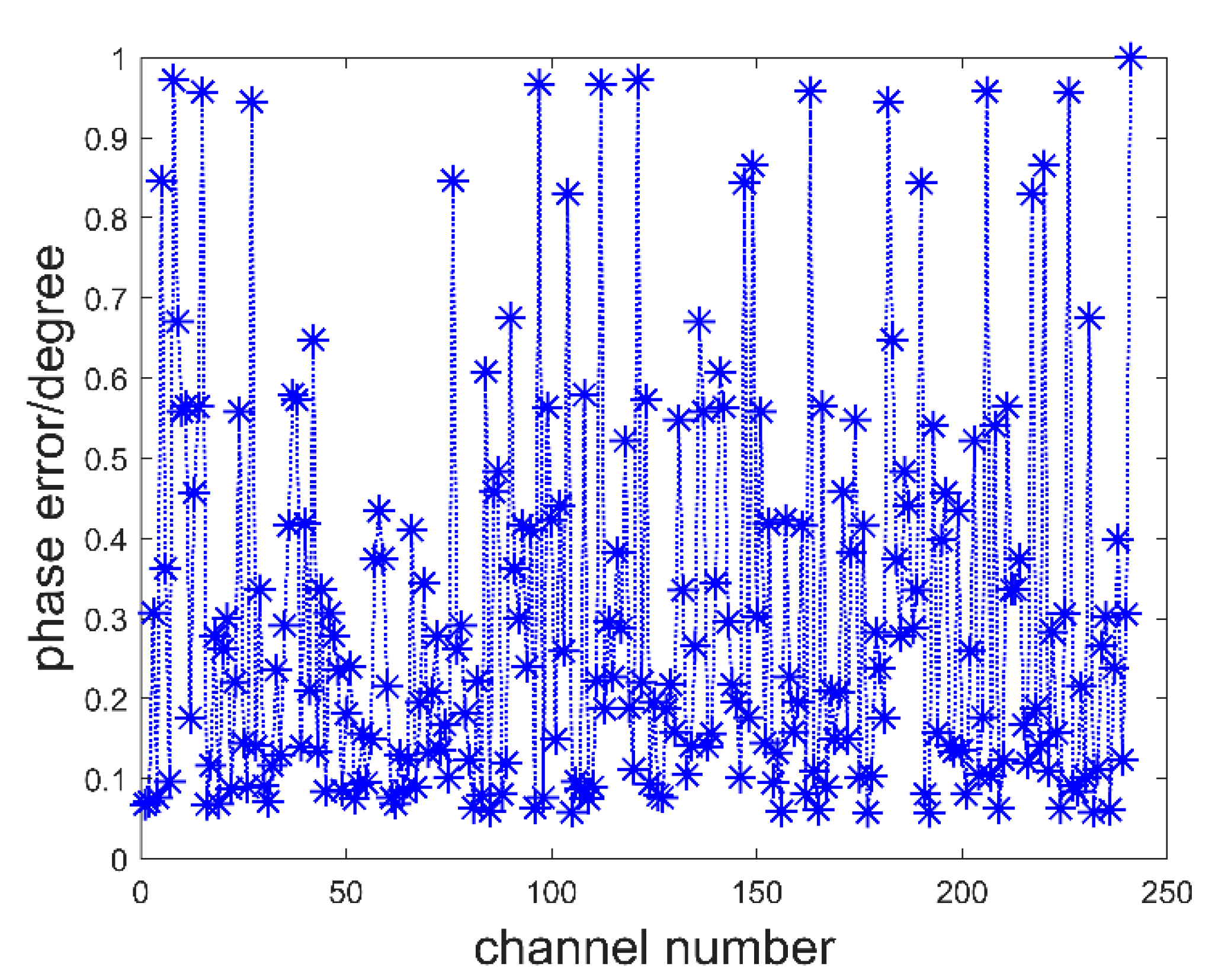
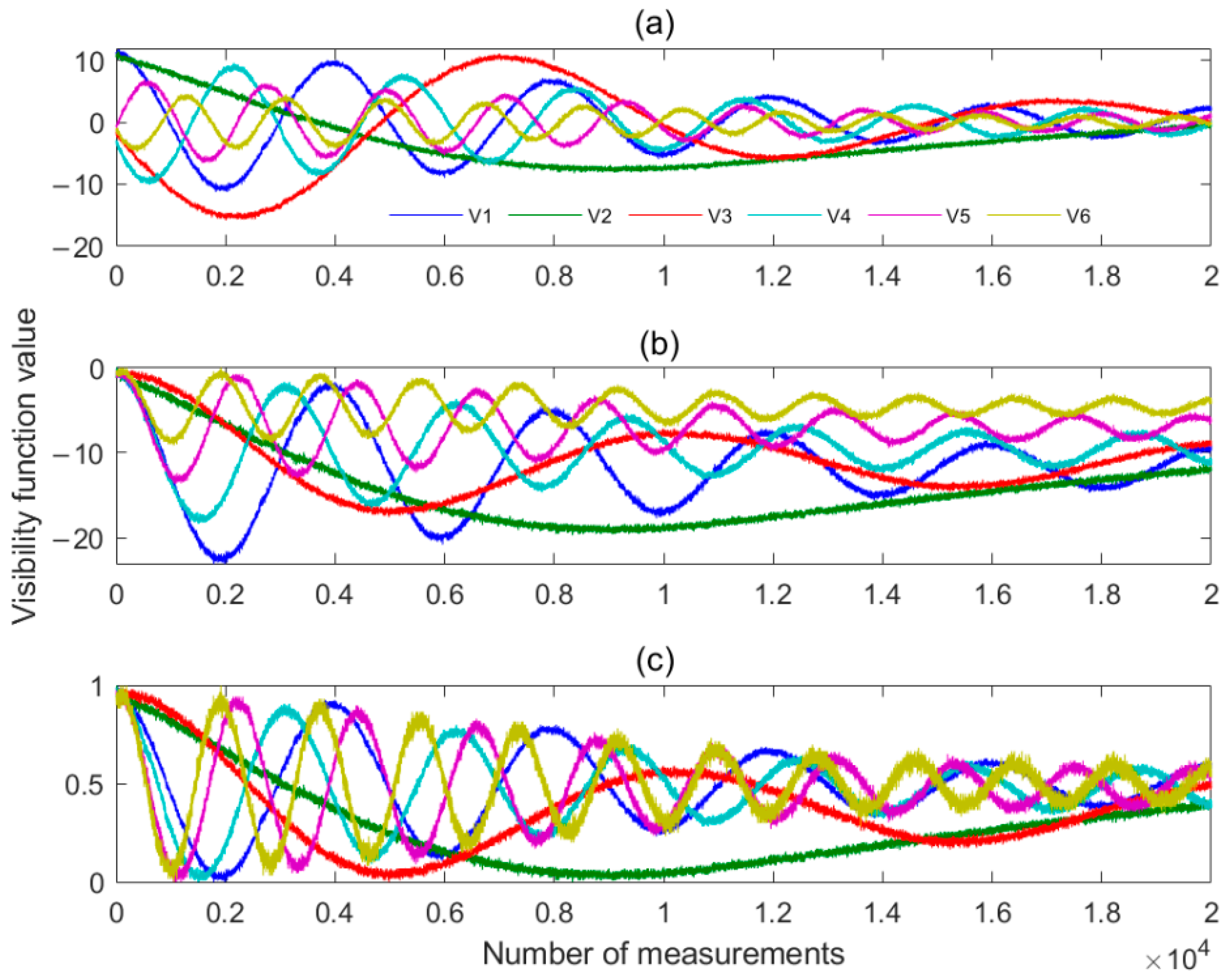
2.3. Error Compensation Method Based on Visibility Function
3. Results and Discussion
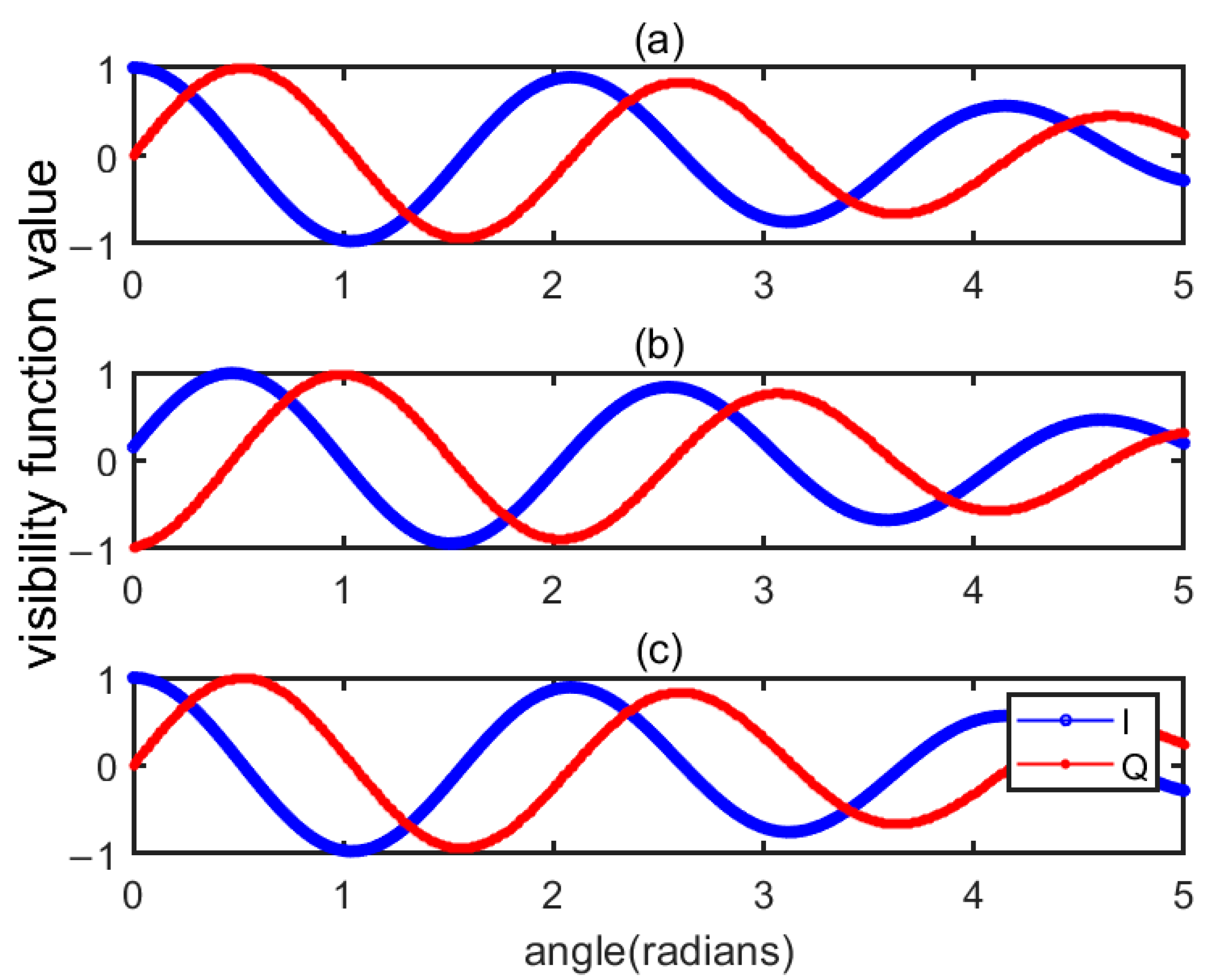
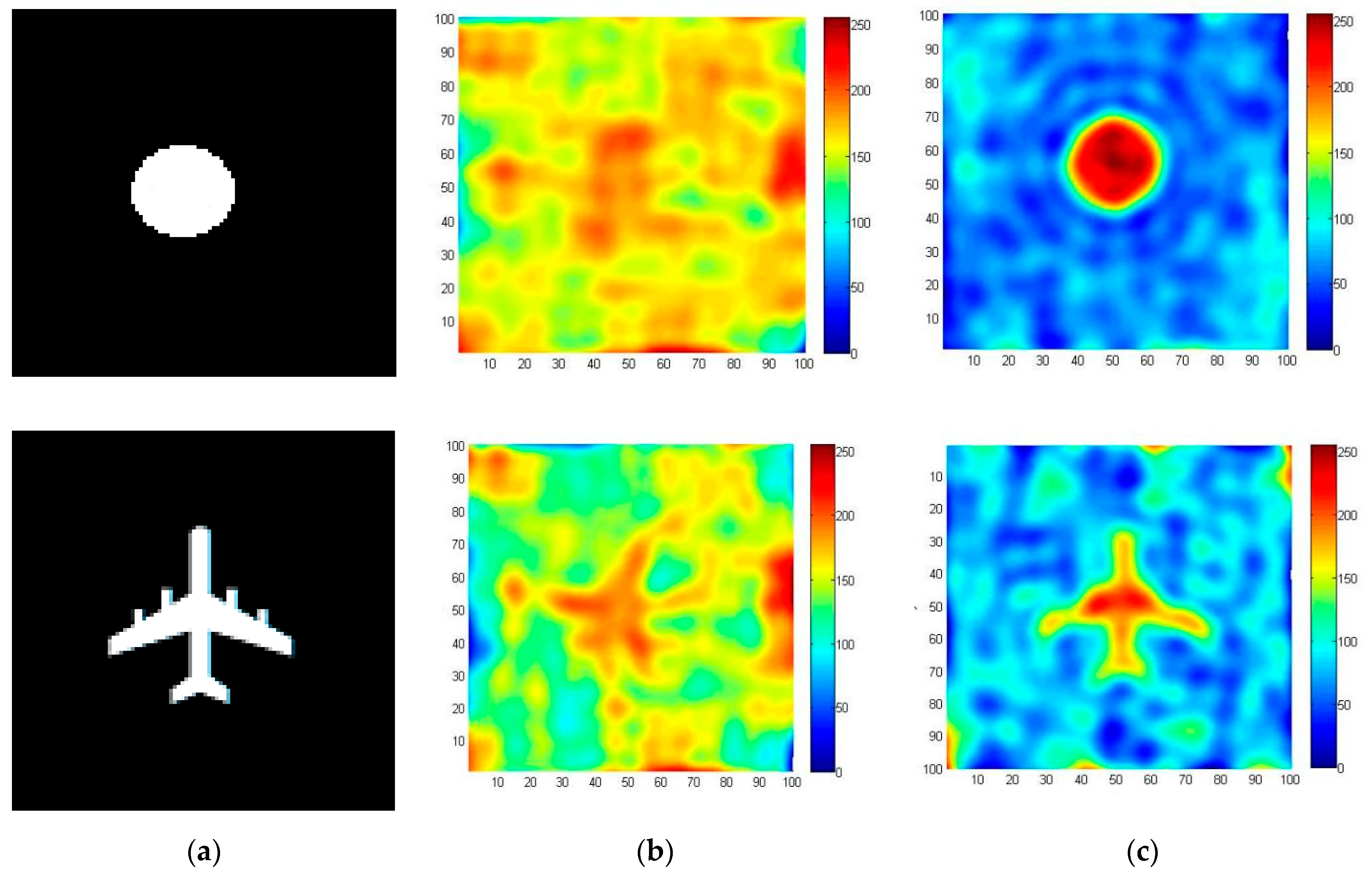
3.1. Simulation Verification
3.2. Experimental Result
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Le Vine, D.; Swift, C.; Haken, M. Development of the synthetic aperture microwave radiometer, ESTAR. IEEE Trans. Geosci. Remote Sens. 2001, 39, 199–202. [Google Scholar] [CrossRef]
- Kerr, Y.; Waldteufel, P.; Wigneron, J.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements of the Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Brown, M.; Torres, F.; Corbella, I.; Colliander, A. SMOS Calibration. IEEE Trans. Geosci. Remote Sens. 2008, 46, 646–658. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Uusitalo, J.; Kainulainen, J.; Rautiainen, K.; Fabritius, N.; Levander, M.; Kangas, V.; Greus, H.; Pihlflyckt, J.; Kontu, A.; et al. SMOS Calibration Subsystem. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3691–3700. [Google Scholar] [CrossRef]
- Tanner, A.; Wilson, W.; Lambrigsten, B.; Dinardo, S.; Brown, S.; Kangaslahti, P.; Gaier, T.; Ruf, C.; Gross, S.; Lim, B.; et al. Initial Results of the Geostationary Synthetic Thinned Array Radiometer (GeoSTAR) Demonstrator Instrument. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1947–1957. [Google Scholar] [CrossRef]
- Torres, F.; Tanner, A.; Brown, S.; Lambrigsten, B. Analysis of Array Distortion in a Microwave Interferometric Radiometer: Application to the GeoSTAR Project. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1958–1966. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, H.; Yan, J.Y.; Sun, W.Y.; Zhang, S.W.; Liu, H.G.; Wu, J. Imaging Algorithm and Experimental Demonstration of Rotating Scanning Interferometric Radiometer. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; 2010. [Google Scholar]
- Chen, K.; Zhu, Y.; Guo, X.; Guo, W.; Li, Q.; Gui, L.; Ni, W. Design of 8 mm-band Aperture Synthetic Radiometer and Imaging Experiment. J. Infrared Millim. Terahertz Waves 2010, 31, 724–734. [Google Scholar]
- Chen, L.; Li, Q.; Yi, G.; Zhu, Y. One-Dimensional Mirrored Interferometric Aperture Synthesis: Performances, Simulation, and Experiments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2960–2968. [Google Scholar] [CrossRef]
- Dong, J.; Li, Q.; Jin, R.; Zhu, Y.; Huang, Q.; Gui, L. A Method for Seeking Low-Redundancy Large Linear Arrays in Aperture Synthesis Microwave Radiometers. IEEE Trans. Antennas Propag. 2010, 58, 1913–1921. [Google Scholar] [CrossRef]
- Yujiri, L.; Shoucri, M.; Moffa, P. Passive millimeter-wave imaging. IEEE Microw. Mag. 2003, 4, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Lettington, A. Design and development of a high-performance passive millimeter-wave imager for aeronautical applications. Opt. Eng. 2005, 44, 093202. [Google Scholar] [CrossRef]
- Le Vine, D.M. The sensitivity of synthetic aperture radiometers for remote sensing applications from space. Radio Sci. 1990, 25, 441–453. [Google Scholar] [CrossRef]
- Ruf, C.S.; Swift, C.T.; Tanner, A.B.; Le Vine, D.M. Interferometric synthetic aperture microwave radiometry for remote sensing of the earth. IEEE Trans. Geosci. Remote Sens. 1988, 26, 597–611. [Google Scholar] [CrossRef]
- Chen, H.; Chao, K.; Zhao, Z.; Lang, R.; Jin, Y. Analysis of two-dimensional circle-array synthetic aperture microwave radiometer channel errors. In Proceedings of the 2010 International Conference on Microwave and Millimeter Wave Technology, Chengdu, China, 8–11 November 2010. [Google Scholar]
- Corbella, I.; Torres, F.; Camps, A.; Duffo, N.; Vall-llossera, M.; Rautiainen, K.; Martin-Neira, M.; Colliander, A. Analysis of correlation and total power radiometer front-ends using noise waves. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2452–2459. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Wu, J.; Niu, L.; Zhang, C. Research on the Preprocessing Method for the Visibility Functions in Synthetic Aperture Radiometer and the Time Domain Simulation. J. Electron. Inf. Technol. 2013, 34, 2475–2481. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, S. Fast Image Reconstruction for Non-uniform Sampling of Thinned Array of Synthesis Aperture Radiometer. J. Electron. Inf. Technol. 2014, 35, 927–932. [Google Scholar] [CrossRef]
- Stogryn, A. Estimates of brightness temperatures from scanning radiometer data. IEEE Trans. Antennas Propag. 1978, 26, 720–726. [Google Scholar] [CrossRef]
- Liu, H.; Wu, J.; Wu, Q. Some further consideration for the image retrieving of synthetic aperture radiometer. In Proceedings of the 24th Asian Conference on Remote Sensing (ACRS), Busan, Korea, 3 November 2003. [Google Scholar]
- Ruf, C. Error analysis of image reconstruction by a synthetic aperture interferometric radiometer. Radio Sci. 1991, 26, 1419–1434. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Wang, J.; Li, Y.; Zhang, Y. Regularization Imaging Algorithm with Accurate G Matrix for Near-Field Mmw Synthetic Aperture Imaging Radiometer. Prog. Electromagn. Res. B 2014, 58, 193–203. [Google Scholar] [CrossRef] [Green Version]
- Yao, X. Analysis and Correction the Inter-channel Mismatch of Synthetic Aperture Radiometer. TELKOMNIKA Indones. J. Electr. Eng. 2013, 11, 7190–7196. [Google Scholar] [CrossRef]


| Parameter | Specifications |
|---|---|
| Operating Frequency | 15.2 GHz |
| antenna elements | 16 |
| bandwidth | 300 MHz |
| integration time | 10 ms |
| Brightness temperature measurement range | 5–350 K |
| System sensitivity | ≤2 K (at 10 ms) |
| Spatial resolution | 0.005 rad |
| Detection distance | ≥5 km |
| Antennas | Location (Radian) | |||
|---|---|---|---|---|
| 16 | 0.086 | 1.670 | 3.338 | 4.865 |
| 0.495 | 2.137 | 3.689 | 5.162 | |
| 0.995 | 2.444 | 3.969 | 5.769 | |
| 1.212 | 2.897 | 4.536 | 6.102 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Ge, J.; Kong, D.; Zhao, Z.; Zhu, Q. A Real-Time Monitoring Method for Civil Aircraft Take-Off and Landing Based on Synthetic Aperture Microwave Radiation Technology. Sensors 2022, 22, 3675. https://doi.org/10.3390/s22103675
Chen H, Ge J, Kong D, Zhao Z, Zhu Q. A Real-Time Monitoring Method for Civil Aircraft Take-Off and Landing Based on Synthetic Aperture Microwave Radiation Technology. Sensors. 2022; 22(10):3675. https://doi.org/10.3390/s22103675
Chicago/Turabian StyleChen, Houcai, Junxiang Ge, Deqing Kong, Zhenwei Zhao, and Qinglin Zhu. 2022. "A Real-Time Monitoring Method for Civil Aircraft Take-Off and Landing Based on Synthetic Aperture Microwave Radiation Technology" Sensors 22, no. 10: 3675. https://doi.org/10.3390/s22103675
APA StyleChen, H., Ge, J., Kong, D., Zhao, Z., & Zhu, Q. (2022). A Real-Time Monitoring Method for Civil Aircraft Take-Off and Landing Based on Synthetic Aperture Microwave Radiation Technology. Sensors, 22(10), 3675. https://doi.org/10.3390/s22103675





