Simulation and Experimental Research on a Beam Homogenization System of a Semiconductor Laser
Abstract
:1. Introduction
2. Methods
2.1. Spot Quality Evaluation
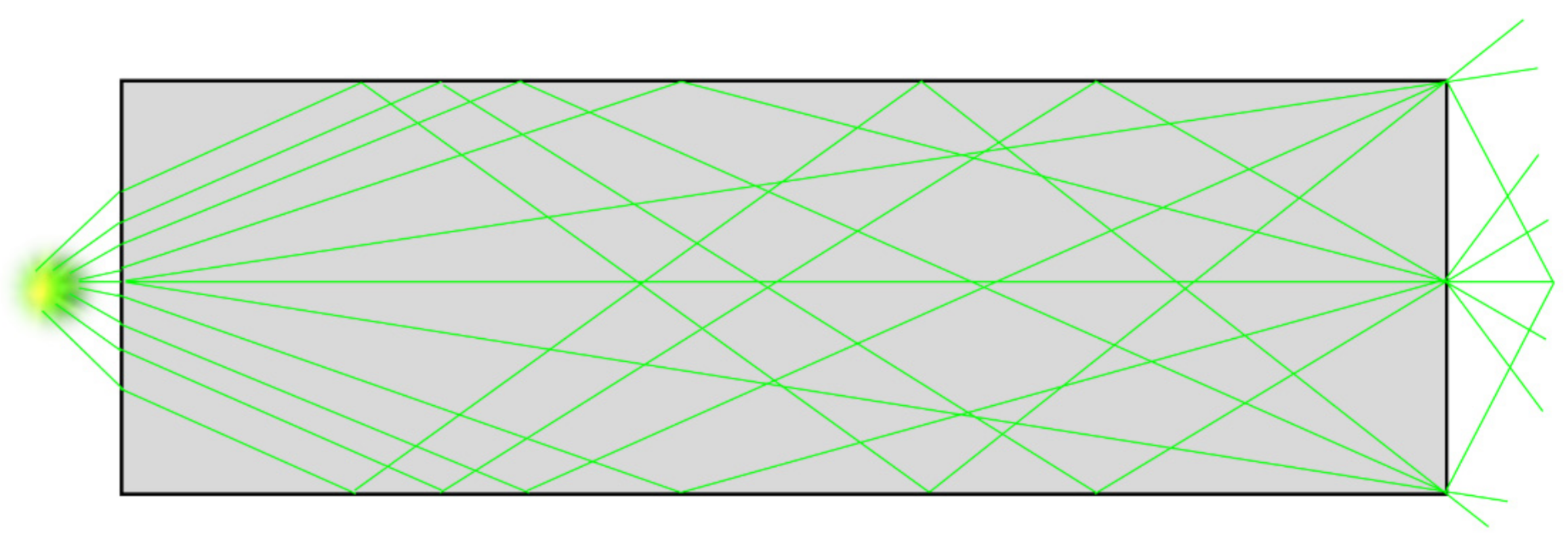
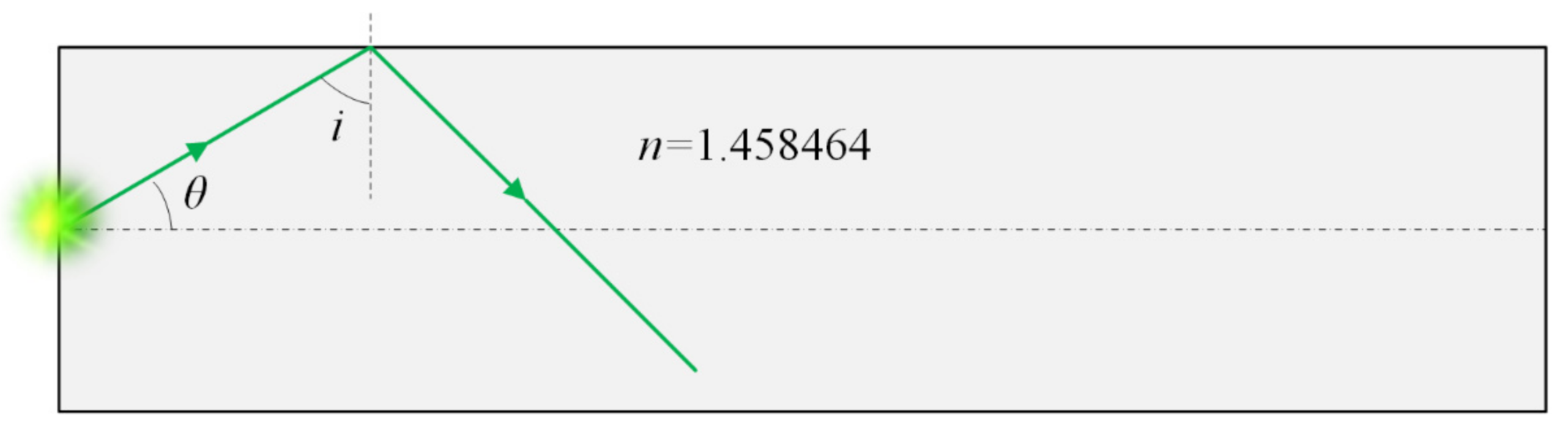
2.2. Principle of Homogenizing Pipe
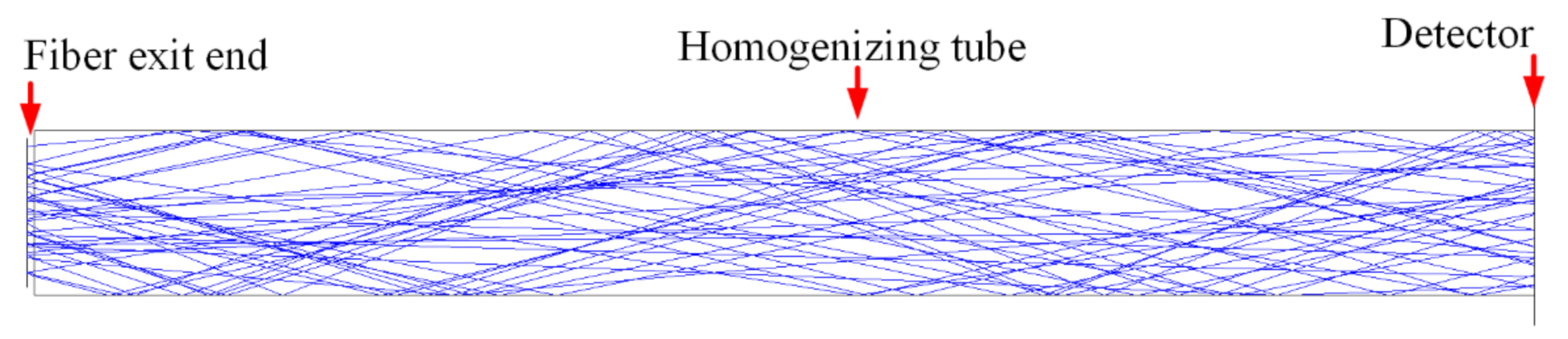
2.3. Simulation
2.3.1. Light Source
2.3.2. Homogenizing Pipe
2.4. Experiment
2.4.1. Illumination System
2.4.2. Imaging Detection System
3. Results and Discussion
3.1. Simulation Results
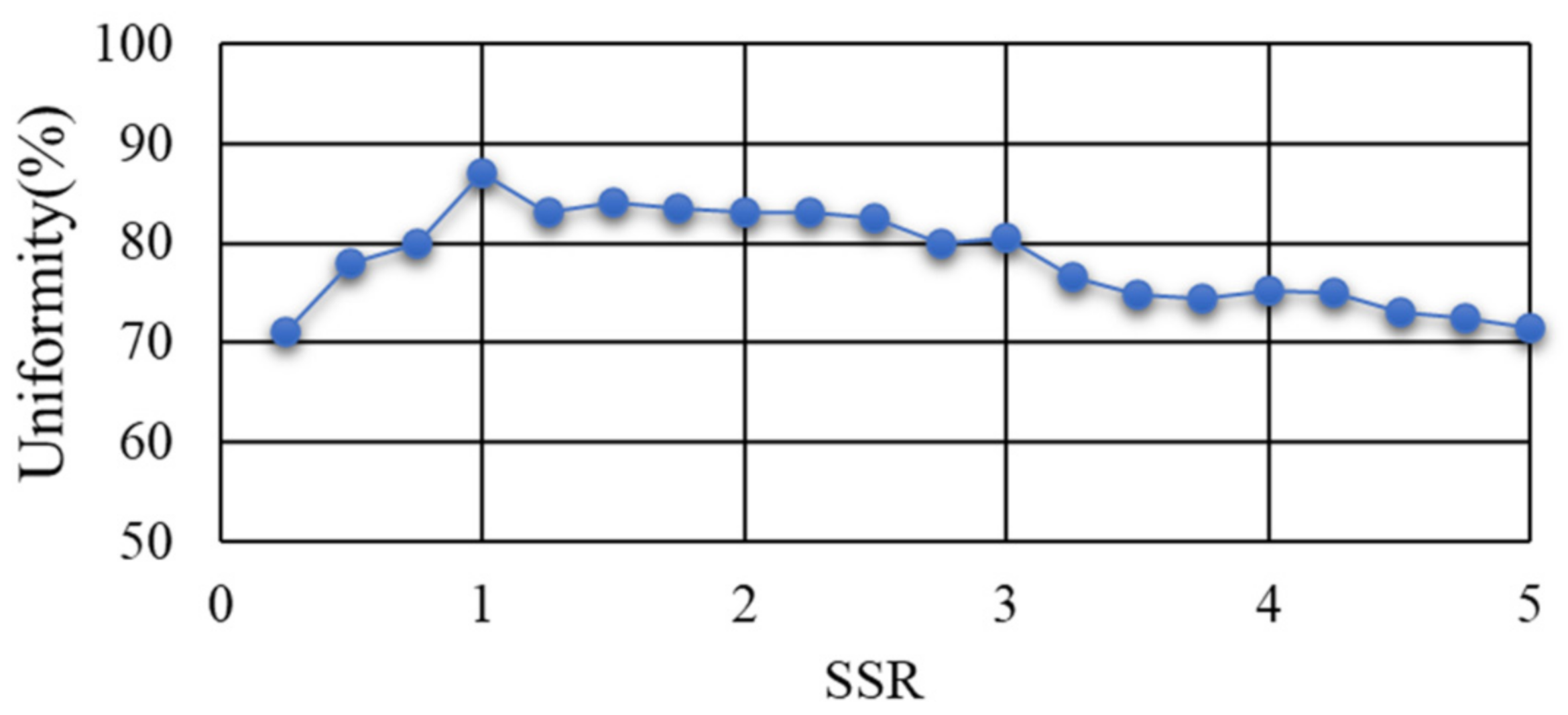
3.1.1. Influence of Aperture Size
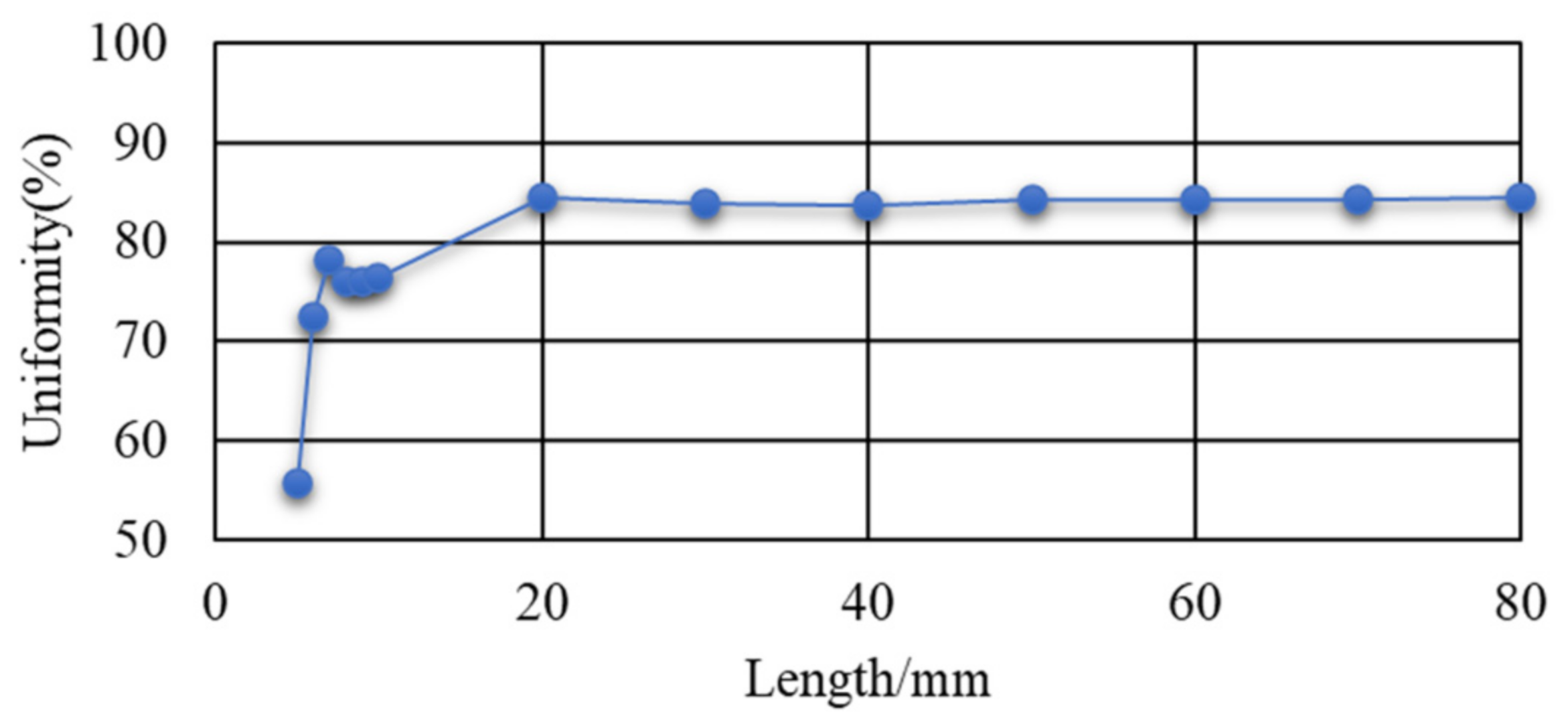
3.1.2. Influence of Length
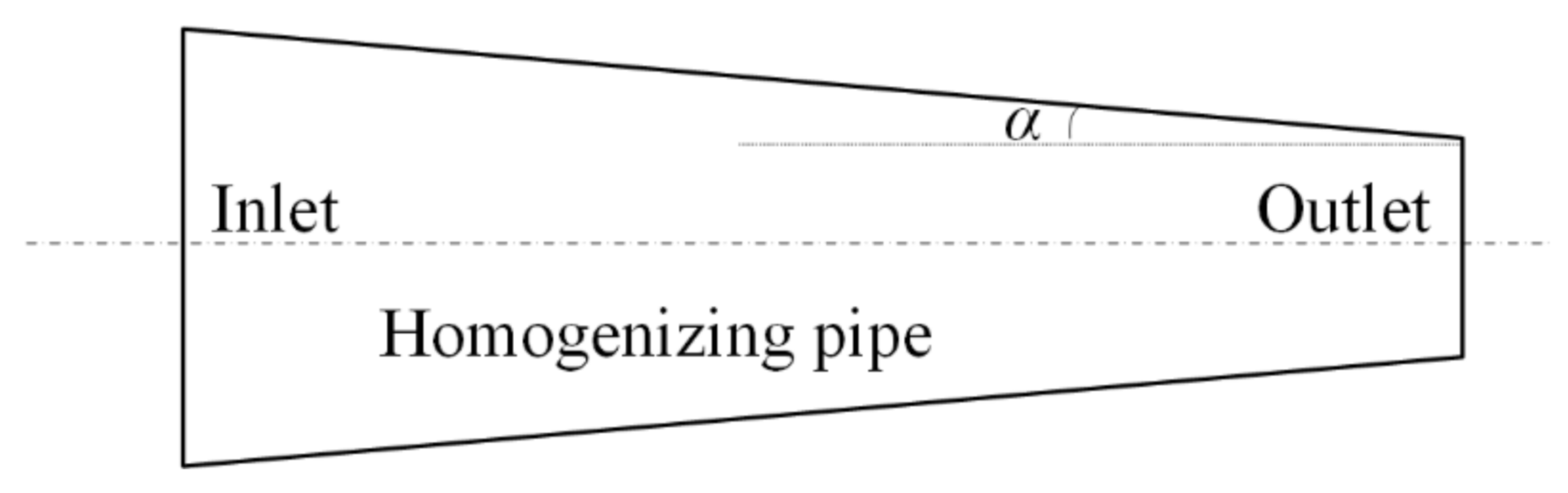
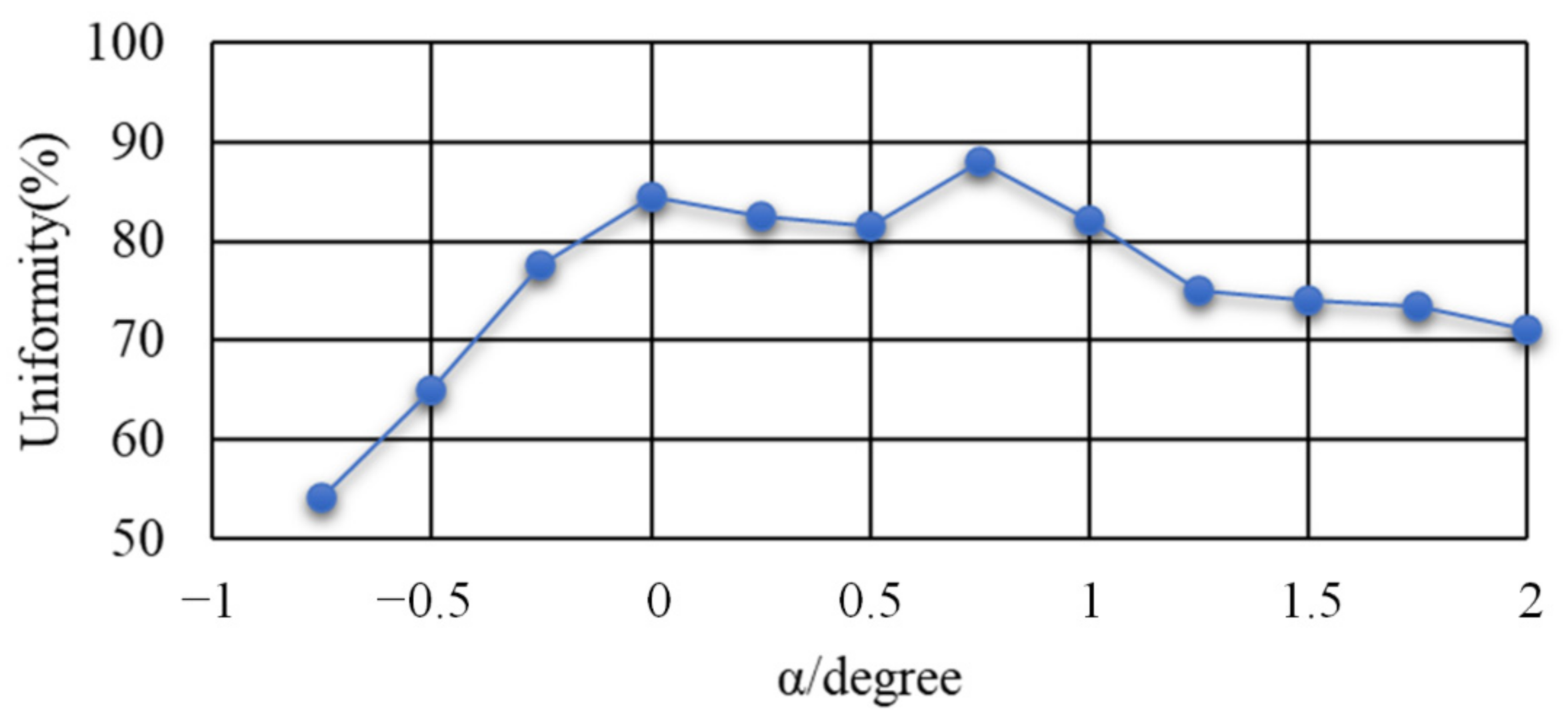
3.1.3. Influence of Taper
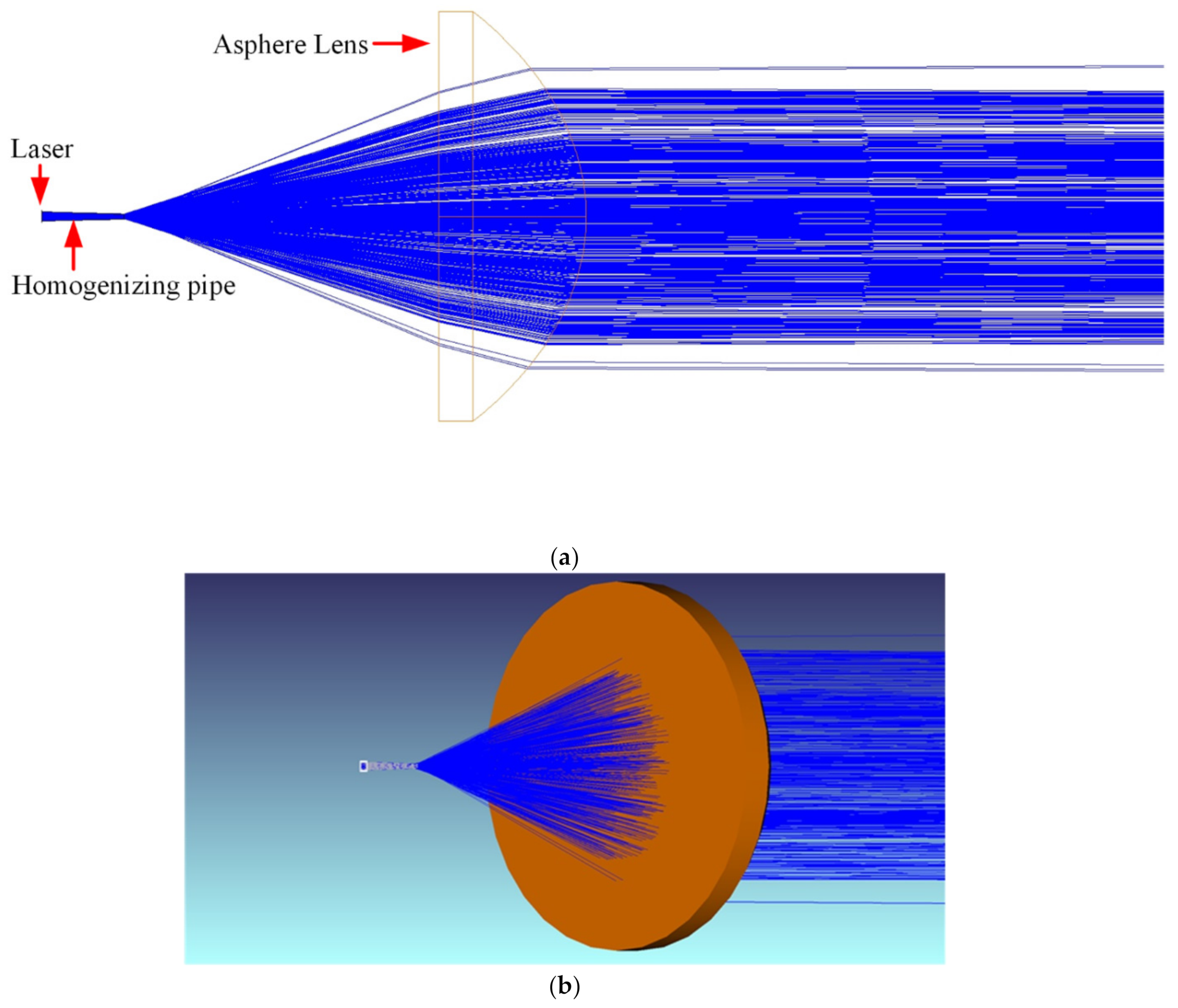
3.1.4. Illumination System
3.2. Experimental Results
3.2.1. Energy Loss
3.2.2. Far-Field Light Spot
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Zhao, W.; Xiong, L.; Liu, H. Packaging of High Power Semiconductor Lasers; Springer: Berlin/Heidelberg, Germany, 2015; pp. 103–123. [Google Scholar] [CrossRef]
- Graf, T.; Balmer, J.E. High-ower Nd: YLF laser end pumped by a diode-laser bar. Opt. Lett. 1993, 18, 1317–1319. [Google Scholar] [CrossRef] [PubMed]
- Hall, R. Coherent light emission from p-n junctions. Solid-State Electron. 1963, 6, 405–408. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, S. Gaussian beam shaping of round spot based on spheric-aspheric cylindrical lens. Laser Optoelectron. Prog. 2018, 55, 060801. [Google Scholar] [CrossRef]
- Wei, Y.; Cheng, X.; Li, X. Integrated double-sided random microlens array used for laser beam homogenization. Micromachines 2021, 12, 673. [Google Scholar] [CrossRef] [PubMed]
- Frieden, B.R. Lossless Conversion of a Plane Laser Wave to a Plane Wave of Uniform Irradiance. Appl. Opt. 1965, 4, 1400–1403. [Google Scholar] [CrossRef]
- Yu, X.; Sang, X.; Gao, X.; Yan, B.; Chen, D.; Liu, B.; Liu, L.; Gao, C.; Wang, P. 360-degree tabletop 3D light-field display with ring-shaped viewing range based on aspheric conical lens array. Opt. Express 2019, 27, 26738–26748. [Google Scholar] [CrossRef] [PubMed]
- Siemion, A. The Magic of Optics—An Overview of Recent Advanced Terahertz Diffractive Optical Elements. Sensors 2020, 21, 100. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, R.; Liu, P.; Zheng, Z.; Li, H.; Liu, X. Double freeform surfaces design for laser beam shaping with Monge–Ampère equation method. Opt. Commun. 2014, 331, 297–305. [Google Scholar] [CrossRef]
- Liu, Z.; Shi, Z.; Yang, H. Homogenization of semiconductor laser using diffractive micro-lens array. Infrared Laser Eng. 2014, 43, 2092–2096. [Google Scholar]
- Prossotowicz, M.; Heimes, A.; Flamm, D.; Jansen, F.; Otto, H.-J.; Budnicki, A.; Killi, A.; Morgner, U. Coherent beam combining with micro-lens arrays. Opt. Lett. 2020, 45, 6728–6731. [Google Scholar] [CrossRef] [PubMed]
- Xue, L.; Pang, Y.; Liu, W.; Liu, L.; Pang, H.; Cao, A.; Shi, L.; Fu, Y.; Deng, Q. Fabrication of Random Microlens Array for Laser Beam Homogenization with High Efficiency. Micromachines 2020, 11, 338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Zhu, G.; Huang, Y.; Zhu, X.; Zhu, C. Analytical model of microlens array system homogenizer. Opt. Laser Technol. 2015, 75, 214–220. [Google Scholar] [CrossRef]
- Sun, Y. Research of Beam Homogenizing Technology for Diode Laser. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2019. [Google Scholar]
- Traub, M.; Hans-Dieter, H. Homogenization of high power diode laser beams for pumping and direct applications. In Proceedings of the High-Power Diode Laser Technology and Applications IV, San Jose, CA, USA, 21–26 January 2006; Volume 6104, p. 61040. [Google Scholar]
- Chen, M.M.; Berkowitz-Mattuck, J.B.; Glaser, P.E. The Use of a Kaleidoscope to Obtain Uniform Flux Over a Large Area in a Solar or Arc Imaging Furnace. Appl. Opt. 1963, 2, 265–271. [Google Scholar] [CrossRef]
- Bartnicki, E.; Bourdet, G.L. Simulation and experimental results of kaleidoscope homogenizers for longitudinal diode pumping. Appl. Opt. 2010, 49, 1636–1642. [Google Scholar] [CrossRef] [PubMed]
- Beach, R.J. Theory and optimization of lens ducts. Appl. Opt. 1996, 35, 2005–2015. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, Y.; Itagaki, Y.; Toyoda, K.; Namba, S. A simple optical device for generating square flat-top intensity irradiation from a gaussian laser beam. Opt. Commun. 1983, 48, 44–46. [Google Scholar] [CrossRef]
- Köhler, B.; Ahnepohl, F.; Rotter, K.; Biesenbach, J. New approach for high-power diode laser modules with homogenized intensity distribution. In Proceedings of the High-Power Diode Laser Technology and Applications IX, San Francisco, CA, USA, 22–27 January 2011; p. 79180U. [Google Scholar] [CrossRef]
- Lutz, Y.; Metzger, N. Near infrared laser illuminator for very long-range flash active imaging applications. In Proceedings of the Illumination Optics II, Marseille, France, 5–8 September 2011; p. 81700C. [Google Scholar] [CrossRef]
- Laurenzis, M.; Lutz, Y.; Christnacher, F.; Matwyschuk, A.; Poyet, J.-M. Homogeneous and speckle-free laser illumination for range-gated imaging and active polarimetry. Opt. Eng. 2012, 51, 061302-1. [Google Scholar] [CrossRef]
- Song, Y.; Chen, Y.; Xin, J.; Sun, T. Two-dimensional beam shaping and homogenization of high power laser diode stack with rectangular waveguide. Front. Optoelectron. 2018, 12, 311–316. [Google Scholar] [CrossRef]
- Fantone, S.D. Kaleidoscopes: More than fun. Opt. Photon. News 1991, 2, 68–69. [Google Scholar] [CrossRef]
- Lü, B.; Zhang, B.; Luo, S. Far-field intensity distribution, M2 factor, and propagation of flattened Gaussian beams. Appl. Opt. 1999, 38, 4581–4584. [Google Scholar] [CrossRef] [PubMed]














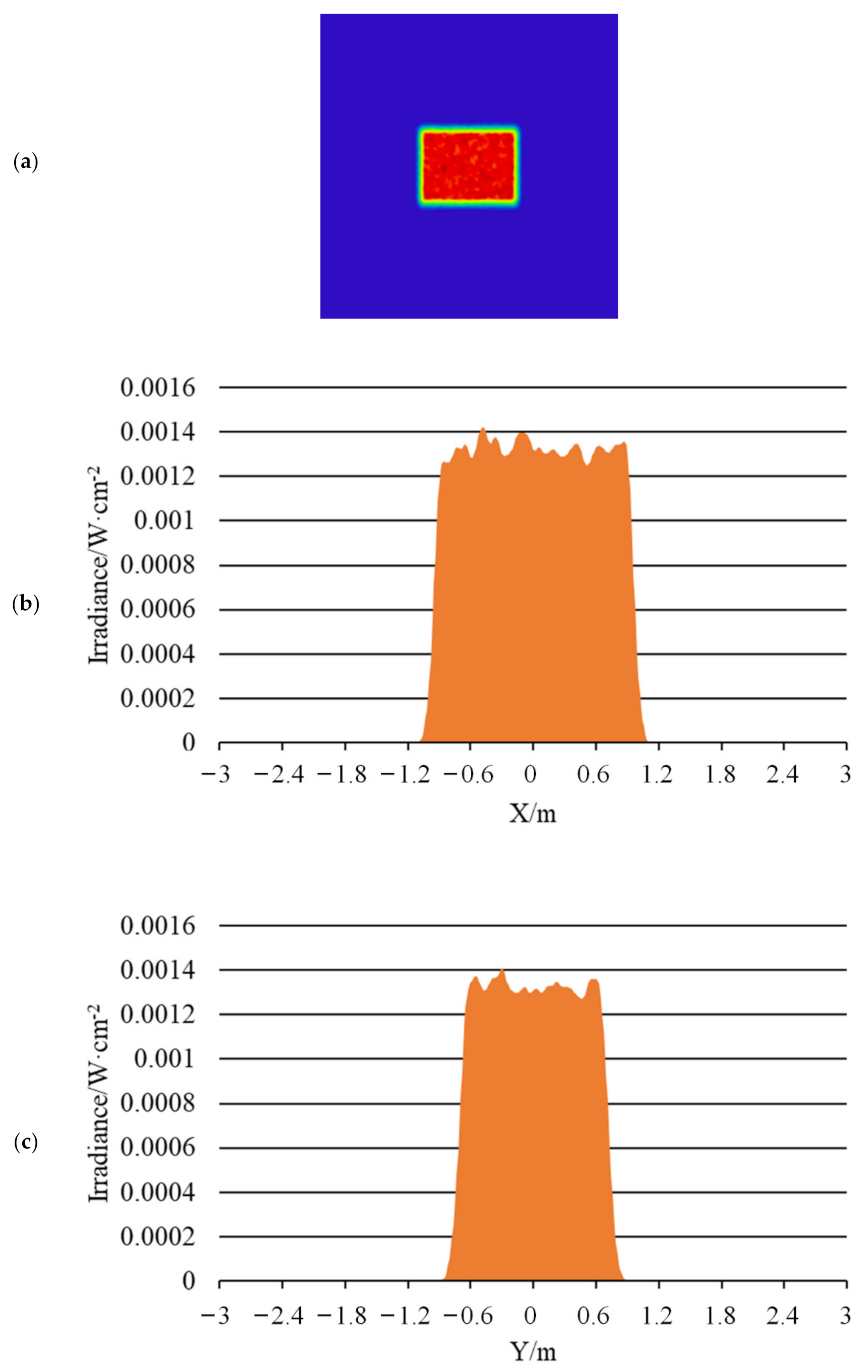


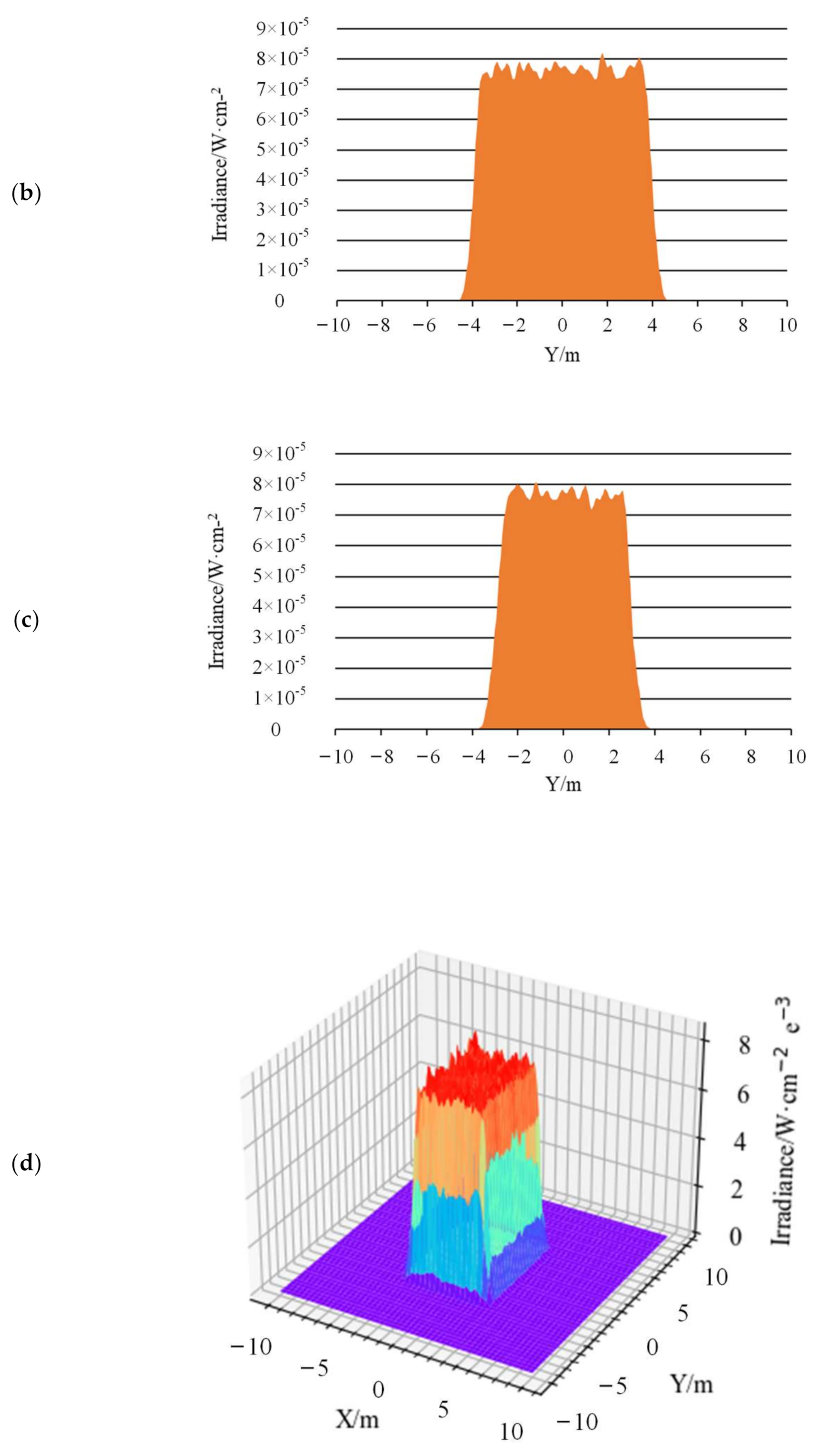


| Type | Inlet Size | Outlet Size | Length | Material |
|---|---|---|---|---|
| pipe 1 | 2 mm × 2 mm | 1.6 mm × 1.2 mm | 20 mm | Silica |
| pipe 2 | 2 mm × 2 mm | 1.6 mm × 1.2 mm | 50 mm | Silica |
| Element | Power of Laser Outlet | Power through Element | Transmittance |
|---|---|---|---|
| pipe 1 | 0.213 W | 0.176 W | 82.6% |
| pipe 2 | 0.213 W | 0.158 W | 74.2% |
| AL5040-B | 0.213 W | 0.184 W | 86.4% |
| Results | Uniformity | Diagonal Length | Divergence Angle |
|---|---|---|---|
| Simulation results | 85.6% | 0.2 m | 10 mrad |
| Experimental results | 87.7% | 0.26 m | 13 mrad |
| Relative error | 2.4% | 23.1% | 23.1% |
| Results | Uniformity | Diagonal Length | Divergence Angle |
|---|---|---|---|
| Simulation results | 91.5% | 1.2 m | 10 mrad |
| Experimental results | 93.3% | 1.8 m | 15 mrad |
| Relative error | 2.4% | 33% | 30% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Sun, H.; Zhang, H.; Li, Y.; Guo, H.; Zhang, L.; Li, R.; Yin, Q. Simulation and Experimental Research on a Beam Homogenization System of a Semiconductor Laser. Sensors 2022, 22, 3725. https://doi.org/10.3390/s22103725
Zheng H, Sun H, Zhang H, Li Y, Guo H, Zhang L, Li R, Yin Q. Simulation and Experimental Research on a Beam Homogenization System of a Semiconductor Laser. Sensors. 2022; 22(10):3725. https://doi.org/10.3390/s22103725
Chicago/Turabian StyleZheng, Haijing, Huayan Sun, Huaili Zhang, Yingchun Li, Huichao Guo, Laixian Zhang, Rong Li, and Qiang Yin. 2022. "Simulation and Experimental Research on a Beam Homogenization System of a Semiconductor Laser" Sensors 22, no. 10: 3725. https://doi.org/10.3390/s22103725
APA StyleZheng, H., Sun, H., Zhang, H., Li, Y., Guo, H., Zhang, L., Li, R., & Yin, Q. (2022). Simulation and Experimental Research on a Beam Homogenization System of a Semiconductor Laser. Sensors, 22(10), 3725. https://doi.org/10.3390/s22103725





