Structural Responses Estimation of Cable-Stayed Bridge from Limited Number of Multi-Response Data
Abstract
:1. Introduction
2. Estimation Algorithm
3. Validation Process
4. Numerical Model for Validation
4.1. Validation Model
4.2. Initial Shape Analysis
4.3. Target Model
4.4. Structural Shape Function (SSF)
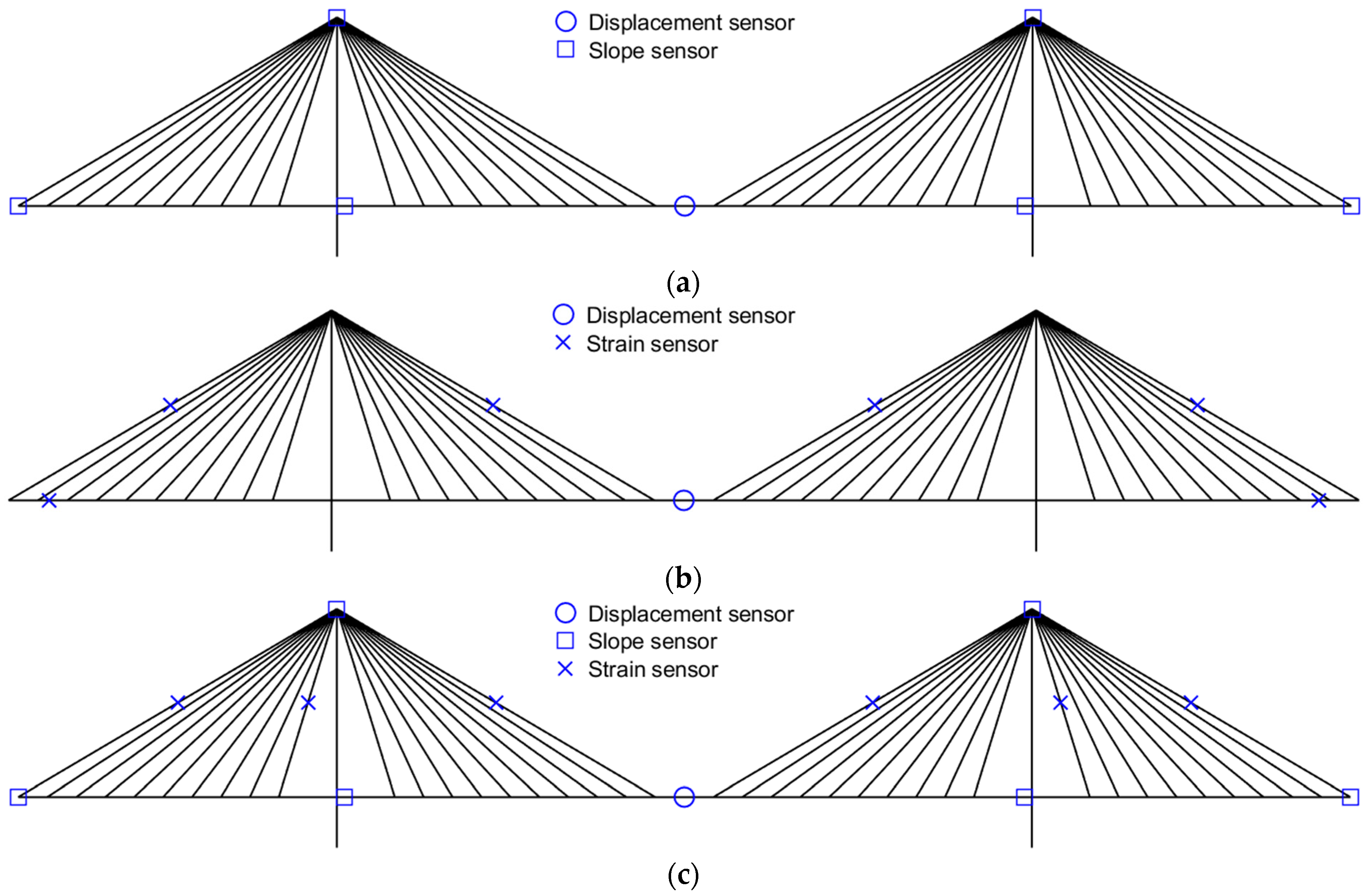
4.5. Measurement Location
5. Validation Results
5.1. Deformed Shape
5.2. Internal Force
5.2.1. Girder Axial Force
5.2.2. Girder Moment
5.2.3. Cable Axial Force
6. Conclusions
- The deformed shape of the cable-stayed bridge can be well estimated by SRALMR using various combinations of displacement, slope, and strain data. In addition, estimation results show that slope and strain data can enhance the estimation accuracy and reduce the required number of displacement data.
- From the deformed shape estimated by SRALMR, internal force (girder axial force, girder bending moment, cable axial force) can be properly determined according to the limited amount of response data. A greater amount of used response data enhances the accuracy of internal force estimation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jang, S.; Jo, H.; Cho, S.; Mechitov, K.; Rice, J.A.; Sim, S.; Jung, H.; Yun, C.; Spencer, B.F.J.; Agha, G. Structural Health Monitoring of a Cable-Stayed Bridge Using Smart Sensor Technology: Deployment and Evaluation. Smart Struct. Syst. 2010, 6, 439–459. [Google Scholar] [CrossRef] [Green Version]
- Cho, S.; Jo, H.; Jang, S.; Park, J.; Jung, H.; Yun, C.; Spencer, B.F.J.; Seo, J. Structural Health Monitoring of a Cable-Stayed Bridge Using Wireless Smart Sensor Technology: Data Analyses. Smart Struct. Syst. 2010, 6, 461–480. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Qiu, G.; Chen, Z. Structural Health Monitoring Methods of Cables in Cable-Stayed Bridge: A Review. Measurement 2021, 168, 108343. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B.; Mariani, S. Big Data Analytics and Structural Health Monitoring: A Statistical Pattern Recognition-Based Approach. Sensors 2020, 20, 2328. [Google Scholar] [CrossRef] [Green Version]
- Son, H.; Pham, V.-T.; Jang, Y.; Kim, S.-E. Damage Localization and Severity Assessment of a Cable-Stayed Bridge Using a Message Passing Neural Network. Sensors 2021, 21, 3118. [Google Scholar] [CrossRef]
- Lee, Y.; Park, W.J.; Kang, Y.J.; Kim, S. Response pattern analysis-based structural health monitoring of cable-stayed bridges. Struct. Control. Health Monit. 2021, 28, e2822. [Google Scholar] [CrossRef]
- Oh, B.K.; Glisic, B.; Kim, Y.; Park, H.S. Convolutional neural network-based wind-induced response estimation model for tall buildings. Comput. Aided Civ. Infrastruct. Eng. 2019, 34, 843–858. [Google Scholar] [CrossRef] [Green Version]
- Wu, R.-T.; Jahanshahi, M.R. Deep Convolutional Neural Network for Structural Dynamic Response Estimation and System Identification. J. Eng. Mech. 2019, 145, 04018125. [Google Scholar] [CrossRef]
- Pamuncak, A.P.; Salami, M.R.; Adha, A.; Budiono, B.; Laory, I. Estimation of structural response using convolutional neural network: Application to the Suramadu bridge. Eng. Comput. 2021, 38, 4047–4065. [Google Scholar] [CrossRef]
- Park, K.-T.; Kim, S.-H.; Park, H.-S.; Lee, K.-W. The Determination of Bridge Displacement Using Measured Acceleration. Eng. Struct. 2005, 27, 371–378. [Google Scholar] [CrossRef]
- Lee, H.S.; Hong, Y.H.; Park, H.W. Design of an FIR Filter for the Displacement Reconstruction Using Measured Acceleration in Low-Frequency Dominant Structures. Int. J. Numer. Methods Eng. 2010, 82, 403–434. [Google Scholar] [CrossRef]
- Park, J.W.; Sim, S.H.; Jung, H.J.; Jr, B. Development of a Wireless Displacement Measurement System Using Acceleration Responses. Sensors 2013, 13, 8377–8392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, X.; Yang, X.; Huang, Q. Using Inclinometers to Measure Bridge Deflection. J. Bridge Eng. 2005, 10, 564–569. [Google Scholar] [CrossRef]
- Foss, G.C.; Haugse, E.D. Using Modal Test Results to Develop Strain to Displacement Transformation. In Proceedings of the 13th International Modal Analysis Conference, Nashville, TN, USA, 13–16 February 1995; pp. 112–118. [Google Scholar]
- Shin, S.; Lee, S.-U.; Kim, Y.; Kim, N.-S. Estimation of Bridge Displacement Responses Using FBG Sensors and Theoretical Mode Shapes. Struct. Eng. Mech. 2012, 42, 229–245. [Google Scholar] [CrossRef]
- Cho, S.; Yun, C.-B.; Sim, S.-H. Displacement Estimation of Bridge Structures Using Data Fusion of Acceleration and Strain Measurement Incorporating Finite Element Model. Smart Struct. Syst. 2015, 15, 645–663. [Google Scholar] [CrossRef] [Green Version]
- Kang, L.-H.; Kim, D.-K.; Han, J.-H. Estimation of dynamic structural displacements using fiber Bragg grating strain sensors. J. Sound Vib. 2007, 305, 534–542. [Google Scholar] [CrossRef]
- Rapp, S.; Kang, L.-H.; Han, J.-H.; Mueller, U.C.; Baier, H. Displacement field estimation for a two-dimensional structure using fiber Bragg grating sensors. Smart Mater. Struct. 2009, 18, 025006. [Google Scholar] [CrossRef]
- Li, L.; Zhong, B.-S.; Li, W.-Q.; Sun, W.; Zhu, X.-J. Structural shape reconstruction of fiber Bragg grating flexible plate based on strain modes using finite element method. J. Intell. Mater. Syst. Struct. 2017, 29, 463–478. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, H.; Wang, J.; Zhang, J.; Ma, M.; Zhong, X. Modal learning displacement–strain transformation. Rev. Sci. Instrum. 2019, 90, 075113. [Google Scholar] [CrossRef]
- Kliewer, K.; Glisic, B. A Comparison of Strain-Based Methods for the Evaluation of the Relative Displacement of Beam-Like Structures. Front. Built Environ. 2019, 5, 118. [Google Scholar] [CrossRef] [Green Version]
- Park, J.-W.; Sim, S.-H.; Jung, H.-J. Displacement Estimation Using Multimetric Data Fusion. IEEE/ASME Trans. Mechatron. 2013, 18, 1675–1682. [Google Scholar] [CrossRef]
- Cho, S.; Sim, S.; Park, O.; Lee, J. Extension of indirect displacement estimation method using acceleration and strain to various types of beam structures. Smart Struct. Syst. 2014, 14, 699–718. [Google Scholar] [CrossRef] [Green Version]
- Cho, S.; Park, J.-W.; Palanisamy, R.P.; Sim, S.-H. Reference-Free Displacement Estimation of Bridges Using Kalman Filter-Based Multimetric Data Fusion. J. Sens. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Sarwar, M.Z.; Park, J.-W. Bridge Displacement Estimation Using a Co-Located Acceleration and Strain. Sensors 2020, 20, 1109. [Google Scholar] [CrossRef] [Green Version]
- Won, J.; Park, J.-W.; Park, J.; Shin, J.; Park, M. Development of a Reference-Free Indirect Bridge Displacement Sensing System. Sensors 2021, 21, 5647. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, X.; Sun, Z.; Ren, L. A Smart Multi-Rate Data Fusion Method for Displacement Reconstruction of Beam Structures. Sensors 2022, 22, 3167. [Google Scholar] [CrossRef]
- Choi, J.; Lee, K.; Lee, J.; Kang, Y. Evaluation of quasi-Static Responses Using Displacement Data from a Limited Number of Points on a Structure. Int. J. Steel Struct. 2017, 17, 1211–1224. [Google Scholar] [CrossRef]
- Choi, J.; Lee, K.; Kang, Y. Quasi-Static Responses Estimation of a Cable-Stayed Bridge from Displacement Data at a Limited Number of Points. Int. J. Steel Struct. 2017, 17, 789–800. [Google Scholar] [CrossRef]
- Byun, N.; Lee, J.; Lee, K.; Kang, Y.-J. Estimation of Structural Deformed Configuration for Bridges Using Multi-Response Measurement Data. Appl. Sci. 2021, 11, 4000. [Google Scholar] [CrossRef]
- Wang, P.H.; Yang, C.G. Parametric Studies on Cable-Stayed Bridges. Comput. Struct. 1996, 60, 243–260. [Google Scholar] [CrossRef]
- Ren, W.X. Ultimate Behavior of Long-Span Cable-Stayed Bridges. J. Bridge Eng. 1999, 4, 30–37. [Google Scholar] [CrossRef]
- Wang, P.H.; Tseng, T.C.; Yang, C.G. Initial Shape of Cable-Stayed Bridges. Comput. Struct. 1993, 47, 111–123. [Google Scholar] [CrossRef]
- Kim, J.C. Determination of Initial Equilibrium State and Construction Geometry on Cable-Stayed Bridges. Ph.D. Dissertation, Seoul National University, Seoul, Korea, 1999. [Google Scholar]
- Kim, K.S.; Lee, H.S. Analysis of Target Configurations Under Dead Loads for Cable-Supported Bridges. Comput. Struct. 2001, 79, 2681–2692. [Google Scholar] [CrossRef]
- Kammer, D.C. Sensor Placement for On-Orbit Modal Identification and Correlation of Large Space Structures. J. Guid. Control Dyn. 1991, 14, 251–259. [Google Scholar] [CrossRef]
- Papadopoulos, M.; Garcia, E. Sensor Placement Methodologies for Dynamic Testing. AIAA J. 1998, 36, 256–263. [Google Scholar] [CrossRef]














| Girder | Pylon | Cable | |
|---|---|---|---|
| Elastic modulus E (kN/m2) | 2.1 × 108 | 2.1 × 108 | 2.1 × 108 |
| Sectional A (m2) | 0.749 | 0.374 | 0.02 |
| 2nd moment of inertia I (m4) | 1.446 | 3.143 | − |
| Unit weight γ (kN/m3) | 218.27 | 76.90 | 76.90 |
| Force (kN) | ||||
|---|---|---|---|---|
| TM1 | TM2 | TM3 | TM4 | |
| P1 | 5000 | 5000 | 5000 | 2000 |
| P2 | - | - | 3000 | 2500 |
| P3 | - | - | - | 3000 |
| TM1 | TM2 | TM3 | TM4 | |
|---|---|---|---|---|
| Case 1 | 1.471 | 2.275 | 2.819 | 2.382 |
| Case 2 | 0.332 | 0.074 | 0.157 | 0.115 |
| Case 3 | 0.002 | 0.021 | 0.022 | 0.019 |
| TM1 | TM2 | TM3 | TM4 | |
|---|---|---|---|---|
| Case1 | 6.024 | 7.127 | 12.891 | 12.410 |
| Case2 | 2.240 | 3.261 | 6.647 | 8.035 |
| Case3 | 0.345 | 2.238 | 3.458 | 4.164 |
| TM1 | TM2 | TM3 | TM4 | |
|---|---|---|---|---|
| Case1 | 2.905 | 3.320 | 3.495 | 3.406 |
| Case2 | 0.773 | 0.335 | 0.615 | 0.580 |
| Case3 | 0.008 | 0.143 | 0.132 | 0.146 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Byun, N.; Lee, J.; Won, J.-Y.; Kang, Y.-J. Structural Responses Estimation of Cable-Stayed Bridge from Limited Number of Multi-Response Data. Sensors 2022, 22, 3745. https://doi.org/10.3390/s22103745
Byun N, Lee J, Won J-Y, Kang Y-J. Structural Responses Estimation of Cable-Stayed Bridge from Limited Number of Multi-Response Data. Sensors. 2022; 22(10):3745. https://doi.org/10.3390/s22103745
Chicago/Turabian StyleByun, Namju, Jeonghwa Lee, Joo-Young Won, and Young-Jong Kang. 2022. "Structural Responses Estimation of Cable-Stayed Bridge from Limited Number of Multi-Response Data" Sensors 22, no. 10: 3745. https://doi.org/10.3390/s22103745
APA StyleByun, N., Lee, J., Won, J.-Y., & Kang, Y.-J. (2022). Structural Responses Estimation of Cable-Stayed Bridge from Limited Number of Multi-Response Data. Sensors, 22(10), 3745. https://doi.org/10.3390/s22103745







