Smart Sensorization Using Propositional Dynamic Logic
Abstract
:1. Introduction
2. Design of an Intelligent Solar Water Heating System (ISWHS)
- In traditional systems, the cold water that enters from the network is heated to replenish the hot water consumed when there is not enough solar radiation. In our case, the accumulator is left emptying and the only contribution of the electrical resistance is usually used to keep the water in the accumulator hot (but at a low level of the accumulator volume). Once the solar contribution is recovered, cold water is introduced from the network but it is heated by solar energy. This is a significant energy saving.
- As no cold water is introduced during the first stage, in which the water of the accumulator is emptied by the consumption of hot water by the users, there is no decrease of the water temperature in the accumulator by the inlet of cold water, which is normal since the cold water inlet valve is closed. This system keeps the water hot for longer.
- During the second stage, the hot water consumed is replaced by cold water from the network heated by the electrical resistance. However, since the water volume of the accumulator is lower (not the entire tank, but a quarter), the heat input of the resistance is also lower than a traditional system. Therefore, the energy saving also occurs at this stage.
- During the third stage, the accumulator is filled with cold water from the network to return to the initial situation and the solar collectors are heating the water. The temperature of the water inside the accumulator decreases and therefore the temperature difference in relation to the water temperature of the solar collectors is maximum. For this reason, this design ensures maximum efficiency of the solar panels, since the differential of temperature of the water passing through the panels with the water of the accumulator will always be maximum. This produces the maximum performance of the solar collectors.
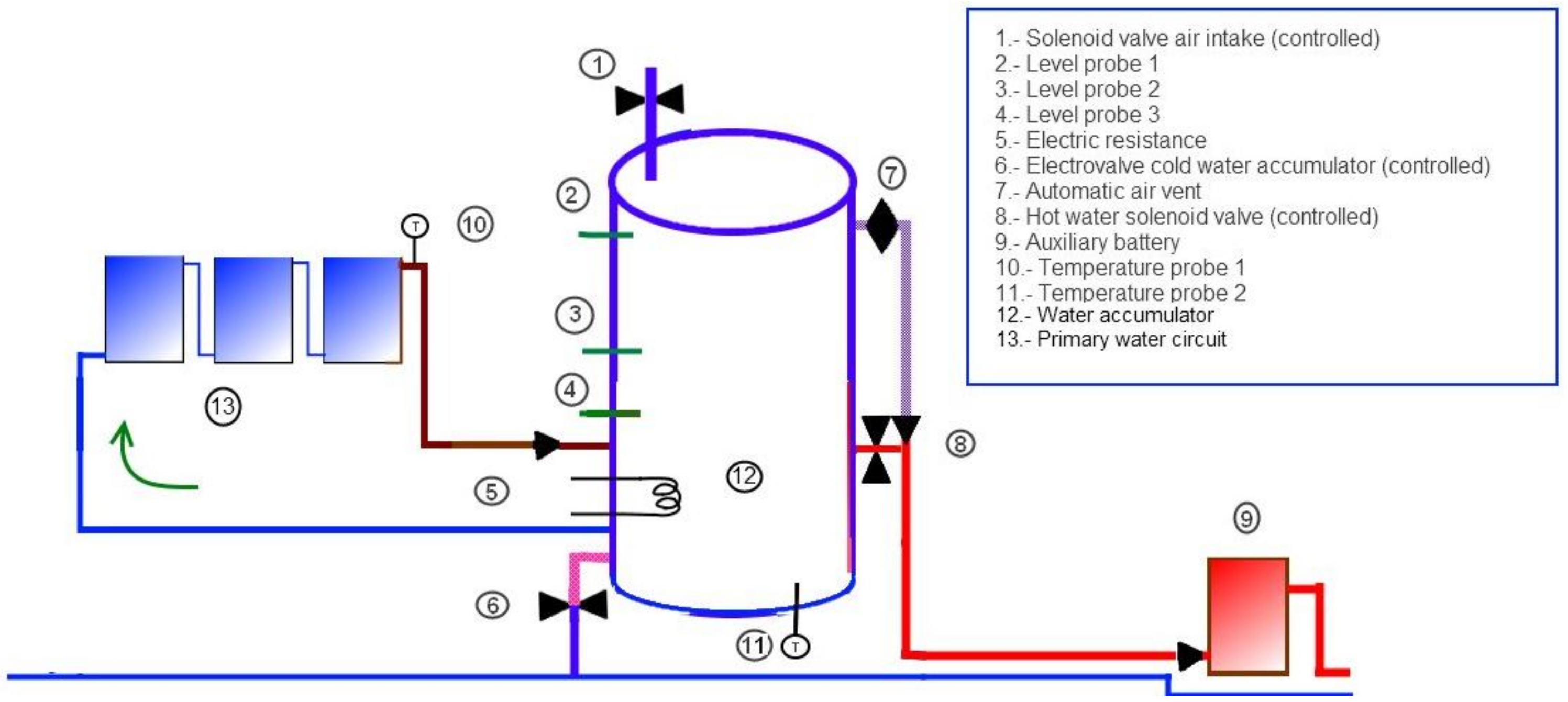
2.1. System Description
- -
- The air inlet to the accumulator (A).
- -
- The cold water inlet from the network to the accumulator (CW).
- -
- The hot water outlet from the accumulator (HW)(located in the figure in the places ①, ⑥, and ⑧, respectively).
- -
- The temperature of the water inside the accumulator (AT), measured by the temperature probe ⑪.
- -
- The temperature of the water passing through the panels (PT) measured by the temperature probe ⑩.
- -
- The temperature requested by the user or setpoint temperature (ST).
2.2. System Operation
- The operation of the primary circuit is automatic: when the temperature of the water leaving the panels (the same water passes through them, one after another, since they are in series) is greater than that of the water inside the accumulator, water circulates due to the thermosyphon effect. When this is not the case, the water will not flow. This does not need control since it is a physical phenomenon.
- Let us describe the operation of the rest of the circuit:
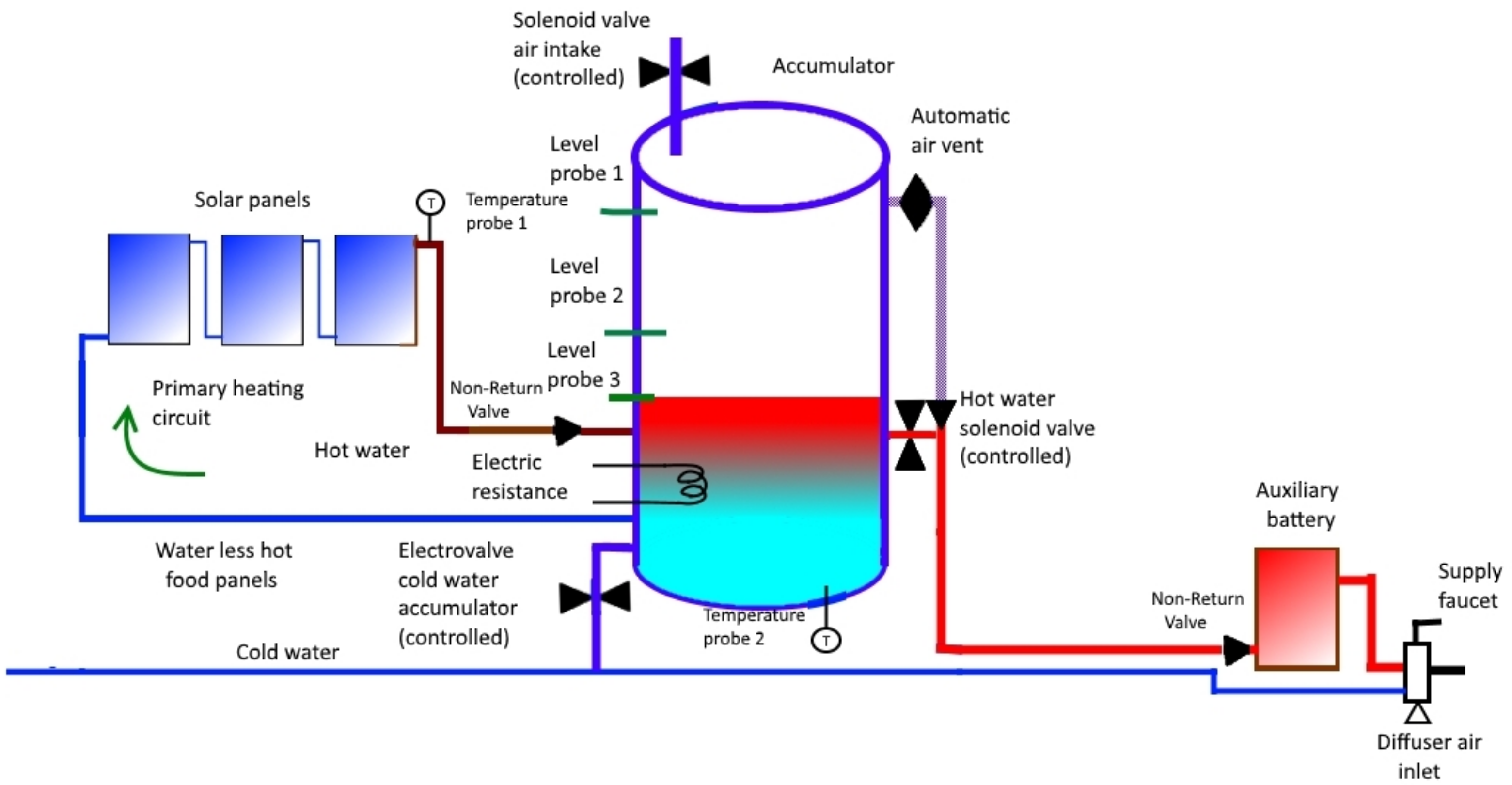
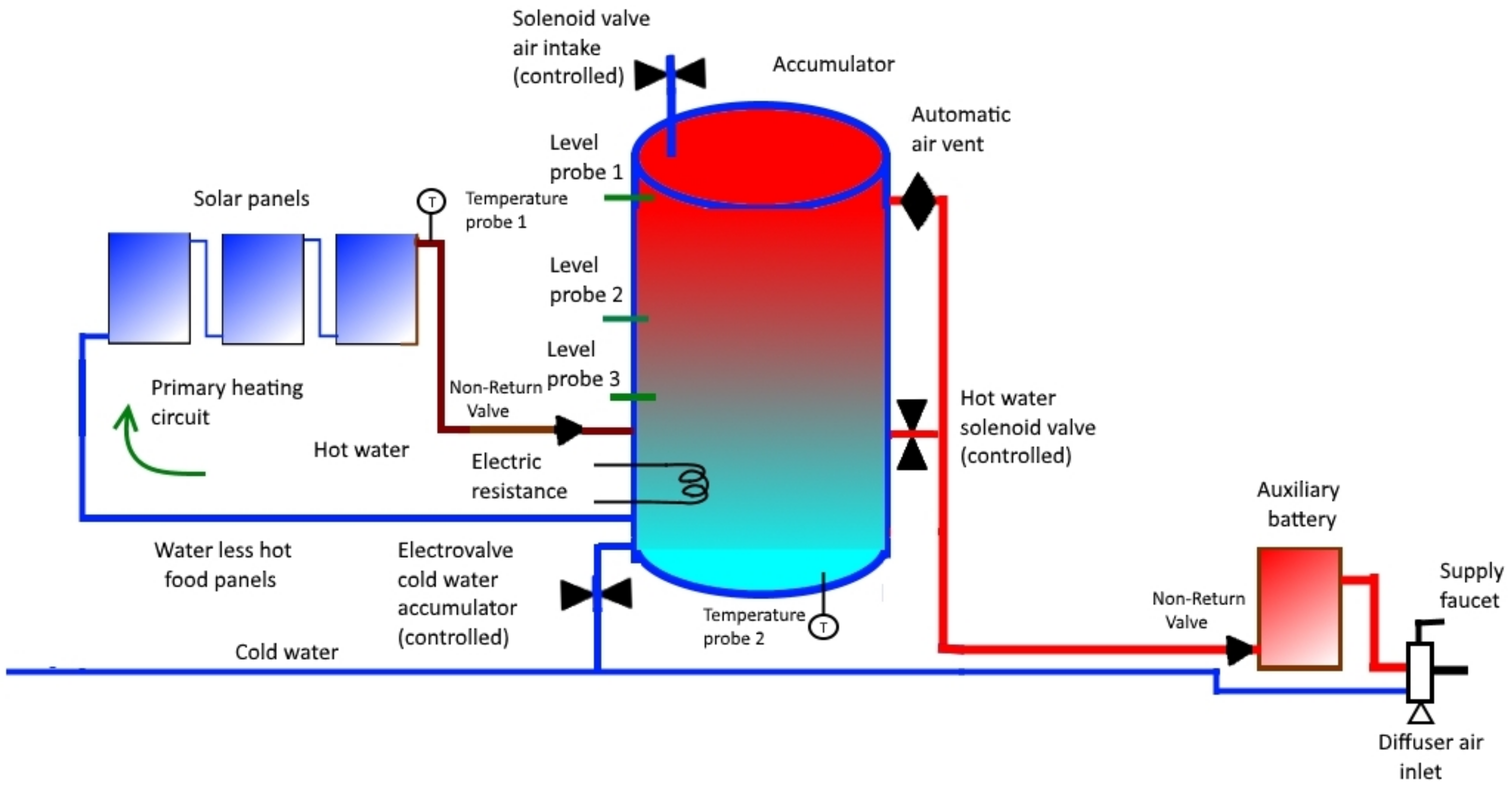
- When AT is greater than PT, the three solenoid valves will be activated as follows: CW closes, while A and HW open.The three valves remain in their respective states until the water level inside the accumulator reaches the position of the level probe 3 (LP3) (see Figure 2).At that time, CW opens and we proceed to activate, or not, the electrical resistance (ER), according to the comparison between AT and ST as follows:
- -
- If AT is lower than ST, then ER is activated to the hot state;
- -
- If AT = ST, then ER is activated to the normal state;
- -
- if AT is greater than ST, then ER must be deactivated (cold state).
In addition, cold water will continue to enter until the water level inside the accumulator reaches the level probe 2 (LP2). In this case, CW is closed.This process will allow the water level to be between probe 2 and 3 while the hot water is being used to consume through the lower outlet of the accumulator (see Figure 3). - When PT is greater than or equal to AT, CW will open and ER will be deactivated; when the water reaches level probe 1 (LP1), A and HW will close (see Figure 4).
It should be noted that this process will lead to AT being greater than or equal to PT (again, previous case). Recall that previously we started from the situation we have now reached with respect to the three solenoid valves: CW is open while A and HW are closed; this describes a circuit.
Algorithm 1 Procedure of an intelligent water heating system (PIWHS) |
Initial situation: the accumulator is full of water, CW is open, and A and HW are closed. begin //Compare AT and PT// while
true
do if AT > PT then Close CW and Open A and HW; if the water level of the accumulator reaches the probe 3 then CW; if AT < ST ⇒ pass ER intensity to hot; AT = ST ⇒ pass ER intensity to normal; AT > ST ⇒ Turn off ER;//ER must be in cold state// fi end if if the water level of the accumulator reaches the probe 2 then Close CW; end if else //AT ≤ PT// Open CW and Turn off ER; if the water level of the accumulator reaches the probe 1 then Close A and HW; end if end if end while end |
3. The Logic Dom
3.1. Notation and Basic Concepts
3.2. Syntax
- (increase): This program means that we must increase the level of the values of the positions of x, respectively, by the positive labels , using a sum operation + (qualitative or numerical). A simultaneous replacement of by is carried out; e.g., increase a little the temperature of the living room.
- (decrease): This program means that we must decrease the level of the values of the positions of x, respectively, by the negative labels , using a sum operation + (qualitative or numerical); e.g., decrease much the intensity of the kitchen light.
- (change): This program means that we must replace simultaneously the state labels of the positions … of x (i.e., , …, ), respectively, by the state labels , …, (e.g., set the room temperature to C, …).
- (watch): This program means that we simply watch the state labels of the positions of x; it is assumed that these would be maintained if there are no actions that change them. The purpose of this program is to explicitly check that these labels do not change even if those in other positions do.
- (“regulator”), whereand are positions of x, all different, and at least one ( is not empty.
- (“turn on all the positions of x”).
- (“turn off all the positions of x”).
- . This program combines and , where and are sets of distinguished positions of different x.
- (“exchange on and off”) is a generic modification of the previous program , that simply does not require previous identification of the positions to be activated/deactivated (the system reads the status of all positions and performs this order automatically, going through all of them). In actuality, are all positions in the scene with off and are all positions in the scene with on. This program activates in x all positions that are deactivated and at the same time deactivates all positions that are enabled; e.g., one result would be to turn all lights on (that are off) and turn off all lights (that are on) simultaneously.
- , where , + is an operation defined for and is a positive label of the set (chosen for ).
- , where , + is an operation defined for and is a negative label of the set (chosen for ).
- , where and .
- and .
3.3. Semantics
- The meaning function m is required to fulfill the following:
- (a)
- , for every atomic formula .
- (b)
- , for every scene formula and .
- (c)
- For all there exists a scene formula such that (all the states of a model are described by a scene formula).
- (d)
- For all and , if , then x is unique, that is, for all different from x (in the sense of Definition 1) we have .
- We define now the semantics of the specific program regulator. if is a state formula, then
- -
- Finally, if and are formulas and are programs, then we have the following:
- (a)
- ;
- (b)
- ;
- (c)
- ;
- (d)
- ;
- (e)
- = ;
- (f)
- (reflexive and transitive closure of relation );
- (g)
- .
4. Formalizing ISWHS
4.1. System States
- denotes the temperature of the water accumulated in the accumulator (AT).
- denotes the temperature of the water passing through the solar panels (PT).
- denotes the status of the cold water solenoid valve of the network to the accumulator (CW).
- denotes the status of the solenoid valve in the upper part of the accumulator (A).
- denotes the status of the solenoid valve of the lower hot water outlet of the accumulator (HW).
- denotes the status of the electrical resistance (ER).
- denotes the set point temperature defined by the user (ST).
- denotes that the water level inside the accumulator reaches the probe of the upper level i ().
- .
- , off}.
- .
- = a finite subset of (to choose).
4.2. Composition Operations
4.3. Logical Description of System Behaviour
4.4. Detecting Failures in System Operation
5. Conclusions
- Efficiency: The proposed solution increases the efficiency of domestic hot water heating systems using renewable energies. Normally, the thermal profitability of this type of installation, powered by solar energy, represents a saving of around of that required for heating [1]. The use of the system presented in this paper represents an additional saving of (depending on the position x of the lowest level sensor with respect to the bottom of the tank).
- Multiplicity: The water heater itself has three different behaviors, depending on its load level. In principle, when the solar thermal input is sufficient, it works as a conventional domestic hot water storage tank powered by solar thermal energy. In a second state, when the heat transfer fluid coming from the panels has a lower temperature than the water in the tank to be heated, it cuts off the external supply and becomes atmospheric, allowing the interior water to be used without any possible mixing with the water at a lower temperature from the network. In the third state, when a minimum level is reached, it will behave similar to an electric heater, powered by renewable or non-renewable energies, working on a minimum level of water compared to the original.
- Economy: The system would allow an estimated global saving of based on the conventional energy used for the heating process. In addition, it allows to use all the water contained in the tank at the maximum temperature reached (until reaching the minimum load level marked by the probe located in the lowest zone) without mixing it with the water coming from the supply network (which would cool the mixture at a considerable speed). Likewise, when the outside temperature does not allow the stored water to be heated, it considerably reduces the consumption of electrical energy by significantly reducing the volume of water that will be used from that moment onwards (it practically becomes a heating as the water flow passes through).
- Complexity: The resolution by means of propositional dynamic logic has overcome the disadvantages of traditional systems to detect faults in the logical operation of the system. In addition, it contains programs that allow qualitative control of the states of the variables, with built-in qualitative addition operations, which gives the system great flexibility. This type of operation is very useful in home automation as many applications require qualitative regulation.
6. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guzmán, F.; Merino, S. Domótica: Gestión de la Energía y Gestión Técnica de Edificios; RA-MA Editorial: Madrid, Spain, 2015. [Google Scholar]
- Kawamura, H.; Naka, K.; Yonekura, N.; Yamanaka, S.; Kawamura, H.; Ohno, H.; Naito, K. Simulation of I–V characteristics of a PV module with shaded PV cells. Sol. Energy Mater. Sol. Cells 2003, 75, 613–621. [Google Scholar] [CrossRef]
- Merino, S.; Guzmán, F.; Martínez, J. Metadomotic optimization using genetic algorithms. Appl. Math. Comput. 2015, 267, 170–178. [Google Scholar] [CrossRef]
- Moretón, R.; Lorenzo, E.; Navarrete, L. Experimental observations on hot-spots and derived acceptance/rejection criteria. Sol. Energy 2015, 118, 28–40. [Google Scholar] [CrossRef] [Green Version]
- Orozco, M.L.; Ramírez-Scarpetta, J.M.; Spagnuolo, G.; Ramos-Paja, C.A. A method for simulating large PV arrays that include reverse biased cells. Appl. Energy 2014, 123, 157–167. [Google Scholar] [CrossRef]
- Petrone, G.; Spagnuolo, G.; Zhao, Y.; Lehman, B.; Ramos-Paja, C.A.; Orozco, M.L. Control of Photovoltaic Arrays, Dynamical Reconfiguration for Fighting Mismatched Conditions and Meeting Load Requests. IEEE Ind. Electron. Mag. 2015, 9, 62–76. [Google Scholar]
- Orozco-Gutiérrez, M.L.; Spagnuolo, G.; Ramírez-Scarpetta, J.M.; Petrone, G.; Ramos-Paja, C.A. Optimized Configuration of Mismatched Photovoltaic Arrays. IEEE J. Photovolt. 2016, 6, 1210–1220. [Google Scholar] [CrossRef]
- Sánchez, F.J.; Sotorrío, P.J.; Heredia, J.R.; Pérez, F.; Sidrach-de-Cardona, M. PLC-Based PV Plants Smart Monitoring System: Field Measurements and Uncertainty Estimation. IEEE Trans. Instrum. Meas. 2014, 63, 2215–2222. [Google Scholar] [CrossRef]
- Selen, J.; Adan, I.; Kapodistria, S.; Van Leeuwaarden, J. Steady-state analysis of shortest expected delay routing. Queueing Syst. 2016, 84, 309–354. [Google Scholar] [CrossRef] [Green Version]
- Quashing, V.; Hanitsch, R. Numerical simulation of current-voltage characteristics of photovoltaic systems with shaded solar cells. Sol. Energy 1996, 56, 513–520. [Google Scholar] [CrossRef]
- Chan, C.; Coghill, G.; Liu, H. Recent advances in Fuzzy Qualitative Reasoning. Int. J. Uncertainty Fuzziness Knowl. Based Syst. 2011, 19, 417–422. [Google Scholar] [CrossRef]
- Chavez, G.; Zerkle, D.; Key, B.; Shevitz, D. Relating confidence to measured information uncertainty in qualitative reasoning. In Proceedings of the 2011 Annual Meeting of the North American Information Processing Society, El Paso, TX, USA, 18–20 March 2011; pp. 1–6. [Google Scholar]
- Duckham, M.; Lingham, J.; Mason, K.; Worboys, M. Qualitative reasoning about consistency in geographic information. Inf. Sci. 2006, 176, 601–627. [Google Scholar] [CrossRef] [Green Version]
- Kuipers, B.; Byun, Y.T. A robot exploration and mapping strategy based on a semantic hierarchy of spatial representations. Robot. Auton. Syst. 1991, 8, 47–63. [Google Scholar] [CrossRef]
- Liu, H.; Brown, D.; Coghill, G. Fuzzy qualitative robot kinematics. IEEE Trans. Fuzzy Syst. 2008, 16, 808–822. [Google Scholar]
- Mossakowski, T.; Moratz, R. Qualitative reasoning about relative direction of oriented points. Artif. Intell. 2012, 180, 34–45. [Google Scholar] [CrossRef] [Green Version]
- Dubois, D.; Ali, A.H.; Prade, H. Making fuzzy absolute and fuzzy relative orders of magnitude consistent. Fuzzy Sets Syst. 2003, 2003, 694–701. [Google Scholar]
- Ali, A.H.; Dubois, D.; Prade, H. Qualitative reasoning based on fuzzy relative orders of magnitude. IEEE Trans. Fuzzy Syst. 2003, 11, 9–23. [Google Scholar] [CrossRef]
- Agell, N.; Sánchez, M.; Prats, F. Modelos cualitativos de órdenes de magnitud: Introducción a los modelos mixtos. Rev. Iberoam. Intel. Artif. 2000, 4, 58–65. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy arithmetic in qualitative reasoning. Model. Control. Syst. 1989, 121, 457–467. [Google Scholar]
- Travé-Massuyès, L.; Piera, N. The orders of magnitude models as qualitative algebras. Proc. Elev. Ijcai 1989, 2, 1261–1266. [Google Scholar]
- Piera, N.; Sánchez, M.; Travé-Massuyès, L. Qualitative operators for order of magnitude calculus: Robustness and precision. In Proceedings of the 13th IMACS World Congress on Computation and Applied Mathematics, Dublin, Ireland, 22–26 July 1991; Volume 22, pp. 1–6. [Google Scholar]
- Harel, D.; Kozen, D.; Tyurin, J. Dynamic Logic; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Bonner, J.; Kiffer, J. An overview of transaction logic. Theor. Comput. Sci. 1994, 133, 205–265. [Google Scholar] [CrossRef] [Green Version]
- Kowalski, R.A.; Sergot, M.J. A logic–based calculus of events. New Gener. Comput. 1986, 4, 67–95. [Google Scholar] [CrossRef]
- McCarthy, J.; Hayes, P.J. Some Philosophical Problems from the Standpoint of Artificial Intelligence. In Machine Intelligence; Meltzer, B., Michie, D., Eds.; Edinburgh University Press: Edinburgh, UK, 1969; Volume 4, pp. 463–502. [Google Scholar]
- Pratt, V.R. A near-optimal method for reasoning about action. J. Comput. Syst. Sci. 1980, 20, 231–254. [Google Scholar] [CrossRef] [Green Version]
- Goré, R.; Widmann, F. An optimal on-the-fly tableau-based decision procedure for PDL-satisfiability. Lect. Notes Comput. Sci. 2009, 5663, 437–452. [Google Scholar]
- De Giacomo, G.; Massacci, F. Combining deduction and model checking into tableaux and algoritms for converse—PDL. Inf. Comput. 2000, 162, 117–137. [Google Scholar] [CrossRef] [Green Version]
- Hudstadt, U.; Schmidt, R.A. A comparison of solvers for propositional dynamic logic. In Proceedings of the Second International Workshop on Practical Aspects of Automated Reasoning (PAAR-2010), Edinburgh, UK, 14 July 2012; Volume 9, pp. 63–73. [Google Scholar]
- Lange, M. Model checking propositional dynamic logic with all extras. J. Appl. Log. 2006, 4, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Burrieza, A.; Guzmán, F.; Martínez, J.; Merino, S. Acumulador, Sistema y Procedimiento Para Proporcionar Agua Caliente Sanitaria. Patent ES2627209B2, 31 March 2017. [Google Scholar]

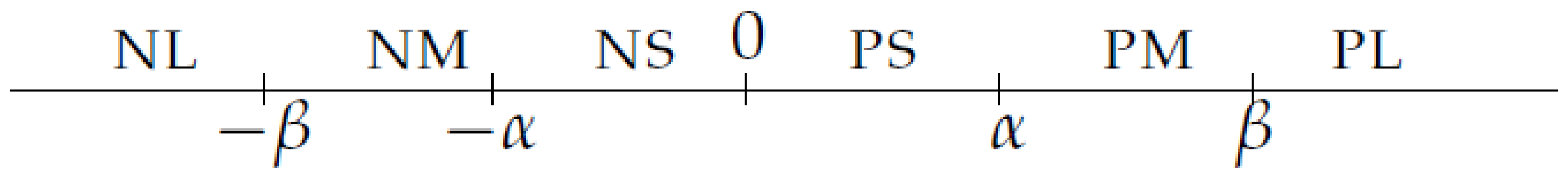
| NL | NM | NS | 0 | PS | PM | PL | |
|---|---|---|---|---|---|---|---|
| nl | nl | nl | nl | nl | nl, nm | nl, nm, ns | 1 |
| nm | nl | nl, nm | nm | nm, ns | ns, 0, ps | ps, pm, pl | |
| ns | nm, ns | ns | ns, 0, ps | ps, pm | pm, pl | ||
| 0 | 0 | ps | pm | pl | |||
| ps | ps, pm | pm, pl | pl | ||||
| pm | pl | pl | |||||
| pl | pl |
| NL | NM | NS | 0 | PS | PM | PL | |
|---|---|---|---|---|---|---|---|
| vc | vc | vc | vc | vc | vc, c | vc, c, n | 1 |
| c | vc | vc | vc, c | c | c, n | n | n, h, vh |
| n | vc, c | vc, c, n | c, n | n | n, h | n, h, vh | h, vh |
| h | vc, c, n | n | n, h | h | h, vh | vh | vh |
| vh | 1 | n, h, vh | h, vh | vh | vh | vh | vh |
| NL | NM | NS | 0 | PS | PM | PL | |
|---|---|---|---|---|---|---|---|
| c | c | c | c | c | c, n | c, n | 1 |
| n | c | c, n | c, n | n | n, h | n, h | h |
| h | 1 | n, h | n, h | h | h | h | h |
| Scene Formula x | w | v | Trouble |
|---|---|---|---|
| , | A | ||
| , | HW | ||
| , | CW | ||
| (where ) | ER |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merino, S.; Burrieza, A.; Guzman, F.; Martinez, J. Smart Sensorization Using Propositional Dynamic Logic. Sensors 2022, 22, 3899. https://doi.org/10.3390/s22103899
Merino S, Burrieza A, Guzman F, Martinez J. Smart Sensorization Using Propositional Dynamic Logic. Sensors. 2022; 22(10):3899. https://doi.org/10.3390/s22103899
Chicago/Turabian StyleMerino, Salvador, Alfredo Burrieza, Francisco Guzman, and Javier Martinez. 2022. "Smart Sensorization Using Propositional Dynamic Logic" Sensors 22, no. 10: 3899. https://doi.org/10.3390/s22103899
APA StyleMerino, S., Burrieza, A., Guzman, F., & Martinez, J. (2022). Smart Sensorization Using Propositional Dynamic Logic. Sensors, 22(10), 3899. https://doi.org/10.3390/s22103899






