Hot Spot Detection of Photovoltaic Module Based on Distributed Fiber Bragg Grating Sensor
Abstract
:1. Introduction
2. Hot Spot Effect of Photovoltaic Module and Its Influence
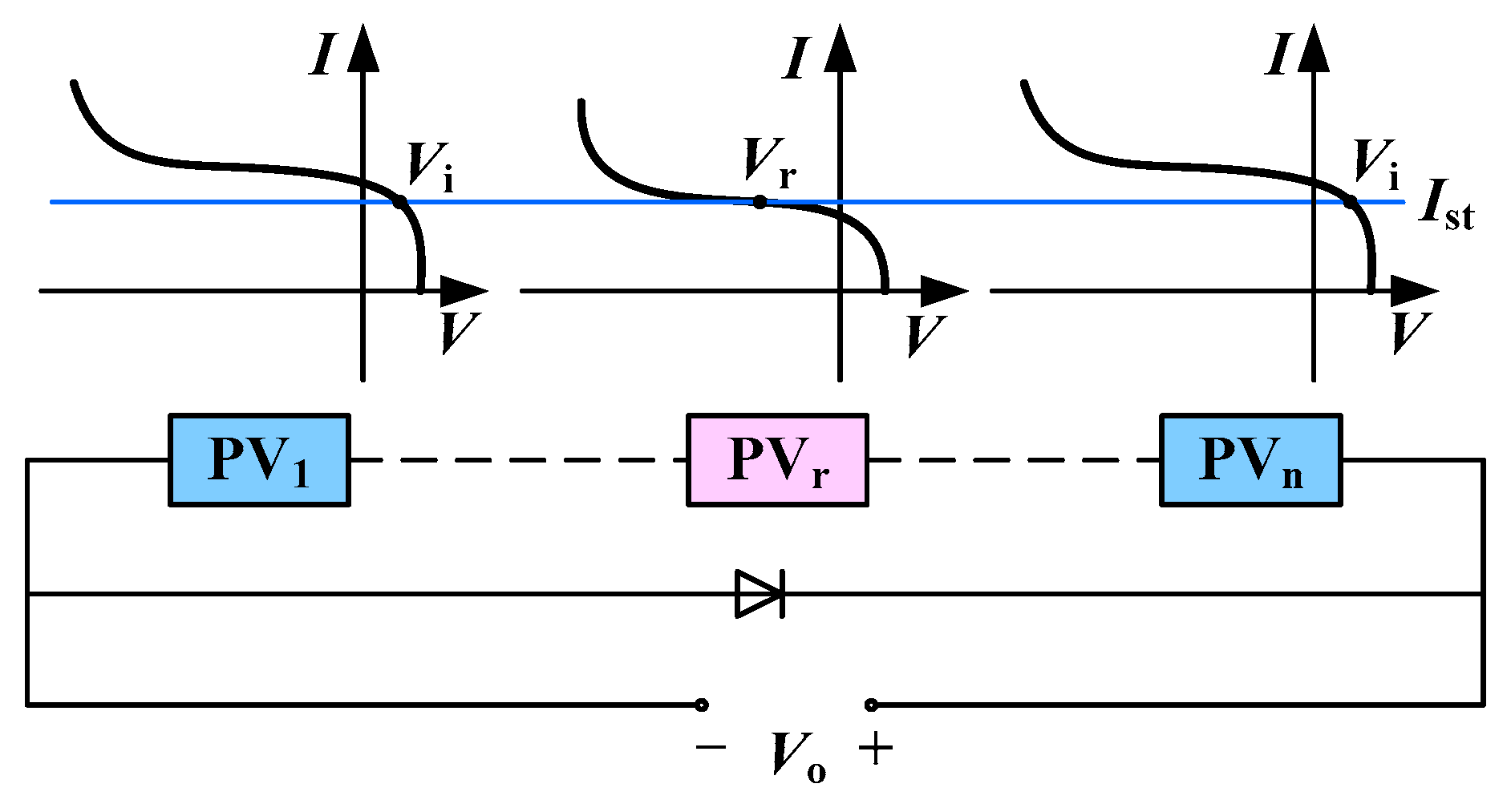
2.1. Hot Spot Effect of Photovoltaic Module
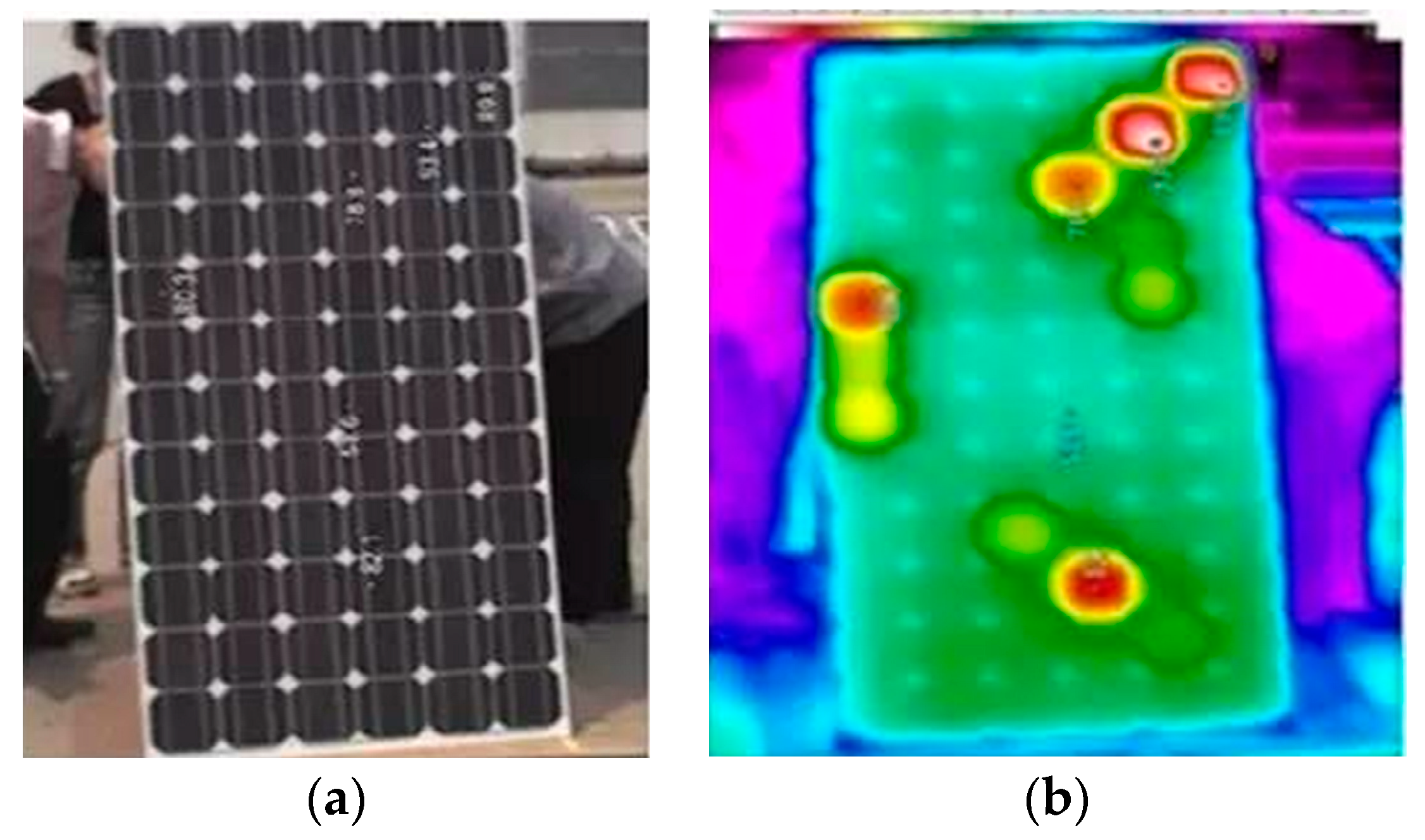
2.2. Influence Analysis of Hot Spot Effect
3. Hot Spot Detection of Photovoltaic Module Based on FBG
3.1. FBG Temperature Detection Principle
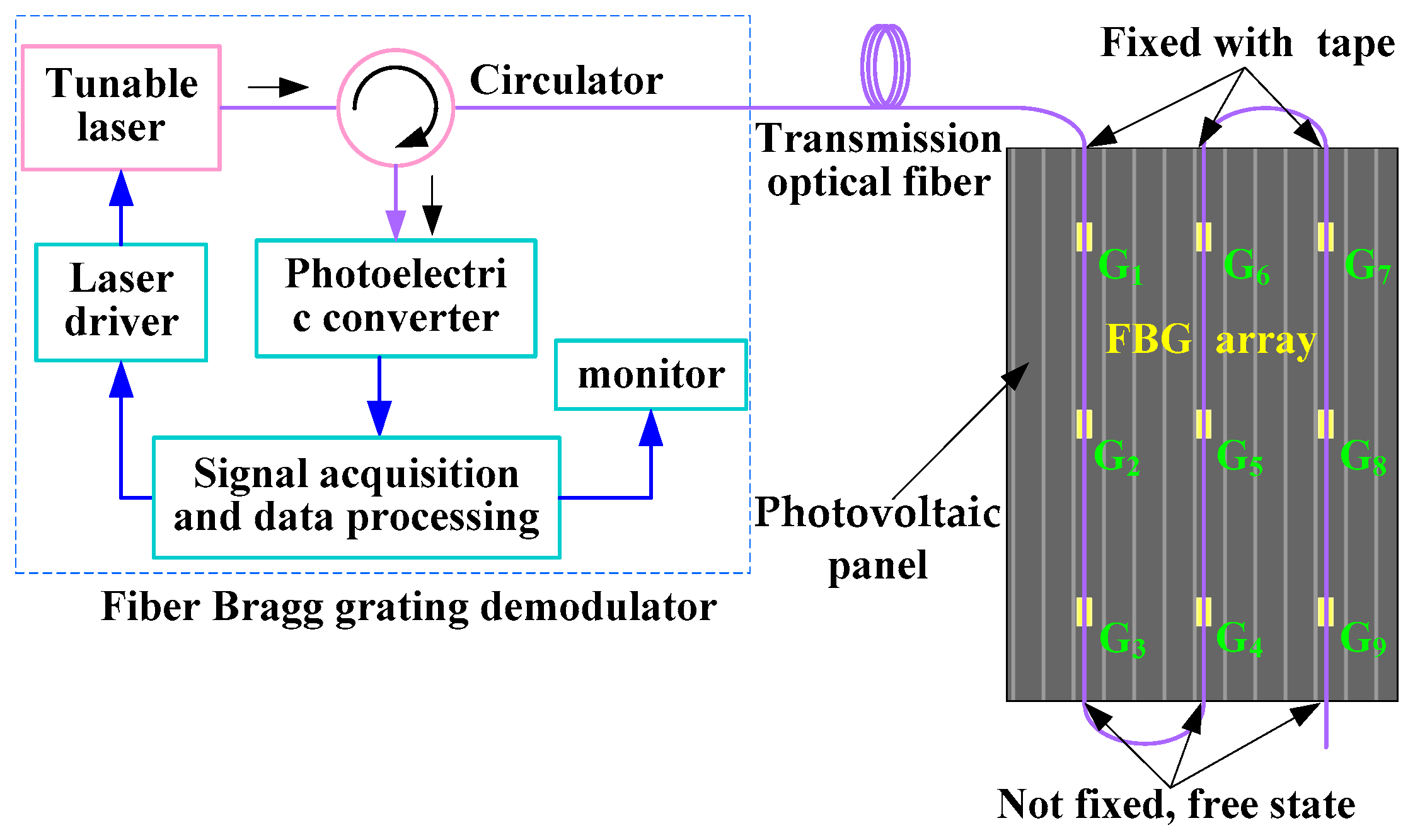
3.2. Hot Spot Detection Method of Photovoltaic Module Based on FBG
4. Experiment and Analysis
4.1. Experimental Materials and Equipment
4.2. Experimental Results and Analysis
4.2.1. FBG Calibration
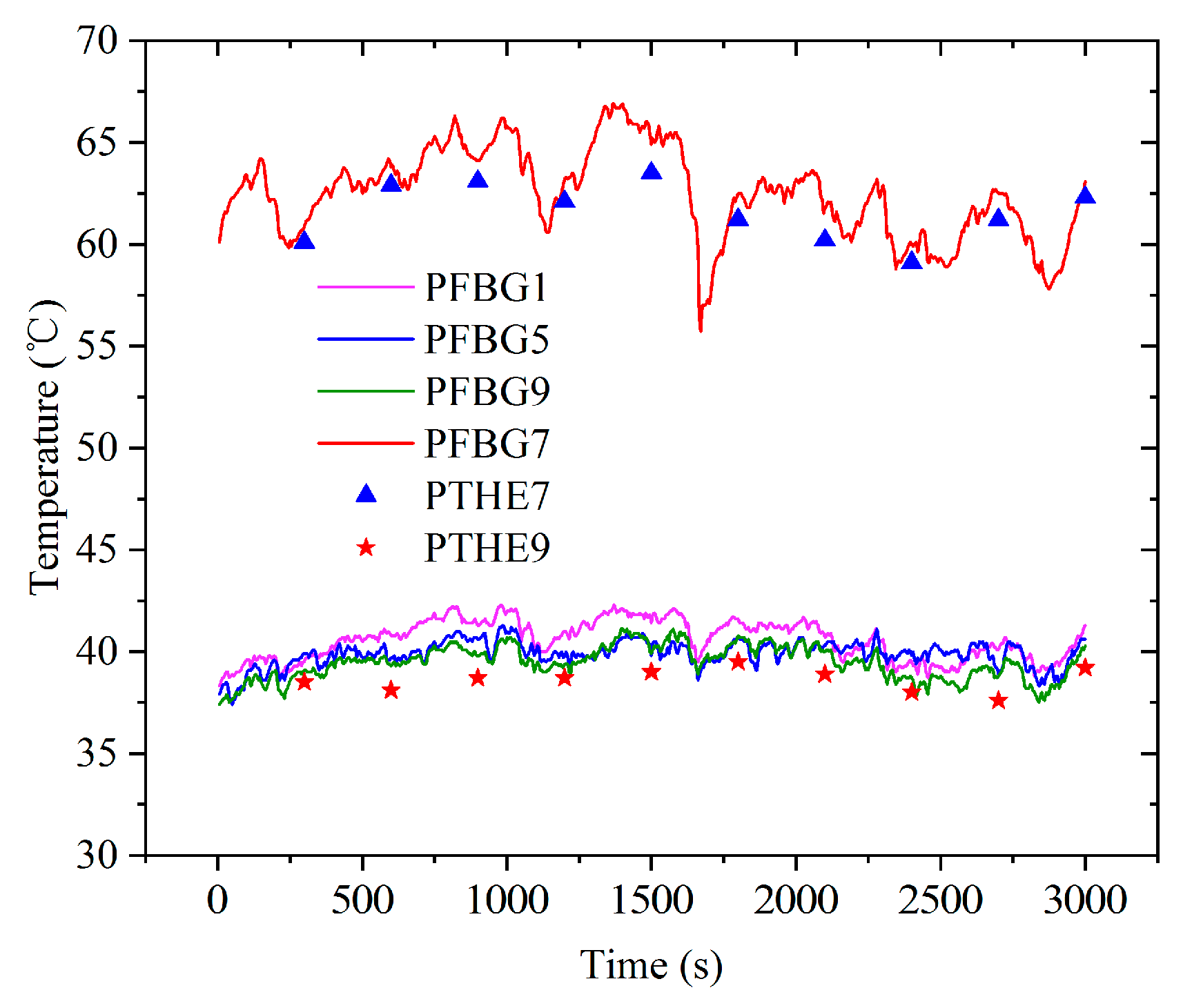
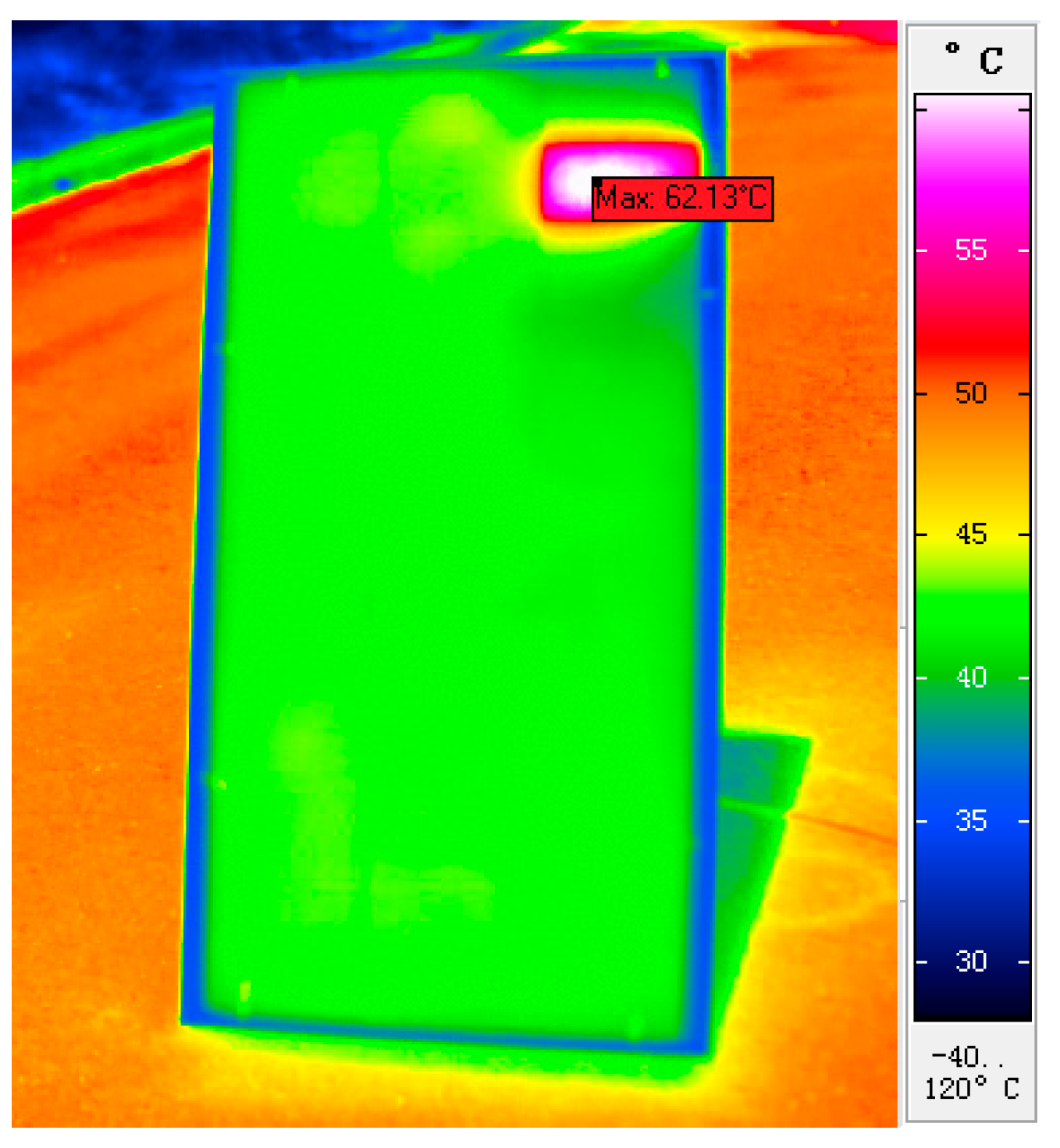
4.2.2. Photovoltaic Panel Temperature Measurement and Hot Spot Identification
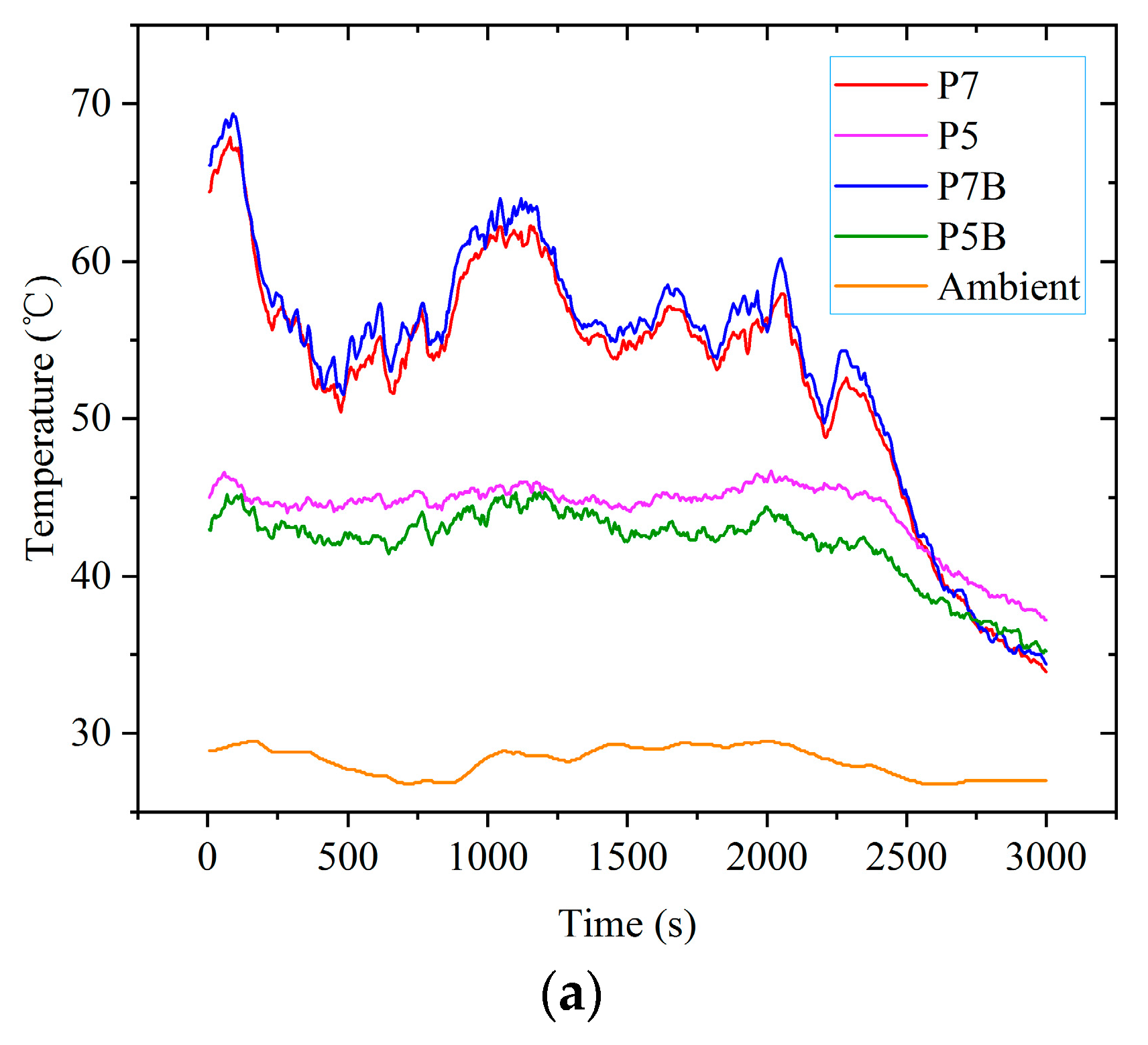
4.2.3. Measurement Experiment of Photovoltaic Panel Temperature and Environmental Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wang, Y.; Gao, M.; Wang, J.; Wang, S.; Liu, Y.; Zhu, J.; Tan, Z. Measurement and key influencing factors of the economic benefits for China’s photovoltaic power generation: A LCOE-based hybrid model. Renew. Energy 2021, 169, 935–952. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Renewable Capacity Statistics 2022; IRENA: Masdar City Abu Dhabi, United Arab Emirates, 2022. [Google Scholar]
- International Energy Agency. IEA Technology Roadmaps, Solar Photovoltaic Energy; OECD/IEA: Paris, France, 2014. [Google Scholar]
- Van Dyk, E.E.; Scott, B.J.; Meyer, E.L.; Leitch, A.W.R. Temperature dependence of performance of crystalline silicon photovoltaic modules. S. Afr. J. Sci. 2000, 4, 198–200. [Google Scholar]
- Skoplai, E.P.; Paiyvos, J.A. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 5, 614–624. [Google Scholar] [CrossRef]
- Bayrakci, M.; Choi, Y.; Brownson, J.R.S. Temperature dependent power modeling of photovoltaics. Energy Procedia 2014, 57, 745–754. [Google Scholar] [CrossRef]
- Zhang, Z.; Shan, L.; Wang, L.; Wu, J.; Quan, P.; Jiang, M. Study on case analysis and effect factors of hot spot fault for photovoltaic module. Acta Energiae Sol. Sin. 2017, 1, 271–278. [Google Scholar]
- Geisemeyer, I.; Fertig, F.; Warta, W.; Rein, S.; Schubert, M.C. Prediction of silicon PV module temperature for hot spots and worst case partial shading situations using spatially resolved lock-in thermography. Sol. Energy Mater. Sol. Cells 2014, 120, 259–269. [Google Scholar] [CrossRef]
- Jiang, L.; Su, J.; Shi, Y.; Lai, J.; Wang, H. Hot spots detection of operating PV arrays through IR thermal image. Acta Energiae Sol. Sin. 2020, 8, 180–184. [Google Scholar]
- Kim, K.A.; Seo, G.S.; Cho, B.H.; Krein, P.T. Photovoltaic hot-spot detection for solar panel substrings using AC parameter characterization. IEEE Trans. Power Electron. 2015, 2, 1121–1130. [Google Scholar] [CrossRef]
- Liu, H.; Ma, M.; Zhang, Z.; Yun, P.; Zhang, X. Study on I-V curve analysis and characteristic simulation of silicon photovoltaic module with hot spot. Acta Energ. Sol. Sin. 2021, 4, 239–246. [Google Scholar]
- Wu, C.; Zhou, D.; Li, Z.; Fu, L. Hot spot detection and fuzzy optimization control method of PV module. Proc. CSEE 2013, 36, 50–61. [Google Scholar]
- Jia, R.; Li, Y.; Zhang, H.; Han, J. Multi-sensor fault detection and positioning method of photovoltaic array based on improved BP neural network. Acta Energiae Sol. Sin. 2018, 1, 110–116. [Google Scholar]
- Bohorquez, M.A.M.; Gomez, J.M.E.; Marquez, J.M.A. A new and inexpensive temperature-measuring system: Application to photovoltaic solar facilities. Sol. Energy 2009, 6, 883–890. [Google Scholar] [CrossRef]
- Tsanakas, J.A.; Botsaris, P. On the detection of hot spots in operating photovoltaic arrays through thermal image analysis and a simulation model. Mater. Eval. 2013, 4, 457–465. [Google Scholar]
- Tsanakas, J.A.; Chrysostomou, D.; Botsaris, P.N.; Gasteratos, A. Fault diagnosis of photovoltaic modules through image processing and canny edge detection on field thermographic measurements. Int. J. Sustain. Energy 2015, 6, 351–372. [Google Scholar] [CrossRef]
- Niazuk, A.K.; Akhtar, W.; Khan, H.A.; Yang, Y.; Athar, S. Hotspot diagnosis for solar photovoltaic modules using a Naïve Bayes classifier. Sol. Energy 2019, 190, 34–43. [Google Scholar]
- Jiang, L.; Su, J.; Li, X.; Wang, H. Hot spot detection of photovoltaic array based on fusion of visible and infrared thermal images. Acta Energiae Sol. Sin. 2022, 1, 393–397. [Google Scholar]
- Mao, X.; Li, Y. Infrared image stitching of UAV in fault detection of photovoltaic array. Acta Energiae Sol. Sin. 2020, 41, 262–269. [Google Scholar]
- Chen, G.; Cai, L.; Zhang, L.; Zuo, Y.; Shu, S. Photovoltaic hotspot simulation modeling and thermal imaging analysis. J. Electron. Meas. Instrum. 2021, 8, 191–197. [Google Scholar]
- Lamberti, A.; Luyckx, G.; Van Paepegem, W.; Rezayat, A.; Vanlanduit, S. Detection, localization and quantification of impact events on a stiffened composite panel with embedded fiber Bragg grating sensor networks. Sensors 2017, 17, 743. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, Z.; Zhang, L.; Chen, J.; Ji, C.; Pham, D.T. Strain modal analysis of small and light pipes using distributed fibre Bragg grating sensors. Sensors 2016, 16, 1583. [Google Scholar] [CrossRef]
- Kokhanovskiy, A.; Shabalov, N.; Dostovalov, A.; Wolf, A. Highly dense FBG temperature sensor assisted with deep learning algorithms. Sensors 2021, 21, 6188. [Google Scholar] [CrossRef] [PubMed]
- Falcetelli, F.; Martini, A.; Di Sante, R.; Troncossi, M. Strain Modal Testing with Fiber Bragg Gratings for Automotive Applications. Sensors 2022, 22, 946. [Google Scholar] [CrossRef] [PubMed]
- Kumar, J.; Prakash, O.; Agrawal, S.K.; Mahakud, R.; Mokhariwale, A.; Dixit, S.K.; Nakhe, S.V. Distributed fiber Bragg grating sensor for multipoint temperature monitoring up to 500 °C in high-electromagnetic interference environment. Opt. Eng. 2016, 9, 90502. [Google Scholar] [CrossRef]
- Da Silva Marques, R.; Prado, A.R.; Da Costa Antunes, P.F.; De Brito André, P.S.; Ribeiro, M.R.N.; Frizera-Neto, A.; Pontes, M.J. Corrosion resistant FBG-based quasi-distributed sensor for crude oil tank dynamic temperature profile monitoring. Sensors 2015, 15, 30693–30703. [Google Scholar] [CrossRef]
- De Vita, E.; Zaltieri, M.; De Tommasi, F.; Massaroni, C.; Faiella, E.; Zobel, B.B.; Iadicicco, A.; Schena, E.; Grasso, R.F.; Campopiano, S. Multipoint temperature monitoring of microwave thermal ablation in bones through fiber Bragg grating sensor arrays. Sensors 2020, 20, 3200. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Tang, J.; Jiang, Y.; Cheng, C.; Yang, M. An enhanced distributed acoustic sensor with large temperature tolerance based on ultra-weak fiber Bragg grating array. IEEE Photonics J. 2020, 4, 1–11. [Google Scholar] [CrossRef]
- Cheng, Z.; Gong, L.; Liu, Y. The influence of optical losses on monocrystalline silicon solar cells parameters. Trans. China Electrotech. Soc. 2016, 17, 217–223. [Google Scholar]
- Markowski, K.; Araszkiewicz, P.; Bojarczuk, J.; Perlicki, K. High-sensitivity chirped tapered fiber-Bragg-grating-based Fabry–Perot cavity for strain measurements. Opt. Lett. 2020, 45, 2838–2841. [Google Scholar] [CrossRef]




| Equipment | Model | Manufacturer |
|---|---|---|
| Photovoltaic panel | Polycrystalline, 960 mm × 480 mm | —— |
| FBG demodulator | BLY-FBG-5S, 1525~1565 nm | China Wuxi Brillouin Electronic Technology Co., Ltd. (Wuxi, China) |
| Digital thermometer | TASI-TA612C | China Suzhou TASI Electronic Industry Co., Ltd. (Suzhou, China) |
| Infrared thermal imager | VarioCAM®HD inspect 980 | Germany InfraTec (Dresden, Germany) |
| Solar power meter | TES-1333R | China TES Electrical Electronic Corp (Taibei, China) |
| Anemometer | Benetech GM8907 | China Shenzhen Jumaoyuan Science And Technology Co., Ltd. (Shenzhen, China) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Wang, F.; Feng, F.; Wei, B. Hot Spot Detection of Photovoltaic Module Based on Distributed Fiber Bragg Grating Sensor. Sensors 2022, 22, 4951. https://doi.org/10.3390/s22134951
Li G, Wang F, Feng F, Wei B. Hot Spot Detection of Photovoltaic Module Based on Distributed Fiber Bragg Grating Sensor. Sensors. 2022; 22(13):4951. https://doi.org/10.3390/s22134951
Chicago/Turabian StyleLi, Guoli, Fang Wang, Fei Feng, and Bo Wei. 2022. "Hot Spot Detection of Photovoltaic Module Based on Distributed Fiber Bragg Grating Sensor" Sensors 22, no. 13: 4951. https://doi.org/10.3390/s22134951
APA StyleLi, G., Wang, F., Feng, F., & Wei, B. (2022). Hot Spot Detection of Photovoltaic Module Based on Distributed Fiber Bragg Grating Sensor. Sensors, 22(13), 4951. https://doi.org/10.3390/s22134951






