Narrow Linewidth Half-Open-Cavity Random Laser Assisted by a Three-Grating Ring Resonator for Strain Detection
Abstract
1. Introduction
2. Experimental Setup and Principle
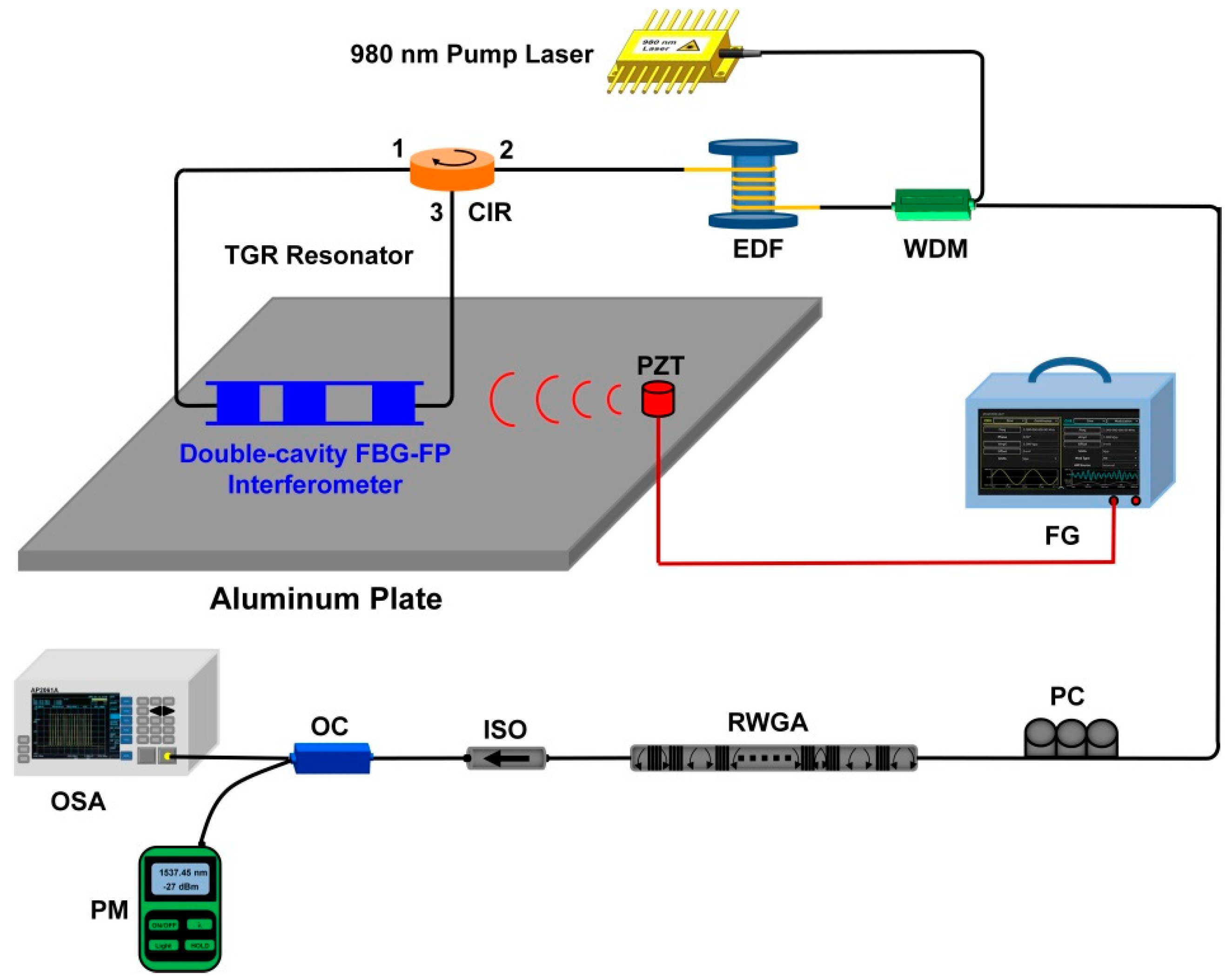
2.1. Configuration of the RFL Strain Sensor
2.2. Operation Principle of TGR Resonator
2.3. Linewidth Compression Principle of the Half-Open-Cavity of RFL
2.4. Strain-Sensing Principle of the Proposed RFL Sensor
3. Experimental Results and Discussion
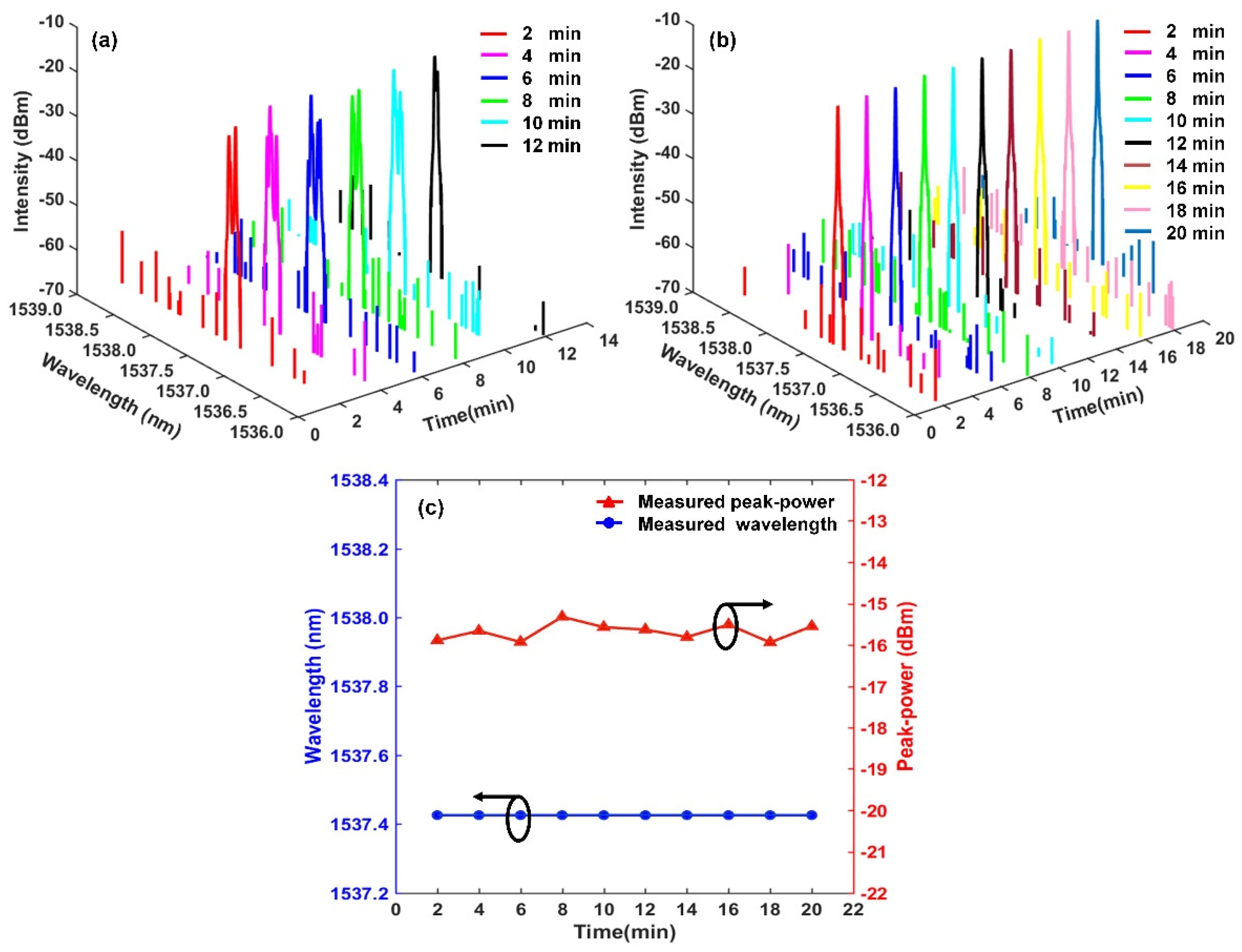
3.1. Output Charateristics of RFL
3.2. Frequency Characteristics of RFL
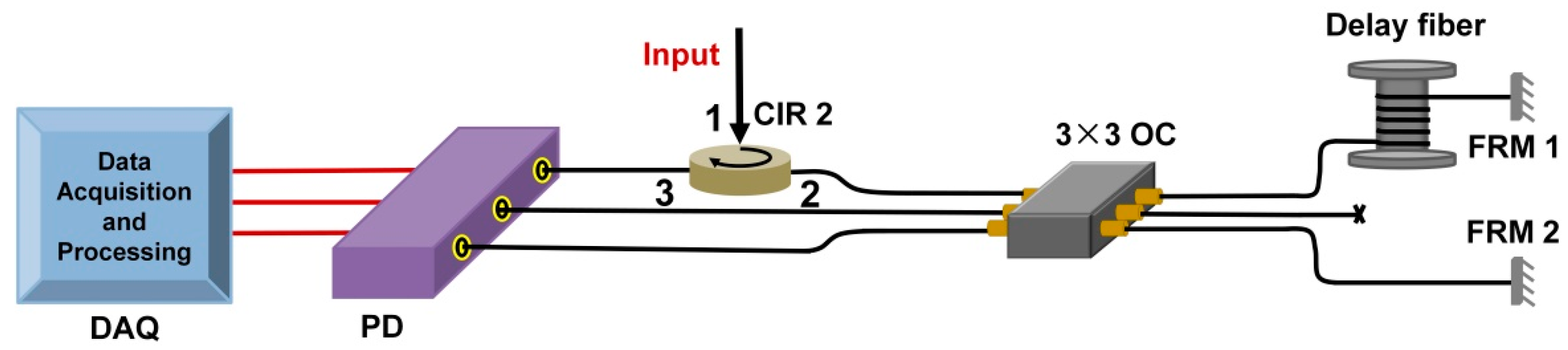
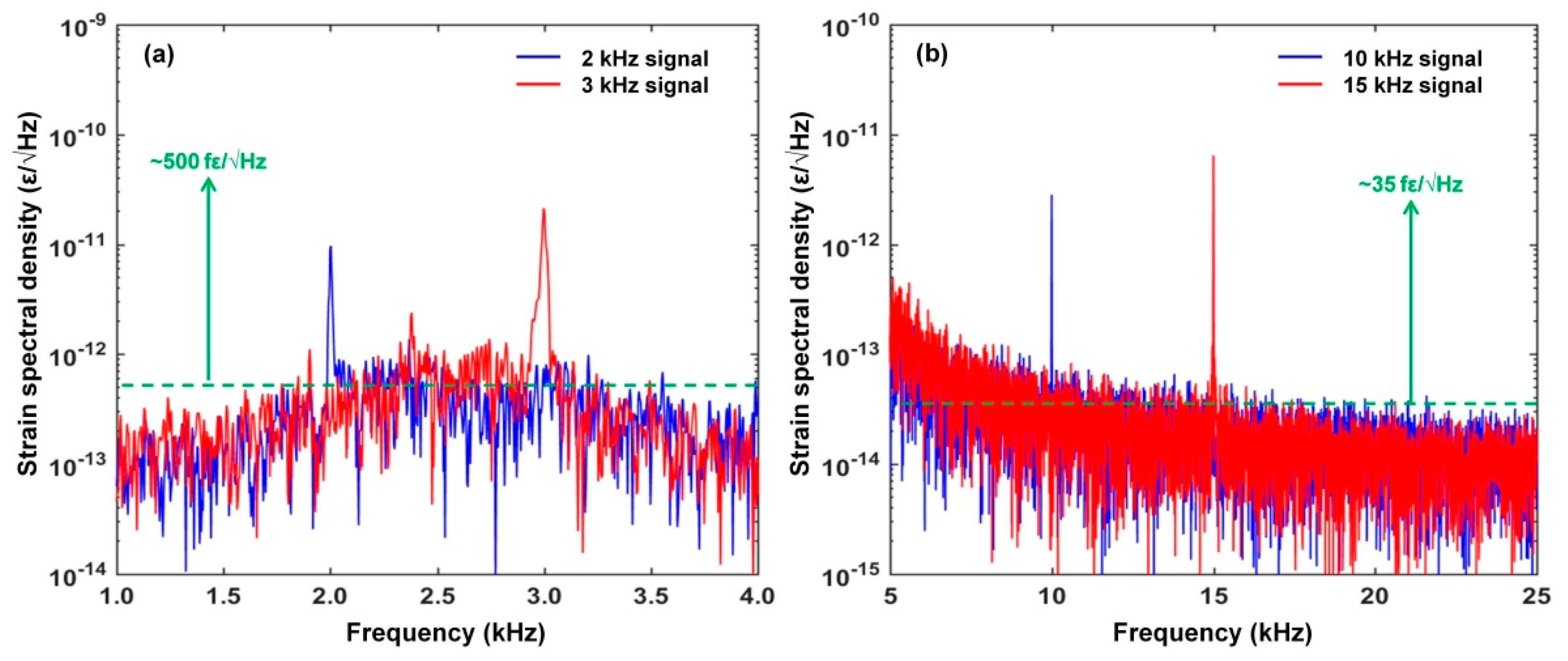
3.3. Strain Detection Characteristics of RFL
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Q.L.; Zhang, Z.T.; Wu, B.; Tan, T.Y.; Yang, C.S.; Gan, J.L.; Cheng, H.H.; Feng, Z.M.; Peng, M.Y.; Yang, Z.M.; et al. Noise-sidebands-free and ultra-low-RIN 1.5 mu m single-frequency fiber laser towards coherent optical detection. Photon. Res. 2018, 6, 326–331. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Zhao, Q.L.; Yang, C.S.; Guan, X.C.; Tan, T.Y.; Wang, Y.F.; Zhou, K.J.; Feng, Z.M.; Yang, Z.M.; Xu, S.H. Noise-sideband-free and narrow-linewidth photonic microwave generation based on an optical heterodyne technique of low-noise fiber lasers. Appl. Opt. 2020, 59, 7907–7911. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhao, Q.; Lin, W.; Li, C.; Yang, C.; Mo, S.; Feng, Z.; Deng, H.; Yang, Z.; Xu, S. Linewidth suppression mechanism of self-injection locked single-frequency fiber laser. Opt. Express 2016, 24, 18907–18916. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Gao, S.; Zhang, M.; Zhang, J.; Qiao, L.; Wang, T.; Gao, F.; Hu, X.; Li, S.; Zhu, Y. Advances in Random Fiber Lasers and Their Sensing Application. Sensors 2020, 20, 6122. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Chen, C.; Lu, P.; Mihailov, S.; Chen, L.; Bao, X. Random Fiber Grating Characterization Based on OFDR and Transfer Matrix Method. Sensors 2020, 20, 6071. [Google Scholar] [CrossRef] [PubMed]
- Skvortsov, M.; Wolf, A.; Dostovalov, A.; Egorova, O.; Semjonov, S.L.; Babin, S. Narrow-linewidth Er-doped fiber lasers with random distributed feedback provided by artificial Rayleigh scattering. J. Light. Technol. 2021, 40, 1829–1835. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Babin, S.A.; Churkin, D.V.; Vatnik, I.D.; Nikulin, M.; Podivilov, E.V. Random distributed feedback fibre lasers. Phys. Rep. 2014, 542, 133–193. [Google Scholar] [CrossRef]
- Jaharudin, N.A.N.; Cholan, N.A.; Omar, M.A.; Talib, R.; Ngajikin, N.H. Remote temperature sensing with a low-threshold-power erbium-doped fiber laser. Appl. Opt. 2019, 58, 6003–6006. [Google Scholar] [CrossRef] [PubMed]
- Leandro, D.; deMiguel-Soto, V.; López-Amo, M. High-Resolution Sensor System Using a Random Distributed Feedback Fiber Laser. J. Light. Technol. 2016, 34, 4596–4602. [Google Scholar] [CrossRef]
- Lizárraga, N.; Puente, N.P.; Chaikina, E.I.; Leskova, T.A.; Méndez, E.R. Single-mode Er-doped fiber random laser with distributed Bragg grating feedback. Opt. Express 2009, 17, 395–404. [Google Scholar] [CrossRef] [PubMed]
- Lv, B.; Zhang, W.; Huang, W.; Li, F. Low Frequency-Noise Ring Random Fiber Laser with a Dual-Cavity FBG Fabry-Perot Filter. J. Light. Technol. 2022, 40, 5286–5293. [Google Scholar] [CrossRef]
- Lv, B.; Zhang, W.; Huang, W.; Li, F. Switchable and compact dual-wavelength random fiber laser based on random Bragg grating array. Opt. Fiber Technol. 2022, 70, 102858. [Google Scholar] [CrossRef]
- Zhang, W.L.; Song, Y.B.; Zeng, X.P.; Ma, R.; Yang, Z.J.; Rao, Y. Temperature-controlled mode selection of Er-doped random fiber laser with disordered Bragg gratings. Photon. Res. 2016, 4, 102–105. [Google Scholar] [CrossRef]
- Zhang, A.; Hao, L. Random phase-shift Bragg grating-based random fiber laser with a half-open cavity. Appl. Opt. 2018, 57, 10017–10021. [Google Scholar] [CrossRef]
- Skvortsov, M.I.; Abdullina, S.R.; Wolf, A.A.; Dostovalov, A.V.; Churin, A.E.; Egorova, O.N.; Semjonov, S.L.; Proskurina, K.V.; Babin, S.A. Single-frequency erbium-doped fibre laser with random distributed feedback based on disordered structures produced by femtosecond laser radiation. Quantum Electron. 2021, 51, 1051–1055. [Google Scholar] [CrossRef]
- Wang, X.; Chen, D.; Mao, B.-M.; Wu, G. Random fiber laser based on an artificially controlled backscattering Erbium-Doped fiber. Opt. Fiber Technol. 2020, 54, 102125. [Google Scholar] [CrossRef]
- Deng, J.; Han, M.; Xu, Z.; Du, Y.; Shu, X. Stable and low-threshold random fiber laser via Anderson localization. Opt. Express 2019, 27, 12987–12997. [Google Scholar] [CrossRef]
- Miao, S.; Zhang, W.; Song, Y. Random Bragg-gratings-based narrow linewidth random fiber laser with a π-phase-shifted FBG. Chin. Opt. Lett. 2019, 17, 090605. [Google Scholar] [CrossRef]
- Li, Y.; Lu, P.; Baset, F.; Ou, Z.; Song, J.; Alshehri, A.; Ravi, V.; Bhardwaj, V.R.; Bao, X. Narrow linewidth low frequency noise Er-doped fiber ring laser based on femtosecond laser induced random feedback. Appl. Phys. Lett. 2014, 105, 101105. [Google Scholar] [CrossRef]
- Willberry, J.; Papaelias, M.; Fernando, G. Structural Health Monitoring Using Fibre Optic Acoustic Emission Sensors. Sensors 2020, 20, 6369. [Google Scholar] [CrossRef]
- Gong, J.; MacAlpine, J.; Jin, W.; Liao, Y. Locating Acoustic Emission with an Amplitude-Multiplexed Acoustic Sensor Array Based on a Modified Mach-Zehnder Interferometer. Appl. Opt. 2002, 40, 6199–6202. [Google Scholar] [CrossRef][Green Version]
- Lu, Y.; Zhu, T.; Chen, L.; Bao, X. Distributed Vibration Sensor Based on Coherent Detection of Phase-OTDR. J. Light. Technol. 2010, 28, 3243–3249. [Google Scholar] [CrossRef]
- Li, W.; Xu, C.; Chun, S.; Ho, M.; Wang, B.; Song, G. Monitoring Concrete Deterioration Due to Reinforcement Corrosion by Integrating Acoustic Emission and FBG Strain Measurements. Sensors 2017, 17, 657. [Google Scholar] [CrossRef]
- Barot, D.; Wang, G.; Duan, L. High-Resolution Dynamic Strain Sensor Using a Polarization-Maintaining Fiber Bragg Grating. IEEE Photonics Technol. Lett. 2019, 31, 709–712. [Google Scholar] [CrossRef]
- Liu, B.; Ruan, Y.; Yu, Y.; Xi, J.; Guo, Q.; Tong, J.; Rajan, G. Laser Self-Mixing Fiber Bragg Grating Sensor for Acoustic Emission Measurement. Sensors 2018, 18, 1956. [Google Scholar] [CrossRef] [PubMed]
- Miao, S.; Gao, L.; Tong, F.; Zhong, Y. Research on high precision optical fiber acoustic emission system for weak damage location on concrete. Constr. Build. Mater. 2022, 347, 128331. [Google Scholar] [CrossRef]
- Liu, P.; Huang, W.; Zhang, W.; Li, F. Ultrahigh resolution optic fiber strain sensor with a frequency-locked random distributed feedback fiber laser. Opt. Lett. 2018, 43, 2499–2502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Lu, P.; Zhou, Z.; Wang, Y.; Mihailov, S.; Chen, L.; Bao, X. High-efficiency random fiber laser based on strong random fiber grating for MHz ultrasonic sensing. IEEE Sens. J. 2020, 20, 5885–5892. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Gao, S.; Lu, P.; Mihailov, S.; Bao, X. Highly sensitive fiber random-grating-based random laser sensor for ultrasound detection. Opt. Lett. 2017, 42, 1353–1356. [Google Scholar] [CrossRef]
- Miao, S.; Zhang, W.; Song, Y.; Huang, W. High-resolution random fiber laser acoustic emission sensor. Opt. Express 2020, 28, 12699–12708. [Google Scholar] [CrossRef]
- Muriel, M.A.; Carballar, A.; Azana, J. Field distributions inside fiber gratings. IEEE J. Quantum Electron. 1999, 35, 548–558. [Google Scholar] [CrossRef]
- Shapira, O.; Fischer, B. Localization of light in a random-grating array in a single-mode fiber. J. Opt. Soc. Am. B 2005, 22, 2542–2552. [Google Scholar] [CrossRef]
- Xu, O.; Lu, S.; Dong, X.; Li, B.; Ning, T.; Jian, S. Theoretical analysis of transmission characteristics for all fiber, multi-cavity Fabry-Perot filters based on fiber Bragg gratings. Sci. China Ser. F Inf. Sci. 2008, 51, 1391–1400. [Google Scholar] [CrossRef]
- Lv, B.; Zhang, W.; Huang, W.; Li, F. Simulation analysis of random mode suppression using two-cavity FBG-FP in random Bragg grating array. Proc. SPIE 2021, 11763, 117634J. [Google Scholar]
- Lv, B.; Zhang, W.; Huang, W.; Li, F. Random Bragg-grating-based wavelength-tunable random fiber laser with a full-open cavity. Chin. Opt. Lett. 2021, 19, 5. [Google Scholar] [CrossRef]
- Rønnekleiv, E. Frequency and Intensity Noise of Single Frequency Fiber Bragg Grating Lasers. Opt. Fiber Technol. 2001, 7, 206–235. [Google Scholar] [CrossRef]
- Gatti, D.; Galzerano, G.; Janner, D.; Longhi, S.; Laporta, P. Fiber strain sensor based on a π-phase-shifted Bragg grating and the Pound-Drever-Hall technique. Opt. Express 2008, 16, 1945–1950. [Google Scholar] [CrossRef]
- Chow, J.H.; Littler, I.C.M.; McClelland, D.E.; Gray, M.B. Laser frequency-noise-limited ultrahigh resolution remote fiber sensing. Opt. Express 2006, 14, 4617–4624. [Google Scholar] [CrossRef]
- Chow, J.H.; Littler, I.C.M.; Vine, G.d.; McClelland, D.E.; Gray, M.B. Phase-Sensitive Interrogation of Fiber Bragg Grating Resonators for Sensing Applications. J. Light. Technol. 2005, 23, 1881. [Google Scholar] [CrossRef]
- Gagné, M.; Kashyap, R. Random fiber Bragg grating Raman fiber laser. Opt. Lett. 2014, 39, 2755–2758. [Google Scholar] [CrossRef]
- Milner, V.; Genack, A.Z. Photon Localization Laser: Low-Threshold Lasing in a Random Amplifying Layered Medium via Wave Localization. Phys. Rev. Lett. 2005, 94, 073901. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, W.; Zhanga, W.; Li, F.; Du, Y. Demonstration of High-resolution DFB Fiber Laser Acoustic Emission Sensing System for CFRP Laminates. IEEE Sens. J. 2021, 21, 18806–18814. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. J. Light. Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef]








| Cavity Type | Sensing Structure | Resolution | References |
|---|---|---|---|
| Ring | Random grating array | ~720 fε/√Hz | [29] |
| Half−open−cavity | π−FBG | ~280 fε/√Hz | [31] |
| Ring | π−FBG | ~140 fε/√Hz | [28] |
| Half−open−cavity | double−cavity FBG-FP 1 | ~35 fε/√Hz | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, B.; Zhang, W.; Huang, W.; Li, F.; Li, Y. Narrow Linewidth Half-Open-Cavity Random Laser Assisted by a Three-Grating Ring Resonator for Strain Detection. Sensors 2022, 22, 7882. https://doi.org/10.3390/s22207882
Lv B, Zhang W, Huang W, Li F, Li Y. Narrow Linewidth Half-Open-Cavity Random Laser Assisted by a Three-Grating Ring Resonator for Strain Detection. Sensors. 2022; 22(20):7882. https://doi.org/10.3390/s22207882
Chicago/Turabian StyleLv, Bing, Wentao Zhang, Wenzhu Huang, Fang Li, and Yongqian Li. 2022. "Narrow Linewidth Half-Open-Cavity Random Laser Assisted by a Three-Grating Ring Resonator for Strain Detection" Sensors 22, no. 20: 7882. https://doi.org/10.3390/s22207882
APA StyleLv, B., Zhang, W., Huang, W., Li, F., & Li, Y. (2022). Narrow Linewidth Half-Open-Cavity Random Laser Assisted by a Three-Grating Ring Resonator for Strain Detection. Sensors, 22(20), 7882. https://doi.org/10.3390/s22207882








