Study on TLS Point Cloud Registration Algorithm for Large-Scale Outdoor Weak Geometric Features
Abstract
:1. Introduction
- We used the NARF algorithm and SIFT algorithm to extract stable and repeatable points as the important elements of point cloud registration, which overcame the problem of enormous point cloud data in field scenes.
- The maximum entropy theory was used to search for the source point cloud viewpoints that contained the largest amount of information to ensure that the registration work could be carried out under reasonable initial conditions.
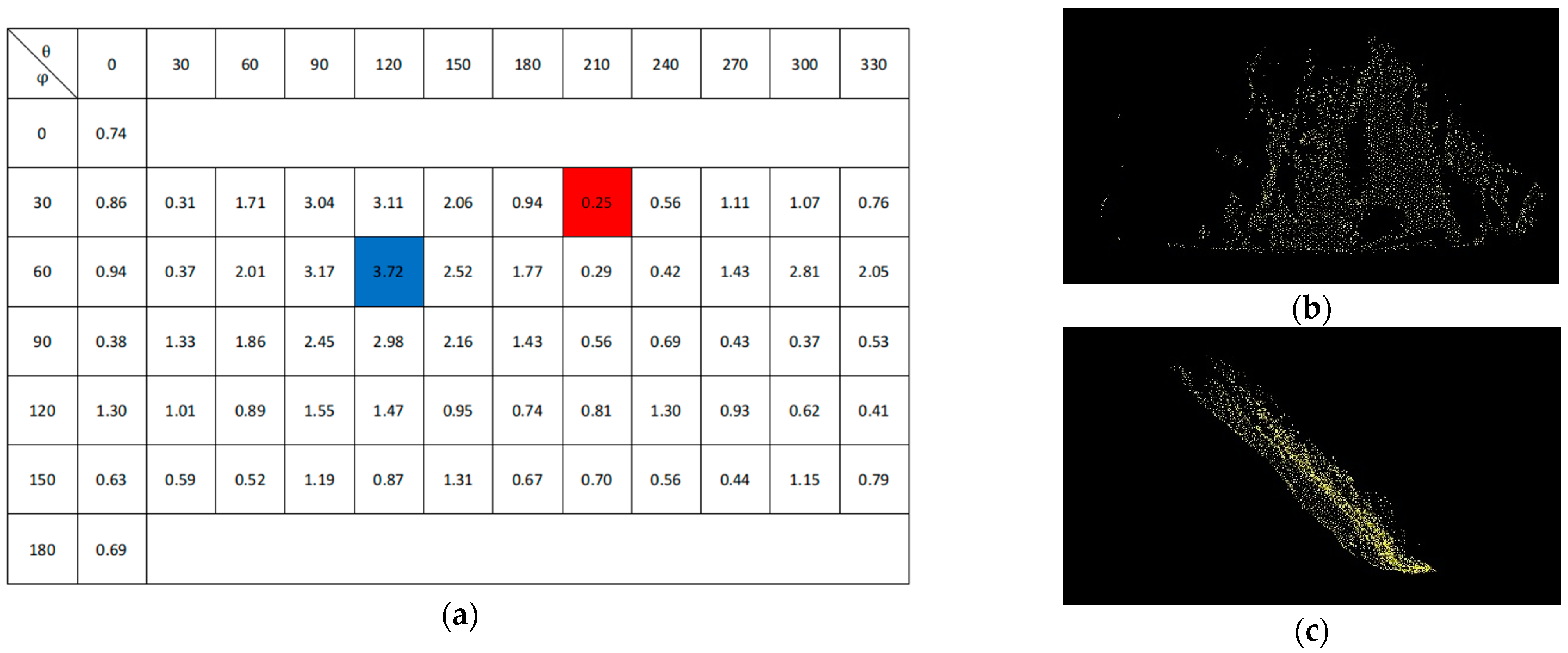
- We proposed a novel iterative structure for the target plate. Twenty-five viewpoints were tested each time, and GPU-accelerated computation was invoked to rapidly narrow down the search area for the best viewpoint.
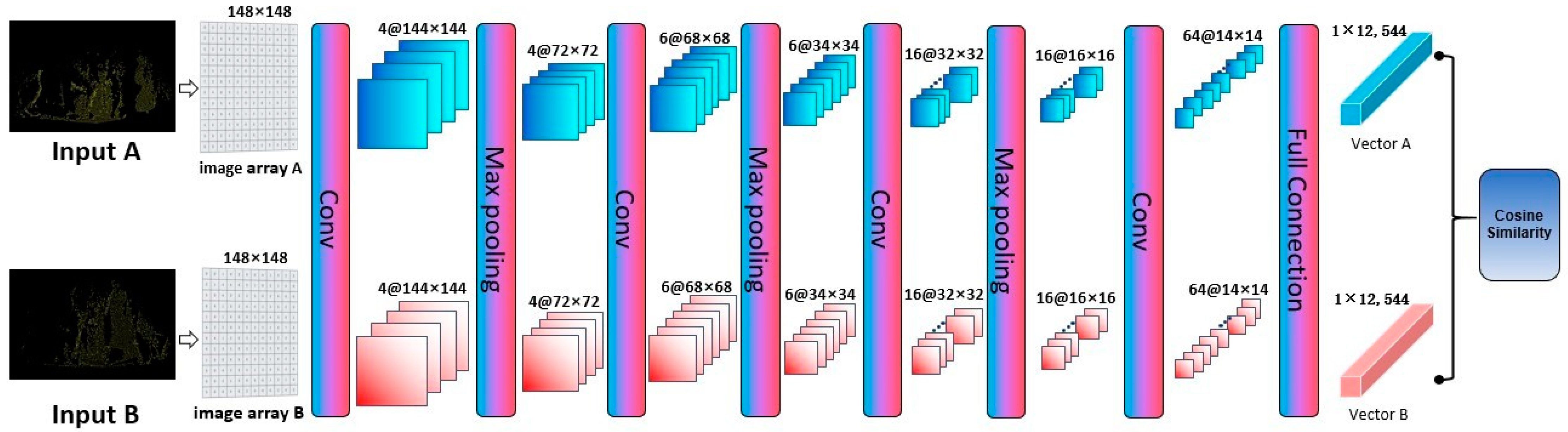
- We designed the point cloud multi-view convolution neural network (PC-MVCNN) model. In this model, the feature of the image matrix was extracted and the matching value was calculated using cosine similarity. The point with the highest score was recorded as the best viewpoint of this iteration and involved in the next iteration. A dynamic threshold of error was used as a limit to prevent infinite iterations.
2. Related Work
2.1. Point Cloud Filtering
2.2. Feature Descriptor
2.3. TLS Point Cloud Registration
3. Method
3.1. Key Points Extraction
3.1.1. Voxel Filtering
3.1.2. NARF Key Points
3.1.3. SIFT Key Points
- 1.
- Generate the scale space. The scale space of an image was defined as
- 2.
- Detect the extreme points in the scale space and construct the difference of the Gaussian (DOG) function:
- 3.
- Accurately locate the extreme point.
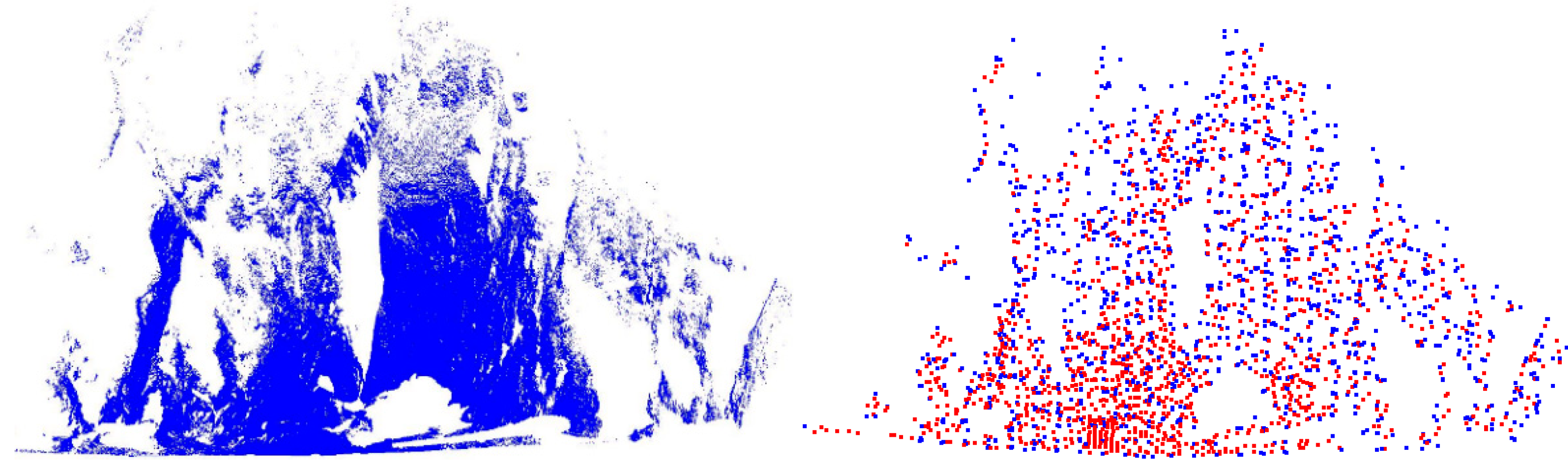
3.2. Extract the Maximum Information Viewpoint from the Source Point Cloud
- Images are paired. Only by ensuring good images are provided by the source point cloud can we pave the way for matching calculations in the early stages.
- The designed CNN must allow images of different sizes to ensure that the source point cloud and the target point cloud can calculate the matching degrees normally.
| Algorithm1. Minimum Bounding Sphere |
| Count MB (P, R), Returns the minimum bounding sphere |
| 1: if P = ∅ or |R| = 3, then |
| 2: else |
| 3: Select a point randomly |
| 4: D←MB (P − {p}, R); |
| 5: if D exists and p ∉ D, then |
| 6: end if; |
| 7: end if; |
3.3. Optimal Viewpoint Matching
3.3.1. Image Matrix
3.3.2. Convolution Process
3.3.3. Calculate the Match
3.3.4. Iterative Computations
3.4. GPU-Accelerated Matrix Computing
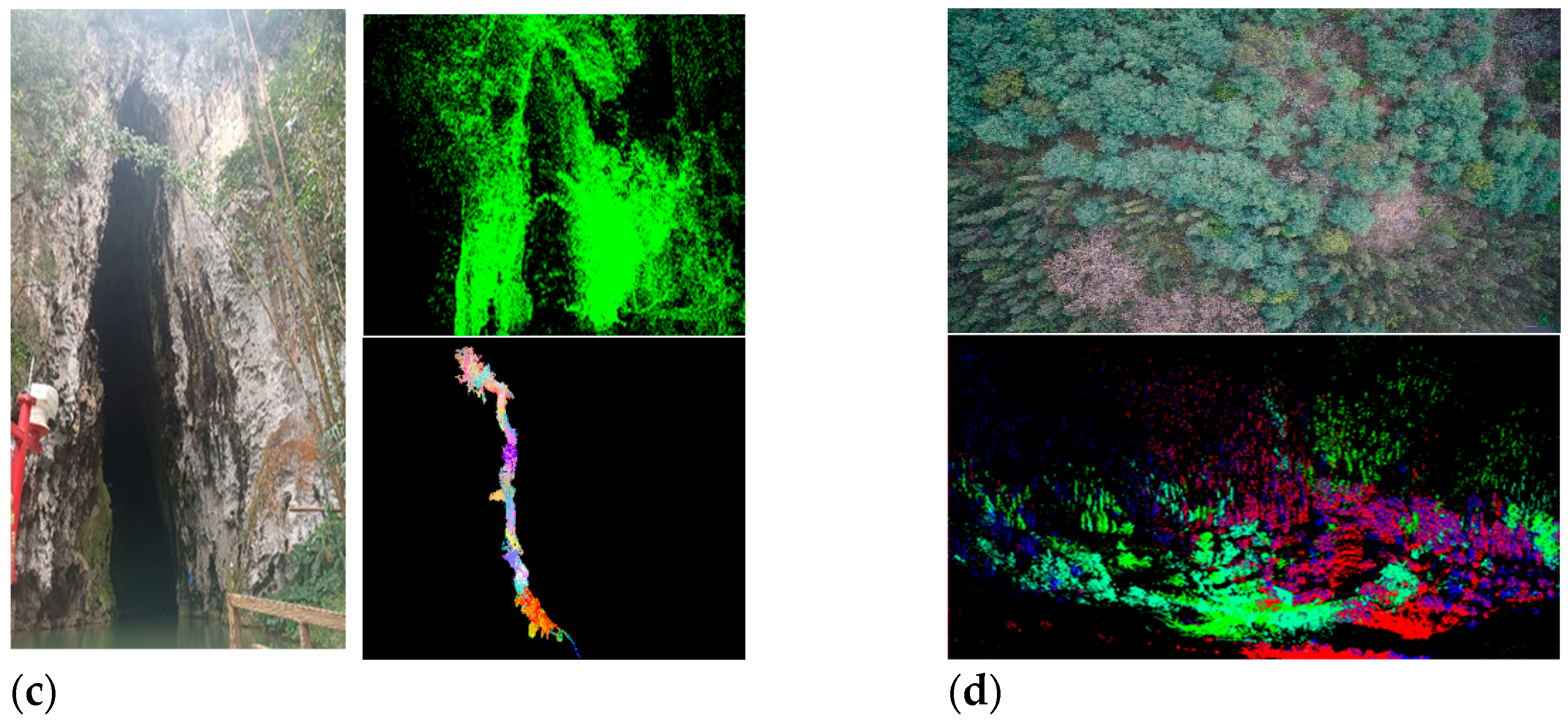
4. Experiment and Analysis Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J. Field engineering surveying and mapping based on digital mapping system. Silicon Val. 2015, 4, 114–115. [Google Scholar]
- Besl, P.; McKay, N. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Xiao, P.; Zhao, R.; Li, D.; Zeng, Z.; Qi, S.; Yang, X. As-Built Inventory and Deformation Analysis of a High Rockfill Dam under Construction with Terrestrial Laser Scanning. Sensors 2022, 22, 521. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Tan, J.; Liu, H.; Xie, H.; Chen, C. Automatic Registration of TLS-TLS and TLS-MLS Point Clouds Using a Genetic Algorithm. Sensors 2017, 17, 1979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qi, C.; Hao, S.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in A Metric Space. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; Volume 18, pp. 5099–5108. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. PointNetLK: Robust & Efficient Point Cloud Registration Using PointNet. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 7156–7165. [Google Scholar]
- Su, H.; Subhransu, M.; Evangelos, K.; Erik, G. Learned-Miller. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Li, Z.; Wang, H.; Li, J. Auto-MVCNN: Neural Architecture Search for Multi-view 3D Shape Recognition. arXiv 2020, arXiv:2012.05493. [Google Scholar]
- Parisotto, T.; Kasaei, H. MORE: Simultaneous Multi-View 3D Object Recognition and Pose Estimation. arXiv 2021, arXiv:2103.09863. [Google Scholar]
- Angrish, A.; Bharadwaj, A.; Starly, B. MVCNN++: Computer-Aided Design Model Shape Classification and Retrieval Using Multi-view Convolutional Neural Networks. J. Comput. Inf. Sci. Eng. 2021, 21, 1–11. [Google Scholar] [CrossRef]
- Steder, B.; Rusu, R.B.; Konolige, K.; Burgard, W. Point feature extraction on 3D range scans taking into account object boundaries. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2601–2608. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Jia, C.C.; Wang, C.J.; Yang, T.; Fan, B.H.; He, F.G. A 3D Point Cloud Filtering Algorithm based on Surface Variation Factor Classification. Procedia Comput. Sci. 2019, 154, 54–61. [Google Scholar] [CrossRef]
- Tuba, K.; BEŞDOK, E. 3-Dimensional Point Cloud Filtering Using Differential Evolution Algorithm. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 653–657. [Google Scholar]
- Zaman, F.; Wong, Y.P.; Ng, B.Y. Density-based Denoising of Point Cloud. arXiv 2016, arXiv:1602.05312. [Google Scholar]
- Zhong, Y. Intrinsic shape signatures: A shape descriptor for 3D object recognition. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 689–696. [Google Scholar]
- Rusu, R.; Blodow, N.; Márton, Z.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Rusu, R.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Salti, S.; Tombari, F.; Stefano, L.D. SHOT: Unique signatures of histograms for surface and texture description. Comput. Vis. Image Underst 2014, 125, 251–264. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE Features. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 214–227. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary robust independent elementary features. In Proceedings of the European Conference on Computer Vision (ECCV 2010), Heraklion, Crete, Greece, 5–11 September 2010; Volume 6314, pp. 778–792. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust invariant scalable keypoints. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2580–2593. [Google Scholar]
- Tola, E.; Lepetit, V.; Fua, P. DAISY: An Efficient Dense Descriptor Applied to Wide-Baseline Stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 815–830. [Google Scholar] [CrossRef] [Green Version]
- Yew, Z.J.; Gim, H.L. 3DFeat-Net: Weakly Supervised Local 3D Features for Point Cloud Registration. arXiv 2018, arXiv:1807.09413. [Google Scholar]
- Zeng, A.; Song, S.; Nießner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 199–208. [Google Scholar]
- Wang, Y.; Yang, B.; Chen, Y.; Liang, F.; Dong, Z. JoKDNet: A joint keypoint detection and description network for large-scale outdoor TLS point clouds registration. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 1–11. [Google Scholar] [CrossRef]
- Zang, Y.; Lindenbergh, R. An improved coherent point drift method for TLS point cloud registration of complex scenes. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, W13, 1169–1175. [Google Scholar] [CrossRef] [Green Version]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-points congruent sets for robust pairwise surface registration. In ACM SIGGRAPH 2008 Papers; ACM: San Antonio, TX, USA, 2008; pp. 1–10. [Google Scholar]
- Lu, F.; Chen, G.; Liu, Y.; Zhang, L.; Qu, S.; Liu, S.; Gu, R. HRegNet: A Hierarchical Network for Large-scale Outdoor LiDAR Point Cloud Registration. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 15994–16003. [Google Scholar]
- Ao, S.; Hu, Q.; Yang, B.; Markham, A.; Guo, Y. SpinNet: Learning a General Surface Descriptor for 3D Point Cloud Registration. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11753–11762. [Google Scholar]
- Jang, T.Y.; Hwang, S.S.; Kim, H.D.; Kim, S.D. Bounding volume estimation algorithm for image-based 3D object reconstruction. IEIE Trans. Smart Processing Comput. 2014, 3, 59–64. [Google Scholar] [CrossRef]
- Magnusson, M. The Three-Dimensional Normal-Distributions Transform: An Efficient Representation for Registration, Surface Analysis, and Loop Detection. Ph.D. Thesis, Örebro University, Örebro, Sweden, 2013. [Google Scholar]
- Dong, Z.; Yang, B.; Liu, Y.; Liang, F.; Li, B.; Zhang, Y. A novel binary shape context for 3D local surface description. ISPRS J. Photogramm. Remote Sens. 2017, 130, 431–452. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, B.; Liang, F.; Huang, R.; Scherer, S. Hierarchical registration of unordered TLS point clouds based on binary shape context descriptor. ISPRS J. Photogramm. Remote Sens. 2018, 144, 61–79. [Google Scholar] [CrossRef]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppä, J.; et al. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 163, 327–342. [Google Scholar] [CrossRef]





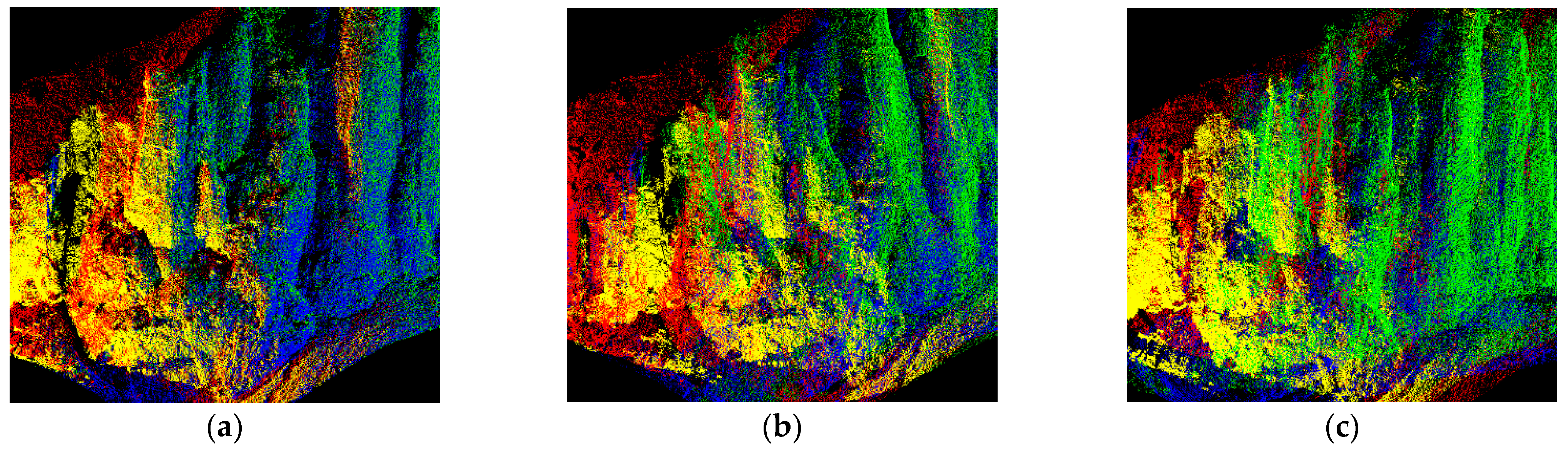

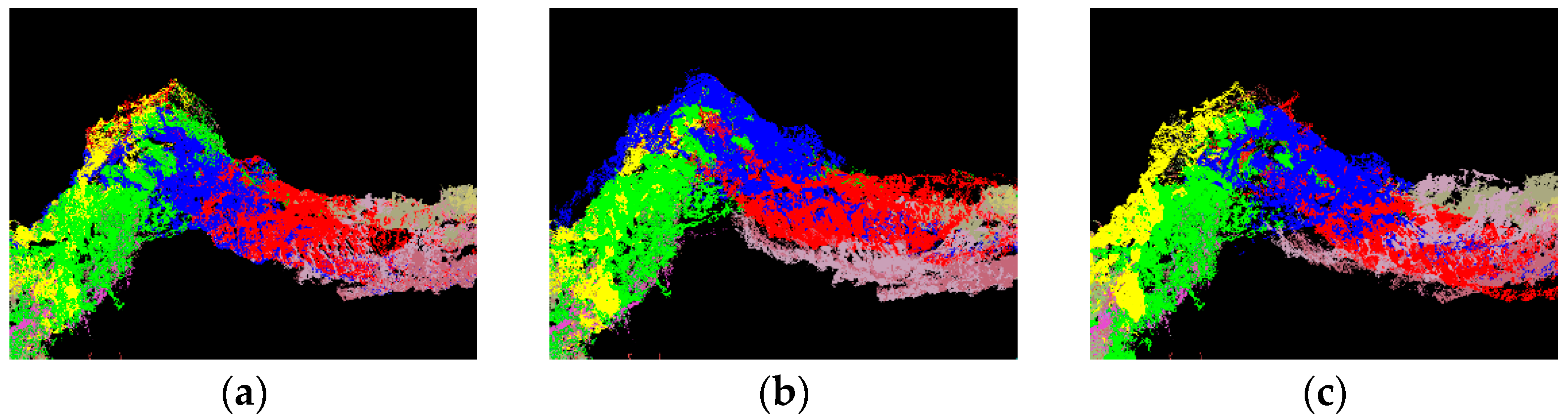



| Device | Import Data Time (s) | Iteration Time (s) |
|---|---|---|
| CPU: Platinum 8358Q | 17.91 | 1.412 |
| GPU: GTX 3080Ti | 18.42 | 0.257 |
| Point Cloud Data | Scan | Point Numbers |
|---|---|---|
| WHU-TLS Mountain [37,38,39] | 6 | 19,612,517 |
| Cliff Wall | 8 | 14,372,836 |
| Tangna Karst Cave | 21 | 45,164,268 |
| Haikou Forest | 4 | 9,615,756 |
| Registration Algorithm | Registration Time (s) | RMSE (m) |
|---|---|---|
| PC-MVCNN | 78.312 | 0.035 |
| Improved CPD [31] | 120.454 | 0.058 |
| PointNetLK [8] | 114.630 | 0.087 |
| 3D-NDT [36] | 155.718 | 0.064 |
| SAC + ICP [3] | 209.112 | 0.096 |
| Registration Algorithm | Registration Time (s) | RMSE (m) |
|---|---|---|
| PC-MVCNN | 104.506 | 0.041 |
| Improved CPD [31] | 177.622 | 0.065 |
| PointNetLK [8] | 210.815 | 0.094 |
| 3D-NDT [36] | 204.227 | 0.075 |
| SAC + ICP [3] | 231.855 | 0.091 |
| Registration Algorithm | Registration Time (s) | RMSE (m) |
|---|---|---|
| PC-MVCNN | 445.912 | 0.080 |
| Improved CPD [31] | 514.363 | 0.097 |
| PointNetLK [8] | 691.705 | 0.284 |
| 3D-NDT [36] | 556.711 | 0.352 |
| SAC + ICP [3] | 627.316 | 0.211 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Xia, Y.; Yang, M.; Wu, X. Study on TLS Point Cloud Registration Algorithm for Large-Scale Outdoor Weak Geometric Features. Sensors 2022, 22, 5072. https://doi.org/10.3390/s22145072
Li C, Xia Y, Yang M, Wu X. Study on TLS Point Cloud Registration Algorithm for Large-Scale Outdoor Weak Geometric Features. Sensors. 2022; 22(14):5072. https://doi.org/10.3390/s22145072
Chicago/Turabian StyleLi, Chen, Yonghua Xia, Minglong Yang, and Xuequn Wu. 2022. "Study on TLS Point Cloud Registration Algorithm for Large-Scale Outdoor Weak Geometric Features" Sensors 22, no. 14: 5072. https://doi.org/10.3390/s22145072
APA StyleLi, C., Xia, Y., Yang, M., & Wu, X. (2022). Study on TLS Point Cloud Registration Algorithm for Large-Scale Outdoor Weak Geometric Features. Sensors, 22(14), 5072. https://doi.org/10.3390/s22145072







