Design of a Fiber Bragg Grating Pressure Sensor Based on a Metal Diaphragm and Lever Structure
Abstract
:1. Introduction
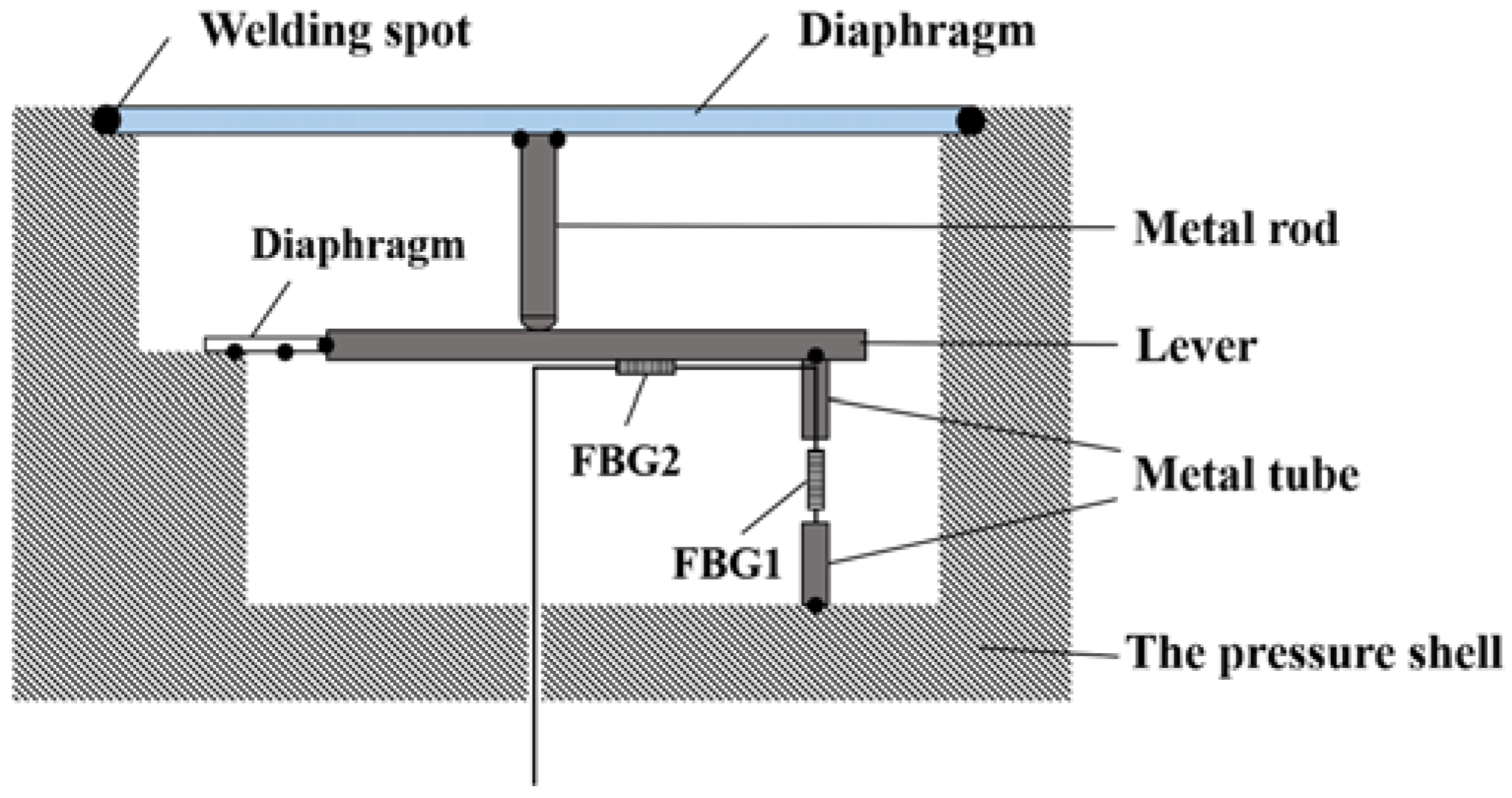
2. Structural Design and Principle
2.1. Principle of Temperature Compensation
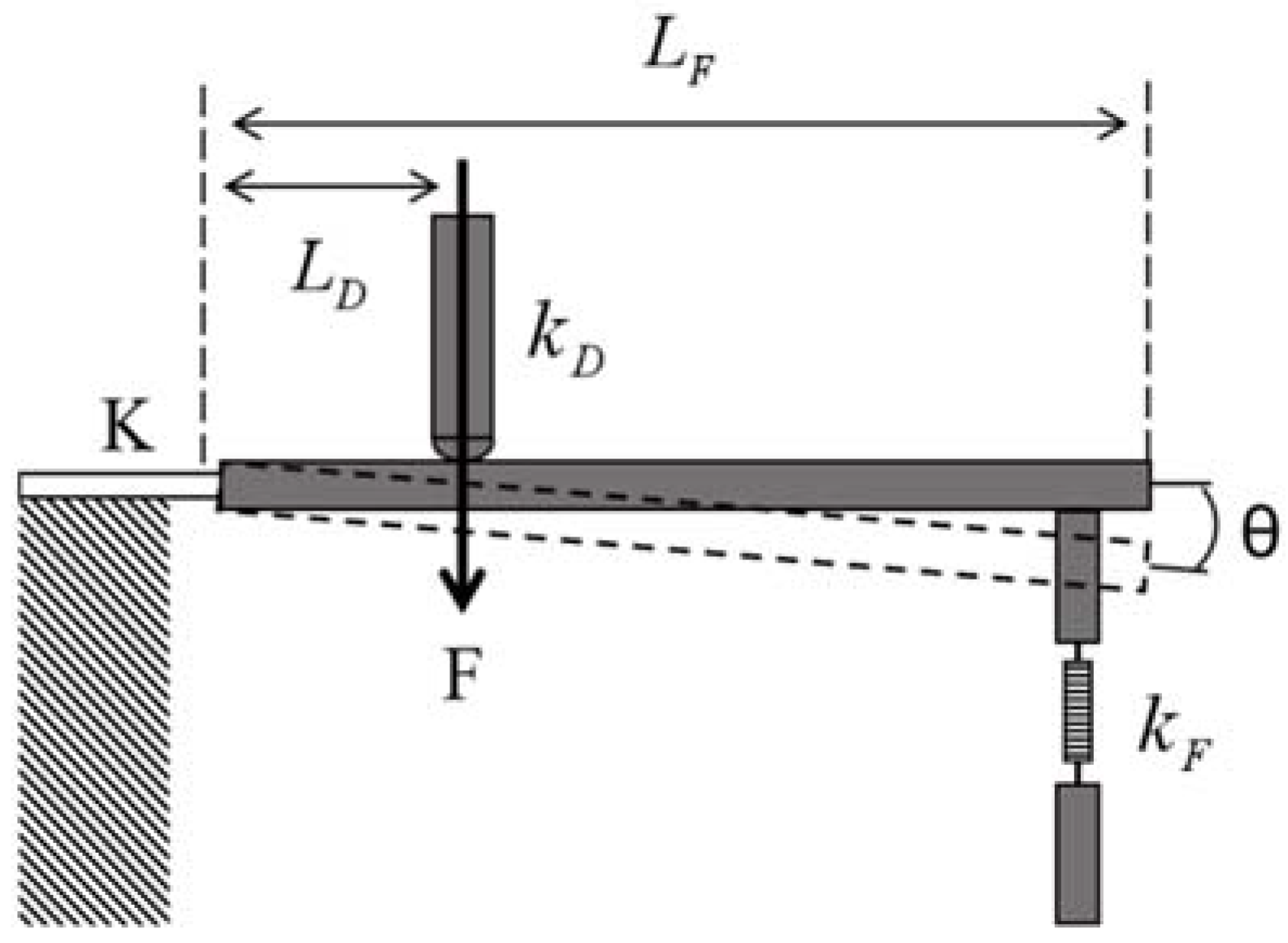
2.2. The Principle of Pressure Sensing
3. Simulation and Analysis
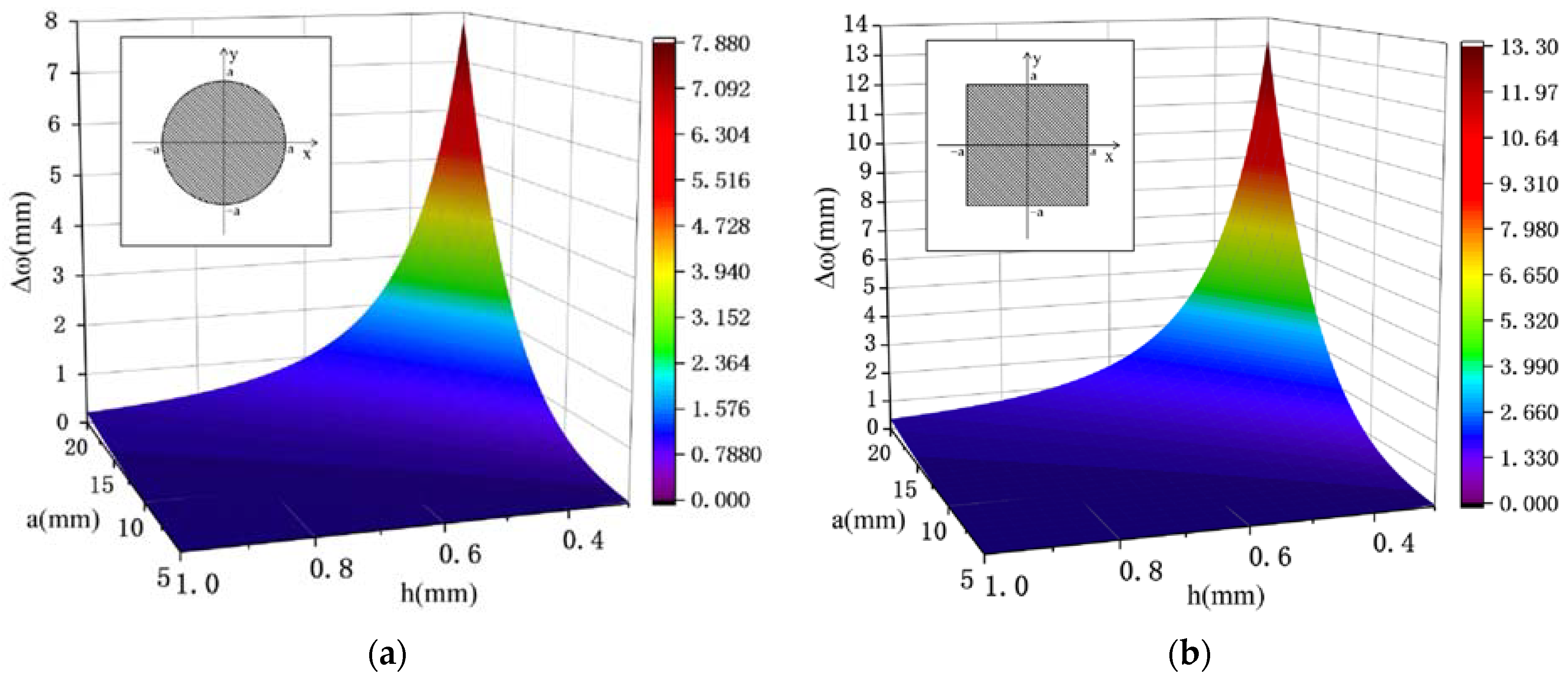
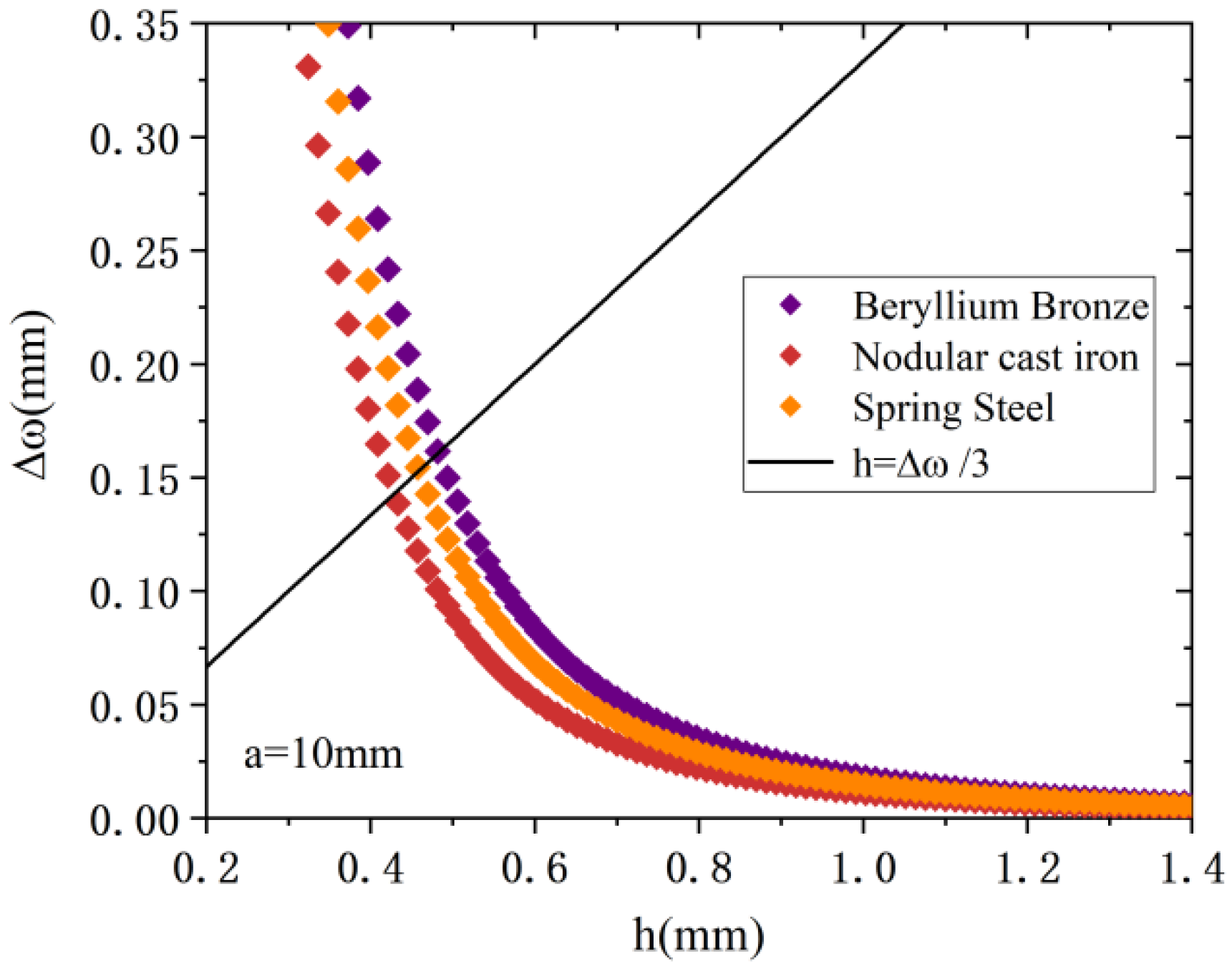
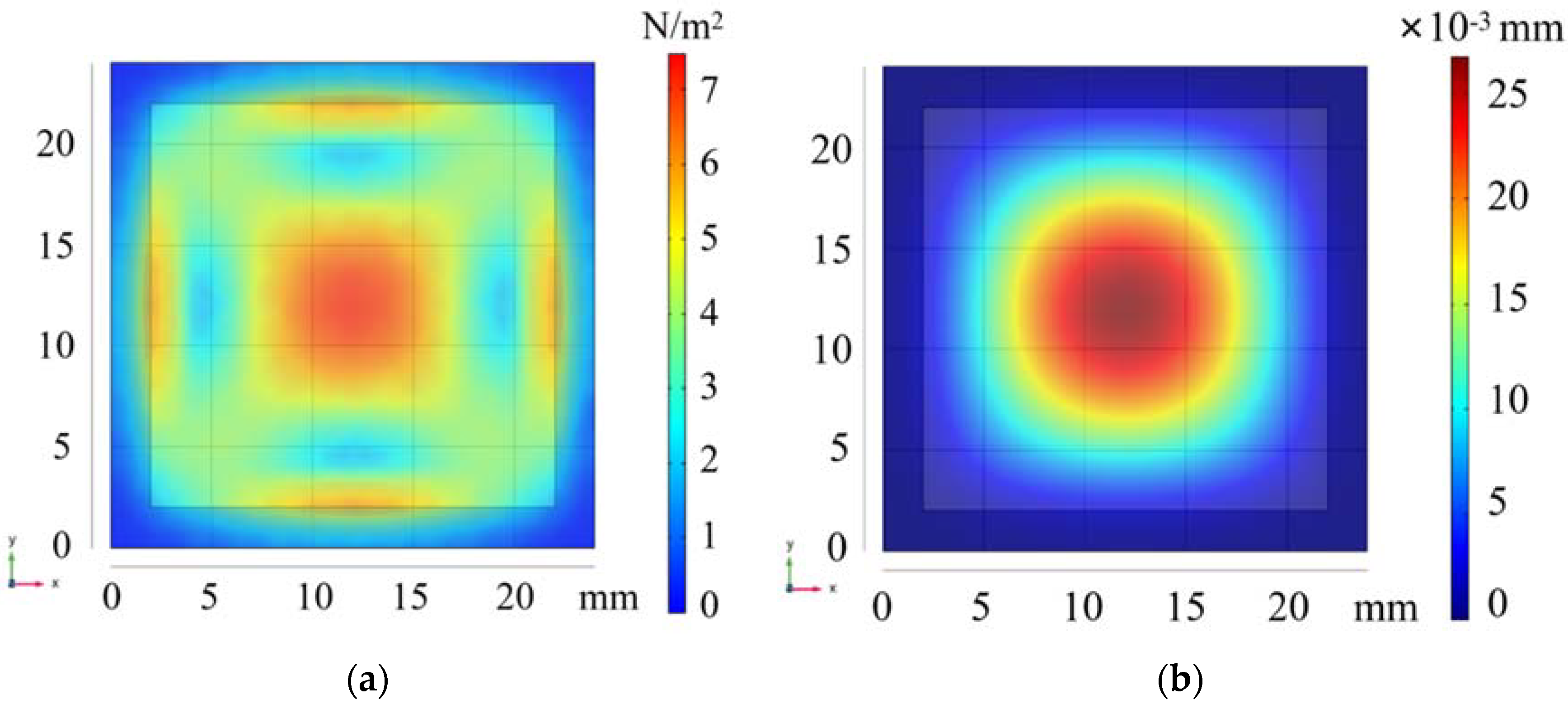
3.1. Analysis of the Metal Film Sheet
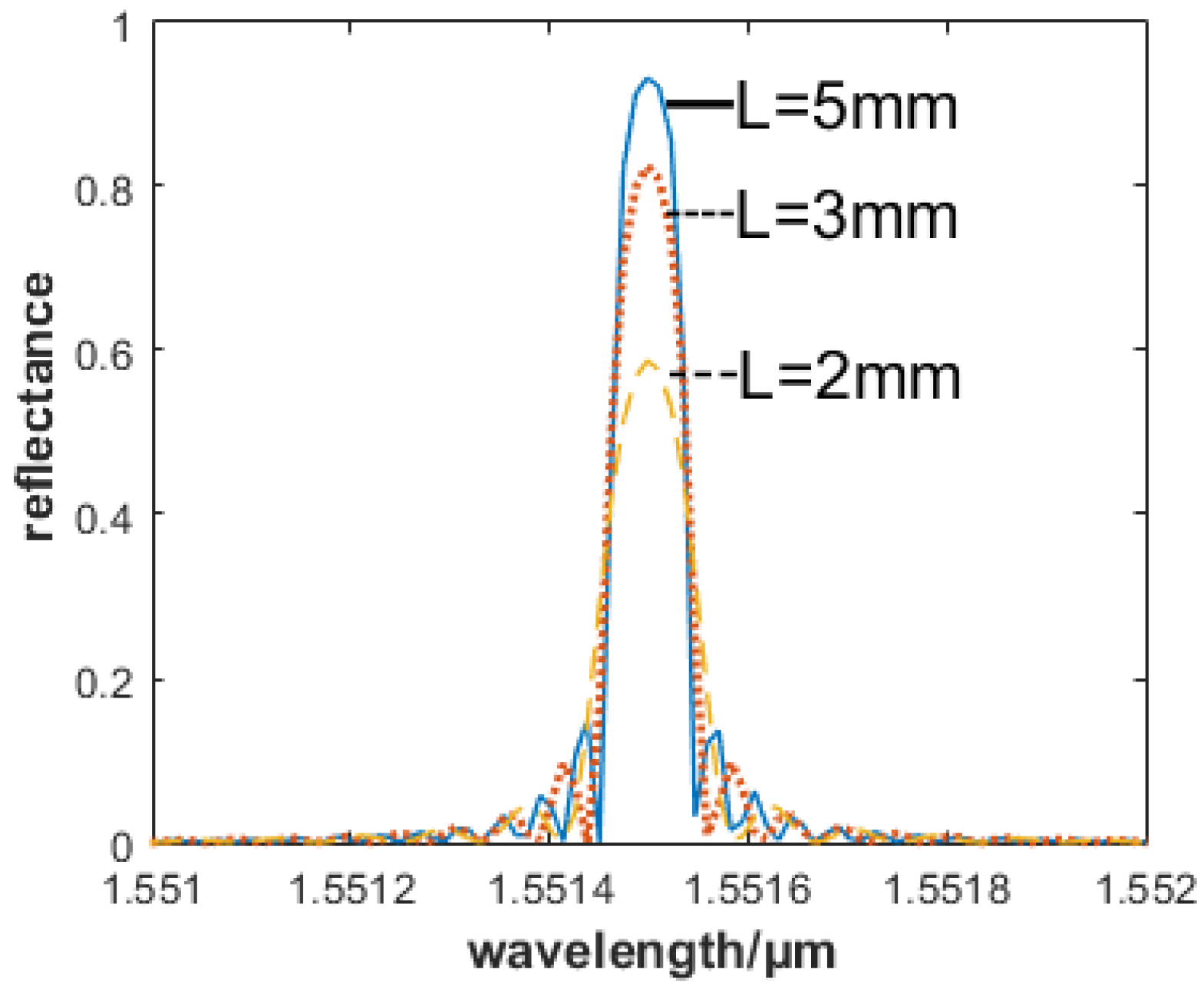
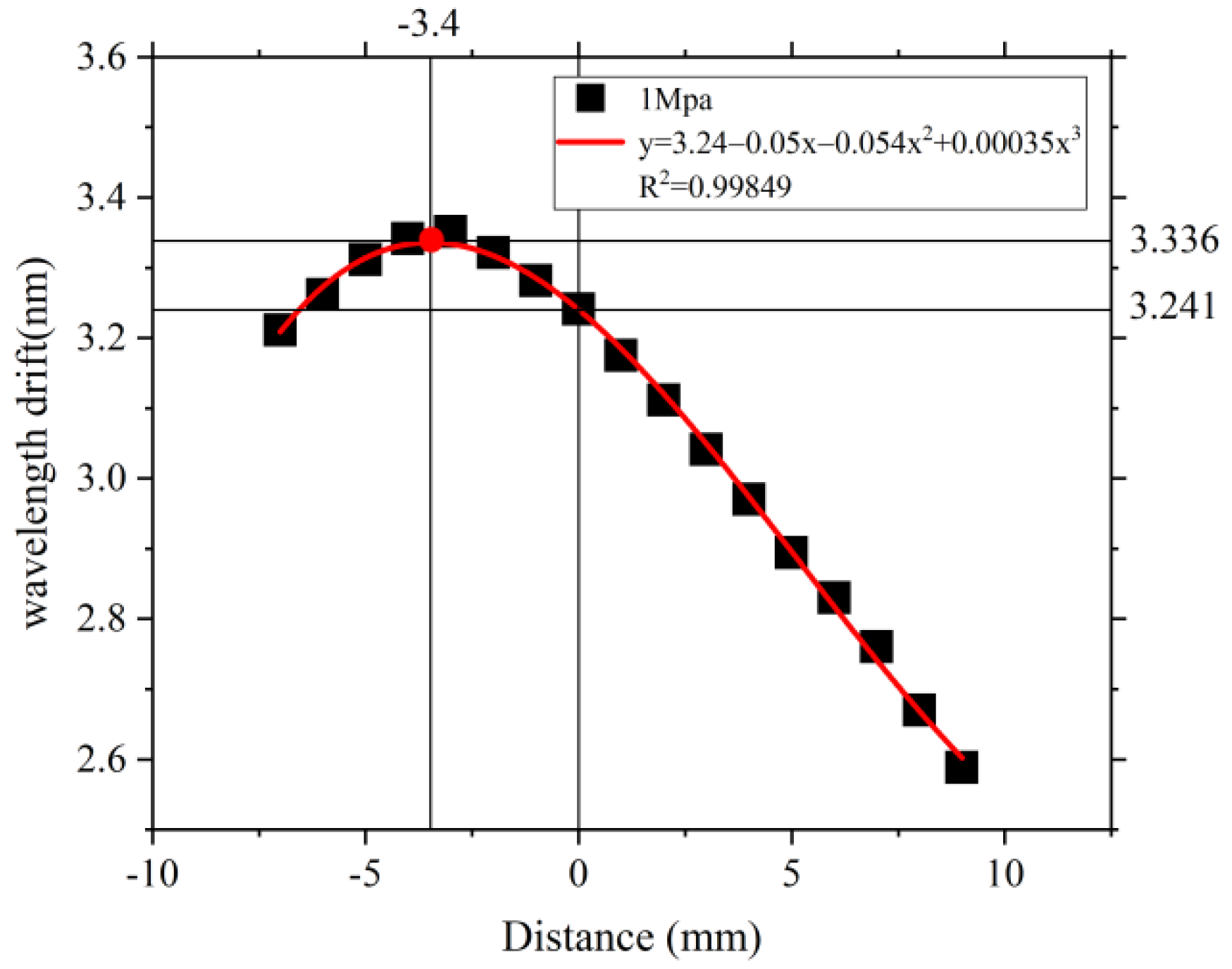
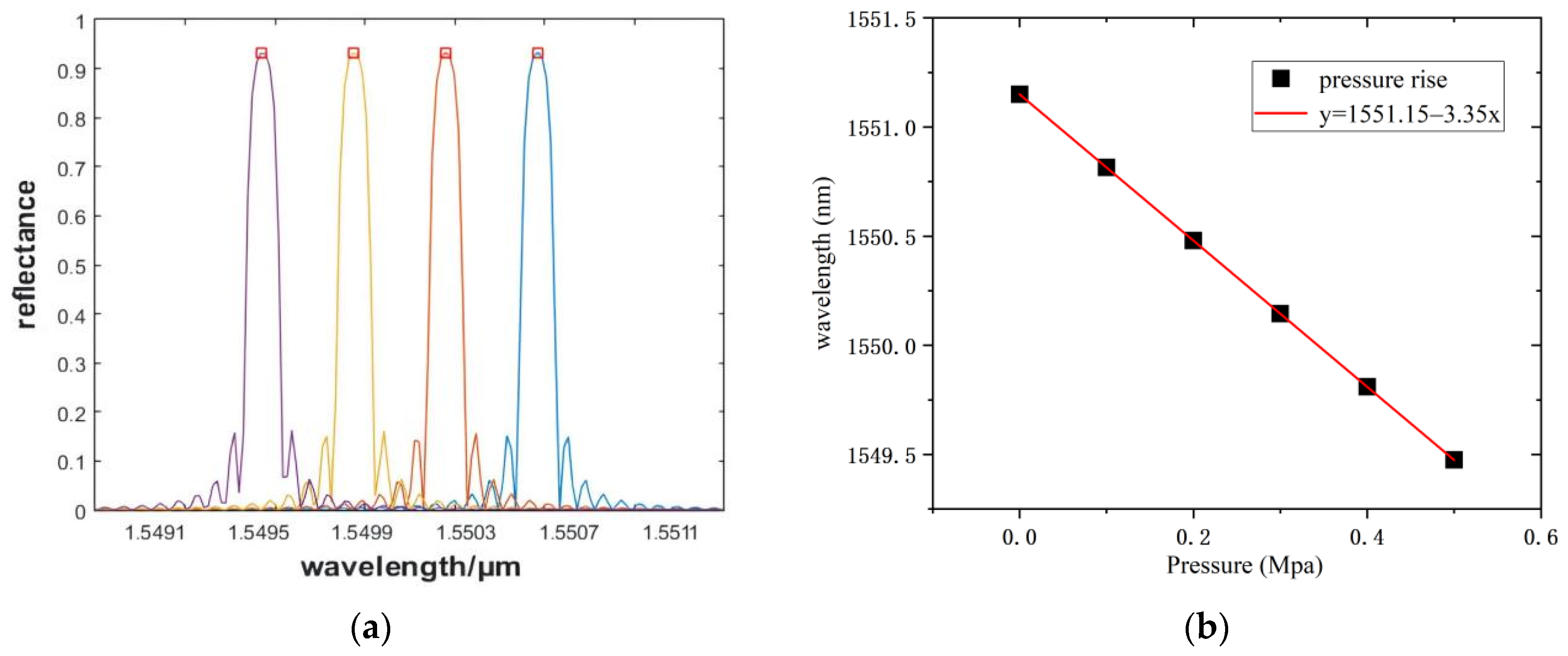
3.2. Sensing Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mihailov, S.J. Fiber bragg grating sensors for harsh environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed]
- Lee, B. Review of the present status of optical fifiber sensors. Opt. Fiber. Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Allwood, G.; Wild, G.; Lubansky, A.; Hinckley, S. A highly sensitive fifiber bragg grating diaphragm pressure transducer. Opt. Fiber. Technol. 2015, 25, 25–32. [Google Scholar] [CrossRef]
- Chen, Z.G.; Zhong, X.R.; Lian, X.J.; Niu, J.F. Leakage detection in pipelines based on bragg fifiber technique. Appl. Mech. Mater. 2014, 687–691, 929–933. [Google Scholar] [CrossRef]
- Guo, H.; Xiao, G.; Mrad, N.; Yao, J. Fiber optic sensors for structural health monitoring of air platforms. Sensors 2011, 11, 3687–3705. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yuan, W.; Sun, Y.; Lei, G.; Zhang, Z.; Zhang, W.; Zhao, P.; Yin, Y. Using custom fifiber bragg grating-based sensors to monitor artifificial landslides. Sensors 2016, 16, 1417. [Google Scholar] [CrossRef]
- Zhao, Z.G.; Zhang, Y.J.; Li, C.; Wan, Z.; Li, Y.N.; Wang, K.; Xu, J.F. Monitoring of coal mine roadway roof separation based on fifiber bragg grating displacement sensors. Int. J. Rock Mech. Min. 2015, 74, 128–132. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, Z.; Zhang, D.; Chen, J.; Li, L.; Deng, X. Design and application of a fiber Bragg grating tension sensor for anchor rope. Adv. Mech. Eng. 2013, 5, 125404. [Google Scholar] [CrossRef]
- Luo, Y.T.; Wang, H.B.; Ma, G.M.; Song, H.T.; Li, C.; Jiang, J. Research on high sensitive D-shaped FBG hydrogen sensors in power transformer oil. Sensors 2016, 16, 1641. [Google Scholar] [CrossRef] [Green Version]
- Shiryayev, O.; Vahdati, N.; Yap, F.F.; Butt, H. Compliant Mechanism-Based Sensor for Large Strain Measurements Employing Fiber Optics. Sensors 2022, 22, 3987. [Google Scholar] [CrossRef] [PubMed]
- Lesiak, P.; Pogorzelec, K.; Bochenek, A.; Sobotka, P.; Bednarska, K.; Anuszkiewicz, A.; Osuch, T.; Sienkiewicz, M.; Marek, P.; Nawotka, M.; et al. Three-Dimensional-Printed Mechanical Transmission Element with a Fiber Bragg Grating Sensor Embedded in a Replaceable Measuring Head. Sensors 2022, 22, 3381. [Google Scholar] [CrossRef]
- Liang, M.; Fang, X.; Wu, G.; Xue, G.-Z.; Li, H.-W. A fiber Bragg grating pressure sensor with temperature compensation based on diaphragm-cantilever structure. Optik 2017, 145, 503–512. [Google Scholar] [CrossRef]
- Zhao, Q.; Zheng, H.-K.; Lv, R.-Q.; Gu, Y.-F.; Zhao, Y.; Yang, Y. Novel integrated optical fiber sensor for temperature, pressure and flow measurement. Sens. Actuators A Phys. 2018, 280, 68–75. [Google Scholar] [CrossRef]
- Pachava, V.R.; Kamineni, S.; Madhuvarasu, S.S.; Putha, K.; Mamidi, V.R. FBG based high sensitive pressure sensor and its low-cost interrogation system with enhanced resolution. Photonic Sens. 2015, 5, 321–329. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Zhao, Y.; Lv, R.; Yang, Y. A practical FBG sensor based on a thin-walled cylinder for hydraulic pressure measurement. IEEE Photon. Technol. Lett. 2016, 28, 2569–2572. [Google Scholar] [CrossRef]
- Wei, Z.; Song, D.; Zhao, Q.; Cui, H. High pressure sensor based on fiber Bragg grating and carbon fiber laminated composite. IEEE Sens. J. 2008, 8, 1615–1619. [Google Scholar] [CrossRef]
- Song, D.; Wei, Z.; Zou, J.L.; Cui, H. Pressure sensor based on fiber Bragg grating and carbon fiber ribbon-wound composite cylindrical shell. IEEE Sens. J. 2009, 9, 828–831. [Google Scholar] [CrossRef]
- Diaz, C.A.R.; Leal-Junior, A.G.; Andre, P.S.B.; Antunes, P.F.d.C.; Pontes, M.J.; Frizera-Neto, A.; Riberiro, M.R.N. Liquid level measurement based on FBG-embedded diaphragms with temperature compensation. IEEE Sens. J. 2018, 18, 193–200. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera, A.; Díaz, C.; Marques, C.; Ribeiro, M.; Pontes, M.J. Material features based compensation technique for the temperature effffects in a polymer diaphragm-based FBG pressure sensor. Opt. Express 2018, 26, 20590. [Google Scholar] [CrossRef]
- Vorathin, E.; Hafifizi, Z.M.; Aizzuddin, A.M.; Lim, K.S. A natural rubber diaphragm based transducer for simultaneous pressure and temperature measurement by using a single FBG. Opt. Fiber Technol. 2018, 45, 8–13. [Google Scholar] [CrossRef]
- Yuan, W.; Khan, L.; Webb, D.J.; Kalli, K.; Rasmussen, H.K.; Stefani, A.; Bang, O. Humidity insensitive TOPAS polymer fiber Bragg grating sensor. Opt. Express 2011, 19, 19731–19739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, C.C.; Dulieu-Barton, J.M.; Webb, D.J.; Zhang, C.; Peng, G.D.; Chambers, A.R.; Lennard, F.J.; Eastop, D.D. Applications of polymer optical fiber grating sensors to condition monitoring of textiles. J. Phys. Conf. Ser. 2009, 178, 012020. [Google Scholar] [CrossRef] [Green Version]
- Hegde, G.; Prasad, M.V.N.; Asokan, S. Temperature compensated diaphragm based Fiber Bragg Grating (FBG) sensor for high pressure measurement for space applications. Microelectron. Eng. 2021, 248, 111615. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Wang, J.; Li, F. A high spatial resolution FBG sensor array for measuring ocean temperature and depth. Photonic Sens. 2020, 10, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Jia, Z.; Fan, Q.; Feng, D.; Yu, D.; Zhao, X.; Yang, K. Design and investigation of the fiber Bragg grating pressure sensor based on square diaphragm and truss-beam structure. Opt. Eng. 2019, 58, 097109. [Google Scholar] [CrossRef]
- Fan, Q.; Feng, D.; Yong, Z. Highly sensitive FBG pressure sensor based on square diaphragm. Optik 2021, 225, 165559. [Google Scholar] [CrossRef]

| Material | Spring Steel | Beryllium Bronze | Nodular Cast Iron |
|---|---|---|---|
| Young’s modulus/105 MPa | 2.06 | 1.24 | 1.59 |
| Poisson ratio | 0.3 | 0.35 | 0.28 |
| Parameter | P/MPa | E/105 MPa | μ | a/mm | h/mm | /nm | L/mm | x/mm | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 1.0 | 0.22 | 1.24 | 0.35 | 10 | 0.5 | 1551.15 | 10 | 3 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zeng, L.; Xu, K.; Li, Z.; Chen, H.; Qiao, Z.; Qu, Y.; Liu, G.; Li, L. Design of a Fiber Bragg Grating Pressure Sensor Based on a Metal Diaphragm and Lever Structure. Sensors 2022, 22, 5096. https://doi.org/10.3390/s22145096
Liu Z, Zeng L, Xu K, Li Z, Chen H, Qiao Z, Qu Y, Liu G, Li L. Design of a Fiber Bragg Grating Pressure Sensor Based on a Metal Diaphragm and Lever Structure. Sensors. 2022; 22(14):5096. https://doi.org/10.3390/s22145096
Chicago/Turabian StyleLiu, Zhaoyue, Lina Zeng, Ke Xu, Zaijin Li, Hao Chen, Zhongliang Qiao, Yi Qu, Guojun Liu, and Lin Li. 2022. "Design of a Fiber Bragg Grating Pressure Sensor Based on a Metal Diaphragm and Lever Structure" Sensors 22, no. 14: 5096. https://doi.org/10.3390/s22145096
APA StyleLiu, Z., Zeng, L., Xu, K., Li, Z., Chen, H., Qiao, Z., Qu, Y., Liu, G., & Li, L. (2022). Design of a Fiber Bragg Grating Pressure Sensor Based on a Metal Diaphragm and Lever Structure. Sensors, 22(14), 5096. https://doi.org/10.3390/s22145096






