One-Step Initial Alignment Algorithm for SINS in the ECI Frame Based on the Inertial Attitude Measurement of the CNS
Abstract
:1. Introduction
- The high-precision attitude measured by the CNS is used as the reference information for the initial alignment. Compared with the traditional initial alignment algorithm, the algorithm proposed in this paper has better performance in alignment accuracy, speed, and stability.
- Compared with the alignment dynamic model in the navigation frame, the model established in the ECI frame is more simplified and avoids the influence of the approximate error caused by the dynamic deflection angle.
- The attitude matching algorithm in the ECI frame proposed in this paper is independent of position parameters and can be used for both dynamic and static conditions.
- Based on the attitude matching algorithm, the velocity measurement information is added to the optimal estimation process to form the attitude and velocity matching algorithm, which further improves the accuracy and speed of the initial alignment under static conditions.
- The hull deformation is considered in the attitude optimal estimation, which can realize a fast and high-precision initial alignment of the SINS installed in various parts of the carrier.
- The CNS is immune to electromagnetic interference and has no navigation error accumulation over time, such as SINS, so the algorithms based on the CNS have important military application values and wider applicability.
2. Frame Definition and Composition of the Initial Alignment System
3. Attitude Measurement Principle of the CNS
4. Initial Alignment Model in the Navigation Frame
5. Attitude Matching Initial Alignment Algorithm in the ECI Frame
5.1. Attitude Error Equation in the ECI Frame
5.2. Dynamic Deflection Deformation Model
5.3. Attitude Measurement Model
5.4. The Kalman Filter for the Attitude Matching Algorithm
5.4.1. The State Equation
5.4.2. The Measurement Equation
6. Attitude and Velocity Matching Algorithm in the ECI Frame
6.1. Velocity Error Equation in the ECI Frame
6.2. The Kalman Filter for the Attitude and Velocity Matching Algorithm
6.2.1. The State Equation
6.2.2. The Measurement Equation
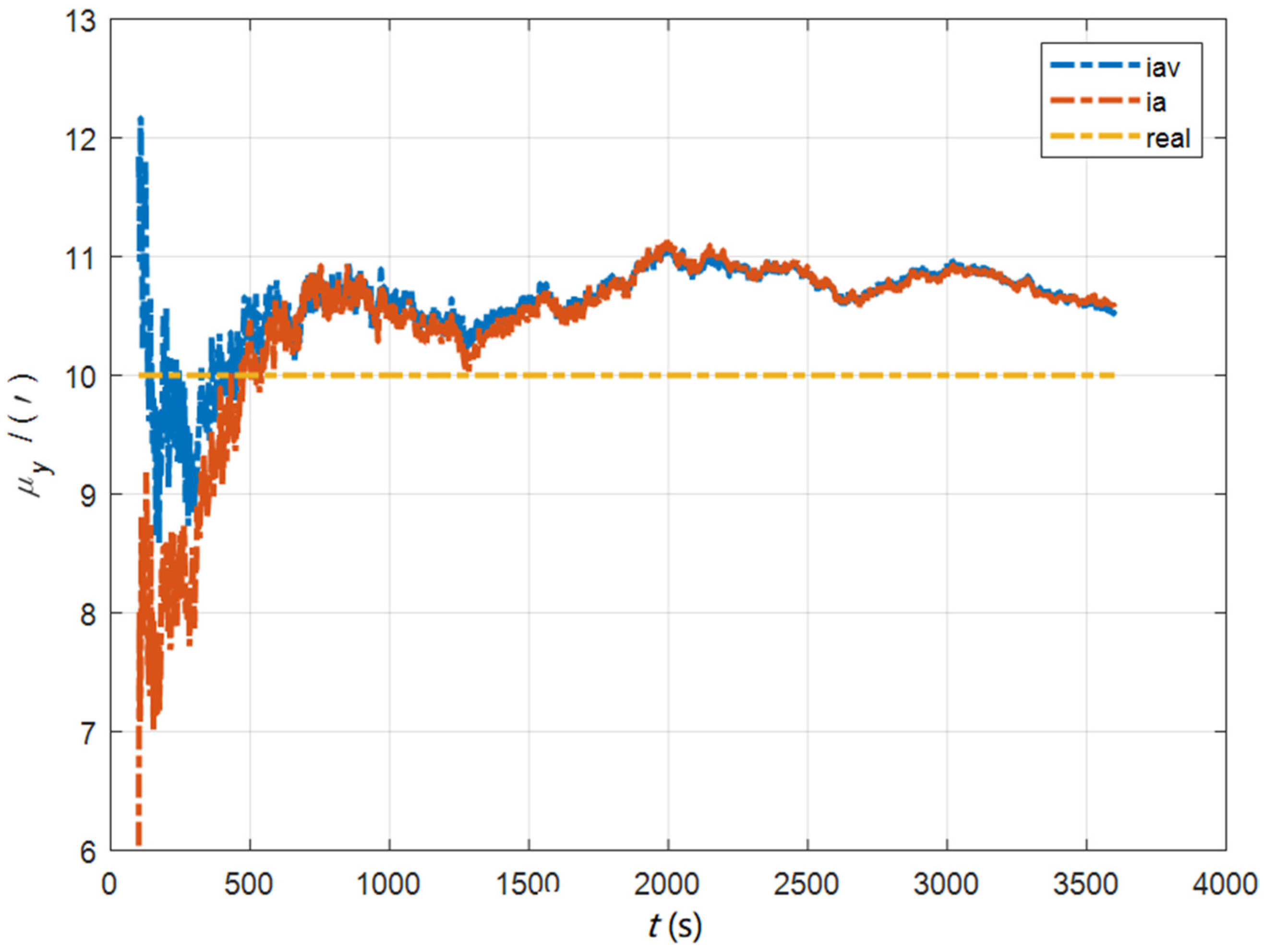
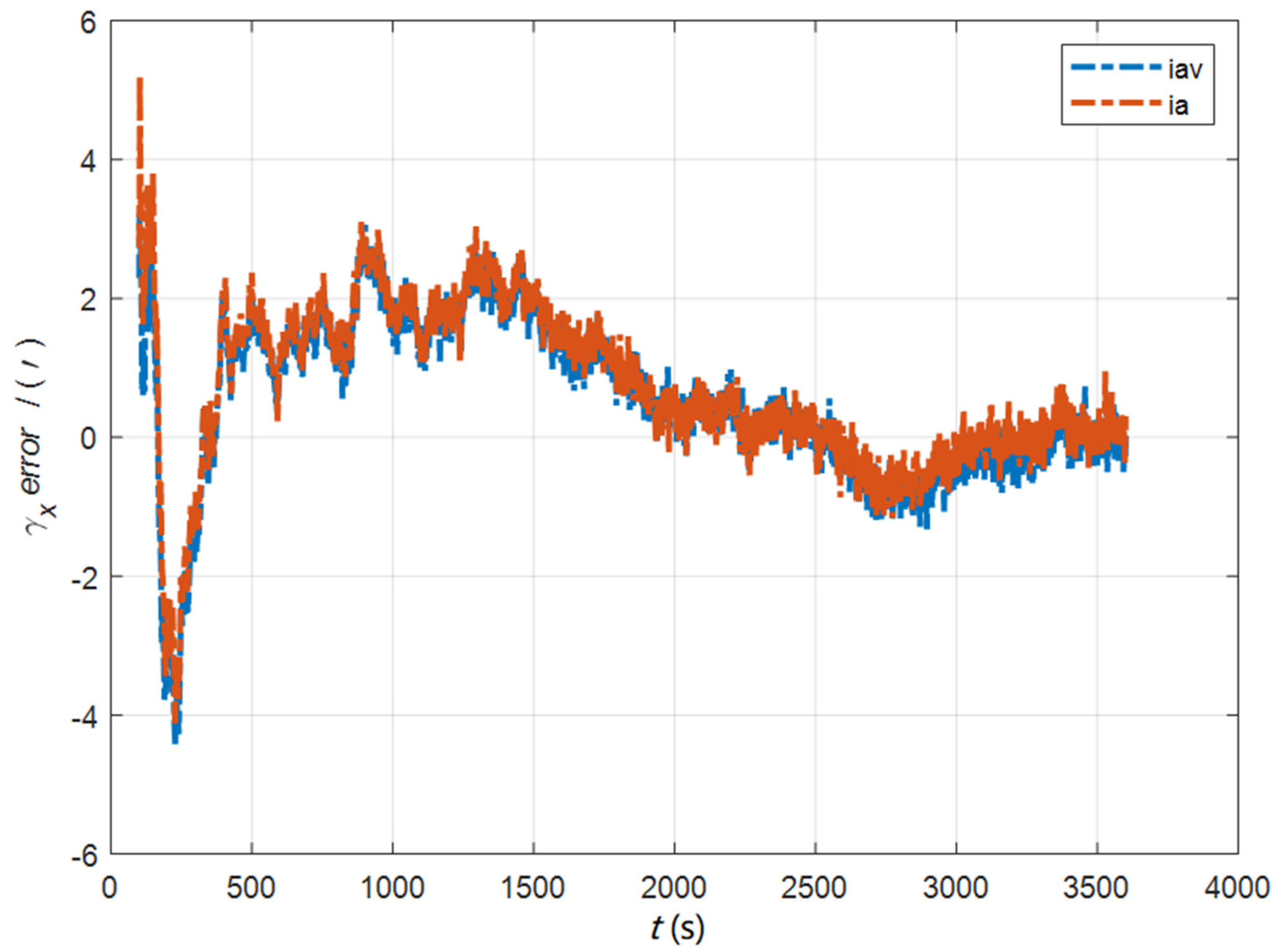
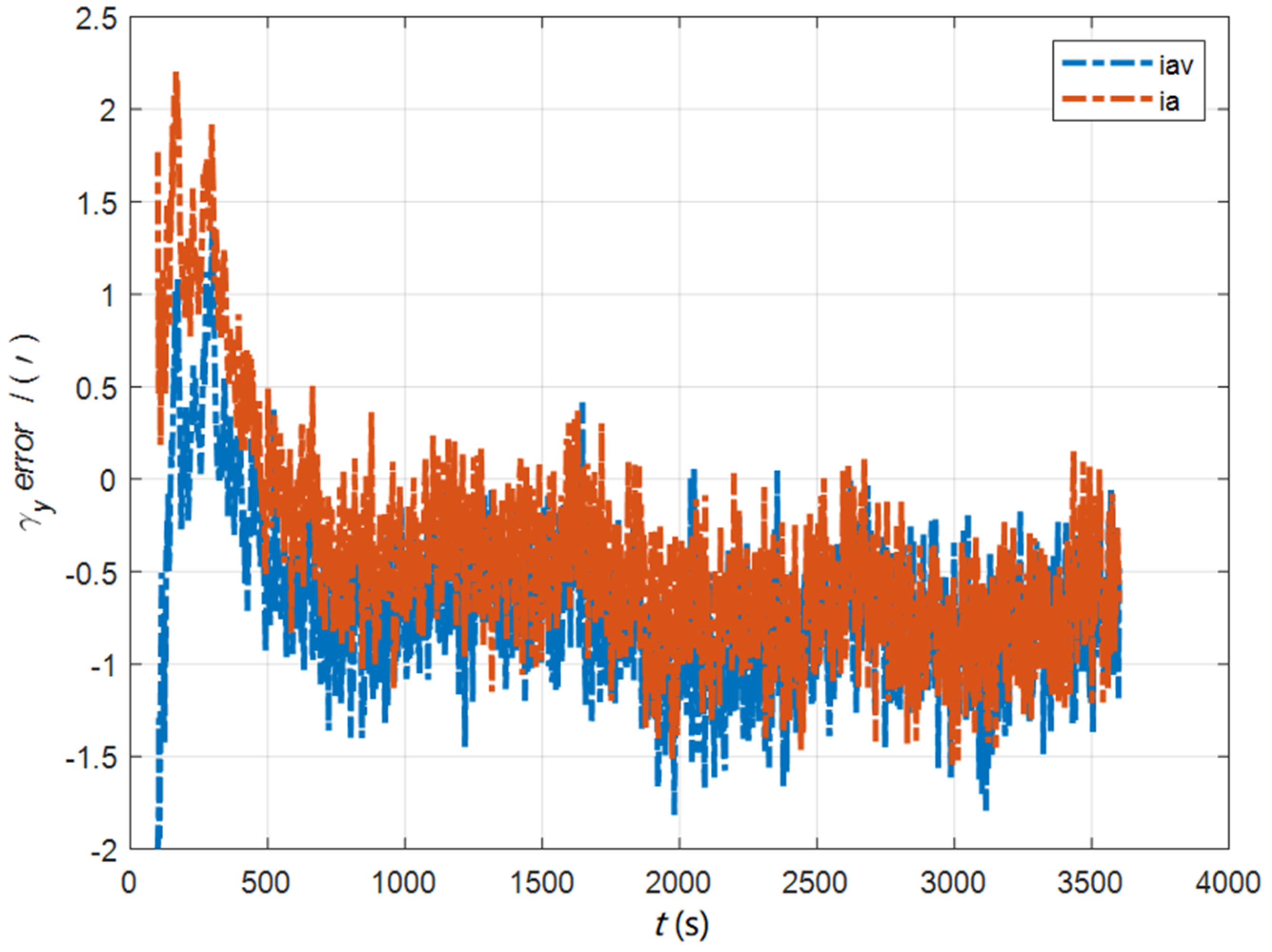
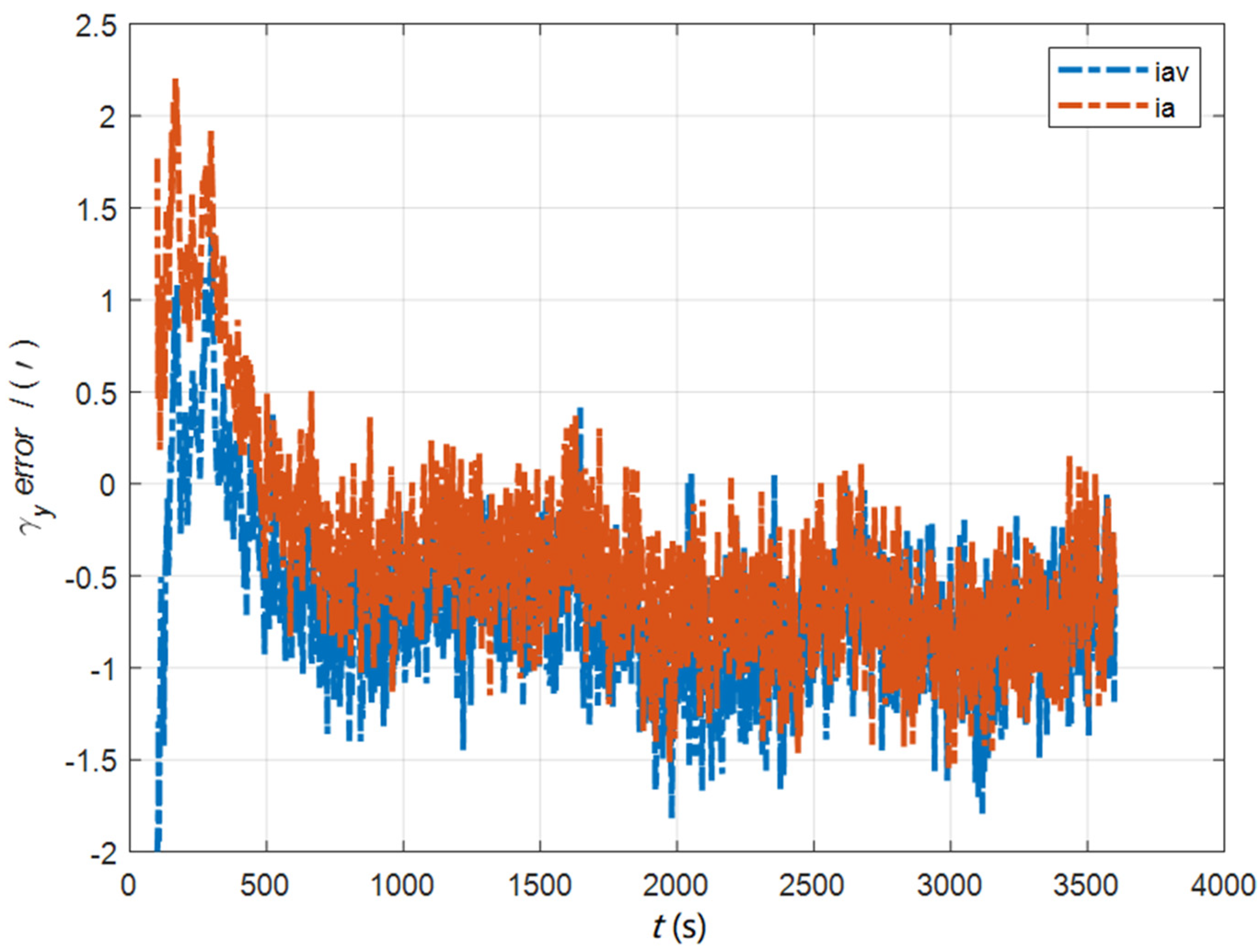
7. Experimental Verification and Discussion
7.1. The Simulation Experiment for the Initial Alignment
7.1.1. The Simulation Experiment for the Initial Alignment in Quasi-Static Swing Base
7.1.2. The Simulation Experiment for the Initial Alignment in the Dynamic Swing Base
7.2. The Simulation Experiment for Deformation Measurement
7.2.1. The Simulation Experiment for Deformation Measurement in Quasi-Static Swing Base
7.2.2. The Simulation Experiment for Deformation Measurement in the Dynamic Swing Base
8. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Titterton, D.H.; Weston, J.L. Strapdown Inertial Navigation Technology: The Institute of Electrical Engineers, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems; Artech House: Norwood, MA, USA, 2008. [Google Scholar]
- Chang, L.; Li, J.; Chen, S. Initial alignment by attitude estimation for strapdown inertial navigation systems. IEEE Trans. Instrum. Meas. 2014, 64, 784–794. [Google Scholar] [CrossRef]
- Li, J.; Xu, J.; Chang, L.; Zha, F. An improved optimal method for initial alignment. J. Navig. 2014, 67, 727–736. [Google Scholar] [CrossRef]
- Fu, Q.; Liu, Y.; Liu, Z.; Li, S.; Guan, B. Autonomous in-motion alignment for land vehicle strapdown inertial navigation system without the aid of external sensors. J. Navig. 2018, 71, 1312–1328. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Li, Y.; Fang, J. Anti-disturbance initial alignment method based on quadratic integral for airborne distributed POS. IEEE Sens. J. 2018, 18, 4536–4543. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Wang, J. Research on initial alignment and self-calibration of rotary strapdown inertial navigation systems. Sensors 2015, 15, 3154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiancheng, F.; Sheng, Y. Study on innovation adaptive EKF for in-flight alignment of airborne POS. IEEE Trans. Instrum. Meas. 2011, 60, 1378–1388. [Google Scholar] [CrossRef]
- Chang, L.B.; Hu, B.; Li, A.; Qin, F. Strapdown inertial navigation system alignment based on marginalised unscented Kalman filter. IET Sci. Meas. Technol. 2013, 7, 128–138. [Google Scholar] [CrossRef]
- Chang, L.; Hu, B.; Li, Y. Backtracking integration for fast attitude determination-based initial alignment. IEEE Trans. Instrum. Meas. 2014, 64, 795–803. [Google Scholar] [CrossRef]
- Chang, L.; Li, J.; Li, K. Optimization-based alignment for strapdown inertial navigation system: Comparison and extension. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1697–1713. [Google Scholar] [CrossRef]
- Chang, L.; Zha, F.; Qin, F. Indirect Kalman filtering based attitude estimation for low-cost attitude and heading reference systems. IEEE/ASME Trans. Mechatron. 2017, 22, 1850–1858. [Google Scholar] [CrossRef]
- Chang, L.; Qin, F.; Li, A. A novel backtracking scheme for attitude determination-based initial alignment. IEEE Trans. Autom. Sci. Eng. 2014, 12, 384–390. [Google Scholar] [CrossRef]
- Chang, L.; Hu, B.; Chang, G. Modified unscented quaternion estimator based on quaternion averaging. J. Guid. Control Dyn. 2014, 37, 305–309. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, B.; Chang, L.; Xue, B.Y. Nonlinear Initial Alignment based on Quaternion Error Model. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–6. [Google Scholar]
- Chang, L.; Qin, F.; Xu, J. Strapdown Inertial Navigation System Initial Alignment Based on Group of Double Direct Spatial Isometries. IEEE Sens. J. 2021, 22, 803–818. [Google Scholar] [CrossRef]
- Luo, L.; Huang, Y.; Zhang, Z.; Zhang, Y. A new Kalman filter-based in-motion initial alignment method for DVL-aided low-cost SINS. IEEE Trans. Veh. Technol. 2021, 70, 331–343. [Google Scholar] [CrossRef]
- Chang, L.; Li, Y.; Xue, B. Initial alignment for a Doppler velocity log-aided strapdown inertial navigation system with limited information. IEEE/ASME Trans. Mechatron. 2016, 22, 329–338. [Google Scholar] [CrossRef]
- Chang, L.; He, H.; Qin, F. In-motion initial alignment for odometer-aided strapdown inertial navigation system based on attitude estimation. IEEE Sens. J. 2016, 17, 766–773. [Google Scholar] [CrossRef]
- Wang, B.; Ye, W.; Liu, Y. An improved real-time transfer alignment algorithm based on adaptive noise estimation for distributed POS. IEEE Access 2020, 8, 102119–102127. [Google Scholar] [CrossRef]
- Xu, X.; Guo, Z.; Yao, Y.; Zhang, T. Robust initial alignment for SINS/DVL based on reconstructed observation vectors. IEEE/ASME Trans. Mechatron. 2020, 25, 1659–1667. [Google Scholar] [CrossRef] [Green Version]
- Han, S.; Wang, J. A novel initial alignment scheme for low-cost INS aided by GPS for land vehicle applications. J. Navig. 2010, 63, 663–680. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Chang, L. A new fast in-motion coarse alignment method for GPS-aided low-cost SINS. IEEE/ASME Trans. Mechatron. 2018, 23, 1303–1313. [Google Scholar] [CrossRef]
- Lu, Y. Study of CNS/INS Integrated Navigation System Based on Speed Damping Technology. Opt. Optoelectron. Technol. 2012, 10, 62–67. [Google Scholar]
- Qi, Z. Research on the Key Technology of Warship SINS/CNS/DVL Integrated Navigation System. Ph.D. Thesis, Dept. Automation. Eng. Harbin Engineering Univ., Harbin, China, 2015. [Google Scholar]
- Li, D.; Wang, Q.; Liu, C.; Zhu, Z. Application of SINS/CNS/DNS integrated navigation in ship navigation system. J. Nanjing Univ. Inf. Sci. Technol. (Nat. Sci. Ed.) 2014, 6, 321–325. [Google Scholar]
- Chen, W.; Yang, Z.; Gu, S.; Wang, Y.; Tang, Y. Adaptive transfer alignment method based on the observability analysis for airborne pod strapdown inertial navigation system. Sci. Rep. 2022, 12, 946. [Google Scholar] [CrossRef] [PubMed]
- Ju, H.; Cho, S.Y.; Park, C.G. The Effectiveness of Acceleration Matching According to the Sensor Performance in Shipboard Rapid Transfer Alignment. J. Navig. 2020, 73, 1–15. [Google Scholar] [CrossRef]
- Geng, X.; Tang, K.; Wu, M. Design of a fast transfer alignment matching algorithm. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1654, p. 012088. [Google Scholar]
- Wang, Q.; Li, Y.; Diao, M.; Gao, W.; Qi, Z. Performance Enhancement of INS/CNS Integration Navigation System Based on Particle Swarm Optimization Back Propagation Neural Network. Ocean Eng. 2015, 108, 33–45. [Google Scholar] [CrossRef]
- Du, H.; Cao, Y.; Hao, Q.; Yin, H.; Yang, M. The federated filtering algorithm based on INS/GPS/CNS. Ship Sci. Technol. 2018, 40, 128–131. [Google Scholar]
- He, Z.; Qin, S.; Wang, S.; Tan, W.; Liu, D. Star Sensor Technology Applications and Future Trends in the Field of Unmanned Combat. J. Ordnance Equip. Eng. 2016, 37, 137–141. [Google Scholar]
- He, Y.; Peng, X.; Zhang, X.; Hu, X. A model-free hull deformation measurement method with time delay compensation. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718810695. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, D.; Tong, J. A hull deformation measurement method based on fiber optic gyro angular rate matching in complex sea conditions. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 236, 34–47. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Peng, X.; Hu, X.; Xu, D. Research on hull deformation measurement for large azimuth misalignment angle based on attitude quaternion. Optik 2019, 182, 159–169. [Google Scholar] [CrossRef]


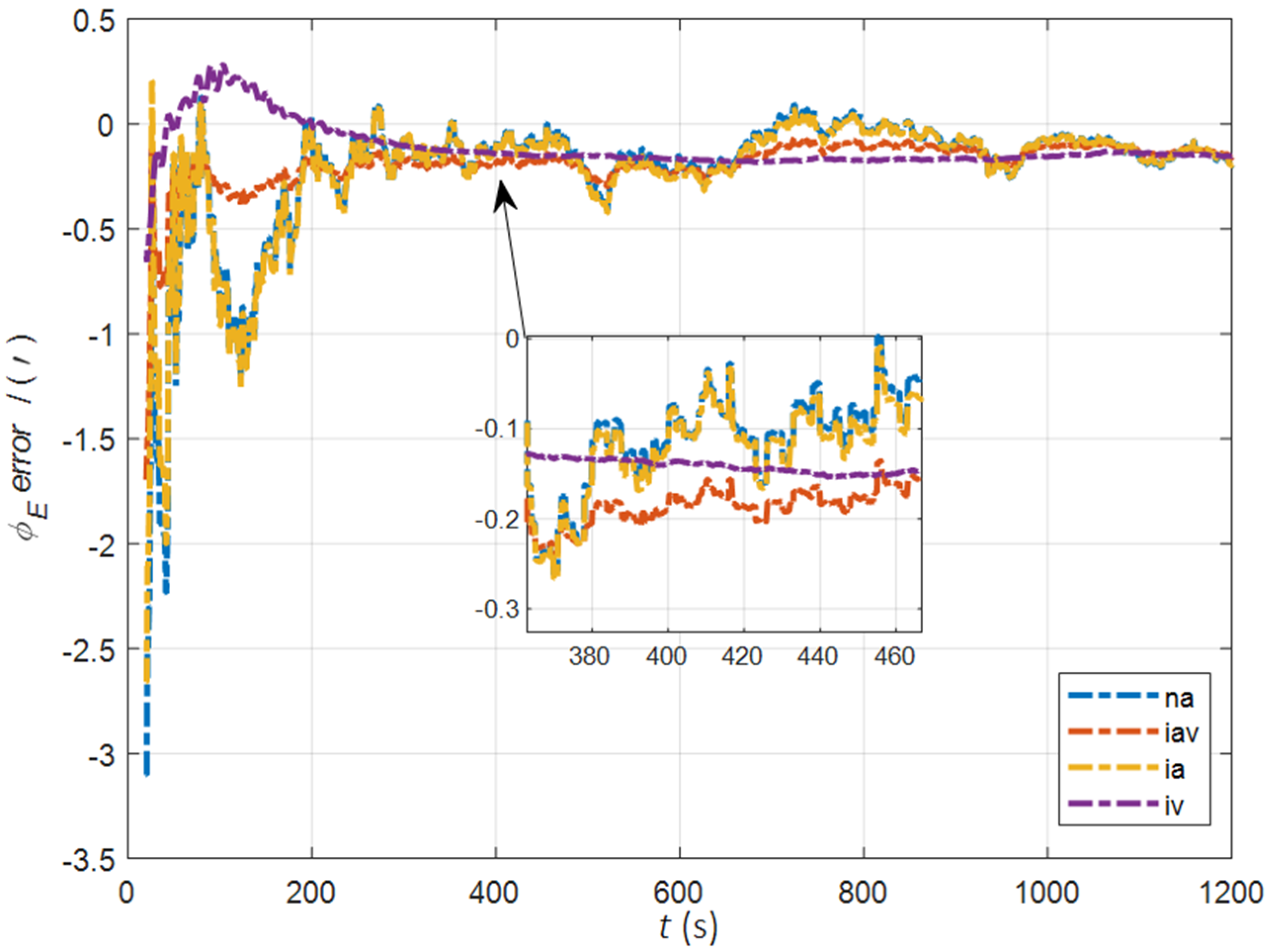

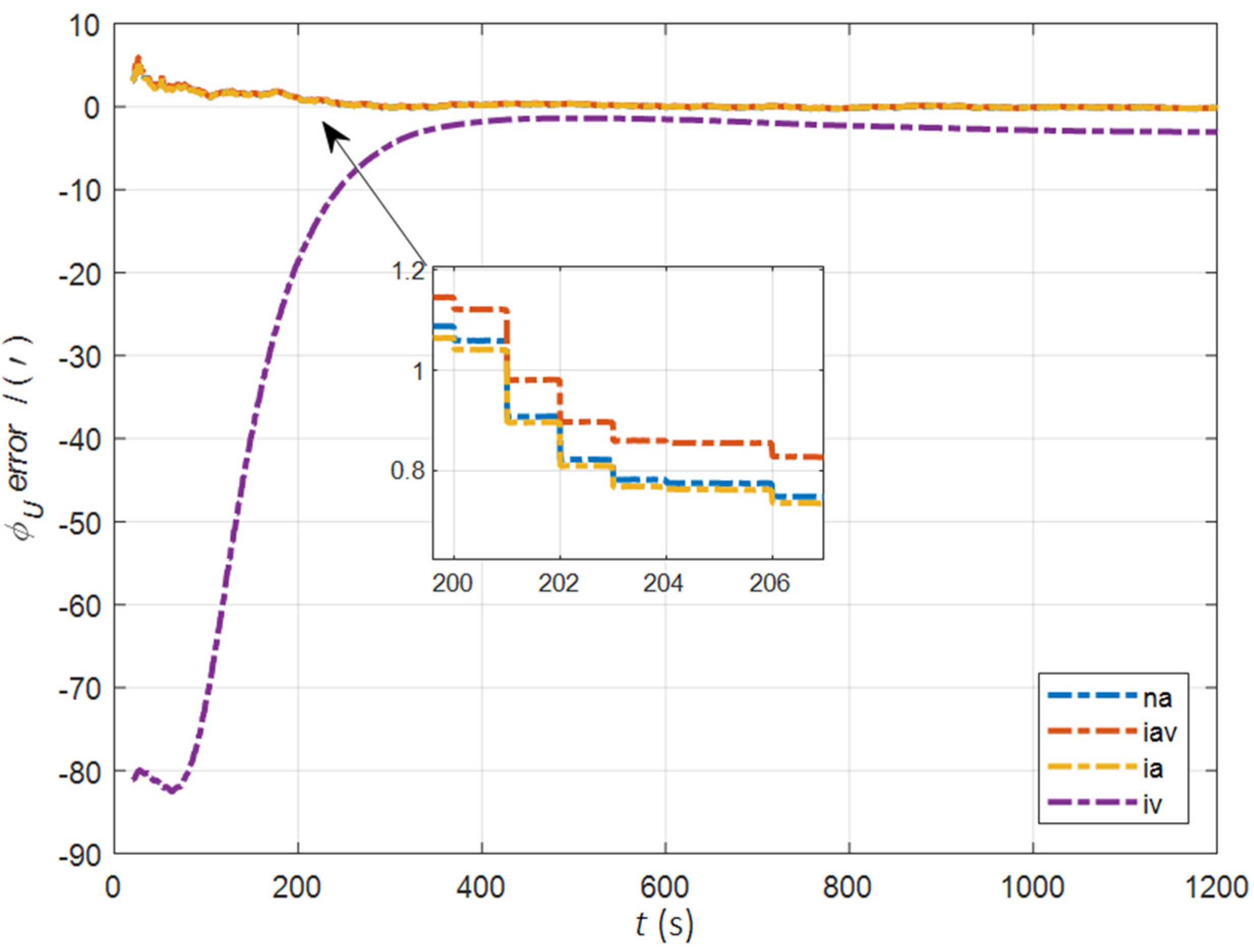
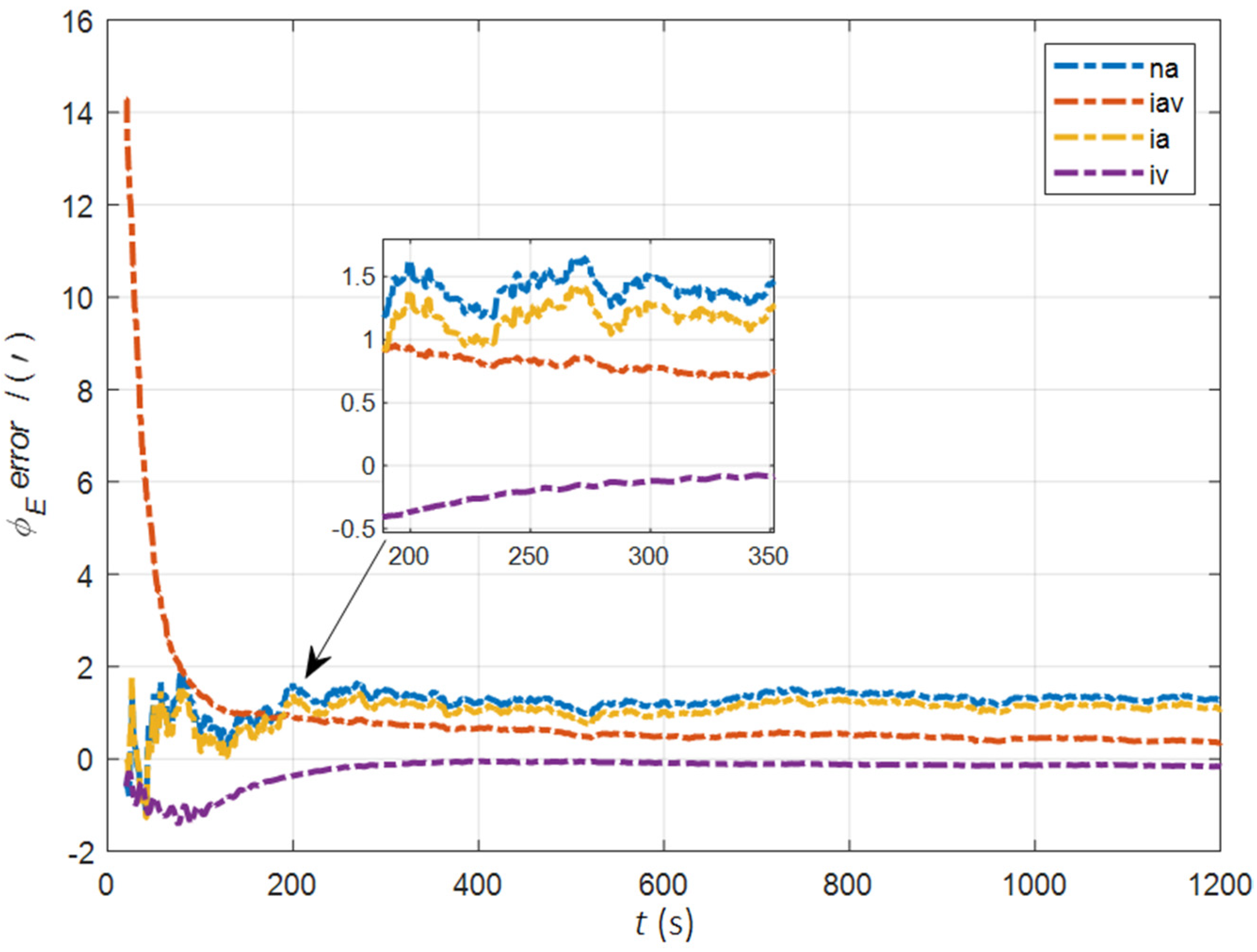


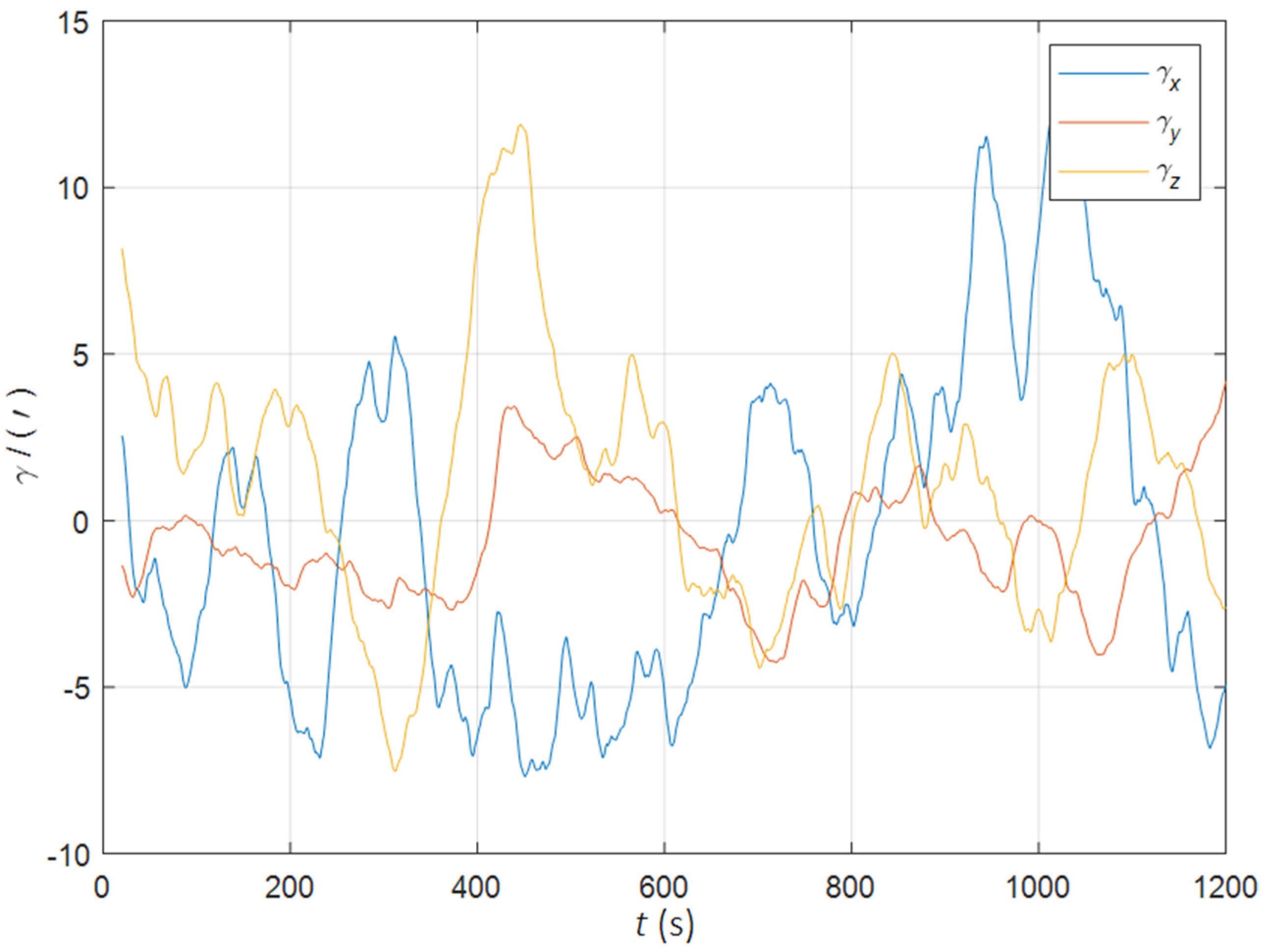
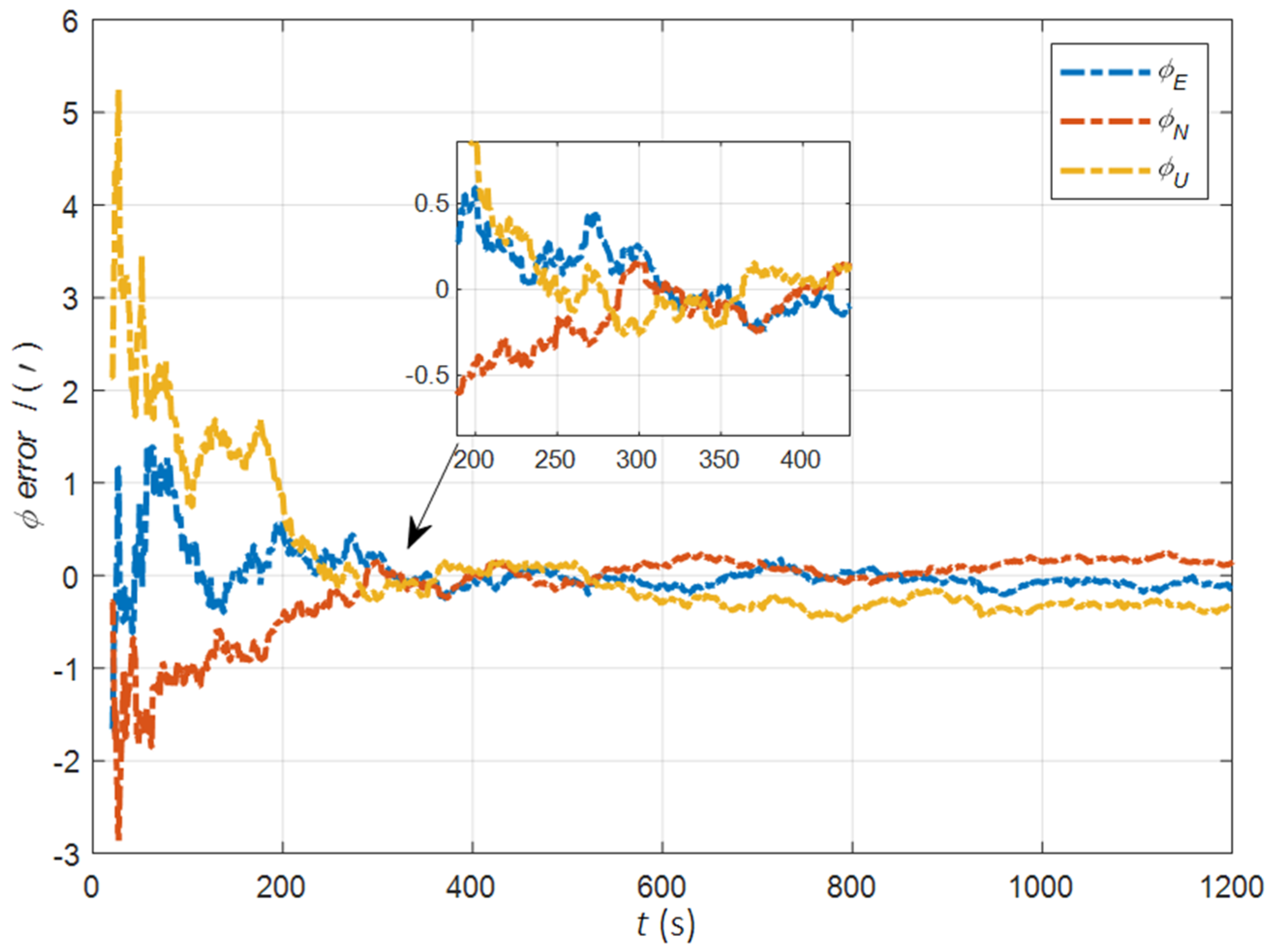
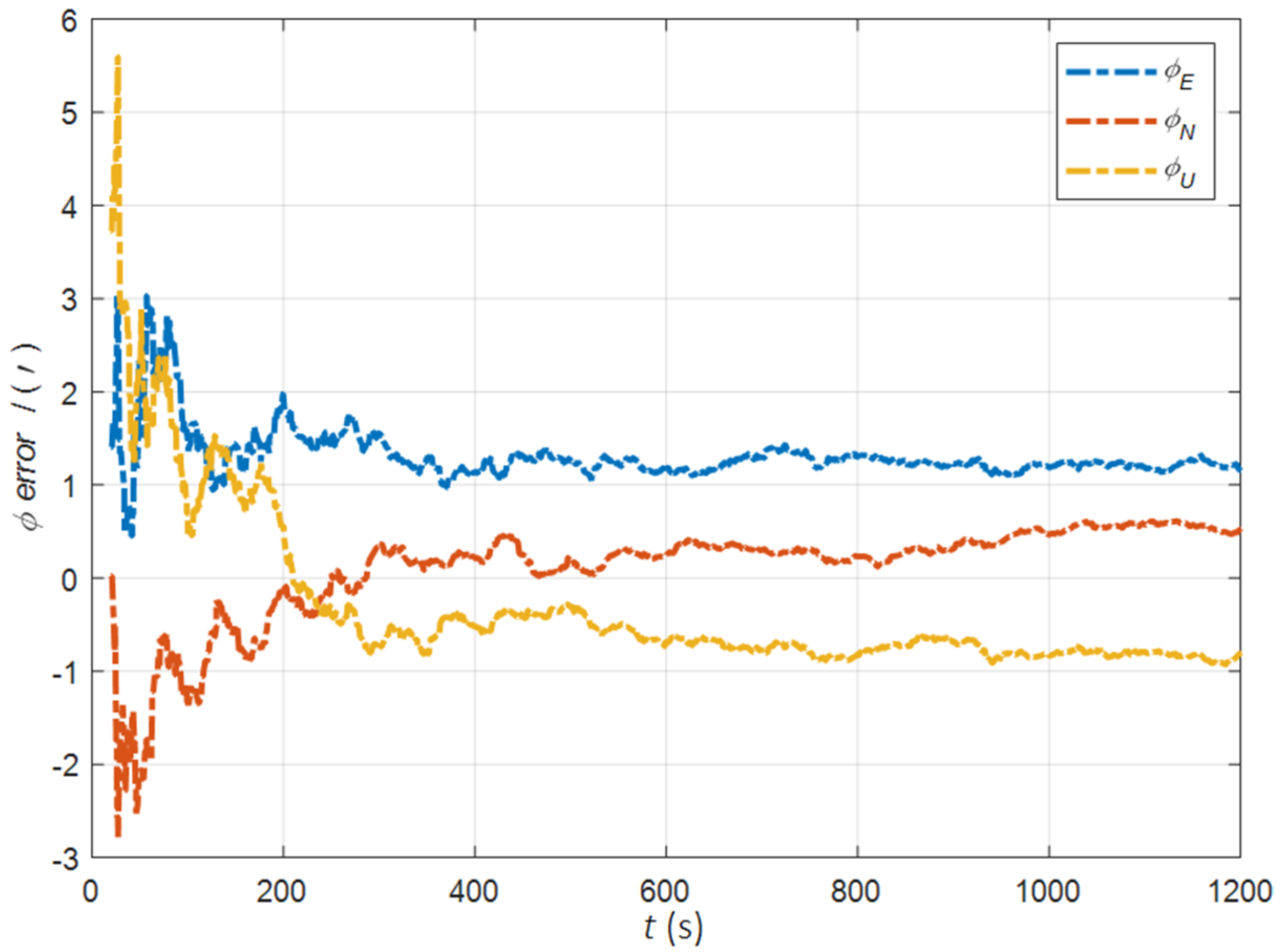
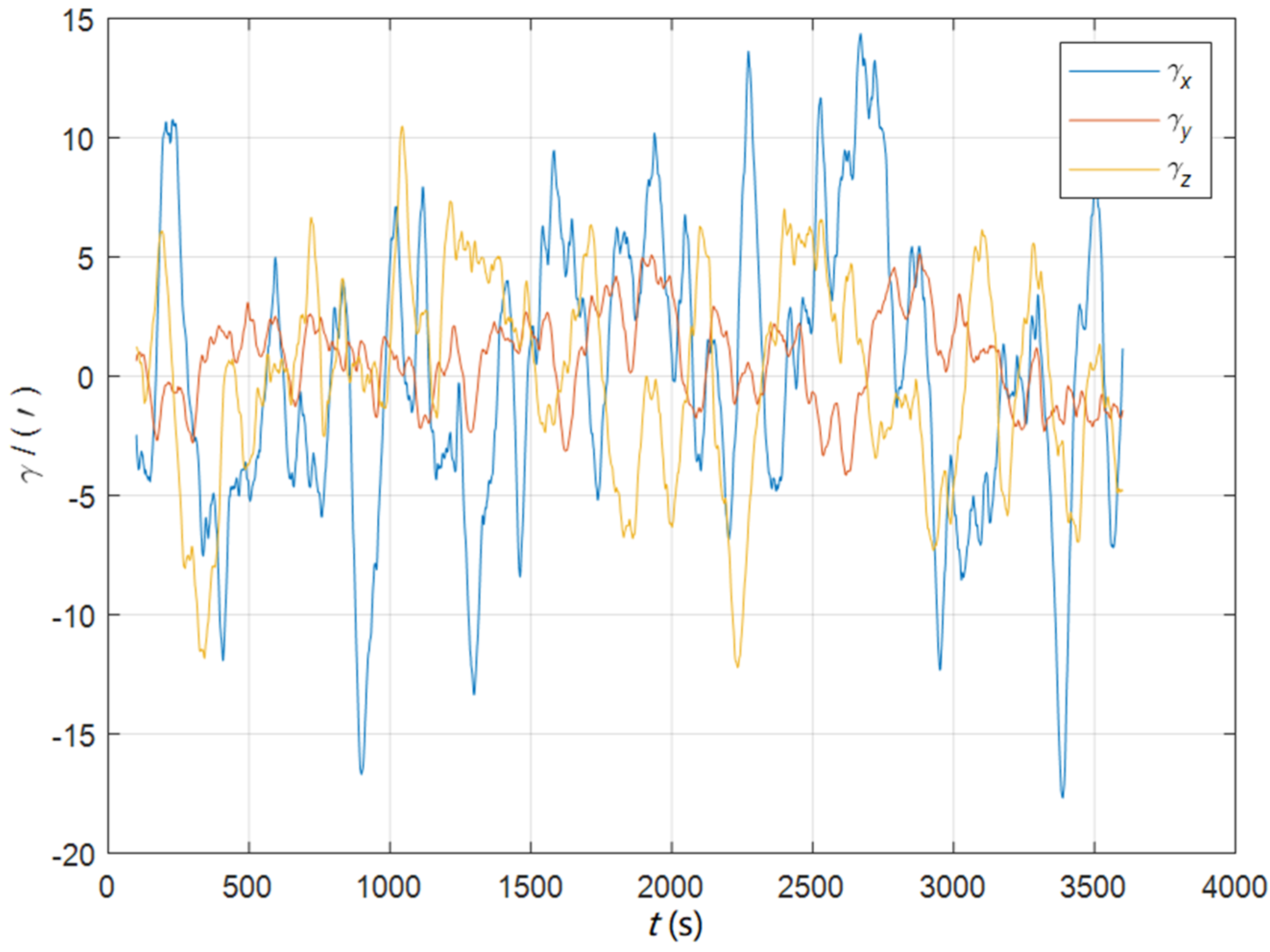
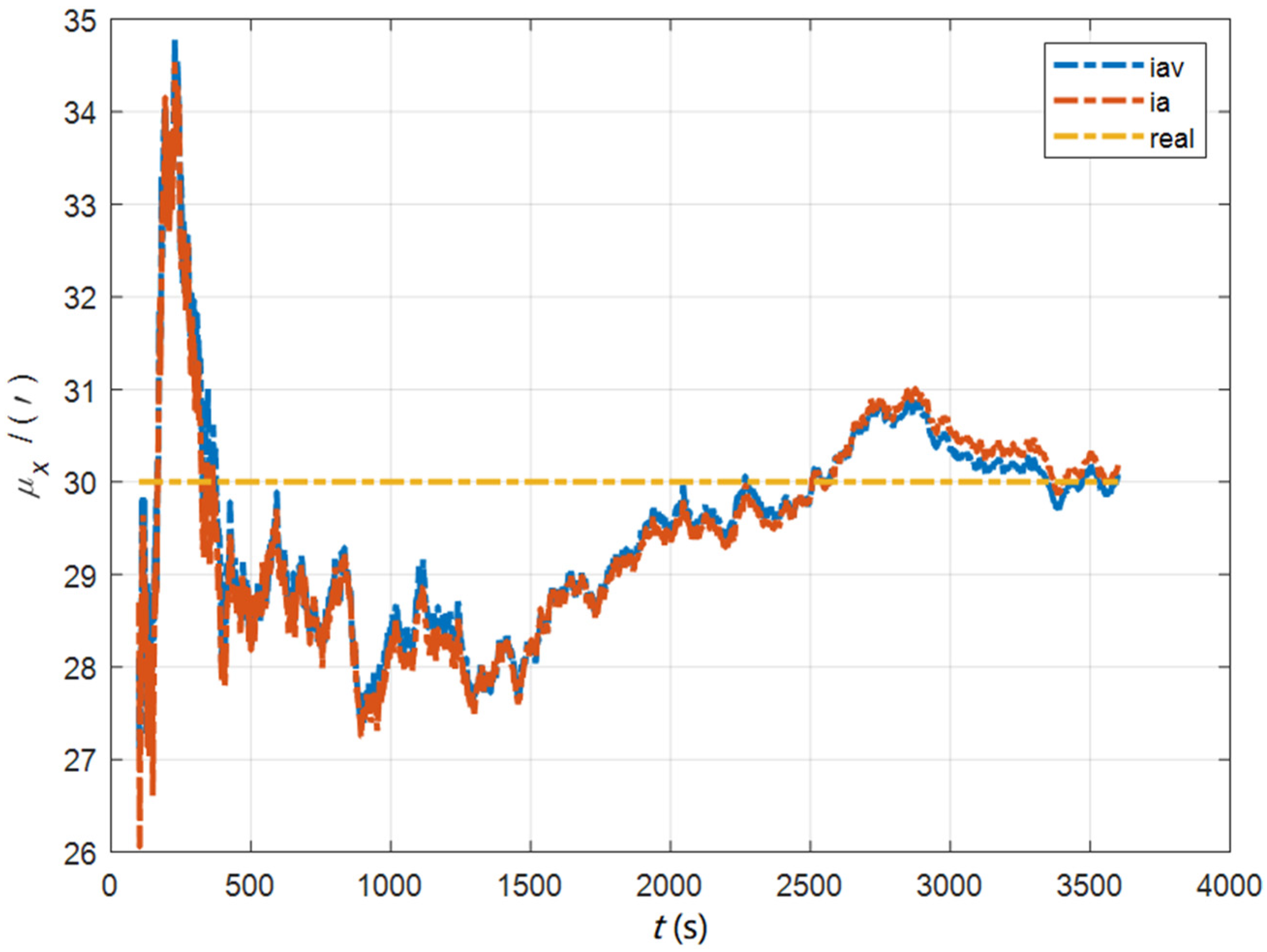

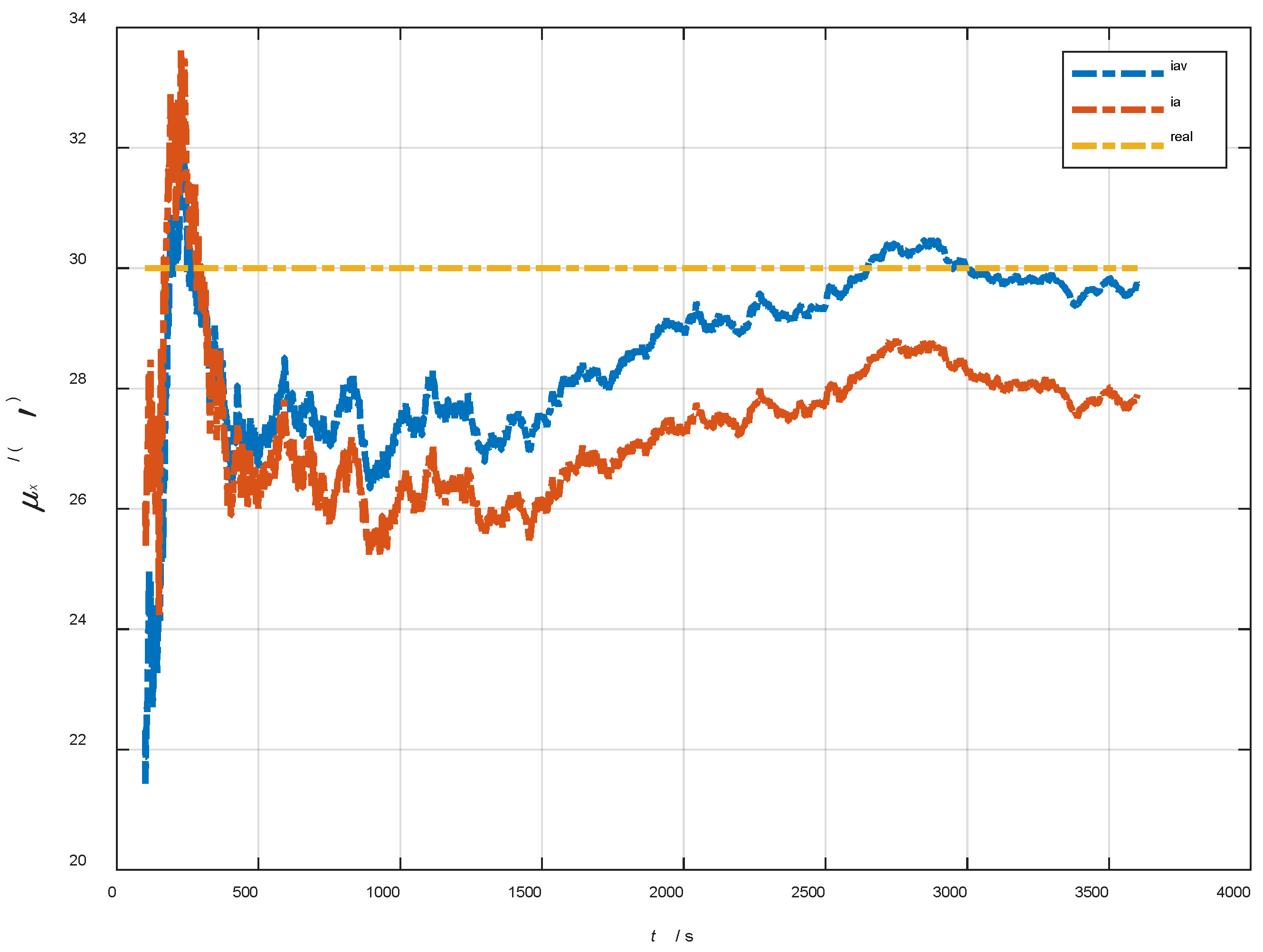
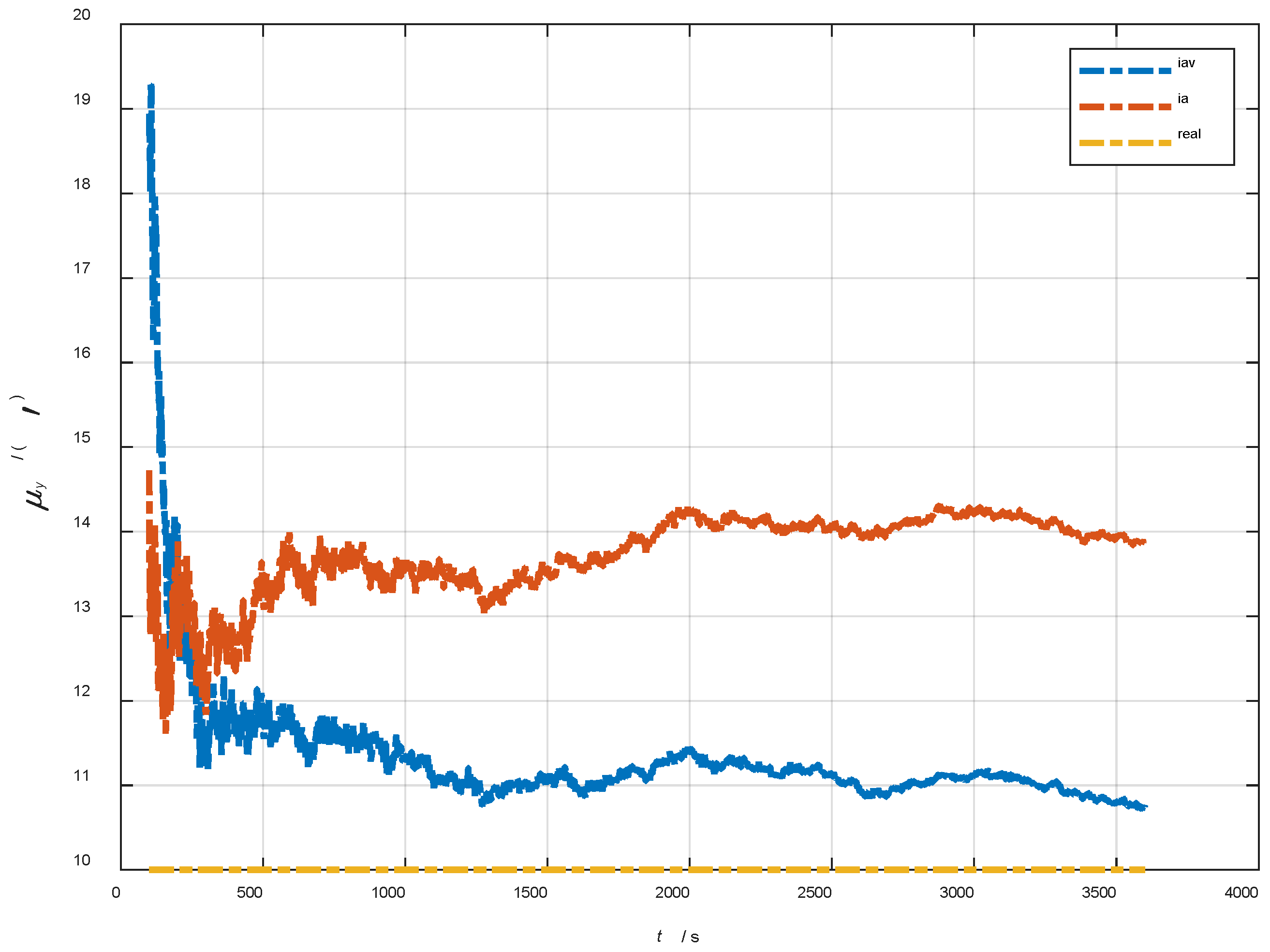
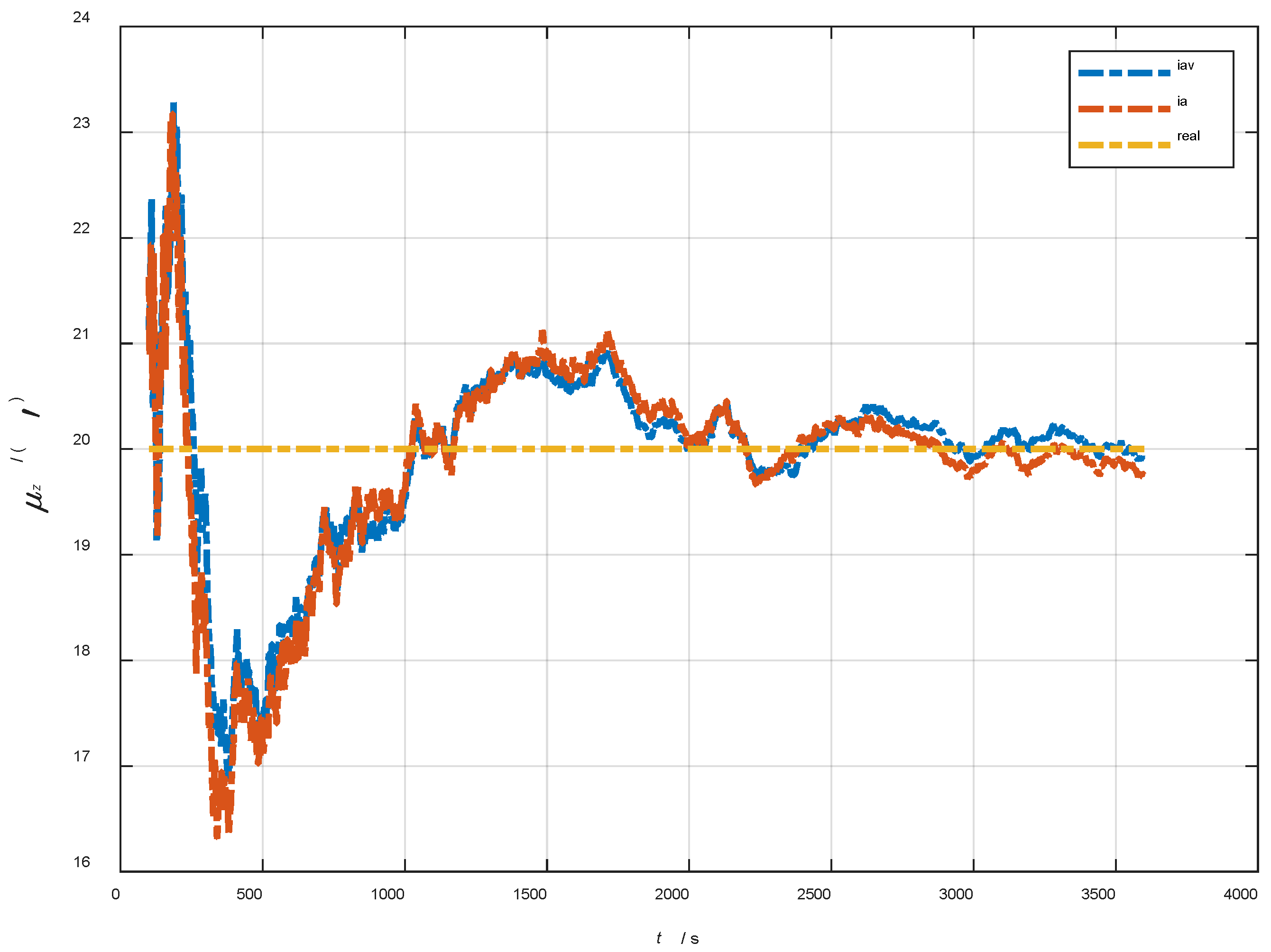


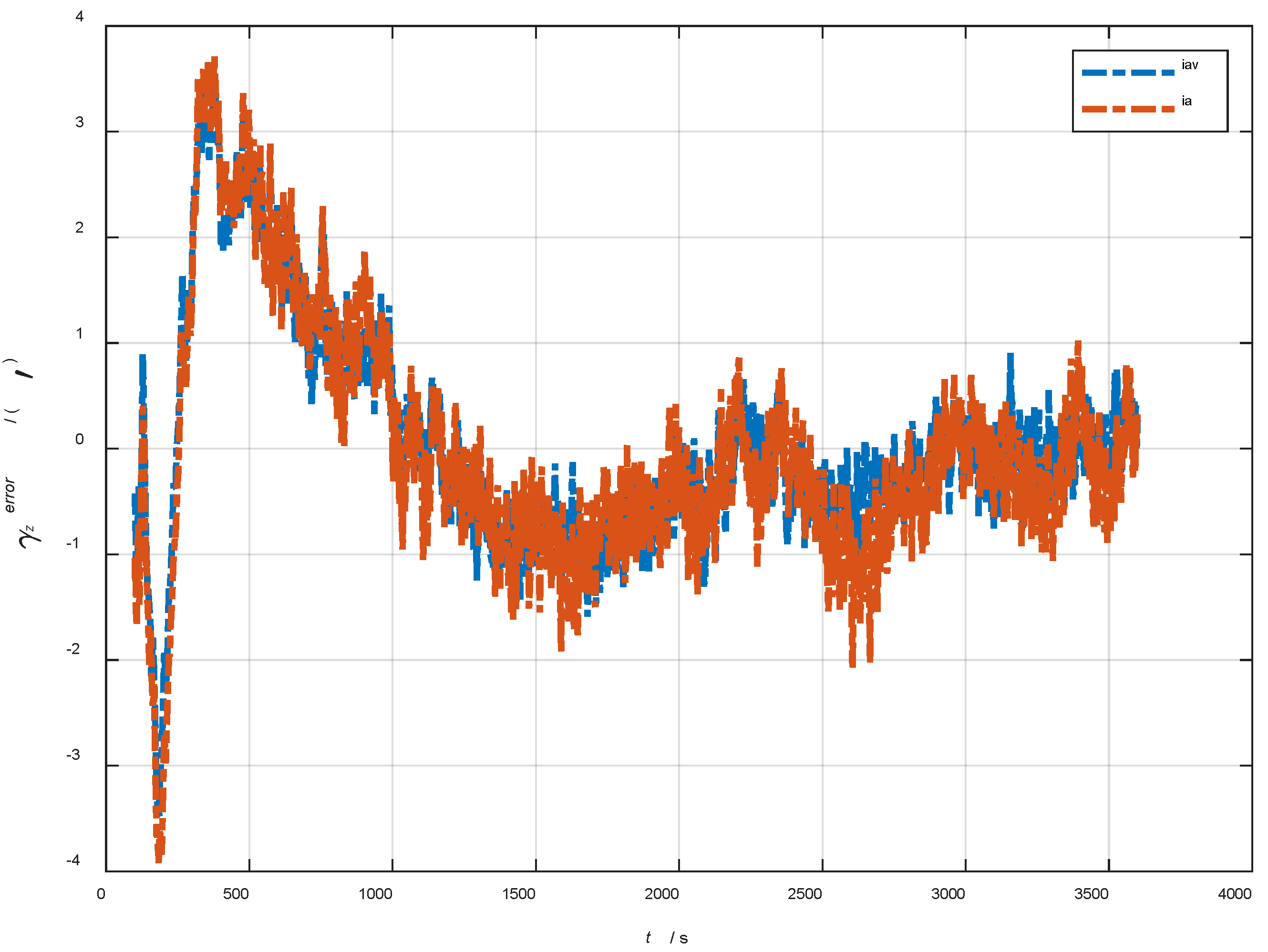
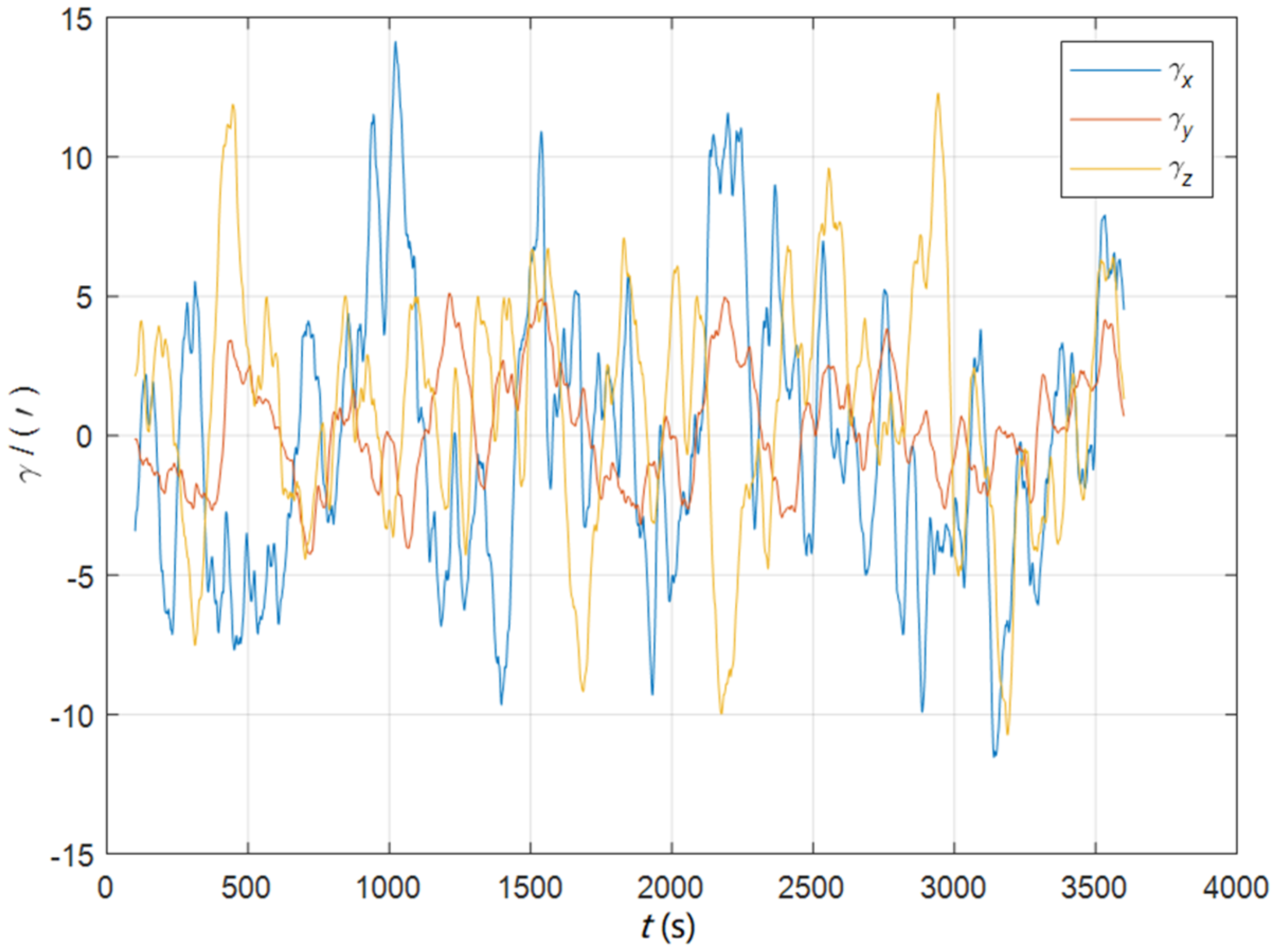

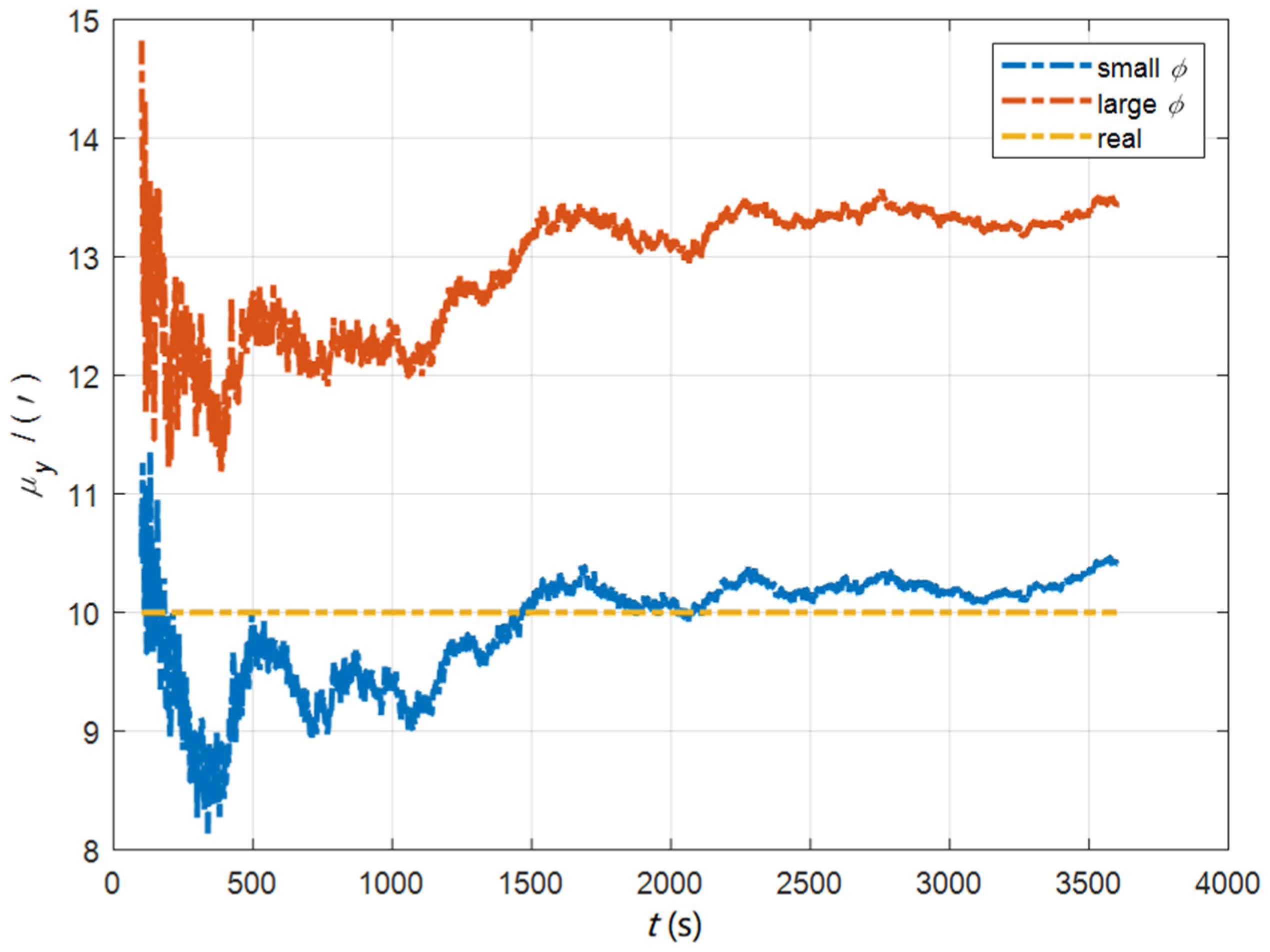
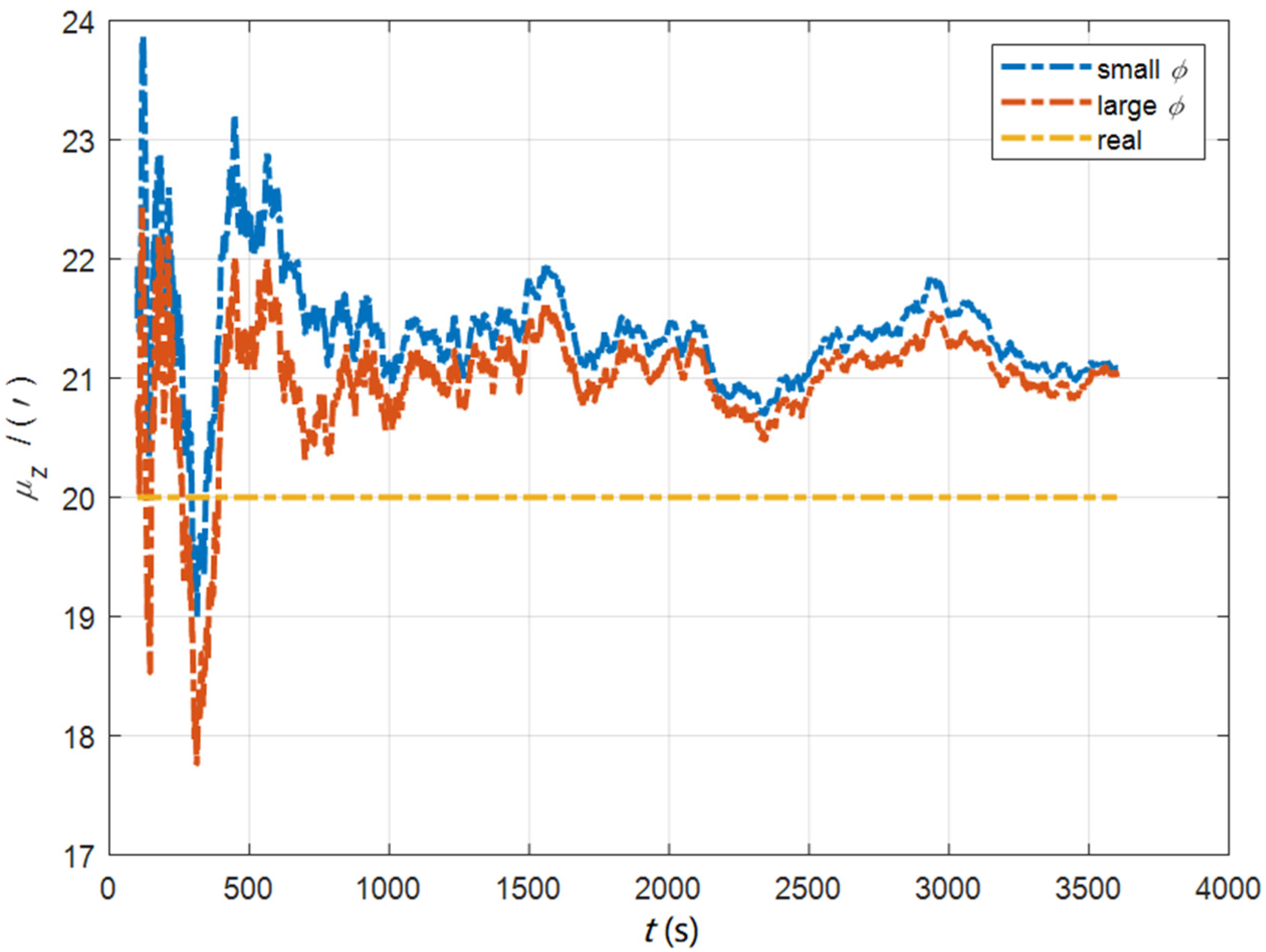



| Method | |||
|---|---|---|---|
| na | 0.15 | 0.22 | 0.21 |
| iav | 0.16 | 0.11 | 0.23 |
| ia | 0.16 | 0.22 | 0.21 |
| iv | 0.15 | 0.16 | 4.07 |
| Method | |||
|---|---|---|---|
| na | 1.32 | 1.08 | 0.85 |
| iav | 0.56 | 0.07 | 0.30 |
| ia | 1.12 | 0.43 | 0.49 |
| iv | 0.13 | 0.16 | 9.52 |
| 0.12 | 0.15 | 0.27 | |
| 1.26 | 0.35 | 0.68 |
| Method | ||||||
|---|---|---|---|---|---|---|
| iav | 0.36 | 0.73 | 0.10 | 0.43 | 0.85 | 0.29 |
| ia | 0.48 | 0.71 | 0.20 | 0.39 | 0.81 | 0.26 |
| Method | ||||||
|---|---|---|---|---|---|---|
| iav | 0.29 | 0.98 | 0.11 | 0.36 | 1.00 | 0.27 |
| ia | 1.92 | 4.09 | 0.13 | 0.76 | 1.47 | 0.39 |
| 0.36 | 0.24 | 1.35 | 0.32 | 0.29 | 1.05 | |
| 2.59 | 3.33 | 1.14 | 0.47 | 0.85 | 0.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Bian, H.; Ma, H.; Wang, R. One-Step Initial Alignment Algorithm for SINS in the ECI Frame Based on the Inertial Attitude Measurement of the CNS. Sensors 2022, 22, 5123. https://doi.org/10.3390/s22145123
Tang J, Bian H, Ma H, Wang R. One-Step Initial Alignment Algorithm for SINS in the ECI Frame Based on the Inertial Attitude Measurement of the CNS. Sensors. 2022; 22(14):5123. https://doi.org/10.3390/s22145123
Chicago/Turabian StyleTang, Jun, Hongwei Bian, Heng Ma, and Rongying Wang. 2022. "One-Step Initial Alignment Algorithm for SINS in the ECI Frame Based on the Inertial Attitude Measurement of the CNS" Sensors 22, no. 14: 5123. https://doi.org/10.3390/s22145123
APA StyleTang, J., Bian, H., Ma, H., & Wang, R. (2022). One-Step Initial Alignment Algorithm for SINS in the ECI Frame Based on the Inertial Attitude Measurement of the CNS. Sensors, 22(14), 5123. https://doi.org/10.3390/s22145123





