Event Collapse in Contrast Maximization Frameworks
Abstract
:1. Introduction
- (1)
- A study of the event collapse phenomenon in regard to event warping and objective functions (Section 3.3 and Section 4).
- (2)
- Two principled metrics of event collapse (one based on flow divergence and one based on area-element deformations) and their use as regularizers to mitigate the above-mentioned phenomenon (Section 3.4 to Section 3.6).
- (3)
- Experiments on publicly available datasets that demonstrate, in comparison with other strategies, the effectiveness of the proposed regularizers (Section 4).
2. Related Work
2.1. Contrast Maximization
2.2. Event Collapse
3. Method
3.1. How Event Cameras Work
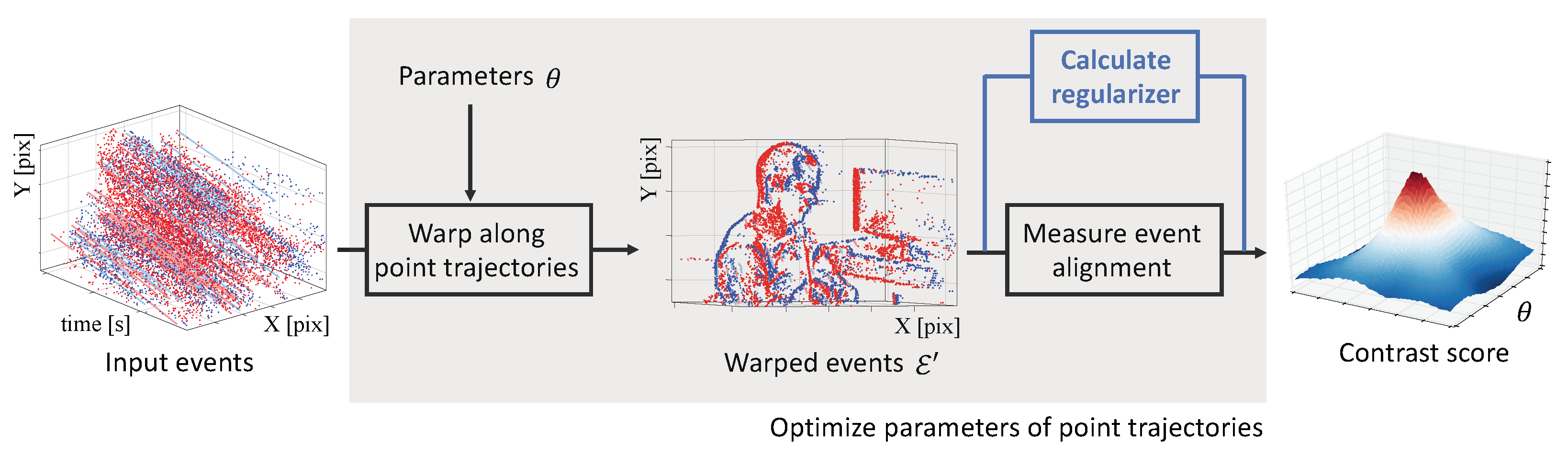
3.2. Mathematical Description of the CMax Framework
3.3. Simplest Example of Event Collapse: 1 DOF
Discussion
3.4. Proposed Regularizers
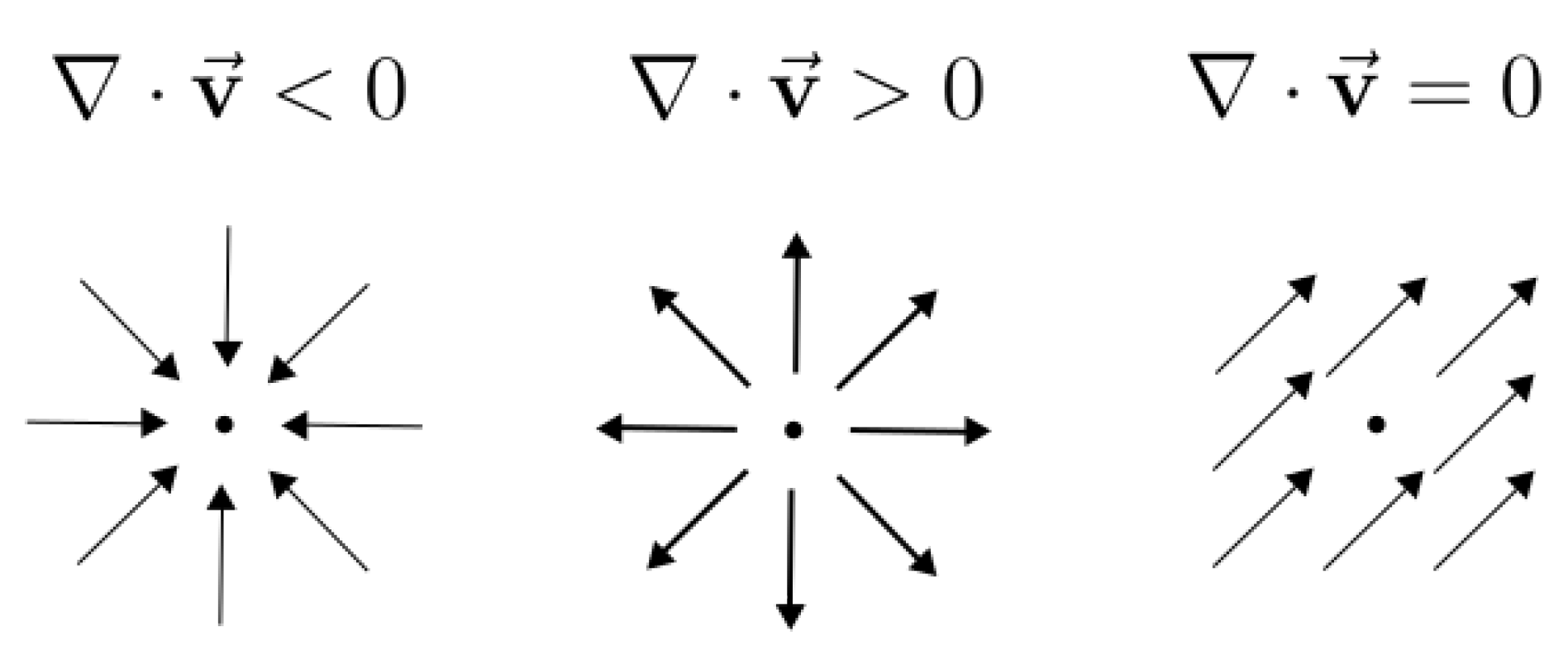
3.4.1. Divergence of the Event Transformation Flow
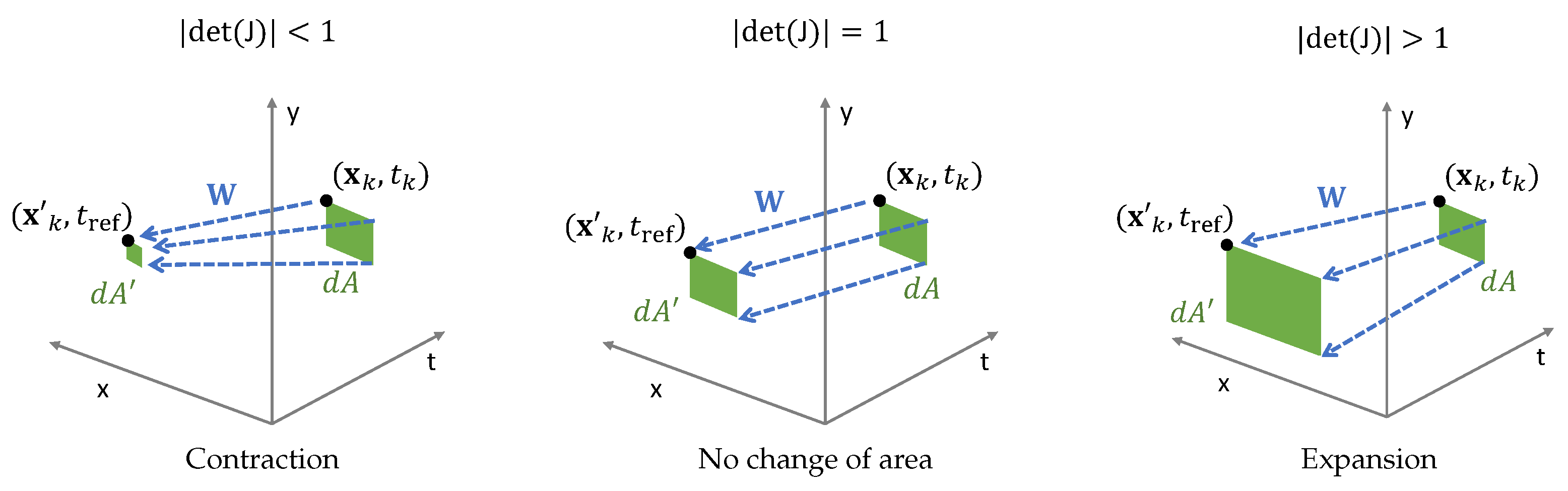
3.4.2. Area-Based Deformation of the Event Transformation
3.5. Higher DOF Warp Models
3.5.1. Feature Flow
3.5.2. Rotational Motion
3.5.3. Planar Motion
3.5.4. Similarity Transformation
3.6. Augmented Objective Function
4. Experiments
4.1. Evaluation Datasets and Metrics
4.1.1. Datasets
4.1.2. Metrics
4.2. Effect of the Regularizers on Collapse-Enabled Warps
4.3. Effect of the Regularizers on Well-Posed Warps
4.4. Sensitivity Analysis
4.5. Computational Complexity
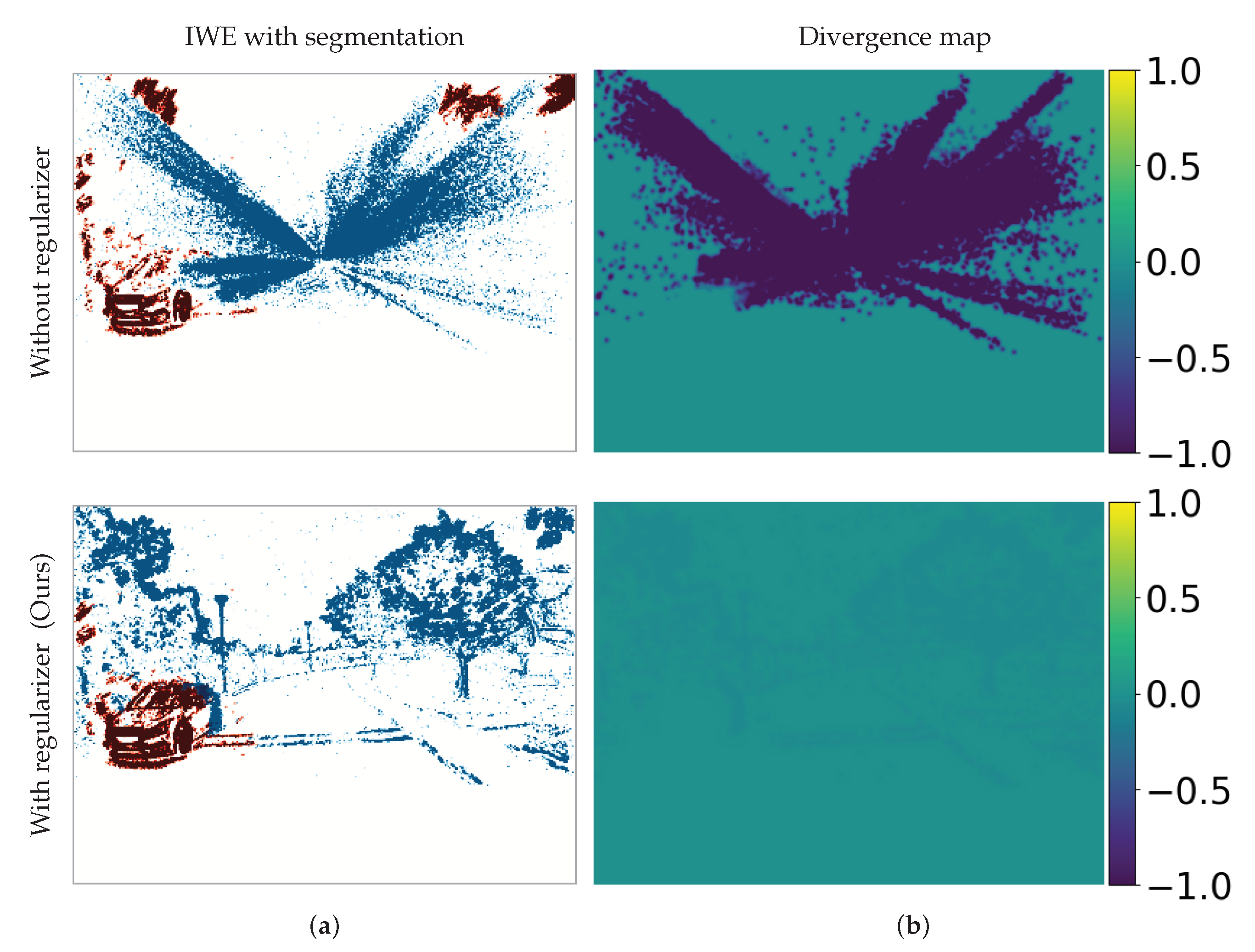
4.6. Application to Motion Segmentation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
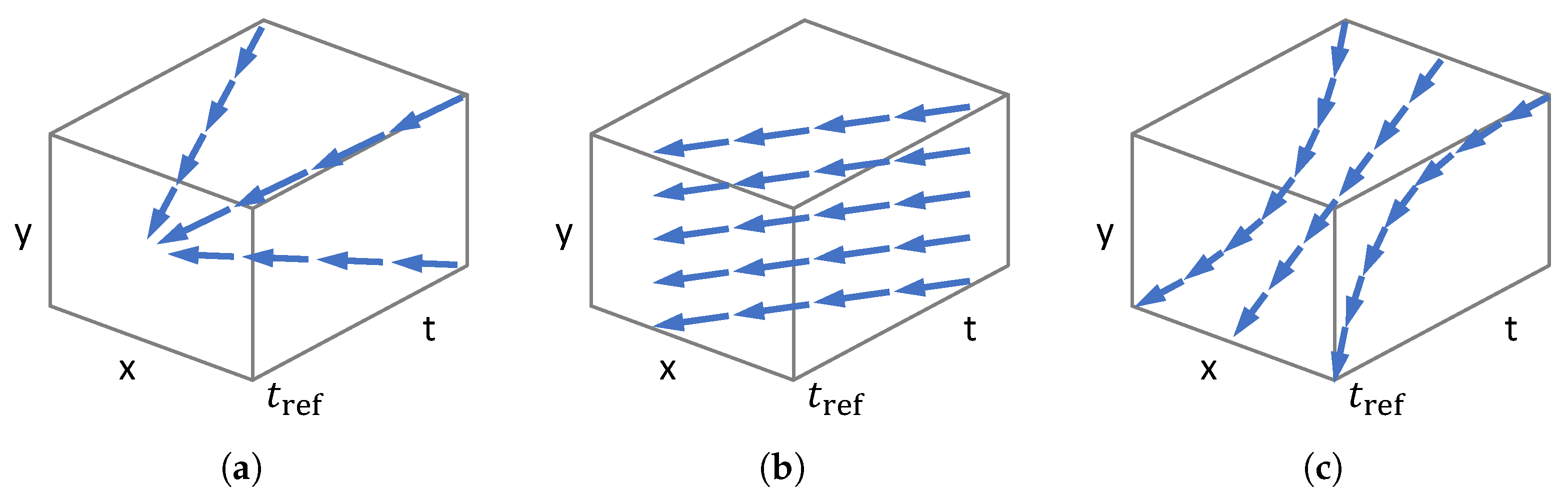
Appendix A. Warp Models, Jacobians and Flow Divergence
Appendix A.1. Planar Motion — Euclidean Transformation on the Image Plane, SE(2)
Appendix A.2. 3-DOF Camera Rotation, SO(3)
Connection between Divergence and Deformation Maps
Appendix A.3. 4-DOF In-Plane Camera Motion Approximation
- 1-DOF Zoom in/out (). .
- 2-DOF translation (). .
- 1-DOF “rotation” (). .Using a couple of approximations of the exponential map in , we obtainHence, plays the role of a small angular velocity around the camera’s optical axis Z, i.e., in-plane rotation.
- 3-DOF planar motion (“isometry”) (). Using the previous result, the warp splits into translational and rotational components:
Appendix A.4. 4-DOF Similarity Transformation on the Image Plane, Sim(2)
References
- Delbruck, T. Frame-free dynamic digital vision. In Proceedings of the International Symposium on Secure-Life Electronics, Tokyo, Japan, 6–7 March 2008; pp. 21–26. [Google Scholar] [CrossRef]
- Suh, Y.; Choi, S.; Ito, M.; Kim, J.; Lee, Y.; Seo, J.; Jung, H.; Yeo, D.H.; Namgung, S.; Bong, J.; et al. A 1280x960 Dynamic Vision Sensor with a 4.95-μm Pixel Pitch and Motion Artifact Minimization. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020. [Google Scholar] [CrossRef]
- Finateu, T.; Niwa, A.; Matolin, D.; Tsuchimoto, K.; Mascheroni, A.; Reynaud, E.; Mostafalu, P.; Brady, F.; Chotard, L.; LeGoff, F.; et al. A 1280x720 Back-Illuminated Stacked Temporal Contrast Event-Based Vision Sensor with 4.86 μm Pixels, 1.066GEPS Readout, Programmable Event-Rate Controller and Compressive Data-Formatting Pipeline. In Proceedings of the IEEE International Solid- State Circuits Conference-(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 112–114. [Google Scholar] [CrossRef]
- Gallego, G.; Delbruck, T.; Orchard, G.; Bartolozzi, C.; Taba, B.; Censi, A.; Leutenegger, S.; Davison, A.; Conradt, J.; Daniilidis, K.; et al. Event-based Vision: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 154–180. [Google Scholar] [CrossRef] [PubMed]
- Gallego, G.; Scaramuzza, D. Accurate Angular Velocity Estimation with an Event Camera. IEEE Robot. Autom. Lett. 2017, 2, 632–639. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Kim, H.J. Real-Time Rotational Motion Estimation with Contrast Maximization Over Globally Aligned Events. IEEE Robot. Autom. Lett. 2021, 6, 6016–6023. [Google Scholar] [CrossRef]
- Zhu, A.Z.; Atanasov, N.; Daniilidis, K. Event-Based Feature Tracking with Probabilistic Data Association. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4465–4470. [Google Scholar] [CrossRef]
- Zhu, A.Z.; Atanasov, N.; Daniilidis, K. Event-based Visual Inertial Odometry. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5816–5824. [Google Scholar] [CrossRef]
- Seok, H.; Lim, J. Robust Feature Tracking in DVS Event Stream using Bezier Mapping. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass, CO, USA, 1–5 March 2020; pp. 1647–1656. [Google Scholar] [CrossRef]
- Stoffregen, T.; Kleeman, L. Event Cameras, Contrast Maximization and Reward Functions: An Analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12292–12300. [Google Scholar] [CrossRef]
- Dardelet, L.; Benosman, R.; Ieng, S.H. An Event-by-Event Feature Detection and Tracking Invariant to Motion Direction and Velocity. TechRxiv 2021. [Google Scholar] [CrossRef]
- Gallego, G.; Rebecq, H.; Scaramuzza, D. A Unifying Contrast Maximization Framework for Event Cameras, with Applications to Motion, Depth, and Optical Flow Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3867–3876. [Google Scholar] [CrossRef] [Green Version]
- Gallego, G.; Gehrig, M.; Scaramuzza, D. Focus Is All You Need: Loss Functions For Event-based Vision. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12272–12281. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Gao, L.; Wang, Y.; Kneip, L. Globally-Optimal Contrast Maximisation for Event Cameras. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3479–3495. [Google Scholar] [CrossRef]
- Rebecq, H.; Gallego, G.; Mueggler, E.; Scaramuzza, D. EMVS: Event-based Multi-View Stereo—3D Reconstruction with an Event Camera in Real-Time. Int. J. Comput. Vis. 2018, 126, 1394–1414. [Google Scholar] [CrossRef] [Green Version]
- Zhu, A.Z.; Yuan, L.; Chaney, K.; Daniilidis, K. Unsupervised Event-based Learning of Optical Flow, Depth, and Egomotion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 989–997. [Google Scholar] [CrossRef] [Green Version]
- Paredes-Valles, F.; Scheper, K.Y.W.; de Croon, G.C.H.E. Unsupervised Learning of a Hierarchical Spiking Neural Network for Optical Flow Estimation: From Events to Global Motion Perception. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2051–2064. [Google Scholar] [CrossRef] [Green Version]
- Hagenaars, J.J.; Paredes-Valles, F.; de Croon, G.C.H.E. Self-Supervised Learning of Event-Based Optical Flow with Spiking Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Virtual-only Conference, 7–10 December 2021; Volume 34, pp. 7167–7179. [Google Scholar]
- Shiba, S.; Aoki, Y.; Gallego, G. Secrets of Event-based Optical Flow. In Proceedings of the European Conference on Computer Vision (ECCV), Tel-Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Mitrokhin, A.; Fermuller, C.; Parameshwara, C.; Aloimonos, Y. Event-based Moving Object Detection and Tracking. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- Stoffregen, T.; Gallego, G.; Drummond, T.; Kleeman, L.; Scaramuzza, D. Event-Based Motion Segmentation by Motion Compensation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 7243–7252. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Gallego, G.; Lu, X.; Liu, S.; Shen, S. Event-based Motion Segmentation with Spatio-Temporal Graph Cuts. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–13. [Google Scholar] [CrossRef]
- Parameshwara, C.M.; Sanket, N.J.; Singh, C.D.; Fermüller, C.; Aloimonos, Y. 0-MMS: Zero-shot multi-motion segmentation with a monocular event camera. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar] [CrossRef]
- Lu, X.; Zhou, Y.; Shen, S. Event-based Motion Segmentation by Cascaded Two-Level Multi-Model Fitting. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 4445–4452. [Google Scholar] [CrossRef]
- Duan, P.; Wang, Z.; Shi, B.; Cossairt, O.; Huang, T.; Katsaggelos, A. Guided Event Filtering: Synergy between Intensity Images and Neuromorphic Events for High Performance Imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Zhang, Z.; Yezzi, A.; Gallego, G. Image Reconstruction from Events. Why learn it? arXiv 2021, arXiv:2112.06242. [Google Scholar]
- Nunes, U.M.; Demiris, Y. Robust Event-based Vision Model Estimation by Dispersion Minimisation. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef] [PubMed]
- Gu, C.; Learned-Miller, E.; Sheldon, D.; Gallego, G.; Bideau, P. The Spatio-Temporal Poisson Point Process: A Simple Model for the Alignment of Event Camera Data. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 13495–13504. [Google Scholar] [CrossRef]
- Liu, D.; Parra, A.; Chin, T.J. Globally Optimal Contrast Maximisation for Event-Based Motion Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 6348–6357. [Google Scholar] [CrossRef]
- Stoffregen, T.; Kleeman, L. Simultaneous Optical Flow and Segmentation (SOFAS) using Dynamic Vision Sensor. In Proceedings of the Australasian Conference on Robotics and Automation (ACRA), Sydney, Australia, 11–13 December 2017. [Google Scholar]
- Ozawa, T.; Sekikawa, Y.; Saito, H. Accuracy and Speed Improvement of Event Camera Motion Estimation Using a Bird’s-Eye View Transformation. Sensors 2022, 22, 773. [Google Scholar] [CrossRef] [PubMed]
- Lichtsteiner, P.; Posch, C.; Delbruck, T. A 128 × 128 120 dB 15 μs latency asynchronous temporal contrast vision sensor. IEEE J. Solid-State Circuits 2008, 43, 566–576. [Google Scholar] [CrossRef] [Green Version]
- Ng, M.; Er, Z.M.; Soh, G.S.; Foong, S. Aggregation Functions For Simultaneous Attitude And Image Estimation with Event Cameras At High Angular Rates. IEEE Robot. Autom. Lett. 2022, 7, 4384–4391. [Google Scholar] [CrossRef]
- Zhu, A.Z.; Thakur, D.; Ozaslan, T.; Pfrommer, B.; Kumar, V.; Daniilidis, K. The Multivehicle Stereo Event Camera Dataset: An Event Camera Dataset for 3D Perception. IEEE Robot. Autom. Lett. 2018, 3, 2032–2039. [Google Scholar] [CrossRef] [Green Version]
- Murray, R.M.; Li, Z.; Sastry, S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Gallego, G.; Yezzi, A. A Compact Formula for the Derivative of a 3-D Rotation in Exponential Coordinates. J. Math. Imaging Vis. 2014, 51, 378–384. [Google Scholar] [CrossRef] [Green Version]
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB; Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Gallego, G.; Yezzi, A.; Fedele, F.; Benetazzo, A. A Variational Stereo Method for the Three-Dimensional Reconstruction of Ocean Waves. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4445–4457. [Google Scholar] [CrossRef]
- Gehrig, M.; Aarents, W.; Gehrig, D.; Scaramuzza, D. DSEC: A Stereo Event Camera Dataset for Driving Scenarios. IEEE Robot. Autom. Lett. 2021, 6, 4947–4954. [Google Scholar] [CrossRef]
- Mueggler, E.; Rebecq, H.; Gallego, G.; Delbruck, T.; Scaramuzza, D. The Event-Camera Dataset and Simulator: Event-based Data for Pose Estimation, Visual Odometry, and SLAM. Int. J. Robot. Res. 2017, 36, 142–149. [Google Scholar] [CrossRef]
- Gehrig, M.; Millhäusler, M.; Gehrig, D.; Scaramuzza, D. E-RAFT: Dense Optical Flow from Event Cameras. In Proceedings of the International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021. [Google Scholar] [CrossRef]
- Nagata, J.; Sekikawa, Y.; Aoki, Y. Optical Flow Estimation by Matching Time Surface with Event-Based Cameras. Sensors 2021, 21, 1150. [Google Scholar] [CrossRef]
- Taverni, G.; Moeys, D.P.; Li, C.; Cavaco, C.; Motsnyi, V.; Bello, D.S.S.; Delbruck, T. Front and Back Illuminated Dynamic and Active Pixel Vision Sensors Comparison. IEEE Trans. Circuits Syst. II 2018, 65, 677–681. [Google Scholar] [CrossRef] [Green Version]
- Zhu, A.Z.; Yuan, L.; Chaney, K.; Daniilidis, K. EV-FlowNet: Self-Supervised Optical Flow Estimation for Event-based Cameras. In Proceedings of the Robotics: Science and Systems (RSS), Pittsburgh, PA, USA, 26–30 June 2018. [Google Scholar] [CrossRef]
- Rosinol Vidal, A.; Rebecq, H.; Horstschaefer, T.; Scaramuzza, D. Ultimate SLAM? Combining Events, Images, and IMU for Robust Visual SLAM in HDR and High Speed Scenarios. IEEE Robot. Autom. Lett. 2018, 3, 994–1001. [Google Scholar] [CrossRef] [Green Version]
- Rebecq, H.; Horstschäfer, T.; Gallego, G.; Scaramuzza, D. EVO: A Geometric Approach to Event-based 6-DOF Parallel Tracking and Mapping in Real-Time. IEEE Robot. Autom. Lett. 2017, 2, 593–600. [Google Scholar] [CrossRef] [Green Version]
- Mueggler, E.; Gallego, G.; Rebecq, H.; Scaramuzza, D. Continuous-Time Visual-Inertial Odometry for Event Cameras. IEEE Trans. Robot. 2018, 34, 1425–1440. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Gallego, G.; Shen, S. Event-based Stereo Visual Odometry. IEEE Trans. Robot. 2021, 37, 1433–1450. [Google Scholar] [CrossRef]
- Brandli, C.; Berner, R.; Yang, M.; Liu, S.C.; Delbruck, T. A 240 × 180 130 dB 3 μs Latency Global Shutter Spatiotemporal Vision Sensor. IEEE J. Solid-State Circuits 2014, 49, 2333–2341. [Google Scholar] [CrossRef]
- Stoffregen, T.; Scheerlinck, C.; Scaramuzza, D.; Drummond, T.; Barnes, N.; Kleeman, L.; Mahony, R. Reducing the Sim-to-Real Gap for Event Cameras. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Granada, Spain, 12–15 December 2011; Volume 24. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The KITTI dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Barfoot, T.D. State Estimation for Robotics—A Matrix Lie Group Approach; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]



| Variance | Gradient Magnitude | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AEE ↓ | 3PE ↓ | 10PE ↓ | 20PE ↓ | FWL ↑ | AEE ↓ | 3PE ↓ | 10PE ↓ | 20PE ↓ | FWL ↑ | ||
| Ground truth flow | _ | _ | _ | _ | 1.05 | _ | _ | _ | _ | 1.05 | |
| Identity warp | 4.85 | 60.59 | 10.38 | 0.31 | 1.00 | 4.85 | 60.59 | 10.38 | 0.31 | 1.00 | |
| 1 DOF | No regularizer | 89.34 | 97.30 | 95.42 | 92.39 | 1.90 | 85.77 | 93.96 | 86.24 | 83.45 | 1.87 |
| Whitening [27] | 89.58 | 97.18 | 96.77 | 93.76 | 1.90 | 81.10 | 90.86 | 89.04 | 86.20 | 1.85 | |
| Divergence (Ours) | 4.00 | 46.02 | 2.77 | 0.05 | 1.12 | 2.87 | 32.68 | 2.52 | 0.03 | 1.17 | |
| Deformation (Ours) | 4.47 | 52.60 | 5.16 | 0.13 | 1.08 | 3.97 | 48.79 | 3.21 | 0.07 | 1.09 | |
| Div. + Def. (Ours) | 3.30 | 33.09 | 2.61 | 0.48 | 1.20 | 2.85 | 32.34 | 2.44 | 0.03 | 1.17 | |
| 4 DOF [20] | No regularizer | 90.22 | 90.22 | 96.94 | 93.86 | 2.05 | 91.26 | 99.49 | 95.06 | 91.46 | 2.01 |
| Whitening [27] | 90.82 | 99.11 | 98.04 | 95.04 | 2.04 | 88.38 | 98.87 | 92.41 | 88.66 | 2.00 | |
| Divergence (Ours) | 7.25 | 81.75 | 18.53 | 0.69 | 1.09 | 5.37 | 66.18 | 10.81 | 0.28 | 1.14 | |
| Deformation (Ours) | 8.13 | 87.46 | 18.53 | 1.09 | 1.03 | 5.25 | 64.79 | 13.18 | 0.37 | 1.15 | |
| Div. + Def. (Ours) | 5.14 | 65.61 | 10.75 | 0.38 | 1.16 | 5.41 | 66.01 | 13.19 | 0.54 | 1.14 | |
| Variance | Gradient Magnitude | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AEE ↓ | 3PE ↓ | 10PE ↓ | 20PE ↓ | FWL ↑ | AEE ↓ | 3PE ↓ | 10PE ↓ | 20PE ↓ | FWL ↑ | ||
| Ground truth flow | _ | _ | _ | _ | 1.09 | _ | _ | _ | _ | 1.09 | |
| Identity warp | 5.84 | 60.45 | 16.65 | 3.40 | 1.00 | 5.84 | 60.45 | 16.65 | 3.40 | 1.00 | |
| 1 DOF | No regularizer | 156.13 | 99.88 | 99.33 | 98.18 | 2.58 | 156.08 | 99.93 | 99.40 | 98.11 | 2.58 |
| Whitening [27] | 156.18 | 99.95 | 99.51 | 98.26 | 2.58 | 156.82 | 99.88 | 99.38 | 98.33 | 2.58 | |
| Divergence (Ours) | 12.49 | 69.86 | 20.78 | 6.66 | 1.43 | 5.47 | 63.48 | 14.66 | 1.35 | 1.34 | |
| Deformation (Ours) | 9.01 | 68.96 | 18.86 | 4.77 | 1.40 | 5.79 | 64.02 | 16.11 | 2.75 | 1.36 | |
| Div. + Def. (Ours) | 6.06 | 68.48 | 17.08 | 2.27 | 1.36 | 5.53 | 64.09 | 15.06 | 1.37 | 1.35 | |
| 4 DOF [20] | No regularizer | 157.54 | 99.97 | 99.64 | 98.67 | 2.64 | 157.34 | 99.94 | 99.53 | 98.44 | 2.62 |
| Whitening [27] | 157.73 | 99.97 | 99.66 | 98.71 | 2.60 | 156.12 | 99.91 | 99.26 | 97.93 | 2.61 | |
| Divergence (Ours) | 14.35 | 90.84 | 41.62 | 10.82 | 1.35 | 10.43 | 91.38 | 41.63 | 9.43 | 1.21 | |
| Deformation (Ours) | 15.12 | 94.96 | 62.59 | 22.62 | 1.25 | 10.01 | 90.15 | 39.45 | 8.67 | 1.25 | |
| Div. + Def. (Ours) | 10.06 | 90.65 | 40.61 | 8.58 | 1.26 | 10.39 | 91.02 | 41.81 | 9.40 | 1.23 | |
| boxes_rot | dynamic_rot | |||
|---|---|---|---|---|
| RMS ↓ | FWL ↑ | RMS ↓ | FWL ↑ | |
| Ground truth pose | _ | 1.559 | _ | 1.414 |
| No regularizer | 8.858 | 1.562 | 4.823 | 1.420 |
| Divergence (Ours) | 9.237 | 1.558 | 4.826 | 1.420 |
| Deformation (Ours) | 8.664 | 1.561 | 4.822 | 1.420 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiba, S.; Aoki, Y.; Gallego, G. Event Collapse in Contrast Maximization Frameworks. Sensors 2022, 22, 5190. https://doi.org/10.3390/s22145190
Shiba S, Aoki Y, Gallego G. Event Collapse in Contrast Maximization Frameworks. Sensors. 2022; 22(14):5190. https://doi.org/10.3390/s22145190
Chicago/Turabian StyleShiba, Shintaro, Yoshimitsu Aoki, and Guillermo Gallego. 2022. "Event Collapse in Contrast Maximization Frameworks" Sensors 22, no. 14: 5190. https://doi.org/10.3390/s22145190
APA StyleShiba, S., Aoki, Y., & Gallego, G. (2022). Event Collapse in Contrast Maximization Frameworks. Sensors, 22(14), 5190. https://doi.org/10.3390/s22145190







