Pose Estimation and Damage Characterization of Turbine Blades during Inspection Cycles and Component-Protective Disassembly Processes
Abstract
:1. Introduction
2. Borescopic Fringe Projection
3. In-Situ Inspection of Turbine Blades
3.1. Film-Cooling Hole Detection
3.2. Data Registration
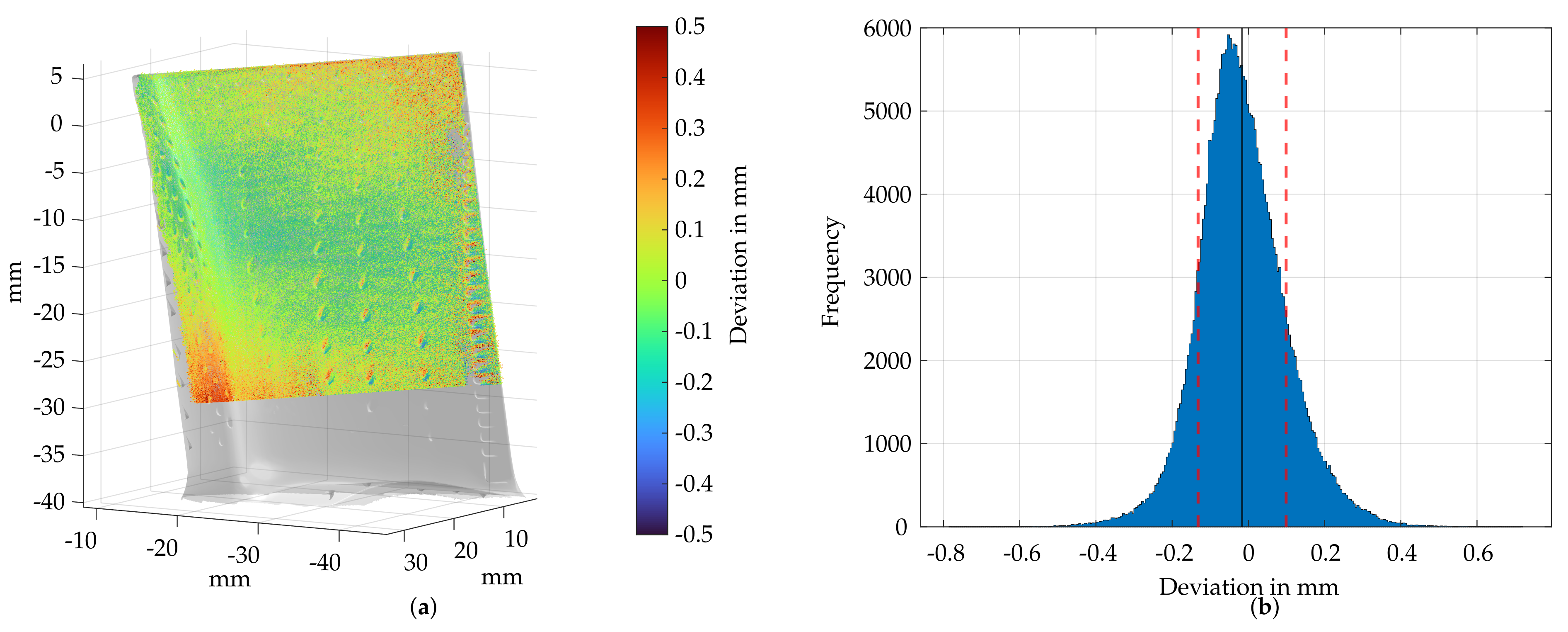
3.3. Damage Derivation
4. Disassembly of Turbine Blades
4.1. Component-Protective Disassembly
4.2. Determination of the Force Limit
4.3. Inspection of Blade Roots after Disassembly
5. Discussion
5.1. Suitability of the Measuring System
5.2. Film-Cooling Hole Detection and Point Cloud Evaluation
5.3. Evaluation of Component Protection
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CAD | Computer-Aided Design |
| DB Scan | Density-Based clustering procedure |
| DMD | Digital Micromirror Device |
| HDR | High Dynamic Range |
| ICP | Iterative Closest Point |
| K-NN | K-Nearest Neighbor |
| MIPI | Mobile Industry Processor Interface |
| RANSAC | Random Sample Consensus |
| SX | Single Crystal |
Appendix A

References
- Aschenbruck, J.; Adamczuk, R.; Seume, J.R. Recent Progress in Turbine Blade and Compressor Blisk Regeneration. Procedia CIRP 2014, 22, 256–262. [Google Scholar] [CrossRef] [Green Version]
- Drury, C.G.; Spencer, F.W.; Schurman, D.L. Measuring Human Detection Performance in Aircraft Visual Inspection. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 1997, 41, 304–308. [Google Scholar] [CrossRef]
- See, J. Visual Inspection: A Review of the Literature; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- Aust, J.; Pons, D. Comparative Analysis of Human Operators and Advanced Technologies in the Visual Inspection of Aero Engine Blades. Appl. Sci. 2022, 12, 2250. [Google Scholar] [CrossRef]
- Meng, J.; Luo, Y. A Damage Assessment System for Aero-engine Borscopic Inspection Based on Support Vector Machines. In Proceedings of the 2009 Ninth International Conference on Hybrid Intelligent Systems, Shenyang, China, 12–14 August 2009; Volume 2, pp. 3–8. [Google Scholar] [CrossRef]
- Samir, B.; Pereira, M.; Paninjath, S.; Jeon, C.U.; Chung, D.H.; Yoon, G.S.; Jung, H.Y. Improvement in accuracy of defect size measurement by automatic defect classification. In Photomask Technology 2015; Hayashi, N., Kasprowicz, B.S., Eds.; SPIE: Bellingham, WA, USA, 2015. [Google Scholar] [CrossRef]
- Svensen, M.; Hardwick, D.; Powrie, H. Deep Neural Networks Analysis of Borescope Images. In Proceedings of the PHM Society European Conference, Utrecht, The Netherlands, 3–6 July 2018. [Google Scholar] [CrossRef]
- Shen, Z.; Wan, X.; Ye, F.; Guan, X.; Liu, S. Deep Learning based Framework for Automatic Damage Detection in Aircraft Engine Borescope Inspection. In Proceedings of the 2019 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 18–21 February 2019. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lee, J.R. Videoscope-based inspection of turbofan engine blades using convolutional neural networks and image processing. Struct. Health Monit. 2019, 18, 2020–2039. [Google Scholar] [CrossRef]
- Kim, H.S.; Park, Y.S. Object Dimension Estimation for Remote Visual Inspection in Borescope Systems. KSII Trans. Internet Inf. Syst. 2019, 13, 4160–4173. [Google Scholar] [CrossRef]
- Liu, L.; Tan, E.; Cai, Z.Q.; Zhen, Y.; Yin, X.J. An Integrated Coating Inspection System for Marine and Offshore Corrosion Management. In Proceedings of the 2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 18–21 November 2018; pp. 1531–1536. [Google Scholar] [CrossRef]
- Holm, E.; Transeth, A.A.; Knudsen, O.; Stahl, A. Classification of corrosion and coating damages on bridge constructions from images using convolutional neural networks. In Proceedings of the Twelfth International Conference on Machine Vision (ICMV 2019), Amsterdam, The Netherlands, 16–18 November 2019; Osten, W., Nikolaev, D.P., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2020; Volume 11433, pp. 549–556. [Google Scholar] [CrossRef]
- Aust, J.; Shankland, S.; Pons, D.; Mukundan, R.; Mitrovic, A. Automated Defect Detection and Decision-Support in Gas Turbine Blade Inspection. Aerospace 2021, 8, 30. [Google Scholar] [CrossRef]
- He, W.; Li, C.; Nie, X.; Wei, X.; Li, Y.; Li, Y.; Luo, S. Recognition and detection of aero-engine blade damage based on Improved Cascade Mask R-CNN. Appl. Opt. 2021, 60, 5124–5133. [Google Scholar] [CrossRef] [PubMed]
- Hedrich, K.; Hinz, L.; Reithmeier, E. Damage segmentation using small convolutional neuronal networks and adversarial training methods on low-quality RGB video data. In AI and Optical Data Sciences III; Jalali, B., Kitayama, K., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2022; Volume 12019, pp. 1–10. [Google Scholar] [CrossRef]
- Geng, J.; Xie, J. Review of 3-D Endoscopic Surface Imaging Techniques. IEEE Sens. J. 2014, 14, 945–960. [Google Scholar] [CrossRef]
- Schlobohm, J.; Pösch, A.; Kästner, M.; Reithmeier, E. On the development of a low-cost rigid borescopic fringe projection system. In Photonics, Devices, and Systems VI; SPIE: Bellingham, WA, USA, 2015. [Google Scholar] [CrossRef] [Green Version]
- Schlobohm, J. Borescopic 3D Inspection of Complex Geometries. Ph.D. Thesis, Institute of Measurement and Automatic Control, Leibniz University Hannover, Hanover, Germany, 2018. [Google Scholar]
- IAE. International Aero Engine. V2500 Maintenance Manual, Borescope Inspection, Standard Practices ATA 70-00-03 2000. Technical Report. Available online: https://www.slideshare.net/RafaelHernandezM/v2500-bsi-issue-01 (accessed on 26 May 2022).
- Qin, Y.F.; Cao, J.B.; Cao, J.Q. Application of Wavelet Transform in Image Processing in Aviation Engine Damage. Appl. Mech. Mater. 2013, 347–350, 3576–3580. [Google Scholar] [CrossRef]
- Frankowski, G.; Hainich, R. DLP-based 3D metrology by structured light or projected fringe technology for life sciences and industrial metrology. In Emerging Digital Micromirror Device Based Systems and Applications; Hornbeck, L.J., Douglass, M.R., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2009; Volume 7210, pp. 102–113. [Google Scholar] [CrossRef]
- Middendorf, P.; Hedrich, K.; Kästner, M.; Reithmeier, E. Miniaturization of borescopic fringe projection systems for the inspection in confined spaces: A methodical analysis. In Emerging Digital Micromirror Device Based Systems and Applications XIII; Online, 6–11 March 2021, Lee, B.L., Ehmke, J., Eds.; SPIE: Bellingham, WA, USA, 2021. [Google Scholar] [CrossRef]
- ISO/IEC 14496-14:2003; Information Technology—Coding of Audio-Visual Objects—Part 14: MP4 File Format. Technical Report; International Organization for Standardization: Geneva, Swizerland, 2003.
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Brown, D. Close-Range Camera Calibration. Photogramm. Eng. 2002, 37, 855–866. [Google Scholar]
- Matthias, S.; Schlobohm, J.; Kästner, M.; Reithmeier, E. Fringe projection profilometry using rigid and flexible endoscopes. Tech. Mess. 2017, 84, 123–129. [Google Scholar] [CrossRef]
- DIN 26343-2; Optical 3-D Measuring Systems, Optical Systems Based on Area Scanning. Deutsches Institut für Normung e. V.: Berlin, Germany, 2012.
- ISO/IEC GUIDE 98-3:2008; Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995). International Organization for Standardizatio: Geneva, Switzerland, 2008.
- Hoppe, H.; DeRose, T.; Duchamp, T.; McDonald, J.; Stuetzle, W. Surface reconstruction from unorganized points. ACM SIGGRAPH Comput. Graph. 1992, 26, 71–78. [Google Scholar] [CrossRef]
- Friedman, J.H.; Bentley, J.L.; Finkel, R.A. An Algorithm for Finding Best Matches in Logarithmic Expected Time. ACM Trans. Math. Softw. 1977, 3, 209–226. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise; AAAI Press: Palo Alto, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Hinz, L.; Kästner, M.; Reithmeier, E. Metal Forming Tool Monitoring Based on a 3D Measuring Endoscope Using CAD Assisted Registration. Sensors 2019, 19, 2084. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Besl, P.; McKay, H. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Kabsch, W. A solution for the best rotation to relate two sets of vectors. Acta Crystallogr. Sect. A 1976, 32, 922–923. [Google Scholar] [CrossRef]
- Bluemel, R.; Raatz, A. Experimental Validation of a Solidification Model for Automated Disassembly; Institutionelles Repositorium der Leibniz Universität Hannover: Hannover, Germany, 2021; pp. 339–348. [Google Scholar] [CrossRef]
- Reed, R.C. The Superalloys; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Wang, F.; Ma, D.; Zhang, J.; Bogner, S.; Bührig-Polaczek, A. A high thermal gradient directional solidification method for growing superalloy single crystals. J. Mater. Process. Technol. 2014, 214, 3112–3121. [Google Scholar] [CrossRef]
- Harris, K.; Wahl, J. Improved Single Crystal Superalloys, CMSX-4 (SLS)[La+Y] and CMSX-486. In Proceedings of the Superalloys 2004 (Tenth International Symposium), TMS, Warrendale, PA, USA, 19–23 September 2004. [Google Scholar] [CrossRef]
- Hinz, L.; Metzner, S.; Müller, P.; Schulte, R.; Besserer, H.B.; Wackenrohr, S.; Sauer, C.; Kästner, M.; Hausotte, T.; Hübner, S.; et al. Fringe Projection Profilometry in Production Metrology: A Multi-Scale Comparison in Sheet-Bulk Metal Forming. Sensors 2021, 21, 2389. [Google Scholar] [CrossRef] [PubMed]
- Smith, I. LSGE: The Least Squares Geometric Elements Library. 2004. Available online: http://www.eurometros.org/gen_report.php?category=distributions&pkey=14 (accessed on 31 May 2022).















| Component | Device Number | Manufacturer |
|---|---|---|
| Camera sensor | OV2740 | OmniVision Technologies, Inc. (Santa Clara, CA, USA) |
| Camera module | MP-FPC31105-18350-200 | MISUMI Electronics Corp. (New Taipei, Taiwan) |
| Frame grabber board | See3CAM_CX3RDK | e-con Systems India Pvt Ltd. (Chennai, Tamil Nadu, India) |
| Borescope | 86290CF | KARL STORZ SE & Co. KG (Tuttlingen, Germany) |
| Borescope lens | 20200043 C-MOUNT lens | KARL STORZ SE & Co. KG (Tuttlingen, Germany) |
| Projector | DLP 4500 EVM | Texas Instruments Inc. (Dallas, TX, USA) |
| Label | P51 | P10 | P40 | 2 | P48 | N26 | - | - |
|---|---|---|---|---|---|---|---|---|
| Force in kN | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 100 |
| Surface Pressure in MPa | 44.2 | 66.3 | 88.4 | 110.0 | 132.6 | 154.7 | 176.8 | 221.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Middendorf, P.; Blümel, R.; Hinz, L.; Raatz, A.; Kästner, M.; Reithmeier, E. Pose Estimation and Damage Characterization of Turbine Blades during Inspection Cycles and Component-Protective Disassembly Processes. Sensors 2022, 22, 5191. https://doi.org/10.3390/s22145191
Middendorf P, Blümel R, Hinz L, Raatz A, Kästner M, Reithmeier E. Pose Estimation and Damage Characterization of Turbine Blades during Inspection Cycles and Component-Protective Disassembly Processes. Sensors. 2022; 22(14):5191. https://doi.org/10.3390/s22145191
Chicago/Turabian StyleMiddendorf, Philipp, Richard Blümel, Lennart Hinz, Annika Raatz, Markus Kästner, and Eduard Reithmeier. 2022. "Pose Estimation and Damage Characterization of Turbine Blades during Inspection Cycles and Component-Protective Disassembly Processes" Sensors 22, no. 14: 5191. https://doi.org/10.3390/s22145191
APA StyleMiddendorf, P., Blümel, R., Hinz, L., Raatz, A., Kästner, M., & Reithmeier, E. (2022). Pose Estimation and Damage Characterization of Turbine Blades during Inspection Cycles and Component-Protective Disassembly Processes. Sensors, 22(14), 5191. https://doi.org/10.3390/s22145191






