RBF Neural Network Sliding Mode Control for Passification of Nonlinear Time-Varying Delay Systems with Application to Offshore Cranes
Abstract
:1. Introduction
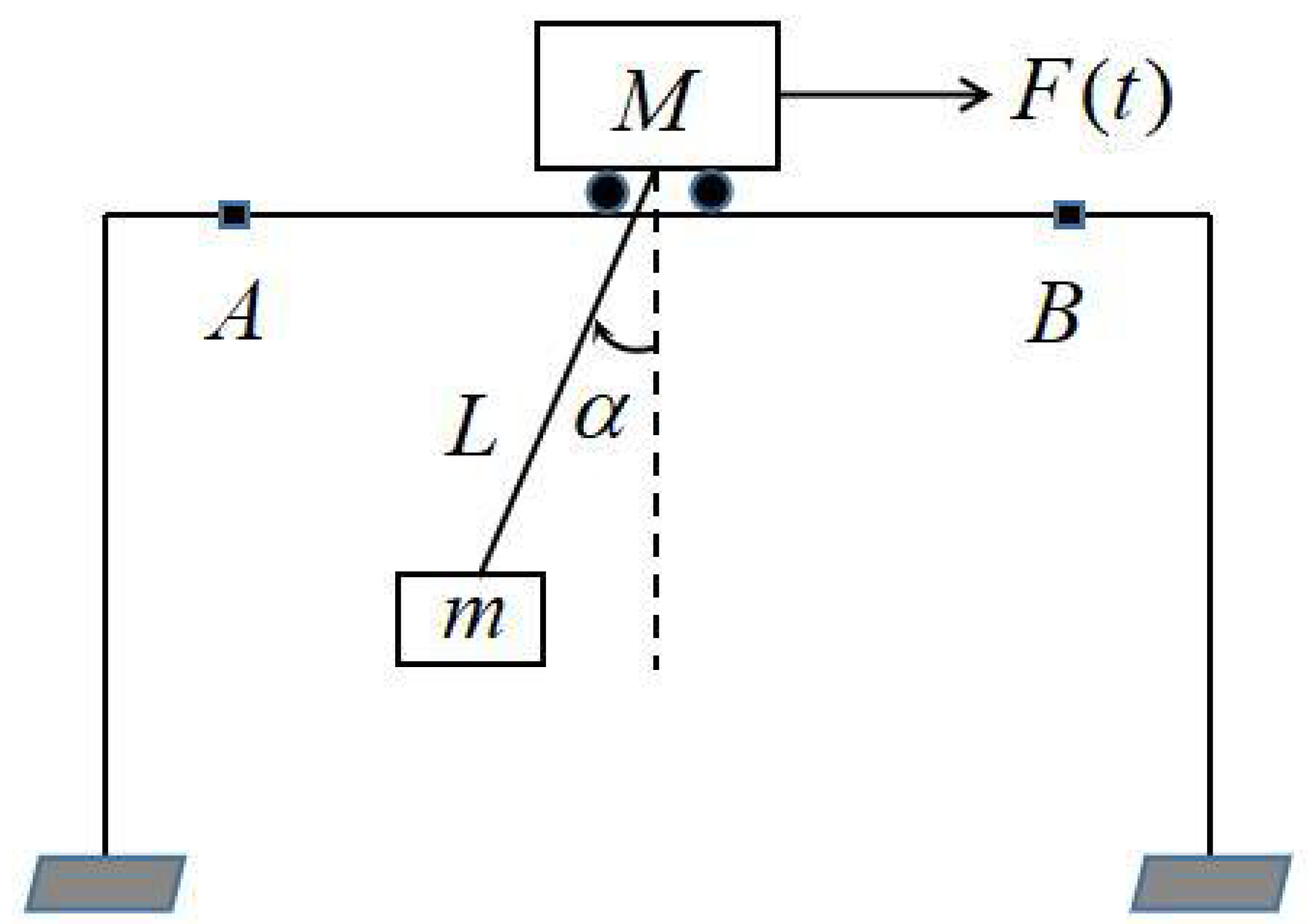
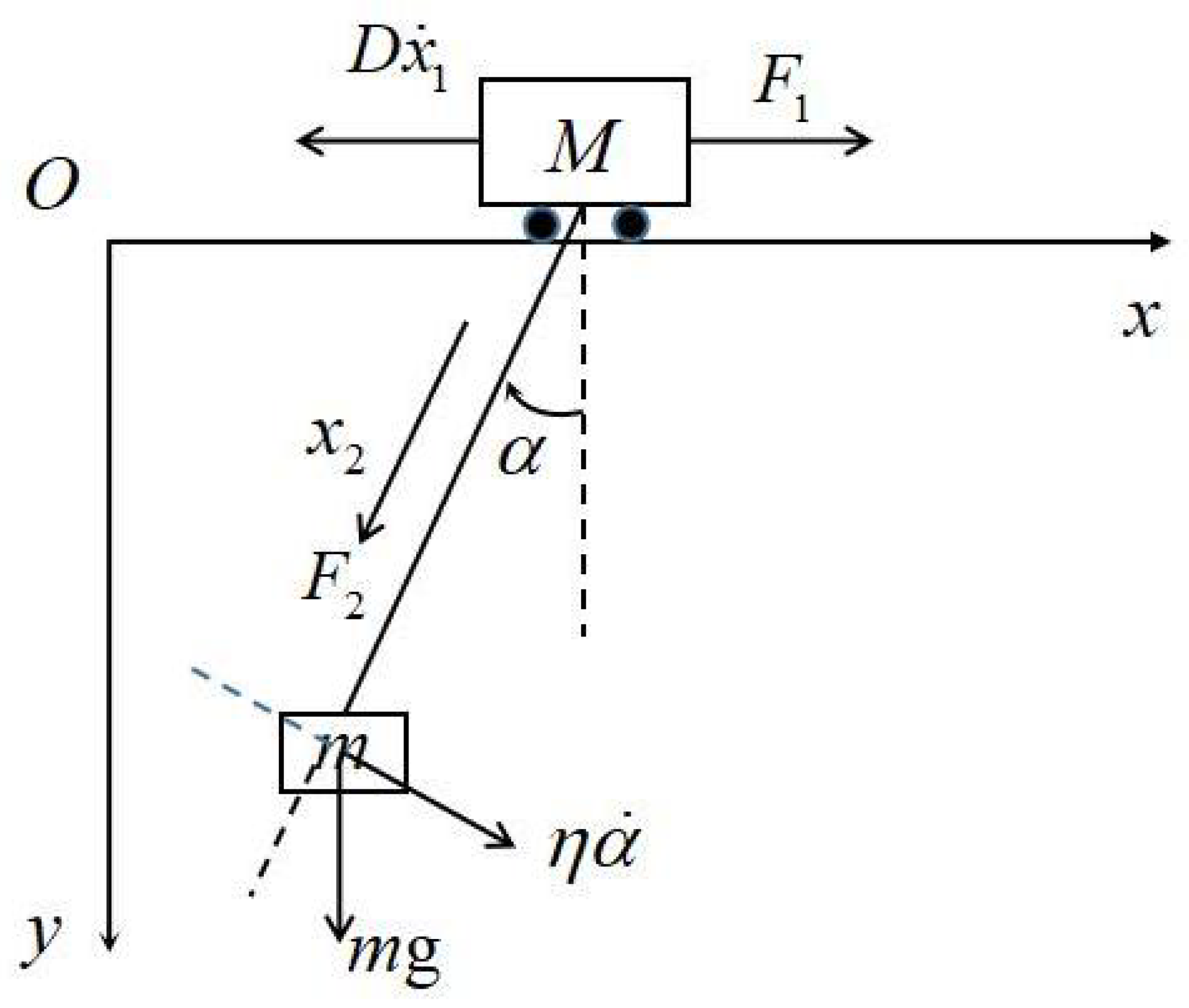
2. Model Establishing and Problem Statement
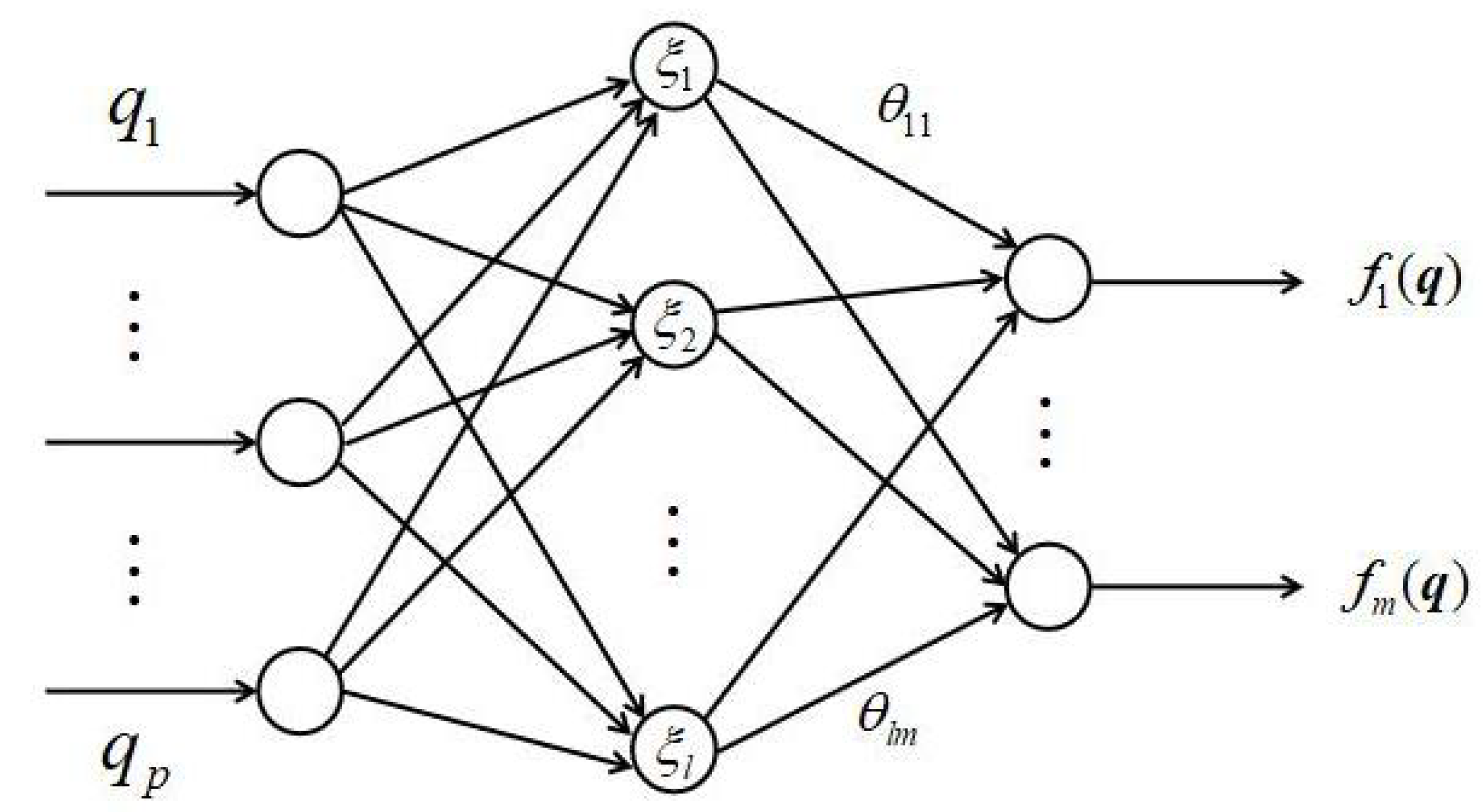
3. Main Results
3.1. Sliding Motion Design
3.2. Stability Analysis
3.3. Computation of Gain Matrix
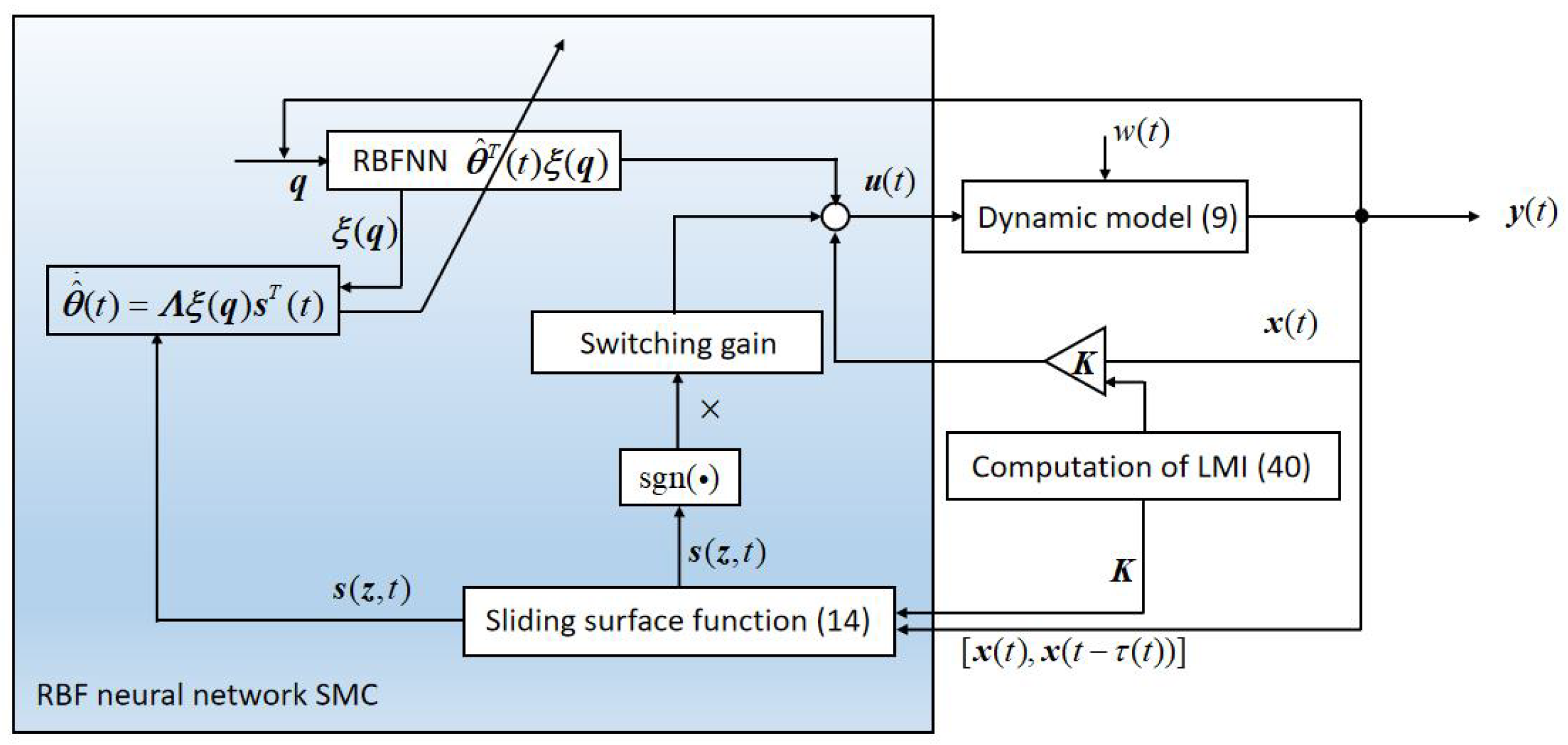
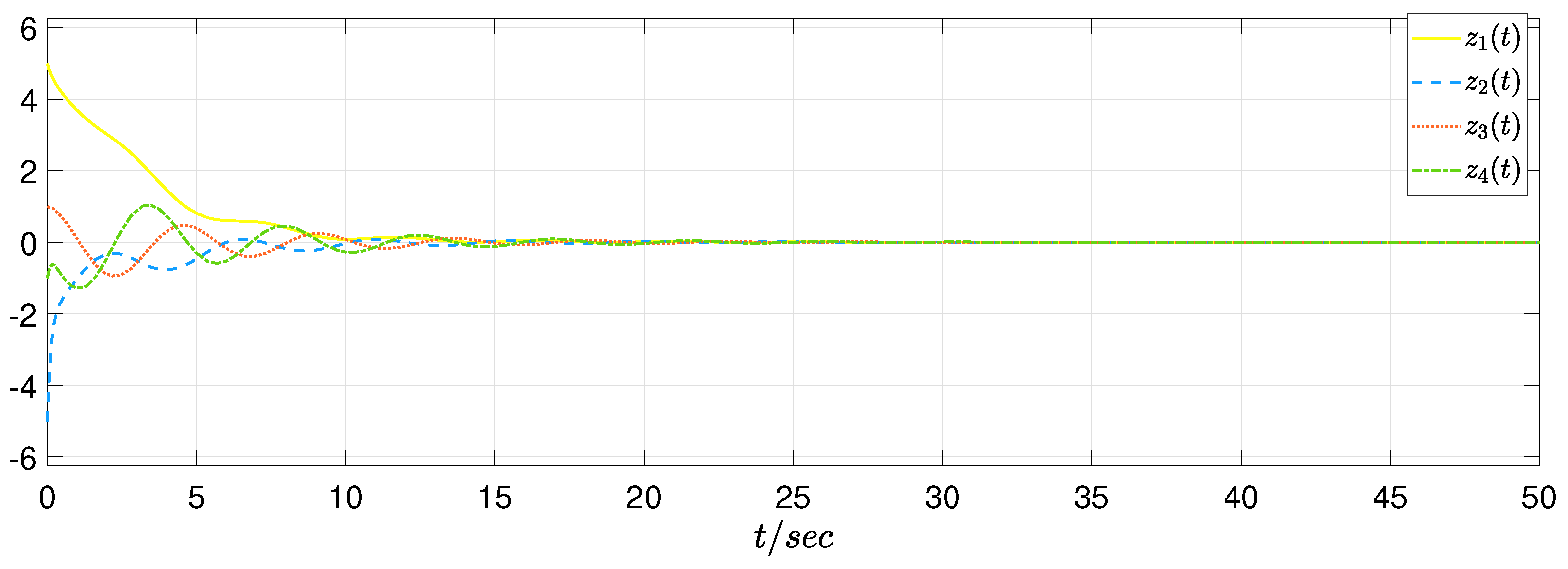
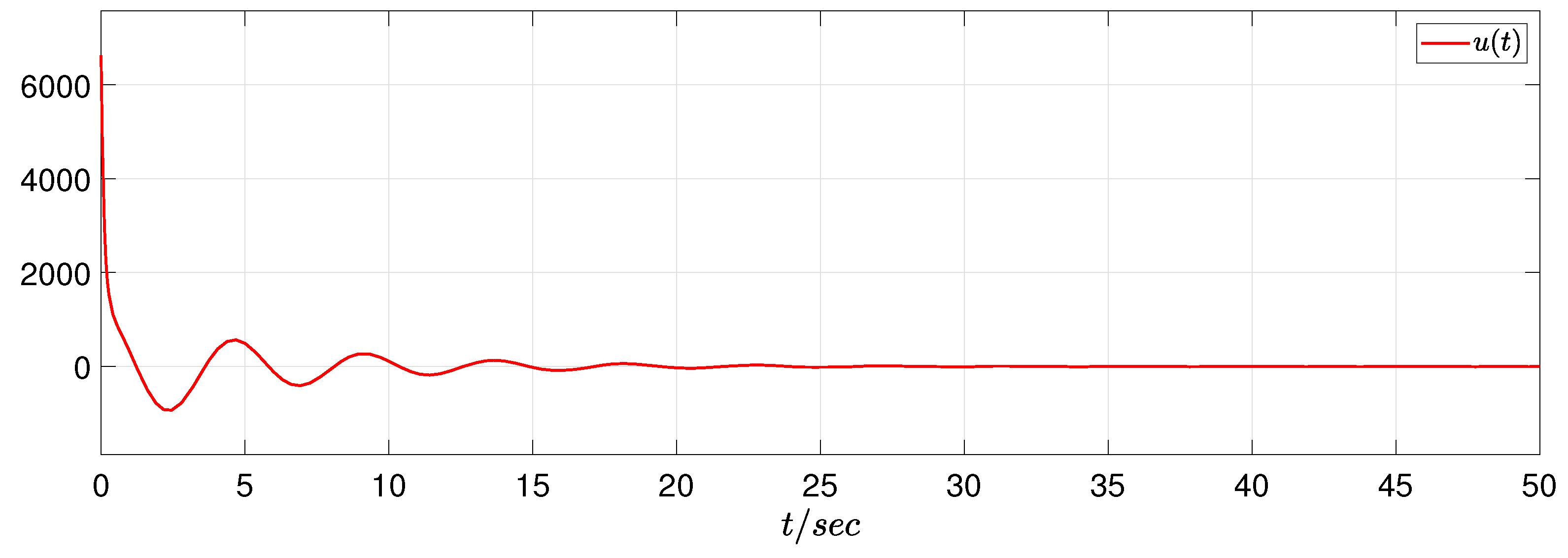
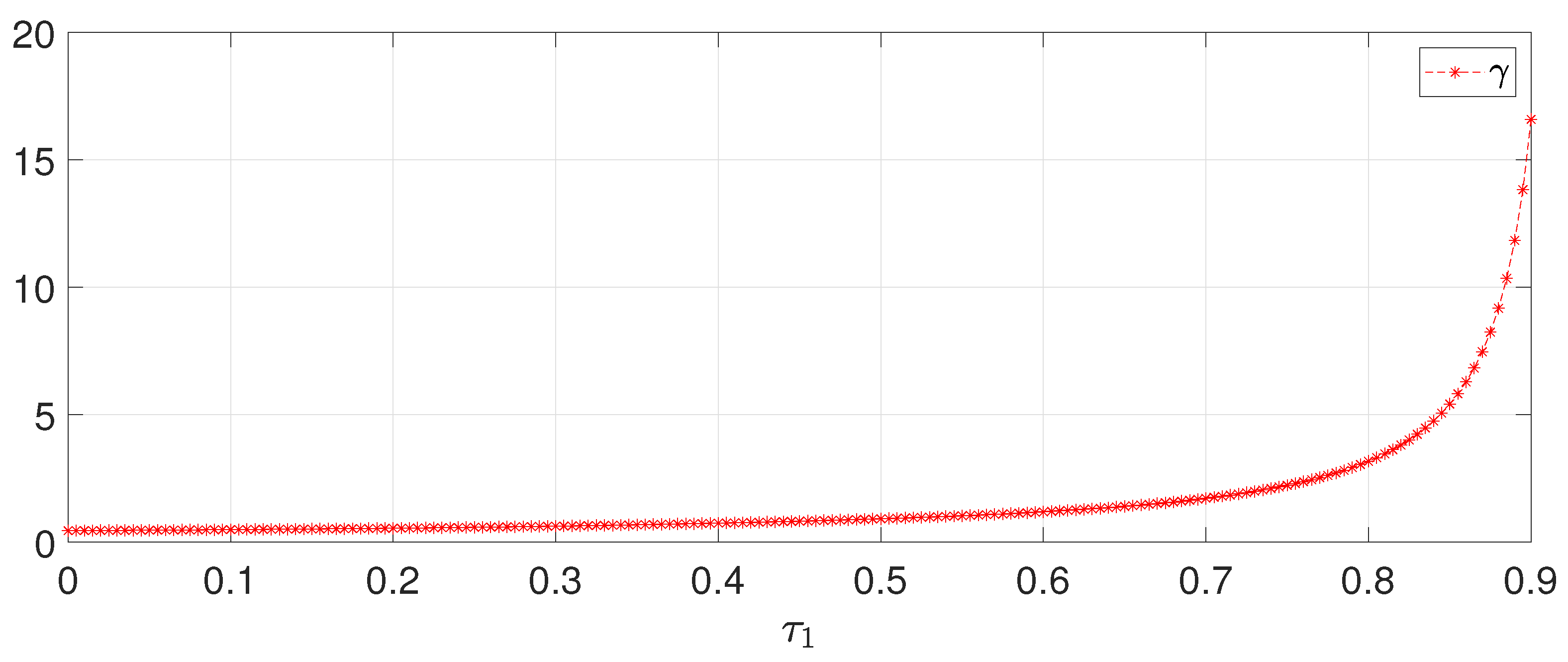
4. Simulation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, X.; Chen, X.; Xu, S.; Zhang, B.; Zhang, Z. Adaptive output feedback control of nonlinear time-delay systems with application to chemical reactor systems. IEEE Trans. Ind. Electron. 2017, 64, 4792–4799. [Google Scholar] [CrossRef]
- Yi, S.; Ulsoy, A.G.; Nelson, P.W. Design of observer-based feedback control for time-delay systems with application to automotive powertrain control. J. Frankl. Inst. 2010, 347, 358–376. [Google Scholar] [CrossRef]
- Boussaada, I.; Tliba, S.; Niculescu, S.I.; Ünal, H.U.; Vyhlídal, T. Further remarks on the effect of multiple spectral values on the dynamics of time-delay systems. Application to the control of a mechanical system. Linear Algebra Its Appl. 2018, 542, 589–604. [Google Scholar] [CrossRef] [Green Version]
- Gopalsamy, K. Stability and Oscillations in Delay Differential Equations of Population Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Arik, S. An analysis of stability of neutral-type neural systems with constant time delays. J. Frankl. Inst. 2014, 351, 4949–4959. [Google Scholar] [CrossRef]
- Xu, X.; Liu, L.; Feng, G. Consensus of heterogeneous linear multiagent systems with communication time-delays. IEEE Trans. Cybern. 2017, 47, 1820–1829. [Google Scholar] [CrossRef]
- Wu, M.; He, Y.; She, J.H.; Liu, G.P. Delay-dependent criteria for robust stability of time-varying delay systems. Automatica 2004, 40, 1435–1439. [Google Scholar] [CrossRef]
- Wu, L.; Su, X.; Shi, P.; Qiu, J. A new approach to stability analysis and stabilization of discrete-time TS fuzzy time-varying delay systems. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2010, 41, 273–286. [Google Scholar] [CrossRef]
- Karimi, H.R. Robust delay-dependent H∞ control of uncertain time-delay systems with mixed neutral, discrete, and distributed time-delays and Markovian switching parameters. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1910–1923. [Google Scholar] [CrossRef]
- Feng, Z.; Lam, J. Integral partitioning approach to robust stabilization for uncertain distributed time-delay systems. Int. J. Robust Nonlinear Control 2012, 22, 676–689. [Google Scholar] [CrossRef]
- Wang, Y.E.; Wu, D.; Karimi, H.R. Robust stability of switched nonlinear systems with delay and sampling. Int. J. Robust Nonlinear Control 2022, 32, 2570–2584. [Google Scholar] [CrossRef]
- Xiao, H.; Zhu, Q.; Karimi, H.R. Stability of stochastic delay switched neural networks with all unstable subsystems: A multiple discretized Lyapunov-Krasovskii functionals method. Inf. Sci. 2022, 582, 302–315. [Google Scholar] [CrossRef]
- Wei, Y.; Karimi, H.R.; Yang, S. New results on sampled-data output-feedback control of linear parameter-varying systems. Int. J. Robust Nonlinear Control 2022, 32, 5070–5085. [Google Scholar] [CrossRef]
- Utkin, V.I.; Vadim, I. Sliding mode control. Var. Struct. Syst. Princ. Implement. 2004, 66, 1. [Google Scholar]
- Baek, J.; Jin, M.; Han, S. A new adaptive sliding-mode control scheme for application to robot manipulators. IEEE Trans. Ind. Electron. 2016, 63, 3628–3637. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Karimi, H.R.; Shen, H.; Fang, Z. Sliding mode control of fuzzy singularly perturbed systems with application to electric circuit. IEEE Trans. Syst. Man Cybern. Syst. 2018, 29, 1667–1675. Available online: https://re.public.polimi.it/handle/11311/1036437?mode=full.738 (accessed on 11 June 2022).
- Wang, Y.; Jiang, B.; Wu, Z.G.; Xie, S.; Peng, Y. Adaptive sliding mode fault-tolerant fuzzy tracking control with application to unmanned marine vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6691–6700. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system. IEEE Trans. Power Electron. 2019, 35, 4117–4126. [Google Scholar] [CrossRef]
- Sumantri, B.; Uchiyama, N.; Sano, S. Least square based sliding mode control for a quad-rotor helicopter and energy saving by chattering reduction. Mech. Syst. Signal Process. 2016, 66, 769–784. [Google Scholar] [CrossRef]
- Utkin, V. Discussion aspects of high-order sliding mode control. IEEE Trans. Autom. Control 2015, 61, 829–833. [Google Scholar] [CrossRef]
- Guo, X.; Liu, Z.; Gao, C. Fault-tolerant adaptive control for uncertain switched systems with time-varying delay and actuator faults based on sliding mode technique. J. Frankl. Inst. 2022, 359, 5231–5250. [Google Scholar] [CrossRef]
- Jiang, B.; Karimi, H.R.; Yang, S.; Gao, C.; Kao, Y. Observer-based adaptive sliding mode control for nonlinear stochastic Markov jump systems via TšCS fuzzy modeling: Applications to robot arm model. IEEE Trans. Ind. Electron. 2020, 68, 466–477. [Google Scholar] [CrossRef]
- Palraj, J.; Mathiyalagan, K.; Shi, P. New results on robust sliding mode control for linear time-delay systems. IMA J. Math. Control Inf. 2021, 38, 320–336. [Google Scholar]
- Jiang, B.; Gao, C.C. Decentralized adaptive sliding mode control of large-scale semi-Markovian jump interconnected systems with dead-zone input. IEEE Trans. Autom. Control 2022, 67, 1521–1528. [Google Scholar]
- Liu, Z.; Karimi, H.R.; Yu, J. Passivity-based robust sliding mode synthesis for uncertain delayed stochastic systems via state observer. Automatica 2020, 111, 108596. [Google Scholar]
- Jiang, B.; Wu, Z.; Karimi, H.R. A distributed dynamic event-triggered mechanism to HMM-based observer design for H∞ sliding mode control of Markov jump systems. Automatica 2022, 142, 110357. [Google Scholar]
- Lewis, F.W.; Jagannathan, S.; Yesildirak, A. Neural Network Control of Robot Manipulators and Non-Linear Systems; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Vasickaninova, A.; Bakosova, M.; Meszaros, A.; Klemeš, J.J. Neural network predictive control of a heat exchanger. Appl. Therm. Eng. 2011, 31, 2094–2100. [Google Scholar]
- Aguiar, C.; Leite, D.; Pereira, D.; Andonovski, G.; Skrjanc, I. Nonlinear modeling and robust LMI fuzzy control of overhead crane systems. J. Frankl. Inst. 2021, 358, 1376–1402. [Google Scholar]
- Chen, Y.; Xue, A.; Lu, R.; Zhou, S. On robustly exponential stability of uncertain neutral systems with time-varying delays and nonlinear perturbations. Nonlinear Anal. Theory, Methods Appl. 2008, 68, 2464–2470. [Google Scholar]
- Wu, Z.G.; Park, J.H.; Su, H.; Chu, J. Delay-dependent passivity for singular Markov jump systems with time-delays. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 669–681. [Google Scholar]
- Gu, K.; Chen, J.; Kharitonov, V.L. Stability of Time-Delay Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]

| 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | |
| 0.730 | 0.768 | 0.793 | 0.811 | 0.824 | 0.835 | 0.844 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Liu, D.; Karimi, H.R.; Li, B. RBF Neural Network Sliding Mode Control for Passification of Nonlinear Time-Varying Delay Systems with Application to Offshore Cranes. Sensors 2022, 22, 5253. https://doi.org/10.3390/s22145253
Jiang B, Liu D, Karimi HR, Li B. RBF Neural Network Sliding Mode Control for Passification of Nonlinear Time-Varying Delay Systems with Application to Offshore Cranes. Sensors. 2022; 22(14):5253. https://doi.org/10.3390/s22145253
Chicago/Turabian StyleJiang, Baoping, Dongyu Liu, Hamid Reza Karimi, and Bo Li. 2022. "RBF Neural Network Sliding Mode Control for Passification of Nonlinear Time-Varying Delay Systems with Application to Offshore Cranes" Sensors 22, no. 14: 5253. https://doi.org/10.3390/s22145253
APA StyleJiang, B., Liu, D., Karimi, H. R., & Li, B. (2022). RBF Neural Network Sliding Mode Control for Passification of Nonlinear Time-Varying Delay Systems with Application to Offshore Cranes. Sensors, 22(14), 5253. https://doi.org/10.3390/s22145253







