RCA-LF: Dense Light Field Reconstruction Using Residual Channel Attention Networks
Abstract
:1. Introduction
2. Related Work
2.1. LF Representation
2.2. LF Reconstruction
2.2.1. Traditional Approaches
2.2.2. Deep Learning Depth-Based Approaches
2.2.3. Deep Learning Non-Depth-Based Approaches
3. Methodology
3.1. Problem Formulation
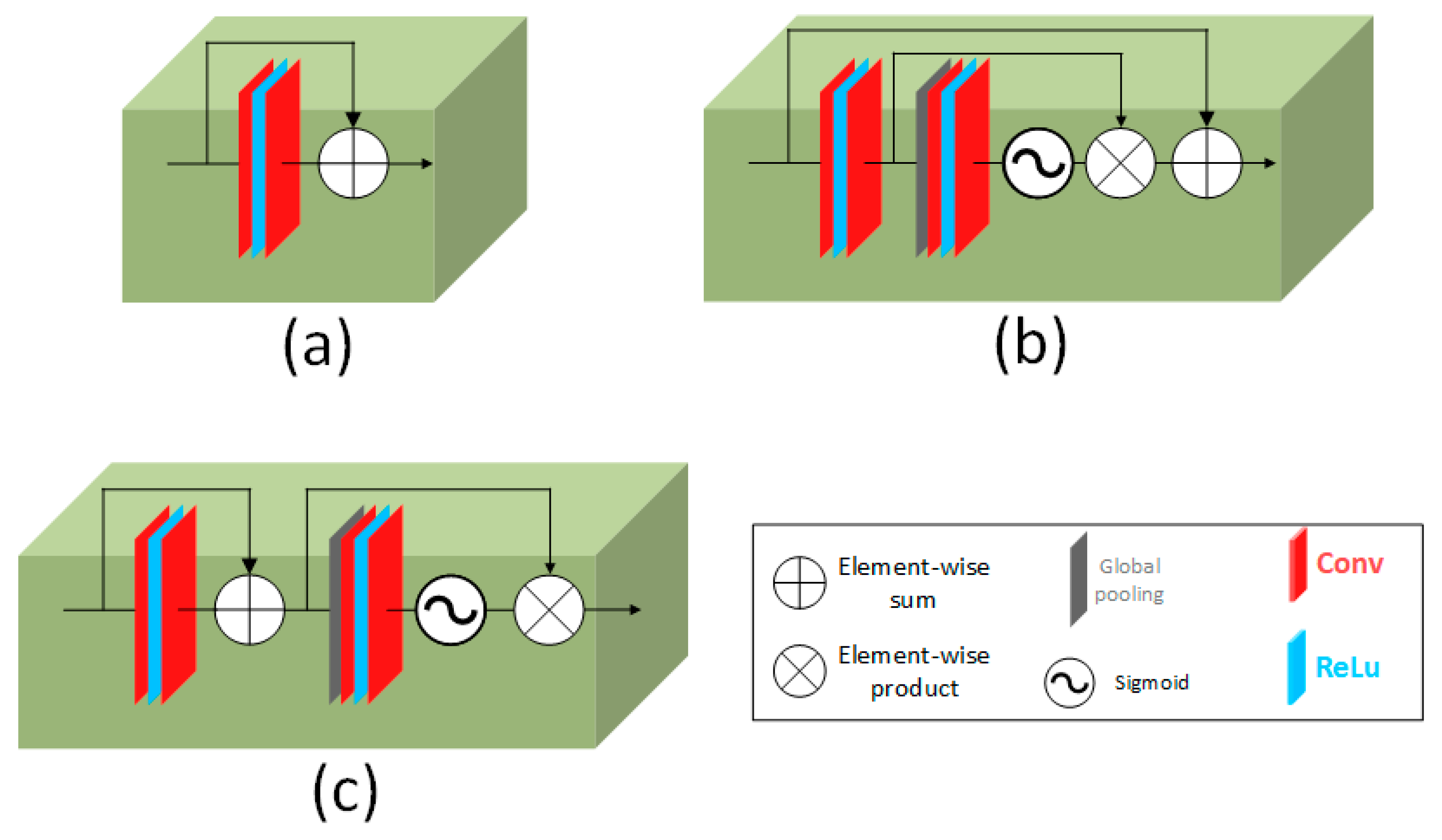
3.2. Network Architecture
3.3. Implementation Details
4. Experiments and Discussion
4.1. Different Reconstruction Tasks
4.1.1. Task 3 × 3–7 × 7
| Dataset | Wu [31] | Wu [32] | Liu [36] | Zhang [37] | Salem [38] | Proposed |
|---|---|---|---|---|---|---|
| 30 Scenes | 41.40/0.980 | 43.592/0.986 | 44.86/0.991 | 45.68/0.992 | 45.96/0.991 | 46.41/0.992 |
| Reflective | 42.19/0.974 | 43.092/0.977 | 44.31/0.980 | 44.92/0.982 | 45.45/0.983 | 45.73/0.984 |
| Occlusions | 37.25/0.925 | 39.748/0.948 | 40.16/0.957 | 40.80/0.955 | 41.21/0.957 | 41.41/0.951 |
| Average | 40.28/0.959 | 42.14/0.971 | 43.11/0.976 | 43.80/0.976 | 44.21/0.977 | 44.51/0.976 |

4.1.2. Task 2 × 2–8 × 8, Extrapolation 0
4.1.3. Task 2 × 2–8 × 8, Extrapolation 1, 2
| Dataset | Wu [31] | Kalantari [15] | Shi [16] | Yeung [46] | Zhang [37] | Salem [40] | Proposed |
|---|---|---|---|---|---|---|---|
| 30 Scenes | 35.25/0.928 | 40.11/0.979 | 41.12/0.985 | 41.21/0.982 | 41.98/0.986 | 42.33/0.985 | 42.69/0.986 |
| Reflective | 35.15/0.940 | 37.35/0.954 | 38.10/0.958 | 38.09/0.959 | 38.71/0.962 | 38.86/0.962 | 39.45/0.967 |
| Occlusions | 31.77/0.881 | 33.21/0.911 | 34.41/0.929 | 34.50/0.921 | 34.76/0.918 | 34.69/0.922 | 35.41/0.928 |
| Average | 34.06/0.916 | 36.89/0.948 | 37.88/0.957 | 37.93/0.954 | 38.48/0.955 | 38.62/0.956 | 39.18/0.960 |
| Dataset | Yeung [46] | Zhang [37] | Salem [40] | Proposed |
|---|---|---|---|---|
| 30 Scenes | 42.47/0.985 | 43.57/0.989 | 43.76/0.988 | 44.26/0.989 |
| Reflective | 41.61/0.973 | 42.33/0.975 | 42.44/0.974 | 43.16/0.979 |
| Occlusions | 37.28/0.934 | 37.61/0.937 | 37.93/0.948 | 38.47/0.943 |
| Average | 40.45/0.964 | 41.17/0.967 | 41.38/0.970 | 41.96/0.970 |
| Dataset | Yeung [46] | Zhang [37] | Salem [40] | Proposed |
|---|---|---|---|---|
| 30 Scenes | 42.74/0.986 | 43.41/0.989 | 43.43/0.987 | 43.92/0.989 |
| Reflective | 41.52/0.972 | 42.09/0.975 | 42.26/0.975 | 42.81/0.978 |
| Occlusions | 36.96/0.937 | 37.60/0.944 | 37.91/0.945 | 38.25/0.935 |
| Average | 40.41/0.965 | 41.03/0.969 | 41.20/0.969 | 41.66/0.967 |


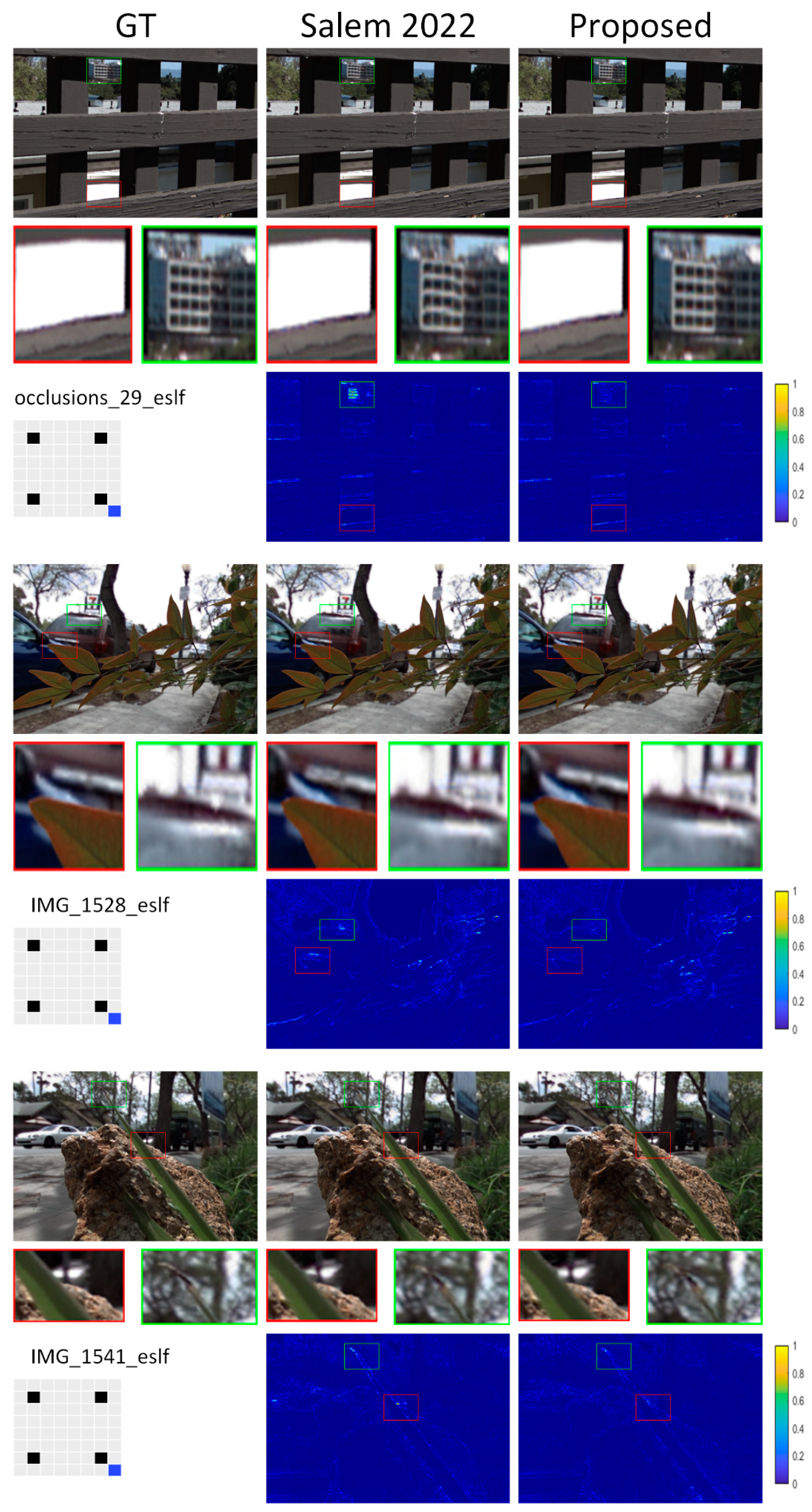
4.2. Reconstruction Time
4.3. Ablation Study
| Model 3 × 3–7 × 7 | 30 Scenes | Reflective | Occlusions | Average |
|---|---|---|---|---|
| No CA | 44.86/0.990 | 44.74/0.981 | 40.06/0.951 | 43.22/0.974 |
| CA inside RB | 46.20/0.992 | 45.71/0.984 | 41.35/0.954 | 44.42/0.976 |
| CA separated from RB | 46.41/0.992 | 45.73/0.984 | 41.41/0.951 | 44.51/0.976 |
5. Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Wu, T.; Yang, J.; Wang, L.; An, W.; Guo, Y. DeOccNet: Learning to see through foreground occlusions in light fields. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 118–127. [Google Scholar]
- Li, Y.; Yang, W.; Xu, Z.; Chen, Z.; Shi, Z.; Zhang, Y.; Huang, L. Mask4D: 4D convolution network for light field occlusion removal. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 2480–2484. [Google Scholar]
- Wang, W.; Lin, Y.; Zhang, S. Enhanced spinning parallelogram operator combining color constraint and histogram integration for robust light field depth estimation. IEEE Signal Process. Lett. 2021, 28, 1080–1084. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Liang, Z.; Yang, J.; An, W.; Guo, Y. Occlusion-Aware Cost Constructor for Light Field Depth Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 19809–19818. [Google Scholar]
- Shi, J.; Jiang, X.; Guillemot, C. A framework for learning depth from a flexible subset of dense and sparse light field views. IEEE Trans. Image Process. 2019, 28, 5867–5880. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Liu, Y.; Zhang, S.; Poppe, R.; Wang, M. Light field saliency detection with deep convolutional networks. IEEE Trans. Image Process. 2020, 29, 4421–4434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piao, Y.; Jiang, Y.; Zhang, M.; Wang, J.; Lu, H. PANet: Patch-Aware Network for Light Field Salient Object Detection. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.; Zhu, L.; Li, J.; Zou, X.; Tang, Y. Collision-free path planning for a guava-harvesting robot based on recurrent deep reinforcement learning. Comput. Electron. Agric. 2021, 188, 106350. [Google Scholar] [CrossRef]
- Lin, G.; Tang, Y.; Zou, X.; Wang, C. Three-dimensional reconstruction of guava fruits and branches using instance segmentation and geometry analysis. Comput. Electron. Agric. 2021, 184, 106107. [Google Scholar] [CrossRef]
- Wu, G.; Masia, B.; Jarabo, A.; Zhang, Y.; Wang, L.; Dai, Q.; Chai, T.; Liu, Y. Light field image processing: An overview. IEEE J. Sel. Top. Signal Process. 2017, 11, 926–954. [Google Scholar] [CrossRef] [Green Version]
- Georgiev, T.G.; Lumsdaine, A. Focused plenoptic camera and rendering. J. Electron. Imaging 2010, 19, 021106. [Google Scholar]
- Raytrix. Available online: https://raytrix.de/ (accessed on 6 May 2022).
- Wu, G.; Zhao, M.; Wang, L.; Dai, Q.; Chai, T.; Liu, Y. Light field reconstruction using deep convolutional network on EPI. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6319–6327. [Google Scholar]
- Hu, Z.; Chung, Y.Y.; Ouyang, W.; Chen, X.; Chen, Z. Light field reconstruction using hierarchical features fusion. Expert Syst. Appl. 2020, 151, 113394. [Google Scholar] [CrossRef]
- Kalantari, N.K.; Wang, T.-C.; Ramamoorthi, R. Learning-based view synthesis for light field cameras. ACM Trans. Graph. (TOG) 2016, 35, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Jiang, X.; Guillemot, C. Learning fused pixel and feature-based view reconstructions for light fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–20 June 2020; pp. 2555–2564. [Google Scholar]
- Cheng, Z.; Xiong, Z.; Chen, C.; Liu, D.; Zha, Z.-J. Light field super-resolution with zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 10010–10019. [Google Scholar]
- Ko, K.; Koh, Y.J.; Chang, S.; Kim, C.-S. Light field super-resolution via adaptive feature remixing. IEEE Trans. Image Process. 2021, 30, 4114–4128. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Chang, S.; Lin, Y. End-to-end light field spatial super-resolution network using multiple epipolar geometry. IEEE Trans. Image Process. 2021, 30, 5956–5968. [Google Scholar] [CrossRef] [PubMed]
- Bergen, J.R.; Adelson, E.H. The plenoptic function and the elements of early vision. Comput. Models Vis. Process. 1991, 1, 8. [Google Scholar]
- Levoy, M.; Hanrahan, P. Light field rendering. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 4–9 August 1996; pp. 31–42. [Google Scholar]
- Wanner, S.; Goldluecke, B. Spatial and angular variational super-resolution of 4D light fields. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 608–621. [Google Scholar]
- Mitra, K.; Veeraraghavan, A. Light field denoising, light field superresolution and stereo camera based refocussing using a GMM light field patch prior. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 18–20 June 2012; pp. 22–28. [Google Scholar]
- Pujades, S.; Devernay, F.; Goldluecke, B. Bayesian view synthesis and image-based rendering principles. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 3906–3913. [Google Scholar]
- Chaurasia, G.; Duchene, S.; Sorkine-Hornung, O.; Drettakis, G. Depth synthesis and local warps for plausible image-based navigation. ACM Trans. Graph. 2013, 32, 1–12. [Google Scholar] [CrossRef]
- Zhang, F.-L.; Wang, J.; Shechtman, E.; Zhou, Z.-Y.; Shi, J.-X.; Hu, S.-M. Plenopatch: Patch-based plenoptic image manipulation. IEEE Trans. Vis. Comput. Graph. 2016, 23, 1561–1573. [Google Scholar] [CrossRef] [Green Version]
- Vagharshakyan, S.; Bregovic, R.; Gotchev, A. Light field reconstruction using shearlet transform. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 133–147. [Google Scholar] [CrossRef] [Green Version]
- Salem, A.; Ibrahem, H.; Kang, H.-S. Dual Disparity-Based Novel View Reconstruction for Light Field Images Using Discrete Cosine Transform Filter. IEEE Access 2020, 8, 72287–72297. [Google Scholar] [CrossRef]
- Jin, J.; Hou, J.; Yuan, H.; Kwong, S. Learning light field angular super-resolution via a geometry-aware network. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 11141–11148. [Google Scholar]
- Yeung, H.W.F.; Hou, J.; Chen, X.; Chen, J.; Chen, Z.; Chung, Y.Y. Light field spatial super-resolution using deep efficient spatial-angular separable convolution. IEEE Trans. Image Process. 2018, 28, 2319–2330. [Google Scholar] [CrossRef]
- Wu, G.; Liu, Y.; Fang, L.; Dai, Q.; Chai, T. Light field reconstruction using convolutional network on EPI and extended applications. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1681–1694. [Google Scholar] [CrossRef]
- Wu, G.; Liu, Y.; Fang, L.; Chai, T. Revisiting light field rendering with deep anti-aliasing neural network. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Meng, N.; So, H.K.-H.; Sun, X.; Lam, E.Y. High-dimensional dense residual convolutional neural network for light field reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 873–886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mildenhall, B.; Srinivasan, P.P.; Ortiz-Cayon, R.; Kalantari, N.K.; Ramamoorthi, R.; Ng, R.; Kar, A. Local light field fusion: Practical view synthesis with prescriptive sampling guidelines. ACM Trans. Graph. 2019, 38, 1–14. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Zhang, K.; Wang, Z.; Sun, Z.; Tan, T. High-fidelity view synthesis for light field imaging with extended pseudo 4DCNN. IEEE Trans. Comput. Imaging 2020, 6, 830–842. [Google Scholar] [CrossRef]
- Liu, D.; Huang, Y.; Wu, Q.; Ma, R.; An, P. Multi-angular epipolar geometry based light field angular reconstruction network. IEEE Trans. Comput. Imaging 2020, 6, 1507–1522. [Google Scholar] [CrossRef]
- Zhang, S.; Chang, S.; Shen, Z.; Lin, Y. Micro-Lens Image Stack Upsampling for Densely-Sampled Light Field Reconstruction. IEEE Trans. Comput. Imaging 2021, 7, 799–811. [Google Scholar] [CrossRef]
- Salem, A.; Ibrahem, H.; Kang, H.-S. Light Field Reconstruction Using Residual Networks on Raw Images. Sensors 2022, 22, 1956. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Salem, A.; Ibrahem, H.; Yagoub, B.; Kang, H.-S. End-to-End Residual Network for Light Field Reconstruction on Raw Images and View Image Stacks. Sensors 2022, 22, 3540. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Raj, A.S.; Lowney, M.; Shah, R.; Wetzstein, G. Stanford Lytro Light Field Archive; Stanford Computational Imaging Lab: Stanford, CA, USA, 2016. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. {TensorFlow}: A System for {Large-Scale} Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Yeung, H.W.F.; Hou, J.; Chen, J.; Chung, Y.Y.; Chen, X. Fast light field reconstruction with deep coarse-to-fine modeling of spatial-angular clues. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 137–152. [Google Scholar]
- Wang, Y.; Liu, F.; Wang, Z.; Hou, G.; Sun, Z.; Tan, T. End-to-end view synthesis for light field imaging with pseudo 4DCNN. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 333–348. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salem, A.; Ibrahem, H.; Kang, H.-S. RCA-LF: Dense Light Field Reconstruction Using Residual Channel Attention Networks. Sensors 2022, 22, 5254. https://doi.org/10.3390/s22145254
Salem A, Ibrahem H, Kang H-S. RCA-LF: Dense Light Field Reconstruction Using Residual Channel Attention Networks. Sensors. 2022; 22(14):5254. https://doi.org/10.3390/s22145254
Chicago/Turabian StyleSalem, Ahmed, Hatem Ibrahem, and Hyun-Soo Kang. 2022. "RCA-LF: Dense Light Field Reconstruction Using Residual Channel Attention Networks" Sensors 22, no. 14: 5254. https://doi.org/10.3390/s22145254
APA StyleSalem, A., Ibrahem, H., & Kang, H.-S. (2022). RCA-LF: Dense Light Field Reconstruction Using Residual Channel Attention Networks. Sensors, 22(14), 5254. https://doi.org/10.3390/s22145254






