Generalized Cross-Correlation Strain Demodulation Method Based on Local Similar Spectral Scanning
Abstract
:1. Introduction
2. Theory
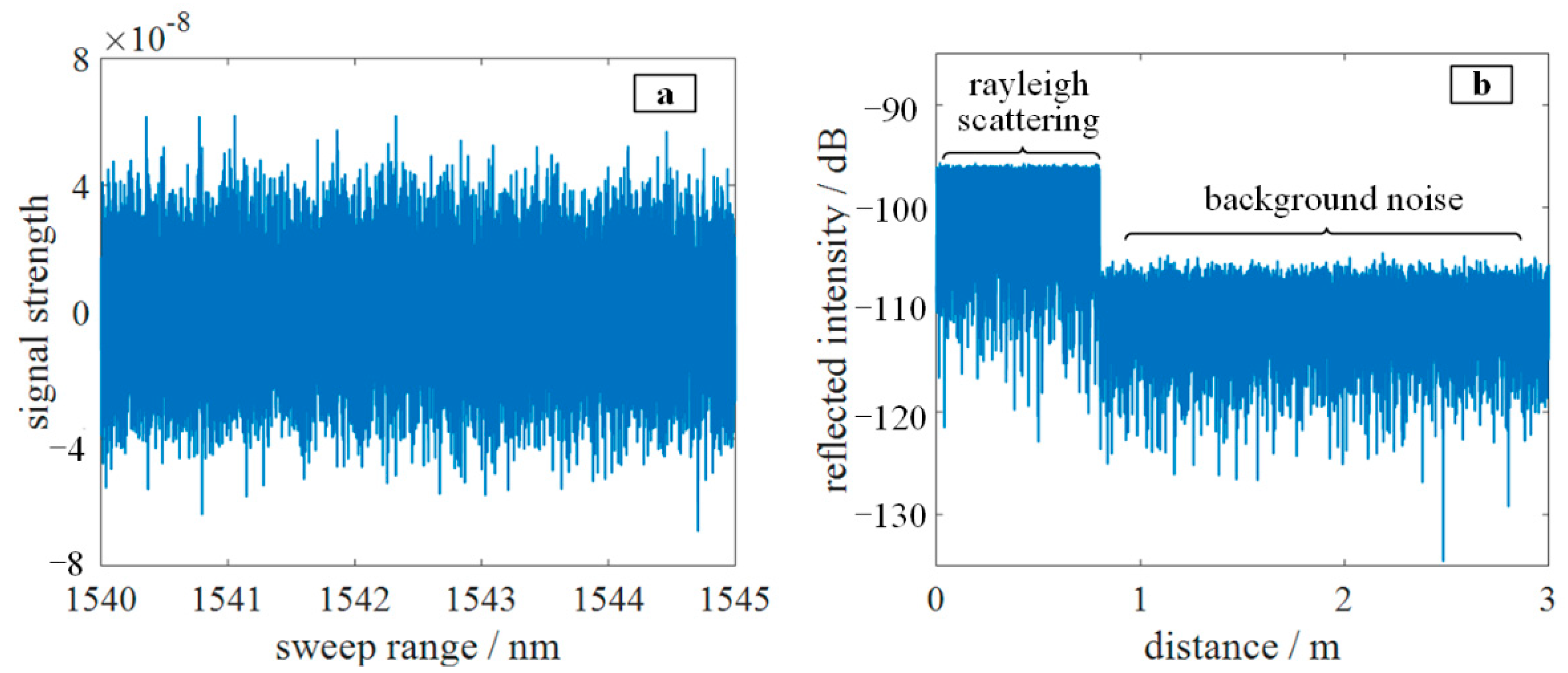
2.1. Rayleigh Scattering in Optical Fibers
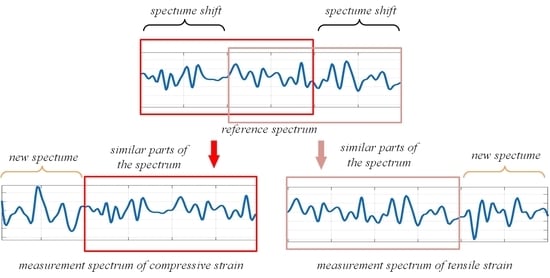
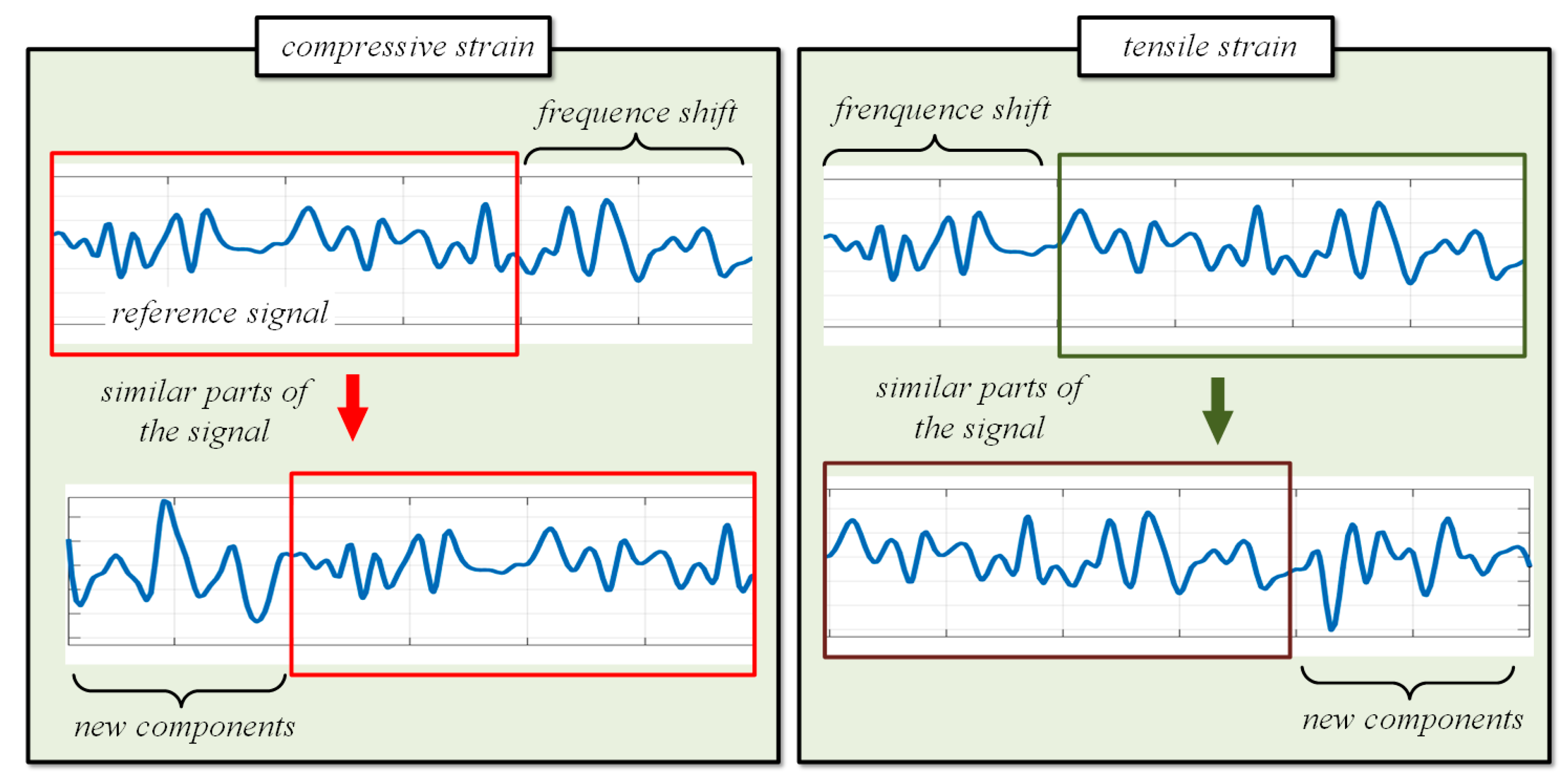
2.2. Local Similar Scanning Algorithm
- (1)
- The tuning range of the incident light source is kept consistent, and the Rayleigh signals in the frequency domain under the strain-free and strain states of the sensing fiber are collected as the reference Rayleigh signal and the measured Rayleigh signal, respectively.
- (2)
- The reference Rayleigh signal and the measured Rayleigh signal in the frequency domain are converted into the distance domain using Fourier transform, and they are denoted as the reference Rayleigh spectrum and the measured Rayleigh spectrum, respectively.
- (3)
- The reference Rayleigh spectrum and the measured Rayleigh spectrum are intercepted by a rectangular window with length N.
- (4)
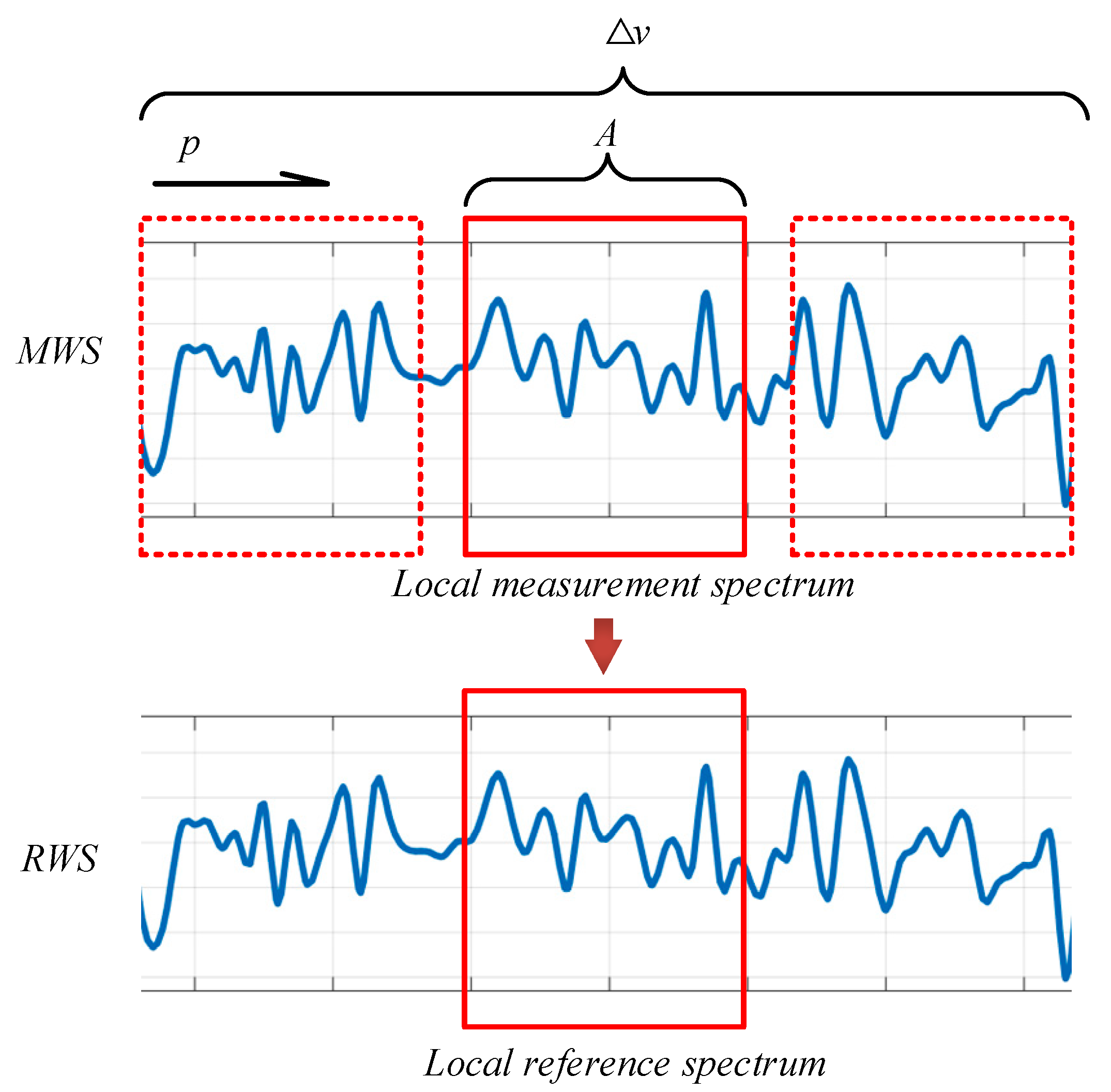
- The reference Rayleigh spectrum and the measured Rayleigh spectrum are supplemented with zero to number K, and then they are converted to the frequency domain using inverse Fourier transform to obtain the reference whole Rayleigh scattering signal (RWS) and the measured whole Rayleigh scattering signal (MWS) at a certain location. It should be noted that the bandwidth of the signal is the tuning range of the light source.
- (5)
- The rectangular window with length A is used to traverse the measured Rayleigh scattering signals in the whole tuning range. The signals of each intercepted region are recorded as local measured Rayleigh signals (LMSs), and the positions are represented by p.
- (6)
- At the center of the reference whole Rayleigh scattering signal, a rectangular window with a length of A is intercepted and recorded as the local reference Rayleigh signal (LRS). The correlation coefficients between the local reference Rayleigh signal and the local measured Rayleigh signal in each region are calculated step by step. The position with the greatest similarity is the shift caused by strain. When p = 0, the sensing fiber has no strain, and −D < p < D (D represents the boundary of the search region in the optical frequency domain).
- (7)
- The strain of the sensing fiber is calculated according to Formula (9):
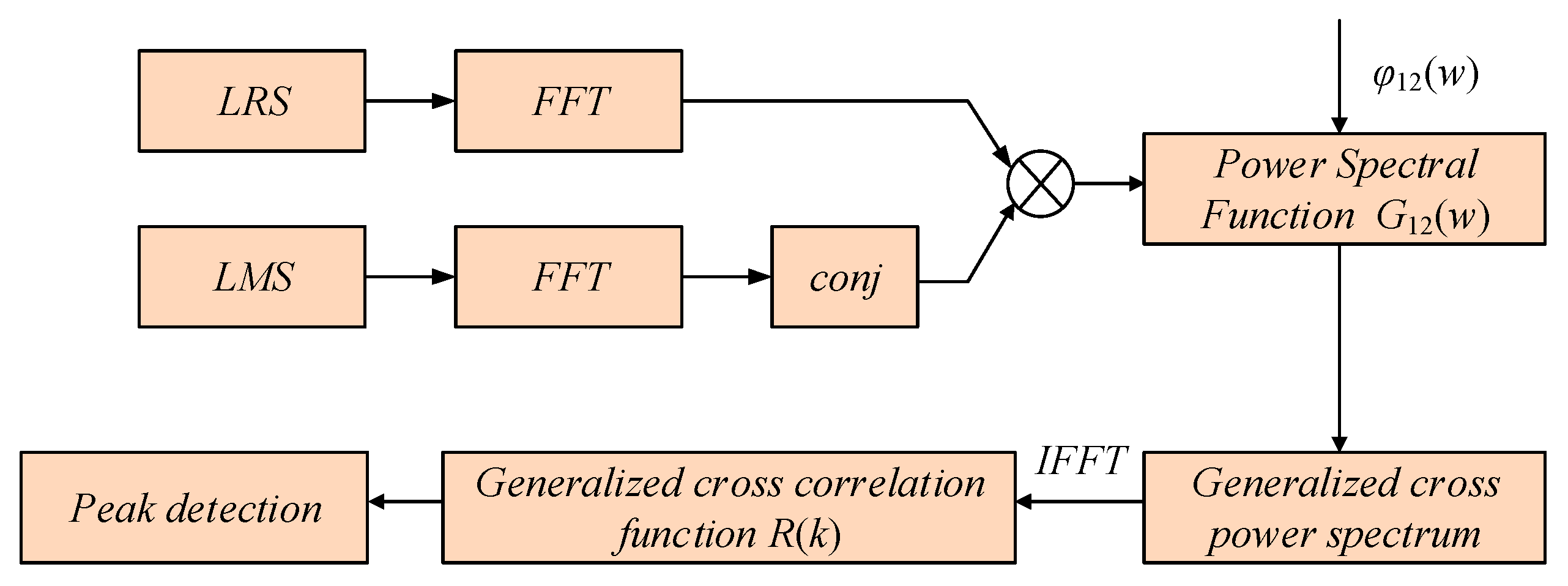
2.3. Generalized Cross-Correlation Algorithm
- (1)
- The local reference signal and the local measurement signal are Fourier transformed.
- (2)
- The conjugate of the transformed local measurement signal is taken, and the two signals are convoluted to obtain the cross-correlation power spectrum G12(w) as follows:
- (3)
- The weighting function of the cross-power spectrum is calculated:
3. Experimental Results
3.1. Experiment
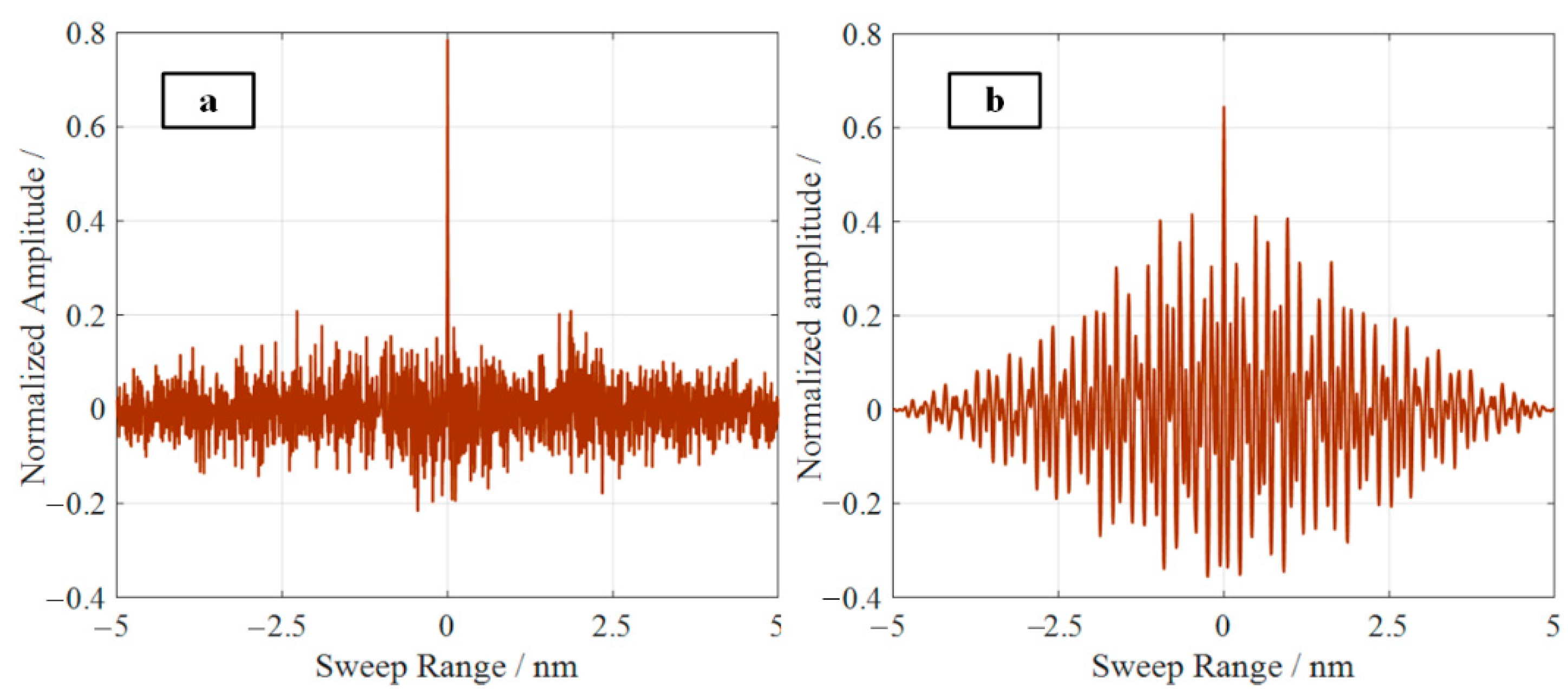
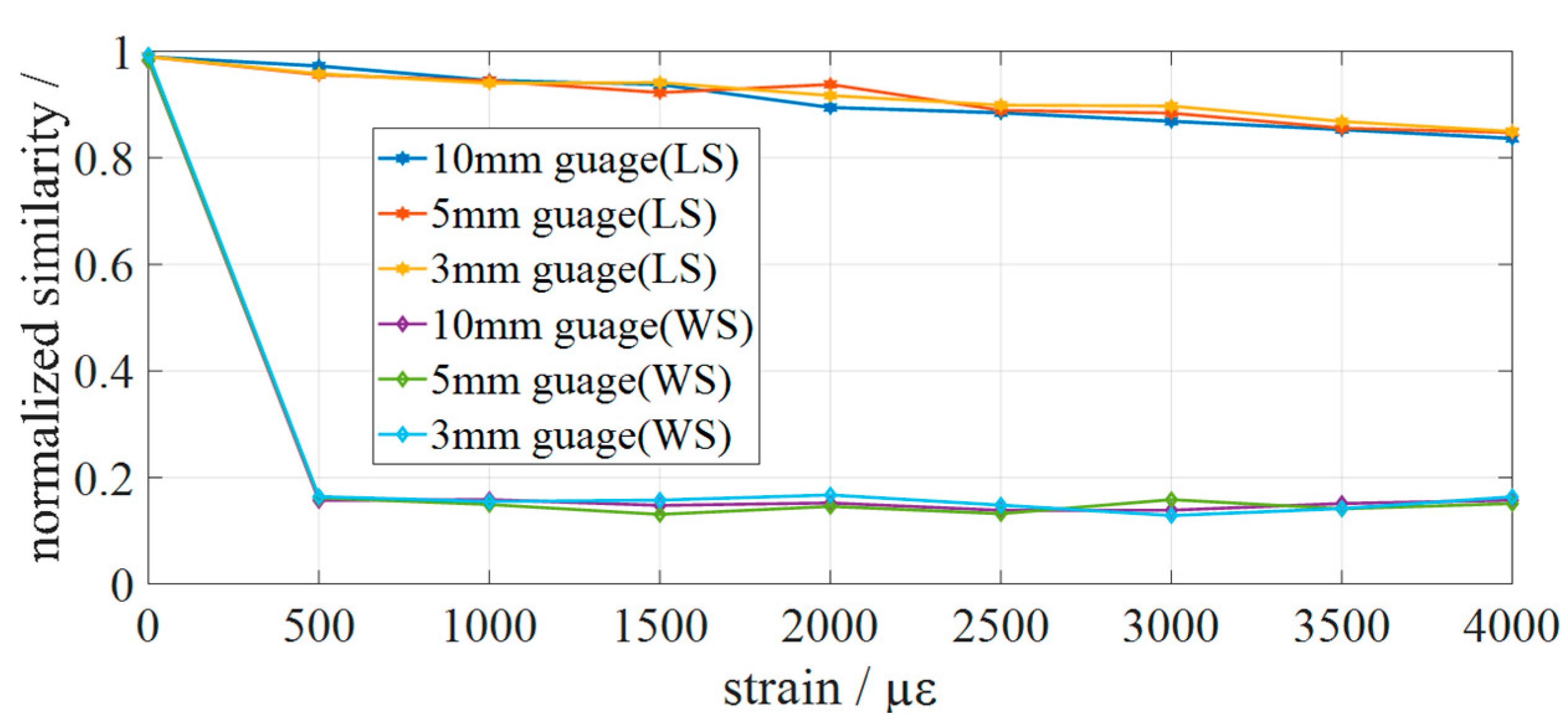
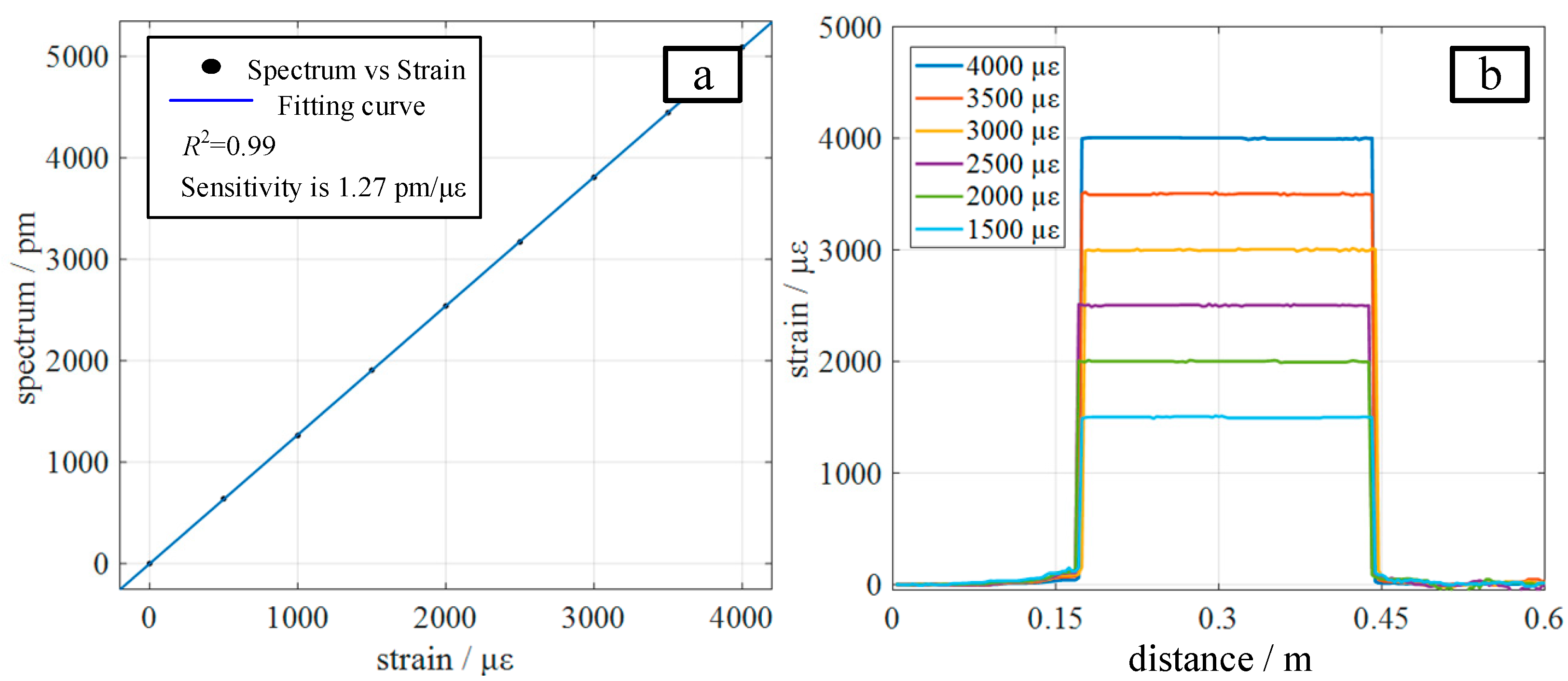
3.2. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bong, J.W.; Lim, S.B. Transanal minimally invasive surgery as a treatment option for a completely occluded anastomosis after low anterior resection: A new approach to severe anastomotic stenosis. Asian J. Endosc. Surg. 2019, 12, 175–177. [Google Scholar] [CrossRef] [PubMed]
- Yayac, M.; Detweiler, M.; Depasse, J.M.; Galetta, M.S.; Divi, S.; Goyal, D.K.C.; Kepler, C.K.; Schroeder, G.D.; Vaccaro, A.R. Minimally invasive surgery of the thoracic spine. Contemp. Spine Surg. 2020, 21, 1–7. [Google Scholar] [CrossRef]
- Templeton, E.H.; Kominsky, D.; Brown, T.; Nesnas, I. A novel sensing tether for rovers. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Burgner-Kahrs, J.; Rucker, D.C.; Choset, H. Continuum robots for medical applications: A survey. IEEE Trans. Robot. 2015, 31, 1261–1280. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalva, S. A review of distributed optical fiber sensors for civil engineering applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Froggatt, M.; Moore, J. High-spatial-resolution distributed strain measurement in optical fiber with Rayleigh scatter. Appl. Opt. 1998, 37, 1735–1740. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.P.; Qin, Z.G.; Li, W.H.; Chen, L.; Bao, X.Y. Distributed vibration sensing with time-resolved optical frequency-domain reflectometry. Opt. Express 2012, 20, 13138–13145. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Yang, D.; Du, Y.; Zhou, Y.; Xu, Z.; Liu, K.; Jiang, J.; Liu, T. Note: Improving distributed strain sensing sensitivity in OFDR by reduced-cladding single mode fiber. Rev. Sci. Instrum. 2016, 87, 126106. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Gan, J.; Zhang, Z.; Heng, X.; Yang, C.; Qian, Q.; Xu, S.; Yang, Z. High spatial resolution distributed fiber strain sensor based on phase-OFDR. Opt. Express 2017, 25, 27913–27922. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kim, M.J.; Rho, B.S.; Kim, Y.H. Measurement range enhancement of Rayleighbased optical frequency domain reflectometry with bi-directional determination. Photonics J. 2017, 9, 7106308. [Google Scholar]
- Heinze, S.; Echtermeyer, A.T. A running reference analysis method to greatly improve optical backscatter reflectometry strain data from the inside of hardening and shrinking materials. Appl. Sci. 2018, 8, 1137. [Google Scholar] [CrossRef] [Green Version]
- Loranger, S.; Gagné, M.; Lambin-Iezzi, V.; Kashyap, R. Rayleigh scatter based order of magnitude increase in distributed temperature and strain sensing by simple UV exposure of optical fibre. Sci. Rep. 2015, 5, 11177. [Google Scholar] [CrossRef] [PubMed]
- Kreger, S.T.; Sang, A.K.; Gifford, D.K.; Froggatt, M.E. Distributed strain and temperature sensing in plastic optical fiber using Rayleigh scatter. Proc. SPIE Int. Soc. Opt. Eng. 2009, 7316, 85–92. [Google Scholar]
- Yan, A.; Huang, S.; Li, S.; Chen, R.; Ohodnicki, P.; Buric, M.; Lee, S.; Li, M.; Chen, K.P. Distributed optical fiber sensors with ultrafast laser enhanced Rayleigh backscattering profiles for real-time monitoring of solid oxide fuel cell operations. Sci. Rep. 2017, 7, 9360. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Cui, J.; Xu, Z.; Tan, J. Generalized Cross-Correlation Strain Demodulation Method Based on Local Similar Spectral Scanning. Sensors 2022, 22, 5378. https://doi.org/10.3390/s22145378
Tian Y, Cui J, Xu Z, Tan J. Generalized Cross-Correlation Strain Demodulation Method Based on Local Similar Spectral Scanning. Sensors. 2022; 22(14):5378. https://doi.org/10.3390/s22145378
Chicago/Turabian StyleTian, Yuqi, Jiwen Cui, Zaibin Xu, and Jiubin Tan. 2022. "Generalized Cross-Correlation Strain Demodulation Method Based on Local Similar Spectral Scanning" Sensors 22, no. 14: 5378. https://doi.org/10.3390/s22145378
APA StyleTian, Y., Cui, J., Xu, Z., & Tan, J. (2022). Generalized Cross-Correlation Strain Demodulation Method Based on Local Similar Spectral Scanning. Sensors, 22(14), 5378. https://doi.org/10.3390/s22145378