Convergence Analysis of Path Planning of Multi-UAVs Using Max-Min Ant Colony Optimization Approach
Abstract
:1. Introduction
2. Problem Statement
3. Preliminaries of Unmanned Aerial vehicles
3.1. Path Planning
3.2. Collision Avoidance Protocol
3.3. Environmental Threats
4. Hybrid Algorithm
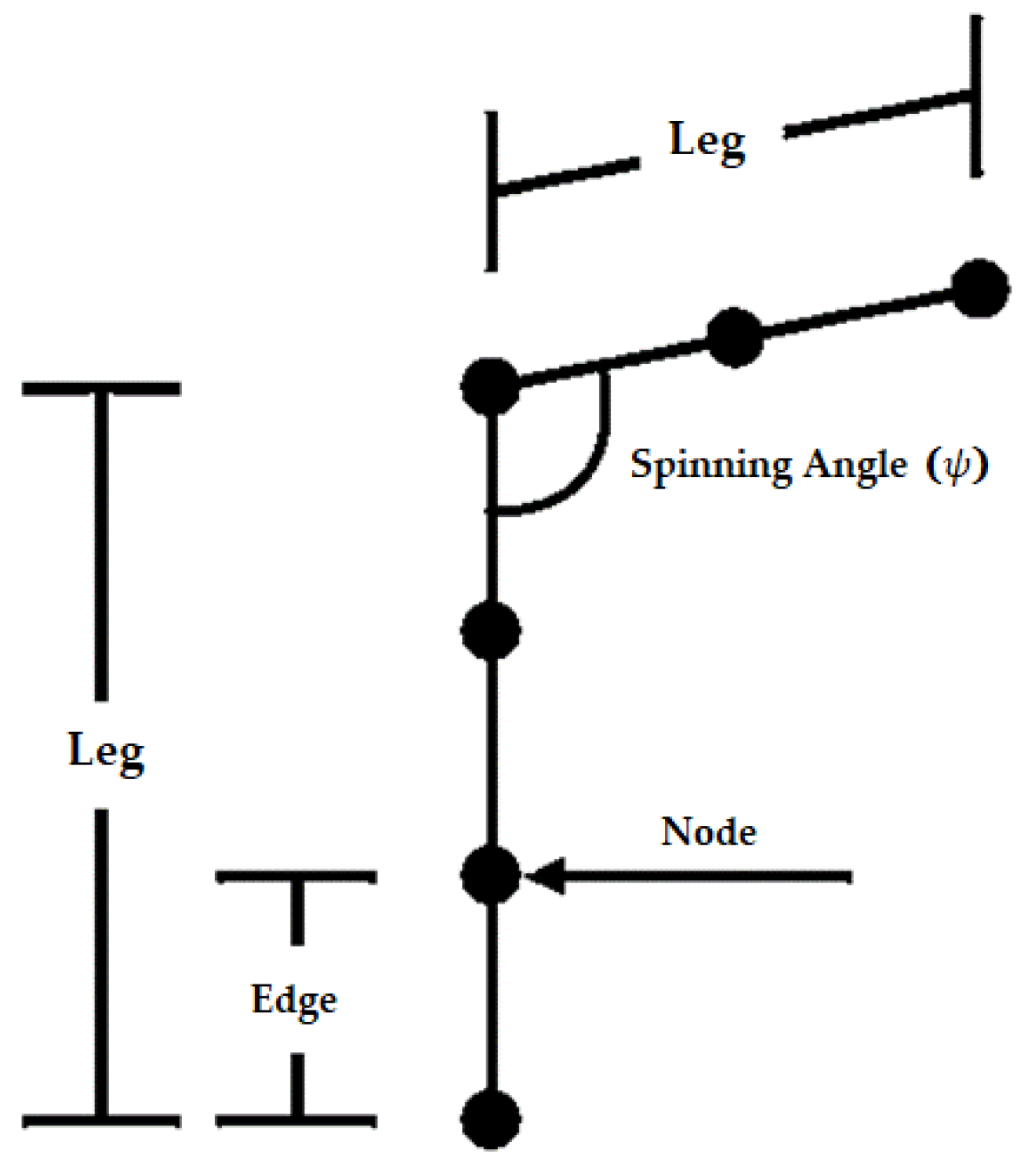
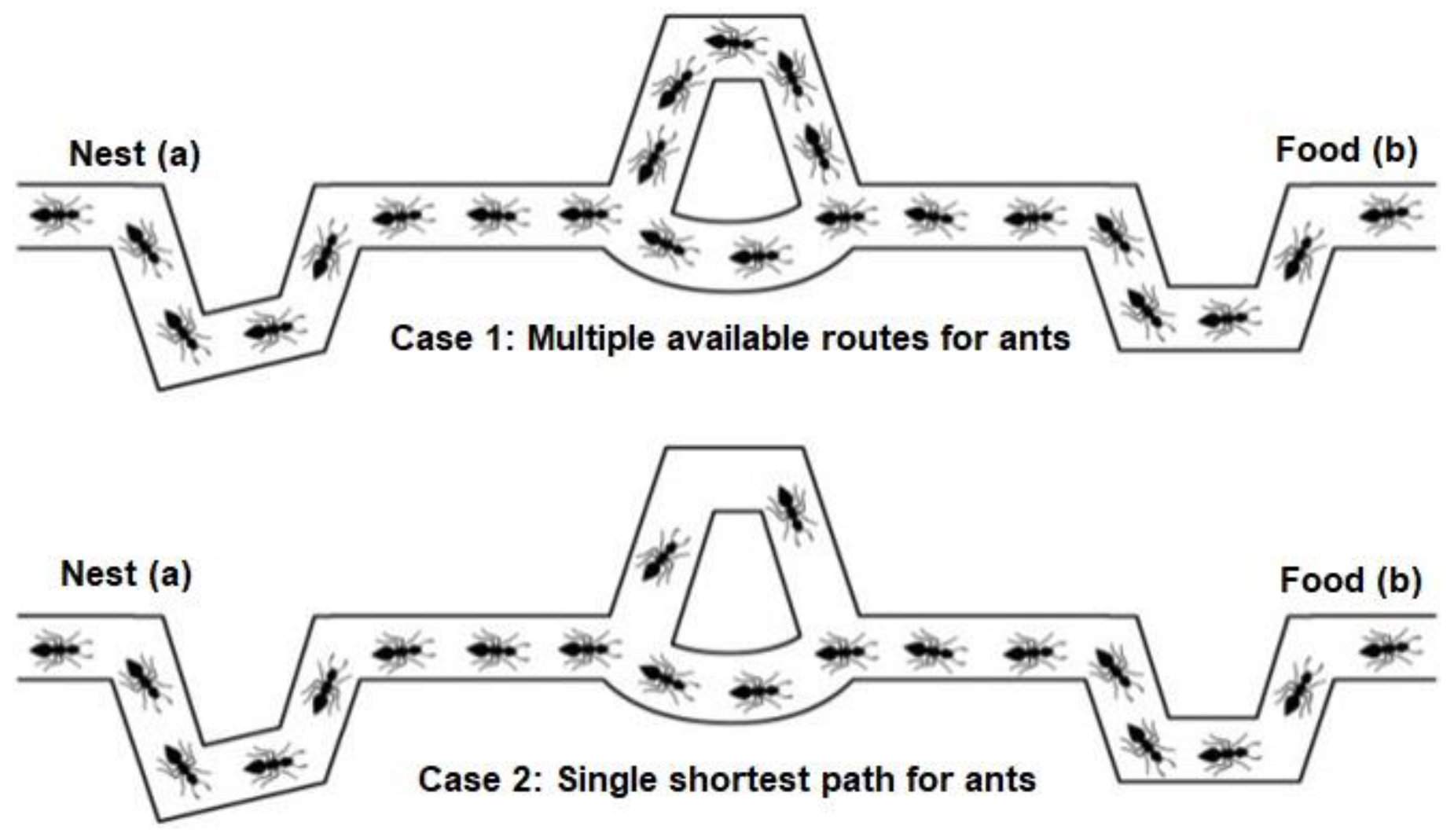
4.1. Ant Colony Optimization
4.2. Maximum Minimum Ant Colony Optimization
4.2.1. Maximum Minimum Ant Colony Optimization with Differential Evolution
4.2.2. Maximum Minimum Ant Colony Optimization with Cauchy Mutant Operator
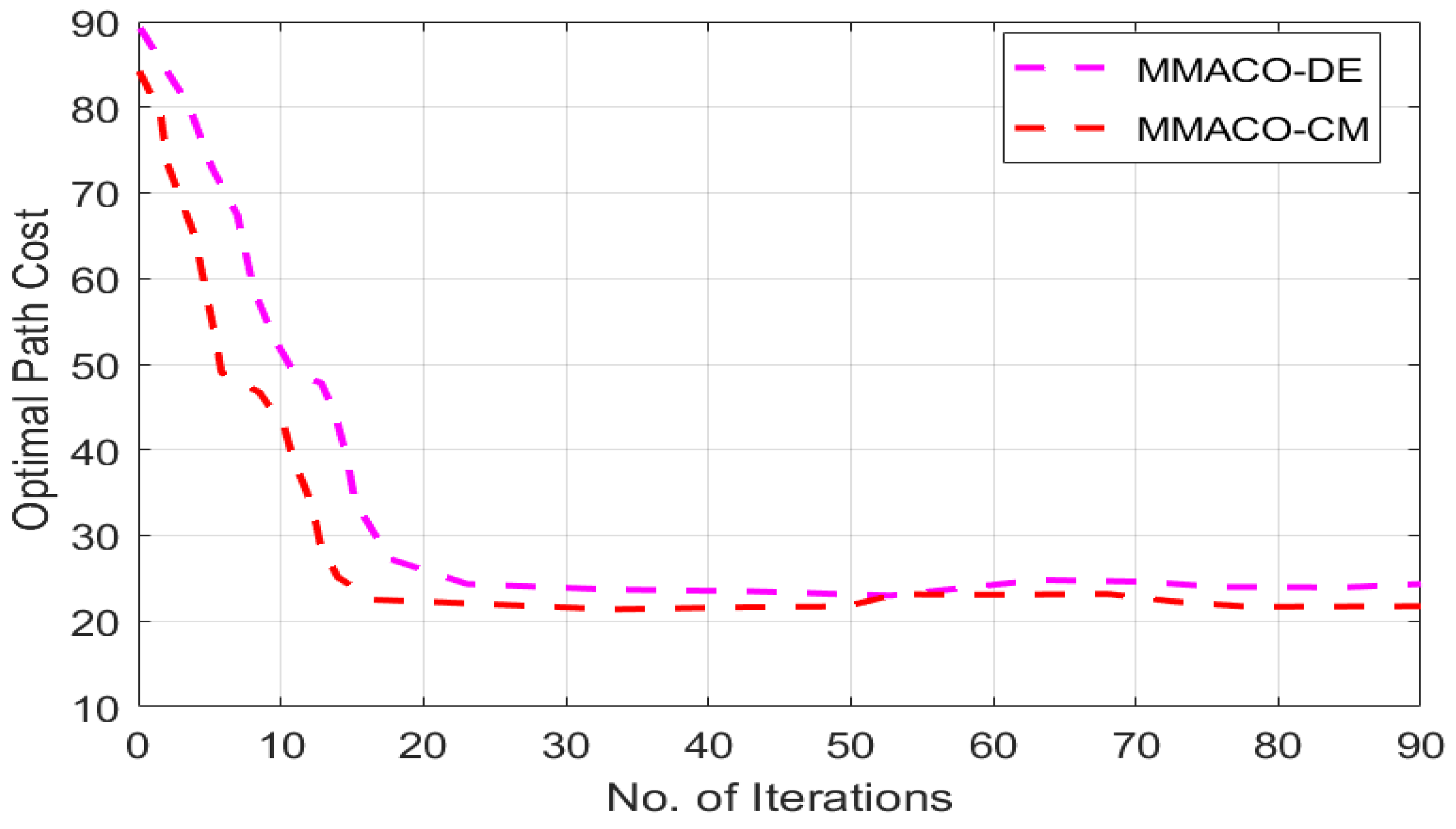
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Shima, T.; Rasmussen, S. (Eds.) UAV Cooperative Decision and Control: Challenges and Practical Approaches; Society for Industrial and Applied Mathematics: Philadelphia, PE, USA, 2009. [Google Scholar]
- Lemaire, T.; Rachid, A.; Lacroix, S. A distributed tasks allocation scheme in multi-UAV context. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 4, pp. 3622–3627. [Google Scholar]
- Roldán, J.J.; del Cerro, J.; Barrientos, A. A proposal of methodology for multi-UAV mission modeling. In Proceedings of the 23rd Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015; pp. 1–7. [Google Scholar]
- Samad; Manan, A.; Kamarulzaman, N.; Hamdani, M.A.; Mastor, T.A.; Hashim, K.A. The potential of Unmanned Aerial Vehicle (UAV) for civilian and mapping application. In Proceedings of the IEEE 3rd International Conference on System Engineering and Technology, Shah Alam, Malaysia, 19–20 August 2013; pp. 313–318. [Google Scholar]
- Glade, D. Unmanned Aerial Vehicles: Implications for Military Operations; Center for Strategy and Technology, Air War College, Air University: Montgomery, AL, USA, 2000. [Google Scholar]
- Iida, F. Biologically inspired visual odometer for navigation of a flying robot. Robot. Auton. Syst. 2003, 44, 201–208. [Google Scholar] [CrossRef] [Green Version]
- Yakıcı, E. Solving location and routing problem for UAVs. Comput. Ind. Eng. 2016, 102, 294–301. [Google Scholar] [CrossRef]
- Chen, Y.B.; Yu, J.Q.; Su, X.L.; Luo, G.C. Path planning for multi-UAV formation. J. Intell. Robot. Syst. 2015, 77, 229–246. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Blum, C. Ant colony optimization: Introduction and recent trends. Phys. Life Rev. 2005, 2, 353–373. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]
- Hajiyev, C.; Soken, H.E. Robust adaptive Kalman filter for estimation of UAV dynamics in the presence of sensor/actuator faults. Aerosp. Sci. Technol. 2013, 28, 376–383. [Google Scholar] [CrossRef]
- Duan, H.; Luo, Q. New progresses in swarm intelligence–based computation. Int. J. Bio-Inspired Comput. 2015, 7, 26–35. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wang, G.-G.; Gandomi, A.H. A survey of learning-based intelligent optimization algorithms. Arch. Comput. Methods Eng. 2021, 28, 3781–3799. [Google Scholar] [CrossRef]
- Duan, H.; Qiao, P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Wang, L.; Zhang, Q.; Wan, N. Simulation study on searching for food by cooperation of multi-robots with swarm intelligence. In Proceedings of the IEEE International Conference on Automation and Logistics, Washington, DC, USA, 18–21 August 2007; pp. 2296–2300. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the travelling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef] [Green Version]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, J.; Xuan, J.; Ren, Z.; Hu, Y. A hybrid ACO algorithm for the next release problem. In Proceedings of the 2nd International Conference on Software Engineering and Data Mining, Chengdu, China, 23–25 June 2010; pp. 166–171. [Google Scholar]
- Rivas, A.E.L.; Gallego Pareja, L.A.; Abrão, T. Coordination of distance and directional overcurrent relays using an extended continuous domain ACO algorithm and an hybrid ACO algorithm. Electr. Power Syst. Res. 2019, 170, 259–272. [Google Scholar] [CrossRef]
- Shuang, B.; Chen, J.; Li, Z. Study on hybrid PS-ACO algorithm. Appl. Intell. 2011, 34, 64–73. [Google Scholar] [CrossRef]
- Stützle, T.; Hoos, H.H. MAX–MIN ant system. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Karakaya, M. UAV route planning for maximum target coverage. arXiv 2014, arXiv:1403.2906. [Google Scholar] [CrossRef]
- Li, B.; Qi, X.; Yu, B.; Liu, L. Trajectory planning for UAV based on improved ACO algorithm. IEEE Access 2019, 8, 2995–3006. [Google Scholar] [CrossRef]
- Duan, H.; Yu, Y.; Zhang, X.; Shao, S. Three-dimension path planning for UCAV using hybrid meta-heuristic ACO-DE algorithm. Simul. Model. Pract. Theory 2010, 18, 1104–1115. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Al-Ani, A.; AlSukker, A.; Al-Jumaily, A. A combined ant colony and differential evolution feature selection algorithm. In Ant Colony Optimization and Swarm Intelligence, Proceedings of the 6th International Conference on Ant Colony Optimization and Swarm Intelligence, Brussels, Belgium, 22–24 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–12. [Google Scholar]
- Ali, Z.A.; Zhangang, H.; Zhengru, D. Path planning of multiple UAVs using MMACO and DE algorithm in dynamic environment. Meas. Control 2020, 53, 0020294020915727. [Google Scholar] [CrossRef]
- Ali, Z.A.; Zhangang, H.; Hang, W.B. Cooperative path planning of multiple UAVs by using max–min ant colony optimization along with Cauchy mutant operator. Fluct. Noise Lett. 2021, 20, 2150002. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially known environments. In Intelligent Unmanned Ground Vehicles; Springer: Boston, MA, USA, 1997; pp. 203–220. [Google Scholar]
- Forsmo, E.J. Optimal Path Planning for Unmanned Aerial Systems. Master’s Thesis, Institutt for Teknisk Kybernetikk, Trondheim, Norway, 2012. [Google Scholar]
- Latombe, J.-C. Robot Motion Planning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 124. [Google Scholar]
- Kavraki, L.E.; Svestka, P.; Latombe, J.-C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef] [Green Version]
- Lumelsky, V.J.; Harinarayan, K.R. Decentralized motion planning for multiple mobile robots: The cocktail party model. Auton. Robot. 1997, 4, 121–135. [Google Scholar] [CrossRef]
- Saunders, J.; Call, B.; Curtis, A.; Beard, R.; McLain, T. Static and dynamic obstacle avoidance in miniature air vehicles. In Proceedings of the Infotech@ Aerospace, Arlington, VA, USA, 26–29 September 2005; p. 6950. [Google Scholar]
- Gasparetto, A.; Zanotto, V. A new method for smooth trajectory planning of robot manipulators. Mech. Mach. Theory 2007, 42, 455–471. [Google Scholar] [CrossRef]
- Najm, A.A.; Ibraheem, I.K. Nonlinear PID controller design for a 6-DOF UAV quadrotor system. Eng. Sci. Technol. Int. J. 2019, 22, 1087–1097. [Google Scholar] [CrossRef]
- Kim, J.-H.; Sukkarieh, S.; Wishart, S. Real-time Navigation, Guidance, and Control of a UAV using Low-cost Sensors. In Field and Service Robotics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 299–309. [Google Scholar]
- Zhang, C.; Zhen, Z.; Wang, D.; Li, M. UAV path planning method based on ant colony optimization. In Proceedings of the Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010; pp. 3790–3792. [Google Scholar]
- Park, J.-W.; Oh, H.-D.; Tahk, M.-J. UAV collision avoidance based on geometric approach. In Proceedings of the SICE Annual Conference, Tokyo, Japan, 20–22 August 2008; pp. 2122–2126. [Google Scholar]
- Zhang, W.; Ning, Y.; Suo, C. A method based on multi-sensor data fusion for UAV safety distance diagnosis. Electronics 2019, 8, 1467. [Google Scholar] [CrossRef] [Green Version]
- Jackson, B.A.; Frelinger, D.; Lostumbo, M.; Button, R.W. Evaluating Novel Threats to the Homeland: Unmanned Aerial Vehicles and Cruise Missiles; Rand Corporation: Santa Monica, CA, USA, 2008; Volume 626. [Google Scholar]
- Yan, F.; Liu, Y.-S.; Xiao, J.-Z. Path planning in complex 3D environments using a probabilistic roadmap method. Int. J. Autom. Comput. 2013, 10, 525–533. [Google Scholar] [CrossRef]
- Al Salami, N.M.A. Ant colony optimization algorithm. UbiCC J. 2009, 4, 823–826. [Google Scholar]
- Bell, W.J. Searching behavior patterns in insects. Annu. Rev. Entomol. 1990, 35, 447–467. [Google Scholar] [CrossRef]
- Hassell, M.P.; Southwood, T.R.E. Foraging strategies of insects. Annu. Rev. Ecol. Syst. 1978, 9, 75–98. [Google Scholar] [CrossRef]
- Cain, M.L. Random search by herbivorous insects: A simulation model. Ecology 1985, 66, 876–888. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 2, pp. 1470–1477. [Google Scholar]
- Vander, M.; Robert, K.; Leeanne, E. Alonso. Pheromone directed behavior in ants. In Pheromone Communication in Social Insects; CRC Press: Boca Raton, FL, USA, 1998; pp. 159–192. [Google Scholar]



| Static Obstacle | Dynamic Obstacle | |
|---|---|---|
| Complete Information Known | 1st Scenario | 2nd Scenario |
| Partial Information Known | 3rd Scenario | 4th Scenario |
| No. | Constraints | Radius, Center Coordinates | Unit |
|---|---|---|---|
| 1 | Radius | 1.8 | km |
| Center | (7,6,1) | ||
| 2 | Radius | 2.5 | km |
| Center | (6,14,1) | ||
| 3 | Radius | 1.3 | km |
| Center | (16,6,0.9) | ||
| 4 | Radius | 0.8 | km |
| Center | (15,12,1) |
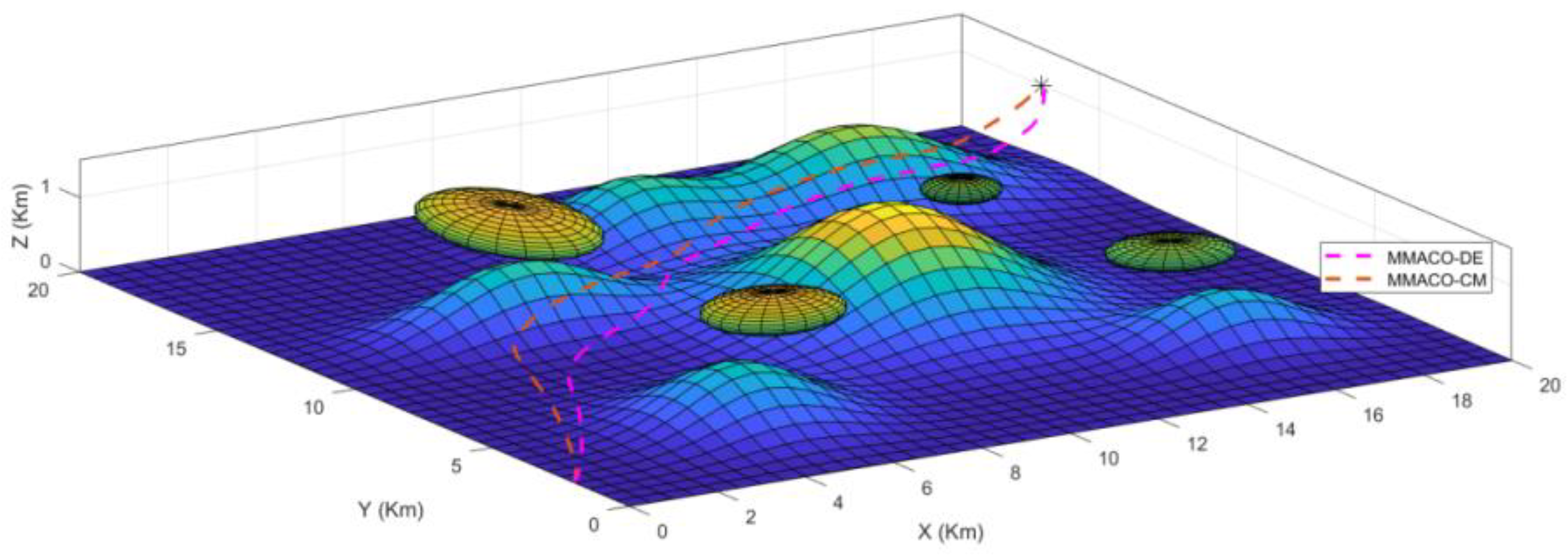
| UAV | Algorithm Applied | Initial Point (x,y,z) | Target Point (x,y,z) | Distance Travelled (in KM) |
|---|---|---|---|---|
| UAV1 | MMACO-DE | (0,2,0) | (20,20,1) | 23.5 |
| UAV2 | MMACO-CM | (0,2,0) | (20,20,1) | 24.1 |
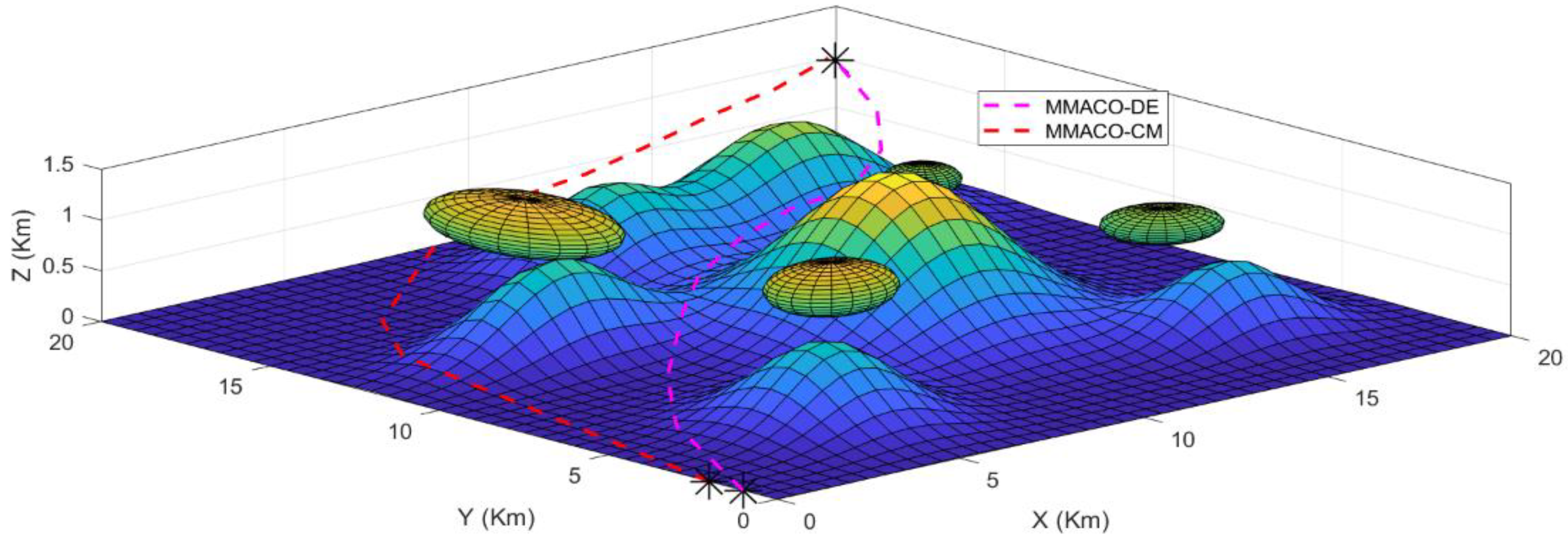
| UAV | Algorithm Applied | Initial Point (x,y,z) | Target Point (x,y,z) | Distance Travelled (in KM) |
|---|---|---|---|---|
| UAV1 | MMACO-DE | (0,1,0) | (19.8,20,1) | 24.221 |
| UAV2 | MMACO-CM | (0,2,0) | (19.8,19.8,1) | 27.242 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shafiq, M.; Ali, Z.A.; Israr, A.; Alkhammash, E.H.; Hadjouni, M.; Jussila, J.J. Convergence Analysis of Path Planning of Multi-UAVs Using Max-Min Ant Colony Optimization Approach. Sensors 2022, 22, 5395. https://doi.org/10.3390/s22145395
Shafiq M, Ali ZA, Israr A, Alkhammash EH, Hadjouni M, Jussila JJ. Convergence Analysis of Path Planning of Multi-UAVs Using Max-Min Ant Colony Optimization Approach. Sensors. 2022; 22(14):5395. https://doi.org/10.3390/s22145395
Chicago/Turabian StyleShafiq, Muhammad, Zain Anwar Ali, Amber Israr, Eman H. Alkhammash, Myriam Hadjouni, and Jari Juhani Jussila. 2022. "Convergence Analysis of Path Planning of Multi-UAVs Using Max-Min Ant Colony Optimization Approach" Sensors 22, no. 14: 5395. https://doi.org/10.3390/s22145395
APA StyleShafiq, M., Ali, Z. A., Israr, A., Alkhammash, E. H., Hadjouni, M., & Jussila, J. J. (2022). Convergence Analysis of Path Planning of Multi-UAVs Using Max-Min Ant Colony Optimization Approach. Sensors, 22(14), 5395. https://doi.org/10.3390/s22145395








