2D and 3D Angles-Only Target Tracking Based on Maximum Correntropy Kalman Filters
Abstract
:1. Introduction
2. Problem Formulation
2.1. Process Model
2.2. Measurement Model
3. Correntropy Measure
4. Gaussian Kernel Based Maximum Correntropy Estimation Framework
5. Cauchy Kernel Based Maximum Correntropy Estimation Framework
6. Nonlinear State Estimators
6.1. Unscented Kalman Filter (UKF)
6.2. New Sigma Point Kalman Filter (NSKF)
| Algorithm 1: For MC-UKF-CK and MC-NSKF-CK |
Posterior mean: . Posterior covariance: . |
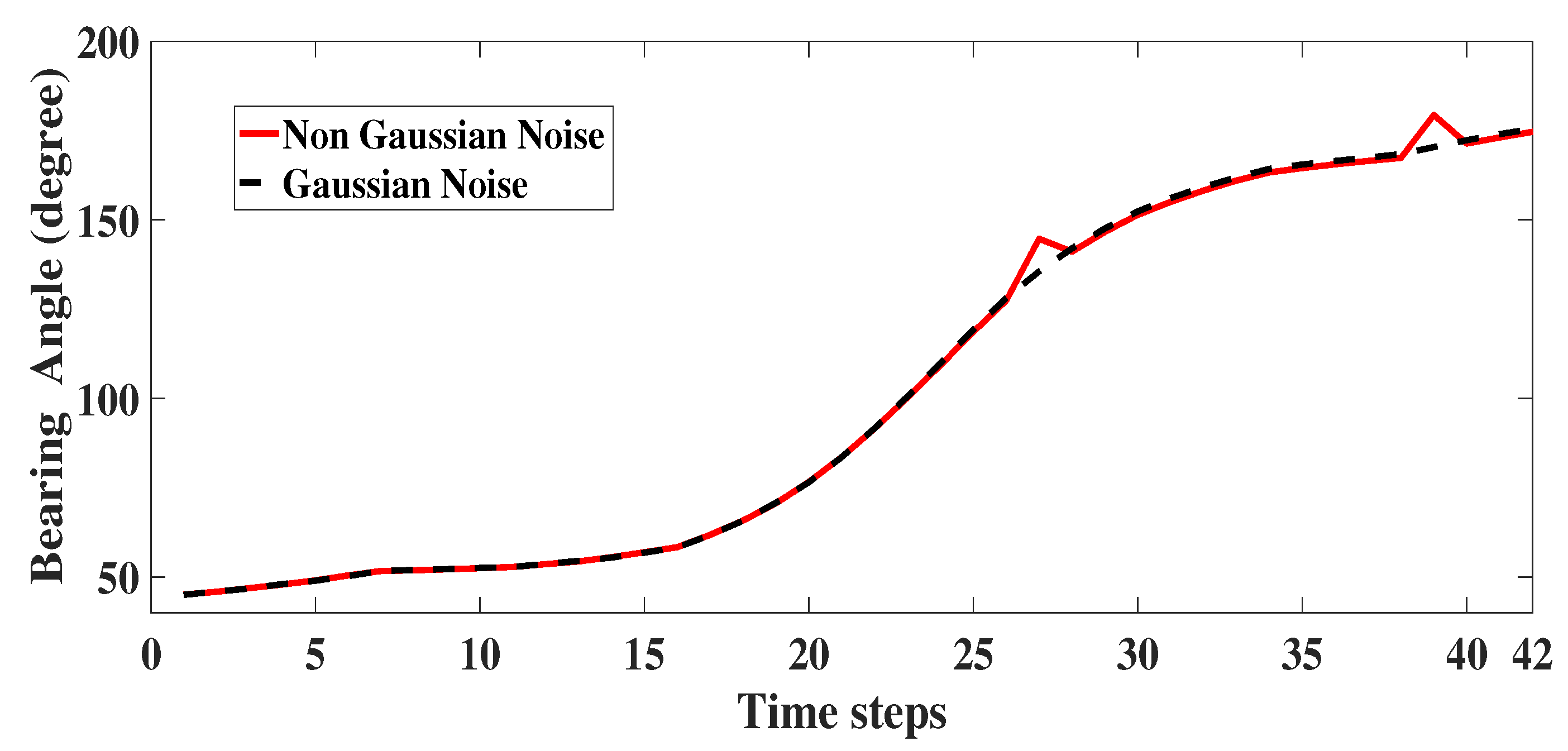
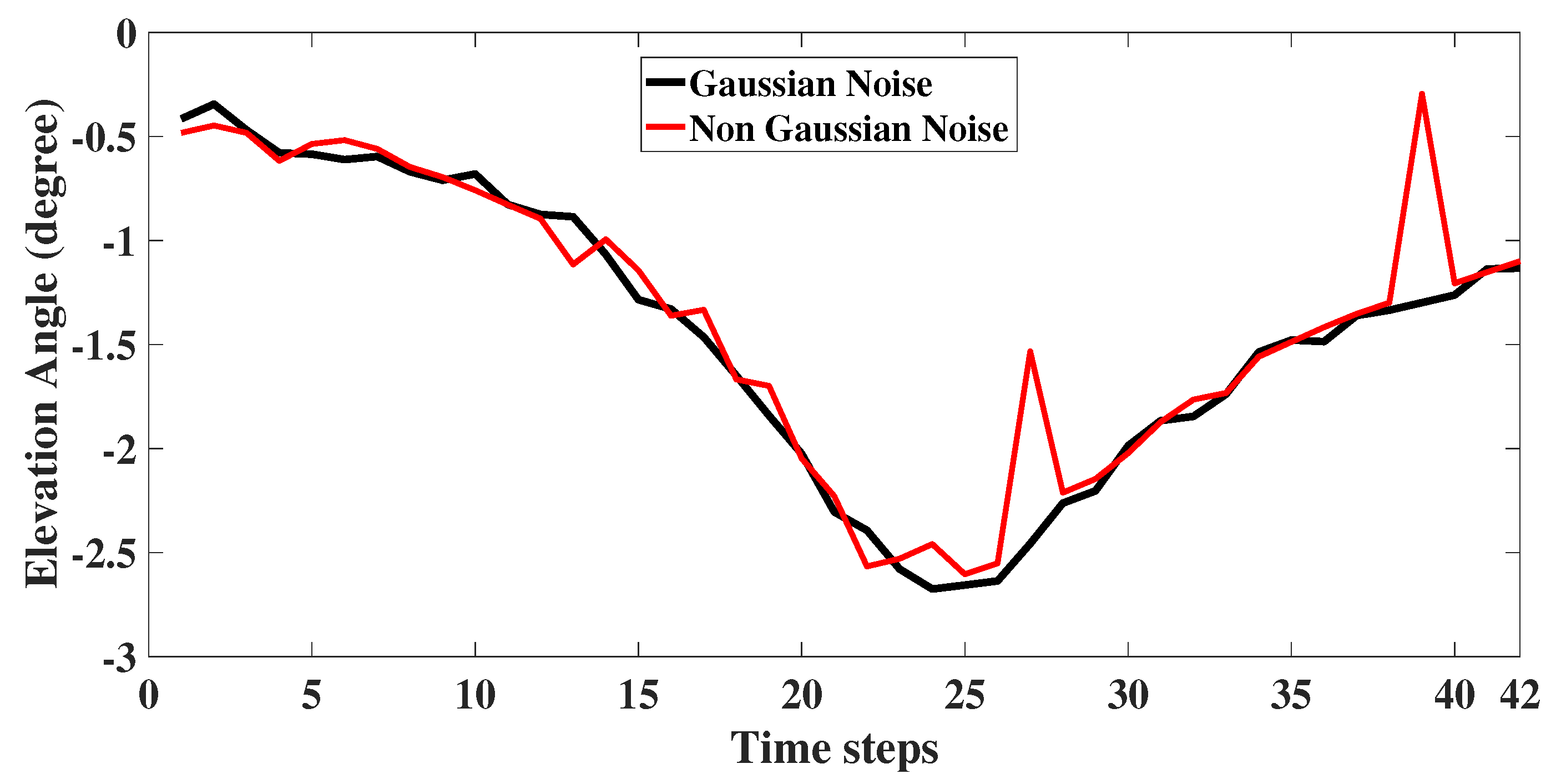
7. Modelling of Non Gaussian Noise in Angular Measurements
8. Simulation Results
8.1. 2D Scenario and Filter Initialisation
8.2. 3D Scenario and Filter Initialisation
8.3. Performance Metrics
- 1.
- RMSE: Root-mean-square error in resultant target position is computed as follows
- 2.
- Track Divergence: In order to identify if a track is divergent or not, a certain threshold value () is set according to the position error computed at the final time instant of observation () as
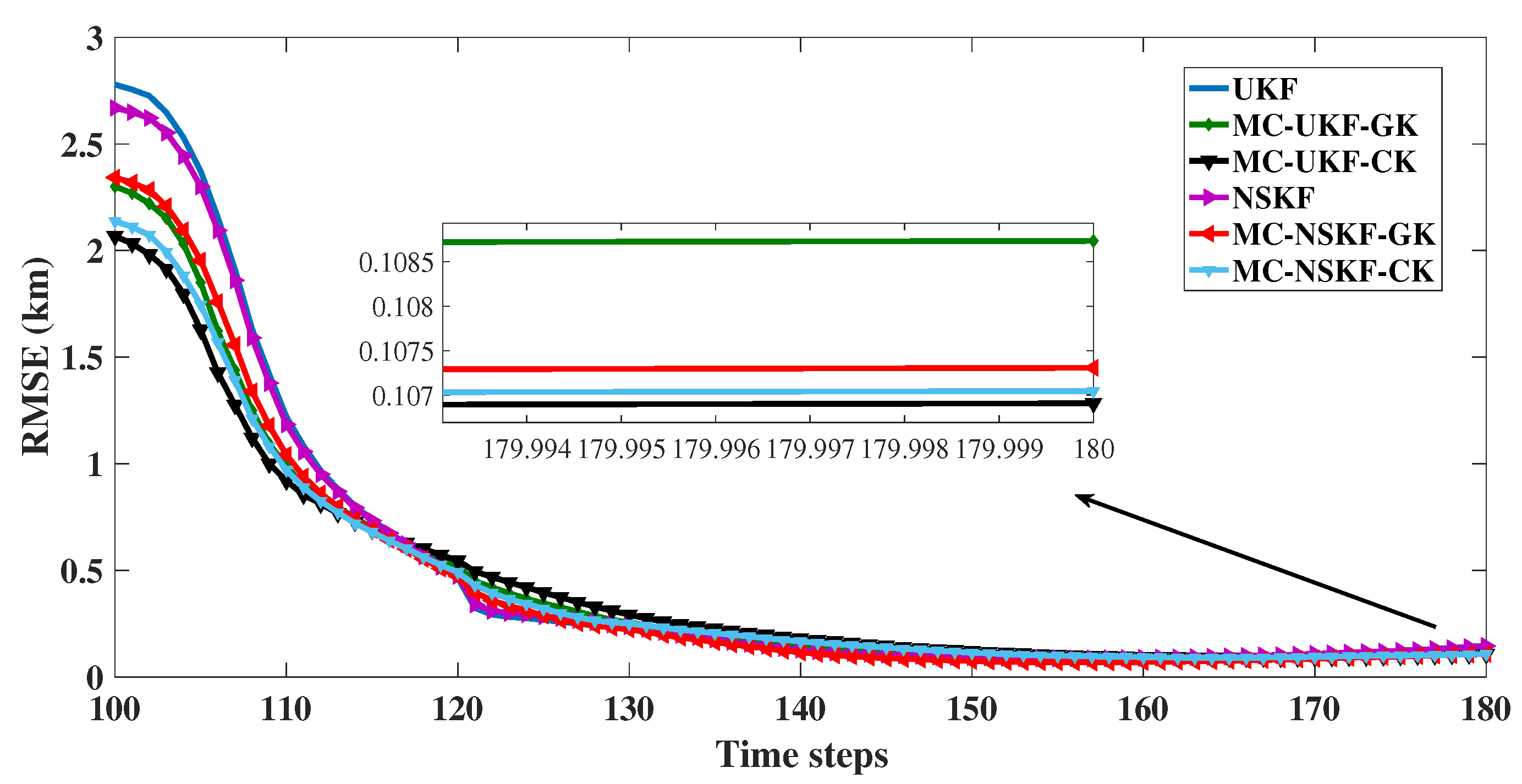
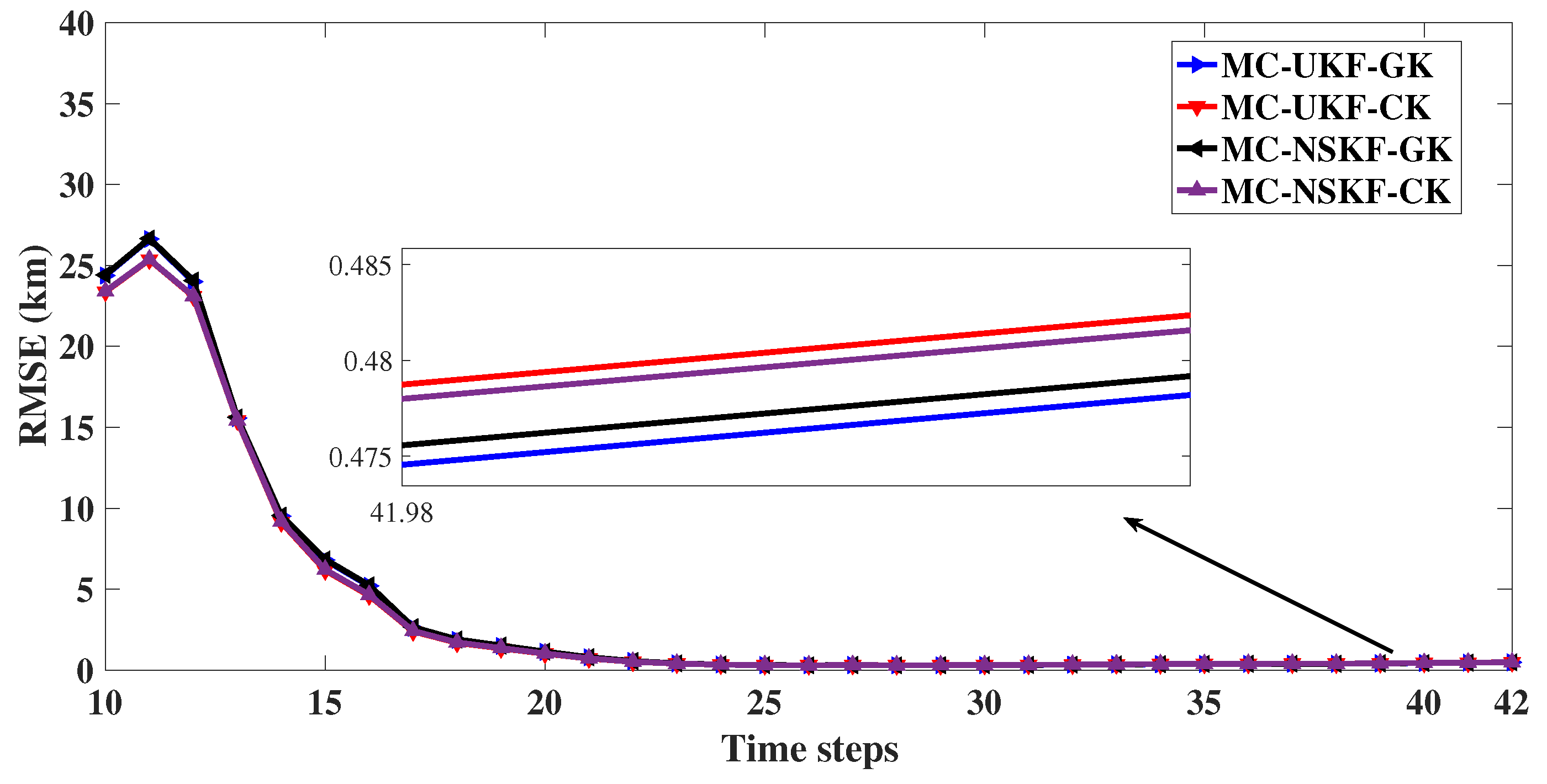
8.4. Performance Analysis
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Target state vector at sample k | |
| Observer state vector at sample k | |
| Relative state vector at sample k | |
| Zero mean Gaussian process noise | |
| Process covariance | |
| State transition matrix | |
| T | Sampling time |
| Power spectral densities of the process noise along the X, Y, and Z axes | |
| Measurement vector at sample k | |
| Non Gaussian measurement noise at sample k | |
| Range vector | |
| and | Bearing and Elevation angle measurement |
| Measurement noise covariance matrix at sample k | |
| and | Standard deviations of error in bearing and elevation angles |
| Kernel function | |
| and | Gaussian kernel and Gaussian bandwidth |
| and | Cauchy kernel and Cauchy bandwidth |
| Prior mean at sample k | |
| Prior covariance at sample k | |
| Weights at sample k | |
| Measurement slope matrix | |
| Cross covariance | |
| Measurement covariance | |
| Cost function | |
| ℘ and | Adjustable weights |
| Gaussian scalar term | |
| Gaussian Kalman gain | |
| Posterior mean at sample k | |
| Posterior covariance at sample k | |
| Initial course estimate | |
| and | True initial bearing and elevation measurement estimate |
| and | Bearing and Elevation angle heading |
| Threshold | |
| RMSE | Root Mean Square Error |
| MMSE | Minimum Mean Square Error |
| MC-UKF-GK | Maximum correntropy unscented Kalman filter Gaussian kernel |
| MC-UKF-CK | Maximum correntropy unscented Kalman filter Cauchy kernel |
| MC-NSKF-GK | Maximum correntropy new sigma point Kalman filter Gaussian kernel |
| MC-NSKF-CK | Maximum correntropy new sigma point Kalman filter Cauchy kernel |
Appendix A. Power Series Expansion of Cauchy Kernel Function
Appendix B. Derivation of Kalman Gain
References
- Auger, F.; Hilairet, M.; Guerrero, J.M.; Monmasson, E.; Orlowska-Kowalska, T.; Katsura, S. Industrial applications of the Kalman filter: A review. IEEE Trans. Ind. Electron. 2013, 60, 5458–5471. [Google Scholar] [CrossRef] [Green Version]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech house: Norwood, MA, USA, 2003. [Google Scholar]
- Mallick, M.; Tian, X.; Zhu, Y.; Morelande, M. Angle-Only Filtering of a Maneuvering Target in 3D. Sensors 2022, 22, 1422. [Google Scholar] [CrossRef]
- Reif, K.; Gunther, S.; Yaz, E.; Unbehauen, R. Stochastic stability of the discrete-time extended Kalman filter. IEEE Trans. Autom. Control. 1999, 44, 714–728. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef] [Green Version]
- Haykin, S.; Arasaratnam, I. Cubature kalman filters. IEEE Trans. Autom. Control. 2009, 54, 1254–1269. [Google Scholar]
- Radhakrishnan, R.; Yadav, A.; Date, P.; Bhaumik, S. A new method for generating sigma points and weights for nonlinear filtering. IEEE Control. Syst. Lett. 2018, 2, 519–524. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, J.; Zhang, X.; Ma, W.; Chen, B.; Senior Member, I. Kernel recursive maximum correntropy. Signal Process. 2015, 117, 11–16. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Bhaumik, S.; Tomar, N.K. Gaussian sum shifted Rayleigh filter for underwater bearings-only target tracking problems. IEEE J. Ocean. Eng. 2018, 44, 492–501. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Asfia, U.; Sharma, S. Gaussian sum state estimators for three dimensional angles-only underwater target tracking problems. IFAC-PapersOnLine 2022, 55, 333–338. [Google Scholar] [CrossRef]
- Kotecha, J.H.; Djuric, P.M. Gaussian sum particle filtering. IEEE Trans. Signal Process. 2003, 51, 2602–2612. [Google Scholar] [CrossRef] [Green Version]
- Karlgaard, C.D. Nonlinear regression Huber–Kalman filtering and fixed-interval smoothing. J. Guid. Control. Dyn. 2015, 38, 322–330. [Google Scholar] [CrossRef]
- Li, W.; Jia, Y. H-infinity filtering for a class of nonlinear discrete-time systems based on unscented transform. Signal Process. 2010, 90, 3301–3307. [Google Scholar] [CrossRef]
- Liu, W.; Pokharel, P.P.; Principe, J.C. Correntropy: A localized similarity measure. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 4919–4924. [Google Scholar]
- Liu, W.; Pokharel, P.P.; Principe, J.C. Correntropy: Properties and applications in non-Gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Cinar, G.T.; Príncipe, J.C. Hidden state estimation using the correntropy filter with fixed point update and adaptive kernel size. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–6. [Google Scholar]
- Cinar, G.T.; Príncipe, J.C. Adaptive background estimation using an information theoretic cost for hidden state estimation. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 489–494. [Google Scholar]
- Chen, B.; Liu, X.; Zhao, H.; Principe, J.C. Maximum correntropy Kalman filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Izanloo, R.; Fakoorian, S.A.; Yazdi, H.S.; Simon, D. Kalman filtering based on the maximum correntropy criterion in the presence of non-Gaussian noise. In Proceedings of the 2016 Annual Conference on Information Science and Systems (CISS), Princeton, NJ, USA, 16–18 March 2016; pp. 500–505. [Google Scholar]
- Liu, X.; Qu, H.; Zhao, J.; Chen, B. Extended Kalman filter under maximum correntropy criterion. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1733–1737. [Google Scholar]
- Liu, X.; Qu, H.; Zhao, J.; Yue, P.; Wang, M. Maximum correntropy unscented Kalman filter for spacecraft relative state estimation. Sensors 2016, 16, 1530. [Google Scholar] [CrossRef]
- Qin, W.; Wang, X.; Cui, N. Maximum correntropy sparse Gauss–Hermite quadrature filter and its application in tracking ballistic missile. IET Radar Sonar Navig. 2017, 11, 1388–1396. [Google Scholar] [CrossRef]
- Wang, G.; Li, N.; Zhang, Y. Maximum correntropy unscented Kalman and information filters for non-Gaussian measurement noise. J. Frankl. Inst. 2017, 354, 8659–8677. [Google Scholar] [CrossRef]
- Wang, G.; Gao, Z.; Zhang, Y.; Ma, B. Adaptive maximum correntropy Gaussian filter based on variational Bayes. Sensors 2018, 18, 1960. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Lyu, D.; He, Z.; Zhou, H.; Wang, D. Cauchy kernel-based maximum correntropy Kalman filter. Int. J. Syst. Sci. 2020, 51, 3523–3538. [Google Scholar] [CrossRef]
- Song, H.; Ding, D.; Dong, H.; Yi, X. Distributed filtering based on Cauchy-kernel-based maximum correntropy subject to randomly occurring cyber-attacks. Automatica 2022, 135, 110004. [Google Scholar] [CrossRef]
- Best, R.A.; Norton, J. A new model and efficient tracker for a target with curvilinear motion. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 1030–1037. [Google Scholar] [CrossRef]
- Cai, X.; Sun, F. Two-layer IMM tracker with variable structure for curvilinear maneuvering targets. Wirel. Pers. Commun. 2018, 103, 727–740. [Google Scholar] [CrossRef]
- Blackman, S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Norwood, MA, USA, 1999. [Google Scholar]
- Cavallaro, A.; Maggio, E. Video Tracking: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hewer, G.; Martin, R.; Zeh, J. Robust preprocessing for Kalman filtering of glint noise. IEEE Trans. Aerosp. Electron. Syst. 1987, 120–128. [Google Scholar] [CrossRef]
- Wu, W.R.; Cheng, P.P. A nonlinear IMM algorithm for maneuvering target tracking. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 875–886. [Google Scholar]
- Souza, C.R. Kernel functions for machine learning applications. Creat. Commons Attrib.-Noncommercial-Share Alike 2010, 3, 1. [Google Scholar]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control. 2000, 45, 477–482. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.R. Target racking with glint noise. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 174–185. [Google Scholar]
- Mallick, M.; Morelande, M.; Mihaylova, L.; Arulampalam, S.; Yan, Y. Angle-only filtering in three dimensions. In Integrated Tracking, Classification, and Sensor Management: Theory and Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2012; Volume 1, pp. 3–42. [Google Scholar]
- Asfia, U.; Radhakrishnan, R.; Sharma, S. Three-Dimensional Bearings-Only Target Tracking: Comparison of Few Sigma Point Kalman Filters. In Communication and Control for Robotic Systems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 273–289. [Google Scholar]
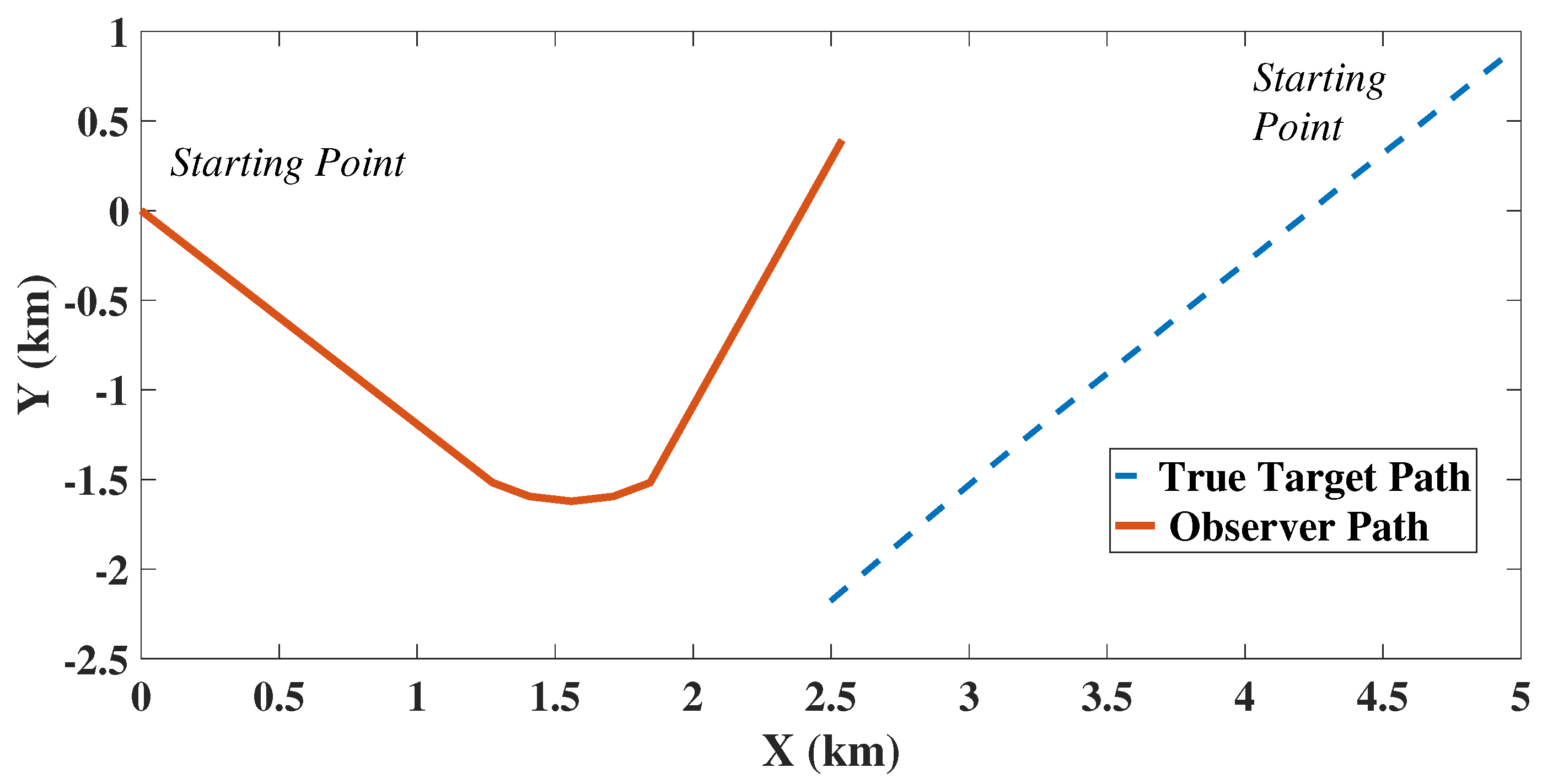
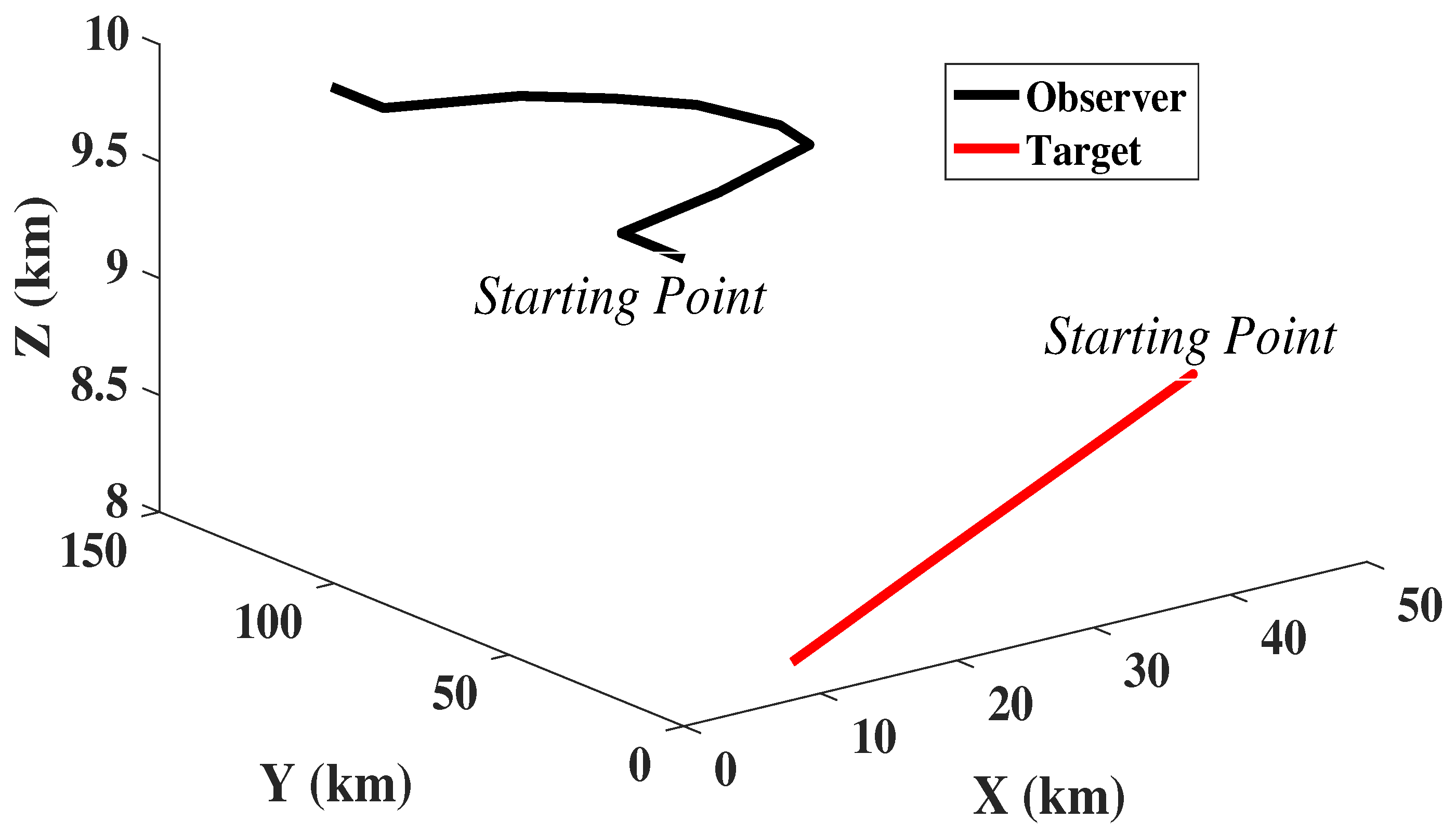
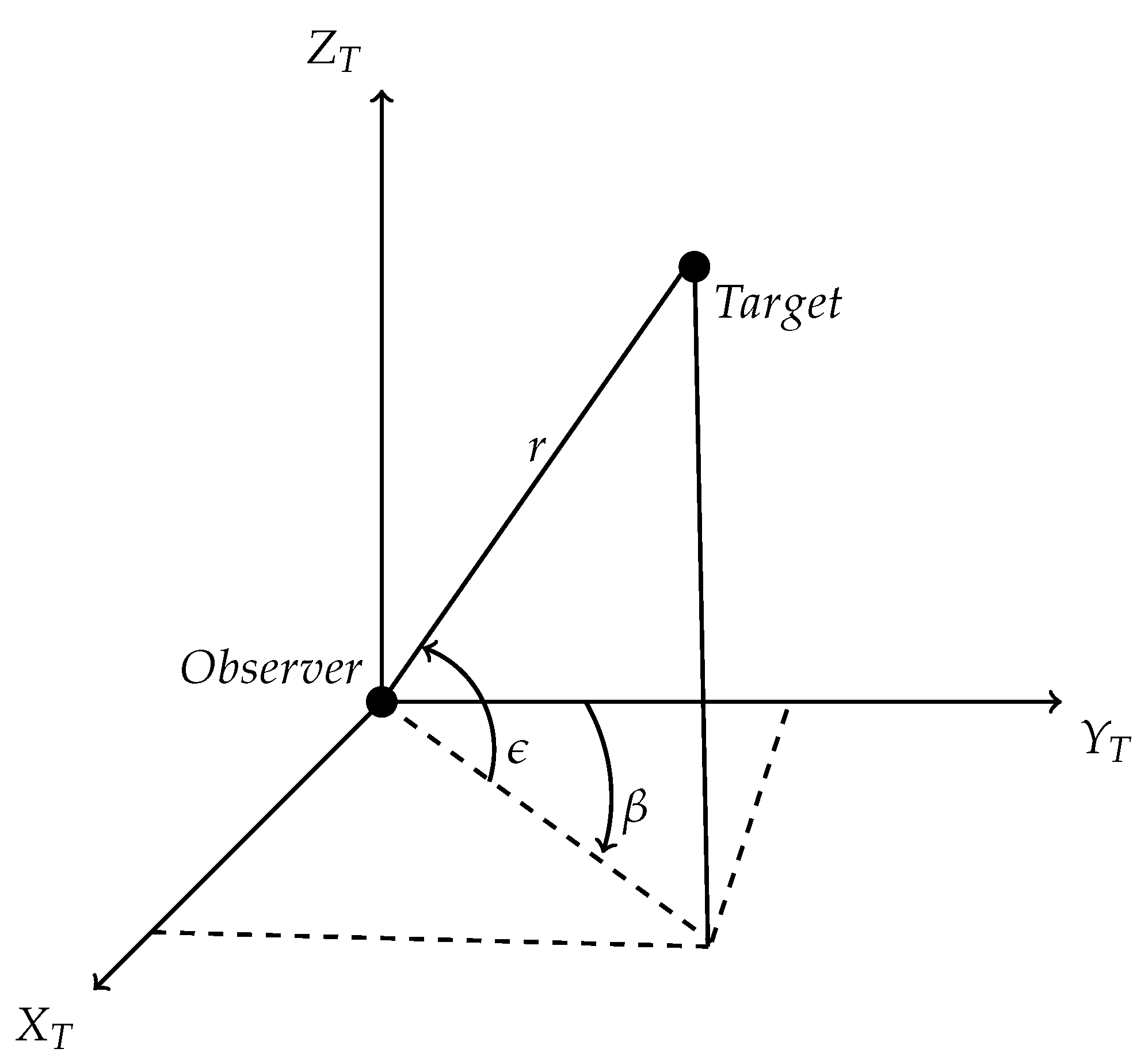

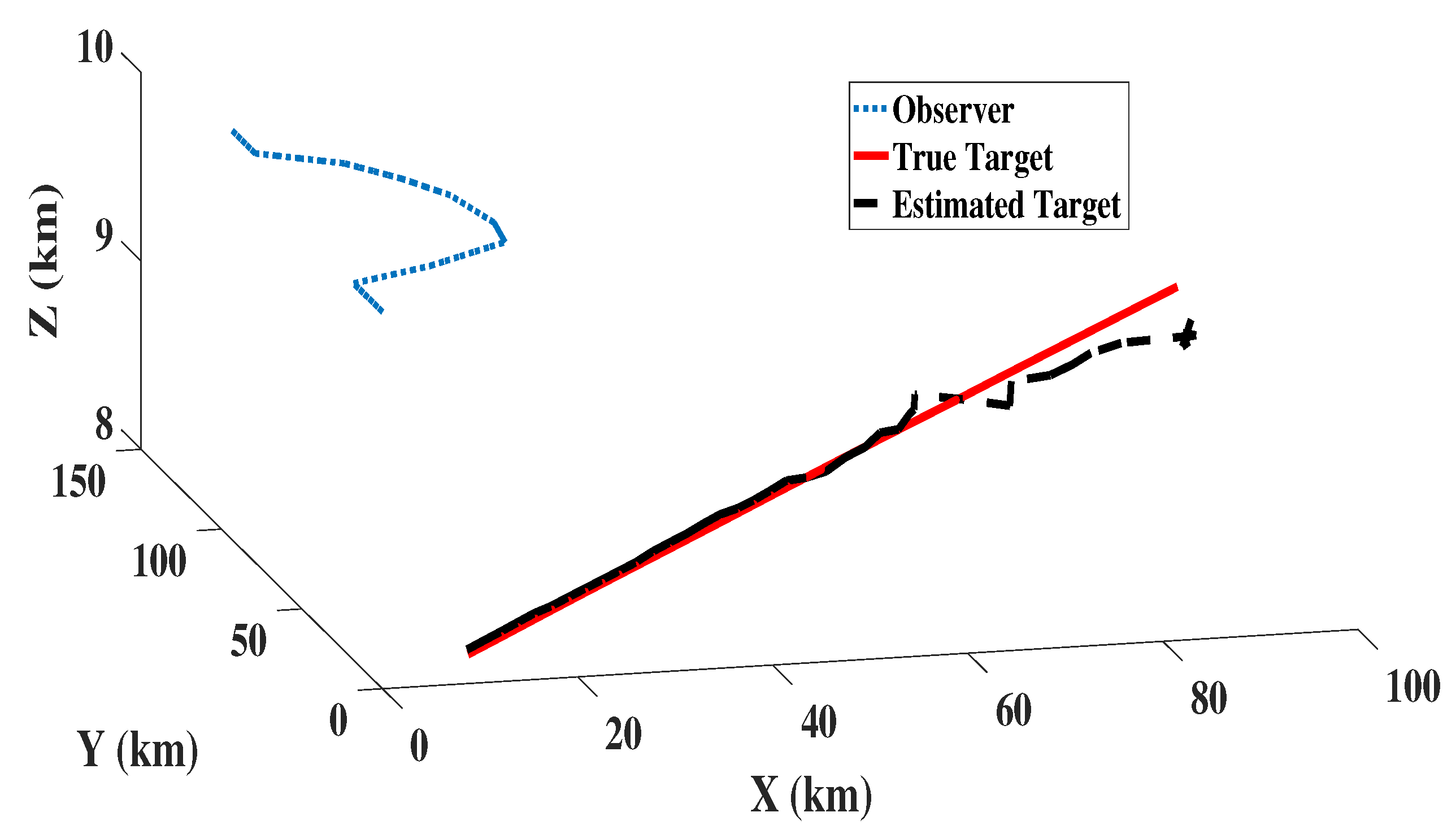

| Parameters | Values |
|---|---|
| Initial Target Position | (km) |
| Initial Observer Position | (km) |
| Initial Target Speed (s) | 4 (knots) |
| Initial Observer Speed | 5 (knots) |
| Target Course | |
| Observer manoeuvre | From 780 to 1020 (s) |
| Initial Range (r) | 5 (km) |
| Observation time | 1800 (s) |
| , | 9 () |
| 2 (km) | |
| 2 (knots) | |
| Sampling time | (s) |
| Initial Observer Course | |
| Final Observer Course | |
| Parameters | Values |
|---|---|
| Initial Target Position | (km) |
| Initial Observer Position | (km) |
| Initial Target Speed (s) | 0.297 (km/s) |
| Initial Observer Speed (s) | 0.297 (km/s) |
| Target Course | |
| Observer manoeuvre | From 70 to 370 (s) |
| Initial Range (r) | 150 (km) |
| Observation time | 420 (s) |
| , | |
| , | |
| 13.6 (km) | |
| 41.6 (m/s) | |
| Elevation Angle | |
| Sampling time | (s) |
| Filters | % Track Loss | RMSE (m) |
|---|---|---|
| UKF | 4.4 | 152.8 |
| MC-UKF-GK | 1.1 | 111.0 |
| MC-UKF-CK | 1.1 | 108.9 |
| NSKF | 2.8 | 151.1 |
| MC-NSKF-GK | 1.2 | 109.6 |
| MC-NSKF-CK | 0.5 | 108.8 |
| Filters | % Track Loss | RMSE (m) |
|---|---|---|
| UKF | 100 | - |
| MC-UKF-GK | 14 | 496.1 |
| MC-UKF-CK | 13.5 | 499.8 |
| NSKF | 100 | - |
| MC-NSKF-GK | 14 | 496.8 |
| MC-NSKF-CK | 13.5 | 498.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urooj, A.; Dak, A.; Ristic, B.; Radhakrishnan, R. 2D and 3D Angles-Only Target Tracking Based on Maximum Correntropy Kalman Filters. Sensors 2022, 22, 5625. https://doi.org/10.3390/s22155625
Urooj A, Dak A, Ristic B, Radhakrishnan R. 2D and 3D Angles-Only Target Tracking Based on Maximum Correntropy Kalman Filters. Sensors. 2022; 22(15):5625. https://doi.org/10.3390/s22155625
Chicago/Turabian StyleUrooj, Asfia, Aastha Dak, Branko Ristic, and Rahul Radhakrishnan. 2022. "2D and 3D Angles-Only Target Tracking Based on Maximum Correntropy Kalman Filters" Sensors 22, no. 15: 5625. https://doi.org/10.3390/s22155625
APA StyleUrooj, A., Dak, A., Ristic, B., & Radhakrishnan, R. (2022). 2D and 3D Angles-Only Target Tracking Based on Maximum Correntropy Kalman Filters. Sensors, 22(15), 5625. https://doi.org/10.3390/s22155625







