Low CP Overhead Waveform Design for Multi-Path Channels with Timing Synchronization Error
Abstract
:1. Introduction
- A novel waveform, i.e., SR-OFDM, is developed, aiming to lower the overhead of CP, whilst satisfying the orthogonality of a multi-carrier modulation system.
- Under the designed paradigm, we mathematically show that the multi-path channels can be overcome via the single-tap equalizer without any interference, even under a timing synchronization error.
- With a rigorous complexity analysis, it is demonstrated that the CP overhead is reduced significantly by the proposed SR-OFDM at the cost of an acceptable complexity.
- Two estimation methods are devised for SR-OFDM together with the theoretical analysis on its key performance features, such as, spectral efficiency, peak to average power ratio (PAPR), and complexity.
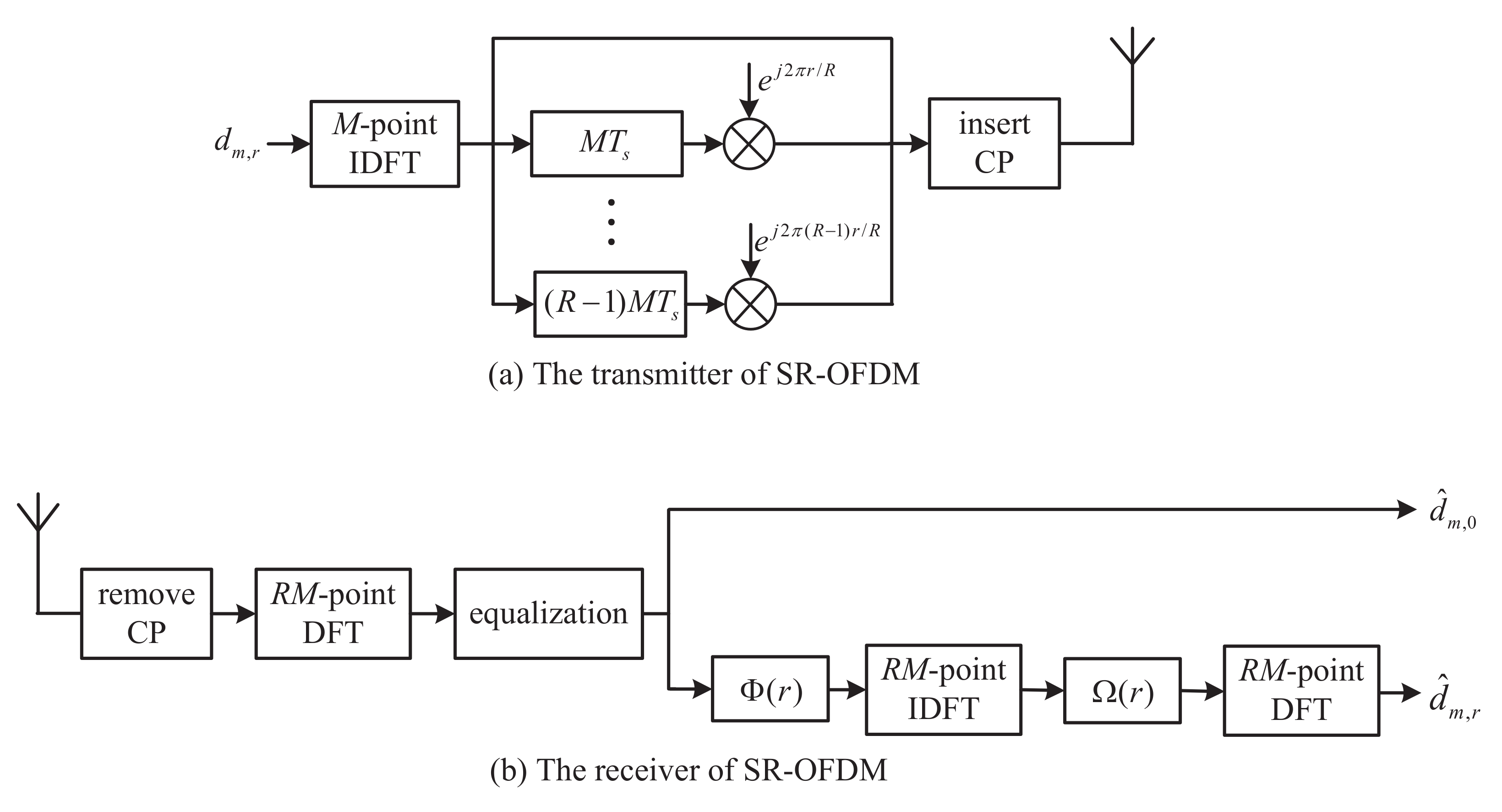
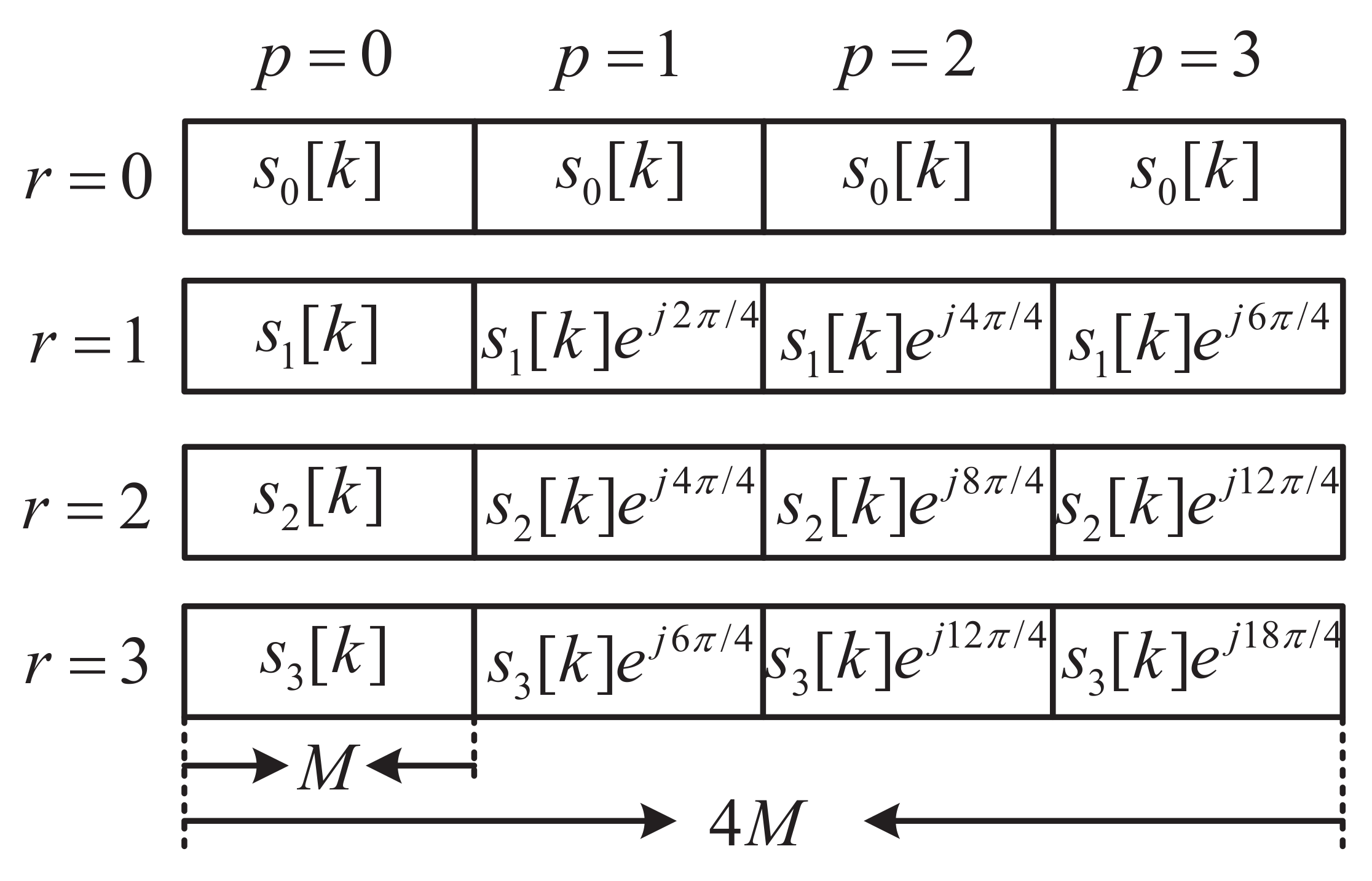
2. Proposed SR-OFDM
2.1. SR-OFDM Transmitter
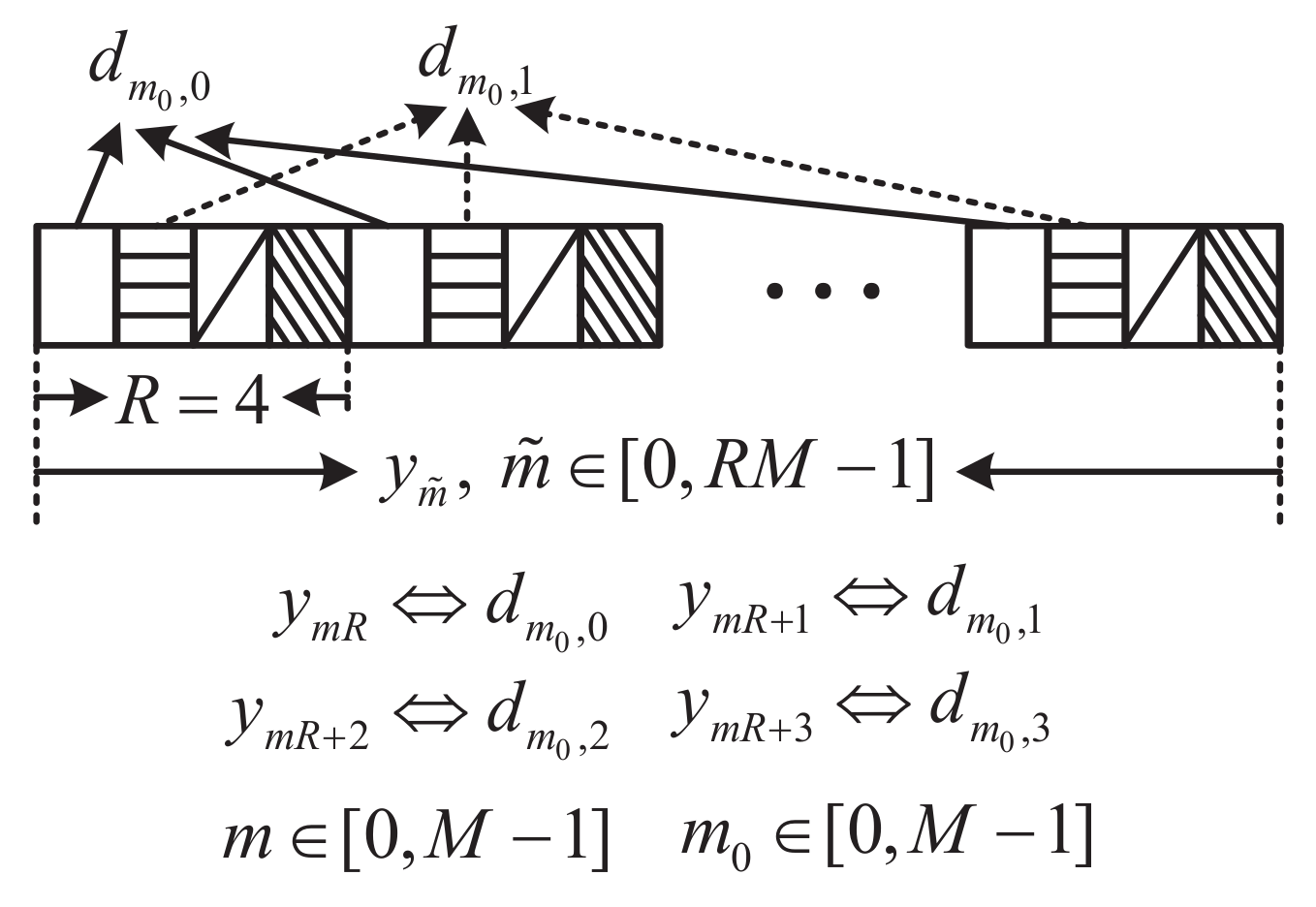
2.2. SR-OFDM Receiver
2.2.1. Symbol Demodulation of
2.2.2. Symbol Demodulation of
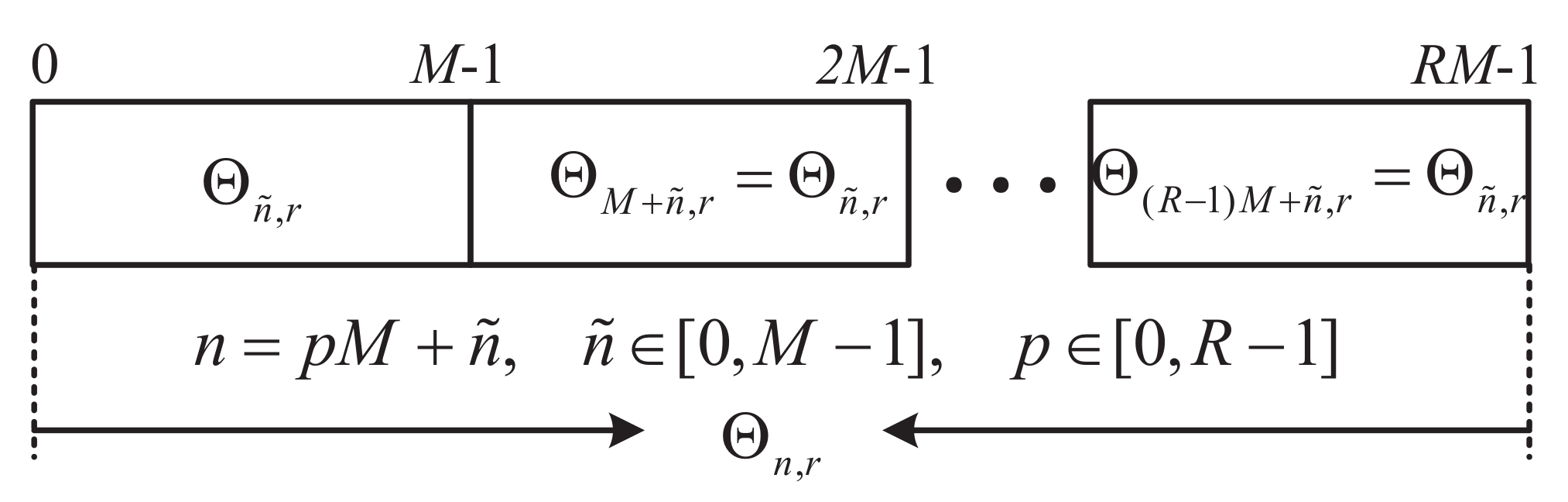
3. SR-OFDM under a Timing Synchronization Error
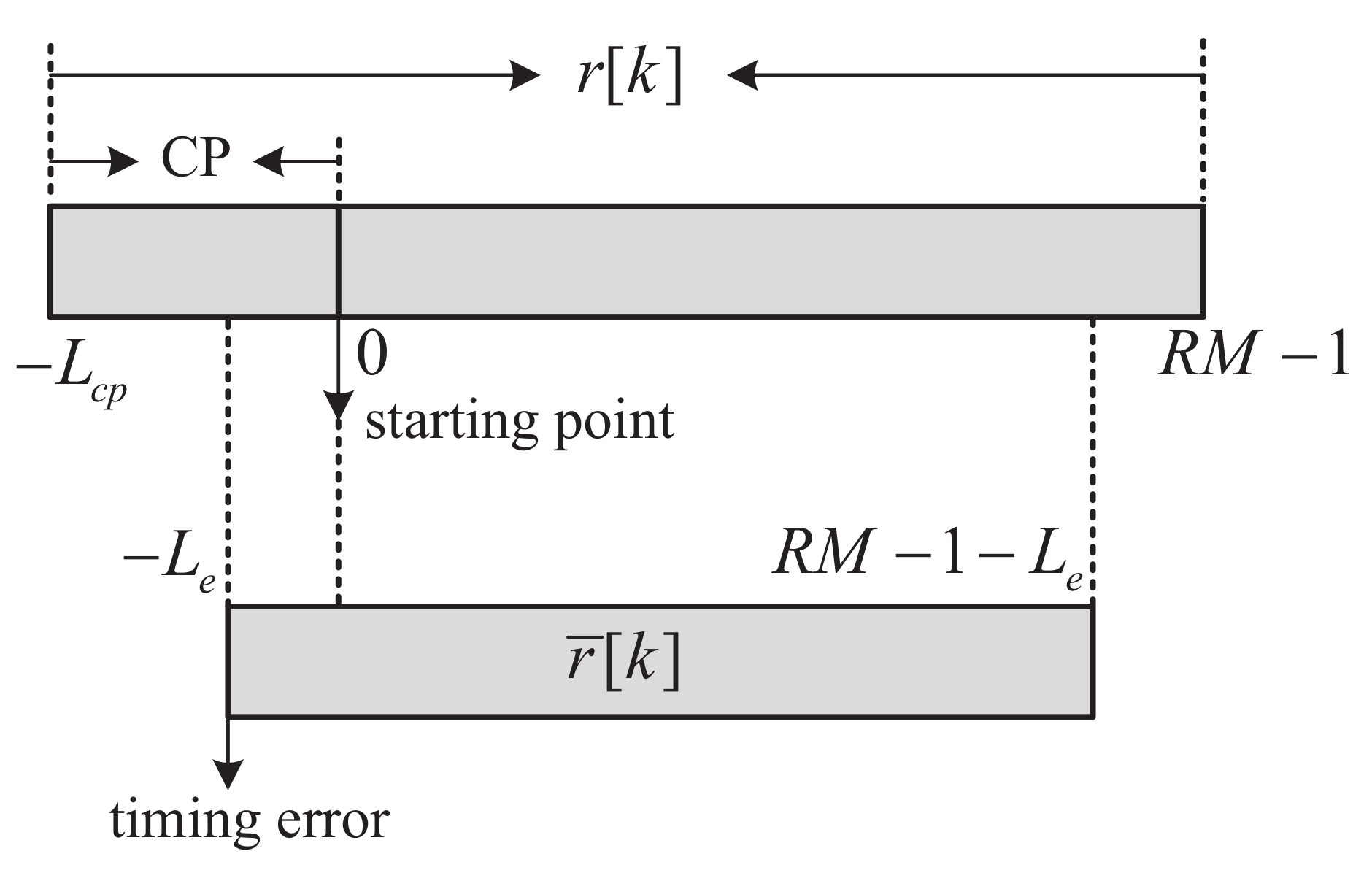
3.1. Received Signal with Timing Synchronization Error
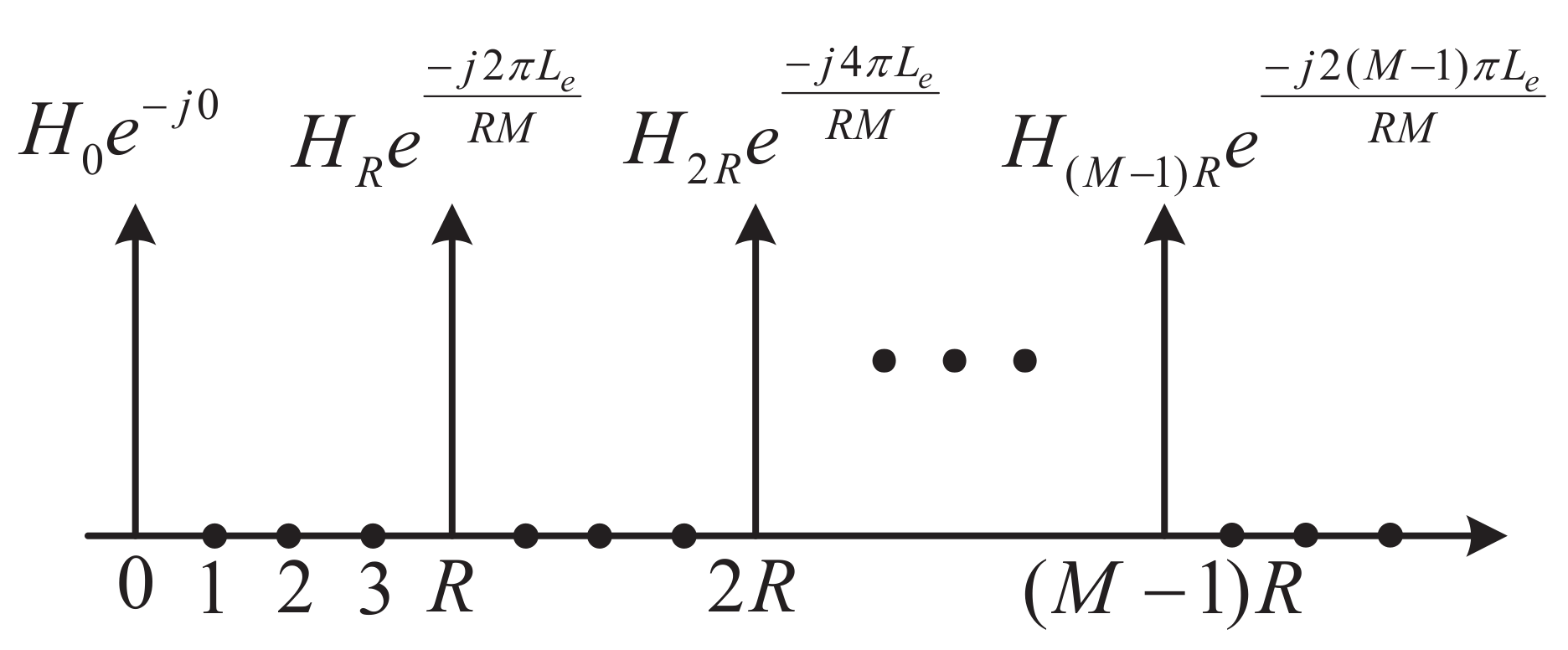
3.2. Symbol Demodulation under Timing Synchronization Error
3.2.1. DFT-Based Estimation
3.2.2. Linear Interpolation Estimation
4. Performance Analysis
4.1. Spectral Efficiency
4.2. Complexity Comparison
4.3. PAPR Comparison
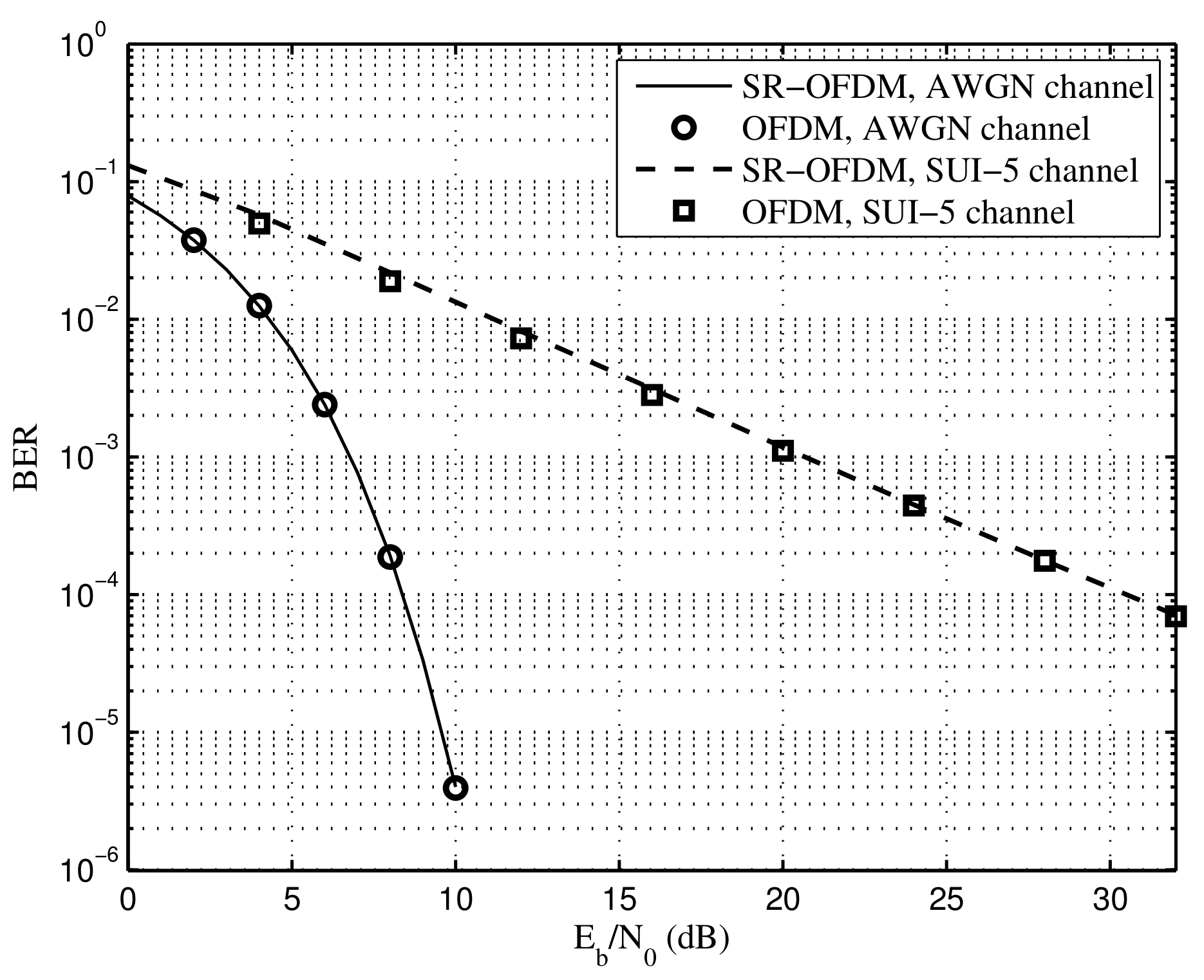
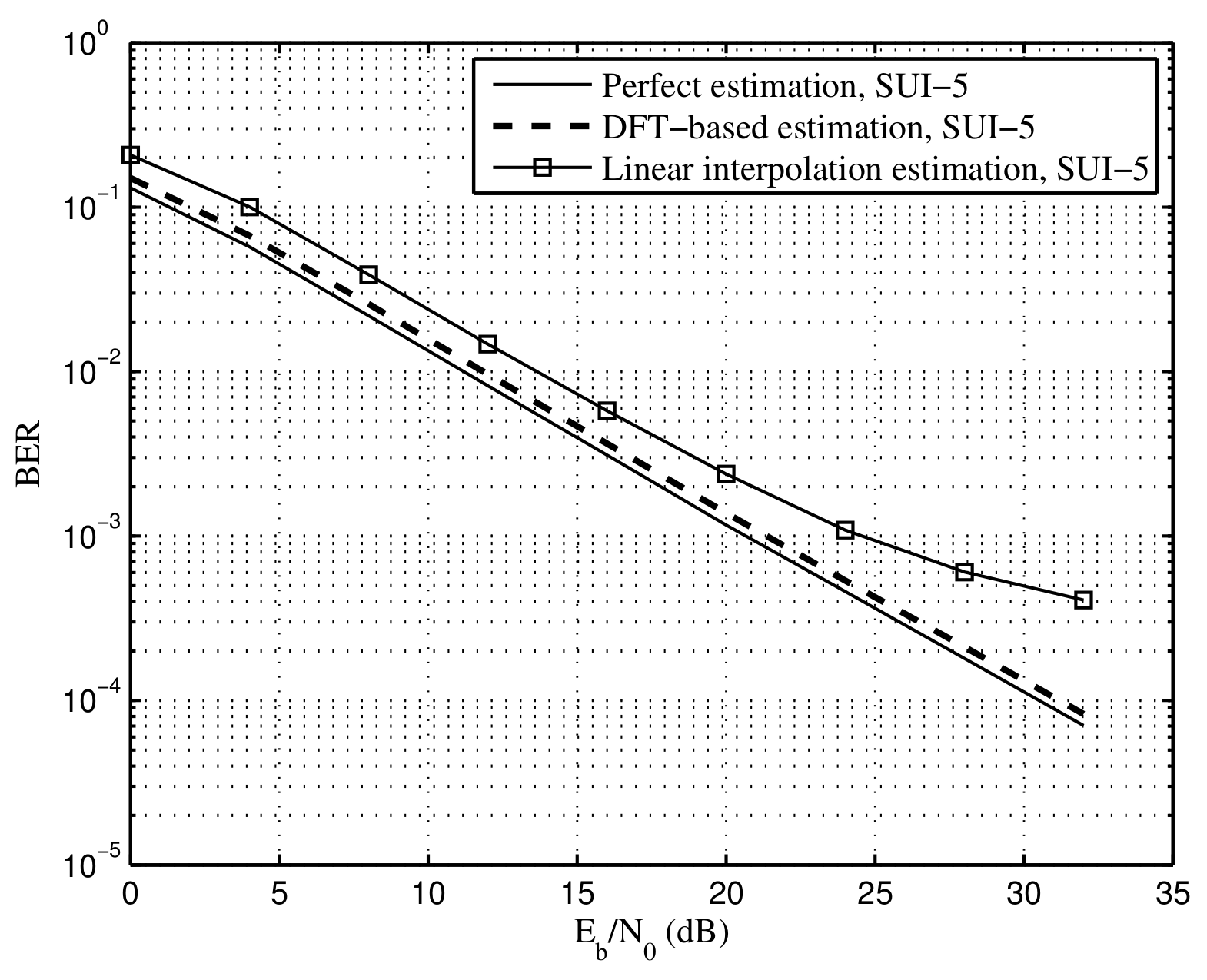
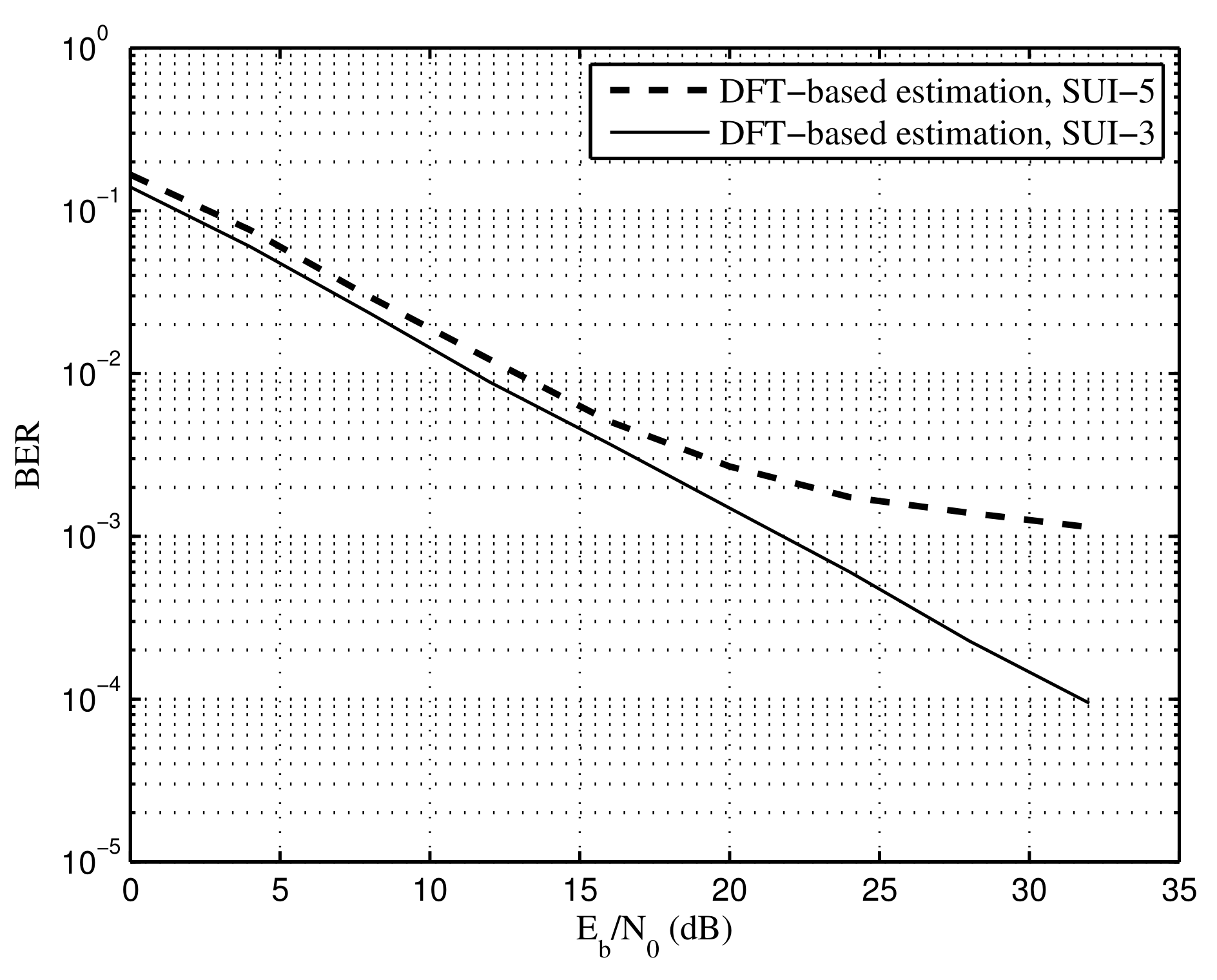
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ericsson Mobility Report. Available online: https://www.ericsson.com/en/mobility-report (accessed on 30 November 2020).
- Cui, Y.; Li, R.; Wang, P. A Novel Broadband Planar Antenna for 2G/3G/LTE Base Stations. IEEE Trans. Antennas Propag. 2013, 61, 2767–2774. [Google Scholar] [CrossRef]
- NR. Physical Channels and Modulation (Release 15). Available online: http://www.3gpp.org/ftp//Specs/archive/38_series/38.211/38211-f10.zip (accessed on 3 April 2018).
- Tse, D.N.C.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kong, D.; Xia, X.G.; Liu, P.; Zhu, Q. MMSE channel estimation for two-port demodulation reference signals in new radio. Sci. China Inf. Sci. 2021, 64, 169303. [Google Scholar] [CrossRef]
- Chakrapani, A. NB-IoT uplink receiver design and performance study. IEEE Internet Things J. 2020, 7, 2469–2482. [Google Scholar] [CrossRef] [Green Version]
- Chakrapani, A. CPLink: Interference-free reuse of cyclic-prefix intervals in OFDM-based networks. IEEE Trans. Wireless Commun. 2019, 18, 665–679. [Google Scholar]
- IEEE Std 802.11a-1999; IEEE Standard for Telecommunications and Information Exchange Between Systems—LAN/MAN Specific Requirements—Part 11: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications: “High Speed Physical Layer in the 5 GHz Band”. The Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 1999; pp. 1–102.
- Kim, N.; Shin, O.; Lee, K.B. Sum rate maximization with shortened cyclic prefix in a MIMO-OFDM system. IEEE Trans. Veh. Technol. 2018, 67, 12416–12420. [Google Scholar] [CrossRef]
- Torres, P.; Gusma˜o, A. Iterative receiver technique for reduced-CP, reduced-PMEPR OFDM transmission. In Proceedings of the 2007 IEEE 65th Vehicular Technology Conference—VTC2007-Spring, Dublin, Ireland, 22–25 April 2007; pp. 1981–1985. [Google Scholar]
- Liu, X.; Chen, H.-H.; Meng, W.; Lyu, B.-Y. Successive multipath interference cancellation for CP-free OFDM systems. IEEE Syst. J. 2019, 13, 1125–1134. [Google Scholar] [CrossRef]
- Hueske, K.; Götze, J. Ov-OFDM: A reduced PAPR and cyclic prefix free multicarrier transmission system. In Proceedings of the IEEE International Symposium on Wireless Communication Systems, Siena, Italy, 7–10 September 2009. [Google Scholar]
- Ngebani, Y.L.I.; Xia, X.-G.; Høst-Madsen, A. On performance of vector OFDM with linear receivers. IEEE Trans. Signal Process. 2012, 60, 5268–5280. [Google Scholar]
- Ngebani, I.; Li, Y.; Xia, X.-G.; Zhao, M. EM-Based Phase Noise Estimation in Vector OFDM Systems Using Linear MMSE Receivers. IEEE Trans. Veh. Technol. 2016, 65, 110–122. [Google Scholar] [CrossRef]
- Kong, D.; Xu, Y.; Song, G.; Li, J.; Jiang, T. A CP reduction scheme based on symbol repetition for narrow-band IoT systems. IEEE Internet Things J. 2021, 8, 12880–12891. [Google Scholar] [CrossRef]
- Wang, X.; Shen, X.; Ma, S. A Time-reversal based CP-free OFDM system for underwater acoustic communication. In Proceedings of the OCEANS 2019—Marseille, Marseille, France, 17–20 June 2019; pp. 1–6. [Google Scholar]
- Liu, L.; Yuen, C.; Guan, Y.L.; Li, Y.; Huang, C. Gaussian message passing for overloaded massive MIMO-NOMA. IEEE Trans. Wireless Commun. 2019, 18, 210–226. [Google Scholar] [CrossRef] [Green Version]
- Shu, T.; He, J.; Zhang, Y.; Dakulagi, V. 3-D Near-Field Source Localization Using a Spatially Spread Acoustic Vector Sensor. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 180–188. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Zhang, Z. Generalized spatial smoothing in bistatic EMVS-MIMO radar. Signal Process. 2022, 193, 108406. [Google Scholar] [CrossRef]
- Zheng, G.; Song, Y.; Chen, C. Height Measurement with Meter Wave Polarimetric MIMO Radar: Signal Model and MUSIC-like Algorithm. Signal Process. 2022, 190, 108344. [Google Scholar] [CrossRef]
- Zheng, G.; Song, Y.; Chen, C. On Parameter Identifiability of Diversity-Smoothing-Based MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1660–1675. [Google Scholar] [CrossRef]
- Kong, D.; Qu, D.; Jiang, T. Time domain channel estimation for OQAM-OFDM systems: Algorithms and performance bounds. IEEE Trans. Signal Process. 2014, 62, 322–330. [Google Scholar] [CrossRef]
- Kong, D.; Zheng, X.; Zhang, Y.; Jiang, T. Frame repetition: A solution to imaginary interference cancellation in FBMC/OQAM systems. IEEE Trans. Signal Process. 2020, 68, 1259–1273. [Google Scholar] [CrossRef]
- Telatar, E. Capacity of multi-antenna Gaussian channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]
- Liu, P.; Luo, K.; Chen, D.; Jiang, T. Spectral efficiency analysis of cell-free massive MIMO systems with zero-forcing detector. IEEE Trans. Wirel. Commun. 2020, 19, 795–807. [Google Scholar] [CrossRef] [Green Version]
- Sesia, S.; Toufik, I.; Baker, M. LTE-The UMTS Long Term Evolution: From Theory to Practice; Wiley Publishing: Hoboken, NJ, USA, 2009. [Google Scholar]
- Wang, X.; Wu, Y.; Chouinard, J.-Y.; Wu, H.-C. On the design and performance analysis of multisymbol encapsulated OFDM systems. IEEE Trans. Veh. Technol. 2006, 55, 990–1002. [Google Scholar] [CrossRef]
- Jiang, T.; Wu, Y. An overview: Peak-to-average power ratio reduction techniques for OFDM signals. IEEE Trans. Broadcast. 2008, 54, 257–268. [Google Scholar] [CrossRef]
- Evolved Universal Terrestrial Radio Access (E-UTRA); Physical Channels and Modulation. Available online: ftp://ftp.3gpp.org/specs/2019-03/Rel-15/36_series/ (accessed on 24 June 2020).
- Jain, R. Channel Models A Tutorial; WiMAX Forum AATG. Available online: https://www.cse.wustl.edu/~jain/cse574-08/ftp/channel_model_tutorial.pdf (accessed on 21 February 2007).





| imaginary unit | |
| M | subcarrier number |
| R | number of symbol repetition |
| transmitted symbol | |
| index of branch in SR-OFDM, not the index of repetition | |
| index of subcarrier | |
| timing synchronization error | |
| the received signal after DFT, , |
| Multiplications | OFDM(R Symbols) | SR-OFDM |
|---|---|---|
| Transmitter | ||
| Receiver |
| Channel | SUI-3 | SUI-5 |
|---|---|---|
| Sampling Frequency (MHz) | 30.72 | 30.72 |
| Number of Paths | 3 | 3 |
| Power Profile (in dB) | 0, −5.0, −10.0 | 0, −5.0, −10.0 |
| Delay Profile (s) | 0, 0.4, 0.9 | 0, 4, 10 |
| Frequency selectivity | low | high |
| Element | Attribute | Characteristic |
|---|---|---|
| Ov-OFDM [12] | Propose a CP-free method for OFDM systems based on overlapping MMSE. | Remaining interference, applicable to low SNR. |
| Vector OFDM [13] | Propose a unit matrix for precoding multiple symbols so that multiple symbols only include one CP. | No inter-symbol interference, high complexity compared to other two methods. |
| SR-OFDM | Propose a novel waveform to make multiple symbols share one CP based on the concept of symbol repetition. | No inter-symbol interference, acceptable increased complexity. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Wang, B.; Guo, J.; Shan, X.; Kong, D. Low CP Overhead Waveform Design for Multi-Path Channels with Timing Synchronization Error. Sensors 2022, 22, 5772. https://doi.org/10.3390/s22155772
Chen J, Wang B, Guo J, Shan X, Kong D. Low CP Overhead Waveform Design for Multi-Path Channels with Timing Synchronization Error. Sensors. 2022; 22(15):5772. https://doi.org/10.3390/s22155772
Chicago/Turabian StyleChen, Jing, Baobing Wang, Jianzhong Guo, Xin Shan, and Dejin Kong. 2022. "Low CP Overhead Waveform Design for Multi-Path Channels with Timing Synchronization Error" Sensors 22, no. 15: 5772. https://doi.org/10.3390/s22155772
APA StyleChen, J., Wang, B., Guo, J., Shan, X., & Kong, D. (2022). Low CP Overhead Waveform Design for Multi-Path Channels with Timing Synchronization Error. Sensors, 22(15), 5772. https://doi.org/10.3390/s22155772






