Research on Vibration Reduction Performance of Electromagnetic Active Seat Suspension Based on Sliding Mode Control
Abstract
:1. Introduction
2. Dynamic Model
2.1. Establishment of “Seat–Body–Tire” Dynamic Model
2.2. Electromagnetic Vibration Damping System
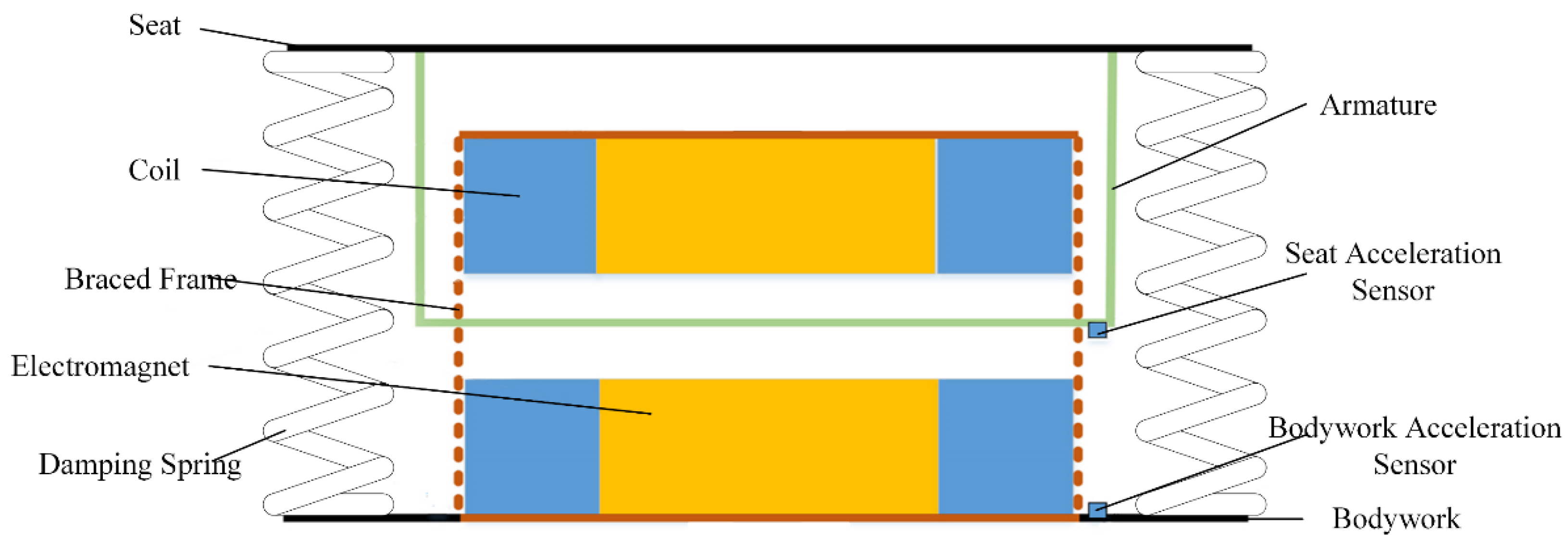
2.2.1. Structure of Electromagnetic Vibration Reduction System
2.2.2. Dynamic Model of Electromagnetic Vibration Damping System
- (1)
- Establishment of electromagnetic force equation:
- (1)
- Idealized assumptions: (a) the armature is rigid and the stiffness coefficient is large enough; (b) the armature mass is evenly distributed; (c) when the armature is in the balanced position, the air gap between the armature and the upper and lower electromagnets is the same and is very small, to ensure that the magnetic line of force passes through vertically; (d) the magnetic flux passes through the magnetic circuit with the cross section S of the magnetic pole; (e)the permeability is ; and (f) flux leakage is ignored.
- (2)
- The electromagnetic force equation is expressed by the coil current and the air gap .
- (2)
- Establishment of the three-degrees-of-freedom model and dynamic equation of “seat–body–tire” system:
2.3. Establishment of State-Space Equation and Feedback Linearization
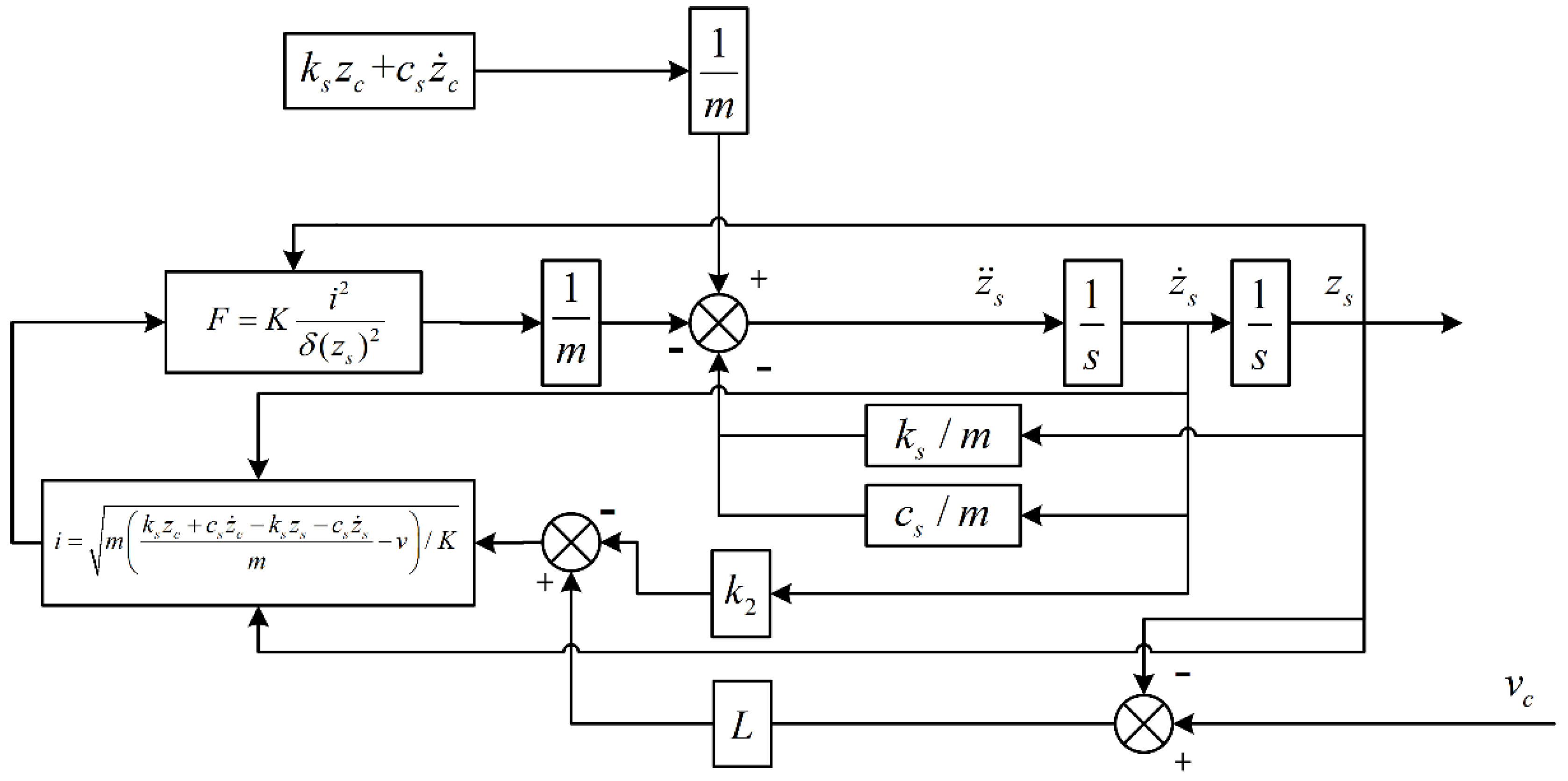
2.3.1. Electromagnetic Vibration Damping Seat System Model
2.3.2. Linearization Process
- (1)
- Test relative order condition
- (2)
- Linearization calculation:
3. Design of Feedback Controller
3.1. Design of State Feedback Controller
3.2. Design of Integral Sliding Mode Controller
4. Establishment of Simulation Test Model
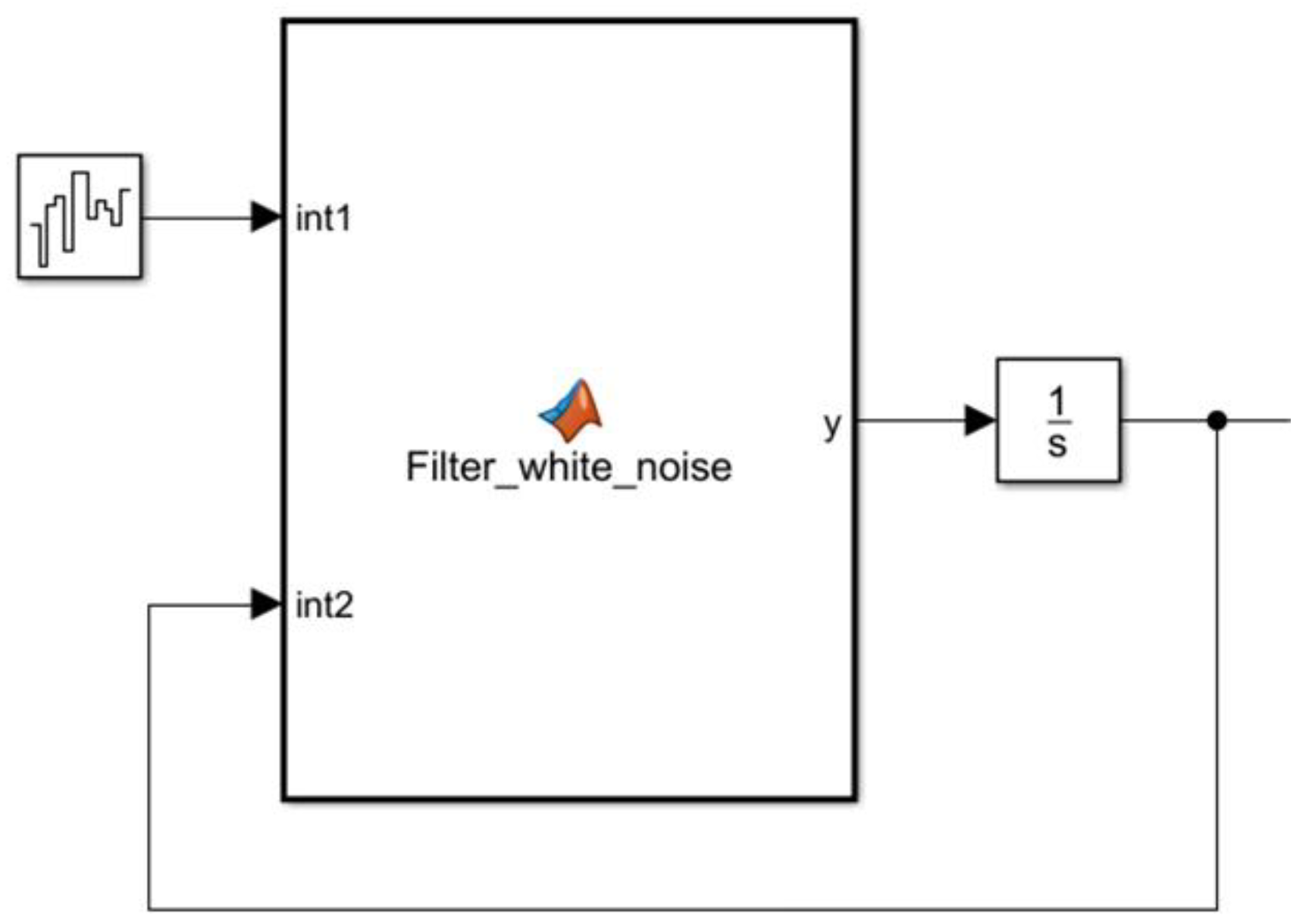
4.1. Establishment of Pavement Spectrum Model
4.2. Establishment of Simulation Model
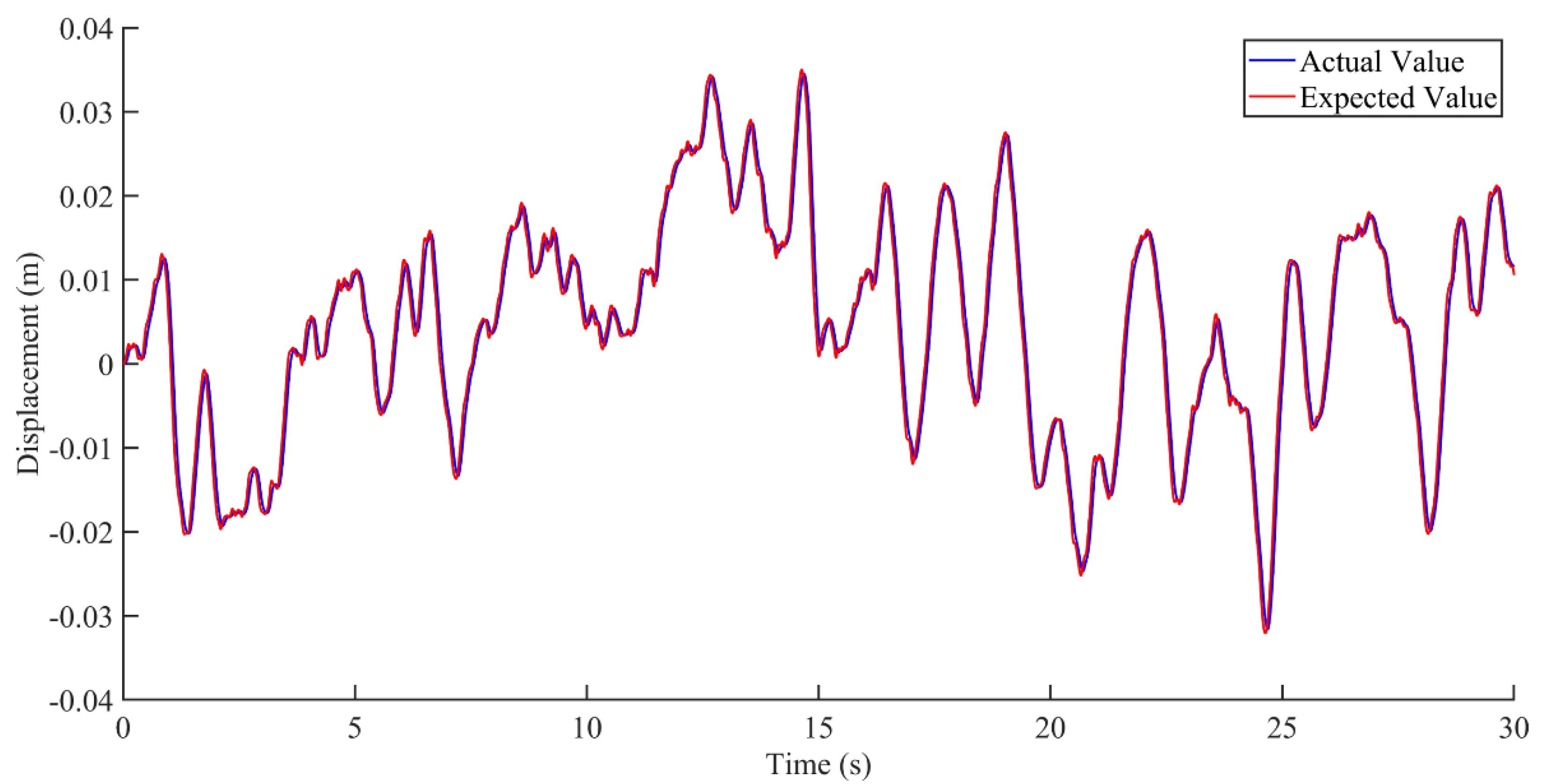
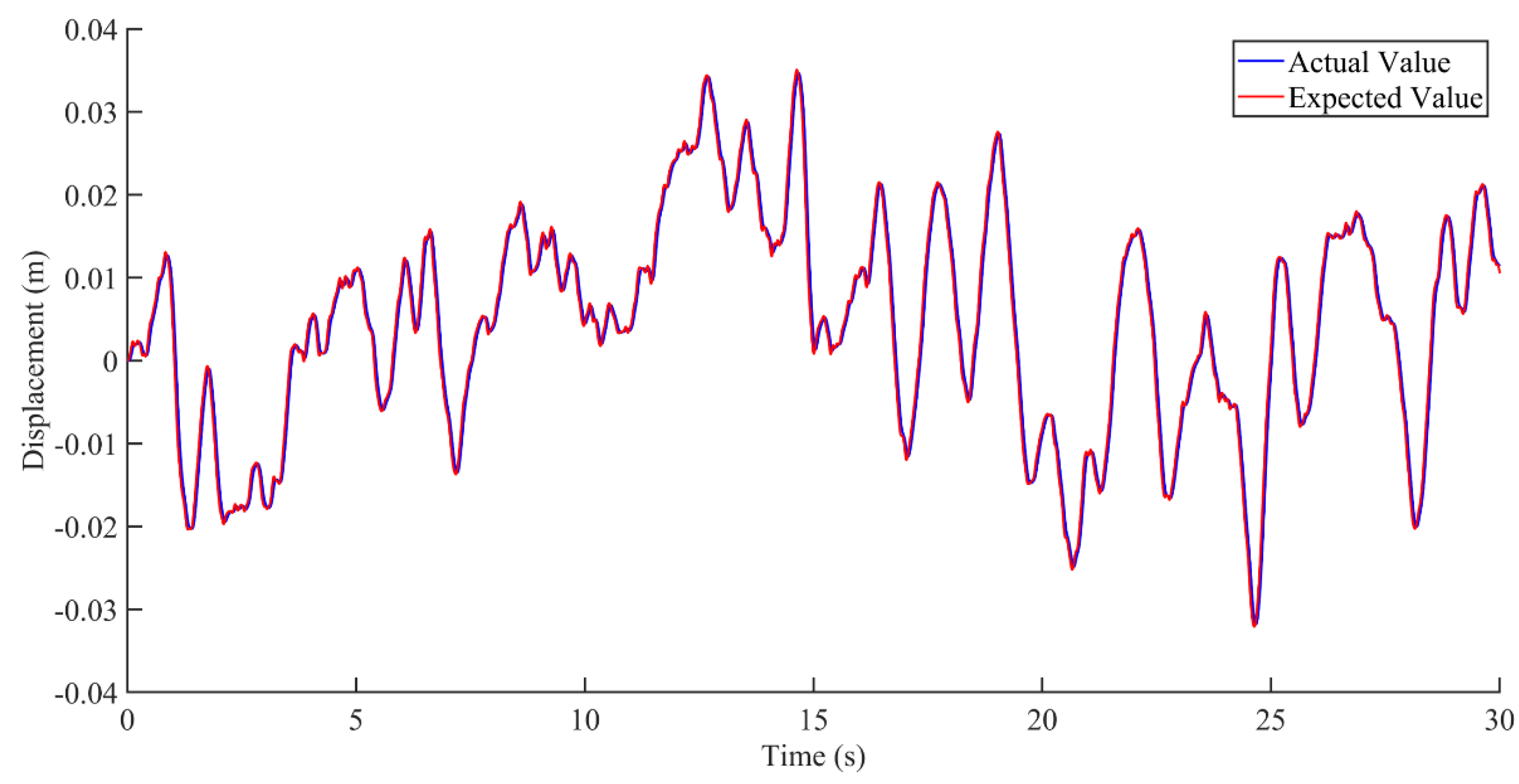
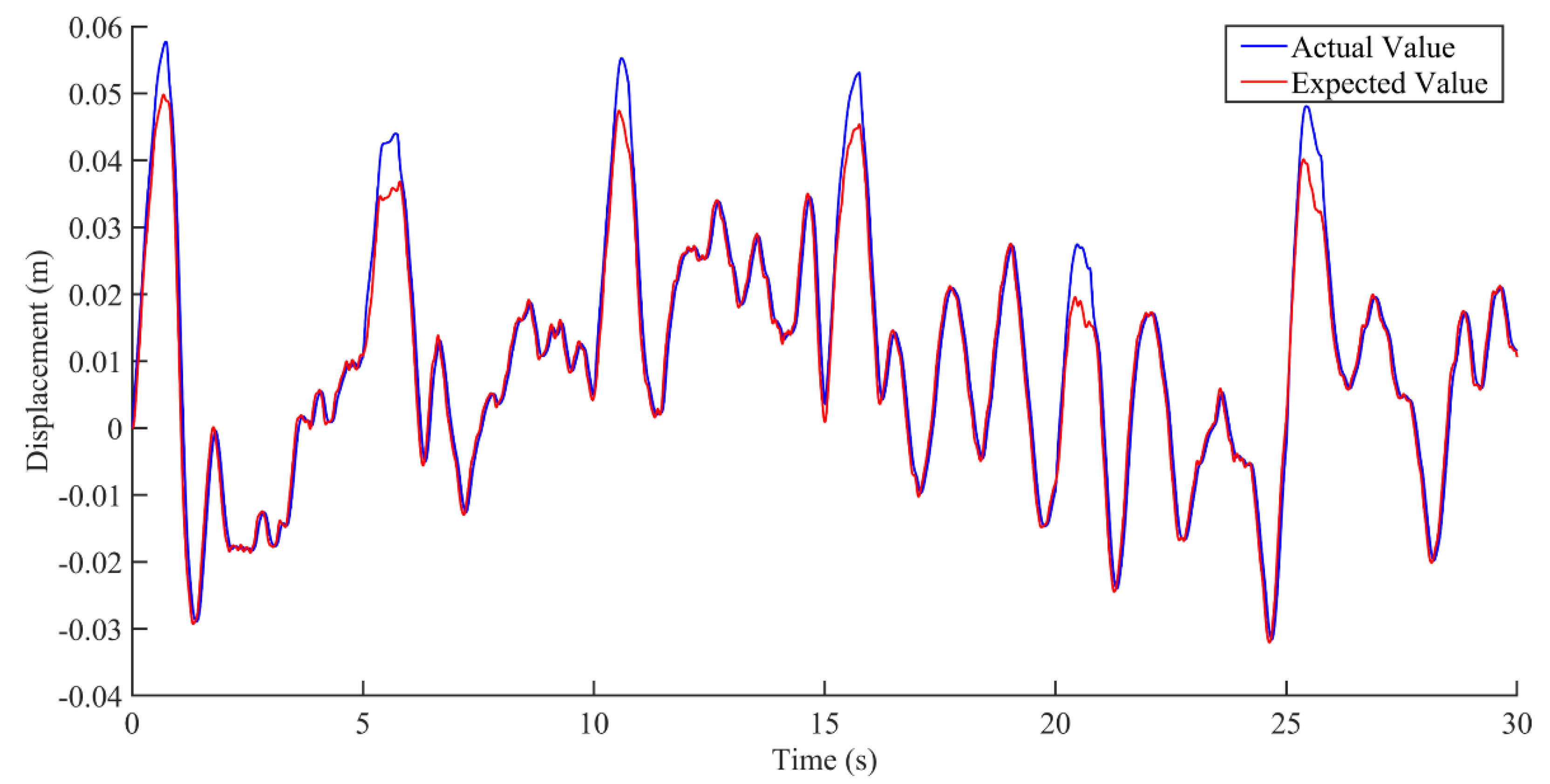
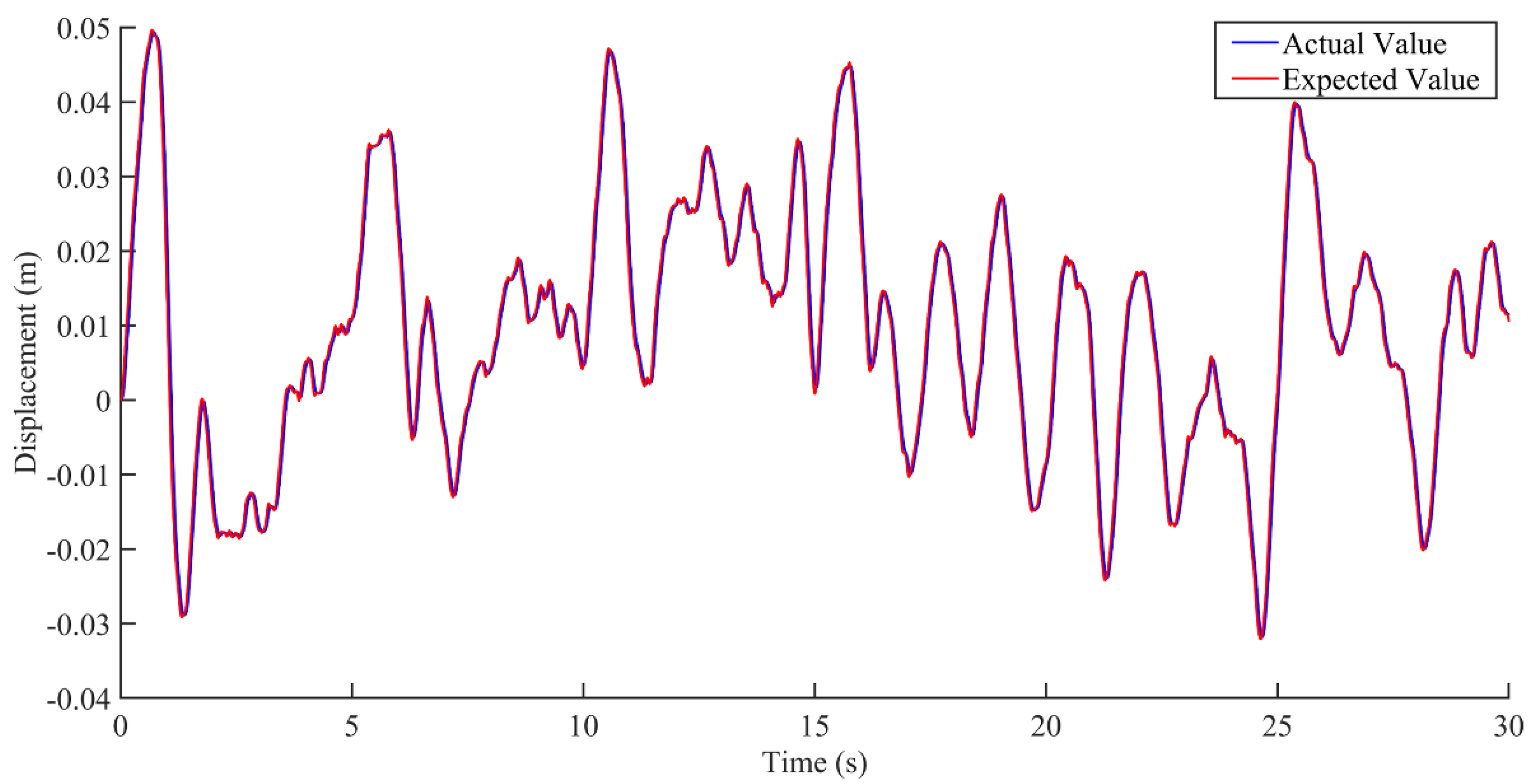
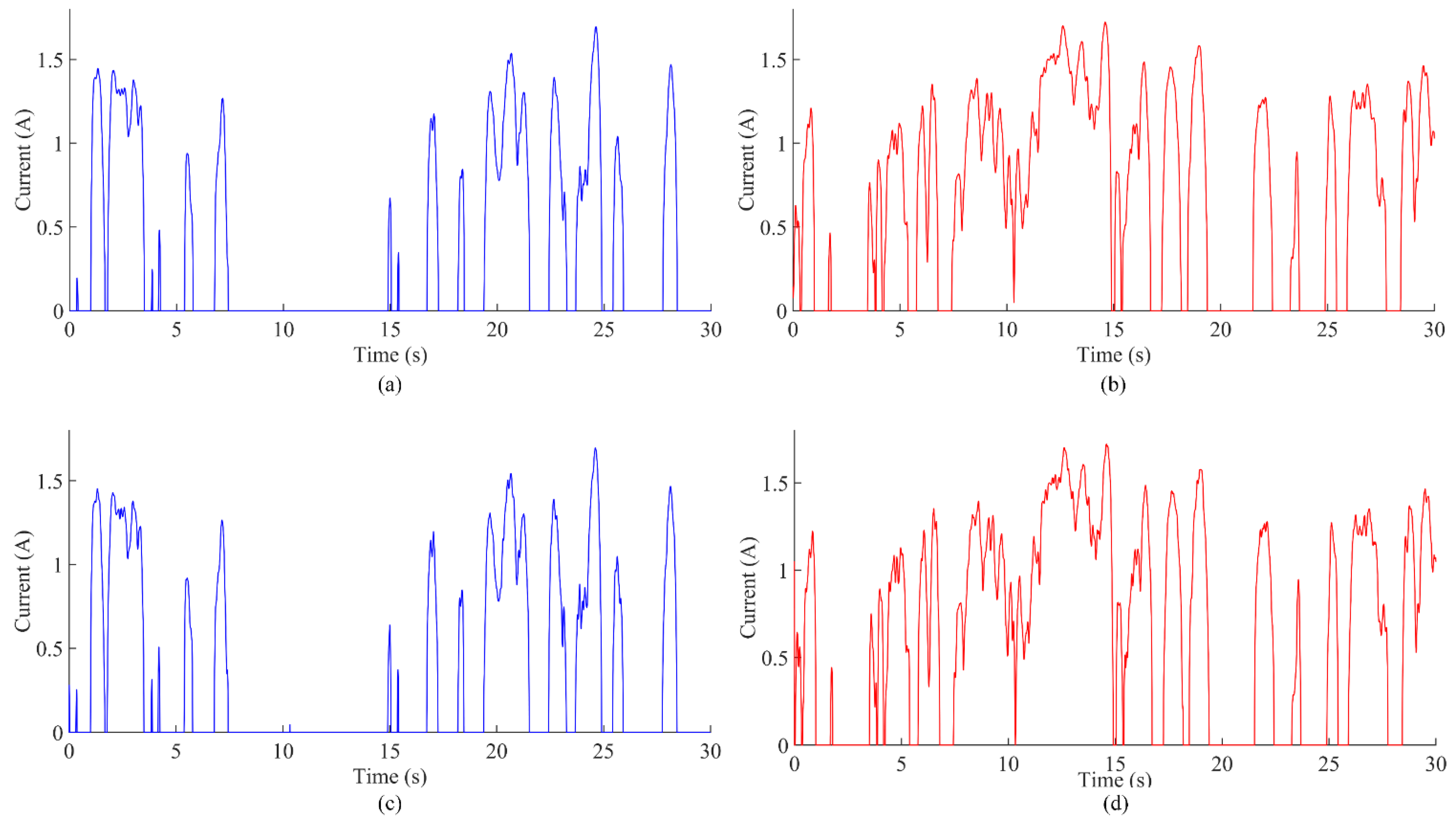
5. Simulation Results and Discussion
5.1. Vibration Study
5.2. Calculation of Electromagnet Energy Consumption
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krajnak, K. Health effects associated with occupational exposure to hand-arm or whole body vibration. J. Toxicol. Environ. Health-Part B-Crit. Rev. 2018, 21, 320–334. [Google Scholar] [CrossRef] [PubMed]
- Tiemessen, I.J.H.; Hulshof, C.T.J.; Frings-Dresen, M.H.W. Low back pain in drivers exposed to whole body vibration: Analysis of a dose-response pattern. Occup. Environ. Med. 2008, 65, 667–675. [Google Scholar] [CrossRef] [PubMed]
- Slota, G.P.; Granata, K.P.; Madigan, M.L. Effects of seated whole-body vibration on postural control of the trunk during unstable seated balance. Clin. Biomech. 2008, 23, 381–386. [Google Scholar] [CrossRef] [PubMed]
- Johanning, E. Diagnosis of whole-body vibration related health problems in occupational medicine. J. Low Freq. Noise Vib. Act. Control 2011, 30, 207–220. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Wang, X. A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems. Appl. Sci. 2019, 9, 3326. [Google Scholar] [CrossRef] [Green Version]
- Oshinoya, Y.; Arai, H.; Ishibashi, K. Experimental study on active seat suspension for a small vehicle. Int. J. Appl. Electromagn. Mech. 2004, 19, 437–443. [Google Scholar] [CrossRef]
- Maciejewski, I.; Meyer, L.; Krzyzynski, T. The vibration damping effectiveness of an active seat suspension system and its robustness to varying mass loading. J. Sound Vib. 2010, 329, 3898–3914. [Google Scholar] [CrossRef]
- Sun, W.C.; Li, J.F.; Zhao, Y.; Gao, H.J. Vibration control for active seat suspension systems via dynamic output feedback with limited frequency characteristic. Mechatronics 2011, 21, 250–260. [Google Scholar] [CrossRef]
- Pan, G.Y.; Hao, X.L. Research on Active Control of Driver’s Seat Suspension System. In Proceedings of the International Conference on Vibration, Structural Engineering and Measurement (ICVSEM 2011), Shanghai, China, 21–23 October 2011; pp. 701–704. [Google Scholar]
- Maciejewski, I. Control system design of active seat suspensions. J. Sound Vib. 2012, 331, 1291–1309. [Google Scholar] [CrossRef]
- Pan, G.Y.; Yang, H.; Liu, Y.T. Study of Commercial Vehicle Active Seat Suspension. In Proceedings of the 3rd International Conference on Machinery Electronics and Control Engineering (ICMECE 2013), Jinan, China, 29–30 November 2013; pp. 641–644. [Google Scholar]
- Maciejewski, I.; Glowinski, S.; Krzyzynski, T. Active control of a seat suspension with the system adaptation to varying load mass. Mechatronics 2014, 24, 1242–1253. [Google Scholar] [CrossRef]
- Gan, Z.; Hillis, A.J.; Darling, J. Adaptive control of an active seat for occupant vibration reduction. J. Sound Vib. 2015, 349, 39–55. [Google Scholar] [CrossRef] [Green Version]
- Ning, D.H.; Sun, S.S.; Li, H.Y.; Du, H.P.; Li, W.H. Active control of an innovative seat suspension system with acceleration measurement based friction estimation. J. Sound Vib. 2016, 384, 28–44. [Google Scholar] [CrossRef]
- Ning, D.H.; Sun, S.; Zhang, J.W.; Du, H.P.; Li, W.H.; Wang, X. An active seat suspension design for vibration control of heavy-duty vehicles. J. Low Freq. Noise Vib. Act. Control 2016, 35, 264–278. [Google Scholar] [CrossRef]
- Maciejewski, I.; Krzyzynski, T.; Meyer, H. Modeling and vibration control of an active horizontal seat suspension with pneumatic muscles. J. Vib. Control 2018, 24, 5938–5950. [Google Scholar] [CrossRef]
- Chouinard, P.; Begin, M.A.; Fortin, J.M.; Berry, A.; Masson, P.; Plante, J.S. Preventing Lower Back Pain among Truck Drivers: Design and Performance of a Controlled Slippage Magnetorheological Actuator for an Active Seat Suspension. In Proceedings of the 38th American-Society-of-Mechanical-Engineers (ASME) Computers and Information in Engineering (CIE) Conference in Conjunction with the International Design Engineering Technical Conferes (IDETC), Quebec City, QC, Canada, 26–29 August 2018. [Google Scholar]
- Alfadhli, A.; Darling, J.; Hillis, A.J. The control of an active seat with vehicle suspension preview information. J. Vib. Control 2018, 24, 1412–1426. [Google Scholar] [CrossRef] [Green Version]
- Ning, D.H.; Sun, S.S.; Du, H.P.; Li, W.H. Integrated active and semi-active control for seat suspension of a heavy duty vehicle. J. Intell. Mater. Syst. Struct. 2018, 29, 91–100. [Google Scholar] [CrossRef] [Green Version]
- Maciejewski, I.; Zlobinski, M.; Krzyzynski, T.; Glowinski, S. Vibration control of an active horizontal seat suspension with a permanent magnet synchronous motor. J. Sound Vib. 2020, 488, 115655. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Alashmori, M.; Bi, F.R.; Wang, X. Parameter identification and robust vibration control of a truck driver’s seat system using multi-objective optimization and genetic algorithm. Appl. Acoust. 2021, 173, 107697. [Google Scholar] [CrossRef]
- Xia, X.J.; Zheng, M.Y.; Liu, P.F.; Zhang, N.; Ning, D.H.; Du, H.P. Friction observer-based hybrid controller for a seat suspension with semi-active electromagnetic damper. Mechatronics 2021, 76, 102568. [Google Scholar] [CrossRef]
- Cvok, I.; Hrgetic, M.; Hoic, M.; Deur, J.; Ivanovic, V. Design of a linear motor-based shaker rig for testing driver’s perceived ride comfort. Mechatronics 2021, 75, 102521. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Liu, Y.J. Adaptive fuzzy fault-tolerant control of seat active suspension systems with actuator fault. IET Control Theory Appl. 2021, 15, 1104–1114. [Google Scholar] [CrossRef]
- Yang, H.; Liu, J.; Li, M.; Zhang, X.L.; Liu, J.Z.; Zhao, Y.L. Adaptive Kalman Filter with L-2 Feedback Control for Active Suspension Using a Novel 9-DOF Semi-Vehicle Model. Actuators 2021, 10, 267. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Ren, C.A.B.; Ma, K.H.; Xu, Z.; Zhou, P.C.; Chen, Y.J. Effect of delayed resonator on the vibration reduction performance of vehicle active seat suspension. J. Low Freq. Noise Vib. Act. Control 2022, 41, 387–404. [Google Scholar] [CrossRef]
- Maciejewski, I.; Blazejewski, A.; Pecolt, S.; Krzyzynski, T. A sliding mode control strategy for active horizontal seat suspension under realistic input vibration. J. Vib. Control 2022, 1–13. [Google Scholar] [CrossRef]
- Liu, L.; Li, X.S. Event-Triggered Tracking Control for Active Seat Suspension Systems With Time-Varying Full-State Constraints. IEEE Trans. Syst. Man Cybern. -Syst. 2022, 52, 582–590. [Google Scholar] [CrossRef]
- Chunfang, L.; Qingguang, C.; Limei, W.; Qingding, G. Studding of NC tool crossbeam magnetic levitation system based on dynamic integral sliding mode control. In Proceedings of the 2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, China, 24–26 August 2010; pp. 402–405. [Google Scholar]
- Wang, L.-M.; Jin, F.-Y.; Liu, C.-F. Sliding mode control of cnc electromagnetic levitation system based on feedback linearization. In Proceedings of the 2009 Chinese and Decision Conference, Guilin, China, 17–19 June 2009; pp. 2706–2709. [Google Scholar]










| Parameters | Physical Meaning | Value | Units |
|---|---|---|---|
| Tire mass | 45 | kg | |
| Body mass | 330 | kg | |
| Seat and human mass | 80 | kg | |
| Tire stiffness | 170,000 | N/m | |
| Body suspension stiffness | 13,000 | N/m | |
| Seat suspension stiffness | 35,000 | N/m | |
| Seat suspension damping | 300 | N/(m/s) | |
| Body suspension damping | 2000 | N/(m/s) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, P.; Che, Y.; Liu, Z.; Wang, G. Research on Vibration Reduction Performance of Electromagnetic Active Seat Suspension Based on Sliding Mode Control. Sensors 2022, 22, 5916. https://doi.org/10.3390/s22155916
Xie P, Che Y, Liu Z, Wang G. Research on Vibration Reduction Performance of Electromagnetic Active Seat Suspension Based on Sliding Mode Control. Sensors. 2022; 22(15):5916. https://doi.org/10.3390/s22155916
Chicago/Turabian StyleXie, Pengshu, Yusong Che, Zhengbin Liu, and Guoqiang Wang. 2022. "Research on Vibration Reduction Performance of Electromagnetic Active Seat Suspension Based on Sliding Mode Control" Sensors 22, no. 15: 5916. https://doi.org/10.3390/s22155916
APA StyleXie, P., Che, Y., Liu, Z., & Wang, G. (2022). Research on Vibration Reduction Performance of Electromagnetic Active Seat Suspension Based on Sliding Mode Control. Sensors, 22(15), 5916. https://doi.org/10.3390/s22155916





