Adaptive Fault-Tolerant Formation Control of Heterogeneous Multi-Agent Systems under Directed Communication Topology
Abstract
:1. Introduction
- UAVs and USVs differ notably in structure, model parameters, and state dimensions. Furthermore, the task changing is random, making it difficult to complete air–sea coordinated formation tasks.
- During the process of formation, the UAVs and USVs may inevitably be subjected to internal and external uncertainties, such as parameter uncertainties and external disturbances caused by modeling techniques and external environment.
- Unsatisfactory faults caused by a lot of damage to the actuator of the multiple UAVs and USVs system may affect the tracking performance.
- The adaptive fault-tolerant formation control is developed for the HMASs with parameter uncertainties, external disturbances, and actuator faults including loss of effectiveness and bias under directed communication topology. Some existing results have been researched for time-varying formation control, such as [16,34,35,36,37]. However, these results only consider the formation control of single vehicle or the HMASs consisting of a UAV and a USV. In this paper, the fault-tolerant time-varying formation for multiple UAVs and USVs can be achieved.
- In order to handle parameter uncertainties and external disturbances, the adaptive control method and the radial basis function neural network (RBFNN) are combined to ensure that the formation errors and tracking errors of the closed-loop system are uniformly ultimately bounded.
2. Preliminaries and Problem Formulation
2.1. Graph Theory
2.2. Problem Formulation
2.3. Radial Basis Function Neural Network
2.4. Control Objective
3. Distributed Fault-Tolerant Formation Control Scheme and Performance Analysis
3.1. Distributed Fault-Tolerant Formation Controller Design
3.2. Performance Analysis
4. Decentralized Formation Controller Design and Performance Analysis
4.1. Decentralized Formation Controller Design
4.2. Performance Analysis
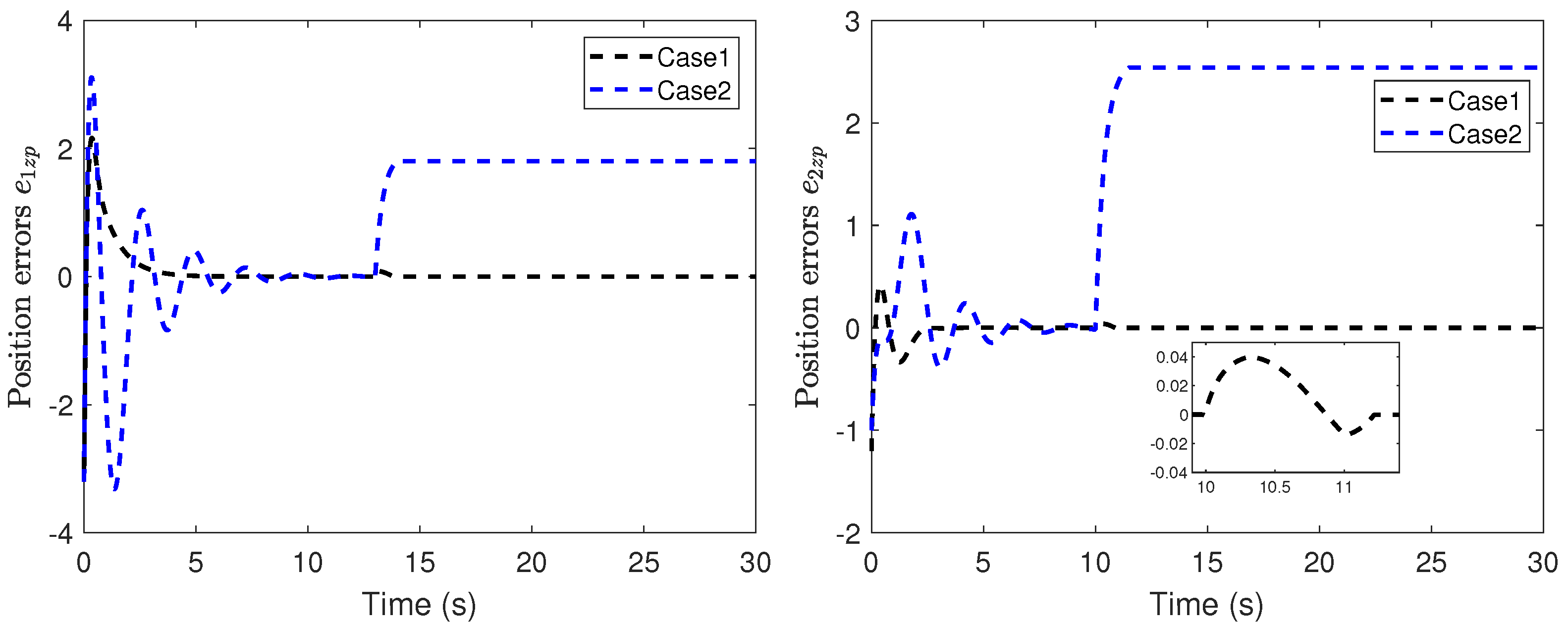
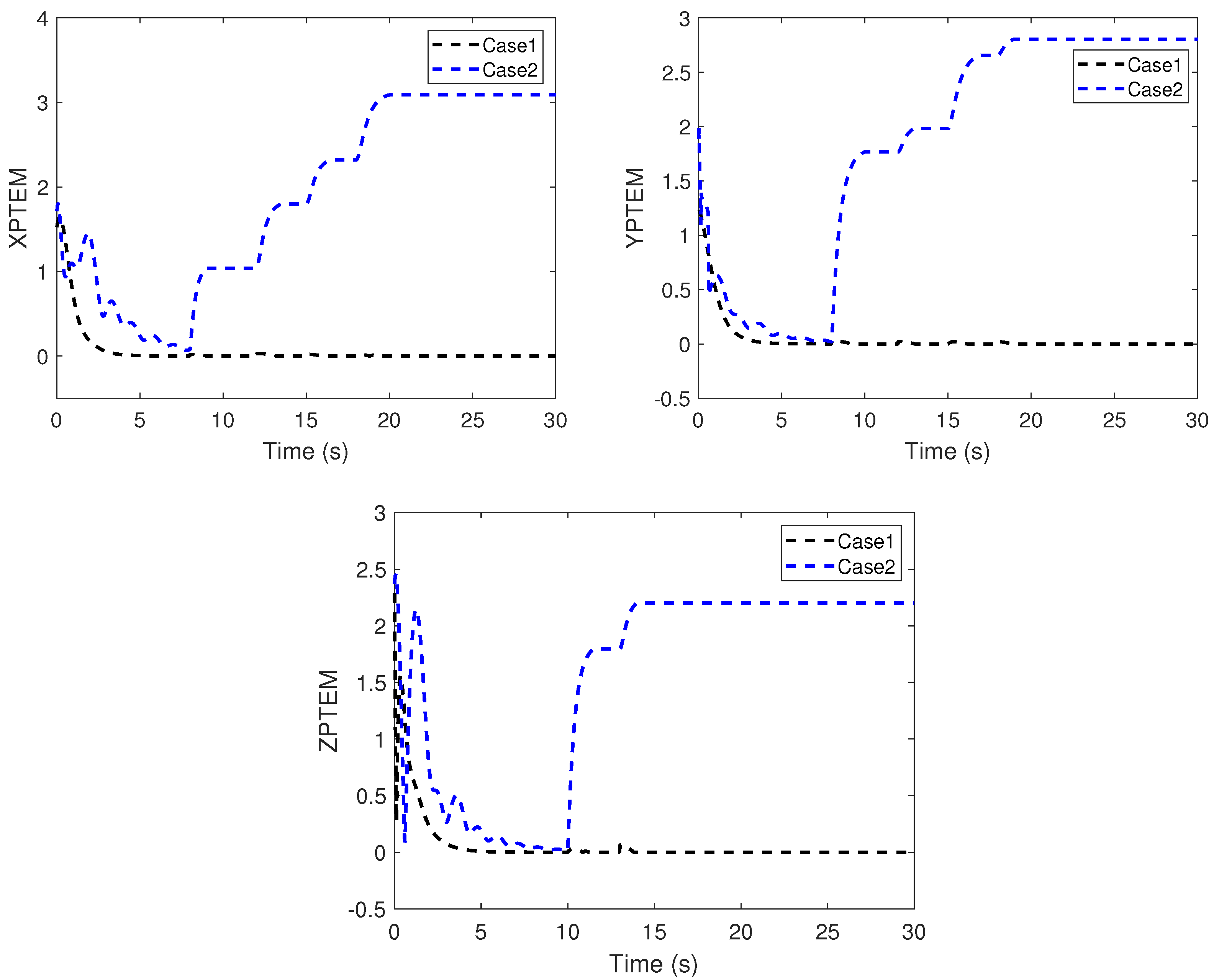
5. Simulation Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, Z.; Zhang, Y.; Jiang, B.; Yu, X.; Fu, J.; Jin, Y.; Chai, T. Distributed adaptive fault-tolerant close formation flight control of multiple trailing fixed-wing UAVs. ISA Trans. 2020, 106, 181–199. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Jiang, B.; Zhang, K.; Patton, R.J. Distributed Fault-Tolerant Consensus Tracking Control of Multi-Agent Systems under Fixed and Switching Topologies. IEEE Trans. Circuits Syst. I 2021, 68, 1646–1658. [Google Scholar] [CrossRef]
- Yazdani, S.; Haeri, M. Robust adaptive fault-tolerant control for leader-follower flocking of uncertain multi-agent systems with actuator failure. ISA Trans. 2017, 71, 227–234. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Li, T.; Qiu, Q.; Zhao, C. A Fully Distributed Protocol with an Event-Triggered Communication Strategy for Second-Order Multi-Agent Systems Consensus with Nonlinear Dynamics. Sensors 2021, 21, 4059. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An Overview of Recent Progress in the Study of Distributed Multi-Agent Coordination. IEEE Trans. Ind. Informat. 2013, 9, 427–438. [Google Scholar] [CrossRef]
- Ding, Z.; Li, Z. Distributed adaptive consensus control of nonlinear output-feedback systems on directed graphs. Automatica 2016, 72, 46–52. [Google Scholar] [CrossRef]
- Shi, Y.; Yin, Y.; Wang, S.; Liu, Y.; Liu, F. Distributed leader-following consensus of nonlinear multi-agent systems with nonlinear input dynamics. Neurocomputing 2018, 286, 193–197. [Google Scholar] [CrossRef]
- Qin, J.; Ma, Q.; Shi, Y.; Wang, L. Recent Advances in Consensus of Multi-Agent Systems: A Brief Survey. IEEE Trans. Ind. Electron. 2017, 64, 4972–4983. [Google Scholar] [CrossRef]
- Sakthivel, R.; Parivallal, A.; Kaviarasan, B.; Lee, H.; Lim, Y. Finite-time consensus of Markov jumping multi-agent systems with time-varying actuator faults and input saturation. ISA Trans. 2018, 83, 89–99. [Google Scholar] [CrossRef]
- Fu, J.; Wen, G.; Yu, W.; Ding, Z. Finite-Time Consensus for Second-Order Multi-Agent Systems with Input Saturation. IEEE Trans. Circuits Syst. II 2018, 65, 1758–1762. [Google Scholar] [CrossRef]
- Tan, C.; Cui, Y.; Li, Y. Global Consensus of High-Order Discrete-Time Multi-Agent Systems with Communication Delay and Saturation Constraint. Sensors 2022, 22, 1007. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Liu, H.; Liu, H. Robust finite-time consensus control for multi-agent systems with disturbances and unknown velocities. ISA Trans. 2018, 80, 73–80. [Google Scholar] [CrossRef]
- He, L.; Sun, X.; Lin, Y. Distributed output-feedback formation tracking control for unmanned aerial vehicles. Int. J. Syst. Sci. 2016, 47, 3919–3928. [Google Scholar] [CrossRef]
- Wang, R.; Dong, X.; Li, Q.; Ren, Z. Distributed Time-Varying Output Formation Control for General Linear Multiagent Systems with Directed Topology. IEEE Trans. Control Netw. Syst. 2019, 6, 609–620. [Google Scholar] [CrossRef]
- Du, H.; Zhu, W.; Wen, G.; Duan, Z.; Lü, J. Distributed Formation Control of Multiple Quadrotor Aircraft Based on Nonsmooth Consensus Algorithms. IEEE Trans. Cybern. 2019, 49, 342–353. [Google Scholar] [CrossRef]
- Chen, F.; Dimarogonas, D.V. Leader-Follower Formation Control with Prescribed Performance Guarantees. IEEE Trans. Control Netw. Syst. 2021, 8, 450–461. [Google Scholar] [CrossRef]
- Zuo, S.; Song, Y.; Lewis, F.L.; Davoudi, A. Time-Varying Output Formation Containment of General Linear Homogeneous and Heterogeneous Multiagent Systems. IEEE Trans. Control Netw. Syst. 2019, 6, 537–548. [Google Scholar] [CrossRef]
- Hua, Y.; Dong, X.; Hu, G.; Li, Q.; Ren, Z. Distributed Time-Varying Output Formation Tracking for Heterogeneous Linear Multiagent Systems with a Nonautonomous Leader of Unknown Input. IEEE Trans. Autom. Control 2019, 64, 4292–4299. [Google Scholar] [CrossRef]
- Rahimi, R.; Abdollahi, F.; Naqshi, K. Time-varying formation control of a collaborative heterogeneous multi agent system. Rob. Auton. Syst. 2014, 62, 1799–1805. [Google Scholar] [CrossRef]
- Mehrabian, A.R.; Khorasani, K. Constrained distributed cooperative synchronization and reconfigurable control of heterogeneous networked Euler–Lagrange multi-agent systems. Inf. Sci. 2016, 370–371, 578–597. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Yang, H.; Han, Q.L.; Ge, X.; Ding, L.; Xu, Y.; Jiang, B.; Zhou, D. Fault-Tolerant Cooperative Control of Multiagent Systems: A Survey of Trends and Methodologies. IEEE Trans. Ind. Informat. 2020, 16, 4–17. [Google Scholar] [CrossRef]
- Yin, S.; Luo, H.; Ding, S.X. Real-Time Implementation of Fault-Tolerant Control Systems with Performance Optimization. IEEE Trans. Ind. Electron. 2014, 61, 2402–2411. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, G.; Zhang, W.; Yu, L. Cooperative Fault Tolerant Tracking Control for Multiagent Systems: An Intermediate Estimator-Based Approach. IEEE Trans. Cybern. 2018, 48, 2972–2980. [Google Scholar] [CrossRef] [PubMed]
- Khalili, M.; Zhang, X.; Cao, Y.; Polycarpou, M.M.; Parisini, T. Distributed adaptive fault-tolerant leader-following formation control of nonlinear uncertain second-order multi-agent systems. Int. J. Robust Nonlinear Control 2018, 28, 4287–4308. [Google Scholar] [CrossRef]
- Hua, Y.; Dong, X.; Li, Q.; Ren, Z. Distributed Fault-Tolerant Time-Varying Formation Control for Second-Order Multi-Agent Systems with Actuator Failures and Directed Topologies. IEEE Trans. Circuits Syst. II 2018, 65, 774–778. [Google Scholar] [CrossRef]
- Ma, H.; Yang, G. Adaptive Fault Tolerant Control of Cooperative Heterogeneous Systems with Actuator Faults and Unreliable Interconnections. IEEE Trans. Autom. Control 2016, 61, 3240–3255. [Google Scholar] [CrossRef]
- Yadegar, M.; Meskin, N. Fault-tolerant control of nonlinear heterogeneous multi-agent systems. Automatica 2021, 127, 109514. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, C.; Meng, Y. Fully distributed time-varying formation tracking control of linear multi-agent systems with input delay and disturbances. Syst. Control Lett. 2020, 146, 104814. [Google Scholar] [CrossRef]
- Dong, C.; Zhang, W.; Wang, Q.; Liu, Y. Time-varying anti-disturbance formation control for high-order non-linear multi-agent systems with switching directed topologies. IET Control Theory Appl. 2020, 14, 271–282. [Google Scholar] [CrossRef]
- Lin, H.; Wei, Q.; Liu, D.; Ma, H. Adaptive tracking control of leader-following linear multi-agent systems with external disturbances. Int. J. Syst. Sci. 2016, 47, 3167–3179. [Google Scholar] [CrossRef]
- Dong, Y.; Su, Y.; Liu, Y.; Xu, S. An internal model approach for multi-agent rendezvous and connectivity preservation with nonlinear dynamics. Automatica 2018, 89, 300–307. [Google Scholar] [CrossRef]
- Zhu, G.; Ma, Y.; Li, Z.; Malekian, R.; Sotelo, M. Event-Triggered Adaptive Neural Fault-Tolerant Control of Underactuated MSVs with Input Saturation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7045–7057. [Google Scholar] [CrossRef]
- Park, B.S.; Kwon, J.W.; Kim, H. Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica 2017, 77, 353–359. [Google Scholar] [CrossRef]
- Kou, B.; Liu, Z.Q.; Xu, L.X. Fault-tolerant Control for Trajectory Tracking of Underactuated Unmanned Surface Vehicles with Actuator Faults. In Proceedings of the 2021 IEEE International Conference on Recent Advances in Systems Science and Engineering (RASSE), Shanghai, China, 12–14 December 2021; pp. 1–6. [Google Scholar]
- Gonzalez-Garcia, A.; Miranda-Moya, A.; Castañeda, H. Robust Visual Tracking Control Based on Adaptive Sliding Mode Strategy: Quadrotor UAV—Catamaran USV Heterogeneous System. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 666–672. [Google Scholar]
- Zhou, S.Q.; Hua, H.C.; Dong, X.W.; Li, Q.D.; Ren, Z. Air-ground time varying formation tracking control for heterogeneous UAV-UGV swarm system. Aero Weapon. 2019, 26, 54–59. [Google Scholar]
- Mei, J.; Ren, W.; Chen, J. Distributed Consensus of Second-Order Multi-Agent Systems with Heterogeneous Unknown Inertias and Control Gains under a Directed Graph. IEEE Trans. Autom. Control 2016, 61, 2019–2034. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, R.; Zhang, K.; Jiang, B.; Tao, G. Robust Backstepping Sliding-Mode Control and Observer-Based Fault Estimation for a Quadrotor UAV. IEEE Trans. Ind. Electron. 2016, 63, 5044–5056. [Google Scholar] [CrossRef]
- Song, Y.; He, L.; Zhang, D.; Qian, J.; Fu, J. Neuroadaptive Fault-Tolerant Control of Quadrotor UAVs: A More Affordable Solution. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1975–1983. [Google Scholar] [CrossRef]
- Chen, S.; Ho, D.W.C.; Li, L.; Liu, M. Fault-Tolerant Consensus of Multi-Agent System with Distributed Adaptive Protocol. IEEE Trans. Cybern. 2015, 45, 2142–2155. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Song, Y.D. Robust fault-tolerant cooperative control of multi-agent systems: A constructive design method. J. Frankl. Inst. 2015, 352, 4045–4066. [Google Scholar] [CrossRef]
- Li, J.H.; Lee, P.M.; Jun, B.H.; Lim, Y.K. Point-to-point navigation of underactuated ships. Automatica 2008, 44, 3201–3205. [Google Scholar] [CrossRef]






| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| 2 | kg | 0.725 | |||
| g | 9.8 | 0.89 | |||
| 1.5 | −1.9 | ||||
| 0.012 | −1.33 | ||||
| 25.8 | kg | −36.47 | |||
| 33.8 | kg | −0.75 | |||
| 2.76 | kg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Jiang, B.; Mao, Z.; Ma, Y. Adaptive Fault-Tolerant Formation Control of Heterogeneous Multi-Agent Systems under Directed Communication Topology. Sensors 2022, 22, 6212. https://doi.org/10.3390/s22166212
Liu S, Jiang B, Mao Z, Ma Y. Adaptive Fault-Tolerant Formation Control of Heterogeneous Multi-Agent Systems under Directed Communication Topology. Sensors. 2022; 22(16):6212. https://doi.org/10.3390/s22166212
Chicago/Turabian StyleLiu, Shangkun, Bin Jiang, Zehui Mao, and Yajie Ma. 2022. "Adaptive Fault-Tolerant Formation Control of Heterogeneous Multi-Agent Systems under Directed Communication Topology" Sensors 22, no. 16: 6212. https://doi.org/10.3390/s22166212







