Computational Analysis of a Multi-Layered Skin and Cardiac Pacemaker Model Based on Neural Network Approach †
Abstract
:1. Introduction
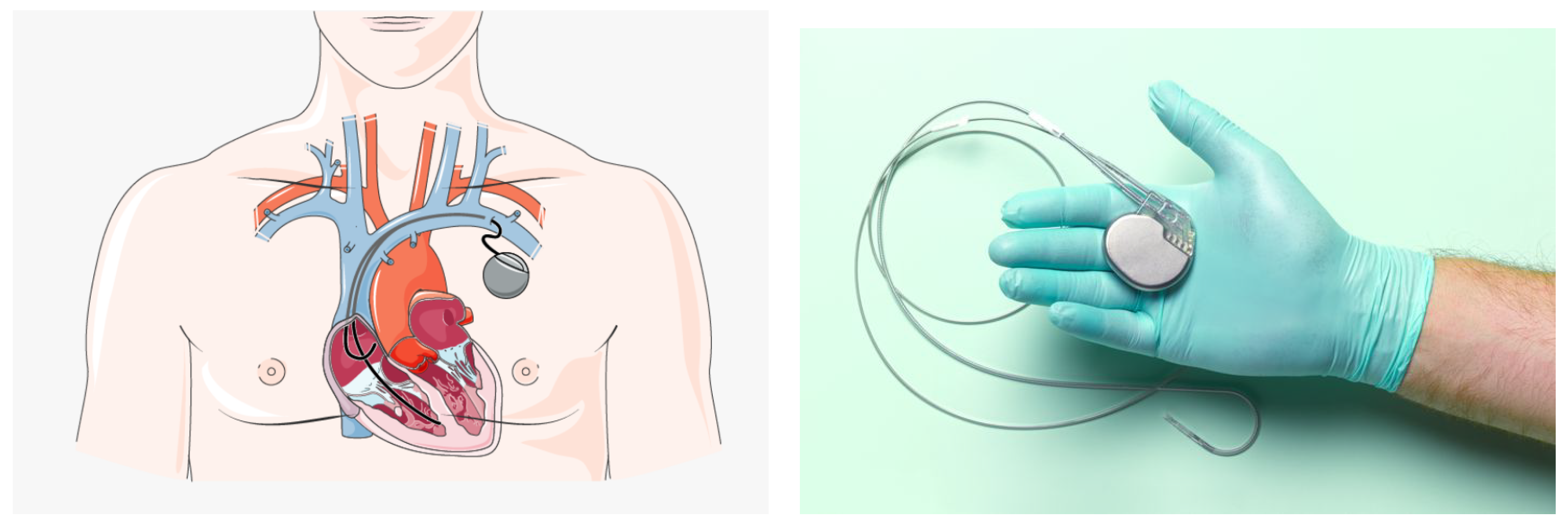
2. Pacemaker Implantation
3. Numerical Modeling of Electromagnetic Field (EMF)
3.1. Electromagnetic Field Source
- c is the speed of the light;
- is the width of the top plate of PIFA;
- is the length of the top plate of PIFA;
- is the resonant frequency.
- is the width of the shorting plate;
- ;
- ;
- .
3.2. Multilayered Tissue Model
4. Neural Network Basic
5. Analysis of the Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Papa, A. Vivere con un Pacemaker: Rischi e Prevenzione. Available online: https://www.cardiologiaoggi.com/vivere-con-un-pacemaker-rischi-e-prevenzione/#:~:text=Il%20rischio%20che%20la%20cintura,)%3A%20non%20sono%20previste%20limitazioni (accessed on 5 August 2022).
- Srivastava, S.K.; Manna, K. Recent Advancements in Electromagnetic Interference Shielding Performance of Nanostructured Materials and their Nanocomposites: A Review. J. Mater. Chem. A 2022, 10, 7431–7496. [Google Scholar] [CrossRef]
- Boyer, A.; Dhia, S.B.; Sicard, E. Characterization of the electromagnetic susceptibility of integrated circuits using a near field scan. Electron. Lett. 2007, 43, 15. [Google Scholar] [CrossRef]
- Mariscotti, A. Assessment of human exposure (including interference to implantable devices) to low-frequency electromagnetic field in modern microgrids, power systems and electric transports. Energies 2021, 14, 6789. [Google Scholar] [CrossRef]
- Li, X.; Qu, Y.; Wang, X.; Bian, H.; Wu, W.; Dai, H. Flexible graphene/silver nanoparticles/aluminum film paper for high-performance electromagnetic interference shielding. Mater. Des. 2022, 213, 110296. [Google Scholar] [CrossRef]
- Zhu, G.; Giraldo Isaza, L.; Huang, B.; Dufresne, A. Multifunctional Nanocellulose/Carbon Nanotube Composite Aerogels for High-Efficiency Electromagnetic Interference Shielding. ACS Sustain. Chem. Eng. 2022, 10, 2397–2408. [Google Scholar] [CrossRef]
- Nadeem, F.; Tran, C.T.; Torbey, E.; Philbin, D.; Morales, C.; Wu, M. Interference by Modern Smartphones and Accessories with Cardiac Pacemakers and Defibrillators. Curr. Cardiol. Rep. 2022, 24, 347–353. [Google Scholar] [CrossRef] [PubMed]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP); Bernhardt, J.H.; Ahlbom, A.; Bergqvist, U.; Césarini, J.-P.; Court, L.A.; Grandolfo, M.; Hietanen, M.; McKinlay, A.F.; Repacholi, M.H.; et al. Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to 300 GHz). Health Phys. 1998, 74, 494–522. [Google Scholar]
- Srivastava, A.; Kumar, R.; Joseph, E.; Kumar, A. Heat exposure study in the workplace in a glass manufacturing unit in India. Ann. Occup. Hyg. 2000, 44, 449–453. [Google Scholar] [CrossRef]
- Lee, S.; Fu, K.; Kohno, T.; Ransford, B.; Maisel, W.H. Clinically significant magnetic interference of implanted cardiac devices by portable headphones. Heart Rhythm. 2009, 6, 1432–1436. [Google Scholar] [CrossRef]
- Hayes, D.L.; Wang, P.J.; Reynolds, D.W.; Estes, N.M.; Griffith, J.L.; Steffens, R.A.; Carlo, G.L.; Findlay, G.K.; Johnson, C.M. Interference with cardiac pacemakers by cellular telephones. N. Engl. J. Med. 1997, 336, 1473–1479. [Google Scholar] [CrossRef]
- Feng, Y.; Li, Z.; Qi, L.; Shen, W.; Li, G. A compact and miniaturized implantable antenna for ISM band in wireless cardiac pacemaker system. Sci. Rep. 2022, 12, 238. [Google Scholar] [CrossRef] [PubMed]
- Azimi, S.; Golabchi, A.; Nekookar, A.; Rabbani, S.; Amiri, M.H.; Asadi, K.; Abolhasani, M.M. Self-powered cardiac pacemaker by piezoelectric polymer nanogenerator implant. Nano Energy 2021, 83, 105781. [Google Scholar] [CrossRef]
- Fonkou, R.; Louodop, P.; Talla, P.; Woafo, P. Dynamic Behavior of Pacemaker Models Subjected to a Arterial Pressure Excitation Simulator: Theoretical and Experimental Study by Microcontroller. Braz. J. Phys. 2021, 51, 1448–1458. [Google Scholar] [CrossRef]
- Erdogan, O. Electromagnetic interference on pacemakers. Indian Pacing Electrophysiol. 2002, 2, 74–78. [Google Scholar]
- Bernardeschi, C.; Domenici, A.; Masci, P. Integrated Simulation of Implantable Cardiac Pacemaker Software and Heart Models; 2d International Congress on Cardiovascular Technology; SciTePress: Setubal, Portugal, 2014; pp. 55–59. [Google Scholar]
- Ryu, H.; Park, H.M.; Kim, M.K.; Kim, B.; Myoung, H.S.; Kim, T.Y.; Yoon, H.J.; Kwak, S.S.; Kim, J.; Hwang, T.H.; et al. Self-rechargeable cardiac pacemaker system with triboelectric nanogenerators. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Wang, M.; Liu, H.; Zhang, P.; Zhang, X.; Yang, H.; Zhou, G.; Li, L. Broadband implantable antenna for wireless power transfer in cardiac pacemaker applications. IEEE J. Electromagn. Microwaves Med. Biol. 2020, 5, 2–8. [Google Scholar] [CrossRef]
- Chen, T.; Diciolla, M.; Kwiatkowska, M.; Mereacre, A. A simulink hybrid heart model for quantitative verification of cardiac pacemakers. In Proceedings of the 16th International Conference on Hybrid Systems: Computation and Control, Philadelphia, PA, USA, 8–11 April 2013; pp. 131–136. [Google Scholar]
- Kourtiche, D.; Nadi, M.; Souques, M.; Magne, I. Implants médicaux et champs électromagnétiques basses fréquences 0–100 kHz. Radioprotection 2014, 49, 241–248. [Google Scholar] [CrossRef]
- Bazaka, K.; Jacob, M.V. Implantable devices: Issues and challenges. Electronics 2012, 2, 1–34. [Google Scholar] [CrossRef]
- Razek, A. Biological and Medical Disturbances Due to Exposure to Fields Emitted by Electromagnetic Energy Devices—A Review. Energies 2022, 15, 4455. [Google Scholar] [CrossRef]
- Niedermeier, A.; Vitali-Serdoz, L.; Fischlein, T.; Kirste, W.; Buia, V.; Walaschek, J.; Rittger, H.; Bastian, D. Perioperative Sensor and Algorithm Programming in Patients with Implanted ICDs and Pacemakers for Cardiac Resynchronization Therapy. Sensors 2021, 21, 8346. [Google Scholar] [CrossRef]
- Özkartal, T.; Demarchi, A.; Caputo, M.L.; Baldi, E.; Conte, G.; Auricchio, A. Perioperative Management of Patients with Cardiac Implantable Electronic Devices and Utility of Magnet Application. J. Clin. Med. 2022, 11, 691. [Google Scholar] [CrossRef] [PubMed]
- Carrión-Camacho, M.R.; Marín-León, I.; Molina-Doñoro, J.M.; González-López, J.R. Safety of permanent pacemaker implantation: A prospective study. J. Clin. Med. 2019, 8, 35. [Google Scholar] [CrossRef] [PubMed]
- Martis, A.; Gusetu, G.; Cismaru, G.; Zdrenghea, D.; Leucuta, D.C.; Pop, D. Improvement of Cognitive Function and Interleukin 1 Beta Serum Concentrations Following Cardiac Pacemaker Implantation in Patients with Symptomatic Bradycardia. J. Pers. Med. 2021, 11, 770. [Google Scholar] [CrossRef] [PubMed]
- Kotsakou, M.; Kioumis, I.; Lazaridis, G.; Pitsiou, G.; Lampaki, S.; Papaiwannou, A.; Karavergou, A.; Tsakiridis, K.; Katsikogiannis, N.; Karapantzos, I.; et al. Pacemaker insertion. Ann. Transl. Med. 2015, 3. Available online: https://atm.amegroups.com/article/view/5793 (accessed on 5 August 2022).
- Haghjoo, M. Techniques of Permanent Pacemaker Implantation. In Current Issues and Recent Advances in Pacemaker Therapy; IntechOpen: Rijeka, Croatia, 2012. [Google Scholar]
- López-Liria, R.; López-Villegas, A.; Enebakk, T.; Thunhaug, H.; Lappegård, K.T.; Catalán-Matamoros, D. Telemonitoring and quality of life in patients after 12 months following a pacemaker implant: The Nordland study, a randomised trial. Int. J. Environ. Res. Public Health 2019, 16, 2001. [Google Scholar] [CrossRef]
- Rippa, A.L.; Kalabusheva, E.P.; Vorotelyak, E.A. Regeneration of dermis: Scarring and cells involved. Cells 2019, 8, 607. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Rinkevich, Y. Scars or regeneration?—Dermal fibroblasts as drivers of diverse skin wound responses. Int. J. Mol. Sci. 2020, 21, 617. [Google Scholar] [CrossRef]
- Virtanen, H.; Keshvari, J.; Lappalainen, R. Interaction of radio frequency electromagnetic fields and passive metallic implants—A brief review. Bioelectromagn. J. Bioelectromagn. Soc. Soc. Phys. Regul. Biol. Med. Eur. Bioelectromagn. Assoc. 2006, 27, 431–439. [Google Scholar] [CrossRef]
- Walendziuk, W. SAR and thermal computations with the use of parallel FDTD algorithm. In Proceedings of the IEEE International Conference on Parallel Computing in Electrical Engineering, Warsaw, Poland, 22–25 September 2002; pp. 282–287. [Google Scholar]
- Golio, M. The RF and Microwave Handbook; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Kumar, N.; Thakur, A.; Sharma, J. Study of Planar Inverted-F Antenna (PIFA) for Mobile Devices. Int. J. Electron. Commun. Technol. (IJECT) 2013, 4, 83–85. [Google Scholar]
- Chattha, H.T.; Huang, Y.; Zhu, X.; Lu, Y. An empirical equation for predicting the resonant frequency of planar inverted-F antennas. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 856–860. [Google Scholar] [CrossRef]
- Madhav, B.; Soumya, K.; Dasari, G. Design and parametric simulation of planar inverted folded antenna. Int. J. Appl. Eng. Res. 2014, 9, 2897–2902. [Google Scholar]
- Chattha, H.T.; Huang, Y.; Ishfaq, M.K.; Boyes, S.J. A comprehensive parametric study of planar inverted-F antenna. Wirel. Eng. Technol. 2012, 3, 1. [Google Scholar] [CrossRef]
- Chen, H.M.; Lin, Y.F.; Cheng, P.S.; Lin, H.H.; Song, C.; Hall, P. Parametric study on the characteristics of planar inverted-F antenna. IEE Proc.-Microwaves Antennas Propag. 2005, 152, 534–538. [Google Scholar] [CrossRef]
- Foundation, I. Tissue Properties Database V3.0; IT’IS Foundation: Zurich, Switzerland, 2015. [Google Scholar]
- Psenakova, Z.; Smondrk, M.; Sciuto, G.L.; Benova, M. Evaluation of radiofrequency field (2.4 GHz) effects to multilayer structure of human skin and pacemaker. In Proceedings of the Conference of Information Technologies in Biomedicine, Kamien Slaski, Poland, 20–22 June 2016; pp. 245–254. [Google Scholar]
- Psenakova, Z.; Smondrk, M.; Barabas, J.; Sciuto, G.L.; Benova, M. Simulation and assessment of pacemaker RF exposure (2.4 GHz) by PIFA antenna. In Proceedings of the IEEE 2016 ELEKTRO, Strbske Pleso, Slovakia, 16–18 May 2016; pp. 569–573. [Google Scholar]
- Dawson, T.W.; Caputa, K.; Stuchly, M.A.; Shepard, R.B.; Kavet, R.; Sastre, A. Pacemaker interference by magnetic fields at power line frequencies. IEEE Trans. Biomed. Eng. 2002, 49, 254–262. [Google Scholar] [CrossRef]
- Wang, F.; Mi, Z.; Su, S.; Zhao, H. Short-term solar irradiance forecasting model based on artificial neural network using statistical feature parameters. Energies 2012, 5, 1355–1370. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Liu, Z. Application of artificial neural networks for catalysis: A review. Catalysts 2017, 7, 306. [Google Scholar] [CrossRef] [Green Version]





| Parameter | Value | Unit |
|---|---|---|
| Center Frequency | 2450 | MHz |
| Speed of Light | 299,792,458 | m·s−1 |
| Speed of Light/Center Frequency | mm | |
| Cylinder Length | 0.46 | mm |
| Cylinder Radius | 0.001 | mm |
| Layer | Thickness (mm) | (S·m−1) | |
|---|---|---|---|
| Epidermis | 1.5 | 38.1 | 1.44 |
| Dermis | 3 | 25.2 | 5.76 |
| Hypodermis | 2/4/10/18 | 30.5 | 3.6 |
| Pacemaker casing | 0.5 | 50 | 0.267 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Psenakova, Z.; Smondrk, M.; Barabas, J.; Benova, M.; Brociek, R.; Wajda, A.; Kowol, P.; Coco, S.; Sciuto, G.L. Computational Analysis of a Multi-Layered Skin and Cardiac Pacemaker Model Based on Neural Network Approach. Sensors 2022, 22, 6359. https://doi.org/10.3390/s22176359
Psenakova Z, Smondrk M, Barabas J, Benova M, Brociek R, Wajda A, Kowol P, Coco S, Sciuto GL. Computational Analysis of a Multi-Layered Skin and Cardiac Pacemaker Model Based on Neural Network Approach. Sensors. 2022; 22(17):6359. https://doi.org/10.3390/s22176359
Chicago/Turabian StylePsenakova, Zuzana, Maros Smondrk, Jan Barabas, Mariana Benova, Rafał Brociek, Agata Wajda, Paweł Kowol, Salvatore Coco, and Grazia Lo Sciuto. 2022. "Computational Analysis of a Multi-Layered Skin and Cardiac Pacemaker Model Based on Neural Network Approach" Sensors 22, no. 17: 6359. https://doi.org/10.3390/s22176359
APA StylePsenakova, Z., Smondrk, M., Barabas, J., Benova, M., Brociek, R., Wajda, A., Kowol, P., Coco, S., & Sciuto, G. L. (2022). Computational Analysis of a Multi-Layered Skin and Cardiac Pacemaker Model Based on Neural Network Approach. Sensors, 22(17), 6359. https://doi.org/10.3390/s22176359










