Inertial Motion Capture-Based Estimation of L5/S1 Moments during Manual Materials Handling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Procedure
2.2. Transfer Phase Identification
2.3. OMC + PF-Based Computation
2.4. IMC-Based Computation
2.5. Data Analysis
3. Results
4. Discussion
4.1. IMC-Based Estimation Accuracy
4.2. Prospects for Use
4.3. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schiefer, C.; Ellegast, R.P.; Hermanns, I.; Kraus, T.; Ochsmann, E.; Larue, C.; Plamondon, A. Optimization of inertial sensor-based motion capturing for magnetically distorted field applications. J. Biomech. Eng. 2014, 136, 121008. [Google Scholar] [CrossRef] [PubMed]
- Battini, D.; Persona, A.; Sgarbossa, F. Innovative real-time system to integrate ergonomic evaluations into warehouse design and management. Comput. Ind. Eng. 2014, 77, 1–10. [Google Scholar] [CrossRef]
- Labaj, A.; Diesbourg, T.; Dumas, G.; Plamondon, A.; Mercheri, H.; Larue, C. Posture and lifting exposures for daycare workers. Int. J. Ind. Ergon. 2016, 54, 83–92. [Google Scholar] [CrossRef]
- Prairie, J.; Corbeil, P. Paramedics on the job: Dynamic trunk motion assessment at the workplace. Appl. Ergon. 2014, 45, 895–903. [Google Scholar] [CrossRef]
- Cuesta-Vargas, A.I.; Galán-Mercant, A.; Williams, J.M. The use of inertial sensors system for human motion analysis. Phys. Ther. Rev. 2010, 15, 462–473. [Google Scholar] [CrossRef]
- Filippeschi, A.; Schmitz, N.; Miezal, M.; Bleser, G.; Ruffaldi, E.; Stricker, D. Survey of motion tracking methods based on inertial sensors: A focus on upper limb human motion. Sensors 2017, 17, 1257. [Google Scholar] [CrossRef]
- Robert-Lachaine, X.; Mecheri, H.; Muller, A.; Larue, C.; Plamondon, A. Validation of a low-cost inertial motion capture system for whole-body motion analysis. J. Biomech. 2020, 99, 109520. [Google Scholar] [CrossRef]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Validation of inertial measurement units with an optoelectronic system for whole-body motion analysis. Med. Biol. Eng. Comput. 2017, 55, 609–619. [Google Scholar] [CrossRef]
- Kim, S.; Nussbaum, M.A. Performance evaluation of a wearable inertial motion capture system for capturing physical exposures during manual material handling tasks. Ergonomics 2013, 56, 314–326. [Google Scholar] [CrossRef]
- Koopman, A.S.; Kingma, I.; Faber, G.S.; Bornmann, J.; van Dieën, J.H. Estimating the L5S1 flexion/extension moment in symmetrical lifting using a simplified ambulatory measurement system. J. Biomech. 2018, 70, 242–248. [Google Scholar]
- Corbeil, P.; Plamondon, A.; Handrigan, G.; Vallée-Marcotte, J.; Laurendeau, S.; Ten Have, J.; Manzerolle, N. Biomechanical analysis of manual material handling movement in healthy weight and obese workers. Appl. Ergon. 2019, 74, 124–133. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, D.; Plamondon, A.; Larivière, C. A Comparison of lumbar spine and muscle loading between male and female workers during box transfers. J. Biomech. 2018, 81, 76–85. [Google Scholar] [CrossRef] [PubMed]
- Marras, W.S.; Parakkat, J.; Chany, A.M.; Yang, G.; Burr, D.; Lavender, S.A. Spine loading as a function of lift frequency, exposure duration, and work experience. Clin. Biomech. 2006, 21, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Ning, X.; Zhou, J.; Dai, B.; Jaridi, M. The assessment of material handling strategies in dealing with sudden loading: The effects of load handling position on trunk biomechanics. Appl. Ergon. 2014, 45, 1399–1405. [Google Scholar] [CrossRef]
- Plamondon, A.; Denis, D.; Delisle, A.; Larivière, C.; Salazar, E. Biomechanical differences between expert and novice workers in a manual material handling task. Ergonomics 2010, 53, 1239–1253. [Google Scholar] [CrossRef]
- Dutta, T.; Holliday, P.J.; Gorski, S.M.; Baharvandy, M.S.; Fernie, G.R. A biomechanical assessment of floor and overhead lifts using one or two caregivers for patient transfers. Appl. Ergon. 2012, 43, 521–531. [Google Scholar] [CrossRef]
- Faber, G.S.; Koopman, A.S.; Kingma, I.; Chang, C.C.; Dennerlein, J.T.; van Dieën, J.H. Continuous ambulatory hand force monitoring during manual materials handling using instrumented force shoes and an inertial motion capture suit. J. Biomech. 2018, 70, 235–241. [Google Scholar] [CrossRef]
- Liedtke, C.; Fokkenrood, S.A.W.; Menger, J.T.; van der Kooij, H.; Veltink, P.H. Evaluation of instrumented shoes for ambulatory assessment of ground reaction forces. Gait Posture 2007, 26, 39–47. [Google Scholar] [CrossRef]
- Stöggl, T.; Martiner, A. Validation of moticon’s opengo sensor insoles during gait, jumps, balance and cross-country skiing specific imitation movements. J. Sports Sci. 2017, 35, 196–206. [Google Scholar] [CrossRef]
- Ancillao, A.; Tedesco, S.; Barton, J.; O’Flynn, B. Indirect measurement of ground reaction forces and moments by means of wearable inertial sensors: A systematic review. Sensors 2018, 18, 2564. [Google Scholar] [CrossRef]
- Faber, G.S.; Chang, C.C.; Kingma, I.; Dennerlein, J.T.; van Dieën, J.H. Estimating 3D L5/S1 moments and ground reaction forces during trunk bending using a full-body ambulatory inertial motion capture system. J. Biomech. 2016, 49, 904–912. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.J.; Lee, J.K. Inertial motion capture-based wearable systems for estimation of joint kinetics: A systematic review. Sensors 2022, 22, 2507. [Google Scholar] [CrossRef] [PubMed]
- Karatsidis, A.; Bellusci, G.; Schepers, H.; de Zee, M.; Andersen, M.; Veltink, P. Estimation of ground reaction forces and moments during gait using only inertial motion capture. Sensors 2016, 17, 75. [Google Scholar] [CrossRef] [PubMed]
- Yang, E.C.-Y.; Mao, M.-H. 3D Analysis system for estimating intersegmental forces and moments exerted on human lower limbs during walking motion. Measurement 2015, 73, 171–179. [Google Scholar] [CrossRef]
- Guo, Y.; Storm, F.; Zhao, Y.; Billings, S.A.; Pavic, A.; Mazzà, C.; Guo, L.-Z. A new proxy measurement algorithm with application to the estimation of vertical ground reaction forces using wearable sensors. Sensors 2017, 17, 2181. [Google Scholar] [CrossRef]
- Wouda, F.J.; Giuberti, M.; Bellusci, G.; Maartens, E.; Reenalda, J.; Van Beijnum, B.-J.F.; Veltink, P.H. Estimation of vertical ground reaction forces and sagittal knee kinematics during running using three inertial sensors. Front. Physiol. 2018, 9, 218. [Google Scholar] [CrossRef]
- Aurbach, M.; Wagner, K.; Süß, F.; Dendorfer, S. Implementation and validation of human kinematics measured using IMUs for musculoskeletal simulations by the evaluation of joint reaction forces. In CMBEBIH 2017; Badnjevic, A., Ed.; Springer Singapore: Singapore, 2017; Volume 62, pp. 205–211. ISBN 978-981-10-4165-5. [Google Scholar]
- Karatsidis, A.; Jung, M.; Schepers, H.M.; Bellusci, G.; de Zee, M.; Veltink, P.H.; Andersen, M.S. Musculoskeletal model-based inverse dynamic analysis under ambulatory conditions using inertial motion capture. Med. Eng. Phys. 2019, 65, 68–77. [Google Scholar] [CrossRef]
- Konrath, J.M.; Karatsidis, A.; Schepers, H.M.; Bellusci, G. Estimation of the knee adduction moment and joint contact force during daily living activities using inertial motion capture. Sensors 2019, 12, 1681. [Google Scholar] [CrossRef]
- Larsen, F.G.; Svenningsen, F.P.; Andersen, M.S.; de Zee, M.; Skals, S. Estimation of spinal loading during manual materials handling using inertial motion capture. Ann. Biomed. Eng. 2020, 48, 805–821. [Google Scholar] [CrossRef]
- Muller, A.; Pontonnier, C.; Robert-Lachaine, X.; Dumont, G.; Plamondon, A. Motion-based prediction of external forces and moments and back loading during manual material handling tasks. Appl. Ergon. 2020, 82, 102935. [Google Scholar] [CrossRef]
- Muller, A.; Pontonnier, C.; Dumont, G. Motion-based prediction of hands and feet contact efforts during asymmetric handling tasks. IEEE Trans. Biomed. Eng. 2019, 67, 344–352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robert-Lachaine, X.; Corbeil, P.; Muller, A.; Vallée-Marcotte, J.; Mecheri, H.; Denis, D.; Plamondon, A. Combined influence of transfer distance, pace, handled mass and box height on spine loading and posture. Appl. Ergon. 2021, 93, 103377. [Google Scholar] [CrossRef] [PubMed]
- Desjardins, P.; Gagnon, M. A force platform for large human displacements. Med. Eng. Phys. 2001, 23, 143–146. [Google Scholar] [CrossRef]
- Wu, G.; van der Helm, F.C.T.; (DirkJan) Veeger, H.E.J.; Makhsous, M.; Van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef]
- Wu, G.; Siegler, S.; Allard, P.; Kirtley, C.; Leardini, A.; Rosenbaum, D.; Whittle, M.; D’Lima, D.D.; Cristofolini, L.; Witte, H.; et al. ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion—Part I: Ankle, hip, and spine. J. Biomech. 2002, 35, 543–548. [Google Scholar] [CrossRef]
- Puchaud, P.; Sauret, C.; Muller, A.; Bideau, N.; Dumont, G.; Pillet, H.; Pontonnier, C. Accuracy and kinematics consistency of marker-based scaling approaches on a lower limb model: A comparative study with imagery data. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Dumas, R.; Chèze, L.; Verriest, J.-P. Adjustments to McConville et al. and Young et al. Body segment inertial parameters. J. Biomech. 2007, 40, 543–553. [Google Scholar] [CrossRef]
- Lu, T.-W.; O’Connor, J.J. Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J. Biomech. 1999, 32, 129–134. [Google Scholar] [CrossRef]
- Schepers, M.; Giuberti, M.; Bellusci, G. Xsens MVN: Consistent tracking of human motion using inertial sensing. Xsens Technol. 2018, 1–8. [Google Scholar]
- Fluit, R.; Andersen, M.S.; Kolk, S.; Verdonschot, N.; Koopman, H.F.J.M. Prediction of ground reaction forces and moments during various activities of daily living. J. Biomech. 2014, 47, 2321–2329. [Google Scholar] [CrossRef]
- Jung, Y.; Jung, M.; Ryu, J.; Yoon, S.; Park, S.-K.; Koo, S. Dynamically adjustable foot-ground contact model to estimate ground reaction force during walking and running. Gait Posture 2016, 45, 62–68. [Google Scholar] [CrossRef] [PubMed]
- Lavender, S.A.; Andersson, G.B.J.; Schipplein, O.D.; Fuentes, H.J. The effects of initial lifting height, load magnitude, and lifting speed on the peak dynamic l5/s1 moments. Int. J. Ind. Ergon. 2003, 31, 51–59. [Google Scholar] [CrossRef]
- Plamondon, A.; Larivière, C.; Denis, D.; St-Vincent, M.; Delisle, A. Sex differences in lifting strategies during a repetitive palletizing task. Appl. Ergon. 2014, 45, 1558–1569. [Google Scholar] [CrossRef]
- Muller, A.; Pontonnier, C.; Dumont, G. Uncertainty propagation in multibody human model dynamics. Multibody Syst. Dyn. 2017, 40, 177–192. [Google Scholar] [CrossRef]
- Larsen, F.G.; Svenningsen, F.P. Estimation of Spinal Loading Using Inertial Motion Capture and Ground Reaction Force Prediction: A Validation Study. Master’s Thesis, Faculty of Health Science and Technology, Aalborg University, Aalborg, Denmark, 2018. [Google Scholar]
- Diraneyya, M.M.; Ryu, J.; Abdel-Rahman, E.; Haas, C.T. Inertial motion capture-based whole-body inverse dynamics. Sensors 2021, 21, 7353. [Google Scholar] [CrossRef]
- Delisle, A.; Gagnon, M.; Desjardins, P. Kinematic analysis of footstep strategies in asymmetrical lifting and lowering tasks. Int. J. Ind. Ergon. 1999, 23, 451–460. [Google Scholar] [CrossRef]
- Akhavanfar, M.; Uchida, T.K.; Clouthier, A.L.; Graham, R.B. Sharing the load: Modeling loads in opensim to simulate two-handed lifting. Multibody Syst. Dyn. 2022, 54, 213–234. [Google Scholar]
- Shojaei, I.; Vazirian, M.; Croft, E.; Nussbaum, M.A.; Bazrgari, B. Age related differences in mechanical demands imposed on the lower back by manual material handling tasks. J. Biomech. 2016, 49, 896–903. [Google Scholar] [CrossRef]
- Muller, A.; Corbeil, P. Back loading estimation during team handling: Is the use of only motion data sufficient? PLoS ONE 2020, 15, e0244405. [Google Scholar] [CrossRef]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Effect of local magnetic field disturbances on inertial measurement units accuracy. Appl. Ergon. 2017, 63, 123–132. [Google Scholar] [CrossRef]
- Robert-Lachaine, X.; Larue, C.; Denis, D.; Delisle, A.; Mecheri, H.; Corbeil, P.; Plamondon, A. Feasibility of quantifying the physical exposure of materials handlers in the workplace with magnetic and inertial measurement units. Ergonomics 2020, 63, 283–292. [Google Scholar] [CrossRef] [PubMed]



| RMSE | Ground Reaction Force (GRF) | Relative Position of the Center of Pressure (CoP) | L5/S1 Moments | |||
|---|---|---|---|---|---|---|
| Vertical | Transverse | AP | ML | Flexion | Asymmetric | |
| All | 39.6 N | 24.8 N | 3.5 cm | 3.5 cm | 21.4 Nm | 15.6 Nm |
| 2 kg | 27.1 N | 19.2 N | 3.0 cm | 3.3 cm | 15.1 Nm | 12.0 Nm |
| 10 kg | 40.0 N | 24.9 N | 3.5 cm | 3.6 cm | 21.4 Nm | 15.8 Nm |
| 20 kg | 52.9 N | 30.9 N | 4.0 cm | 3.6 cm | 28.5 Nm | 19.1 Nm |
| RMSE | b | CI | R2 | ||
|---|---|---|---|---|---|
| Peak | Flexion | 26.5 Nm | −16.4 Nm | 35.0 Nm | 0.87 |
| Asymmetric | 27.0 Nm | −17.8 Nm | 30.1 Nm | 0.31 | |
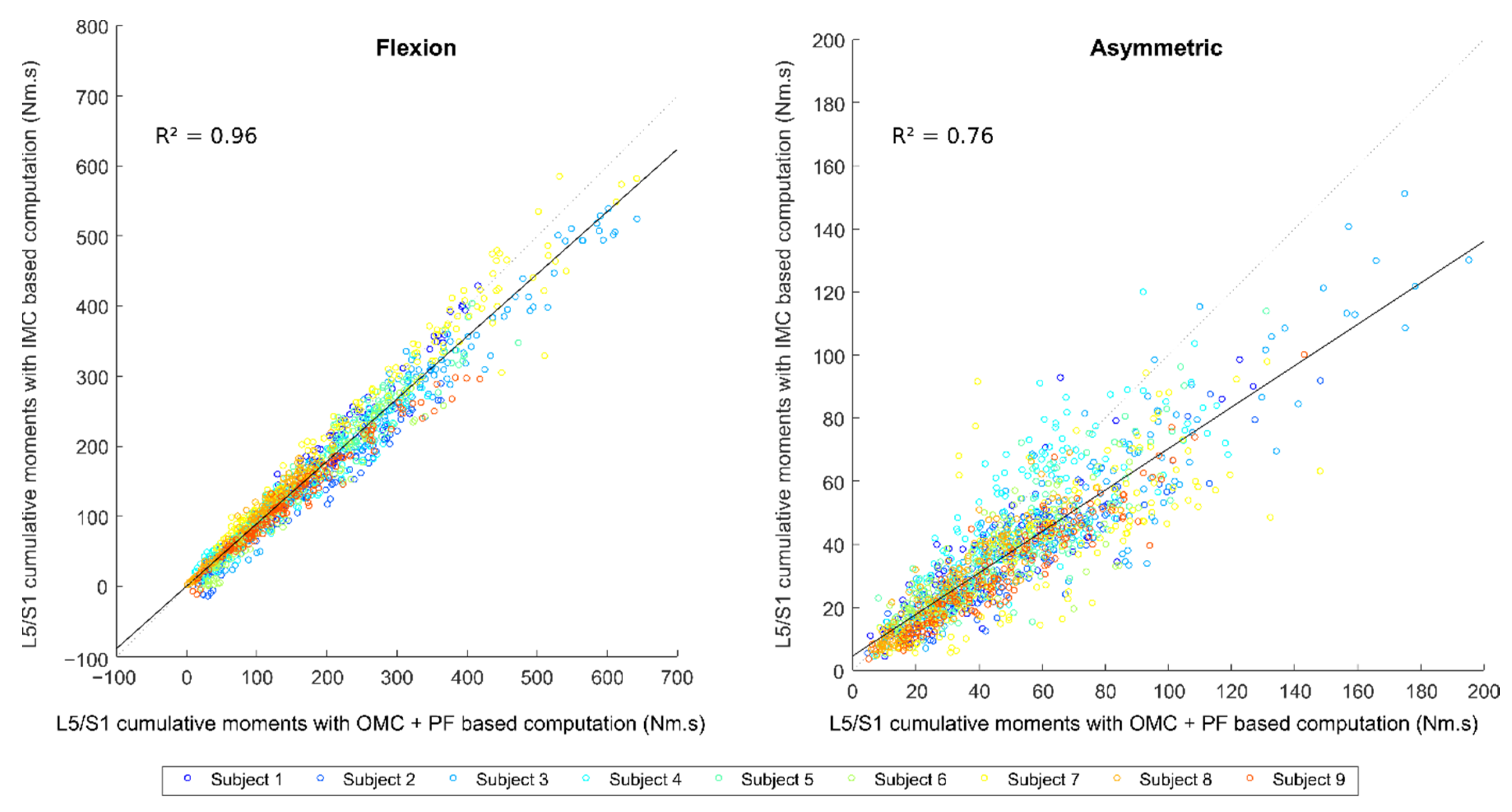
| Cumulative | Flexion | 31.6 Nm·s | −18.3 Nm·s | 41.8 Nm·s | 0.96 |
| Asymmetric | 18.6 Nm·s | −12.1 Nm·s | 22.9 Nm·s | 0.76 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muller, A.; Mecheri, H.; Corbeil, P.; Plamondon, A.; Robert-Lachaine, X. Inertial Motion Capture-Based Estimation of L5/S1 Moments during Manual Materials Handling. Sensors 2022, 22, 6454. https://doi.org/10.3390/s22176454
Muller A, Mecheri H, Corbeil P, Plamondon A, Robert-Lachaine X. Inertial Motion Capture-Based Estimation of L5/S1 Moments during Manual Materials Handling. Sensors. 2022; 22(17):6454. https://doi.org/10.3390/s22176454
Chicago/Turabian StyleMuller, Antoine, Hakim Mecheri, Philippe Corbeil, André Plamondon, and Xavier Robert-Lachaine. 2022. "Inertial Motion Capture-Based Estimation of L5/S1 Moments during Manual Materials Handling" Sensors 22, no. 17: 6454. https://doi.org/10.3390/s22176454
APA StyleMuller, A., Mecheri, H., Corbeil, P., Plamondon, A., & Robert-Lachaine, X. (2022). Inertial Motion Capture-Based Estimation of L5/S1 Moments during Manual Materials Handling. Sensors, 22(17), 6454. https://doi.org/10.3390/s22176454






