Acoustic Limescale Layer and Temperature Measurement in Ultrasonic Flow Meters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fundamentals of the Lamb Wave-Based Flow Meter
2.2. Experimental Methods
2.3. Simulation Methods
3. Results
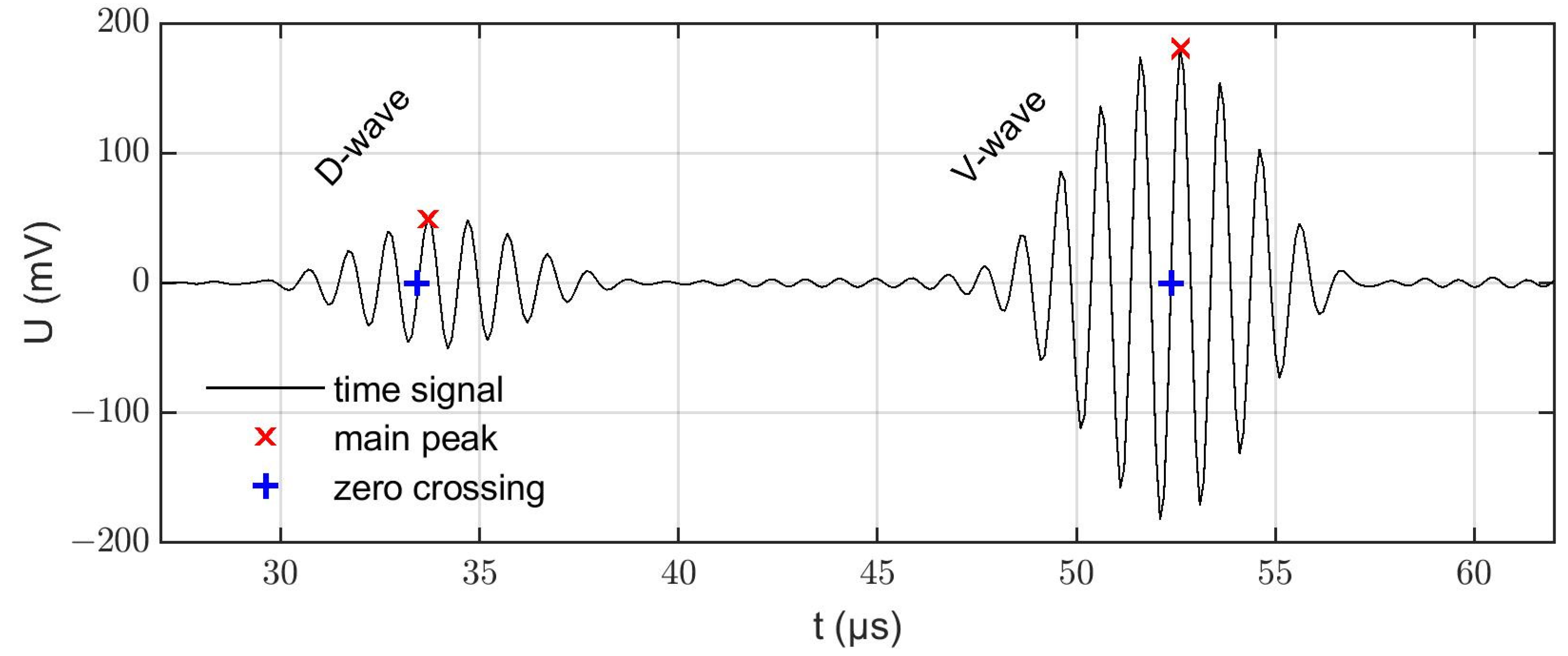
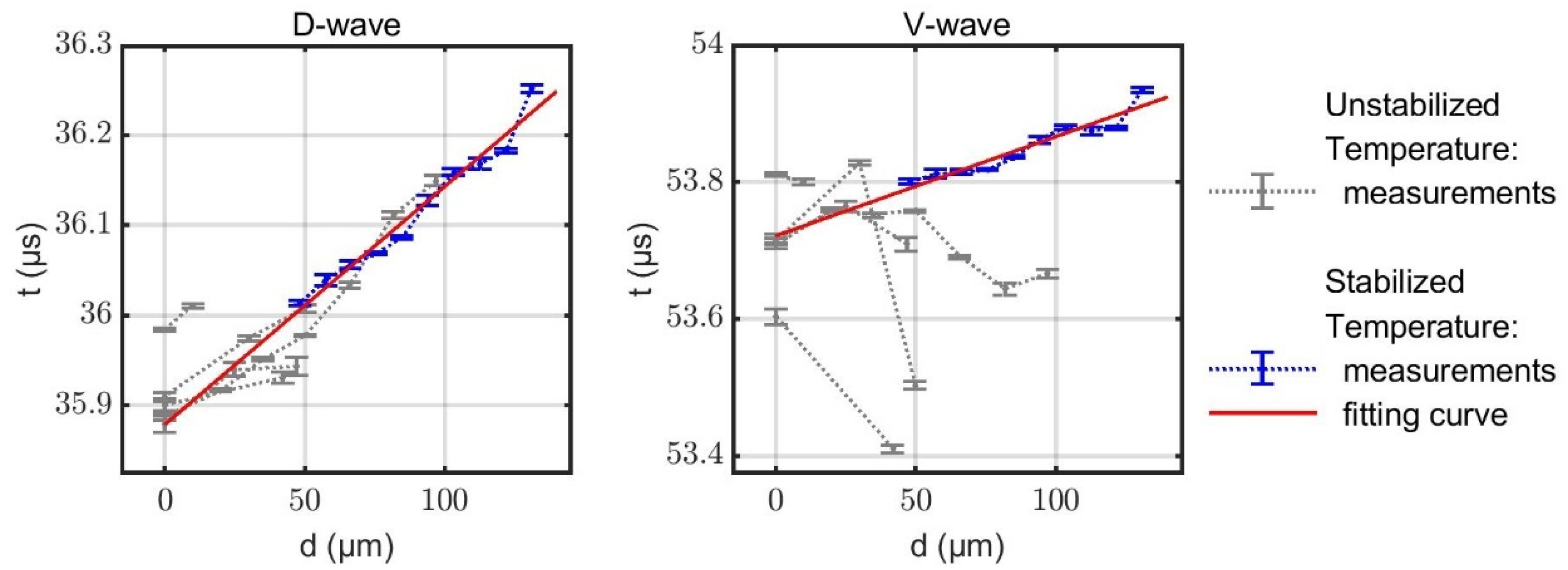
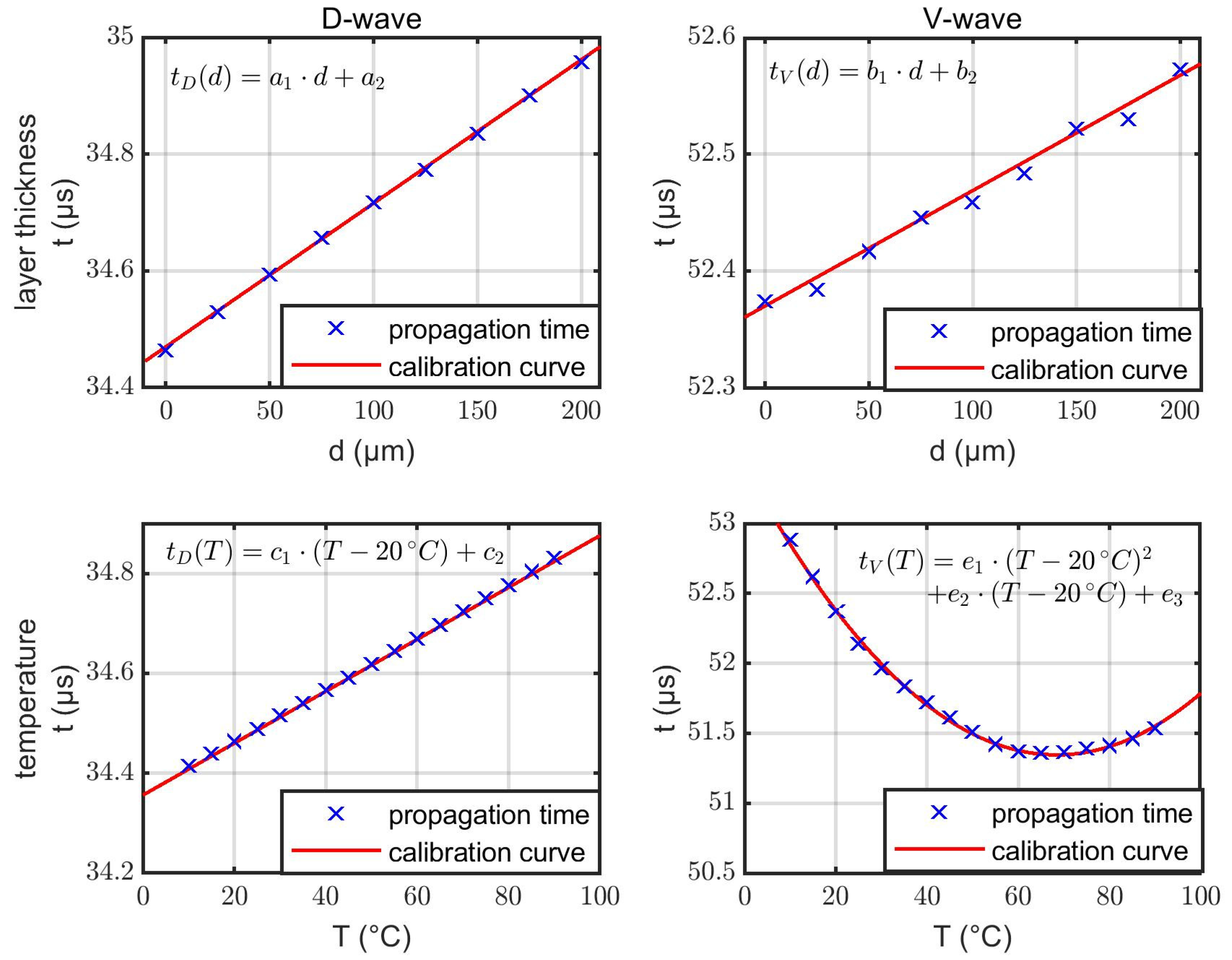
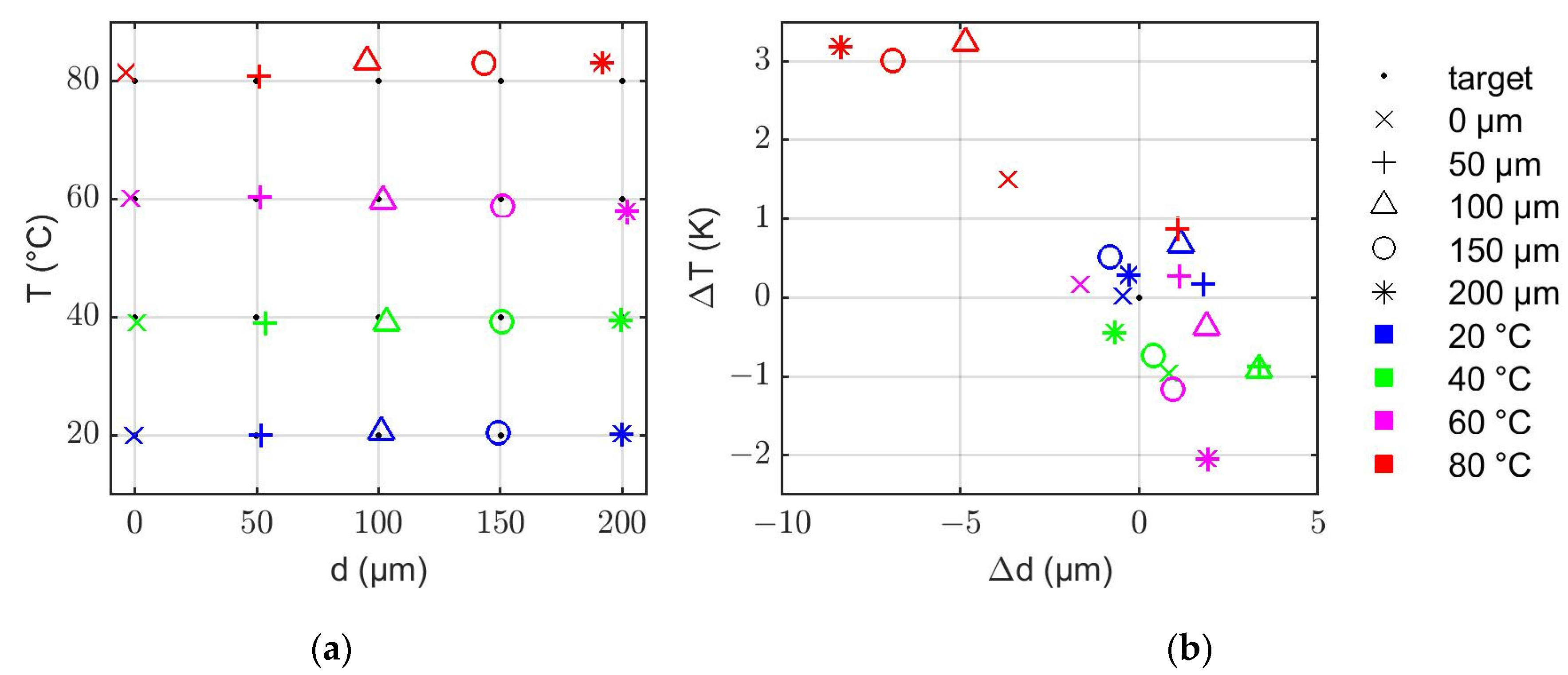
3.1. Experimental Results
3.2. Simulation Results
3.3. Evaluation Algorithm
4. Discussion
5. Outlook and Conclusions
6. Patents
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Chen, T.; Wang, Q. Mineral scale deposits—Analysis and interpretation. In Water-Formed Deposits; Elsevier: Amsterdam, The Netherlands, 2000; pp. 783–794. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Nagy, P.B. Excess attenuation of leaky Lamb waves due to viscous fluid loading. J. Acoust. Soc. Am. 1997, 101, 2649–2658. [Google Scholar] [CrossRef]
- Kocsis, D. Modeling and vibration analysis of limescale deposition in geothermal pipes. Environ. Eng. Manag. J. 2014, 13, 2817–2824. [Google Scholar] [CrossRef]
- Sohaili, J.; Shi, H.S.; Lavania-Baloo; Zardari, N.H.; Ahmad, N.; Muniyandi, S.K. Removal of scale deposition on pipe walls by using magnetic field treatment and the effects of magnetic strength. J. Clean. Prod. 2016, 139, 1393–1399. [Google Scholar] [CrossRef]
- Zeppenfeld, K. Removal of Carbonate Encrustation by Electrolysis of Calcareous Solutions. Chem. Eng. Technol. 1999, 22, 583–587. [Google Scholar] [CrossRef]
- Tyusenkov, A.S.; Cherepashkin, S.E. Scale inhibitor for boiler water systems. Russ. J. Appl. Chem. 2014, 87, 1240–1245. [Google Scholar] [CrossRef]
- Hafid, N.; Belaatar, M.; Ben-Aazza, S.; Hadfi, A.; Ezahri, M.; Driouiche, A. Characterization of Scale Formed in Drinking Water and Hot Water Pipes in the Taliouine Downtown—Morocco. AJAC 2015, 6, 677–686. [Google Scholar] [CrossRef]
- East, C.P.; Schiller, T.L.; Fellows, C.M.; Doherty, W.O. Analytical Techniques to Characterize Scales and Deposits. In Mineral Scales and Deposits; Elsevier: Amsterdam, The Netherlands, 2015; pp. 681–699. [Google Scholar] [CrossRef]
- Woodward, V.; Williams, R.; Amjad, Z. Analytical Techniques for Identifying Mineral Scales and Deposits. In Abstracts of Papers of the American Chemical Society; American Chemical Society: Washington, DC, USA, 2015; pp. 425–445. [Google Scholar] [CrossRef]
- Lee, K.I. Ultrasonic Technique for Measuring the Thickness of Scale on the Inner Surface of Pipes. J. Korean Phy. Soc. 2010, 56, 558–561. [Google Scholar] [CrossRef]
- Saifi, A.; Amiri, A.E.; Elhassnaoui, A.; Obbadi, A.; Errami, Y.; Sahnoun, S. Thermography model for detecting the scale thickness in water pipes. In Proceedings of the 2015 3rd International Renewable and Sustainable Energy Conference (IRSEC), Marrakech, Morocco, 10–13 December 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Guo, D.; Kundu, T. A New Sensor for Pipe Inspection by Lamb Waves. Mater. Eval. 2000, 58, 991–994. [Google Scholar]
- Arregui, F.J.; Pastor-Jabaloyes, L.; Mercedes, A.V.; Gavara, F.J. Accuracy of Solid-State Residential Water Meters under Intermittent Flow Conditions. Sensors 2020, 20, 5339. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, K.; Wang, L.; Yang, M. Design of a High Precision Ultrasonic Gas Flowmeter. Sensors 2020, 20, 4804. [Google Scholar] [CrossRef]
- Bingham, J.; Hinders, M. Lamb Wave Detection of Delaminations in Large Diameter Pipe Coatings. Open Acoust. J. 2009, 2, 75–86. [Google Scholar] [CrossRef]
- Ebrahiminejad, A.; Mardanshahi, A.; Kazemirad, S. Nondestructive evaluation of coated structures using Lamb wave propagation. Appl. Acoust. 2022, 185, 108378. [Google Scholar] [CrossRef]
- Mehrabi, M.; Soorgee, M.H.; Habibi, H.; Kappatos, V. A novel application of ultrasonic Lamb waves: Studying adhesive effects on the inspection of coating debonding in a three-layer waveguide. Nondestruct. Test. Eval. 2021, 36, 616–636. [Google Scholar] [CrossRef]
- Laperre, J.; Thys, W. Experimental and theoretical study of Lamb wave dispersion in aluminum/polymer bilayers. J. Acoust. Soc. Am. 1993, 94, 268–278. [Google Scholar] [CrossRef]
- Liu, Z.; Kleiner, Y. State-of-the-Art Review of Technologies for Pipe Structural Health Monitoring. IEEE Sens. J. 2012, 12, 1987–1992. [Google Scholar] [CrossRef]
- Liu, Z.; Kleiner, Y. State of the art review of inspection technologies for condition assessment of water pipes. Measurement 2013, 46, 1–15. [Google Scholar] [CrossRef]
- Bratton, R.; Datta, S. Analysis of Guided Waves in a Bilayered Plate. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1992; pp. 193–200. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Zhu, Z. The Interfacial Mass Detection with Lamb-Wave Sensors. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1992; pp. 1051–1058. [Google Scholar] [CrossRef]
- Xu, P.-C.; Lindenschmidt, K.-E.; Meguid, S.A. A new high-frequency analysis of coatings using leaky Lamb waves. J. Acoust. Soc. Am. 1993, 94, 2954–2962. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors; Elsevier Science: Amsterdam, The Netherlands, 2014; ISBN 0124201024. [Google Scholar]
- Wu, J.; Zhu, Z. The influence of liquid layers on the propagation of Lamb waves. In Proceedings of the IEEE 1991 Ultrasonics Symposium, Orlando, FL, USA, 8–11 December 1991; pp. 383–386. [Google Scholar] [CrossRef]
- Tietze, S.; Singer, F.; Lasota, S.; Ebert, S.; Landskron, J.; Schwuchow, K.; Drese, K.S.; Lindner, G. Monitoring of Soft Deposition Layers in Liquid-Filled Tubes with Guided Acoustic Waves Excited by Clamp-on Transducers. Sensors 2018, 18, 526. [Google Scholar] [CrossRef]
- Schmitt, M.; Schmidt, K.; Olfert, S.; Rautenberg, J.; Lindner, G.; Henning, B.; Reindl, L.M. Detection of coatings within liquid-filled tubes and containers by mode conversion of leaky Lamb waves. J. Sens. Sens. Syst. 2013, 2, 73–84. [Google Scholar] [CrossRef]
- Lindner, G.; Schmitt, M.; Schmidt, K.; Faustmann, H.; Krempel, S.; Schubert, J. A1.3—Detection of Coatings and Measurement of Coating Thickness on Technical Substrates using Surface Acoustic Waves in a Waveguide Configuration. In Proceedings of the Sensor + Test Conference SENSOR, Nürnberg, Germany, 26–28 May 2009; pp. 36–40. [Google Scholar] [CrossRef]
- Di Lanza Scalea, F.; Salamone, S. Temperature effects in ultrasonic Lamb wave structural health monitoring systems. J. Acoust. Soc. Am. 2008, 124, 161–174. [Google Scholar] [CrossRef]
- Pei, J.; Degertekin, F.L.; Khuri-Yakub, B.T.; Saraswat, K.C. Insitu thin film thickness measurement with acoustic Lamb waves. Appl. Phys. Lett. 1995, 66, 2177–2179. [Google Scholar] [CrossRef]
- Yule, L.; Zaghari, B.; Harris, N.; Hill, M. Modelling and Validation of a Guided Acoustic Wave Temperature Monitoring System. Sensors 2021, 21, 7390. [Google Scholar] [CrossRef] [PubMed]
- Yule, L.; Zaghari, B.; Harris, N.; Hill, M. Surface temperature condition monitoring methods for aerospace turbomachinery: Exploring the use of ultrasonic guided waves. Meas. Sci. Technol. 2021, 32, 52002. [Google Scholar] [CrossRef]
- Zoubi, A.B.; Mathews, V.J. Compensation of Temperature Effects on Lamb Waves Using Mode Decomposition and a Nonlinear Model. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 829–842. [Google Scholar] [CrossRef]
- Thyssenkrupp Materials (UK) Ltd. Stainless Steel 1.4571: Datasheet. Available online: https://ucpcdn.thyssenkrupp.com/_legacy/UCPthyssenkruppBAMXUK/assets.files/material-data-sheets/stainless-steel/stainless-steel-1.4571.pdf (accessed on 10 January 2022).
- Simonetti, F. Lamb wave propagation in elastic plates coated with viscoelastic materials. J. Acoust. Soc. Am. 2004, 115, 2041–2053. [Google Scholar] [CrossRef]
- Lee, Y.-C. Measurement of leaky Lamb wave dispersion curves with application on coating characterization. AIP Conf. Proc. 2001, 557, 196–203. [Google Scholar] [CrossRef]
- Lee, Y.C.; Cheng, S.W. Measuring Lamb wave dispersion curves of a bi-layered plate and its application on material characterization of coating. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 830–837. [Google Scholar] [CrossRef]
- Lindner, G. Sensors and actuators based on surface acoustic waves propagating along solid–liquid interfaces. J. Phys. D: Appl. Phys. 2008, 41, 123002. [Google Scholar] [CrossRef]
- Van Willigen, D.M.; van Neer, P.L.M.J.; Massaad, J.; Jong, N.; de Verweij, M.D.; Pertijs, M.A.P. An Algorithm to Minimize the Zero-Flow Error in Transit-Time Ultrasonic Flowmeters. IEEE Trans. Instrum. Meas. 2021, 70, 7500109. [Google Scholar] [CrossRef]
- Rupitsch, S.J.; Ilg, J. Complete characterization of piezoceramic materials by means of two block-shaped test samples. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1403–1413. [Google Scholar] [CrossRef]
- Schmitt, M.; Faustmann, H.; Schmidt, K.; Lindner, G. Method for Investigating a Structure and Structure for Receiving and/or Conducting a Liquid of Soft Medium. WO 2010/034715 A2, 22 September 2009. [Google Scholar]
- Ebert, S.; Drese, K.S.; Lindner, G.; Tietze, S.; Vogt, T.; Lasota, S.; Schwuchow, K.; Krempel, S.; Landskron, J.; Roßteutscher, I.; et al. Device and Method for Detecting Deposition Layers in a Conduit Conducting a Liquid or a Soft Medium and/or for Level Detection. EP 3 486 619 A1, 17 November 2017. [Google Scholar]
- Mayle, M.; Ploss, P. Verfahren und Messeinrichtung zur Ermittlung einer Fluidgrösse. EP3421945B1, 24 October 2018. [Google Scholar]




| D-Wave | V-Wave | ||
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landskron, J.; Dötzer, F.; Benkert, A.; Mayle, M.; Drese, K.S. Acoustic Limescale Layer and Temperature Measurement in Ultrasonic Flow Meters. Sensors 2022, 22, 6648. https://doi.org/10.3390/s22176648
Landskron J, Dötzer F, Benkert A, Mayle M, Drese KS. Acoustic Limescale Layer and Temperature Measurement in Ultrasonic Flow Meters. Sensors. 2022; 22(17):6648. https://doi.org/10.3390/s22176648
Chicago/Turabian StyleLandskron, Johannes, Florian Dötzer, Andreas Benkert, Michael Mayle, and Klaus Stefan Drese. 2022. "Acoustic Limescale Layer and Temperature Measurement in Ultrasonic Flow Meters" Sensors 22, no. 17: 6648. https://doi.org/10.3390/s22176648
APA StyleLandskron, J., Dötzer, F., Benkert, A., Mayle, M., & Drese, K. S. (2022). Acoustic Limescale Layer and Temperature Measurement in Ultrasonic Flow Meters. Sensors, 22(17), 6648. https://doi.org/10.3390/s22176648







