Application of Teager–Kaiser Energy Operator in the Early Fault Diagnosis of Rolling Bearings
Abstract
:1. Introduction
2. TKEO Envelope Analysis
2.1. Envelope Analysis of the Vibration Signal
2.2. Teager–Kaiser Energy Operator
2.3. Influence of Noise on TKEO
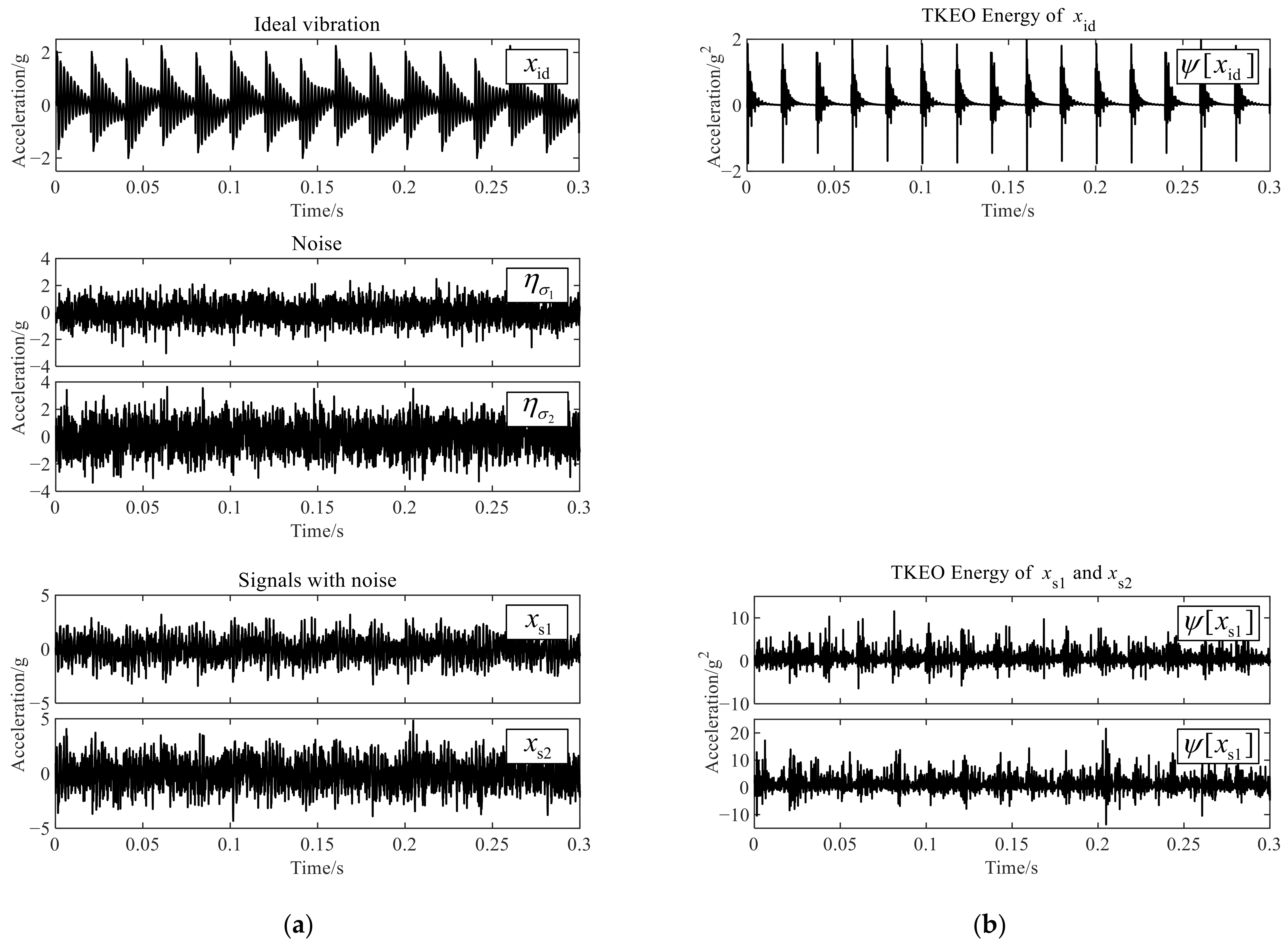
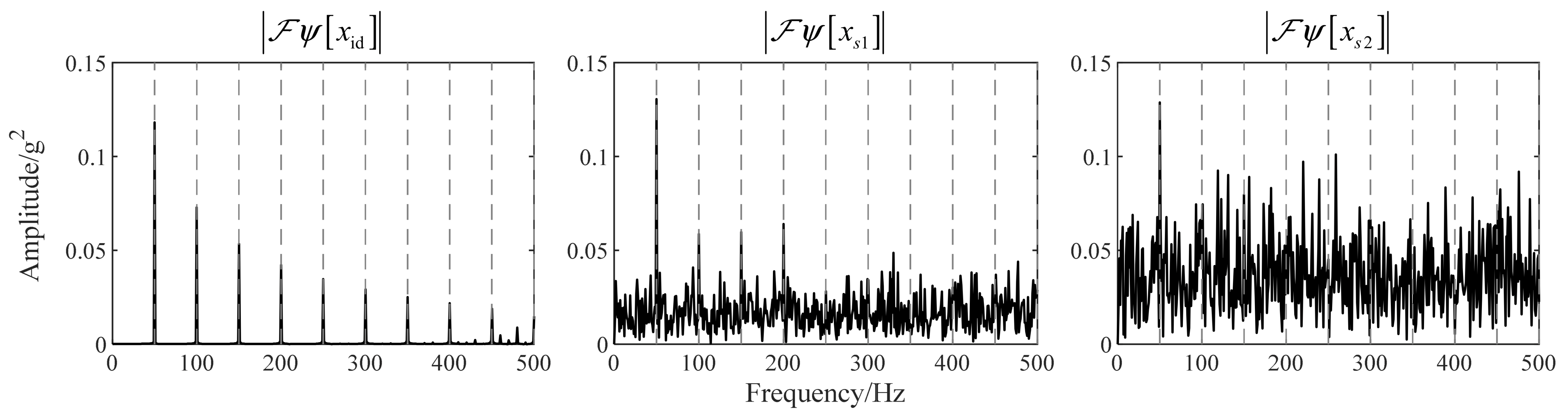
2.4. Simulation Validation
3. Improved TKEO
3.1. Denoising Method Proposed for Vibration Signals
3.1.1. Extract Fault Characteristic Components
3.1.2. Reconstruct the Target Signal
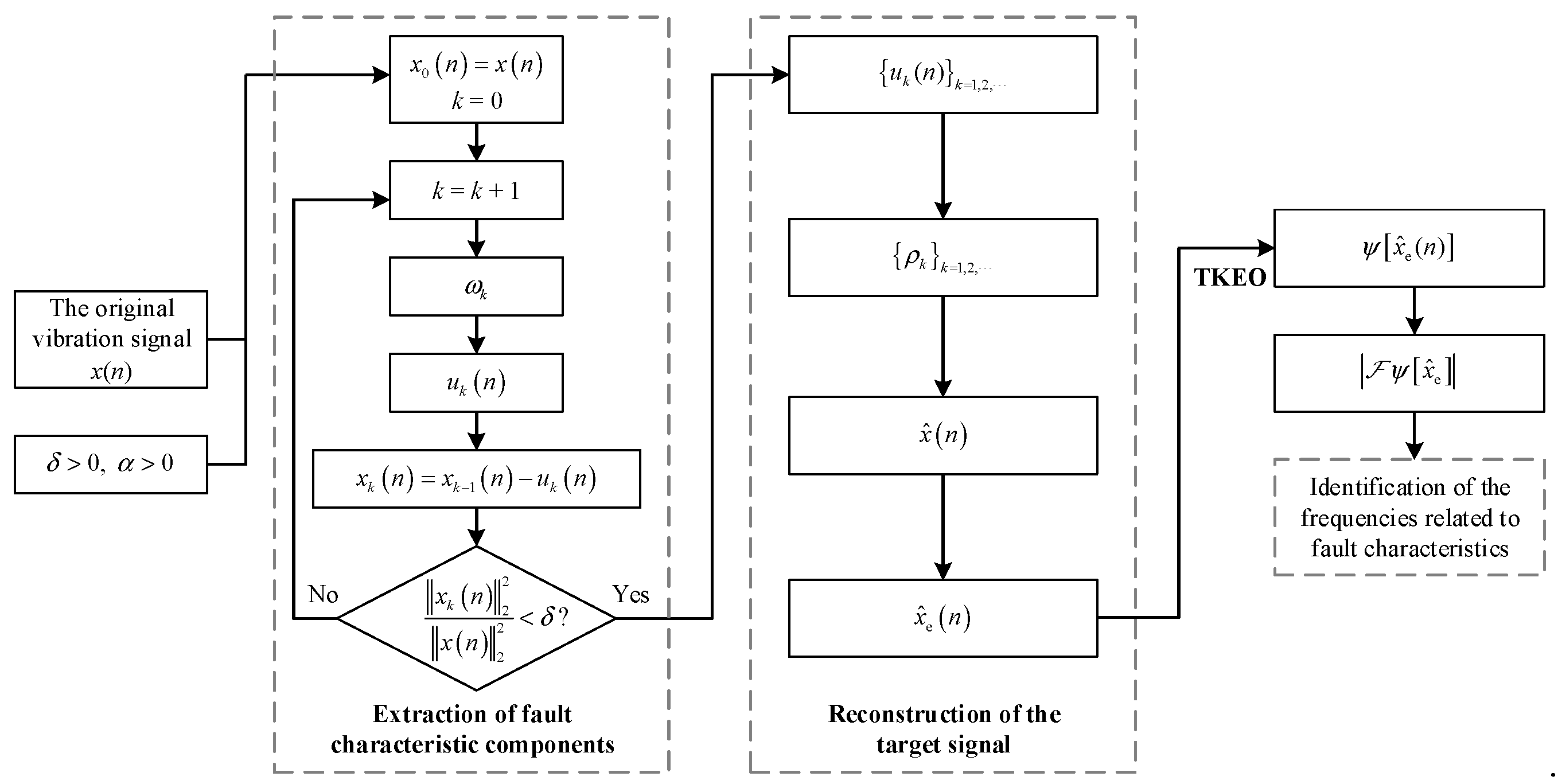
3.2. Complete Flow of Improved TKEO Proposed
- Step 1
- Input the signal , and the parameter , ;
- Step 2
- Set and ;
- Step 3
- Calculate the discrete Fourier transform ;
- Step 4
- ;
- Step 5
- Obtain the center frequency ;
- Step 6
- . Calculate the inverse discrete Fourier transform and obtain ;
- Step 7
- ;
- Step 8
- Judge whether . If not, then go back to Step 3. If yes, stop the iterations and proceed to Part 2.
- Step 9
- Calculate for each by ;
- Step 10
- ;
- Step 11
- ;
- Step 12
- Calculate the TKEO energy ;
- Step 13
- Calculate the TKEO spectrum if necessary for the fault identification.
4. Experiment Data Analysis
4.1. Data Set
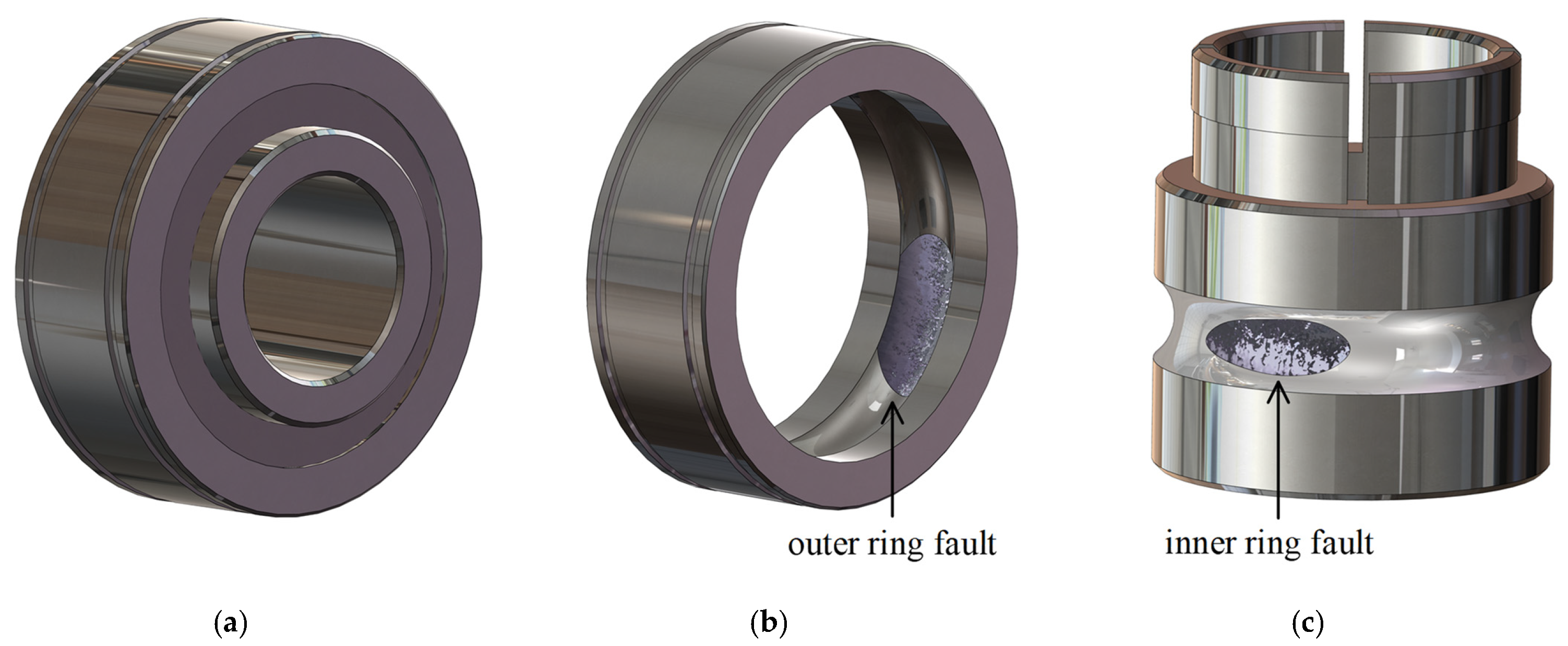
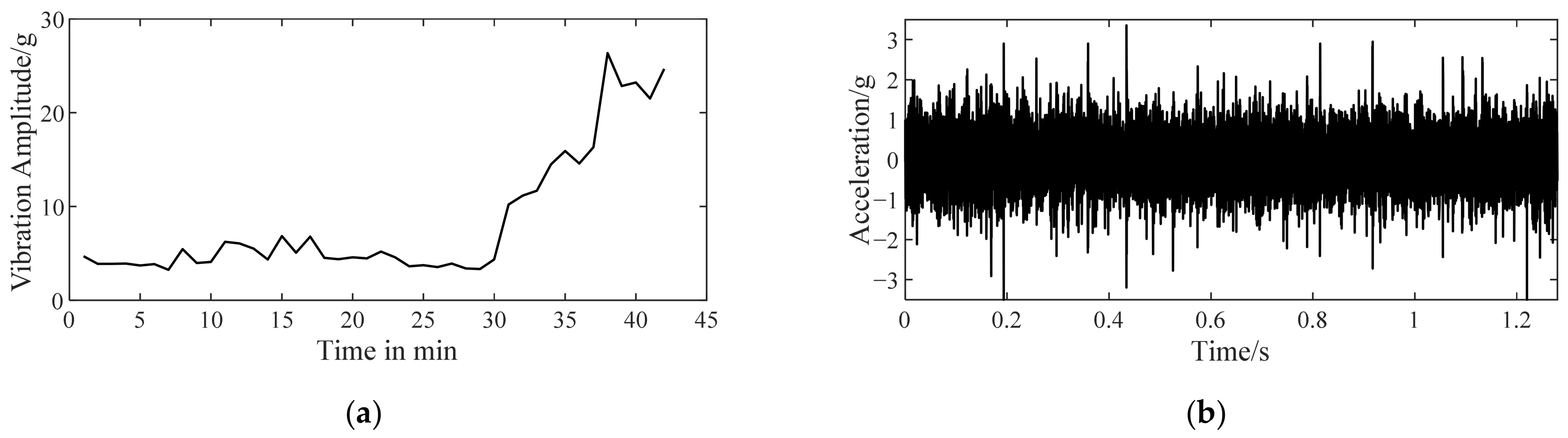
4.2. Outer Ring Defect
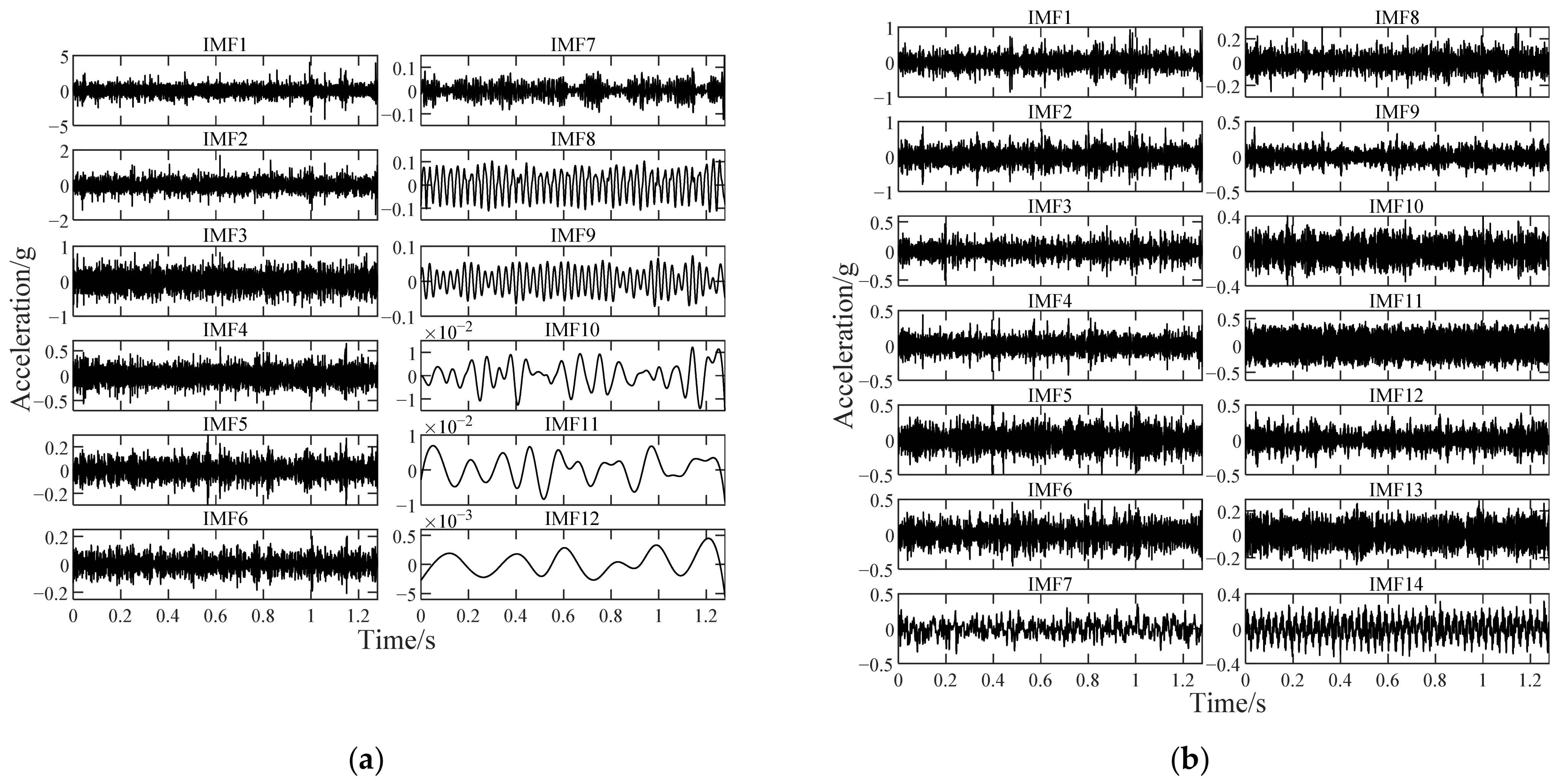
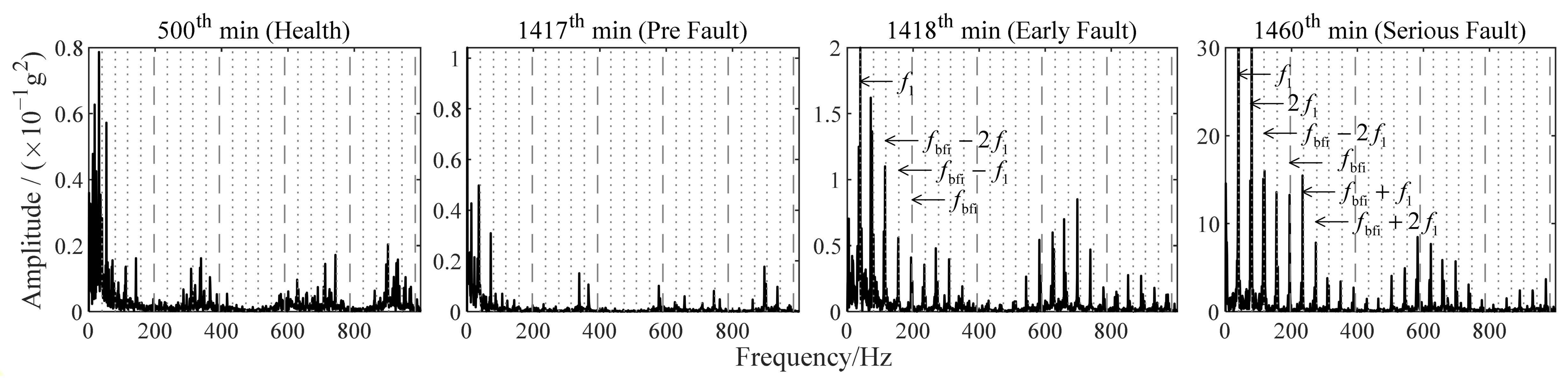
4.2.1. Validation of Improved TKEO
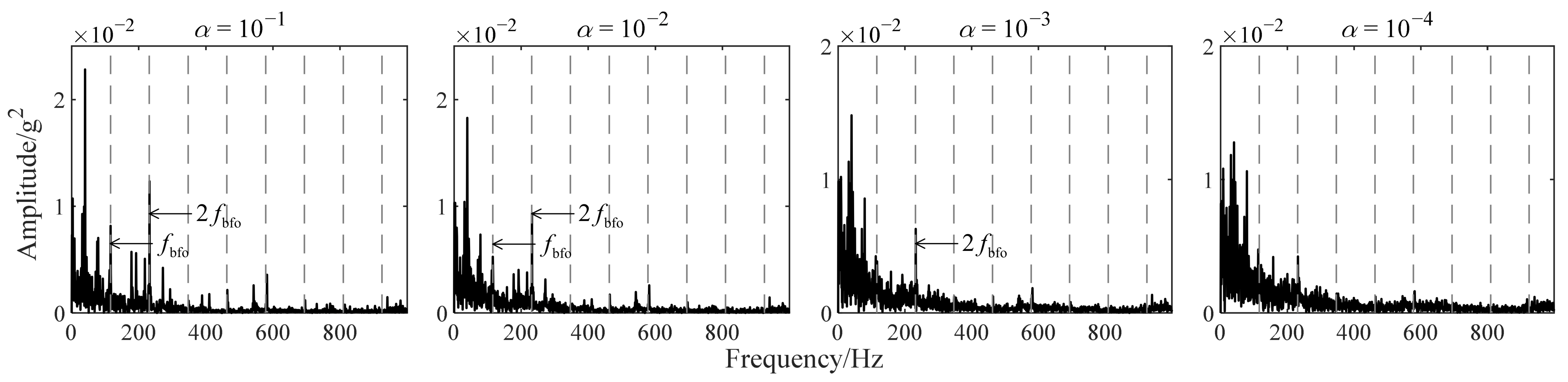
4.2.2. Parameter Setting of Improved TKEO
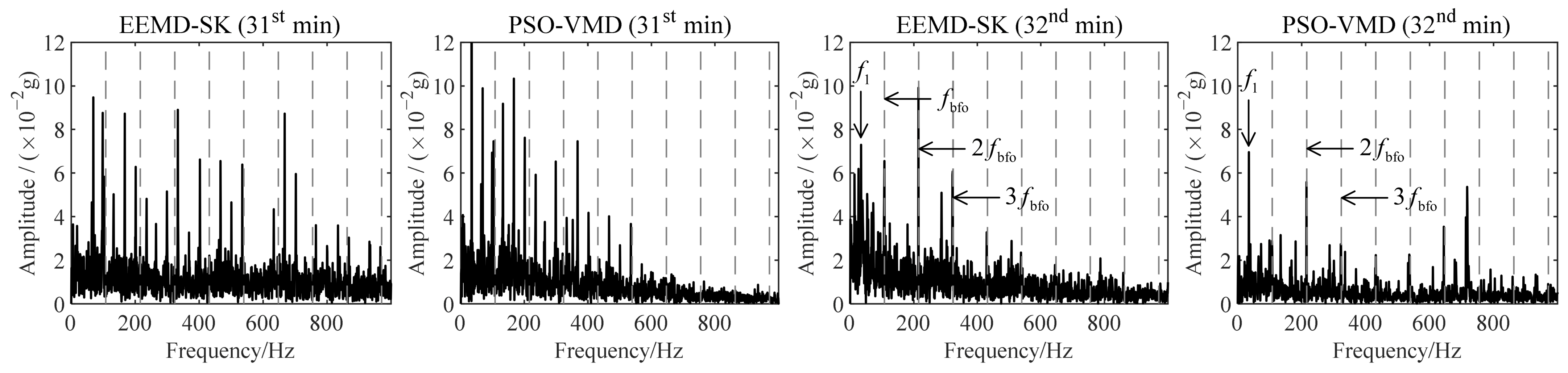
4.2.3. Comparison with Existing Methods
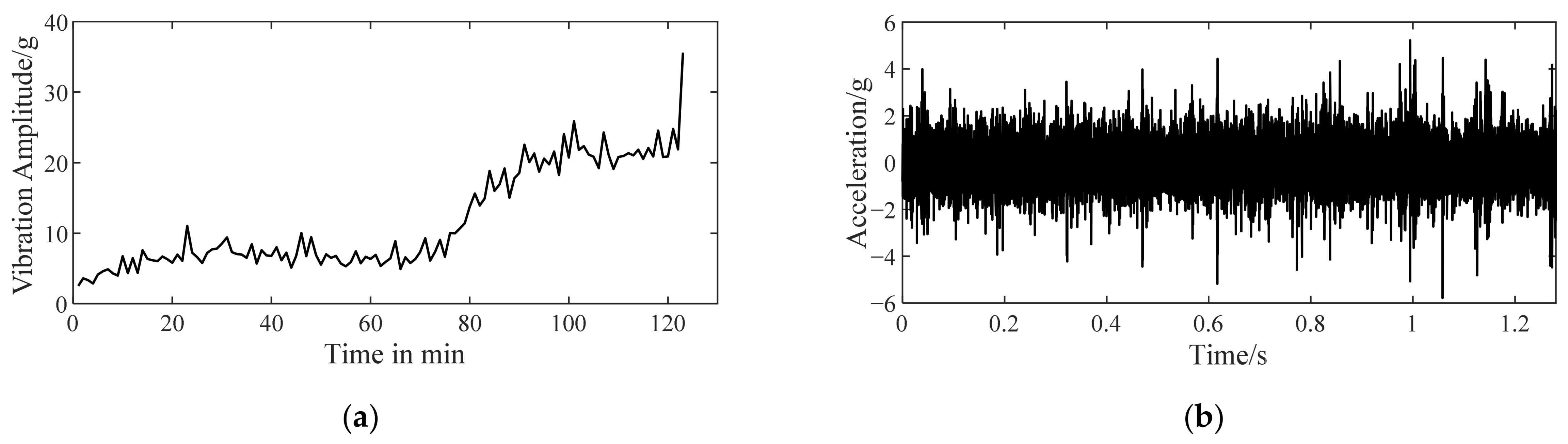
4.3. Inner Ring Defect
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AM | amplitude modulated |
| AM-FM | amplitude-modulated and frequency-modulated |
| the variance operator | |
| the expectation operator | |
| EEMD | ensemble empirical mode decomposition |
| EMD | empirical mode decomposition |
| the notation of Fourier transform | |
| GMPSO | genetic mutation particle swarm optimization |
| IMF | intrinsic modal function |
| SK | spectral kurtosis |
| TKEO | Teager–Kaiser energy operator |
| VMD | variational mode decomposition |
Appendix A


References
- Janssens, O.; Schulz, R.; Slavkovikj, V.; Stockman, K.; Loccufier, M.; Van de Walle, R.; Van Hoecke, S. Thermal Image Based Fault Diagnosis for Rotating Machinery. Infrared Phys. Technol. 2015, 73, 78–87. [Google Scholar] [CrossRef]
- Al-Musawi, A.K.; Anayi, F.; Packianather, M. Three-Phase Induction Motor Fault Detection Based on Thermal Image Segmentation. Infrared Phys. Technol. 2020, 104, 103140. [Google Scholar] [CrossRef]
- Choudhary, A.; Mian, T.; Fatima, S. Convolutional Neural Network Based Bearing Fault Diagnosis of Rotating Machine Using Thermal Images. Measurement 2021, 176, 109196. [Google Scholar] [CrossRef]
- Elasha, F.; Greaves, M.; Mba, D.; Addali, A. Application of Acoustic Emission in Diagnostic of Bearing Faults within a Helicopter Gearbox. Procedia CIRP 2015, 38, 30–36. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Zhang, L. Fault Diagnosis of Industrial Wind Turbine Blade Bearing Using Acoustic Emission Analysis. IEEE Trans. Instrum. Meas. 2020, 69, 6630–6639. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.-M. Bearing Fault Diagnosis Using Grad-CAM and Acoustic Emission Signals. Appl. Sci. 2020, 10, 2050. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, A.; Kumar, N. Motor Current Signature Analysis for Bearing Fault Detection in Mechanical Systems. Procedia Mater. Sci. 2014, 6, 171–177. [Google Scholar] [CrossRef]
- Aviña-Corral, V.; Rangel-Magdaleno, J.; Morales-Perez, C.; Hernandez, J. Bearing Fault Detection in Adjustable Speed Drive-Powered Induction Machine by Using Motor Current Signature Analysis and Goodness-of-Fit Tests. IEEE Trans. Ind. Inform. 2021, 17, 8265–8274. [Google Scholar] [CrossRef]
- Jiang, C.; Li, S.; Habetler, T.G. A review of condition monitoring of induction motors based on stray flux. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 5424–5430. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Osornio-Rios, R.A.; Antonino-Daviu, J.A.; Cureño-Osornio, J.; Saucedo-Dorantes, J.-J. Gradual Wear Diagnosis of Outer-Race Rolling Bearing Faults through Artificial Intelligence Methods and Stray Flux Signals. Electronics 2021, 10, 1486. [Google Scholar] [CrossRef]
- Ni, Z.; Wang, X.; Wu, R.; Du, L. Modeling and Characteristic Analysis of Variable Reluctance Signal Variation of Rolling Bearing Outer Ring Fault. IEEE Access 2022, 10, 49542–49550. [Google Scholar] [CrossRef]
- Dyer, D.; Stewart, R.M. Detection of Rolling Element Bearing Damage by Statistical Vibration Analysis. J. Mech. Des. 1978, 100, 229–235. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. The application of spectral kurtosis to bearing diagnostics. In Proceedings of the 2004 AAS Meeting, Gold Coast, Australia, 3–5 November 2004; Volume 1. [Google Scholar]
- Antoni, J.; Randall, R.B. The Spectral Kurtosis: Application to the Vibratory Surveillance and Diagnostics of Rotating Machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Dybała, J.; Zimroz, R. Rolling Bearing Diagnosing Method Based on Empirical Mode Decomposition of Machine Vibration Signal. Appl. Acoust. 2014, 77, 195–203. [Google Scholar] [CrossRef]
- Yu, D.; Cheng, J.; Yang, Y. Application of EMD Method and Hilbert Spectrum to the Fault Diagnosis of Roller Bearings. Mech. Syst. Signal Process. 2005, 19, 259–270. [Google Scholar] [CrossRef]
- Mohanty; Gupta, K.K.; Raju, K.S. Bearing fault analysis using variational mode decomposition. In Proceedings of the 9th International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Y.; Liao, Z.; Song, L.; Chen, P. A Novel Fast Entrogram and Its Applications in Rolling Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2021, 154, 107582. [Google Scholar] [CrossRef]
- Smith, W.A.; Borghesani, P.; Ni, Q.; Wang, K.; Peng, Z. Optimal Demodulation-Band Selection for Envelope-Based Diagnostics: A Comparative Study of Traditional and Novel Tools. Mech. Syst. Signal Process. 2019, 134, 106303. [Google Scholar] [CrossRef]
- Sun, Y.; Li, S.; Wang, X. Bearing Fault Diagnosis Based on EMD and Improved Chebyshev Distance in SDP Image. Measurement 2021, 176, 109100. [Google Scholar] [CrossRef]
- Dore, P.; Chakkor, S.; El Oualkadi, A. Comparative study between EMD, VMD, SAGE, CLEAN, and ESPRIT-TLS algorithms for real-time fault bearing recognizing in induction machines. In Proceedings of the International Conference on Decision Aid Sciences and Applications (DASA), Chiang Rai, Thailand, 23–25 March 2022; pp. 1572–1576. [Google Scholar] [CrossRef]
- Bensana, T.; Mihoub, M.; Mekhilef, S.; Fnides, M. A Novel Method for Rolling Bearing Fault Diagnosis Based on VMD and SGW. Mechanika 2022, 28, 113–120. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. An Optimized VMD Method and Its Applications in Bearing Fault Diagnosis. Measurement 2020, 166, 108185. [Google Scholar] [CrossRef]
- Kaiser, J.F. On a simple algorithm to calculate the “energy” of a signal. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; Volume 1, pp. 381–384. [Google Scholar] [CrossRef]
- Gałęzia, A.; Gryllias, K. Application of the Combined Teager-Kaiser Envelope for Bearing Fault Diagnosis. Measurement 2021, 182, 109710. [Google Scholar] [CrossRef]
- Kwak, D.-H.; Lee, D.-H.; Ahn, J.-H.; Koh, B.-H. Fault Detection of Roller-Bearings Using Signal Processing and Optimization Algorithms. Sensors 2014, 14, 283–298. [Google Scholar] [CrossRef] [PubMed]
- Azergui, M.; Abenaou, A.; Bouzahir, H. A Teager–Kaiser Energy Operator and Wavelet Packet Transform for Bearing Fault Detection. Smart Sci. 2018, 6, 227–233. [Google Scholar] [CrossRef]
- Pei, X.; Zheng, X.; Wu, J. Intelligent Bearing Fault Diagnosis Based on Teager Energy Operator Demodulation and Multiscale Compressed Sensing Deep Autoencoder. Measurement 2021, 179, 109452. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Li, H.; Zhen, D.; Gu, F.; Ball, A. Improved Cyclostationary Analysis Method Based on TKEO and Its Application on the Faults Diagnosis of Induction Motors. ISA Trans. 2021; in press. [Google Scholar] [CrossRef] [PubMed]
- Henríquez Rodríguez, P.; Alonso, J.B.; Ferrer, M.A.; Travieso, C.M. Application of the Teager–Kaiser Energy Operator in Bearing Fault Diagnosis. ISA Trans. 2013, 52, 278–284. [Google Scholar] [CrossRef]
- Ma, J.; Wu, J.; Fan, Y.; Wang, X. The Rolling Bearing Fault Feature Extraction Based on the LMD and Envelope Demodulation. Math. Probl. Eng. 2015, 2015, e429185. [Google Scholar] [CrossRef] [Green Version]
- Liang, M.; Soltani Bozchalooi, I. An Energy Operator Approach to Joint Application of Amplitude and Frequency-Demodulations for Bearing Fault Detection. Mech. Syst. Signal Process. 2010, 24, 1473–1494. [Google Scholar] [CrossRef]
- Kedadouche, M.; Thomas, M.; Tahan, A. A Comparative Study between Empirical Wavelet Transforms and Empirical Mode Decomposition Methods: Application to Bearing Defect Diagnosis. Mech. Syst. Signal Process. 2016, 81, 88–107. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, Y.; Zhang, Y.; Zhu, C.; Wang, P. Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance. J. Vib. Shock 2013, 32, 76–80. [Google Scholar] [CrossRef]
- Ding, J.; Huang, L.; Xiao, D.; Li, X. GMPSO-VMD Algorithm and Its Application to Rolling Bearing Fault Feature Extraction. Sensors 2020, 20, 1946. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Parameters | |||||
|---|---|---|---|---|---|
| (Hz) | 500 | (Hz) | 2500 | (Hz) | 4000 |
| (s−1) | 100 | (s−1) | 500 | (s−1) | 300 |
| (g) | 2 | (g) | 0.5 | (g) | 0.2 |
| (Hz) | 20 | (Hz) | 50 | (Hz) | 10,000 |
| 0.7138 | 1 | 1.5 | |||
| TKEO Energy | Simulation Results | Theoretical Results | ||
|---|---|---|---|---|
| Expectation | Variance | Expectation | Variance | |
| 0.1047 | 0.0836 | / | / | |
| 0.6199 | 2.456 | 0.6142 | 2.420 | |
| 1.244 | 7.468 | 1.251 | 7.531 | |
| Number of Faulty Bearing | Radial Force (kN) | Motor Speed (r/min) | Fault Location | Fault Characteristic Frequency (Hz) |
|---|---|---|---|---|
| 1 | 12 | 2100 | Outer ring | 107.9 |
| 2 | 11 | 2250 | Outer ring | 115.6 |
| 3 | 12 | 2100 | Outer ring | 107.9 |
| 4 | 10 | 2400 | Inner ring | 196.7 |
| Analysis Methods | Parameter Settings | |||
|---|---|---|---|---|
| Improved TKEO | Filter parameter | 0.05 | / | |
| Termination condition | 0.1 | |||
| TKEO | / | / | ||
| EEMD-SK | EEMD | Envelope Filter | ||
| 1 | 0.25 | order | 10 | |
| Number of ensemble members | 100 | |||
| PSO-VMD | GMPSO | VMD | ||
| Numbers of swarms | 20 | Termination condition | 0.01 | |
| Maximum generation | 30 | |||
| Parameters to optimize | , 2 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Zhang, Z.; Xia, Z.; Li, B.; Gu, X.; Shi, T. Application of Teager–Kaiser Energy Operator in the Early Fault Diagnosis of Rolling Bearings. Sensors 2022, 22, 6673. https://doi.org/10.3390/s22176673
Shi X, Zhang Z, Xia Z, Li B, Gu X, Shi T. Application of Teager–Kaiser Energy Operator in the Early Fault Diagnosis of Rolling Bearings. Sensors. 2022; 22(17):6673. https://doi.org/10.3390/s22176673
Chicago/Turabian StyleShi, Xiangfu, Zhen Zhang, Zhiling Xia, Binhua Li, Xin Gu, and Tingna Shi. 2022. "Application of Teager–Kaiser Energy Operator in the Early Fault Diagnosis of Rolling Bearings" Sensors 22, no. 17: 6673. https://doi.org/10.3390/s22176673
APA StyleShi, X., Zhang, Z., Xia, Z., Li, B., Gu, X., & Shi, T. (2022). Application of Teager–Kaiser Energy Operator in the Early Fault Diagnosis of Rolling Bearings. Sensors, 22(17), 6673. https://doi.org/10.3390/s22176673








